引用本文
熊红凯, 高星, 李劭辉, 徐宇辉, 王涌壮, 余豪阳, 刘昕, 张云飞. 可解释化、结构化、多模态化的深度神经网络. 模式识别与人工智能, 2018,31(1): 1-11
XIONG Hongkai, GAO Xing, LI Shaohui, XU Yuhui, WANG Yongzhuang, YU Haoyang, LIU Xin, ZHANG Yunfei. Interpretable Structured Multi-modal Deep Neural Network. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2018,31(1): 1-11.  
Doi: 10.16451/j.cnki.issn1003-6059.201801001
Permissions
Copyright©2018, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部 所有
可解释化、结构化、多模态化的深度神经网络
熊红凯1, 高星1, 李劭辉1, 徐宇辉1, 王涌壮1, 余豪阳2, 刘昕2, 张云飞3
1.上海交通大学 电子工程系 上海 200240
2.深圳市腾讯计算机系统有限公司 深圳 518000
3.宇龙计算机通信科技有限公司 深圳 518035

通讯作者:熊红凯,博士,教授,主要研究方向为多媒体通信、信号处理、计算机视觉与机器学习.E-mail:xionghongkai@sjtu.edu.cn.

作者简介：高 星,博士研究生,主要研究方向为非监督表示学习.E-mail:williamg-g@sjtu.edu.cn.

李劭辉,硕士研究生,主要研究方向为小波与散射网络.E-mail:lishaohui@sjtu.edu.cn.

徐宇辉,博士研究生,主要研究方向为计算机视觉、机器学习.E-mail:yuhuixu1993@126.com.

王涌壮,硕士研究生,主要研究方向为计算机视觉.E-mail:wyz1036880293@sjtu.edu.cn.

余豪阳,学士,主要研究方向为微服务云平台的研发与运营.E-mail:rainyu@tencent.com.

刘 昕,学士,主要研究方向为网络通信、云计算.E-mail:xinliu@tencent.com.

张云飞,博士,高级工程师,主要研究方向为多媒体通信、5G、下一代互联网、智能终端.E-mail:13701196523@189.cn.

收稿日期: 2017-09-26 接受日期: 2017-11-26
摘要

深度学习方法依赖于大规模的标签数据,通过端到端的监督训练,在计算机视觉、自然语言处理领域都取得优异性能.但是,现有方法通常针对单一模态数据,忽视数据的内在结构,缺乏理论支撑.针对上述问题,文中从基于小波核学习的深度滤波器组网络设计、基于结构化学习的深度学习、基于多模态学习的深度学习3个角度阐述结合深度学习方法与小波理论、结构化预测的潜在方法,以及其拓展到多模态数据的可行机制.

关键词: 深度学习; 滤波器组; 小波理论; 结构化学习; 多模态学习
Interpretable Structured Multi-modal Deep Neural Network
XIONG Hongkai1, GAO Xing1, LI Shaohui1, XU Yuhui1, WANG Yongzhuang1, YU Haoyang2, LIU Xin2, ZHANG Yunfei3
1.Department of Electronic Engineering, Shanghai Jiao Tong University, Shanghai 200240
2.Shenzhen Tencent Computer System Co., Ltd, Shenzhen 518000
3.Yulong Computer Communication Technology Co., Ltd, Shenzhen 518035
Corresponding author ：XIONG Hongkai, Ph.D., professor. His research interests include multimedia communication, signal processing, computer vision and machine learning.

About the Author:GAO Xing, Ph.D. candidate. His research interests include unsupervised representation learning.

LI Shaohui, master student. His research interests include wavelet and scattering network.

XU Yuhui, Ph.D. candidate. His research interests include computer vision and machine learning.

WANG Yongzhuang, master student. His research interests include computer vision.

YU Haoyang, bachelor. His research interests include micro-service cloud platform research, development and operations.

LIU Xin, bachelor. His research interests include network communication and cloud computing.

ZHANG Yunfei, Ph.D., senior engineer. His research interests include multimedia communication, 5G, NGI and smart terminals.

Abstract

Deep learning methods achieve excellent performance in the fields of computer vision and natural language processing through end-to-end supervised training dependent on large scale labeled datasets. However, the existing methods are often targeted for single modal data, ignoring the inherent structure of the data with the lack of theoretical support. Therefore, the wavelet theory based deep convolution networks, the structured deep learning and the multi-modal deep learning are discussed in this paper to demonstrate the potential methods of the combination of deep learning techniques, wavelet theory and structure prediction, and the viable mechanism for extending to multi-modal data is explored as well.

Key words: Deep Learning; Filter Bank; Wavelet Theory; Structured Learning; Multi-modal Learning

人工智能技术的发展在很大程度上给人们的生活带来便捷, 例如人脸识别、人机交互、机器翻译、自动驾驶等.现有的以深度学习为代表的人工智能方法依赖于深度模型的学习能力、图形处理器的强大计算能力和大数据提供的样本多样性, 通过端到端的监督学习, “ 黑箱” 式地提取数据特征, 在处理图像、视频和语音等领域都取得极大的进展.但是, 目前的学习方法仍有一定的局限.首先, 现有深度网络大多依托大规模数据进行参数学习, 而其最优网络结构、最优参数无从可得. 其次, 现有方法多侧重于对网络结构的设计研究, 却忽视多媒体大数据内容本身的信号内在构造.此外, 多数方法针对单一模态的信息进行处理, 如目标检测、人脸识别、图像分类等, 而现实世界中的信息大多来自不同的模态.例如:图像通常与跟它相关的标注或补充文字一起出现; 文字也能因为包含图像的信息而更清楚地表示主旨.

回首审视传统多媒体信号处理的表示方法、其通常针对信号的不同结构特点(平稳性、奇异性等), 通过严格的数理推导得到不同形式的基函数, 用于分解表示信号.因此, 结合信号处理的理论研究体系势必会给人工智能的理论研究深度带来突破, 建立一个基于滤波器组的多方向、多尺度分解的深度卷积网络具有重要意义.基于此网络, 通过组合多维结构建立稀疏表示理论, 提出优化逼近的算法, 探讨其中的稳定重构理论, 建立基于结构化约束的学习网络模型, 并利用小波分析的相关理论减少自由参数的数目, 为最优模型结构提供理论支持.通过随机森林等集成方法, 得到一种参数远小于深度神经网络的模型, 性能可与神经网络模型相媲美, 同时提供理论解释支持以及由滤波器组构建的表示模型.

针对数据内部结构特性的问题, 结构化预测方法提供一种有效机制, 其利用概率图模型, 如条件随机场, 显式地对数据内在的依赖结构建模, 所得的预测模型可以反映数据的结构信息与内在联系.因此如何结合结构化方法与深度学习方法以探索利用信号的内在结构也是一个重要的研究方向.

多模态的数据可以提供更多元的信息, 但不同模态的信息常具有不同的统计特性及各异的表示.多模态学习旨在联合表示不同模态的数据, 并通过捕捉不同模态之间的相似性结构, 填充在传统的任务中缺失的信息.因此, 如何有效协调不同模态的数据, 提取融合多模态数据的表示, 是多模态学习的关键.

本文通过简要阐述基于小波核学习的深度滤波器组网络、基于结构化学习的深度学习、基于多模态的深度学习, 来探讨未来深度学习的发展趋势.

1 基于小波核学习的深度滤波器组 网络

目前主流的深度网络结构大多以深度卷积神经网络为雏形, 在图像识别、语音识别、自然语言处理等多种人工智能任务上取得较好的效果.回顾深度学习的发展, 最早的深度学习网络源于LeCun等[1]提出的LeNet网络架构, 之后随着新网络结构的不断涌现, 如AlexNet[2]、VGGNet[3]、GoogleNet[4]、ResNet[5]等, 深度学习的准确率甚至高于人类的水平.

虽然深度学习领域现已取得举世瞩目的成就, 但反观该方法的特点, 不难发现存在诸多不足之处.1)网络结构的选择在多数情况下源于经验, 频繁地调试参数会浪费大量的时间; 2)对输入的处理是单向的, 不具有信号重构的能力; 3)原理部分具有“ 黑箱” 特点, 可解释性正逐渐成为研究的热点; 4)惊人的性能建立在强大的计算能力之上, 对计算所需的硬件设备要求较高.

同样是对于图像分析的方法, 从信号处理的角度出发的方法所构建的深度网络在原理上具有确定的理论支撑, 避免网络参数调试的盲目性.此外, 这种方法能够完成信息在网络中的双向传递, 具有信号重构性.

接下来的内容与小波分析密切相关, 因此, 先回顾小波分析应用于图像处理领域的发展.最先在图像处理中应用的是由一维小波的张量积构建得到的二维小波, 但是它的基缺乏方向性.为了解决这一问题, 人们提出多尺度几何分析方法, 旨在构建一种最优多维信号表示方法, 分为非自适应和自适应两类.

非自适应的图像多尺度几何表示方法并不需要先验地知道图像本身的几何特性, 它以脊波变换[6]、曲线波变换[7]及轮廓波变换[8]为代表.自适应分析方法一般先进行边缘检测, 再利用边缘信息对原函数进行最优表示, 代表方法有楔波变换[9]、带波变换[10]和方向波变换[11].

近几年, 出现一些新的变换方法, 如图小波变换[12]和散射变换[13].图小波变换提出如何在任意权重图上构造小波的框架, 在图拉普拉斯的谱变换域构造小波函数.散射变换是多层小波滤波操作与平均操作构成的卷积网络, 每一层分解对应一个低频部分与多个不同尺度、不同方向的高频部分, 通过对每层得到的子带重复多尺度多方向分解, 下一层得到更高阶的分解系数, 具有一定程度的平移不变性与形变稳定性.然而, 信号处理方法在弥补深度学习缺点的同时也存在自身的问题, 需要得到更合理且具有自适应性的频率分割方案, 网络的任务性能亟待提升.

深度学习方法性能高但具有原理上的“ 黑箱” 特点及不可重构性, 信号处理方法具有理论上的确定性及可重构性, 但现有方法的频率分解方案有待优化.为此, 深度径向-方向滤波器组网络、深度随机森林网络及反卷积网络的提出有效解决不可重构性问题, 并提出更合理的频率分割方案, 从信号处理领域对深度学习的可解释性做出尝试.

1.1 深度径向-方向滤波器组网络

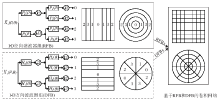
对于上述方法的不足之处, 研究者们针对性地考虑一系列解决方案.首先, 为了解决像散射网络不可逆性这样的问题, 徐璨[14]提出基于小波核学习的深度径向-方向滤波器组网络, 网络框图如图1所示.与散射网络不同的是, 该网络的频域分解按照明确的径向和方向两个角度进行, 因此对输入图像的低频部分和高频部分均进行分解.并且该网络使用迭代滤波器组, 在保证离散实现高效性的同时又使整个网络具有完美重建性.

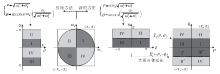
图1 结构化径向、方向滤波器组网络Fig.1 Structured networks based on radial and directional filter banks

其次, 这种方法针对坐标变换系统方面的问题也进行一定的改进.在国内外其他学者的研究中, Bamberger等[15]提出可最大采样及完美重建的二维方向滤波器组, 主要思想是棋盘式滤波器组和棋盘式采样点阵, 可达到精细的方向分解.但是, 具有不同形状和采样操作的滤波器的设计非常困难, 许多研究者考虑在极坐标系中进行构建, 包括Candé s 等[16]在第二代曲波变换中的运用, 即在极傅里叶域构造一个曲波, 然后将其映射回正交坐标下的傅立叶域后逆变换回原时域.但是对于只包含采样器的方向滤波器组, 每个楔形子带对应于不可分离的采样矩阵, 找到这样的矩阵是一项非常重要的任务.

为了更好地利用极坐标上的频率分区的可分离性并克服其在离散化方面的困难, 深度径向-方向滤波器组网络利用伪极傅里叶变换中的坐标映射方法, 形成一种特定的坐标映射系统, 如图2所示.

图2 新坐标映射与传统坐标映射的对比.Fig.2 Comparison of new coordinate and the conventional one

对于这种基于小波核学习的深度径向-方向滤波器组网络的未来发展, 可以考虑结合该网络的可逆重构性与散射网络中的多维不变性(平移、形变、旋转), 加入稀疏的层间连通性, 形成拥有深度网络结构的信号处理框架, 实现泛化的表示学习能力.此外, 该网络也可由对二维图像的处理延伸至对三维视频信号的处理.

回溯最早使用小波进行视频编码的尝试, 从没有运动补偿的纯三维小波视频编码, 到基于小波的可分级视频编码, 实现时域可分级的深度卷积网络层间设计是其中的关键, 这方面可借鉴长短期记忆网络(Long Short-Term Memory, LSTM)的循环神经网络思想, 加入视频序列的帧间状态相关性, 提高视频编码的效率.近几年出现更多的多尺度几何分析方法, 包括以剪切操作代替旋转以改进曲波变换的剪切波变换、对图像局部最优分块并采用不同方向的方向波变换、基于图像内容规律性在任意支集延拓Haar小波的组波变换、对轮廓波改进实现不均匀的方向频率分解等, 这些变换方法的思想也对进一步改进网络结构具有借鉴意义.

1.2 深度随机森林网络

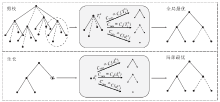
为了进一步探索自适应性的频率分割方案, 引入树结构构造2种寻找最优基的方法.在上述网络的滤波器组迭代分解时, 每个子带都有径向滤波器组分解和方向滤波器组分解两种分解选择, 在这里考虑引入树的结构, 在分解时寻找分解的最优路径.

另外, 为了加快计算, 利用从上到下的搜索方法, 从树的根节点开始, 根据一定的分解准则, 不断向下分解, 这样得到的结果是局部最优的, 如图3所示.

图3 两种自适应寻找最优基的方法Fig.3 Two Adaptive methods for searching the best basis

进一步可以利用自顶向下的树结构构造结构更复杂的随机森林网络.通过在损失函数中引入随机变量, 使得在该随机因子的影响下, 能够得到具有不同分解方式的树结构.对于不需要训练的一些任务, 如压缩、去噪等, 通过在这些树中选择表现较优的结构, 可以使原本只是用于求得局部最优的方法得到的结果更逼近全局最优解.而在需要训练的分类等任务中, 随机变量的引入和不同结构树的组合能够有效地避免对训练数据集的过拟合, 提高分类的泛化能力.

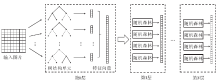
其次, 深度森林网络[17]得到广泛的关注.受此启发, 可以将森林与普通的随机森林堆叠形成网络以实现不同的目的.如图4所示, 在第一层网络中均使用上述的树结构, 那么由叶节点得到的特征向量可以反映通过不同滤波器的图像信号的响应.将这些响应作为特征向量, 输入给下一级的随机森林, 通过随机森林的分类可以得到对图像的分类结果.这样的分类处理过程从计算量上讲要远小于深度神经网络, 同时, 所需的超参数的数量也要远小于神经网络.

图4 随机森林网络Fig.4 Random forest networks

1.3 反卷积网络

针对数据高维度与复杂的空间几何, 也有相关研究开始结合传统信号理论与深度卷积网络结构, 探索研究其内在联系.Zeiler等[18, 19]提出反卷积网络, 非监督地构造层次化的图像表示.这些层次化的图像表示不仅可用于基础应用(如去噪), 也可用于更高级的应用(如对象识别).尽管在形式上与文献[1]中的卷积网络相似, 但是构造上却大不相同.卷积网络以卷积、非线性、降采样等操作对输入信号进行分解; 而反卷积网格通过学习得到的滤波器对特征图进行卷积求和, 生成原始信号的近似信号.正是加入对于信号处理中常用到的重构性考虑, 可以学习到用于分析与合成的丰富的层次化特征.同时反卷积的过程也为滤波器的选取提供新手段.Dosovitskiy等[20]研究深度图像表示的逆过程用于理解深度网络, 提出将浅层次特征与深度特征在不同程度重构的方法, 揭示深度网络与原信号特征之间的联系.基于重构的可视化, 可以判断哪些信息是在深度网络中作为重要信息保存下来的; 而通过探讨滤波器, 可以尝试挖掘这些重要信息是如何保存下来的, 可更进一步理解深度网络.

在反卷积网络[18, 19]基础上, Zhang等[21]提出基于L1/2的反卷积网络, 相比初始的基于L1的反卷积网络, 取得更好的稀疏化表示的效果.该网络局限性主要是其推理能力依然有限, 即进行一连串推导或优化过程以达到一个结果的能力还不足, 计算的步骤受到前向传播的层数限制.深入研究的关键是让深度学习系统学会推理, 能够形成一组可能的输出, 启发结构化预测的结合发展.

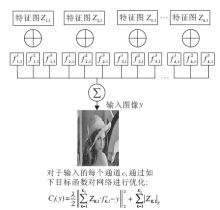
此外, 卷积神经网络中的输入信号单向传播, 无

法通过输出对输入进行有效重构, 也无法保证输出信号的稀疏性.反卷积网络结构如图5所示, 它通过最小化输出与输入的重构误差, 在加入对输出信号的正则化约束后, 得到输入信号的可逆的稀疏表示:

Cl(y)= λ2|| ∑k=1klZk, l· fk, lc-y|| 22+ ∑k=1kl||Zk, l||p.

每一层的滤波器组 fk, lc与特征图Zk, l都是通过迭代地优化上式描述的重构误差以得到.在优化过程中, 对于不同的正则化约束项, 可以设计不同的优化算法.当p> 1时, 梯度下降算法可以解决上式的凸优化问题, 当p< 1时, 交替方向乘子算法(Alternating Direction Method of Multipliers, ADMM)等针对非凸优化的算法可以被应用进行求解.

针对输入信号, 通过优化目标函数得到对于输入的理论最优的滤波器组和特征表示, 经过多层的网络结构, 最终得到输入的层次化的特征表示.得到高维的稀疏信号将被应用到分类、识别等一系列后续任务中.

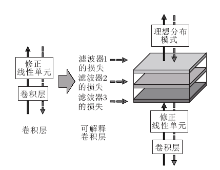
图5 反卷积网络结构Fig.5 Structure of the deconvolutional networks

1.4 卷积神经网络的语义可解释性

从深度神经网络本身结构出发, 利用语义的可解释性对网络进行分析也是近来一个新的热点.与反卷积网络结构类似, 从语义出发的研究希望了解卷积神经网络在学习过程中学习到怎样的信息, 进一步了解网络模型产生某个决策的原因.

与卷积神经网络可解释性有关的工作主要从两个方面进行.首先对网络中的滤波器及特征图进行可视化以及相应的解释, 其中较突出的工作有反卷积网络[20].另外, 模式检索也是语义理解的一种常用方法, 通过检索卷积网络中层特征, 可以恢复对应的原图中的一些信息, 利用这样的关系, 对卷积神经网络提取的特征具有更直接的了解.

早期的语义理解工作常出现在精细粒度识别的任务中, Simon等[22]设计弱监督条件下的部件检测子模型, 在没有位置标定信息以及边框的情况下也可以学习到检测物体部件所需的检测子.该方法的主要思路是通过对有标注的候选区域利用卷积神经网络的卷积层生成特征, 然后利用支持向量机对这些从不同类型候选区得到的特征进行分类, 得到原本卷积网络中不同通道的响应与物体局部信息之间的关系.该方法可以快速构建新的部件检测子, 用于精细粒度识别等任务.

2017年, Zhang等[23]提出可解释卷积神经网络.它与普通的卷积神经网络类似, 但在端到端的学习过程中, 通过对卷积层的滤波器增加约束, 使这些滤波器对物体某类部件(例如动物的头部)响应更明确.图6所示为卷积神经网络与可解释卷积神经网络的结构对比, 其中, 虚线表示网络训练中反向传播的过程, 实线表示正向传播决策的过程.从图中可以看到, 可解释卷积网络在正向传播时和普通神经网络无区别, 但在反向传播的过程中加入新的损失项.新加入的损失项表示图像经过滤波器后得到的特征图分布与物体某个部件的理想分布之间互信息的相反数.

Zhang等[23]展示该网络的可视化实验结果, 证明该网络的滤波器确实能够有针对性地检测物体的具体部件.

图6 卷积神经网络与可解释卷积神经网络的卷积层结构Fig.6 Convolutional layers of convolutional neural networks and interpretable convolutional neural networks

2 基于结构化学习的深度学习

目前的深度学习方法主要利用端对端的训练学习输入空间到输出空间的映射, 忽视输入空间或输出空间自身的结构特性.而信号处理中的一系列结构化学习方法通过不同的方式可以有效挖掘或建模数据的内部结构.因此, 如何以结构化方法如条件随机场、概率图模型等作为理论依据, 指导设计深度学习网络结构, 以及以结构化稀疏表示压缩网络规模实现具有理论指导设计的轻量高性能网络, 是结构化深度学习的重要研究方向.

2.1 结构化学习方法

本文主要探讨2类结构化方法:1)利用图模型对数据间的依赖关系进行显式建模的结构化预测, 如结构化SVM、条件随机场; 2)在数据的表示空间对结构信息进行编码的结构化稀疏方法.

从2007年Bakir 等[24]系统提出结构化学习以来, 基于结构化学习的信号处理取得巨大的发展及突破.结构化预测涉及预测多个相关且具有依赖性的变量的机器学习模型, 主要应用于计算机视觉、语音信号处理、自然语言处理和计算生物学等领域.在这些领域中, 结构化预测能精确反映先验知识、多个任务之间的联系以及各任务之间的约束性.由于其极高的计算复杂度以及推理求解的难度, 学术界热衷于设计具有高效计算特性的精确推理和自主学习的结构化预测模型, 以及一系列近似求解方法[25-31].结构化支持向量机是结构化预测的一种经典模型.相比支持向量机, 结构化支持向量机可以直

接预测多元(结构化)输出:

min 12||w||2+C ∑iξ i, s.t. wTfi(y(i))+ξ i≥ maxy∈Y(i)wTfi(y)+li(y)].

上述公式是关于凸二次规划问题, 形式上与多类支持向量机类似.结构化支持向量机的条件约束项较复杂, 针对这一问题, 衍生许多变形与对应解法.

结构化稀疏是一种信号表示(分解)模型, 即在求解信号特征表示的过程中, 除稀疏性, 同时考虑原始信号在表示空间的潜在先验结构信息, 如分块结构、分层结构、连通性等, 利用结构化范式正则项对优化目标问题进行约束并求解的方法, 如施加混合 L1/L2约束的组Lasso(Group Lasso):

J(w)=Loss(w)+ ∑g=1Gλ ||wg||2.

2.2 结构化预测与神经网络

在深度学习领域, 目前已有部分工作结合深度卷积神经网络与条件随机场(Conditional Random Field, CRF):Tompson 等[32, 33]提出联合学习卷积神经网络特征和结构化输出, 并应用于解决人体姿势估计问题.Gal等[34]提出利用统计学习和深度学习联合生成概率模型, 试图解释深度学习模型.Chu等[35]采用添加隐藏层的策略, 在卷积神经网络的第五层神经单元之后建立一个独立的图模型, 实现信息的传递和特征图之间的交流.此外, Zheng等[36]结合全卷积网络(Fully Convolutional Network, FCN)和CRF, 视作一个循环神经网络(Recurrent Netural Network, RNN)进行求解, 得以端到端解决语义分割问题.其工作的开创性在于将CRF等图模型结构融入深度学习, 使数据内的依赖关系得以有效利用.Belanger等[37]基于结构化支持向量机损失函数, 率先采用卷积网络特性构建结构化预测能量网络, 跳出因子图和置信传播算法的推理求解框架.之后, 又利用基于梯度的后向传播算法直接实现能量最小化, 有效解决复杂非凸能量最小化的问题.

目前人工智能技术, 尤其是深度卷积神经网络技术在计算机视觉、语音信号处理、自然语言处理等领域取得惊人的成绩, 但在深度卷积神经网络的设计上, 更多的是直觉和经验.如何设计结构化的网络, 实现特征图之间的信息交流是当前研究的热点, 也是亟需解决的理论难点.将条件随机场等理论融入深度卷积神经网络结构中, 实现神经网络内部的特征信息交流, 保留和提取数据原有结构信息, 将有效指导深度网络的设计.

2.3 结构化稀疏与神经网络

结构化稀疏学习在稀疏学习简约特性和计算优势的基础上, 进一步将结构信息进行编码, 在多个研究领域及许多计算问题中取得成功.随着各类型结构的发现, 人们相继提出各种结构化正则函数.这些正则函数通过利用特定的结构信息提高稀疏学习算法的性能.通常结构化稀疏学习适用于2种情况:1)模型本身具有稀疏性, 2)即使模型本身不能满足稀疏性条件, 但其仍然可以寻找到最佳的结构化稀疏近似, 使结构化稀疏学习得以适用.

卷积神经网络作为人工智能领域的技术突破, 在图像分类、人脸识别、语义分割、目标检测等领域都取得成功.从LeNet[1]、AlexNet[2]、GoogleNet[4]到ResNet[5], 卷积神经网络的结构趋向于更深更复杂的方向发展.虽然更深更复杂的网络结构能更大程度地利用深度学习特征提取能力, 取得更好的结果, 但不可避免地带来存储空间和能源消耗的增大.高度需求的计算资源和存储空间限制神经网络在移动设备、可穿戴器械上的使用.

近两年, 神经网络的压缩引起众多研究者的兴趣.Han等[38]提出简单的参数裁剪的方法, 去除低于预设阈值的参数, 实现网络参数的稀疏化.之后他又将参数裁剪的方法与矢量量化、霍夫曼编码结合, 进一步压缩网络的大小, 实现参数稀疏化.Li等[39]利用类似的方式对神经网络的滤波器进行裁剪, 极大地减少网络的计算量.然而这些非结构化的裁剪方法需要多次迭代训练, 同时也破坏网络的结构特性, 影响网络的性能.Wei等[40]将结构化稀疏学习应用到神经网络中, 利用Group Lasso约束网络训练, 不但减少网络参数的数量, 而且减少网络通道数和网络层数, 在减少网络冗余的同时保证网络性能.结合结构化稀疏学习与神经网络, 不仅可以避免参数的盲目选取和冗余, 而且便于解释神经网络, 丰富人工智能的理论基础.

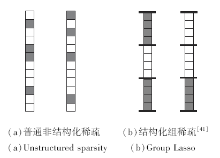
神经网络作为一种网络结构, 本身具有丰富的结构特性, 包含的结构单元有:参数、通道、滤波器、层.每种结构单元都有一定的冗余, 单元相互之间有影响.这就与Group Lasso特性相关, Group Lasso的稀疏约束结果使每个组内的变量都同时为0, 这样的稀疏保证结构特性(如图7).

图7 非结构化稀疏与结构化组稀疏的对比Fig.7 Comparison of unstructured sparsity and group Lasso

将Group Lasso应用到神经网络中, 将通道、滤波器、层这些单元作为Group Lasso的组结构, 在保证结构特性的同时, 被稀疏的单元内部参数全都为0(如图8).

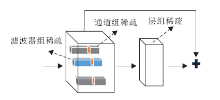图8 卷积神经网络的结构化组稀疏[4]Fig.8 Structured sparsity of convolutional neural networks

利用结构化组稀疏, 卷积神经网络的约束表示为

E(W)=Ec(W)+λ R(W)+λ g ∑l=1LRg(Wl),

其中, W表示神经网络所有参数, Ec(W)表示神经网络原本的损失函数, R(· )表示针对参数非结构化的稀疏约束, Rg(· )表示每一层结构化的组稀疏正则项, λ 和λ g都是常数.将结构化稀疏运用到神经网络中, 在保存网络结构化特性的同时, 整体上极大稀疏网络, 降低网络的存储和运算消耗.

3 基于多模态的深度学习

传统任务大多是对单一模态的信息进行处理, 如基于图像信息的分类、目标检测、语义分割任务, 基于文本信息的词性标注、机器翻译、阅读理解任务, 基于语音信息的语音识别任务等.虽然近几年传统任务取得突破性的进展, 但是这些任务在实际场景中的应用依然非常有限.这是因为在实际生活中, 人类处理的并不仅仅是单一模态的信息, 而往往是视觉、听觉、嗅觉、触觉等多元信息的集合.这些信息往往相互对应、相互补充、相互转换, 共同为人类处理日常任务提供支持.而对于目前的人工智能, 这些操作都非常困难, 但必不可少, 在此背景下, 多模态学习应运而生.

多模态学习的最终目标在于实现多种模态信息的协同学习, 重点为多模态信息在多模态空间中的表示、融合、对齐和转换, 但是这些操作并不是相互独立, 而是在不同任务中有所侧重.除上述重点外, 如何基于其它模态信息预测并填补单一模态信息的缺失也是难点所在.目前在多模态学习领域, 对图像、文本信息的处理相对较成熟, 其中具有代表性的便是图像(视频)描述生成任务和视觉图像问答任务.

以图像描述生成任务为例, 其目标是根据图像内容生成对应的描述语句, 即通过构建图像文本双模态空间, 实现从图像信息到文本信息的转换.但是这一转换过程是基于图像和文本信息的表示与融合, 且往往会通过对齐操作以提高模型效果.

目前图像描述生成任务最成功的模型主要是基于神经网络的模型, 不同于传统方法, 其不再基于特定图像处理任务的结果, 而是直接提取图像的特征作为图像的表示, 然后将图像特征与词向量转换到多模态空间进行协同学习, 最终由多模态空间生成最终的文本描述.在构建多模态空间方面, 主要使用的模型包括对数双线性模型(Log-Bilinear Model, LBL)和RNN.

对数双线性模型最早应用于机器翻译, Kiros等[42]在语言模型的基础上增加图像输入构建多模态空间, 并尝试采用不同的融合方式, 最终分析对比模型结果.除图像描述生成任务以外, 他们同时将模型应用于图像检索任务, 证明多模态空间拥有信息对齐的效果.相比基于特定图像处理任务结果的模型, 多模态对数双线性模型以词向量和图像特征表示为基础, 在一定程度上减少不同信息之间转换产生的信息损失, 模型效果得到一定程度的提升.但是由于对数双线性模型在生成描述语句时仍然基于滑动窗口中的有限单词, 而且多模态信息的融合、对齐仍然相对粗糙, 最终结果距离理想结果仍有较大差距.

而循环神经网络可以有效解决不定长上下文依赖问题, 同时受益于循环神经网络在机器翻译的发展, Vinyals等[43]提出编解码器框架.在基于编解码框架的方法[44, 45, 46]中, 卷积神经网络作为图像编码器提取图像特征, 多模态循环神经网络将其与词向量同时转换到多模态空间进行信息融合, 同时作为解码器生成目标文本, 整个编解码框架作为一个端到端系统进行训练.该类工作虽然构建多模态空间, 但其中的多模态信息是否对齐无法测度.因此, Xu等[47]引入注意机制, 通过注意机制[48, 49, 50]实现在文本生成的同时建立文本与图像的对齐, 较好地提升模型效果.而Lu等[51]在此基础上分别建立当前输出对已生成文本的语法依赖和对图像内容的对齐依赖, 解决图像文本对齐问题中的缺失问题, 使当前模型能力初步接近人类, 展露神经网络模型的潜力.

虽然图像描述生成任务旨在实现从图像到文本信息的转换, 这一转换过程往往通过构建图像文本多模态空间来实现, 但是该空间实质上建立图像与文本信息的对齐关系.因此, 图像描述生成模型往往也用于图像检索、文本检索、视觉问答等相关任务, 如Wu等[52]研究高级语义特征在图像文本多模态空间的作用, 其模型在视觉图像问答任务上也有较好表现.

综上所述, 多模态学习虽然在一些任务上取得不错的成果, 但是仍然处于初级阶段, 需要在如下方面进一步加强研究.

首先, 多模态学习需要一个完整的框架及理论指导.虽然多模态学习的任务目标及基本操作较清楚, 但工作机制仍然缺乏严格意义的理论指导与证明, 目前相关任务模型种类繁多, 一个完整框架是多模态学习发展所必需的.

其次, 多模态信息的表示需要严格的理论解释与证明.在信息表示方面, 多模态学习以特征表示为基础, 相比手工提取特征, 当前深度学习模型为信息的特征提取提供更强大的工具, 而多模态空间的构建正是基于特征的提取.虽然神经网络在特征提取上表现出色, 但其黑箱特性使提取到的特征难以解释, 因此对于不同模态信息的表示将是研究重点之一, 而且如何表示不同模态信息独有的特点也是难点所在, 如文本、语音信息的时序性等.

最后, 多模态信息的处理需要建立普适性方法.在信息处理方面, 目前多模态学习多以任务为驱动, 而对多模态信息融合、对齐、转换等操作的最直接的理论研究基本处于空白状态.由于不同任务对多模态信息的处理要求不同, 目前模型更多的是在多模态学习相关概念指导下解决任务中特有的问题, 导致不同任务之间多模态信息的处理方法多种多样, 而且由于缺乏理论的证明, 研究人员难以判断方法的优劣.目前虽然多种处理方式正是多模态学习取得进步的主要动力, 但是多模态学习的进一步发展迫切需要抛开特定任务的影响, 从而理解信息融合、对齐、转换等操作的工作机制, 建立对应于特定操作的普适性方法.

4 结 束 语

本文从可解释化、结构化及多模态化3个角度探讨深度学习方法的发展历程与趋势.信号处理领域中的小波理论为基于多维度可分解的滤波器组神经网络的设计提供理论的支持, 同时也赋予网络不同模块特定的物理含义.此外, 结合结构化模型对关系显式建模的机制, 结构化深度学习有效地利用数据的内在结构.另一方面, 结构化稀疏理论为优化深度网络提供理论指导, 使神经网络的大规模参数得以有效压缩, 为复杂神经网络在移动端的应用提供解决方案.最后, 深度学习方法在图像描述问题的演示进一步揭示了深度学习处理多模态数据的演化进程及未来趋势.

The authors have declared that no competing interests exist.

参考文献
[1] LECUN Y, BENGIO Y. Convolutional Networks for Images, Speech, and Time-Series in the Hand book of Brain Theory and Neural Networks. Cambridge, USA: The MIT Press, 1995. [本文引用:3]
[2] KRIZHEVSKY A, SUTSKEVER L, HINTON G E. Imagenet Classification with Deep Convolutional Neural Networks[C/OL]. [2017-11-20]. https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf. [本文引用:2]
[3] SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[JOL]. [2017-11-20]. https://arxiv.org/pdf/1409.1556.pdf. [本文引用:1]
[4] SZEGEDY C, LIU W, JIA Y Q, , et al. Going Deeper with Convolutions[C/OL]. [2017-11-20]. https://arxiv.org/pdf/1409.4842.pdf. [本文引用:2]
[5] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE International Conference on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2016: 770-778. [本文引用:2]
[6] DO M N, VETTERLI M. The Finite Ridgelet Transform for Image Representation. IEEE Transactions on Image Processing, 2003, 12(1): 16-28. [本文引用:1]
[7] CANDE S E J, DONOHO D L. Curvelets, Multiresolution Representation, and Scaling Laws[JOL]. [2017-11-20]. http://statweb.stanford.edu/~candes/papers/SPIE_Curvelets.pdf. [本文引用:1]
[8] DO M N, VETTERLI M. The Contourlet Transform: An Efficient Directional Multiresolution Image Representation. IEEE Transactions on Image Processing, 2005, 14(12): 2091-2106. [本文引用:1]
[9] DONOHO D L. Wedgelets: Nearly Minimax Estimation of Edges. The Annals of Statistics, 1999, 27(3): 859-897. [本文引用:1]
[10] LE PENNEC E, MALLAT S. Sparse Geometric Image Representations with Band elets. IEEE Transactions on Image Processing, 2005, 14(4): 423-438. [本文引用:1]
[11] VELISAVLJEVIC V, BEFERULL-LOZANO B, VETTERLI M, et al. Directionlets: Anisotropic Multidirectional Representation with Separable Filtering. IEEE Transactions on Image Processing, 2006, 15(7): 1916-1933. [本文引用:1]
[12] HAMMOND D K, VANDERGHEYNST P, GRIBONVAL R. Wavelets on Graphs via Spectral Graph Theory. Applied and Computational Harmonic Analysis, 2011, 30(2): 129-150. [本文引用:1]
[13] BRUNA J, MALLAT S. Invariant Scattering Convolution Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1872-1886. [本文引用:1]
[14] 徐璨. 可逆深度卷积网络的构建. 硕士学位论文. 上海: 上海交通大学, 2017.
(XU C. The Construction of Reversible Deep Convolution Networks. Master Dissertation. Shanghai, China: Shanghai Jiao Tong University, 2017. ) [本文引用:1]
[15] BAMBERGER R H, SMITH M J. A Filter Bank for the Directional Decomposition of Images: Theory and Design. IEEE Transactions on Signal Processing, 1992, 40(4): 882-893. [本文引用:1]
[16] CANDE S E J, DEMANET L, DONOHO D, et al . Fast Discrete Curvelet Transforms. Multiscale Modeling & Simulation, 2006, 5(3): 861-899. [本文引用:1]
[17] ZHOU Z H, FENG J. Deep Forest: Towards an Alternative to Deep Neural Networks[JOL]. [2017-11-20]. https://arxiv.org/pdf/1702.08835.pdf. [本文引用:1]
[18] ZEILER M D, KRISHNAN D, TAYLOR G W, et al. Deconvolutional Networks // Proc of the IEEE International Conference on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2010: 2528-2535. [本文引用:2]
[19] ZEILER M D, TAYLOR G W, FERGUS R. Adaptive Deconvolutional Networks for Mid and High Level Feature Learning // Proc of the IEEE International Conference on Computer Vision. WashingtonUSA: IEEE, 2011: 2018-2025. [本文引用:2]
[20] DOSOVITSKIY A, BROX T. Inverting Visual Representations with Convolutional Networks[JOL]. [2017-11-20]. https://arxiv.org/pdf/1506.02753.pdf. [本文引用:1]
[21] ZHANG J, ZHONG P, CHEN Y, et al. L1/2-Regularized Deconvolution Network for the Representation and Restoration of Optical Remote Sensing Images. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2617-2627. [本文引用:1]
[22] SIMON M, RODNER E. Neural Activation Constellations: Unsupervised Part Model Discovery with Convolutional Networks // Proc of the IEEE International Conference on Computer Vision. Wa-shington, USA: IEEE, 2015: 1143-1151. [本文引用:1]
[23] ZHANG Q S, WU Y N, ZHU S C. Interpretable Convolutional Neural Networks[JOL]. [2017-11-20]. https://arxiv.org/pdf/1710.00935.pdf. [本文引用:2]
[24] BAKIR G H, HOFMANN T, SCHÖLKOPF B, et al. Predicting Structured Data. Cambridge, USA: The MIT Press, 2007. [本文引用:1]
[25] MESHI D, SONTAG T, JAAKKOLA T, et al. Learning Efficiently with Approximate Inference via Dual Losses // Proc of the 27th International Conference on Machine Learning. New York, USA: Omnipress, 2010: 783-790. [本文引用:1]
[26] HAZAN T, URTASUN R. A Primal-Dual Message-Passing Algorithm for Approximated Large Scale Structured Prediction // Proc of the 23rd International Conference on Neural Information Proce-ssing Systems. Cambridge, USA: The MIT Press, 2010: 838-846. [本文引用:1]
[27] DOMKE J. Parameter Learning with Truncated Message-Passing // Proc of the IEEE International Conference on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2011: 2937-2943. [本文引用:1]
[28] ROSS S, MUNOZ D, HEBERT M, et al. Learning Message-Pa-ssing Inference Machines for Structured Prediction // Proc of the IEEE International Conference on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2011: 2737-2744. [本文引用:1]
[29] STOYANOV V, ROPSON A, EISNER J. Empirical Risk Minimization of Graphical Model Parameters Given Approximate Infe-rence, Decoding, and Model Structure // Proc of the 14th International Conference on Artificial Intelligence and Statistics. New York, USA: ACM, 2011: 725-733. [本文引用:1]
[30] DAUME III H, LANGFORD J, MARCU D. Search-Based Structured Prediction. Machine Learning, 2009, 75(3): 297-325. [本文引用:1]
[31] ROSS G, GORDON G, BAGNELL D. A Reduction of Imitation Learning and Structured Prediction to No-regret Online Learning // Proc of the 14th International Conference on Artificial Intelligence and Statistics. New York, USA: ACM, 2011: 627-635. [本文引用:1]
[32] TOMPSON J, JAIN A, LECUN Y, et al. Joint Training of a Con-volutional Network Joint Training of a Con-volutional Network and a Graphical Model for Human Pose Estimation[C/OL]. [2017-11-20]. https://arxiv.org/pdf/1406.2984.pdf. [本文引用:1]
[33] TOMPSON J, GOROSHIN R, JAIN A, et al. Efficient Object Localization Using Convolutional Networks // Proc of the IEEE International Conference on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2015: 648-656. [本文引用:1]
[34] GAL Y, GHAHRAMANI Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning[C/OL]. [2017-11-20]. https://arxiv.org/pdf/1506.02142.pdf. [本文引用:1]
[35] CHU X, OUYANG W L, LI H S, et al. Structured Feature Lear-ning for Pose Estimation // Proc of the IEEE International Confe-rence on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2016: 4715-4723. [本文引用:1]
[36] ZHENG S, JAYASUMANA S, ROMERA-PAREDES B, et al. Conditional Rand om Fields as Recurrent Neural Networks // Proc of the IEEE International Conference on Computer Vision. Wa-shington, USA: IEEE, 2015: 1529-1537. [本文引用:1]
[37] BELANGER D, MCCALLUM A. Structured Prediction Energy Networks[C/OL]. [2017-11-20]. https://arxiv.org/pdf/1511.06350.pdf. [本文引用:1]
[38] HAN S, POOL J, TRAN J, et al. Learning both Weights and Connections for Efficient Neural Network // CORTES C, LAWRENCE N D, LEE D D, et al. , eds. Advances in Neural Information Processing Systems 25. Cambridge, USA: The MIT Press, 2015: 1135-1143. [本文引用:1]
[39] LI H, KADAV A, DURDANOVIC I. Pruning Filters for Efficient Convnets[C/OL]. [2017-11-20]. https://arxiv.org/pdf/1608.08710v1.pdf. [本文引用:1]
[40] WEI W, WU C P, WANG Y D, et al. Learning Structured Sparsity in Deep Neural Networks[C/OL]. [2017-11-20]. https://arxiv.org/pdf/1608.08710v1.pdf. [本文引用:1]
[41] MAIRAL J, BACH F, PINCE J. Sparse Modeling for Image and Vision Processing[JOL]. [2017-11-20]. https://arxiv.org/pdf/1411.3230.pdf. [本文引用:1]
[42] KIROS R, SALAKHUTDINOV R, ZEMEL R. Multimodal Neural Language Models // Proc of the 31st International Conference on Machine Learning. New York, USA: ACM, 2014: 595-603. [本文引用:1]
[43] VINYALS O, TOSHEV A, BENGIO S, et al. Show and Tell: A Neural Image Caption Generator[JOL]. [2017-11-20]. https://arxiv.org/pdf/1411.4555v1.pdf. [本文引用:1]
[44] KARPATHY A, LI F F. Deep Visual-Semantic Alignments for Generating Image Descriptions // Proc of the IEEE International Conference on Computer Vision and Pattern Recognition. WashingtonUSA: IEEE, 2015: 3128-3137. [本文引用:1]
[45] DONAHUE J, HENDRICKS L A, GUADARRAMA S, et al. Long-Term Recurrent Convolutional Networks for Visual Recognition and Description. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 677-691. [本文引用:1]
[46] MAO J H, XU W, YANG Y, et al. Deep Captioning with Multimodal Recurrent Neural Networks Deep Captioning with Multimodal Recurrent Neural Networks(m-RNN)[JOL]. [2017-11-20]. https://arxiv.org/pdf/1412.6632.pdf. [本文引用:1]
[47] XU K, BA J, KIROS R, et al. Show, Attend and Tell: Neural Image Caption Generation with Visual Attention[JOL]. [2017-11-20]. https://arxiv.org/pdf/1502.03044.pdf. [本文引用:1]
[48] JIA X, GAVVES E, FERNANDO B, et al. Guiding Long-Short Term Memory for Image Caption Generation[JOL]. [2017-11-20]. https://arxiv.org/pdf/1502.03044.pdf. [本文引用:1]
[49] YOU Q Z, JIN H L, WANG Z W, et al. Image Captioning with Semantic Attention[JOL]. [2017-11-20]. https://arxiv.org/pdf/1603.03925.pdf. [本文引用:1]
[50] CHEN L, ZHANG H W, XIAO J, et al. SCA-CNN: Spatial and Channel-Wise Attention in Convolutional Networks for Image Captioning[JOL]. [2017-11-20]. https://arxiv.org/pdf/1611.05594.pdf. [本文引用:1]
[51] LU J S, XIONG C M, PARIKH D, et al. Knowing When to Look: Adaptive Attention via a Visual Sentinel for Image Captioning[JOL]. [2017-11-20]. https://arxiv.org/pdf/1612.01887.pdf. [本文引用:1]
[52] WU Q, SHEN C H, LIU L Q, et al. What Value Do Explicit High Level Concepts Have in Vision to Language Problems?[JOL]. [2017-11-20]. https://arxiv.org/pdf/1506.01144.pdf. [本文引用:1]