试题作为教育中的一类重要的学习资源, 在传统教育和在线教育中都发挥重要作用, 针对试题分析的相关研究吸引许多研究人员的注意.目前, 许多在线学习网站都提供在线题库供学生使用、学习^[2], 智学网、猿题库等学习平台更是搭建以试题练习为主的在线学习环境.因此, 在线学习系统需要提供针对海量试题的收集、整理、存储, 并提供试题下载或在线答题等服务.

1.1.1 试题分析研究现状

图2为智学网中的试题样例, 包含试题类型、题面、知识点等一系列的试题信息.如何有效地对试题题面、知识点及学生在试题上的答题记录等信息进行表征, 并使用试题的数据表征进行试题难度预测、相似试题判定或试题知识点识别, 是在线教育中面向试题研究的重要内容.本文着重介绍基于试题表征方法的难度预测研究.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 智学网试题样例[20]Fig.2 Question sample of ZHIXUE in iFlyTek[20]

试题难度是试题的一项重要特征, 测试试题难度的预估对教学的各方面都具有一定的现实意义^[21].首先, 对试题难度的准确估计和标注可以帮助系统构造更合理的试题库.其次, 做好试题难度估计和标注工作可以辅助教师自动组卷, 在减少人工工作量的同时, 提高组卷的科学性和合理性.最后, 准确的试题难度估计可以帮助在线学习系统为每个学生筛选合适的练习题.

教育心理学中的经典测量理论(Classical Test Theory, CTT)认为, 试题的难度可由一道试题被错误回答的比率表示, 即对一道试题, 答错的学生越多, 那么该试题就越难^[22].然而, 在某些实际情况下, 需要在学生对试题进行作答之前, 进行试题难度的预测和评估.例如, 对于标准化测试(如TOEFL, GRE等), 每个学生可以多次参加考试, 并选择最高分数作为最终分数用于学校申请等工作^[23].因此, 多次考试的试题难度应当一致, 以保障考试成绩的公平性; 对于一些大型的考试(如中国的普通高等学校招生全国统一考试, 简称高考), 对试题的难度预测可以保证测试的质量.

传统的试题难度预测方法可以基于专家经验对试题难度进行人工评估或使用教育心理学中的简单回归模型^[24].然而, 前者存在专家主观性强、费时费力的问题, 后者存在难以使用海量样本、对试题文本特征等利用不足的问题.Huang等^[25]提出基于试题文本的难度预测框架(Test-Aware Attention-Based Convolutional Neural Network, TACNN), 用于自动完成试题的难度预测任务.

1.1.2 基于试题表征方法的难度预测

图3为TACNN框架示意图.具体地, 以英语阅读理解试题为例, TACNN通过使用试题文本信息及学生在试题上的历史答题记录, 预测新的考试中出现的英语阅读理解试题的难度(答错率).

从图3可以看出, TACNN主要由4部分组成, 分别是输入层、句子卷积神经网络层、注意力层、预测层.输入层包含英语阅读理解选择题Q_i的各部分信息:阅读文本张量TD_i、问题矩阵TQ_i、选项矩阵TO_i.TACNN的第2层, 基于卷积神经网络(Con-volutional Neural Network, CNN)对试题中的

每个句子进行表征, 将每句话表示为一个固定长度的向量.第3层注意力层结合学生的阅读习惯处理试题, 包括本文每个句子对试题难度的贡献DA_i及每个选项的难度贡献DO_i.在最终的预测层中, TACNN根据文本难度贡献DA_i、选项难度贡献DO_i及问题的形式化表征, 设计考试范围依赖的偏序训练目标, 消除不同考试的误差, 预测试题难度 P̃i.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 TACNN框架[25]Fig.3 TACNN Framework[25]

TACNN设计统一的表征方法对英语阅读理解试题的各个组成部分(阅读文本、问题、选项)进行语义理解和表示, 并针对每道题量化各部分文本的特征表示, 以区分阅读理解试题阅读文本材料部分中各句子对不同问题的重要性.最重要的是, TACNN设计可以消除不同考试范围误差的框架, 以试题表征的结果均衡因参加考试的学生不同而导致的试题难度无法直接比较的问题, 从而对每道试题进行精确的难度预测.

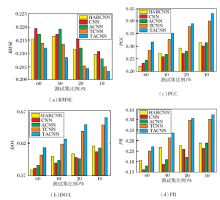
将TACNN框架应用于科大讯飞提供的学生英语阅读答题数据, 使用近300万的学生答题记录和对应题面, 对试题难度进行预测.为了衡量TACNN的性能, 实验中首先使用广泛采用的均方根误差(Root Mean Square Error, RMSE)对比准确度.然后, 使用排序准确度(Degree of Agreement, DOA)从排序的角度衡量试题对之间的难度排序正确百分比.其次, 使用皮尔逊相关系数(Pearson Correlation Coefficient, PCC)衡量试题难度和学生答题表现之间的关系.最后, 使用t检验通过率(Passing Ratio, PR)检测难度评估的置信水平.

这4个不同的评价指标中, RMSE越小, 模型表现越好; 其余指标越大, 模型表现越好.图4为TACNN难度预测结果, 对比方法包括:分层含注意力策略的CNN(Hierarchical Attention-Based CNN, HABCNN)、CNN、含注意力策略的CNN(Attention-Based CNN, ACNN)、文本感知的CNN(Text-Aware CNN, TCNN).从图中可以看出, 相比其它方法, TACNN可更准确地对英语阅读类型试题进行难度预测.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 TACNN难度预测结果[25]Fig.4 Difficulty prediction result of TACNN[25]

学生是在线教育系统服务的主要对象, 准确分析学生的认知水平, 对帮助了解学生状态、构建适当的教学计划都具有极大的帮助^[9].为此, 教育心理学的研究者提出认知诊断评价(Cognitive Diagnosis Assessment, CDA), 进行学生认知水平的全面分析.

1.2.1 认知诊断研究现状

CDA是一个基于认知心理学、统计学和计算机科学的评价体系, 通过对学生的答题数据进行建模分析, 引入试题与知识结构的关联关系, 对学生的认知状态进行诊断, 定量考察学生的个体差异和认知水平^[8].认知诊断理论起源于20世纪50年代, 经过多年的发展, 教育心理学家提出多个不同的认识诊断模型(Cognitive Diagnosis Model, CDM).根据“ 试题-知识点结构” 的关系与“ 学生-知识点” 的掌握类型^[26], 常见的CDM可以分为单维连续型模型和多维离散型模型.这里, “ 维度” 指学生能力(试题所关联知识点、技能)的数目, “ 离散” 、 “ 连续” 对应模型

诊断得到的学生能力值是离散型(0或1)还是连续型.

项目反映理论(Item Response Theory, IRT)是最常用的单维连续认知诊断模型之一^[27], 它假设学生对试题的作答结果服从独立同分布, 并将每位学生的认知状态表示为一个单维连续的能力值, 再结合试题特征(区分度、难度等)建模学生的答题情况.IRT模型的评估函数有多种形式, 较常见的IRT模型的函数形式之一如下:

P(X_ij=1|θ _j, a_i, b_i, c_i)=c_i+ 1-ci1+exp(-1.7ai(θj-bi)),

具体地, 上式通过估计学生j答对试题i的概率诊断分析学生认知能力θ _j, 其中, a_i为试题的区分度, b_i为试题的难度, c_i为试题的猜测度.该模型为三参数逻辑斯蒂回归IRT模型(Three-Parameter Logistic IRT, 3PL-IRT).当不考虑试题猜测度c_i时, 模型退化为双参数逻辑斯蒂回归IRT模型(Two-Parameter Logistic IRT, 2PL-IRT).若只考虑试题的区分度a_i, 该模型为单参数逻辑斯蒂回归IRT模型(One-Para-meter Logistic IRT, 1PL-IRT).根据应用场景及诊断要求的不同, 这3种类型的IRT模型在教育数据挖掘领域均具有较广泛应用.

在所有的多维离散型认知诊断模型中, DINA(Deterministic Input, Noisy AND-gate)^[16]模型是应用较广泛的模型之一.DINA模型认为每个试题由显式的知识点表述, 并将此关联关系使用Q矩阵表示^[26].Q矩阵通常由教育领域专家进行标注, 从图2的智学网试题样例中可以看出, 该题所关联的知识点为“ 不等式和绝对值不等式” .表1为一个Q矩阵示例, 从表中可看出, 试题i₁关联知识点S₁和S₄.DINA模型将学生能力描述为在多维知识点上的离散掌握向量, 表2为2位学生在知识点上的掌握程度示例, 从表中可看出学生j₁掌握知识点S₁和S₃.

表1

Table 1

表1(Table 1)

表1 试题-知识点关联Q矩阵示例 Table 1 Sample of question-knowledge point corresponding Q-matrx 试题 知识点 S1 S2 S3 S4 S5 i1 1 0 0 1 0 i2 0 1 0 1 0

表1 试题-知识点关联Q矩阵示例 Table 1 Sample of question-knowledge point corresponding Q-matrx

表2

Table 2

表2(Table 2)

表2 学生-知识点掌握矩阵示例 Table 2 Sample of student-knowledge point corresponding matrix 学生 知识点 S1 S2 S3 S4 S5 j1 1 0 1 0 0 j2 1 1 0 1 0

表2 学生-知识点掌握矩阵示例 Table 2 Sample of student-knowledge point corresponding matrix

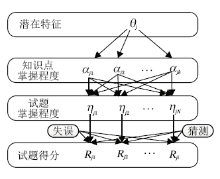
DINA模型同时考虑学生的认知能力及“ 猜测” 和“ 失误” 等心理因素进行认知诊断分析, 对于一个包含K个知识点的测试, 学生j答对试题i的概率X_ij可表示为

P(X_ij=1|θ _j, g_i, s_i)= 1-si, ηij=1gi, ηij=0

其中, g_i和s_i分别为试题i的猜测和失误因素, η _ij= ∏k=1Kθjkqik是学生j对试题i的掌握程度.DINA模型认为, 学生j掌握试题i关联的全部知识点k时, 可正确作答试题i(η _ij=1).由专家标注得到的Q矩阵具有极好的解释性, 因此, DINA模型通过引入试题-知识点关联Q矩阵, 不仅将诊断得到的学生单维认知能力扩展至多维认知状态, 还对每个认知维度赋予实际含义, 诊断得到的学生能力也具有很强的可解释性.

1.2.2 模糊认知诊断分析框架

教育心理学家提出的传统认知诊断模型通常仅基于小样本, 一般只适用于客观题(客观题是让学生从事先拟定的答案中辨认正确答案的题目, 答案非对即错), 难以考虑学生在主观题(学生自由陈述答案, 评分是根据作答情况给出相应分值)上的答题情况进行诊断分析^[8].针对这些传统认知诊断模型的局限性, 随着大数据分析挖掘的不断发展, 出现许多和数据挖掘方法相结合的认知诊断模型.Wu等^[29]提出面向学生个性化学习的模糊认知诊断分析框架(Fuzzy Cognitive Diagnosis Framework, Fu-zzyCDF).

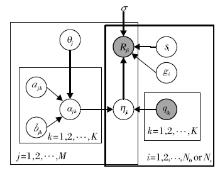
图5为FuzzyCDF的框架图, 此框架同时考虑学生在客观题和主观题上的作答过程, 形式化建模成一个4层的生成模型.第1层是学生自身的潜在特性(能力), 影响学生技能掌握程度的先验, FuzzyCDF模型认为, 学生的技能掌握程度受潜在特征的影响, 假设每个学生j有一个潜在特征θ _j.第2层为学生当前的认知状态(针对技能的掌握程度), 结合学生j潜在特性θ _j和IRT理论中的试题参数共同决定, 概率化学生j在技能k上的掌握程度α _jk.第3层根据学生j的技能掌握程度, 获得学生试题掌握程度η _ji, 在FuzzyCDF的第3层中, 基于模糊系统分别建模学生在主观题和客观题上不同的答题模式.具体地, FuzzyCDF分别考虑主观题和客观题2种测试题型关联的知识点掌握模式(主观题上的技能掌握模式满足教育学中“ 补偿型” 知识点假设, 在客观题上的掌握模式满足“ 链接型” 假设), 并结合专家标注的Q矩阵和模糊系统理论生成学生对试题的掌握程度α _jk(使用模糊并建模“ 补偿型” 知识点关联的客观题, 使用模糊交建模“ 连接型” 知识点关联的主观题).FuzzyCDF的第4层为学生答题结果的生成, 进一步考虑传统认知心理学中学生答题时存在的“ 失误” 和“ 猜测因素” , 即学生j在掌握试题的情况下可能因为失误(s_i)导致对试题i的答题错误, 或是在没有掌握试题的情况下通过猜测(g_i)答对试题i.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 四层FuzzyCDF框架图[29]Fig.5 4-step FuzzyCDF framework[29]

经过此四步的生成模型, FuzzyCDF最终建模得到学生在试题上的最终得分结果.图6为FuzzyCDF的图模型(该模型只需要两类观察变量:观察到学生的做题得分R_ji, 试题关联的知识点q_ik), 与图5中的步骤及本段中的描述相对应.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 FuzzyCDF图模型[29]Fig.6 Graphical model of FuzzyCDF[29]

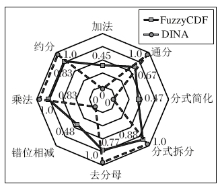
DINA模型只能给出学生的离散化的认知状态诊断结果(即输出的1, 0值分别表示学生在某个知识点上掌握或未掌握), 而FuzzyCDF可以进一步将诊断得到的学生认知状态细化为具有更多信息量的连续值(0~1之间的数值, 越大表示学生掌握程度越高).因此, 通过FuzzyCDF诊断得到的结果具有更强的可扩展性、抗噪声性和可解释性.例如, 图7在同个极坐标下分别展示FuzzyCDF和DINA模型诊断得到的学生知识点掌握程度结果对比.由图可见, 对于知识点“ 去分母” 而言, FuzzyCDF诊断学生在该知识点上的掌握程度为0.77, 这种概率化的诊断结果更精确, 且对在线学习提供的诸多面向学生的应用具有较大帮助.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 FuzzyCDF与DINA的诊断结果对比[29]Fig.7 Comparison of diagnosis result of FuzzyCDF and DINA[29]

1.2.3 学生游戏心理估计与诊断

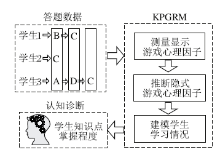
在线学习作为一种基于互联网的新型智能教学方式, 在快速发展的同时也面临着许多传统的线下教育未曾遇到的问题^[30-31].在面向学生的认知诊断分析任务中, 就面临这一情况:学生对试题的作答受自身能力和游戏心理的共同影响.学生自身能力即为知识点掌握程度等潜在特征, 而游戏心理是指通过固定的答题方法或是猜测(敷衍)回答问题.那么, 能否量化学生在作答时的游戏心理?Wu等^[32]提出“ 知识-猜测” 叠加反应模型(Knowledge Plus Gaming Response Model, KPGRM), 对在线学习中的学生游戏心理进行诊断和分析.

图8为学生在线答题的示例, 从图中的答题数据部分可以看出, 学生3通过不断猜测最终选择正确答案, 学生2第一次作答就选择正确答案.对于这两类不同的答题情况, KPGRM通过分析学生在多次答题(Multiple-Attempt Responses, MAR)下的显式游戏心理因子和单次答题(One-Attempt Response, OAR)下的显式和隐式猜测因子, 建模并诊断学生的游戏心理及认知情况.

现有的研究认为, 如果在线选择题的答题形式为学生只有答对当前试题才能进行下一题作答, 那么学生的游戏行为主要有持续作答、系统作答和快速作答这3类^{[33, 34]}.KPGRM基于这3种学生游戏行为, 提出4个用于诊断显式的学生游戏心理的特征:1)在一道题上的答题尝试次数越多, 对应的游戏心理因子越高(持续作答, Len); 2)答题速度越快, 游戏心理越强(快速作答, Spd); 3)答题过渡越高(Cov), 4)选择的选项对所有选项的覆盖度越大, 都标志更高的游戏心理因子(系统作答, Trs).在对学生答题时的4个特征进行观测后, 使用线性组合的方法对这4个特征进行组合, 即可分析出学生的显式游戏心理因子.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 KPGRM框架Fig.8 KPGRM framework

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 KPGRM图模型[32]Fig.9 Graphical model of KPGRM[32]

相比学生对一道试题多次作答的情况, 如果学生在第一次进行猜测时就选到正确答案, 则没有那么丰富的信息用于分析学生的隐式游戏心理.因此, KPGRM使用协同过滤(Collaborative Filtering, CF)对这种隐式的学生游戏心理进行分析.具体地, KPGRM将每位学生、试题都映射到D维的空间中, 使用一个向量描绘学生的潜在心理特征及对应试题的潜在特性.在应用潜在因子模型时, KPGRM将学生的游戏心理因子看作学生与试题间的交互, 并使用已观测到的学生显式游戏心理因子作为基础, 对相似学生的隐式游戏心理因子进行分析.

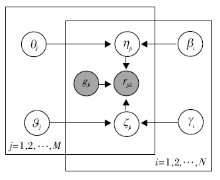
KPGRM使用信号检测模型从含有噪声的观测(首次作答的结果r_ji1)中检测学生j在回答试题i时的游戏心理因子g_ji.分别考虑如下2种情况.

1)学生j在没有任何游戏心理因子的情况下正确回答试题i, 建模学生学习状态η _ji.

2)学生j完全依靠游戏心理因子(如猜测等)正确回答试题i, 建模学生学习状态ζ _ji.

假设学生在每道试题上的作答是独立的情况, 使用伯努利分布建模学生所有的第一次作答情况(答对或答错), 表示如下:

P(r_ji1=1|θ _j, β _i, ϑ _j, γ _i, g_ji)= ηji1-gjiζjigji.

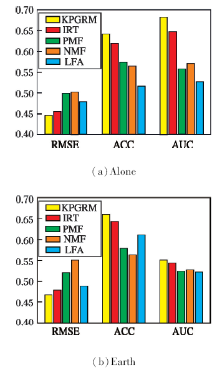
KPGRM模型通过学生多次回答问题时的特征观测显式游戏心理因子, 并使用协同过滤的方法推断隐式游戏心理因子.对比实验方法包括:IRT、概率矩阵分解(Probabilistic Matrix Factorization, PMF)、

非负矩阵分解(Non-negative Matrix Factorization, NMF)和因子分析(Learning Factor Analysis, LFA),

各方法在学生得分预测表现在Alone数据集和Earth数据集上的对比结果如图10所示.从图中可以看出, KPGRM可以对学生得分进行更准确的预测.

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 KPGRM的得分预测结果对比[32]Fig.10 Predicting result comparison of KPGRM[32]

此外, 文献[32]中的实验还补充对游戏心理因子的分析.具体地, 随机选取Alone数据集中20道MAR模式下的学生答题记录, 并邀请11名志愿者进行学生猜测情况标记F(1、 0.5和 0分别表示“ 游戏心理” 、“ 不确定” 和“ 非游戏心理” ), 并计算平均受试者工作特征曲线下的面积(Area Under Receiver

Operating Characteristic Curve, AUC).表3展示模型诊断得到的游戏心理因子和志愿者标注的对比情况, 达到可接受的属性一致分析结果(Fleiss's κ =0.73).从表中可以看出, KPGRM的测量结果和志愿者标注结果相符度较高.

表3

Table 3

表3(Table 3)

表3 KPGRM结果和志愿者标记结果对比[32] Table 3 Results comparison of KPGRM and volunteer 指标 Len Spd Trs Cov F AUC 0.598 0.723 0.923 0.945 0.966

表3 KPGRM结果和志愿者标记结果对比[32] Table 3 Results comparison of KPGRM and volunteer

综上所述, 在结合学生游戏心理因子的情况下, KPGRM使用信号检测模型诊断学生学习状态, 实现学生在线答题时游戏心理的分析, 同时还能更精确地诊断学生的认知状态.

对于智慧教育的研究, 是为了更好地辅导学生学习.因此, 除了面向试题(试题表征)和面向学生(认知诊断), 初步探索在线学习中的智能教学辅助.

1.3.1 教学辅助研究现状

在面向在线学习的教育数据挖掘中, 认知诊断方法可以帮助分析学生的学习状况^[8].学生通常需要不断地进行试题练习, 用于学习、巩固学习的内容, 因此, 在线学习面向教学的核心任务之一就是如何基于学生不同的认知状态(知识点掌握程度)向每个学生推荐适合的习题(试题).

在传统的线下教学过程中, 即使是对于知识点掌握程度不同的学生, 通常也由教师以班级为单位进行作业、习题的布置.从图7的学生知识点掌握雷达图中可以看出, 该学生在“ 分式化简” 和“ 分式拆分” 这两个知识点上的掌握程度区别较大, 因此, 每个具有不同认知状态的学生, 对练习的试题需求也应当不同.伴随在线学习系统中试题库的不断扩充, 传统方法不但难以对每个学生不同的学习状态进行有针对性的训练, 人工筛选试题也会花费大量的时间.所以, 如何自动为每个学生生成、推荐个性化试题, 是在线教育领域中面临的一个重要问题.

近些年, Thai-Nghe等^[35]基于教育领域中的认知诊断思想, 研究基于学生得分预测的试题推荐方法, 将学生的答题结果映射为“ 试题-知识点关联” 及“ 学生-知识点掌握” 两个低秩矩阵(表1、表2即为某种映射的示例).该方法通过预测学生在未知试题上的得分, 选择合适的题目进行推荐.因为学生的知识点掌握状态具有一定的隐蔽性, 诊断结果可能不够准确, 因此, 再使用这类基于认知诊断的试题推荐方法进行试题推荐时, 推荐准确度也会较差.此外, 朱天宇等^[14]使用传统的数据挖掘方法开展学生试题推荐工作, 这类方法基于协同过滤的思想对学生的共性进行建模, 较好地解决教师在筛选试题时耗时耗力的问题.然而, 这类数据挖掘方法的效果易受学生做题数据稀疏性的影响, 最终的题目推荐结果存在可解释性不足的问题, 即难以向学生、教师说明推荐某一道试题的原因(如学生因为对某一知识点掌握程度不足而进行推荐^[16]).因此, 在实际应用中也具有一定的局限性.

针对学生知识点掌握情况的认知诊断分析不仅可用于在线教育的试题推荐, 还可将分析得到的学生认知诊断情况应用于离线的课堂教育中, 对学生群体的分析也是教育数据挖掘中重要的一部分^[36].

班级作为学生离线学习的一个重要单位, 对班级里的学生进行建模, 发现班内学生之间的相似性和差异性对离线教学具有较大帮助.学生协同学习分组^[37]是离线学习中的一种重要学习形式, 它通过将班级内的学生划分为5~8人学习小组的形式, 组织每个学习小组内的学生进行学习, 同一学习小组内的学生通过互相交流、讨论, 达到提升学业水平的目的.传统的协同学习分组有人工选择和自动生成等方式, 学生自主构建学习小组的人工选择方法容易聚集相似的学生, 难以达到分组学习、互相提高的目的, 而教师主导分组的方法分组效率较低, 难以保证分组效果.此外, 基于模拟特征的协同学习分组方法缺乏对分组效果的验证, 而基于学生得分特征的分组方法粒度过粗, 无法根据学生的实际知识点掌握水平进行合理的分组.

1.3.2 基于认知诊断的个性化试题推荐

针对认知诊断在个性化推荐教学辅助方面的应用, 朱天宇等^[14]通过结合数据挖掘的推荐方法, 提出可增强试题推荐结果可靠性和可解释性的试题推荐方法(Probabilistic Matrix Factorization-Cognitive Di-agnosis, PMF-CD), 如图11所示.

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 PMF-CD个性化试题推荐[14]Fig.11 Personalized questions recommended PMF-CD framework[14]

PMF-CD试题推荐框架主要包括数据输入、学生认知诊断、学生得分预测及试题推荐4个步骤.首先根据已有的学生答题记录, 利用教育数据挖掘的认知诊断分析方法获得每个学生的认知状态.然后, 在已知学生知识点掌握程度的情况下, 通过将已观测到的学生答题情况和试题对应的知识点作为先验, 计算学生在每道试题上的实际掌握水平(即排除猜测和失误后的学生真实水平).在获得学生的试题掌握水平后, 再计算学生和试题的先验得分情况, 并将其应用于概率矩阵分解(Probabilistic Matrix Factorization, PMF).PMF可以获得学生和试题的隐向量, 并对学生的答题情况进行预测.最后, 模型根据所需试题的难度范围, 筛选得分预测在适合范围内的试题并形成待推荐试题集.经过PMF-CD模型的处理, 每个学生会得到一份结合自身的知识点掌握情况和相似学生答题情况共同生成的个性化试题.

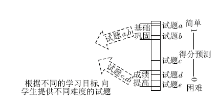
在提出的个性化试题推荐框架中, 可以根据学生的不同学习需求, 有针对性地向学生推荐不同难度的试题.如图12所示.针对需要提升薄弱知识点的掌握程度, 提高知识点掌握程度的学生, 可向其推荐难度较大的试题, 帮助成绩提升.而对于每个知识点的基础巩固, 可以向学生推荐难度较低(简单)的试题.

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 有针对性的试题推荐[14]Fig.12 Question Recommendation[14]

实验将PMF-CD框架应用于两组某市的高中学生实际答题记录的数据集(DATASET1、DATASET2),

并进行试题推荐.从图13中的结果可以看出, PMF-CD在向学生进行不同难度的试题推荐时, 相比未引入认知诊断的推荐方法(PMF), 均可以得到更好的推荐效果(PMF-CD的预测结果更贴近学生真实的答题率, 即推荐的简单题不会过于简单, 推荐的难题不会过于难).

图13

Fig.13

	Figure Option ViewDownloadNew Window
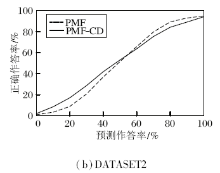	图13 不同推荐难度对推荐效果的影响[14]Fig.13 Influence of difficulty on results[14]

1.3.3 学生协同学习分组推荐

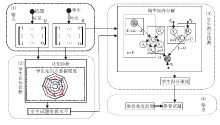
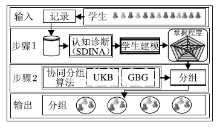
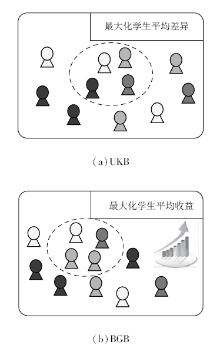
如前所述, 除将对学生的认知诊断结果应用于个性化试题推荐之外, 还可以根据班级内学生的知识点掌握水平, 进行协同学习分组的推荐.针对1.3.1节中提到的学生协同学习分组方法存在的相关问题, Liu等^[38]研究基于学生认知诊断分析的学生协同学习智能分组方法.如图14所示, 该框架分为输入、学生建模、学生分组及输出4个部分.输入部分为班级中待分组的学生及收集的学生答题情况.首先根据学生的试题作答情况对学生进行认知诊断, 分析软性确定性输入噪音与门模型(Soft-Deterministic Inputs Noisy and "Gate", S-DINA), 获得学生在每个独立的知识点上的概率化掌握程度.然后根据每个学生不同的知识点掌握情况, 进行学生分组, 并分别提出基于学生差异的分组算法(Uniform k-means Based, UKB)和基于收益的学生分组算法(Balanced Gain Based, BGB).如图15所示, UKB以学生知识点掌握程度为特征对班级内的学生进行聚类, 旨在将同类的学生分配到不同的学习小组.BGB通过最大化组内所有学生的平均收益, 对学生进行分组.

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 学生协同学习分组框架[38]Fig.14 Collaborative learning team formation framework[38]

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 UKB、BGB分组方法示意图[38]Fig.15 Sketch map of team formation result of UKB, BGB[38]

将学生协同学习分组方法应用于某市高中的班级学生协同学习分组推荐, 图16为某分组中学生知识点掌握水平的柱状图表示, 从图中可以看出, 该分组推荐方法可以平衡小组内学生(SD-Stu₁~SD-Stu₅)的知识点(S₁~S₅)掌握水平, 让学生可以互相学习、共同进步.此外, 实验中还引入授课教师对协同学习分组结果的真实评估.具体地, 该调查分别使用根据学生得分、DINA模型诊断得到的二元技能掌握程度及本文中S-DINA模型诊断得到的概率化技能掌握程度3种特征, 输出学生分组.

图16

Fig.16

	Figure Option ViewDownloadNew Window
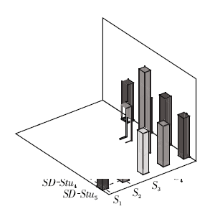	图16 协同学习分组示例[38]Fig.16 Team formation example[38]

表4为授课教师对这些分组的盲选结果, 从命中率来看, 本文所提的概率化技能掌握程度特征可以取得与授课教师意见更相符的协同学习分组结果.

表4

Table 4

表4(Table 4)

表4 授课教师调查结果[38] Table 4 Teacher evaluation % 特征 命中率/% 学生得分 6.6 二元技能掌握程度 26.7 概率化技能掌握程度 66.7

表4 授课教师调查结果[38] Table 4 Teacher evaluation %

Brusilovsky等^[39]提出自适应学习的概念后, 得到国内外研究人员的重视.自适应学习通常指为学生提供学习环境、实例或平台, 通过分析学生的学习过程, 发现并总结理论, 用于学生自主解决问题的学习形式.自适应学习可以看作个性化教育的一种实际应用, 目前, 已有在线学习网站向学生提供自适应学习的解决方案以满足每个学生不断变化的学习需求.“ 智学网” 作为场景覆盖较广、智能化较高的学生答题数据采集、分析、应用平台之一, 全程跟踪学生的学习过程, 为每位学生打造个性化学习路径, 促进学生的个性化学习, 提高学业水平.

当前的自适应学习系统要求及时诊断学生的学习状态, 根据每位学生的不同状态生成个性化学习内容, 保证学习的高效性和合理性^[39].

1.3.1节介绍的个性化试题推荐就是自适应学习系统的一个重要功能.由于国外的自适应学习系统发展较早, 因此, 相对于国内近些年才起步、发展的自适应学习平台, 发展略为成熟.Knewton(https://www.knewton.com)为美国一个个性化教育初创公司开发的较典型的个性化学习产品, 该平台的核心就是向学生提供一系列的自动资源内容评估(评估系统内试题、视屏等学习资源的质量)、自适应诊断技术(学生认知能力诊断)以及推荐功能(针对每个学生的个性化学习资源推荐).目前, 该平台已经覆盖全球120个国家, 《快公司》(Fast Company)杂志(https://www.fastcompany.com)曾将其评为全球大数据领域最具创新力的十大公司之一.

对试题、学生的分析和诊断结果, 不仅可应用于在线的自适应学习平台, 还可用于辅助教师的离线教学^[38].1.3节提到的学生协同学习分组推荐, 就是将学生分析诊断结果应用于离线(课堂)教学的案例之一.除了面向学生分析的离线教学应用之外, 对试题的分析也对离线教学辅助具有一定的帮助, 如根据试题的难度、知识点考察范围等进行自动组卷, 保证试卷整体的科学性与合理性^[39].

目前, 国内的自适应学习在线教育平台大多以系统资源构建和学生能力分析为主要目标, 较难有效利用学习资源向不同能力的学生提供个性化服务, 也难渗透到学生的日常学习教学场景中.为了探索国内K12教育与自适应学习系统结合的可能性, 为学生提供科学、个性化的在线学习环境, 科大讯飞公司智学网(zhixue.com)系统集成一套用于学生自适应学习的在线模块, 并率先与全国各地的中学进行合作试点, 取得一定的初步成效.

在提供在线自适应学习平台的同时, 智学网还伴随式收集离线(在校)的教与学数据, 全面分析学生的学习状态, 并及时向授课教师反馈, 帮助教师精准教研, 帮助学生推荐个性化学习资源, 促使有效提升.也就是说, 在对学生进行认知诊断分析、试题推荐的同时, 也能提供面向教师的班级学生学习状态反馈、智能组卷等服务.

文中介绍的部分教育数据挖掘技术及相关应用成果(如认知诊断分析、试题推荐、自动组卷等)已应用于智学网的学习平台.与此同时, 通过学生对所推荐资源的学习反馈, 形成“ 学习-诊断-推荐-反馈-学习” 的闭环结构.目前, 智学网初步搭建的大数据在线教育平台已覆盖全国29个省230多个城市, 提供的服务让近13 000所学校的千万师生受益.