引用本文
李萍, 倪志伟, 朱旭辉, 宋娟. 联合类间及域间分布适配的迁移学习方法. 模式识别与人工智能, 2020,33(1): 1-10
LI Ping, NI Zhiwei, ZHU Xuhui, SONG Juan. Transfer Learning with Joint Inter-class and Inter-domain Distributional Adaptation. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2020,33(1): 1-10.  
Doi: 10.16451/j.cnki.issn1003-6059.202001001
Permissions
Copyright©2020, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
联合类间及域间分布适配的迁移学习方法
李萍1,2,3, 倪志伟1,3, 朱旭辉1,3, 宋娟1,3
1.合肥工业大学 管理学院 合肥 230009
2.阜阳师范大学 信息工程学院 阜阳 236041
3.合肥工业大学 过程优化与智能决策教育部重点实验室 合肥 230009
通讯作者：

倪志伟,博士,教授,主要研究方向为人工智能、机器学习、云计算.E-mail:zhwnelson@163.com.
作者简介：

李 萍,博士研究生,讲师,主要研究方向为模式识别、机器学习.E-mail:apple151691@126.com.

朱旭辉,博士,讲师,主要研究方向为智能计算、机器学习.E-mail:xuhuihappystar@163.com.

宋 娟,博士研究生,主要研究方向为智能计算、机器学习.E-mail:420074425@qq.com.

收稿日期: 2019-02-17 接受日期: 2019-09-02
资助项目: 国家自然科学基金项目(No.91546108,71490725,71521001)、安徽省自然科学基金项目(No.1708085MG169)、安徽省高校自然科学研究重点项目(No.KJ2019A0949)、安徽省高校教学研究项目(No.2018jyxm0264)资助
摘要

在域间分布适配的过程中,容易丢失一些重要的域自身信息,在源域上难以训练获得一个有效的分类器,影响其在目标域上的泛化与标注性能.基于此种情况,文中提出联合类间及域间分布适配的迁移学习方法.通过学习一个公共投影矩阵,分别将源域与目标域映射到一个公共子空间上.采用最大均值差异方法分别度量类间及域间分布距离.在目标函数的优化过程中,不但显式地使域间分布差异变小,而且增大不同类别间的差异性,提高源域与目标域之间知识迁移的性能.在迁移学习数据集上的实验表明文中方法的有效性.

关键词: 类间分布适配; 特征迁移; 迁移学习; 最大均值差异
中图分类号:TP18
Transfer Learning with Joint Inter-class and Inter-domain Distributional Adaptation
LI Ping1,2,3, NI Zhiwei1,3, ZHU Xuhui1,3, SONG Juan1,3
1. School of Management, Hefei University of Technology, Hefei 230009
2. College of Information Engineering, Fuyang Normal University, Fuyang 236041
3. Key Laboratory of Process Optimization and Intelligent Decision-Making, Ministry of Education, Hefei University of Technology, Hefei 230009
Corresponding author:
NI Zhiwei, Ph.D., professor. His research interests include artificial intelligence, machine learning and cloud computing.
AboutAuthor:

LI Ping, Ph.D. candidate, lecturer. Her research interests include pattern recognition and machine learning.

ZHU Xuhui, Ph.D., lecturer. His research interests include intelligent computing and machine learning.

SONG Juan, Ph.D. candidate. Her research interests include intelligent computing and machine learning.

Fund:National Natural Science Foundation of China(No.91546108,71490725,71521001), Natural Science Foundation of Anhui Province(No.1708085MG169), Key Program of Natural Science of Higher Education Institutions of Anhui Province(No.KJ2019A0949), Teaching Research Program of Higher Education Institutions of Anhui Province(No.2018jyxm0264)
Abstract

Inter-domain information is lost during the process of inter-domain distributional adaptation. Therefore, it is difficult to train an effective classifier in the source domain, and the performance of generalization and tagging in the target domain are affected. Aiming at this problem, an approach, joint inter-class and inter-domain distributional adaptation for transfer learning, is proposed to address this challenge. The proposed method is formulated by learning a projection matrix to map new representations of respective domains into a common subspace. And the distance-measure method of the maximum mean discrepancy is adopted to compute the distance of inter-class and inter-domain distributions. During the optimization procedure, the inter-domain distributional difference is reduced explicitly, and the inter-class distributional difference is enlarged greatly. The capability of knowledge transfer between different domains is improved. Experiments on transfer learning dataset verify the effectiveness of the proposed approach.

Key words: Key Words Inter-class Distribution Adaptation; Feature Transfer; Transfer Learning; Maximum Mean Discrepancy

本文责任编委 王士同

Recommended by Associate Editor WANG Shitong

传统的机器学习方法不但需要足量的训练样本, 还假设训练样本与测试样本服从相同分布.但是在如人物追踪、安全监控、医疗诊断等诸多领域中, 一方面由于数据更新迅速, 导致已有的训练数据与新涌现的数据分布不一致, 另一方面由于很难获得新数据的标签, 因此需要相关技术解决这类领域中新样本的标注问题.

迁移学习通过将源域(分布不同但相关)中的知识迁移到目标域中, 在目标域中复用源域中大量有标注信息的样本, 解决目标域样本的标注问题.迁移学习方法主要包括基于实例的迁移学习[1, 2, 3]、基于特征的迁移学习[4, 5, 6, 7]、基于模型的迁移学习[8, 9, 10]和基于关系的迁移学习[11, 12, 13].

基于特征的迁移学习的主要思想是通过结合某种特征提取方法, 将源域和目标域同时映射到一个新的公共特征空间, 使它们对应的新特征表示之间的分布差异减小, 提高源域与目标域的相似性.Pan等[4]提出迁移成分分析(Transfer Component Analysis, TCA), 使用最大均值差异(Maximum Mean Discrepan-cy, MMD)缩小二者的边缘概率分布差异.Long 等[6]提出联合分布适配方法(Joint Distribution Adaptation, JDA), 使用类条件MMD(Class-Wise MMD)同时减小二者之间的边缘分布差异和条件分布差异.Zhang 等[14]提出联合几何和统计对齐的分布适配方法(Joint Geometrical and Statistical Align-ment for Visual Domain Adaptation, JGSA), 认为保持域内自身的数据性质对于知识迁移同样重要.

上述方法为了简化模型优化过程, 均采用基于主成分分析的特征提取框架, 属于基于矩阵优化的特征迁移方法.近年来, 由于数据量的激增, 基于深度学习的特征迁移方法在工业问题中得到广泛应用[15, 16, 17, 18, 19, 20, 21, 22].Long等[7]提出深度适配网络, 利用多核MMD对网络的最后三层进行适配.进一步地, Long等[23]提出联合适配的深度迁移学习方法, 在网络的多个层中在源域和目标域之间进行联合分布对齐.

域间分布适配的迁移学习方法通过最小化源域与目标域之间的分布差异, 学习新的特征空间.在新特征空间中, 源域与目标域的分布距离最小, 从而直接使用源域上训练的分类器对目标域中的样本进行标注.该方法广泛应用于各种特征迁移学习方法中[7, 24, 25, 26].

然而, 域间分布适配的迁移学习方法在最小化源域与目标域之间的分布差异时, 通常会丢失乃至削弱各领域自身的一些重要性质[27], 如源域中不同类别之间的差异性, 不能保证在源域上训练获得一个有效的分类器, 影响其在目标域中的标注性能.例如JGSA[14]提到不存在一个理想的公共子空间, 使其在源域和目标域的分布完全一致的同时, 各领域自身的性质仍能得到最大化保持.因此, 在对领域之间的分布进行适配的过程中, 考虑领域自身的数据性质同样重要.

基于此种情况, 本文提出联合类间及域间分布适配的迁移学习方法(Transfer Learning with Joint Inter-class and Inter-domain Distributional Adaptation, JCDA).首先, 利用源域样本训练初始分类器, 学习目标域样本的伪标签.再利用MMD度量方法, 通过最小化源域与目标域之间的边缘分布和条件分布距离, 同时最大化源域中不同类别之间样本的分布距离, 建立目标函数, 求解新的特征空间.然后, 利用新特征空间中的源域数据训练分类器, 重新学习目标域样本的伪标签.最后, 通过迭代方式, 得到最终的特征空间, 在新的特征空间上, 提高目标域中样本的分类准确率.鉴于目标域中伪标签的不可靠性, 在计算不同类别之间的样本分布距离时, 仅考虑源域内部不同类别之间的样本分布距离.

1 问题定义

记带有标注信息的源域Ds={Xs, Ys}, 无标注信息的目标域Dt={Xt}, 假设源域与目标域的特征空间相同(Xs=Xt), 标签类别空间相同(Ys=Yt), 但是边缘分布及条件分布不同, 即

Ps(Xs)≠ Pt(Xt), Qs(Ys|Xs)≠ Qt(Yt|Xt).

本文需要解决上述源域与目标域的问题, 寻找新的特征空间ϕ (X), 在新特征空间中

Ps(ϕ (Xs))≈ Pt(ϕ (Xt)), Qs(Ys|(Xs))≈ Qt(Yt|(Xt)),

实现从源域中学习的分类器对目标域样本的有效分类.

本文使用MMD的经验估计[4, 6]度量任意2个样本集X's、X't对应的不同分布P's、P't之间的距离:

Dist(P's, P't)= ||1n's∑i=1n'sϕ(x'si)-1n't∑j=1n'tϕ(x'tj)||2,

其中, n's为X's样本个数, n't为X't样本个数, x 'si、x 'tj分别为X's、X't中样本, ϕ 为特征映射.

2 联合类间及域间分布适配的迁移学习方法
2.1 最优化模型的建立

根据文献[4], 若X经过核变换后又降维到新的k维特征空间ϕ (X), 则源域与目标域的总样本分布的距离为

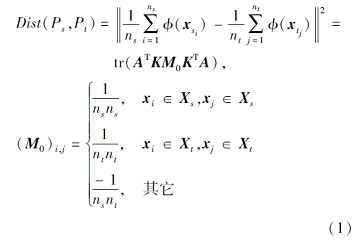
其中, ns为源域样本个数, nt为目标域样本个数, xsi为源域中样本, xtj为目标域中样本, K为源域与目标域样本的核矩阵, A为特征变换矩阵.

根据文献[6], 若X未经核变换直接降维到新的k维特征空间ϕ (X), 则源域与目标域的总样本分布的距离为

Dist(Ps, Pt)= ||1ns∑i=1nsϕ(xsi)-1nt∑j=1ntϕ(xtj)||2=tr(ATXM0XTA),

其中X=[Xs Xt].

为了书写统一, 下面在计算样本集之间距离时, 只考虑样本经核变换后再降维的情况, 对于样本被直接降维的情况具有相应的表示.因此, 源域与目标域的同类样本分布的距离为

Dist( Ps(c), Pt(c))= ∑c=1C||1nsc∑i=1nscϕ(xsic)-1ntc∑j=1ntcϕ(xtjc)||2= ∑c=1C(ATKMcKTA),

(Mc)i, j= 1ns(c)ns(c), xi∈Xs(c), xj∈Xs(c)1nt(c)nt(c), xi∈Xt(c), xj∈Xt(c)-1ns(c)nt(c), xi∈Xs(c)∧xj∈Xt(c)或xi∈Xt(c)∧xj∈Xs(c)0, 其它(2)

其中, c=1, 2, …, C为样本类别号, ns(c)为源域中类别为c的样本总数, nt(c)为目标域中类别为c的样本总数, Xs(c)为源域中类别为c的样本构成的集合, Xt(c)为目标域中类别为c的样本构成的集合, xsi(c)∈ Xs(c), xsj(c)∈ Xt(c).

源域中不同类别样本间距离为

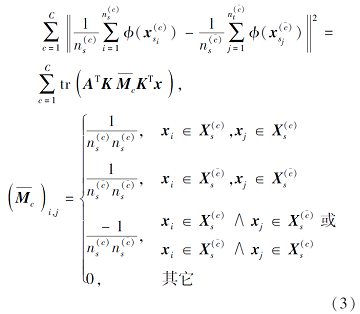
其中, c̅为{1, 2, …, C}中非c的类别号, ns(c)̅为源域中类别不为c的样本总数, Xs(c)̅为源域中类别不为c的样本构成的集合, xsi(c)∈ Xs(c), xsj(c)̅∈ Xs(c)̅.

借助JDA的思想[6], 源域与目标域之间的样本分布距离可表示为Dist(Ps, Pt)+Dist( Ps(c), Pt(c)).

通过最小化域间分布距离、最大化源域内类间分布距离, 利用权重调节系数β 权衡两者之间的重要度, 建立目标函数, 同时使用样本方差作为约束条件, 得到最优化问题:

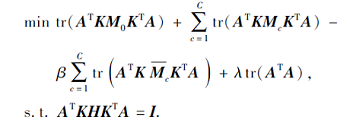
化简如上目标函数, 可得

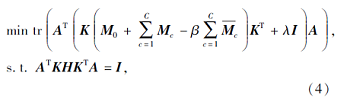
其中

(H)i, j= 1-1ns+nt, i=j-1ns+nt, i≠j(5)

λ 为正则化系数.

鉴于迁移学习主要解决域间差异的问题, 本文考虑为类间差异分配较小的权重, 即β ∈ [0, 1], 当β =0时, 该最优化问题退化为JDA.

JDA作为域分布适配中的一个经典方法, 在TCA和迁移联合匹配(Transfer Joint Matching, TJM)的基础上同时考虑领域间的边缘分布和条件分布差异.然而, 不存在一个理想的公共子空间, 在其源域和目标域的分布完全一致的同时, 领域自身的性质也能得到最大化保持[14].因此, JCDA可以看成JDA的改进版, 不仅考虑域间的两种分布差异, 而且使用已有的MMD定义类间分布距离, 使源域中不同类别样本间分布差异最大, 保持源域良好的类可分性.JCDA不仅保证领域间的相似性, 而且在源域上可以训练获得一个更有效的分类器, 提升在目标域上的标注效果.

2.2 最优化模型的求解

针对带有约束条件的最优化问题(4), 本文采用拉格朗日函数进行求解, 设

Φ =diag(ϕ 1, ϕ 2, …, ϕ k)∈ Rk× k

为拉格朗日乘子, 则式(4)对应的拉格朗日函数:

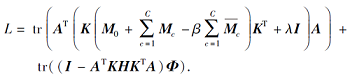
令 ∂L∂A=0, 得

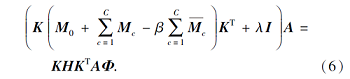
因此, 特征变换矩阵A可通过求解方程(6)所得的前k个最小特征值对应的特征向量构成.记Ks为K的前ns列构成的矩阵, Kt为K的后nt列构成的矩阵, 则ATKs、ATKt即为源域和目标域的新特征表示.

2.3 算法步骤

JCDA通过联合类间分布适配与域间分布适配学习源域与目标域样本的新特征表示.一方面, 最小化源域与目标域之间样本的分布距离, 增强域间样本分布的相似性.另一方面, 为了避免源域中类间样本差异过小导致的难以训练有效分类器的问题, 最大化类间分布距离, 保持类间样本的差异性, 实现源域到目标域知识的有效迁移.具体算法步骤如下.

算法 JCDA

输入 源域样本Xs, 对应的标签Ys,

目标域样本Xt

输出 变换矩阵A,

源域样本的新特征表示Zs=ATKs,

目标域样本的新特征表示Zt=ATKt

step 1 初始化新特征空间维数k、正则化系数λ 、权重调节系数β 、迭代次数T, 标准化处理源域样本和目标域样本, 选择核函数.

step 2 利用有监督学习训练(Xs, Ys)并得到分类器, 利用该分类器学习Xt的标签Yt, 根据核函数计算核矩阵K, 根据式(5)计算H, iter=1.

step 3 根据(Xs, Ys)和(Xt, Yt)分别利用式(1)~式(3)计算M0、Mc及 M¯c.

step 4 求解式(6)对应的广义特征分解问题, 选择前k个最小特征值对应的特征向量构成变换矩阵A, 求解Zs=ATKs, Zt=ATKt.

step 5 利用有监督学习训练(Zs, Ys)并得到分类器, 利用该分类器学习Zt的标签Yt.

step 6 若iter< T, 令iter=iter+1, 转step 3; 否则, 算法结束.

2.4 算法复杂度分析

本文采用渐进法衡量算法的时间复杂度, 源域与目标域的样本总数n=ns+nt, 样本原始特征维数为m, 新特征维数为k≪min(m, n), 迭代次数为T≪min(m, n).设有监督学习采用1-近邻(1-Nearest Neighbor, 1-NN).step 2中有监督学习的时间复杂度为O(n), 其它部分时间复杂度为O(n2).step 3中MMD矩阵的计算复杂度为O(Cn2).step 4中求解广义特征分解问题的时间复杂度为O(km2), 其它部分的时间复杂度为O(mn+n2).step 5中有监督学习的时间复杂度为O(n).所以经过T次迭代算法总共的时间复杂度为O(TCn2+Tkm2+Tmn).

3 实验及结果分析
3.1 实验数据集

本文使用MNST、USPS、PIE、Office、Caltech数据集.具体地, 分别从MNIST、USPS数据集上随机选取2 000和1 800个样本用于实验, 图像大小为28× 28, 类别数为10.这2个数据集构成2对迁移学习任务.

PIE数据集为68人在不同光线强度、姿势、表情下, 从左、上、下、前、右5个角度拍下的人脸图像, 图像大小为32× 32.从5个角度分别随机选出3 321幅、1 629幅、1 632幅、3 329幅、1 632幅图像构成5个样本集, 记为PIE1、PIE2、PIE3、PIE4和PIE5, 两两之间构成20对迁移学习任务.Office数据集是通过3种不同的方式分别得到的31种不同物体的图像集合, 分别为Amazon、Webcam、DSLR.Caltech-256数据集由256种不同物体图像构成.Office+Caltech数据集[5]使用加速稳健特征(Speeded up Robust Features, SURF), 特征维数为800.

为了使标签空间一致, 分别从Amazon、Webcam、DSLR和Caltech中选择10个公共类别, 这4类图像数据集两两之间构成12对迁移学习任务.对比相关的基于深度学习的特征迁移方法, Office-31数据集的深度特征从ResNet-50模型[28]上提取得到, ResNet-50模型在ImageNet上进行预训练, 最终的特征维数为2 048.同样, 来自Office-31的Amazon、Webcam和DSLR两两之间构成6对迁移学习任务.所有数据集的统计信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets
3.2 对比方法和参数设置

对比方法为1-NN, TCA, JDA, 深度适配网络(Deep Adaptation Networks, DAN)[7], 残差迁移网络(Residual Transfer Networks, RTN)[29], 联合适配网络(Joint Adaptation Networks, JAN)[23].设定新特征空间维数k∈ {10, 20, …, 200}, 正则化系数λ ∈ {0.01, 0.1, 1, 10, 100}, 权重调节系数β ∈ {0.1, 0.2, …, 1}.针对各种迁移学习任务, 很难选出一个统一的参数组合, 使所有迁移学习任务都达到最好的学习效果.在实验对比时, TCA、JDA、JCDA统一选取子空间维度k=100, 迭代次数T=10, 对于正则化参数λ , 在MNIST+USPS数据集上取λ =0.1、在PIE数据集上取λ =0.01、在Office+Caltech和Office-31数据集上取λ =1.特别地, 对于本文的权重调节系数设定为β =0.1.而对于本文列出的基于深度学习的特征迁移方法的实验结果均是从对应文献中获得[7, 23, 28, 29], 可认为是该方法的最好结果.

3.3 实验结果对比

JCDA、1-NN、TCA、JDA在MNIST+USPS、PIE、Office+Caltech数据集上的实验结果如表2所示.

表2 各方法在34种迁移学习任务上的学习精度 Table 2 Learning accuracy of different approaches on 34 transfer tasks

由表2可看出, 所有方法均优于1-NN, 体现在跨领域问题中迁移学习技术的有效性和必要性.此外, 相比TCA和JDA, JCDA具有明显优势.具体地, JCDA在所有数据集上的分类精度均优于TCA, 除了在PIE3→ PIE2、Amazon→ DSLR及Webcam→ Amazon上分类精度略低于JDA以外, 在其它31个迁移任务上的分类精度均高于JDA, 验证了本文在其基础上进行改进的有效性, 即源域内的类间分布适配的重要性.

JCDA、1-NN、TCA、JDA、ResNet-50、DAN、RTN、JAN在Office-31数据集上的实验结果如表3所示.由表可看出, 迁移学习方法在跨领域问题中的作用至关重要, 即所有方法均优于1-NN.

表3 各方法在6种迁移学习任务上的学习精度 Table 3 Learning accuracy of different approaches on 6 transfer tasks

此外, 对比在Office-31的深度特征上的迁移学习效果发现, 相比TCA和JDA, JCDA具有明显优势, 进一步验证在JDA基础上所做改进的有效性.而相比深度迁移学习方法DAN、RTN、JAN, JCDA在DSLR→ Webcam、Webcam→ DSLR及Webcam→ Amazon表现较优.

通过观察不同方法在Office-31数据集上迁移任务的平均学习精度可看出, JCDA的平均学习精度最高, 说明尽管本文方法属于基于矩阵优化的特征迁移方法, 但相比基于深度学习的特征迁移方法, 仍具有明显优势.

3.4 有效性分析

本文以迁移任务USPS→ MNIST为实验对象, 分析域间分布距离与类间分布距离在知识迁移过程中的变化.图1分别反映2种统计量基于4种方法(1-NN、TCA、JDA、JCDA)随迭代次数的变化情况.由(a)可看出, 由于1-NN属于非迁移学习方法, 随着迭代次数的增加, 分布距离无任何变化.由于JDA和JCDA均同时最小化边缘分布和条件分布距离, 因此, 相比1-NN和TCA(仅考虑边缘分布距离), JDA和JCDA均取得最低值.

图1 四种方法中两种统计量随迭代次数的变化Fig.1 The variation of 2 statistics by 4 methods with iteration number

由于源域类间距离对于训练一个好的分类器至关重要, 而该分类器最终直接影响在目标域上的识别率, 因此本文提出同时最小化域间分布距离和最大化源域类间距离, 即实现域内类间分布适配.

由图1(b)可看出, 1-NN对应原始特征空间下的源域类间距离, TCA和JDA仅实现域间分布适配, 使源域中不同类别样本之间的距离变小.与之不同的是, 在知识迁移的过程中, JCDA尽可能使源域类间距离最大化, 提出使用MMD定义类间分布距离, 同时实现域间分布和源域类间分布适配.在TCA和JDA的基础上, JCDA一定程度地增大源域类间分布距离, 该方法更有效.

3.5 参数分析

本节通过对参数敏感性的实验分析, 验证本文方法在较大的参数范围内能保持良好的性能, 在对特定参数进行分析时保持其它参数固定不变.

下面分析特征空间维数k与迭代次数T对算法性能的影响, 仅以USPS→ MNIST、PIE1→ PIE2、Caltech→ Amazon(SURF)和Amazon→ Webcam (ResNet)为例.如图2所示, 对于其它迁移学习任务具有类似特点.由(a)可看出, 当k∈ [60, 200]时, 各迁移学习任务的学习精度较稳定.由(b)可看出, 当迭代次数T达到10以上时, 各迁移学习任务的学习精度趋于稳定.因此, k、T对最终的实验结果不敏感.

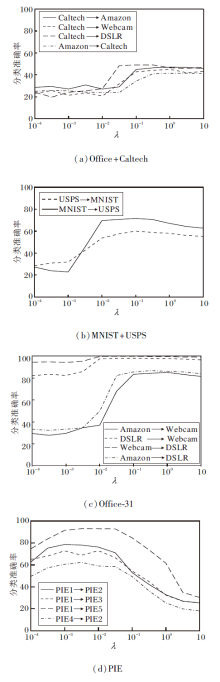
图2 参数对方法性能的影响Fig.2 Influence of parameters on performance of the proposed approach

在对正则化系数λ 进行分析时, 因为不同数据集对λ 的敏感度不同, 因此分别在4个数据集上进行实验.鉴于Office+Caltech、PIE、Office-31数据集涉及的迁移任务较多, 仅针对其中的前四组迁移学习任务, 实验结果如图3所示.

图3 λ 在4个数据集上的敏感性分析Fig.3 Sensitivity analysis of λ on 4 datasets

由图3可看出, 在物体识别数据集Offcie+Caltech、Office-31上, λ 在10-1~10这个较宽范围内的迁移学习准确率较稳定.在手写数字数据集MNIST+USPS和人脸识别数据集PIE上, λ 分别在[10-1.5, 10-0.5]和[10-3.5, 10-2]内的迁移学习准确率较稳定.

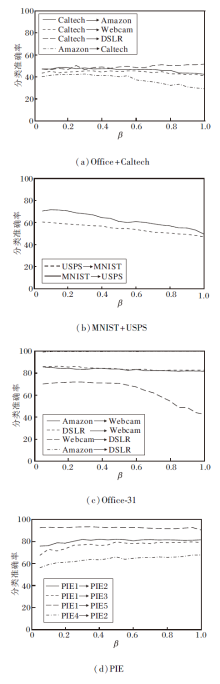
与λ 的分析类似, 为了图形的简洁性, 仅分别给出权重调节系数β 在4个数据集上对部分迁移任务性能的影响, 如图4所示.由图可看出, 对于物体识别数据集Offcie+Caltech、Office-31, 当β ∈ [0.05, 0.55]时, 在这个较宽范围内均能取得较优的迁移学习效果, 当β ∈ [0.6, 1]时, 个别迁移学习任务的学习性能有所提升, 而绝大多数的迁移学习任务的学习性能有所下降.对于手写数字数据集MNIST+USPS, 迁移学习性能对β 较敏感, β 仅在[0.05, 0.2]内时迁移学习性能较优.对于人脸识别数据集PIE, 在β ∈ [0.2, 1]这个宽泛范围内, 各个迁移学习任务均能取得良好效果.

图4 β 在4个数据集上的敏感性分析Fig.4 Sensitivity analysis of β on 4 datasets

上述参数分析实验表明, 新特征空间维数k与迭代次数T能够在统一的范围内使JCDA在各数据集上产生良好的迁移学习效果.正则化系数λ 与权重调节系数β 分别在不同的范围内使JCDA在各数据集上表现较优的迁移学习性能.总之, JCDA能在较宽泛的参数范围内, 提高迁移学习的性能, 实现源域到目标域知识的有效迁移.

4 结束语

本文提出联合类间及域间分布适配的迁移学习方法(JCDA), 借助权重调节因子同时进行类间分布适配与域间分布适配, 学习新特征空间, 实现源域与目标域的分布对齐, 同时保持源域中异类样本间的差异性, 提高迁移学习的性能.在多个数据集上进行对比实验、方法有效性分析及参数分析, 结果表明, 本文方法具有较优的迁移学习性能.今后将对迁移学习中源域与目标域的分布适配产生的域漂移问题进行深入研究, 利用后验概率解决这一问题.

参考文献
[1] DAI W Y, YANG Q, XUE G R, et al. Boosting for Transfer Lear-ning // Proc of the 24th International Conference on Machine Lear-ning. New York, USA: ACM, 2007: 193-200. [本文引用:1]
[2] 张倩, 李明, 王雪松, 等. 一种面向多源领域的实例迁移学习. 自动化学报, 2014, 40(6): 1176-1183.
(ZHANG Q, LI M, WANG X S, et al. Instance-Based Transfer Learning for Multi-source Domains. Acta Automatica Sinica, 2014, 40(6): 1176-1183. ) [本文引用:1]
[3] JIANG S Y, XU Y H, SONG H J, et al. Multi-instance Transfer Metric Learning by Weighted Distribution and Consistent Maximum Likelihood Estimation. Neurocomputing, 2018, 321: 49-60. [本文引用:1]
[4] PAN S J, TSANG I W, KWOK J T, et al. Domain Adaptation via Transfer Component Analysis. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210. [本文引用:4]
[5] GONG B Q, SHI Y, SHA F, et al. Geodesic Flow Kernel for Unsupervised Domain Adaptation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2012: 2066-2073. [本文引用:2]
[6] LONG M S, WANG J M, DING G G, et al. Transfer Feature Lear-ning with Joint Distribution Adaptation // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2013: 2200-2207. [本文引用:5]
[7] LONG M S, CAO Y, WANG J M, et al. Learning Transferable Features with Deep Adaptation Networks // Proc of the 32nd International Conference on Machine Learning. Washington, USA: IEEE, 2015: 97-105. [本文引用:5]
[8] PAN S J, SHEN D, YANG Q, et al. Transferring Localization Models across Space // Proc of the 23rd National Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2008, III: 1383-1388. [本文引用:1]
[9] ZHAO Z T, CHEN Y Q, LIU J F, et al. Cross-People Mobile-Phone Based Activity Recognition // Proc of the 22nd International Joint Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2011, III: 2545-2250. [本文引用:1]
[10] WEI Y, ZHU Y, LEUNG C W, et al. Instilling Social to Physical: Co-regularized Heterogeneous Transfer Learning // Proc of the 30th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2016: 1338-1344. [本文引用:1]
[11] MIHALKOVA L, HUYNH T, MOONEY R J. Mapping and Revising Markov Logic Networks for Transfer Learning // Proc of the 22nd National Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2007, I: 608-614. [本文引用:1]
[12] MIHALKOVA L, MOONEY R J. Transfer Learning by Mapping with Minimal Target Data // Proc of the AAAI Workshop on Transfer Learning for Complex Tasks. Palo Alto, USA: AAAI Press, 2008: 31-36. [本文引用:1]
[13] DAVIS J, DOMINGOS P. Deep Transfer via Second-Order Markov Logic // Proc of the 26th International Conference on Machine Learning. New York, USA: ACM, 2009: 217-224. [本文引用:1]
[14] ZHANG J, LI W Q, OGUNBONA P. Joint Geometrical and Statistical Alignment for Visual Domain Adaptation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 5150-5158. [本文引用:3]
[15] CAO Z J, LONG M S, WANG J M, et al. Partial Transfer Lear-ning with Selective Adversarial Networks // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 2724-2732. [本文引用:1]
[16] CAO Z J, MA L J, LONG M S, et al. Partial Adversarial Domain Adaptation // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 139-155. [本文引用:1]
[17] HAUSSER P, FRERIX T, MORDVINTSEV A, et al. Associative Domain Adaptation // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 2784-2792. [本文引用:1]
[18] HONG W X, WANG Z Z, YANG M, et al. Conditional Generative Adversarial Network for Structured Domain Adaptation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 1335-1344. [本文引用:1]
[19] LONG M S, CAO Z J, WANG J M, et al. Conditional Adversarial Domain Adaptation // Proc of the 32nd Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 1647-1657. [本文引用:1]
[20] MOTIIAN S, PICCIRILLI M, ADJEROH D A, et al. Unified Deep Supervised Domain Adaptation and Generalization // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 5716-5726. [本文引用:1]
[21] PEI Z Y, CAO Z J, LONG M S, et al. Multi-adversarial Domain Adaption // Proc of the 32nd AAAI Conference on Artificial Inte-lligence. Palo Alto, USA: AAAI Press, 2018: 3934-3941. [本文引用:1]
[22] ZHANG J, DING Z W, LI W Q, et al. Importance Weighted Adversarial Nets for Partial Domain Adaptation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8156-8164. [本文引用:1]
[23] LONG M S, WANG J M, JORDAN M I. Deep Transfer Learning with Joint Adaptation Networks // Proc of the 34th International Conference on Machine Learning. Washington, USA: IEEE, 2017: 2208-2217. [本文引用:3]
[24] WANG J D, CHEN Y Q, HAO S J, et al. Balanced Distribution Adaptation for Transfer Learning // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2017: 1129-1134. [本文引用:1]
[25] COURTY N, FLAMARY R, HABRARD A, et al. Joint Distribution Optimal Transportation for Domain Adaptation[C/OL]. [2019-01-25]. https://arxiv.org/pdf/1705.08848.pdf. [本文引用:1]
[26] SUN B C, FENG J S, SAENKO K. Return of Frustratingly Easy Domain Adaptation[C/OL]. [2019-01-25]. https://arxiv.org/pdf/1511.05547.pdf. [本文引用:1]
[27] BAKTASHMOTLAGH M, HARANDI M T, LOVELL B C, et al. Unsupervised Domain Adaptation by Domain Invariant Projection // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2013: 769-776. [本文引用:1]
[28] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:2]
[29] LONG M S, ZHU H, WANG J M, et al. Unsupervised Domain Adaptation with Residual Transfer Networks // LEE D D, SUGIYAMA M, LUXBURG U V, et al. , eds. Advances in Neural Information Processing Systems 29. Cambridge, USA: The MIT Press, 2016: 136-144. [本文引用:2]