作者简介:

林艺东,博士研究生,主要研究方向为粗糙集、概念格等.E-mail:yidong_lin@yeah.net.

张呈玲,硕士研究生,主要研究方向为概念格.E-mail:cl-zhang@163.com.
基于模糊形式背景,文中研究模糊-经典概念的矩阵表示及属性约简的矩阵方法.首先,从矩阵视角提出模糊-经典概念的外延和内涵的矩阵表示,进一步给出属性粒矩阵的概念.为了得到模糊-经典概念格的最小生成组,研究交不可约元的矩阵判定定理.再在保持交不可约元外延不变的约简框架下,通过矩阵刻画属性子集之间的相似性,给出属性内外重要性的度量,提出模糊-经典概念格属性约简的矩阵方法.最后,通过数值实验验证文中方法的有效性.
LI Jinjin, Ph.D., professor. His research interests include topology, rough set and concept lattices.
AboutAuthor:
LIN Yidong, Ph.D. candidate. His research interests include rough set and concept lattices.
ZHANG Chengling, master student. Her research interests include concept lattices.
A matrix representation of fuzzy-crisp formal concepts based on fuzzy formal contexts and a matrix approach of attribute reduction are studied. Firstly, the matrix representations of the extension and intension of fuzzy-crisp concept are developed from the matrix perspective, respectively. The definition and the computing method of attribute granular matrix are formulated subsequently. To find the minimal generation group of fuzzy-crisp concept lattice, matrix judgment theorem of meet-irreducible elements is discussed, and it is utilized to construct the attribute reduction framework preserving the extents of meet-irreducible elements. The significance measure of attribute is proposed by introducing the similarity degree between attribute subsets with aforementioned matrices. And then a heuristic matrix-method of attribute reduction is developed. Finally, numerical experiments verify the effectiveness of the proposed approach.
本文责任编委 张燕平
Recommended by Associate Editor ZHANG Yanping
Wille[1]提出形式概念分析理论(Formal Concept Analysis, FCA), 以形式背景为基础, 通过对象和属性特征之间的Galois连接形成概念, 进而由全体概念生成概念格.概念格刻画概念之间的泛化和特化关系, 具有典型的层次结构.此外, 概念的外延和内涵匹配的完美化在本质上体现数据集上对象和属性的关系.因此, FCA成为有效的数据挖掘和知识表示的工具, 已成功应用于数字图书馆、信息检索、软件工程、机器学习、数据挖掘与知识发现等领域[2, 3, 4, 5].
在经典概念格理论中, 概念格基于精确的形式背景, 通常是0-1二值表, 1表示对象与属性具有关系, 0表示无关系.然而, 在实际应用中, 对象与属性之间的二元关系往往是模糊、不确定的.概念的外延和内涵也不仅限于经典集合.为了克服经典概念格理论的局限性, 学者们将Zedeh的模糊集理论与FCA结合, 研究模糊概念格理论[6, 7, 8, 9, 10, 11, 12].在模糊形式背景中, Kraj
属性约简是概念格理论研究的核心问题.Ganter等[15]提出对象约简和属性约简的概念, 揭示概念格外延和内涵之间的内在关系.Zhang等[16]构造辨识矩阵, 给出属性协调集的概念及判定定理.此后, 国内的研究主要基于文献[16]的约简理论框架.在单边模糊概念格属性约简的研究中, Shao等[7]研究变精度概念格属性约简和对象约简问题.随后, Shao等[8]从粒计算角度研究经典-模糊概念格的属性约简问题, 构造辨识矩阵.针对模糊-经典概念格, Li等[9]提出保持交不可约元外延不变的属性约简概念, 给出不同属性特征的判定定理.Mao等[10]结合定向图理论, 提出模糊-经典概念格属性约简方法.Shi等[17]基于模糊-经典概念格, 提出对象粒约简方法.Li[18]在区间值模糊形式背景中研究多水平属性约简方法.
通常, (模糊)形式背景是一个二元关系表, 可看成一个二元关系矩阵.同时, 概念之间的运算本质上是关于集合的运算, 而集合的运算通常可以转化为矩阵运算.于是, 张清新[19]利用布尔矩阵提出概念格的属性约简方法.张呈玲等[20]进一步在不协调形式背景下提出矩阵型属性约简方法.然而, 基于矩阵研究概念格的相关工作仍然较少见.特别地, 利用矩阵研究模糊形式背景属性约简的成果更少.目前仅有Lin等[21, 22]在经典-模糊概念格的理论框架下进行一些相关工作.
本文受文献[19]启发, 在文献[9]的约简理论框架下, 研究模糊-经典概念格的矩阵表示及其属性约简的矩阵方法.首先提出概念外延与内涵的矩阵表示, 给出属性粒矩阵的概念.再基于矩阵框架给出交不可约元的矩阵判定定理.然后, 通过定义属性子集间的相似性刻画属性的重要度, 进而基于矩阵方法设计属性约简的启发式方法.最后, 通过数值实验评估本文方法效率.
本节主要回顾模糊概念格的基本概念[7, 8]和矩阵运算律.对任意非空集合U, P(U)表示U的幂集, F(U)表示U的模糊幂集.
设 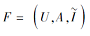
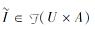
与经典的形式背景不同, 对于任意x∈ U和a∈ A,
f∶ F(U)→ P(A), g∶ P(A)→ F(U),
对任意 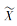
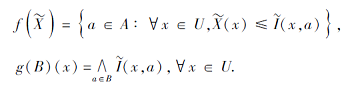
为了方便起见, 简记 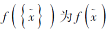
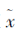
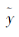
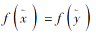
根据映射f和g的定义, 可得如下性质:
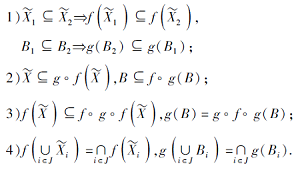
若 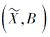
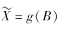
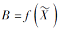
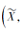
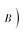
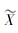
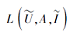


并且
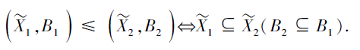
对于C⊆A, 记 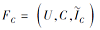
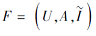
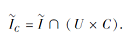
对任意 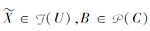
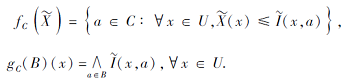
其中
fC∶ F(U)→ P(C), gC∶ P(C)→ F(U).
此外, 若
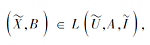
则有

由此可知, 任何一个模糊-经典概念均可表示为由其内涵诱导的属性概念的交.
首先引入特征向量.设论域U={x1, x2, …, xn}, X⊆U的特征向量记为
λ X=(λ X(x1), λ X(x2), …, λ X(xn)),
其中
λ X(xi)=
若
其次, 设A=
1)A≤ B⇔ aij≤ bij, i=1, 2, …, n, j=1, 2, …, m;
2)A∨ B=
3)A∧ B=
4)A· C=
5)A-B=
6)~A=
7)
其中:∨ 表示上确界(supremum), ∧ 表示下确界(infimum).
通常, 模糊形式背景 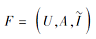
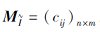
定理 1 设 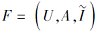
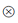
g(B)=~(λ B· (~
证明 记λ B=(t1, t2, …, tm)且
则
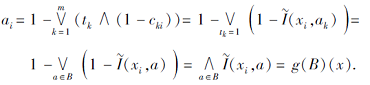
由定理1可知, 任何模糊-经典概念的外延均可通过特征向量与模糊关系矩阵之间的矩阵运算得到.然而, 概念的内涵无法通过类似的运算得到矩阵表示.为了解决这个问题, 定义如下矩阵运算律.
定义 1 设A=
A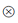
其中
cij= 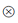
aik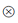
定理 2 设 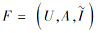
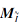

证明
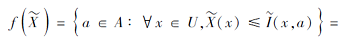

推论 1 设 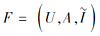
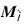
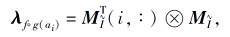
其中 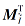
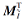
从粒计算角度上看, f°g(ai)反映属性ai的粒结构.另一方面, 模糊形式背景中所有属性的粒结构的特征向量可组成一个矩阵, 称为模糊形式背景的属性粒矩阵, 记为M.
定理 3 设 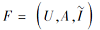
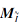
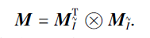
证明 由推论1可得.
显然, M的第i行M(i, ∶ )=为属性ai外延的内涵特征向量.
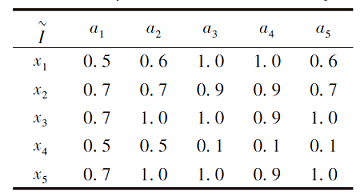
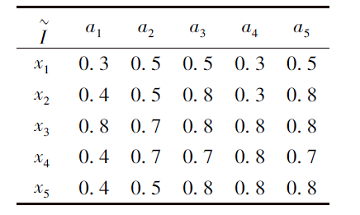
例1F为模糊形式背景, 如表1所示, 其中U={x1, x2, x3, x4, x5}为对象集, A={a1, a2, a3, a4, a5}为属性集.
| 表1 例1中模糊形式背景F Table 1 Fuzzy formal context F of example 1 |
由表1可知, F的模糊关系矩阵

若令
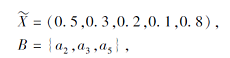
则根据定理1和定理2可得

由定理3可得F的属性粒矩阵:
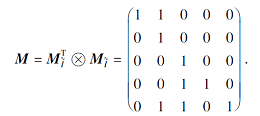
下面基于Li等[9]提出的属性约简框架探讨模糊形式背景属性约简的矩阵方法.∀ C⊆A, 设LC表示 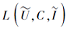
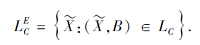
定义 2[9] 设 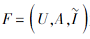
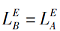
为了利用上述属性粒矩阵研究属性约简, 首先探讨交不可约元的矩阵判定定理.需要注意的是, 对于任意给定的模糊形式背景 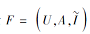
g(a)≠ g(b).
定理 4 设 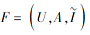
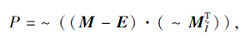
若
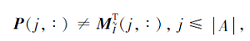
则(g(aj), f°g(aj))为一个交不可约元, 否则为交可约元.
证明 由M(j, ∶ )为f°g(aj)特征向量可知, P(j, ∶ )为g(a)的特征向量.若
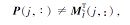
表明
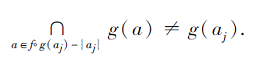
于是
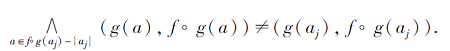
因此, (g(aj), f°g(aj))为交不可约元.
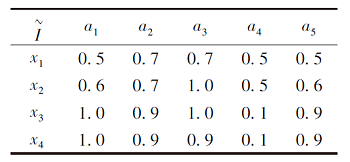
例 2F为模糊形式背景, 如表2所示.
| 表2 例2中模糊形式背景F Table 2 Fuzzy formal context F of example 2 |
由表2可得F的属性粒矩阵:
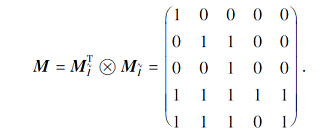
根据定理4可得
P=
观察可得
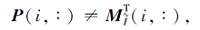
而
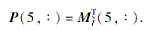
因此F的交不可约元为
(g(ai), f° g(ai)), i=1, 2, 3, 4.
对任意C⊆A, 记
推论 2 设 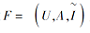
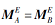
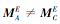
值得注意的是, 对于任意a∈ A, 属性概念(g(a), f°g(a))可能是交不可约元.反之, 任何交不可约元一定是属性概念.因此, ∀ B⊆A, 对∀
1)存在
2)对任意
另一方面,
定义3 设 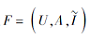
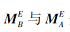
E(B|A)=
推论 3 设 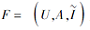
推论 4 设 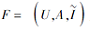
根据上述相似度定义, 给出属性重要度的2种度量.
定义 4 设 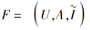
sig(B|a)=E(B|A)-E(B-{a}|A)
为属性a关于B的内重要度; 对任意a∈ A-B, 称
sig(a|B)=E(B∪ {a}|A)-E(B|A)
为属性a关于B的外重要度.
值得注意的是, sig(B|a)和sig(a|B)均通过相似度的变化刻画属性的重要性, 但前者反映当将属性a从B中去掉后相似度发生的变化, 而后者反映将a添加到B中所引起的相似度的变化.
定理 5 设 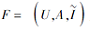
证明 由定义2及推论4可得.
因此
core(F)={a∈ A∶ sigD(A|a)> 0}.
定理 6 设 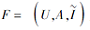
证明 由推论3及定理5可得.
定理 7 设 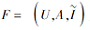
r(A)=A-{ai∶ i∈ T},
则F的约简与模糊形式背景 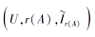
证明 不妨设
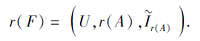
只需证明C={ai∶ i∈ T}为F中所有不必要属性组成的集合.由C的定义易知, 任意ai∈ C都是F中不必要属性.
因此, 根据上述分析, 可设计基于矩阵模糊形式背景属性约简的启发式算法(A Heuristic Algorithm for Attribute Reduction of Fuzzy Context Based on Attribute Granular Matrix, RFAG).
算法 1 RFAG
输入 模糊形式背景 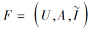
输出F的一个约简RED
step 1 预处理并计算属性粒矩阵MA;
step 2 计算
step 3 输出约简集RED, 算法结束.
容易验证计算属性粒矩阵的时间复杂度为O(|U||A|), 计算
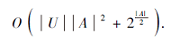
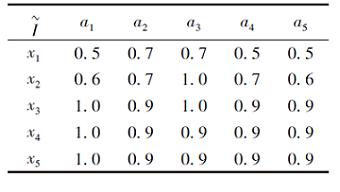
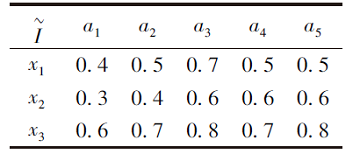
例3F为模糊形式背景, 如表3所示.
| 表3 例3中模糊决策形式背景F Table 3 Fuzzy formal context F of example 3 |
由表3可知F的交不可约元外延矩阵:
由算法1可得sig(A|a5)=0, {a1, a2, a3, a4}为F的约简.
本节基于属性粒矩阵讨论协调模糊决策形式背景的属性约简问题.设 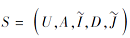
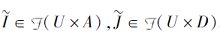
定义 5 称 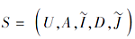
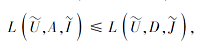
即对 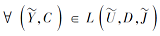
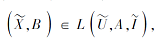
使 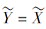
由此给出协调集、约简集及核心定义.
定义 6 设 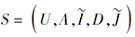
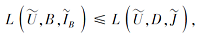
约简是保持S协调性不变的极小条件属性子集.值得注意的是, 对任意
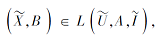
都有
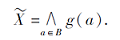
另一方面, 根据定义5, 可发现如下事实.
推论 5 若 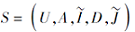
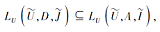
其中 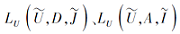
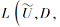
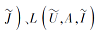
推论 6 若 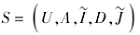
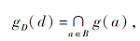
即对任意交不可约元的外延集gD(d)∈
g(
使
gD(d)=
进一步地, 若B⊆A为协调集, 则存在
g(
使
gD(d)=
由第3节可知, 对任意B⊆A,
例4 由例2可知,
N(
定理 8 设 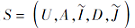
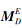
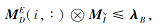
则存在
g(
使
gD(di)=
证明 由已知可得,
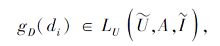
因此
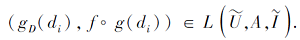
而
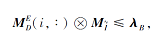
表明 
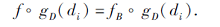
于是

因此存在
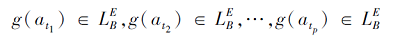
使
gD(di)=
推论 7 设 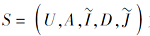
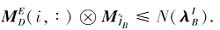
所以由上述定理和推论, 可得如下协调集的判定定理.
定理 9 设 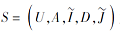
1)若 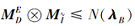
2) 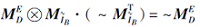
证明 只证明2).
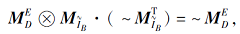
表明∀ gD(d)∈
使
gD(d)=
显然, 定理9中2)等价于
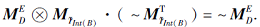
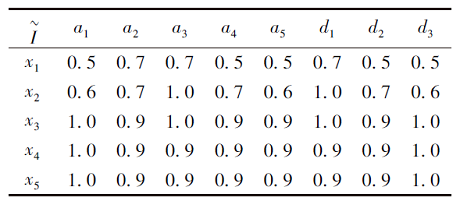
例5S为一个模糊决策形式背景, 如表4所示.
| 表4 例5中模糊决策形式背景S Table 4 Fuzzy decision formal context S of example 5 |
可得在S中条件属性A和决策属性D下的所有概念如表5和表6所示.
| 表5 模糊决策形式背景S中条件属性A对应的概念 Table 5 Concepts with respect to A of fuzzy decision formal context S |
| 表6 模糊决策形式背景S中决策属性D对应的概念 Table 6 Concepts with respect to D of fuzzy decision formal context S |
显然,
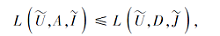
所以模糊决策形式背景S是协调的.另外, 决策属性粒矩阵
MD=
根据定理4可得, 决策属性D对应的交不可约元矩阵
令B={a1, a3, a4, a5}, 由定理8可得
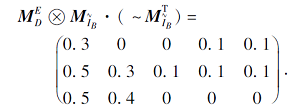
经检验
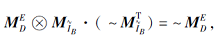
故B为协调集.
对任意B⊆A, 记 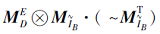
定义 7 设 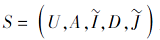
E(B|A, D)=
推论 8 设 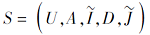
E(B|A, D)=1.
推论 9 设 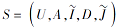
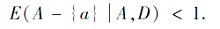
定义 8 设 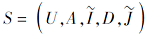
sigD(B|a)=E(B|A, D)-E(B-{a}|A, D)
为属性a关于B的D内重要度.对∀ a∈ A-B, 称
sigD(a|B)=E(B∪ {a}|A, D)-E(B|A, D)
为属性a关于B的D外重要度.
需要注意的是, sigD(B|a)和sigD(a|B)均通过相似度的变化刻画属性的重要性, 但前者刻画从B中除去属性a后相似度发生的变化, 而后者反映将a添加到B中引起的相似度的变化, 因此二者有本质区别.
定理 10 设 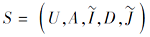
sigD(A|a)> 0,
a是不必要属性当且仅当
sigD(A|a)=0.
证明 由定义6及推论9可得.
因此
core(S)={a∈ A∶ sigD(A|a)> 0}.
定理 11 设 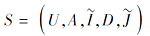
E(B|A, D)=1,
且对于∀ a∈ B, 都有
sigD(B|a)> 0.
证明 由推论8及定理10可得.
因此, 根据上述分析, 可以基于矩阵设计协调模糊决策形式背景属性约简的启发式算法.
算法 2 基于属性粒矩阵的协调模糊决策形式背景
属性约简算法
输入 协调模糊决策形式背景 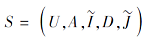
输出S的一个约简RED
step 1 计算属性粒矩阵MA、MD, 令RED← Ø ;
step 2 对∀ a∈ A, 计算
step 3 对∀ a∈ A, 若
RED← RED∪ {a};
step 4 若
step 5 对∀ a∈ A-RED, 计算sigD(a|RED);
step 6 选择属性a∈ A-RED, 满足
sigD(a|RED)=
RED← RED∪ {a};
step 7 对∀ a∈ RED, 若
sigD(RED|a)> 0,
执行step 9;
step 8 若存在a∈ RED, 使
sig(RED|a)=0,
则
RED← RED-{a},
执行step 7;
step 9 输出约简集RED, 算法结束.
计算
实验环境为Windows 10操作系统, Intel (R) Core (TM)i7-6700 CPU @3.41 GHz, 8 GB内存.软件为Matlab 9.3.实验所用数据为由表1、表3、表7、表8的模糊形式背景根据文献[23]方法组合生成以及从UCI获取的公开数据集.
| 表7 实验中第1个模糊形式背景F Table 7 Fuzzy formal context F used in experiment 1 |
| 表8 实验中第2个模糊形式背景F Table 8 Fuzzy formal context F used in experiment 2 |
设F1、F2为2个模糊形式背景.称[
如表9所示, F1、F2和F3分别为表1、表3和表7的模糊形式背景.F4为表7和表8转置的组合.F5先由F4、F1和F2合并, 再与F3组合.F1与2个F2组合及合并, 再与F3组合得到F6.F7为F1、F4的合并先与F1组合, 再与F2和F3的串联.F8为F1~F4的合并.F9先由F2与F3组合, 再与F4串联得到.F4先与F2、F3的组合合并, 再和F1串联得到F10.另外, F11为F3的100倍合并.F12为F4的79倍合并.F13为F5的66倍合并.F14为F6的51倍合并.F15为F7的70倍合并.F16为F8的68倍合并.F17为F9的80倍合并.F18为F10的40倍合并.F19为F4的63倍合并.F20是F10的72倍合并.
| 表9 组合生成的实验数据 Table 9 Experimental datasets generated by combination |
此外, 从UCI公开数据集中选取6个数据集, 检验本文方法在真实数据上的可行性和有效性, 数据见表10.每个数据集均归一化到[0, 1], 保留一位小数.
| 表10 UCI数据集上的实验数据 Table 10 Experimental datasets on UCI dataset |
对比方法为CAR(Computing All Attribute Redu-cts of L(
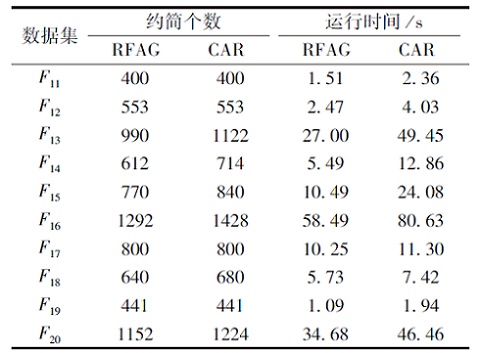
| 表11 两种算法在组合数据集上的实验结果 Table 11 Experimental results of 2 algorithms on composite datasets |
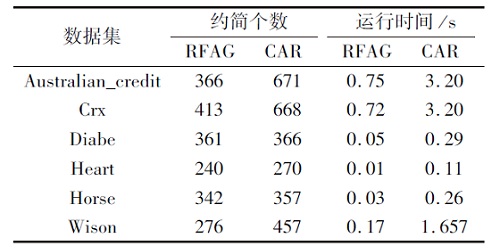
| 表12 两种算法在UCI数据集上的实验结果 Table 12 Experimental results of 2 algorithms on UCI datasets |
由表11可见, RFAG得到的约简个数大部分小于CAR, 这是因为若形式背景存在相同的列时, 由CAR得到的约简存在冗余属性.从运行时间上看, 在每个数据集上, RFAG的运行时间均少于CAR.
由表12可见, 在每个UCI数据集上, 由RFAG得到的约简个数和运行时间均小于CAR.综上可知, RFAG优于CAR.
本文主要研究模糊-经典概念格的矩阵表示及属性约简的矩阵方法.提出概念外延和内涵的矩阵表示方法, 给出属性粒矩阵的定义.利用属性粒矩阵, 给出交不可约元的矩阵判定定理.在保持交不可约元的外延矩阵不变的基础上, 提出属性子集之间的相似性度量, 进而提出属性内外重要度的定义.随后设计属性约简的启发式算法.最后通过数值实验验证本文方法的效率.本项工作不仅丰富模糊-经典概念格的理论基础, 也为形式概念分析的研究提供一种途径.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|