基于LU分解和交替最小二乘法的分布式奇异值分解推荐算法

引用本文

李琳, 王培培, 谷鹏, 解庆. 基于LU分解和交替最小二乘法的分布式奇异值分解推荐算法. 模式识别与人工智能, 2020,33(1): 32-40
LI Lin, WANG Peipei, GU Peng, XIE Qing. Distributed Singular Value Decomposition Recommendation Algorithm Based on LU Decomposition and Alternating Least Square. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2020,33(1): 32-40. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202001004
Permissions

《模式识别与人工智能》编辑部

基于LU分解和交替最小二乘法的分布式奇异值分解推荐算法

李琳¹, 王培培¹, 谷鹏¹, 解庆¹

1.武汉理工大学计算机科学与技术学院武汉 430070

通讯作者：

李琳,博士,教授,主要研究方向为信息检索、推荐系统、机器学习、数据挖掘.E-mail:cathylilin@whut.edu.cn.
作者简介：

王培培,博士研究生,主要研究方向为自然语言处理、推荐系统.E-mail:ppwang07@whut.edu.cn.

谷鹏,硕士,主要研究方向为数据挖掘、组推荐、信息检索.E-mail:380059082@qq.com.

解庆,博士,副教授,主要研究方向为流数据挖掘、模式分析、知识服务、推荐系统.E-mail: felixxq@whut.edu.cn.

收稿日期: 2019-08-20 接受日期: 2019-12-09

资助项目: 国家社会科学基金项目(No.15BGL048)、国家自然科学基金(No.61602353)、湖北省科技支撑计划项目(No.2015BAA072)、中央高校基本科研业务费专项资金(No.WUT:2017II39GX,2016-YS-068)资助

摘要

针对当前分布式潜在因子推荐算法存在时间复杂度较高、运行时间较长的问题,文中提出基于LU分解和交替最小二乘法(ALS)的分布式奇异值分解推荐算法,利用ALS利于分布式求解目标函数的特点,提出网格状分布式粒度分割策略,获取相互独立不相关的特征向量.在更新特征矩阵时,使用LU分解求逆矩阵,加快算法的运行速度.在KDD CUP 2012 Track1中的腾讯微博数据集上的实验表明,文中算法在确保一定推荐精度的前提下,大幅提升推荐速度和算法效率.

关键词: 分布式计算; 交替最小二乘法(ALS); 奇异值分解(SVD); 推荐算法

中图分类号:TP391

Distributed Singular Value Decomposition Recommendation Algorithm Based on LU Decomposition and Alternating Least Square

LI Lin¹, WANG Peipei¹, GU Peng¹, XIE Qing¹

1. School of Computer Science and Technology, Wuhan University of Technology, Wuhan 430070

Corresponding author:
LI Lin, Ph.D., professor. Her research interests include information retrieval, recommender system, machine learning and data mining.
AboutAuthor:

WANG Peipei, Ph.D. candidate. Her research interests include natural language processing and recommender system.

GU Peng, master. His research interests include data mining, group recommendation and information retrieval.

XIE Qing, Ph.D., associate professor. His research interests include stream mining, pa-ttern analysis, knowledge service and reco-mmender system.

Fund:National Social Science Foundation of China(No.15BGL048), National Natural Science Foundation of China(No.61602353), Science and Technology Support Project of Hubei Province(No.2015BAA072), Fundamental Research Funds for the Central Universities(No.WUT:2017II39GX,2016-YS-068)

Abstract

Aiming at the problems of high time complexity and long running time of the current distributed potential factor recommendation algorithm, a distributed singular value decomposition recommendation algorithm based on LU decomposition and alternating least square(ALS) is proposed. Based on the characteristics of ALS for distributed solution of objective function, a grid-like distributed granularity segmentation strategy is proposed to obtain independent and unrelated feature vectors. When the characteristic matrix is updated, LU decomposition is adopted to solve the inverse matrix to speed up the operation of the algorithm. The experiment on Tencent Weibo dataset in KDD CUP 2012 Track1 indicates that the recommendation speed and efficiency of the proposed algorithm is significantly improved on the premise of ensuring a certain recommendation accuracy.

Key words: Key Words Distributed Computing; Alternating Least Square(ALS); Singular Value Decomposition(SVD); Recommender System

文章图片

本文责任编委陈恩红

Recommended by Associate Editor CHEN Enhong

推荐系统通过收集用户和商品的相关信息进行分析和挖掘, 有效帮助用户过滤无关信息^[1], 提高信息的利用率, 帮助用户找到自己感兴趣的信息^[2].随着用户数量及其产生的数据量的指数级增长, 推荐准确度也在不断提高, 但是单机推荐系统的推荐模型日益复杂, 建模时间也随之延长.因此, 近年来分布式推荐算法成为研究热点, 以此加快建模的速度.协同过滤推荐算法是众多推荐算法中应用最广泛的一种^[3], 通常利用邻域推荐^[4]或矩阵分解方法^[5]实现.

为了克服目前单机计算在速度和存储空间上的不足, 通常将基于矩阵分解的推荐模型进行分布式优化处理.现有的矩阵分解方法有奇异值分解(Singular Value Decomposition, SVD)^[6], 隐语义模型(Latent Factor Model, LFM), SVD++等.在分布式数据处理方面以 MapReduce^[7]为主.

在使用分布式文件系统(Distributed File System, DFS)的基础上, 使用Map和Reduce两个步骤重新表达数据处理逻辑.Zhou等^[8]提出在MapReduce框架下, 采用加权正则化的交替最小二乘法(Alternating Least Square with Weighted-λ -Regularization, ALS-WR)实现SVD矩阵分解的分布式算法, 减少获取评分矩阵的时间, 加快推荐效率, 但是推荐效率还有待改进.

相比邻域推荐, 矩阵分解方法能更好地处理数据稀疏性问题.余永红等^[9]提出基于Ranking的泊松矩阵分解的兴趣点推荐方法, 针对社交网络用户中基于地域签到的行为特点, 采用泊松矩阵分解实现兴趣点推荐, 一同处理签到频率数据和传统推荐系统重点评分数据, 拟合用户在兴趣点对上的偏序关系, 在一定程度上解决数据的稀疏性问题.

考虑到大误差的异常值容易支配目标函数, Huang等^[10]提出鲁棒流形非负矩阵分解(Robust Manifold Nonne-gative Matrix Factorization, RMNMF), 使用L_{2, 1}范数, 在相同的聚类框架下集成非负矩阵分解(Non-negative Matrix Factorization, NMF)和谱聚类.通过基于增广拉格朗日法(Augmented Lagrange Method, ALM)解决正交约束的优化问题, 将原始的约束优化问题转化为多变量的约束问题, 每个子问题都有一个封闭的解决方案, 弱化异常值的影响.

近些年, 推荐系统的研究关注矩阵分解模型的分布式化处理, 主要目的是提高矩阵分解的效率.朱夏等^[11]提出基于候选邻居的协同过滤推荐算法(Candidate Neighbor-Based Distributed Collaborative Filtering Algorithm, CN-DCFA), 充分利用候选邻居信息, 设计云计算环境下基于协同过滤的个性化推荐机制, 通过制定分布式评分管理策略, 筛选对推荐结果影响较大的项目集, 构建基于分布式存储系统的2个阶段评分索引, 快速准确定位候选邻居.

基于MapReduce框架的矩阵分解分布式技术, Zhou等^[8]通过Hadoop平台和MapFail文件系统技术, 以MapReduce模式分布式处理特征矩阵的多正则化因子, 最终实现集群上的分布式大数据处理.余志琴^[12]提出基于交替方向乘子法(Alternating Direc-tion Methods of Multipliers, ADMM)框架的随机分布式交替方向乘子法(Distributed Stochastic ADMM, DS-ADMM), 有效提升推荐效率, 但是对于某些问题却不便进行分布式矩阵模型拆分.唐云^[13]应用Spark平台的分布式矩阵分解算法, 提出权衡矩阵运算并发度与数据读写开销的矩阵运算执行策略(Concurrent Replication Based Matrix Multiplication, C-RMM), 根据Spark的特性设计大规模分布式矩阵运算库Marlin, 大幅提高运算效率.

基于上述分析, 本文提出基于LU分解和交替最小二乘法的分布式奇异值分解推荐算法(LU De-composition and Alternating Least Squares with Weighted-λ -Regularization, LUALS-WR), 利用交替最小二乘法(Alternating Least Squares, ALS)利于分布式求解目标函数的特点, 提出网格状分布式粒度分割策略, 获取相互独立不相关的特征向量.在更新特征矩阵时, 使用LU分解求逆矩阵, 加快算法的运行速度.在KDD CUP 2012 Track1中的腾讯微博数据集上的实验表明, 文中算法在确保一定推荐精度的前提下, 大幅提升推荐速度和算法效率.

1 基于LU分解和交替最小二乘法的分布式奇异值分解推荐算法

1.1 奇异值分解算法

大规模的用户评分矩阵通常较稀疏, SVD^[14]有效改善协同过滤推荐算法在大规模稀疏数据集上的不足.SVD是协同过滤算法中一种基于矩阵分解的方法, 将原始矩阵分解成P与Q两个特征矩阵的乘积, 其中P为用户-特征(User-Feature)矩阵, Q为项目-特征(Item-Feature)矩阵.预测评分矩阵

$\hat{R}$ =P^TQ .

取隐因子个数为F, 下标i和u分别为项目和用户的编号, 矩阵所有个体向量表示如下:

${\tilde{r}}_{u, i}$ = $\overset{F}{\sum_{f = 1}}$ p_u_,_fq_i_,_f .

1.2 本文推荐算法步骤

本文研究分析ALS-WR^[5], 找出不足并提出改进算法, 即基于LU分解和ALS的分布式SVD推荐算法(LUALS-WR).

基于MapReduce的LUALS-WR提高分布式SVD分解的速度, 基本思想是采用LU分解作为矩阵分解方法, 使用ALS作为模型的优化函数求解方法, 使某个矩阵中的元保持不变, 通过循环迭代的方法更新另一个矩阵中的元.不断循环更新矩阵找到最优解.LUALS-WR具体步骤如下所示.

1)划分数据集.将评分记录按特定的比例随机分为训练集和测试集.

2)计算ItemRatings.将单位设定为itemID, 确定每个user对该item的评分, 并以< key, value> 的形式存储结果.

3)计算UserRatings.将单位设定为userID, 确定user对每个item的评分, 并以< key, value> 的形式存储结果.

4)计算AverageRatings.将单位设定为itemID, 计算每个item获得评分的平均值.

5)初始化用户特征向量.

6)分布式迭代更新P、Q矩阵.

具体算法的代码如下.

算法1 LUALS-WR

输入评分记录records, 正则化项参数λ ,

迭代次数N, 隐因子数量numFactors,

训练比例系数train_proportion

输出P, Q

(TrainSet, TestSet) =

Datadivide(recordstrain_proportion); /* 划分数据集* /

ItemRatings = item_rat(TrainSet); /* 计算ItemRatings* /

UserRatings = user_rat(TrainSet); /* 计算UserRatings* /

AvgRatings = avg_rat(TrainSet); /* 计算AverageRatings* /

Init p_i; /* 初始化用户特征向量* /

parallelALS Job do /* 分布式迭代更新矩阵* /

For (1 to N) do

Fixed P, Fun(P) do /* P不变, 计算Q* /

FUVector = vec_u(AvgRatings, UserRatings); /* FUVector 为用户特征向量* /

Matrix Mili = T(FUVector); /* 求用户特征向量的转置矩阵Mili * /

Matrix Rili = T(ratingVector); /* 求评分向量的转置矩阵Rili * /

Matrix A_i = T(Mili)* Mili; /* 求Mili的转置矩阵并与Mili做内积* /

Matrix V_i = Mili* Rili;

Matrix U_i= LUDecomposition(A_i); /* 根据LU分解计算A_i的逆矩阵U_i * /

Matrix Q = U_i* V_i;

Return Q;

Fixed Q Fun(Q) do; /* Q不变, 计算P* /

/* 类似上述步骤* /

Return P;

End For

End

算法的时间复杂度与本文设计的分布式方法有关, 如Parallel ALS Job所示.将矩阵A_i分解为L矩阵和U矩阵, A_i=L· U, L为n× k矩阵, U为k× n矩阵, 并将L设置为下三角矩阵, U设置为上三角矩阵.算法外层的循环次数为N, 所以时间复杂度由O(n³)变为O(Nn³).本文超参数主要通过Grid Search进行搜索, 确定合适参数.

所以LUALS-WR的核心问题主要在于利用分布式算法优化P、Q的迭代方法, 具体在于:1)分布式任务粒度的划分(算法中parallelALS Job), 2)任务节点上对特征向量的更新求解.

1.3 基于MapReduce的分布式粒度分割策略

LUALS-WR的一个核心问题是将任务精确到粒度的划分, 并在Hadoop集群上实现, 而任务划分与模型求解相辅相成.损失函数的确定是模型求解的首要步骤, 损失函数的优化主要是利用分布式迭代的方法, 从而最终确定模型参数, 即P、Q, 因此重点在于适合分布式的目标函数优化方法的选取以及设计合适的粒度分割策略.

1.3.1 适合分布式的目标函数优化方法

较常用的优化方法有随机梯度下降(Stochastic Gradient Descent, SGD)^[15]和ALS^[16].

SGD在初始化各项参数和项目评分值后, 不断循环迭代更新整个算法, 在循环过程中调整算法的学习率和隐变量参数, 同时损失函数的值逐步减少, 最后各项参数逐步靠近最优解, 与此同时学习步长也相应调整, 减少震荡.设r为预测评分, γ 为学习步长, λ 为正则化项参数, 求解过程如下:

e_ui=r_ui- ${\tilde{r}}_{ui}$ , bu_←bu₊γ (eu_i_-λ bu₎, bi← _bi+_γ(eui_-λbi)_,pu← p_u+γ ₍eui-_λ_pu), qi← qi₊γ (_eui-λ _qi).

SGD优化损失函数时优化速度较快, 主要是因为每步更新时的参数较多且参数同步更新.但是按照目前顺序执行的方法, 特别是在使用分布式处理大数据问题过程中, 当应用SGD对本文算法中的损失函数进行优化时会出现如下两个问题:数据相关性和数据存储限制.

数据相关性.如今数据量急剧增长, 数据共享为目前常态, 针对数据共享状态在分布式中的应用存在如下问题:要实现任务分布式处理, 其数据一定是分为不同部分分块存储, 而在应用Hadoop时, 将数据分为不同部分, 分别存储在HDFS的不同节点中.在进行分布式多进程SGD处理时, 一个项目和某位用户的隐变量会出现在同个子节点的评分集中, 会引起数据冲突而无法更新数据, 从而对优化结果产生一定影响.

数据存储限制.为了将大数据和分布式方法进行结合, 需要矩阵分解也采用分布式方法, 以此解决在大数据时代数据量巨大而造成的存储和计算的问题, 但SGD也存在一定的不足.例如, 将所选数据集中用户数量预设为m、系统规模大小预设为n、包含因子数量预设为f, 数据集中拟合的参数个数为f(m+n).为了体现SGD在大数据下的局限性, 假设m=2 000 000, n=200 000, f=100, 所有的参数采用8 B的形式存储, 由此可计算算法每循环一次参数所占的空间:

100(2000000+200000)× 8=1.76× 109⁼1.63 GB.

由上可看出, 面对大数据时, SGD极大地占用空间.

ALS是广泛用于优化目标函数的方法.相比SVD, 交叉学习作为ALS的关键要点, 每次更新过程中仅改变一个变量而其它变量需要保持不变, 以这种方式循环优化参数, 找到最优解.损失函数为

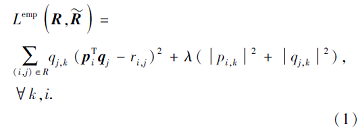
根据ALS的主要思想, 设计损失函数迭代更新方法.首先固定损失函数中用户特征矩阵P或项目特征矩阵Q, 对算法中未固定的矩阵进行矩阵求导, 并根据损失值更新矩阵, 然后更新损失函数值L^emp.式(1)中函数明显为一个非凸函数, 通过循环更新, 当损失值函数收敛后, 确定最后的P、Q, 形成最后的预测评分矩阵 $\tilde{R}$ .ALS伪代码如下.

算法2 ALS^[17]

输入训练数据集TrainSet, λ , N

输出P, Q

Init(P, Q); /* 初始化用户和项目的特征矩阵* /

For 1 to N do /* 迭代n次* /

fixed P; /* 用户特征矩阵P不变, 计算Q* /

Q = ALS_tr(λ , P);

fixed Q; /* 项目特征矩阵Q不变, 计算P* /

P= ALS_tr(λ , Q);

End

算法2的迭代次数为n, 因此ALS计算复杂度为O(n).

借鉴ALS的公式推导步骤, 为了便于求导计算过程, 本文将损失函数使用向量表示如下:

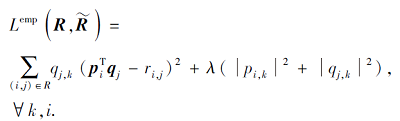
通过求导和消元法, 将上式中的向量和使用矩阵表示如下:

q_j= $(P_{Ij} {P^{T}}_{Ij} {+ λE)}^{- 1}$ P_IjR(I_j, j)^T, ∀ j,

其中, $Q_{I_{i}}$ 表示Q中i∈ I_i列的子矩阵, R(i, I_i)表示R第i行, i∈ I_i列的子矩阵.由此求出:

p_i= $(Q_{Ii} {Q^{T}}_{Ii} {+ λE)}^{- 1}$ Q_IiR(i, I_i)^T, ∀ i.

由上述求解过程可知, 当某个矩阵不变时, 从剩余矩阵中得到彼此没有关联独立的特征向量, 而分布式计算可较好地利用这些从矩阵中分解的独立向量实现分布式更新等, 因此本文在优化损失函数时采用ALS.

1.3.2 粒度分割策略

通过分析上述损失函数的优化方法可看出, ALS在分布式实现方面具有较好的适用性:先固定P, 求Q; 再固定Q, 求P.在求矩阵的过程中, 首先单独求得多个特征向量, 在求解完特征向量并整合后得到特征矩阵.待求特征矩阵的多个特征向量都是独立不相关的, 所以才能将分布式循环更新方法应用于被分解的多个任务中.理论上, P、Q是以行为单位分割, 用户特征矩阵划分为p份, 项目特征矩阵划分为q份, 每个节点的作用是计算p和q中的一份.但是, 根据 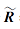=PQ^T可知, 项目特征矩阵Q首先进行转置, 然后代入式(1)中进行计算, 所以在评分矩阵R中区分不同项目时需要取矩阵中与之对应的列向量, 最后得到每个项目的特征向量.

为了实现对数据的分布式处理, 需要对P、Q进行分块, 具体的划分方式如下:设置参数m, n, 将user和item项目依据user%m=x, item%n=y划分为m、n组, 并依据得到的x、y对矩阵的分组进行标记, 最后将分组后的数据组合理分配到Hadoop集群的不同节点中.利用Hadoop良好的分布式计算优势, 确定其中某个矩阵, 循环更新优化另一个矩阵, 得到更新后矩阵的特征向量p_x或q_x.

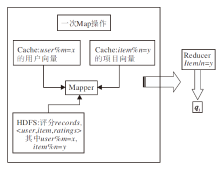
由上述分析可知, 在获取三元组评分记录records后, 首先找出数据块所在的位置, 依据每个数据块的参数x、y将分块后的数据合理分配到不同的节点上, 因为某个固定矩阵中的特征向量并无变化, 依据共享特征向量可以确定特征向量.例如, 当固定P, 更新Q时, 在Map阶段, 读入数据

records< user, item, ratings> ,

则此条记录属于数据块(user/m, item/n).进一步地, 在该节点上通过

q_j= ${(P}_{Ij} {P^{T}}_{Ij} {+ λE)}^{- 1}$ P_IjR(I_j, j)^T, ∀ j

计算此次迭代的特征向量, k=user/m, 即是本文给出的用户特征向量.由此可以得出, k 取值为[0, m-1], 要得到特征向量q_j, 只需融合特征向量值为k的特征向量.与之类似求出用户特征向量p_i, 详细求解q_j的Map/Reduce步骤如图1所示.

	Figure Option View Download New Window
	图1 特征向量求解Map/Reduce示意图Fig.1 Eigenvector computing using Map/Reduce

1.4 基于LU分解的特征向量更新

在求取大规模稀疏矩阵的广义逆矩阵的过程中, 可以采用SVD分解、QR分解和LU分解等方法.虽然SVD最稳定, 但相比后两者, 需要分解成3个矩阵, 在大规模数据集上大幅提高空间复杂度.而在QR分解中, 则

A^-1=(QR)^-1=R^-1Q^-1=R^-1Q^T,

其中, Q为正交酉矩阵, R为一个非奇异上三角矩阵, 在求解A逆矩阵的过程中, 需要先将A分解为Q和R, 再分别求Q和R的逆矩阵, 最后两逆矩阵求积, 时间复杂度为O(2n³).

在保证空间复杂度不变的情况下, LU分解和QR分解的效果不同, 在大多数情况下, LU分解的效果优于QR分解.

本文使用LU分解求取原始矩阵的逆矩阵, 用于更新特征向量, 提高执行速度.具体过程如下.

首先将矩阵LU分解为下三角矩阵L和上三角矩阵U, 即A=LU.然后分别求L和U的逆矩阵L^-¹和U^-¹.最后计算原始矩阵A的逆矩阵

A^-¹=(LU)^-1=U^-¹L^-¹ .

LU分解的具体过程如下.将原始矩阵拆解为下三角矩阵L和上三角矩阵U, 并保证L和U的对角线元都为1.循环逐步计算两个矩阵中的不同元.具体的迭代求解过程为

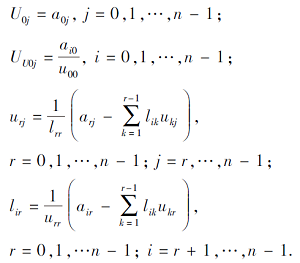
根据上述迭代公式可见, LU分解是先求上三角矩阵U, 后求下三角矩阵L.针对上三角矩阵和下三角矩阵的特性, 上三角矩阵依行进行逐步求解, 而下三角矩阵依列进行逐步求解.

逆矩阵L^-¹和U^-¹的求解过程如下.为了确定L的逆矩阵L^-¹的计算过程, 本文选取一个4阶矩阵, 并将L的逆使用l表示.通过Ll=E, 最后得到的求解公式如下:

l_ij= $l_{ij}^{- 1}$ , i=j; l1₀₌-l0₀₍l1_1L1₀₎…;

l₂₀=-l₀₀(l₂₁L₁₀+l₂₂L₂₀)…; l3₀₌-l0₀₍l3_1L1₀₊l3_2L2₀₊l3_3L3₀₎….

由上述公式可求L的逆矩阵l的各元:

l_ji= $\{\begin{array}{l} l_{ii}^{- 1}, & i = j \\ - l_{ii} (\overset{j}{\sum_{k = i + 1}} L_{jk} l_{ki}), & i < j \\ 0, & i > j \end{array}$

同理可以得到U的逆矩阵u的各元:

u_ji= $\{\begin{array}{l} u_{jj}^{- 1}, & i = j \\ - \frac{1}{u_{jj}} (\overset{i}{\sum_{k = j + 1}} U_{jk} u_{ki}), & i > j \\ 0, & i < j \end{array}$

计算L^-¹和U^-¹之后, 直接由

A^-¹=(LU) ^-¹=U^-¹L^-¹,

计算原始矩阵A的逆矩阵A^-1, 具体的迭代求解公式如下:

$A_{[i] [j]}^{- 1}$ = $\overset{n}{\sum_{k = j}}$ u_[_i_][_k_]l_[_k_][_j_].

观察L、U求逆的过程, 可发现L和U的求逆过程相似, 对于n维矩阵而言, 迭代次数为n-1.L和U的循环过程略有不同, 在迭代过程中, U的列迭代过程为倒序, 而剩余矩阵迭代计算过程都为正序.整个计算直至填满L^-¹和U^-¹时结束.

在n维矩阵的分解上, 若为LU分解, 时间复杂度为O(n³).若为QR分解, 时间复杂度为O(2n³).随着系数变化, 算法的运行时间明显不同, 特别是在数量级都是n³, 但矩阵维度n较大时.所以LU分解比QR分解的速度提升更快, 当n逐渐变大时, 速度提升效果愈加显著.

算法 3 特征向量更新算法^[17]

输入P, λ

输出Q

Fun Q = Update_Q(lAcols, P); /* P不变, 求Q* /

Lam_I = λ · eye(Nf);

Lq = zeros(Nf, Nlq); lQ = single(lQ);

For(q in 1/Nlq)

Users = find(lAcols(q)); /* Q中特征向量q* /

U_q = U(users); /* 共享用户特征向量* /

V_i = U_q· full(lAcols(users, q));

A_i = U_q· ${U_{q}}^{T}$ + locWtQ(q)· lam_I;

Y= A_i/V_i

lQ(q) = Y;

End For

Q = merge(darry(lQ));

End

算法3中求逆矩阵的时间复杂度同算法1, 此处假设项目特征矩阵Q为k维矩阵, 则更新项目算法的时间复杂度为O(n³k).

每个节点中的矩阵都进行LU分解并得到逆矩阵, 通过A_iV_i计算方式求得针对项目的特征向量q_i, 统一融合不同节点中全部的特征向量, 形成最终的特征矩阵Q.算法3以固定P、求Q为例, 给出更新步骤.

2 实验及结果分析

2.1 实验数据集

筛选KDD CUP 2012 Track1数据集, 选取其中的腾讯微博数据集, 从2011年11月11日至2011年12月11日这30天的微博记录中选取1 392 973位用户对4 710个项目的73 209 277个历史评分记录, 数据集规模约为3.8 G.数据集主要由社交关系和用户物品特征等信息组成, 对个人信息进行加密处理, 避免个人信息泄露, 将用户的个人用户名、用户购买商品名称都使用数字的形式替代信息.实验数据集如表1所示.

表1 实验数据统计^[17] Table 1 Experimental data statistics^[17]

数据集中包含大量用户对项目评分的数据, 包含各种不同的数据格式, 并使用三元组的形式表示.训练数据集中用户对项目的评分为1表示用户接受该项目, 值为-1表示用户不接受该项目.在测试数据集中评分略有不同, 测试数据集中出现评分为0的情况, 表示无法确定用户是否接受该项目.

数据集中训练数据和测试数据最大的区别在于, 训练数据中存在用户多次行为后留下的推荐信息, 而测试数据中是不存在这些重复的推荐信息.在另外的5个文件夹中包含用户和项目的特征信息, 如用户接受项目的等级、项目的不同类别、项目之间的关系、用户的选择偏好及所有的用户行为的历史记录.

实验利用Hadoop集群的优越性能, 在集群中设置5个节点, 每个节点都分配8 GB内存、20 GB硬盘空间、双核CPU.同时将5个节点分为1个主节点和4个子节点.

2.2 数据预处理

本文在确保推荐准确度的同时提升推荐效率, 对比不同分布式矩阵分解方法的速度及隐因子数量对推荐精度的影响, 形成最终的社交关系模型, 并充分考虑用户在社交关系中不同权重, 将行为权重加入原本的用户特征中.

用户信息特性复杂, 在文件user_action.txt中将用户针对项目的评论次数和用户转发项目信息次数及用户@信息融合, 对上述信息形成的最终权重进行归一化处理:

R^*= $\frac{r - \min}{\max - \min}$ .

归一化处理后的权重R^*的取值范围为0~1, R^*越大说明用户的积极性越高.处理文件user_action.txt中的用户数据, 找到活跃度高的用户, 按由大到小顺序排列, 形成队列.权重值大的用户为最活跃、积极性最高的用户, 数据集中筛选1 200 000位用户.在rec_log_train.txt中选出在队列中权重值高的用户, 获取这些用户对不同项目的评分, 并进行下一步实验.

后续部分的实验都针对筛选的数据, 数据规模为1.37 G.同时将训练集和测试集以8∶ 2的比例进行随机抽取, 利用训练集合测试集交叉验证的方式, 取30次结果的平均值作为最后的实验结果.

本次实验主要针对如下两点:1)隐因子模型, 选取不同数量的隐因子会在一定程度上影响实验结果的精度, 所以本文选取12组隐因子实验, 隐因子的数量为5, 10, 15, 20, 25, 30, 40, 50, 60, 100, 200, 300.2)推荐效率, 即完成整个推荐过程的耗时.将训练数据和测试数据相互辅助进行验证, 给出30次实验结果的平均值.

2.3 推荐模型评估指标

本文使用均方根误差(Root Mean Square Error, RMSE)作为评估指标:

RMSE= $\sqrt[]{\frac{1}{| Test_Set |} \sum_{\underset{i \in TestSet}{u \in TestSet}} (r_{u, i} - {\tilde{r}}_{u, i})^{2}}$ ,

其中, r_ui为真实打分, ${\tilde{r}}_{ui}$ 为预测打分, Test_Set为测试集.

由上式可看出, RMSE越小, 推荐模型的推荐越准确.采用交叉验证的方式, 取30次结果的平均值作为最终的实验结果, 最终的平均值表示为平均均方根误差(Average RMSE, AVE-RMSE)。

2.4 实验结果

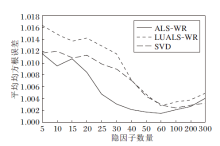
ALS-WR、LUALS-WR、SVD在不同隐因子数量下的平均均方根误差(AVE-RMSE)的变化情况如图2所示.由图可知, 在相同隐因子数量下, SVD的推荐准确度最高.随着隐因子的增加, ALS-WR和LUALS-WR推荐精度也逐步向SVD靠近.LUALS-WR的准确度略低于ALS-WR.LUALS-WR在隐因子较小时, 效果并不理想, 平均RMSE值普遍偏高, 但当隐因子数量大幅增加时, 拟合效果越优, 推荐精度曲线拟合的效果也越优.

	Figure Option View Download New Window
	图2 三种算法平均均方根误差对比Fig.2 AVE_RMSE comparison of 3 algorithms

针对矩阵稀疏度较大的情况, 本文算法具有更好的效果; 在矩阵维度较高的情况下, 本文算法同样取得良好效果.

3种算法在不同隐因子数量下平均运行时间如图3所示.这里仅展示前五组实验.

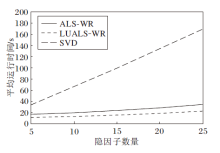	Figure Option View Download New Window
	图3 三种算法在不同隐因子数量下的运行时间对比Fig.3 Running time comparison of 3 algorithms with different number of hidden factors

图4记录实验中当12组隐因子数量分别为5到300时, 3种模型的平均运行时间比值.

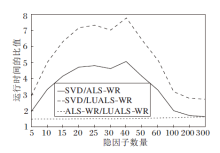	Figure Option View Download New Window
	图4 三种算法在不同隐因子数量下的运行时间比值Fig.4 Running time ratio of 3 algorithms with different number of hidden factors

结合图2~图4可得, 在大规模数据的前提下, 相比SVD, ALS-WR和LUALS-WR在确保推荐准确度的同时, 提升推荐效率.相比ALS-WR, LUALS-WR推荐速度更快, 获得1.5倍左右的速度提升.

3 结束语

用户是互联网所有互动的基石, 特别是互联网用户在各大社交网站上的频繁活动.大规模数据的产生导致推荐效率尤为重要, 直接影响用户体验.针对上述问题, 本文提出基于LU分解和ALS的分布式SVD推荐算法.采用分布式技术完成分解矩阵过程, 改进ALS-WR, 在每个子节点上求特征矩阵的过程中, 提出使用时间复杂度较低的LU分解求逆矩阵, 并设计粒度划分策略和求解算法.实验表明, 在确保一定推荐准确度的前提下, 推荐效率提高1.5倍左右.

今后将进一步改进本文工作, 原因如下.首先, 在建立矩阵分解模型时, 加入的用户间的社交行为和社会关系是在一定时间段内发生的, 并未考虑时间戳的影响.其次, 在采用分布式矩阵分解时, ALS虽然比SGD更方便使用, 但效率较低.SGD应用在分布式处理中也存在一些技术瓶颈, 虽然目前也有一些研究成果实现SGD的分布式计算^[18].最后, 由于Hadoop平台自身的性能限制, 可以考虑Spark平台以进一步提高速度.

参考文献

文献选项

[1]	ZHANG S, YAO L N, SUN A X. Deep Learning Based Recommender System: A Survey and New Perspectives[C/OL]. [2019-07-25]. https://arxiv.org/pdf/1707.07435v3.pdf. [本文引用:1]
[2]	HE X N, HE Z K, SONG J K, et al. NAIS: Neural Attentive Item Similarity Model for Recommendation. IEEE Transactions on Know-ledge and Data Engineering, 2018, 30(12): 2354-2366. [本文引用:1]
[3]	张志鹏, 张尧, 任永功. 基于覆盖约简的个性化协同过滤推荐方法. 模式识别与人工智能, 2019, 32(7): 607-614. (ZHANG Z P, ZHANG Y, REN Y G. Personalized Collaborative Filtering Recommendation Approach Based on Covering Reduction. Pattern Recognition and Artificial Intelligence, 2019, 32(7): 607-614. ) [本文引用:1]
[4]	周孟, 朱福喜. 基于邻居选取策略的人群定向算法. 计算机研究与发展, 2017, 54(7): 1465-1476. (ZHOU M, ZHU F X. An Audience Targeting Algorithm Based on Neighbor Choosing Strategy. Journal of Computer Research and Development, 2017, 54(7): 1465-1476. ) [本文引用:1]
[5]	黄璐, 林川杰, 何军, 等. 融合主题模型和协同过滤的多样化移动应用推荐. 软件学报, 2017, 28(3): 708-720. (HUANG L, LIN C J, HE J, et al. Diversified Mobile App Reco-mmendation Combining Topic Model and Collaborative Filtering. Journal of Software, 2017, 28(3): 708-720. ) [本文引用:2]
[6]	DE PESSEMIER T, VANHECKE K, DOOMS S, et al. Content-Ba-sed Recommendation Algorithms on the Hadoop MapReduce Framework // Proc of the 7th International Conference on Web Information Systems and Technologies. Lisbon, Portugal: SciTe Press, 2011: 237-240. [本文引用:1]
[7]	LÄMMEL R. Google's MapReduce Programming Model-Revisited. Science of Computer Programming, 2008, 70(1): 1-30. [本文引用:1]
[8]	ZHOU Y H, WILKINSON D, SCHREIBER R, et al. Large-Scale Parallel Collaborative Filtering for the Netflix Prize // Proc of the 4th International Conference on Algorithmic Aspects in Information and Management. Berlin, Germany: Springer, 2008: 337-348. [本文引用:2]
[9]	余永红, 高阳, 王皓. 基于Ranking的泊松矩阵分解兴趣点推荐算法. 计算机研究与发展, 2016, 53(8): 1651-1663. (YU Y H, GAO Y, WANG H. A Ranking Based Poisson Matrix Factorization Model for Point-of-Interest Recommendation. Journal of Computer Research and Development, 2016, 53(8): 1651-1663. ) [本文引用:1]
[10]	HUANG J, NIE F P, HUANG H, et al. Robust Manifold Nonne-gative Matrix Factorization. ACM Transactions on Knowledge Discovery from Data, 2014, 8(3). DOI: DOI:10.1145/2601434. [本文引用:1]
[11]	朱夏, 宋爱波, 东方, 等. 云计算环境下基于协同过滤的个性化推荐机制. 计算机研究与发展, 2014, 51(10): 2255-2269. (ZHU X, SONG A B, DONG F, et al. A Collaborative Filtering Recommendation Mechanism for Cloud Computing. Journal of Computer Research and Development, 2014, 51(10): 2255-2269. ) [本文引用:1]
[12]	余志琴. 基于ADMM的分布式矩阵分解. 硕士学位论文. 上海: 上海交通大学, 2015. (YU Z Q. Distributed Factorization via ADMM. Master Dissertation. Shanghai, China: Shanghai Jiaotong University, 2015. ) [本文引用:1]
[13]	唐云. 基于Spark的大规模分布式矩阵运算算法研究与实现. 硕士学位论文. 南京: 南京大学, 2016. (TANG Y. Research and Implementation on Large Scale Distributed Matrix Computation Algorithm with Spark. Master Dissertation. Nanjing, China: Nanjing University, 2016. ) [本文引用:1]
[14]	CUI L Z, HUANG W Y, YAN Q, et al. A Novel Context-aware Recommendation Algorithm with Two-Level SVD in Social Networks. Future Generation Computer Systems, 2018, 86: 1459-1470. [本文引用:1]
[15]	PETRONI F, QUERZONI L. GASGD: Stochastic Gradient Descent for Distributed Asynchronous Matrix Completion via Graph Partitioning // Proc of the 8th ACM Conference on Recommender Systems, New York, USA: ACM, 2014: 241-248. [本文引用:1]
[16]	GIAMPOURAS P V, RONTOGIANNIS A A, KOUTROUMBAS K D. Alternating Iteratively Reweighted Least Squares Minimization for Low-Rank Matrix Factorization. IEEE Transactions on Signal Processing, 2019, 67(2): 490-503. [本文引用:1]
[17]	谷鹏. 分布式群组推荐算法研究. 硕士学位论文. 武汉: 武汉理工大学, 2017. (GU P. Research on Distributed Group Recommendation Algorithm. Master Dissertation. Wuhan, China: Wuhan University of Technology, 2016. ) [本文引用:2]
[18]	GEMULLA R, NIJKAMP E, HAAS P J, et al. Large-Scale Matrix Factorization with Distributed Stochastic Gradient Descent // Proc of the 17th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2011: 69-77. [本文引用:1]

0.0

... 推荐系统通过收集用户和商品的相关信息进行分析和挖掘,有效帮助用户过滤无关信息^[1],提高信息的利用率,帮助用户找到自己感兴趣的信息^[2] ...

2018

0.0

... 推荐系统通过收集用户和商品的相关信息进行分析和挖掘,有效帮助用户过滤无关信息^[1],提高信息的利用率,帮助用户找到自己感兴趣的信息^[2] ...

2019

0.0

... 协同过滤推荐算法是众多推荐算法中应用最广泛的一种^[3],通常利用邻域推荐^[4]或矩阵分解方法^[5]实现 ...

2017

0.0

... 协同过滤推荐算法是众多推荐算法中应用最广泛的一种^[3],通常利用邻域推荐^[4]或矩阵分解方法^[5]实现 ...

2017

0.0

... 协同过滤推荐算法是众多推荐算法中应用最广泛的一种^[3],通常利用邻域推荐^[4]或矩阵分解方法^[5]实现 ...

... 2 本文推荐算法步骤本文研究分析ALS-WR^[5],找出不足并提出改进算法,即基于LU分解和ALS的分布式SVD推荐算法(LUALS-WR) ...

2011

0.0

... 现有的矩阵分解方法有奇异值分解(Singular Value Decomposition, SVD)^[6],隐语义模型(Latent Factor Model, LFM),SVD++等 ...

2008

0.0

... 在分布式数据处理方面以 MapReduce^[7]为主 ...

2008

0.0

... Zhou等^[8]提出在MapReduce框架下,采用加权正则化的交替最小二乘法(Alternating Least Square with Weighted-#cod#x003bb ...

... 基于MapReduce框架的矩阵分解分布式技术,Zhou等^[8]通过Hadoop平台和MapFail文件系统技术,以MapReduce模式分布式处理特征矩阵的多正则化因子,最终实现集群上的分布式大数据处理 ...

2016

0.0

余永红, 高阳, 王皓. 基于Ranking的泊松矩阵分解兴趣点推荐算法. 计算机研究与发展, 2016, 53(8): 1651-1663.

(YU Y

, GAO

, WANG

. A Ranking Based Poisson Matrix Factorization Model for Point-of-Interest Recommendation. Journal of Computer Research and Development, 2016, 53(8): 1651-1663. )

With the rapid growth of location-based social network (LBSN), point-of-interest (POI) recommendation has become an important means to meet users’ personalized demands and alleviate the information overload problem. However, traditional POI recommendation algorithms have the following problems: 1)most of existing POI recommendation algorithms simplify users’ check-in frequencies at a location, i.e., regardless how many times a user checks-in a location, they only use binary values to indicate whether a user has visited a POI; 2)matrix factorization based POI recommendation algorithms totally treat users’ check-in frequencies as ratings in traditional recommender systems and model users’ check-in behaviors using the Gaussian distribution; 3)traditional POI recommendation algorithms ignore that users’ check-in feedback is implicit and only positive examples are observed in POI recommendation. In this paper, we propose a ranking based Poisson matrix factorization model for POI recommendation. Specifically, we first utilize the Poisson distribution instead of the Gaussian distribution to model users’ check-in behaviors. Then, we use the Bayesian personalized ranking metric to optimize the loss objective function of Poisson matrix factorization and fit the partial order of POIs. Finally, we leverage a regularized term encoding geographical influence to constrain the process of Poisson matrix factorization. Experimental results on real-world datasets show that our proposed approach outperforms traditional POI recommendation algorithms.

(State Key Laboratory for Novel Software Technology (Nanjing University), Nanjing 210023) (Collaborative Innovation Center of Novel Software Technology and Industrialization, Nanjing 210023)

随着基于位置社交网络(location-based social network, LBSN)的发展，兴趣点推荐成为满足用户个性化需求、减轻信息过载问题的重要手段.然而，已有的兴趣点推荐算法存在如下的问题：1)多数已有的兴趣点推荐算法简化用户签到频率数据，仅使用二进制值来表示用户是否访问一个兴趣点；2)基于矩阵分解的兴趣点推荐算法把签到频率数据和传统推荐系统中的评分数据等同看待，使用高斯分布模型建模用户的签到行为；3)忽视用户签到数据的隐式反馈属性.为解决以上问题，提出一个基于Ranking的泊松矩阵分解兴趣点推荐算法.首先，根据LBSN中用户的签到行为特点，利用泊松分布模型替代高斯分布模型建模用户在兴趣点上签到行为；然后采用BPR(Bayesian personalized ranking)标准优化泊松矩阵分解的损失函数，拟合用户在兴趣点对上的偏序关系；最后，利用包含地域影响力的正则化因子约束泊松矩阵分解的过程.在真实数据集上的实验结果表明：基于Ranking的泊松矩阵分解兴趣点推荐算法的性能优于传统的兴趣点推荐算法.

... 余永红等^[9]提出基于Ranking的泊松矩阵分解的兴趣点推荐方法,针对社交网络用户中基于地域签到的行为特点,采用泊松矩阵分解实现兴趣点推荐,一同处理签到频率数据和传统推荐系统重点评分数据,拟合用户在兴趣点对上的偏序关系,在一定程度上解决数据的稀疏性问题 ...

2014

0.0

... 考虑到大误差的异常值容易支配目标函数,Huang等^[10]提出鲁棒流形非负矩阵分解(Robust Manifold Nonne-gative Matrix Factorization, RMNMF),使用L_2,1范数,在相同的聚类框架下集成非负矩阵分解(Non-negative Matrix Factorization, NMF)和谱聚类 ...

2014

0.0

朱夏, 宋爱波, 东方, 等. 云计算环境下基于协同过滤的个性化推荐机制. 计算机研究与发展, 2014, 51(10): 2255-2269.

(ZHU

, SONG A

, DONG

, et al. A Collaborative Filtering Recommendation Mechanism for Cloud Computing. Journal of Computer Research and Development, 2014, 51(10): 2255-2269. )

The advent of cloud computing has witnessed a sharp augmentation in the amount of application data, the result of which gives more and more prominence to a personalized recommendation technique, which has been used by different kinds of Web applications. However, traditional collaborative filtering (CF) techniques, when applied to cloud computing which features a huge scale and distributed processing architecture, are confronted with some problems, such as low recommendation accuracy, long recommendation time and high network traffic. Consequently, the performance of recommendation mechanisms degrades drastically. To address this issue, a CF recommendation mechanism for cloud computing (RAC) is proposed in this paper. RAC first employs a candidate neighbor, the definition of which will also be given, to screen those items which exert great influence on the recommendation results. Then a 2-stage rating indexing structure based on distributed storage system will be constructed to ensure the quick and precise location of CN by RAC. On this basis, a CN-based CF recommendation algorithm CN-DCFA which searches k nearest neighbors between candidate neighbors can be provided. Meanwhile, CN-DCFA utilizes similarity to predict the recommendation results top-N of active users. Experiments have showed that our recommendation mechanism RAC, enjoying great efficiency and exactitude, is worthy of recommendation.

(School of Computer Science and Engineering, Southeast University, Nanjing 211189)

随着云计算时代的到来，应用数据量剧增，个性化推荐技术日趋重要.然而由于云计算的超大规模以及分布式处理架构等特点，将传统的推荐技术直接应用到云计算环境时会面临推荐精度低、推荐时延长以及网络开销大等问题，导致推荐性能急剧下降.针对上述问题，提出一种云计算环境下基于协同过滤的个性化推荐机制RAC.该机制首先制定分布式评分管理策略，通过定义候选邻居(candidate neighbor, CN)的概念筛选对推荐结果影响较大的项目集，并构建基于分布式存储系统的2个阶段评分索引，保证推荐机制快速准确地定位候选邻居；在此基础上提出基于候选邻居的协同过滤推荐算法(candidate neighbor-based distribited collaborative filtering algorithm, CN-DCFA)，在候选邻居中搜索目标用户已评分项目的k近邻，预测目标用户的推荐集top-N.实验结果表明，在云计算环境下RAC拥有良好的推荐精度和推荐效率.

... 朱夏等^[11]提出基于候选邻居的协同过滤推荐算法(Candidate Neighbor-Based Distributed Collaborative Filtering Algorithm, CN-DCFA),充分利用候选邻居信息,设计云计算环境下基于协同过滤的个性化推荐机制,通过制定分布式评分管理策略,筛选对推荐结果影响较大的项目集,构建基于分布式存储系统的2个阶段评分索引,快速准确定位候选邻居 ...

2015

0.0

... 余志琴^[12]提出基于交替方向乘子法(Alternating Direc-tion Methods of Multipliers, ADMM)框架的随机分布式交替方向乘子法(Distributed Stochastic ADMM, DS-ADMM),有效提升推荐效率,但是对于某些问题却不便进行分布式矩阵模型拆分 ...

2016

0.0

... 唐云^[13]应用Spark平台的分布式矩阵分解算法,提出权衡矩阵运算并发度与数据读写开销的矩阵运算执行策略(Concurrent Replication Based Matrix Multiplication, C-RMM),根据Spark的特性设计大规模分布式矩阵运算库Marlin,大幅提高运算效率 ...

2018

0.0

... 1 奇异值分解算法大规模的用户评分矩阵通常较稀疏, SVD^[14]有效改善协同过滤推荐算法在大规模稀疏数据集上的不足 ...

2014

0.0

... 较常用的优化方法有随机梯度下降(Stochastic Gradient Descent, SGD)^[15]和ALS^[16] ...

2019

0.0

... 较常用的优化方法有随机梯度下降(Stochastic Gradient Descent, SGD)^[15]和ALS^[16] ...

2017

0.0

... 算法2 ALS^[17] ...

... 算法 3 特征向量更新算法^[17] ...

2011

0.0

... SGD应用在分布式处理中也存在一些技术瓶颈,虽然目前也有一些研究成果实现SGD的分布式计算^[18] ...