基于正交约束的分块不完整多视角聚类

引用本文

姜健伟, 殷俊. 基于正交约束的分块不完整多视角聚类. 模式识别与人工智能, 2020,33(1): 41-49
JIANG Jianwei, YIN Jun. Chunk-by-Chunk Incomplete Multi-view Clustering Based on Orthogonal Constraints. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2020,33(1): 41-49. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202001005
Permissions

《模式识别与人工智能》编辑部

基于正交约束的分块不完整多视角聚类

姜健伟¹, 殷俊¹

1.上海海事大学信息工程学院上海 201306

通讯作者：

殷俊,博士,副教授,主要研究方向为模式识别、机器学习.E-mail:junyin@shmtu.edu.cn.
作者简介：

姜健伟,硕士研究生,主要研究方向为模式识别、机器学习.E-mail:1467450564@qq.com.

收稿日期: 2019-10-14 接受日期: 2019-12-20

资助项目: 国家自然科学基金项目(No.61603243)、中国博士后科学基金项目(No.2017M611503)资助

摘要

在处理数据特征提取问题时,已有的基于非负矩阵分解的不完整多视角聚类算法对局部特征的提取不够准确.针对此问题,文中提出基于正交约束的分块不完整多视角聚类(CIMVCO).利用非负矩阵分解获得所有视角的潜在特征矩阵,通过加入正交约束得到更好的局部特征.对于各个视角的缺失样本,CIMVCO给予较小的权重以减小缺失数据的影响.为了解决大规模数据的聚类问题,CIMVCO逐块处理数据以减少内存需求和处理时间.在Reuters和Digit数据集上的实验验证CIMVCO的有效性.

关键词: 分块; 多视角聚类; 非负矩阵分解(NMF); 正交约束

中图分类号:TP181

Chunk-by-Chunk Incomplete Multi-view Clustering Based on Orthogonal Constraints

JIANG Jianwei¹, YIN Jun¹

1. College of Information Engineering, Shanghai Maritime University, Shanghai 201306

Corresponding author:
YIN Jun, Ph.D., associate professor. His research interests include pattern recognition and machine lear-ning.
AboutAuthor:

JIANG Jianwei, master student. Her research interests include pattern recognition and machine learning.

Fund:Supported by National Natural Science Foundation of China(No.61603243), China Postdoctoral Science Foundation(No.2017M611503)

Abstract

Existing incomplete multi-view clustering algorithms based on nonnegative matrix factorization(NMF) cannot extract local features accuratly. To solve this problem, an algorithm of chunk-by-chunk incomplete multi-view clustering based on orthogonal constraints (CIMVCO) is proposed. A potential feature matrix of all views is obtained by nonnegative matrix factorization, and orthogonal constraints are added to obtain better local features. For missing samples of each view, smaller weights are given to reduce the impact of missing data. To solve the problem of large scale data clustering, data are processed block-by-block to reduce the memory demand and processing time. Experimental results on Reuters and Digit datasets demonstrate the effectiveness of CIMVCO.

Key words: Key Words Chunk-by-Chunk; Multi-view Clustering; Nonnegative Matrix Factorization(NMF); Orthogonal Constraints

文章图片

本文责任编委于剑

Recommended by Associate Editor YU Jian

现实世界的数据通常由多个视角组成或采用不同方式表示.多视角聚类利用数据样本的多个视角特征表示将它们划分到正确的簇中, 即给每个样本都贴上合适的标签.大量的多视角聚类算法^{[1, 2, 3, 4, 5, 6]}利用数据的多个视角信息进行聚类, 多个视角提供语义相同的数据及其一致或互补表示, 使用数据多个视角的特征进行聚类可以比仅使用单视角方法能获得更好的性能.联合非负矩阵分解多视角聚类算法(Multi-view Clustering via Joint Nonnegative Matrix Factori-zation, MultiNMF)^[4]在聚类时, 不同视角下的同个样本多会分配到同个簇中.MultiNMF在非负矩阵分解(Nonnegative Matrix Factorization, NMF)过程中引入一个约束, 并找到多个视角兼容的聚类结果, 减少矩阵维数, 降低聚类复杂度.

已有的多视角聚类算法^{[5, 6]}大多假设每个样本的各视角都完整, 而现实世界的数据常有缺失, 想要获取完整的数据集需耗费的成本极高, 因此需要处理视角不完整数据的多视角聚类方法.目前解决不完整视角聚类的方法^{[7, 8, 9, 10, 11, 12]}在许多数据集上聚类效果较优.部分多视角聚类算法(Partial Multi-view Clu-stering, PVC)^[9]基于NMF建立一个多视角的潜在子空间, 实现簇内相似度较高、簇间相似度较低的聚类效果.L_{2, 1}正则化加权非负矩阵分解不完整多视角聚类算法(Multiple Incomplete Views Clustering via Weighted NMF with L_{2, 1} Regularization, MIC)^[10]基于加权NM-F, 学习所有视角的潜在特征矩阵, 并生成一致矩阵, 以此最小化视角间的差异.

由于互联网的高速发展和普及, 计算机运用领域扩大, 现实世界的数据通常规模较大.一般内存无法容纳庞大的数据, 只有较少的多视角聚类算法^{[13, 14, 15, 16, 17, 18]}可以处理大规模数据集, 在较小的内存占用下对大规模数据集进行高效聚类.加权多视角在线竞争聚类算法(Weighted Multi-view Online Compe-titive Clustering, WMLCC)^[13]同时采用变权策略和在线竞争学习, 将多视角聚类问题转化为一个优化问题进行求解.在线不完整多视角聚类算法(Online Multi-view Clustering with Incomplete Views, OMVC)^[14]将多视角聚类问题看作联合非负矩阵问题和大规模多视角数据的处理, 利用快速投影梯度下降减少计算时间.在线无监督多视角特征选择算法(Online Unsupervised Multi-view Feature Selection, OMVFS)^[15]通过稀疏学习的NMF将无监督特征选择嵌入一个聚类算法中, 利用图正则化保存局部结构信息和选择辨别特征, 通过缓冲技术减少计算量和存储代价.

近些年, NMF广泛应用于聚类并取得良好效果^{[19, 20, 21, 22, 23]}.利用NMF, 本文提出基于正交约束的分块不完整多视角聚类算法(Chunk-by-Chunk Incomplete Multi-view Clustering Based on Orthogonal Constraints, CIMVCO).CIMVCO加入正交约束以得到更好的局部特征, 得到的解具有唯一性.基于正交约束的NMF应用到聚类任务时具有更严密的可解释性, 产生的解更适合聚类.CIMVCO使用动态权重矩阵对缺失数据进行赋值, 降低缺失数据对聚类结果的影响.利用牛顿下降法^{[24, 25]}对目标函数进行迭代优化, 使算法具有较快的收敛速度.通过对数据集进行分块, 减少内存占用, 提高内存利用率, 降低算法复杂度.

1 相关知识

1.1 联合非负矩阵分解聚类算法

给定一个多视角数据集

{X⁽^v⁾, v=1, 2, …, n_v},

其中, X⁽^v⁾∈ $R^{D_{v} \times N}$ 为第v个视角的数据, n_v为总视角数, D_v为第v个视角的特征维度.对于不同视角具有相同数量的样本, 允许每个样本拥有不同的特征尺寸.MultiNMF旨在寻找每个视角的潜在特征矩阵和所有视角集成信息的一致矩阵.

给定一个衡量系数矩阵C⁽^v⁾和一致矩阵C^*, 定义差异度的损失函数^[4]:

D(C⁽^v⁾, C^*)= ${(C^{(v)} - C^{*})}_{F}^{2}$ ,

其中 ${(\cdot)}_{F}$ 为Frobenius范数.把损失函数融入每个视角的非负矩阵分解框架中, 得到如下对于U⁽^v⁾、C⁽^v⁾、C^*, 1≤ v≤ n_v的联合最小化问题:

$\min_{U^{(v)}, C^{(v)}, C^{*}}$ O= $\overset{n_{v}}{\sum_{v = 1}} {(X^{(v)} - U^{(v)} {C^{(v)}}^{T})}_{F}^{2}$ + $\overset{n_{v}}{\sum_{v = 1}}$ v ${((C^{(v)} - C^{*}))}_{F}^{2}$ , s.t. ∀ 1≤ k≤ K, = ${(U_{., k}^{(v)})}_{1}$ , U(v)^≥⁰^, C(v)^≥⁰^, C* ≥ 0^.(1)

其中, α _v为平衡第v个视角的重构误差的权衡参数, U⁽^v⁾∈ $R_{+}^{D_{v} \times K}$ 为基矩阵, C⁽^v⁾∈ $R_{+}^{N \times K}$ 为第v个视角的潜在特征矩阵, C^*∈ $R_{+}^{N \times K}$ 为所有视角的一致潜在特征矩阵, K为期望的约减维度.

1.2 在线不完整多视角聚类算法

给定一个不完整多视角数据集

{X⁽^v⁾, v=1, 2, …, n_v},

为了填补缺失数据, 引入一个对角权重矩阵W⁽^v⁾∈ R^N^×^N, 它的对角元素 $w_{i, i}^{(v)}$ 表示第v个视角的第i个样本的权重, 完整样本给予权重1, 缺失样本给予较低权重.使用l₁正则化强制潜在特征矩阵稀疏, 减少噪声和异常值.得到目标函数:

$\min_{{U^{(v)}}, {C^{(v)}}, C^{*}}$ O= $\overset{n_{v}}{\sum_{v = 1}} {((X^{(v)} - U^{(v)} {C^{(v)}}^{T}) W^{(v)})}_{F}^{2}$ + $\overset{n_{v}}{\sum_{v = 1}}$ α _v ${(W^{(v)} (C^{(v)} - C^{*}))}_{F}^{2}$ + $\overset{n_{v}}{\sum_{v = 1}}$ β _v ${(C^{(v)})}_{1}$ .

由于现实世界数据矩阵过大, 因此OMVC使用一个在线流方法逐块处理数据, 降低计算和存储复杂度.上式改写为

$\min_{{U^{(v)}}, {C^{(v)}}, C^{*}}$ O= $\overset{n_{v}}{\sum_{v = 1}} \overset{「 \frac{N}{s} ⌉}{\sum_{t = 1}} {(W_{t}^{(v)} (X_{t}^{(v)} - U^{(v)} {C_{t}^{(v)}}^{T}))}_{F}^{2}$ +

$\overset{n_{v}}{\sum_{v = 1}} \overset{「 \frac{N}{s} ⌉}{\sum_{t = 1}}$ α _v ${(W_{t}^{(v)} (C_{t}^{(v)} - C_{t}^{*}))}_{F}^{2}$ + $\overset{n_{v}}{\sum_{v = 1}} \overset{「 \frac{N}{s} ⌉}{\sum_{t = 1}}$ β _v ${(C_{t}^{(v)})}_{1}$ ,

其中, s为块大小, t为输入数据块个数, $X_{t}^{(v)}$ 为第v个视角的第t个数据块.

为了确保矩阵分解结果的唯一性和正确性, 在更新过程中采用归一化策略.使用的更新迭代规则为牛顿下降法.牛顿下降法具有二阶收敛且收敛速度较快的优点, 但牛顿下降法是一种迭代算法, 每步都需要求解目标函数的海森矩阵的逆矩阵, 计算较复杂.对式(1)迭代更新U⁽^v⁾、C⁽^v⁾、C^*, 对U⁽^v⁾应用更新规则进行更新, 得

U⁽^v⁾← P[U⁽^v⁾- $δ_{k} H^{- 1}$ [O(U⁽^v⁾, C⁽^v⁾, C^*)]· $\nabla_{U^{(v)}}$ (U(^v⁾^,C(^v⁾^,C* ⁾] ,

其中, k为迭代次数, H^-1[O(U, C)]为海森矩阵的逆, $\nabla_{U}$ O(U, C)为目标函数关于U的一阶导, δ _k为步长, 使用Armijo规则进行选择.P定义为

P[u_i_,_j]= $\{\begin{array}{l} u_{i, j}, & u_{i, j} \geq 0 \\ 0, & 其它 \end{array}$

同样把牛顿下降法应用到其它公式的更新中.

2 基于正交约束的分块不完整多视角聚类

2.1 原理及目标

引入一个指示符矩阵^[6]M∈ $R^{N \times n_{v}}$ , 其中

m_i_,_j= $\{\begin{array}{l} 1, & 存在第 j 个视角的第 i 个样本 \\ 0, & 其它 \end{array}$

每列都表示一个视角下的所有样本,

$\overset{N}{\sum_{i = 1}}$ m_i_,_j< N, j=1, 2, …, n_v.

给定一个不完整多视角数据集

{X⁽^v⁾, v=1, 2, …, n_v},

由于每个视角都存在缺失, 不能直接优化目标函数, 为此每读入一个新的数据块, 都使用已有的特征取平均值填补缺失的数据:

$X_{t}^{(v)}$ = $\frac{\overset{t}{\sum_{i = 1}} m_{i, v} X_{i}^{(v)}}{\overset{t}{\sum_{i = 1}} m_{i, v}}$ .(2)

较大的缺失率对聚类结果会造成较大影响.为了减小缺失数据对实验的影响, 引入对角权重矩阵W⁽^v⁾∈ R^N^×^N, 对角元素 $w_{i, i}^{(v)}$ 设置如下:

$w_{t, t}^{(v)}$ = $\{\begin{array}{l} 1, & 存在视角 v 的第 t 个样本 \\ \frac{1}{t} \overset{t}{\sum_{i = 1}} m_{i, v}, & 其它 \end{array}$ (3)

为了得到更好的局部特征和唯一最优解, 对U给定一个正交约束U^TU=I, 其中U∈ {0, 1}^N^×^K, U中各行元素和为1.由于U满足正交性, 故U形成子空间上的一组基, 可促进几何解释和信息重构.将其看作是原本的聚类指示符约束的松弛型, 该正交约束可以更好地对C⁽^v⁾进行特征选择.下面给出基于正交约束的视角缺失下分块多视角聚类算法的目标函数:

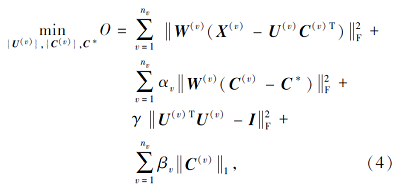
其中, γ > 0为控制正交状态的参数, ${(\cdot)}_{1}$ 为lasso范数, β _v为视角v的重构稀疏性和准确率的权参, U⁽^v⁾∈ $R_{+}^{D_{v} \times K}$ 为基矩阵, C⁽^v⁾∈ $R_{+}^{N \times K}$ 为第v个视角的潜在特征矩阵, C^*∈ $R_{+}^{N \times K}$ 为所有视角的一致潜在特征矩阵.

lasso正则化主要用于稀疏选择, 稀疏正则化可以实现特征的自动选择, 通过学习去除这些没有信息的特征, 即把这些特征对应的权重置为0.此外, 稀疏后的模型更易解释, 如果最后学习到的C⁽^v⁾只有很少的非零元素, 可以认为这些非零元素对应的特征提供的信息是巨大的、决策性的.

为了解决现实应用中数据量较大、内存难以装载的问题, 使用一种小存储和低计算复杂度的分块方法, 按一定大小分块大规模数据, 数据块逐块放入内存.下面使用

{ $X_{t}^{(v)}$ ∈ $R^{s \times D_{v}}$ , v=1, 2, …, n_v}

表示第t次输入的数据块, $X_{t}^{(v)}$ 为第v个视角的第t个数据块.式(4)可改为

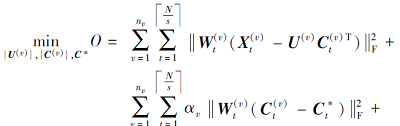
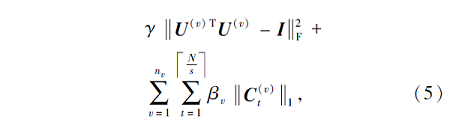
其中, $C_{t}^{(v)}$ ∈ R^s^×^K为第t个数据块的潜在特征矩阵, $W_{t}^{(v)}$ ∈ R^s^×^s为第t个数据块的对角权重矩阵.

2.2 目标优化

由式(5)可以看出, 有3个未知量{U⁽^v⁾}、{ $C_{t}^{(v)}$ }和 $C_{t}^{*}$ , 因此采取交替更新迭代的方法进行求解.

1)固定{ $C_{t}^{(v)}$ }和 $C_{t}^{*}$ , 优化{U⁽^v⁾}.只需优化如下目标函数:

$\min_{{U^{(v)}}, {C^{(v)}}, C^{*}} {O^{(t)}}^{(U^{(v)})}$ = $\overset{t}{\sum_{i = 1}} {((X_{i}^{(v)} - U^{(v)} {C_{i}^{(v)}}^{T}) W_{i}^{(v)})}_{F}^{2}$ +γ ${(U^{(v)} {U^{(v)}}^{T} - I)}_{F}^{2}$ .

目标函数O⁽^t⁾(U⁽^v⁾)关于U⁽^v⁾的一阶偏导为

目标函数O⁽^t⁾(U⁽^v⁾)关于U⁽^v⁾的海森矩阵为

H[U⁽^v⁾]=2 ${W_{i}^{(v)}}^{T} C_{i}^{(v)} {C_{i}^{(v)}}^{T} W_{i}^{(v)}$ + γ (3 ${U^{(v)}}^{T}$ (^v⁾^-I).

使用牛顿下降法, 得到第t次的U⁽^v⁾的更新公式:

$U_{k + 1}^{(v)}$ ← P[ $U_{k}^{(v)}$ -δ _kH^-1[ $U_{k}^{(v)}$ ]Ñ O⁽^t⁾( $U_{k}^{(v)}$ )], (6)

其中k为迭代次数.

2)固定{U⁽^v⁾}和 $C_{t}^{*}$ , 优化{ $C_{t}^{(v)}$ }.只需要优化如下目标函数:

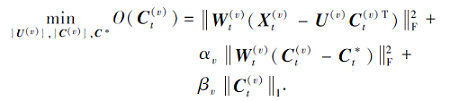
目标函数O( $C_{t}^{(v)}$ )关于 $c_{ti}^{(v)}$ 的一阶偏导为

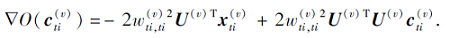
目标函数O( $C_{t}^{(v)}$ )关于 $c_{ti}^{(v)}$ 的海森矩阵为

H[ $c_{ti}^{(v)}$ ]=2 ${w_{ti, ti}^{(v)}}^{2}$ ( ${U^{(v)}}^{T}$ U⁽^v⁾+α _vI_K),

使用牛顿下降法, 得到更新公式:

$c_{ti}^{(v)}$ ← P[ $c_{ti}^{(v)}$ -δ _kH^-1[ $c_{ti}^{(v)}$ ]Ñ ( $c_{ti}^{(v)}$ )], (7)

其中, $c_{ti}^{(v)}$ 为 $C_{t}^{(v)}$ 的第i列, $w_{ti, ti}^{(v)}$ 为 $W_{t}^{(v)}$ 的第i个对角元素.

3)固定{U⁽^v⁾}和{ $C_{t}^{(v)}$ }, 优化 $C_{t}^{*}$ .只需优化如下目标函数:

$\min_{{U^{(v)}}, {C^{(v)}}, C^{*}}$ O( $C_{t}^{*}$ )= $\overset{n_{v}}{\sum_{v = 1}}$ α _v ${(W_{t}^{(v)} (C_{t}^{(v)} - C_{t}^{*}))}_{F}^{2}$ , s.t. α v_>0.

目标函数O( $C_{t}^{*}$ )关于 $C_{t}^{*}$ 求取一阶偏导, 并令其为0, 求得

$c_{t}^{*}$ = $(\overset{n_{v}}{\sum_{v = 1}} α_{v} {W_{i}^{(v)}}^{T} W_{i}^{(v)})^{- 1} \overset{n_{v}}{\sum_{v = 1}}$ α _v ${W_{i}^{(v)}}^{T} W_{i}^{(v)} C_{t}^{(v)}$ .(8)

具体CIMVCO步骤如下.

算法1 CIMVCO

输入多视角数据矩阵{X⁽^v⁾}, 簇数K, 块大小s,

参数{α _v}, {β _v}, γ .

输出基矩阵U⁽^v⁾, 特征选择矩阵C⁽^v⁾,

一致矩阵C^*

step 1 初始化数据矩阵X⁽^v⁾、基矩阵U⁽^v⁾和权重矩阵W⁽^v⁾为空矩阵.

step 2 随机初始化特征选择矩阵C⁽^v⁾.

step 3 对t=1∶ 「 $\frac{N}{s}$ ⌉, 循环step 4~step 10.

step 4 根据式(2)填补缺失数据, 根据式(3)设置权重.

step 5 循环step 6~step 9, 直到收敛.

step 6 对v=1∶ n_v循环step 7、step 8.

step 7 根据式(6)更新U⁽^v⁾.

step 8 根据式(7)更新C⁽^v⁾.

step 9 根据式(8)计算C^*.

step 10 对特征选择矩阵C⁽^v⁾进行K-means聚类.

3 实验及结果分析

3.1 实验数据集

在Digit、Reuters数据集上进行实验, 每个数据集设置不同的样本缺失率和不同的块大小.

Digit数据集包含2 000个手写数字(0~9)样本, 每类200个样本, 共10类.数据集共有6个特征:mfeat-fou、mfeat-fac、mfeat-kar、mfeat-pix、mfeat-zer、mfeat-mor.mfeat-fou表示76维字符形状的傅里叶系数.mfeat-fac表示216维资料相关系数.mfeat-pix表示2× 3窗口下的240个像素平均值.mfeat-zer表示47个Zernike矩.mfeat-mor表示6种形态特征.mfeat-kar表示64维Karhunen-Love系数.实验中使用前5个视角的数据.

Reuters数据集为多视图文本分类测试集, 包含使用5种不同语言(英语、法语、德语、西班牙语和意大利语)编写的111 740个文档特征, 共享同一组标签.在EN、FR、GR、IT、SP这5个文件夹下都有使用该语言编写或翻译的文件索引.例如, EN中包括Index_EN-EN为原本的英文文档; Index_FR-EN为法语文档转换成的英文文档; Index_GR-EN为德语文档转换成的英文文档; Index_IT-EN为意大利语文档转换成的英文文档; Index_SP-EN为西班牙语文档转换成的英文文档.实验中使用上述前5个视角的数据.

3.2 参数设置

CIMVCO的目标函数中共有3个参数:α 、β 和γ , 在Digit数据集上分析这3个参数, 选取一个在绝大部分情况下可获得好的结果参数值.标准化互信息(Normalized Mutual Information, NMI)用于度量2个聚类结果的相近程度, NMI的值域是[0, 1], 值越高表示划分越准.X和Y分别表示训练得到的结果和原始标签, p(x, y)为x和y的联合概率分布:

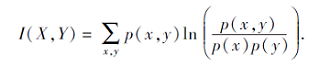
准确率(Accuracy, AC)计算聚类正确的百分比, AC的值域为[0, 1], 值越大表明聚类效果越好:

AC= $\frac{1}{N} \overset{N}{\sum_{i = 1}}$ δ (b_i, r_i),

其中, K为簇数, b_i和r_i分别表示数据x_i对应的获得的标签和真实标签, N为数据总个数,

δ (x, y)= $\{\begin{array}{l} 1, & x = y \\ 0, & 其它 \end{array}$

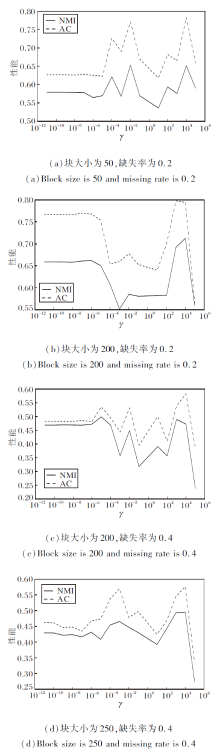
首先固定α _v=10^-2、 β _v=10^-7, 对比不同γ 得到的结果, 找到最佳γ , 结果如图1所示.由图可看出, 在不同块大小和缺失率下, 当γ =10⁴时, 普遍获得较好的聚类结果.在下面的实验中, γ =10⁴.

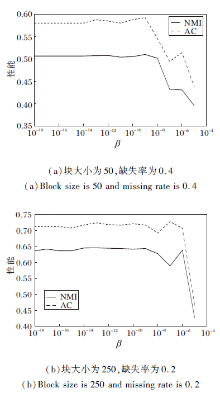
	Figure Option View Download New Window
	图1 固定α 、 β 后γ 的实验结果对比Fig.1 Experimental results comparison of γ after fixing α and β

在γ =10⁴情况下, 选取α 、 β .图2为对β 的对比分析结果.由图可看出, 当β ≤ 10^-9时, 聚类结果趋于稳定, 该方法拥有较好的聚类效果.

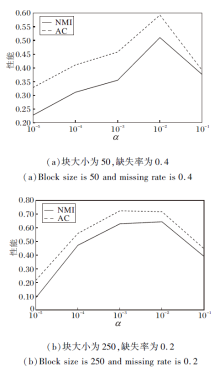
	Figure Option View Download New Window
	图2 固定α 、γ 后β 的实验结果对比Fig.2 Experimental results comparison of β after fixing α and γ

图3是对α 的对比分析, 固定γ =10⁴, β =10^-9.由图可看出, 当α =10^-2时, 聚类效果较好.

	Figure Option View Download New Window
	图3 固定β 、γ 后α 的实验结果对比Fig.3 Experimental results comparison of α after fixing β and γ

3.3 算法对比

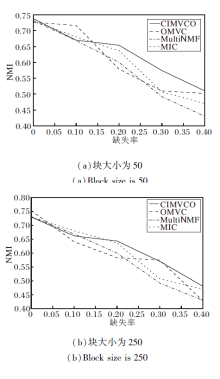
为了验证本文算法的有效性, 在不同的缺失率和块大小情况下对比MultiNMF、MIC、OMVC.实验设置如下:α =10⁴, β =10^-9, γ =10^-2.

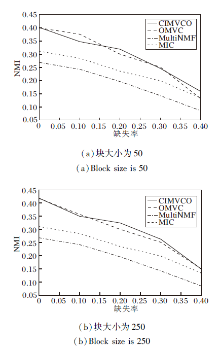
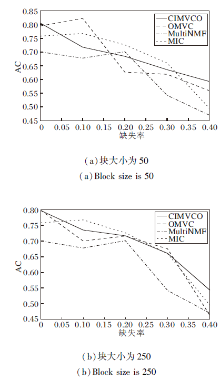
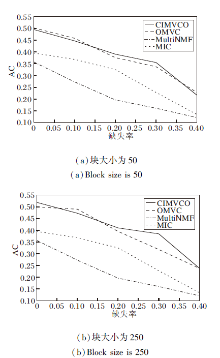
MultiNMF是在视角完整的情况下基于NMF的多视角聚类方法.MIC是视角缺失情况下基于加权NMF的多视角聚类方法.OMVC为基于NMF的在线多视角聚类方法.MultiNMF、MIC直接对整个数据集进行聚类, CIMVCO、OMVC可以利用逐块输入减小内存需求.

图4~图7分别为4种算法在不同缺失率下的NMI值和AC值.由图可看出, 大多数情况下CIMV-CO性能最优, 缺失率增加时性能下降最慢.这是由于正交约束使特征选择矩阵获得更好的局部特征, 增加信息的有效性和可靠性.

	Figure Option View Download New Window
	图4 各算法在Digit数据集上的NMI对比Fig.4 NMI comparison of different algorithms on Digit dataset

	Figure Option View Download New Window
	图5 各算法在Reuters数据集上的NMI对比Fig.5 NMI comparison of different algorithms on Reuters dataset

	Figure Option View Download New Window
	图6 各算法在Digit数据集上的AC对比Fig.6 AC comparison of different algorithms on Digit dataset

	Figure Option View Download New Window
	图7 各算法在Reuters数据集上的AC对比Fig.7 AC comparison of different algorithms on Reuters dataset

另外, 在大多数情况下, 块大小增加, 提升聚类效果.这是因为在补全缺失数据时可利用的已知数据越多, 补全的数据准确性越高.当缺失率增加时, 聚类效果逐渐变差, 这是因为已知数据减少使有效信息变少.

4 结束语

本文提出基于正交约束的分块不完整多视角聚类算法(CIMVCO), 解决视角缺失情况下大规模数据的聚类问题.CIMVCO通过对基矩阵施加正交约束, 得到更好的局部特征和唯一最优解, 应用到聚类任务时具有更严密的可解释性, 产生更适合聚类的解.CIMVCO提供各视角的缺失样本较小的权重, 减小缺失数据的影响.此外, 该算法通过逐块处理大规模数据以减少内存需求和计算量.在Digit、Reuters数据集上实验表明本文算法的有效性.如何自学习选取最优参数将是今后研究工作的重点.

参考文献

文献选项

[1]	BICKEL S, SCHEFFER T. Multi-view Clustering // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2004: 19-26. [本文引用:1]
[2]	YANG Y, WANG H. Multi-view Clustering: A Survey. Big Data Mining and Analytics, 2018, 1(2): 83-107. [本文引用:1]
[3]	ZOU P, LI F Z, ZHANG L. Nonnegative and Adaptive Multi-view Clustering // Proc of the 24th International Conference on Pattern Recognition. Washington, USA: IEEE, 2018: 1247-1252. [本文引用:1]
[4]	LIU J L, WANG C, GAO J, et al. Multi-view Clustering via Joint Nonnegative Matrix Factorization // Proc of the SIAM International Conference on Data Mining. Philadelphia, USA: SIAM, 2013: 252-260. [本文引用:3]
[5]	ZHANG X T, ZHANG X C, LIU H, et al. Multi-task Multi-view Clustering. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3324-3338. [本文引用:2]
[6]	ZHAO L, CHEN Z K, WANG Z J. Unsupervised Multiview Nonnegative Correlated Feature Learning for Data Clustering. IEEE Signal Processing Letters, 2018, 25(1): 60-64. [本文引用:3]
[7]	CHAU V T N, PHUNG N H, TRAN V T N. A Robust and Effective Algorithmic Framework for Incomplete Educational Data Clustering // Proc of the 2nd National Foundation for Science and Technology Development Conference on Information and Computer Science. Washington, USA: IEEE, 2015: 65-70. [本文引用:1]
[8]	GAO H, PENG Y X, JIAN S L. Incomplete Multi-view Clustering // Proc of the International Conference on Intelligent Information Processing. Berlin, Germany: Springer, 2016: 245-255. [本文引用:1]
[9]	LI S Y, JIANG Y, ZHOU Z H. Partial Multi-view Clustering. Proceedings of the National Conference on Artificial Intelligence, 2014, 3: 1968-1974. [本文引用:2]
[10]	SHAO W X, HE L F, YU P S. Multiple Incomplete Views Clustering via Weighted Nonnegative Matrix Factorization with L_{2, 1} Regularization // Proc of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer, 2015: 318-334. [本文引用:2]
[11]	RAI P, TRIVEDI A, DAUMÉ III H, et al. Multiview Clustering with Incomplete Views[C/OL]. [2019-09-22]. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.364.5079&rep=rep1&type=pdf. [本文引用:1]
[12]	WANG S W, LI M M, HU N, et al. K-means Clustering with Incomplete Data. IEEE Access, 2019, 7: 69162-69171. [本文引用:1]
[13]	ZHANG G Y, HUANG D, WANG C D, et al. Weighted Multi-view On-Line Competitive Clustering // Proc of the 2nd IEEE International Conference on Big Data Computing Service and Applications. Washington, USA: IEEE, 2016: 286-292. [本文引用:2]
[14]	SHAO W X, HE L F, LU C T, et al. Online Multi-view Clustering with Incomplete Views // Proc of the IEEE International Confe-rence on Big Data. Washington, USA: IEEE, 2016: 1012-1017. [本文引用:2]
[15]	SHAO W, HE L, LU C, et al. Online Unsupervised Multi-view Feature Selection // Proc of the 16th IEEE International Confe-rence on Data Mining. Washington, USA: IEEE, 2016: 1203-1208. [本文引用:2]
[16]	BU F Y, CHEN Z K, ZHANG Q C, et al. Incomplete Big Data Clustering Algorithm Using Feature Selection and Partial Distance // Proc of the 5th International Conference on Digital Home. Washington, USA: IEEE, 2014: 263-266. [本文引用:1]
[17]	丁祥武, 郭涛, 王梅, 等. 一种大规模分类数据聚类算法及其并行实现. 计算机研究与发展, 2016, 53(5): 1063-1071. (DING X W, GUO T, WANG M, et al. A Clustering Algorithm for Large-Scale Categorical Data and Its Parallel Implementation. Journal of Computer Research and Development, 2016, 53(5): 1063-1071. ) [本文引用:1]
[18]	张建朋, 陈福才, 李邵梅, 等. 基于仿射传播的进化数据流在线聚类算法. 模式识别与人工智能, 2014, 27(5): 443-451. (ZHANG J P, CHEN F C, LI S M, et al. Online Clustering of Evolution Data Stream Based on Affinity Propagation Clustering. Pattern Recognition and Artificial Intelligence, 2014, 27(5): 443-451. ) [本文引用:1]
[19]	SNASEL V, ABDULLA H D. Search Results Clustering Using Non-negative Matrix Factorization(NMF) // Proc of the International Conference on Advances in Social Network Analysis and Mining. Washington, USA: IEEE, 2009: 320-323. [本文引用:1]
[20]	TANG J, CENG X Y, PENG B. New Methods of Data Clustering and Classification Based on NMF // Proc of the International Conference on Business Computing and Global Informatization. Wa-shington, USA: IEEE, 2011: 432-435. [本文引用:1]
[21]	ZHANG X C, ZONG L L, LIU X Y, et al. Constrained Clustering With Nonnegative Matrix Factorization. IEEE Transactions on Neural Networks and Learning Systems, 2015, 27(7): 1514-1526. [本文引用:1]
[22]	GÜRAN A, GANIZ M C, NAIBOGLU H S, et al. NMF Based Dimension Reduction Methods for Turkish Text Clustering // Proc of the IEEE INISTA. Washington, USA: IEEE, 2013: 1-5. [本文引用:1]
[23]	LIU K, WANG H, RISACHER S, et al. Multiple Incomplete Views Clustering via Non-negative Matrix Factorization with Its Application in Alzheimer's Disease Analysis // Proc of the 15th IEEE International Symposium on Biomedical Imaging. Washing-ton, USA: IEEE, 2018: 1402-1405. [本文引用:1]
[24]	KUTIL R, FLATZ M, VAJTERSIC M. Improvements in Approximation Performance and Parallelization of Nonnegative Matrix Factorization with Newton Iteration // Proc of the International Confe-rence on High Performance Computing and Simulation. Washington, USA: IEEE, 2017: 887-888. [本文引用:1]
[25]	BERTSEKAS D P. Projected Newton Methods for Optimization Pro-blems with Simple Constraints. SIAM Journal on Control and Optimization, 1982, 20(2): 221-246. [本文引用:1]

2004

0.0

... 大量的多视角聚类算法^{[1,2,3,4,5,6]}利用数据的多个视角信息进行聚类,多个视角提供语义相同的数据及其一致或互补表示,使用数据多个视角的特征进行聚类可以比仅使用单视角方法能获得更好的性能 ...

2018

0.0

2018

0.0

2013

0.0

... 联合非负矩阵分解多视角聚类算法(Multi-view Clustering via Joint Nonnegative Matrix Factori-zation, MultiNMF)^[4]在聚类时,不同视角下的同个样本多会分配到同个簇中 ...

... ,定义差异度的损失函数^[4]: ...

2016

0.0

... 已有的多视角聚类算法^[5,6]大多假设每个样本的各视角都完整,而现实世界的数据常有缺失,想要获取完整的数据集需耗费的成本极高,因此需要处理视角不完整数据的多视角聚类方法 ...

2018

0.0

... 1 原理及目标引入一个指示符矩阵^[6]M#cod#x02208 ...

2015

0.0