相关滤波算法旨在设计一个具有对目标高响应而对背景低响应的滤波器, 以此进行目标定位与尺度估计.相关滤波算法通过对目标样本进行循环位移以增加训练样本数, 提高跟踪效果.此外, 算法将时域中复杂的矩阵乘积和求逆操作转换为频域中元素的点乘和点除操作, 提高算法速度.相关滤波算法可大致分为学习过程和跟踪过程.

1)学习过程.根据当前已知目标状态训练滤波器.在第t帧中, 以目标位置为中心提取目标图像块x, 并以此为原始样本进行循环位移, 得到样本空间X.之后, 结合训练样本和给定的鉴别标签g, 使用岭回归训练滤波器:

minθ‖ h(x)-g‖ ²+λ ‖ θ ‖ ²,

其中, θ 为滤波器, λ 为正则化系数,

h(x)=Xθ =x$\otimes$θ

为所得响应图, $\otimes$为循环卷积.该岭回归问题可在频域中快速计算, 有闭式解如下:

θ︿= x︿☉g︿x︿* ☉x︿+λ, (1)

其中, ☉为点乘, ·︿为傅里叶变换, · ^* 为共轭, 分数线为点除操作, θ︿为学习的滤波器在频域中的表示.

2)跟踪过程.学习到滤波器后可用它对下一帧目标进行检测定位.在t+1帧中, 根据上一帧目标位置提取检测图像块z, 并与上一帧训练得到的滤波器θ 在频域中进行相关滤波, 转换到时域可得响应图r如下:

r=F^-1( θ︿☉ z︿), (2)

其中F^-1为傅里叶逆变换.响应图r反映当前帧目标与上一帧目标间的位置偏移, 因此, 根据响应图r可以预测t+1帧中目标的位置.

然而, 跟踪过程中往往存在各种干扰因素, 为了防止滤波器的退化, 往往采取如下插值的方式更新滤波器:

θ _t=(1-η )θ _t-1+η θ , (3)

其中, θ _t为第t帧更新后的滤波器, θ 为通过式(1)学习到的第t帧的滤波器, η 为学习率.一般使用θ _t对下一帧目标进行定位跟踪.

相关滤波算法具有较快的跟踪速度, 但算法性能较差.

针对相关滤波算法存在的问题, STRCF^[17]在其基础上引入空间正则化和时间一致性约束, 目标函

数如下:

minθ∑d=1Dxd⊗θd-g2+ ∑d=1D‖ w ☉θ ^d‖ ²+μ ‖ θ - θ _(t-1)‖ ²,

其中, x为当前帧目标图像块, θ 为需要学习的当前帧滤波器, g为鉴别标签, θ _(t-1)为上一帧学到的滤波器, w 为预设的空间正则化矩阵, · ^d为第d个通道, 特征总通道数为D, μ 为正则化系数.

空间正则化即在正则化项中给滤波器添加倒高斯形矩阵w , 赋予滤波器边缘高惩罚系数, 将滤波器能量集中在中心区域, 有效缓解边界效应, 提高滤波器鉴别能力.时间一致性约束要求滤波器在完成当前帧跟踪任务的同时与上一帧滤波器保持结构相似, 其实质为对滤波器引入低秩约束, 增强泛化性能, 进一步提高算法鲁棒性.STRCF具有较好的鲁棒性和跟踪精度, 但仍存在不足之处, 限制算法性能.

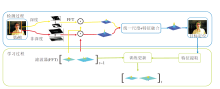
本文就STRCF的不足之处提出多空间分辨率自适应特征融合的改进算法.不同于STRCF等直接将深度特征和浅层特征叠加使用, 而是使用自适应的方式融合两类特征.首先, 使用从不同尺度搜索区域提取深度特征和浅层特征完成目标的检测和滤波器的训练任务.另外, 在检测阶段得到不同特征的响应图后, 以自适应的方式选取权重融合响应图, 更好地发挥深度特征和浅层特征各自的优越性.图1为本文算法框图.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 本文算法框图Fig.1 Framework of the proposed algorithm

首先, 依据当前目标位置分割不同尺度的图像块, 分别从中提取深度特征和浅层特征.再在频域中将其与滤波器点乘, 使用自适应权重融合两类特征响应图.最后, 从融合后的响应图中获取当前帧目标位置, 并以此更新滤波器.特征提取是根据当前目标位置和尺度从视频帧中分割不同尺度的图像块, 并分别从中提取深度特征和浅层特征, 用于对应模板滤波器的训练更新.

2.1.1 不同尺度的搜索区域

相关滤波算法在训练滤波器和检测目标时采用周期性假设以扩充样本.然而, 周期性假设由快速傅里叶变换隐式完成, 带来边界效应问题, 影响算法性能.搜索区域尺度的选择主要考量边界效应和训练样本数.采用直接扩大搜索区域的方式虽然能通过循环位移得到更多的样本数, 但带来的边界效应问题也较大, 导致正训练样本中的背景区域所占面积比更大, 这些干扰信息会严重影响滤波器的鉴别性能.虽然目前存在的多种空间正则化滤波器能有效缓解边界效应, 但问题依然存在.因此, 在确定搜索区域尺度时需在边界效应问题与训练样本数间寻求一个平衡.

深度特征和浅层特征的分辨率不同, 相对来说, 由深层的卷积网络提取的深度特征常具有更小的空间分辨率, 即当两类特征搜索区域尺度一致时, 深度特征对应通道矩阵具有更小的尺度, 可获取的样本数更少, 同时边界效应更小.浅层特征则相反, 在循环位移产生更多样本数的同时也加大边界效应问题对目标检测的影响.现有跟踪算法大多采取相同尺度的搜索区域以提取用于滤波器训练和目标检测的特征, 忽略了上述问题.因此, 为了更好地平衡边界效应与样本数, 采用更大的搜索区域以提取深度特征, 同时采用较小的搜索区域以提取浅层特征.在本文算法的自身验证实验中也证实这种做法的合理性与有效性.

2.1.2 自适应特征融合

在目标检测时, 传统算法直接将各类特征相关滤波得到的响应图进行简单地叠加融合, 无法较好地发挥各类特征的特性.又考虑到在不同跟踪场景中, 各类特征的表示性能也有所不同.在较简单的场景中, 由于浅层特征更具纹理信息和较高的空间分辨率, 有利于精准定位和尺度估计, 应赋予浅层特征更大的权重.而在复杂的场景下, 深度特征更具鲁棒性和鉴别性, 应当赋予深度特征较高的权重.因此, 本文引入自适应权重的融合策略^[22], 用于融合每帧深度特征和浅层特征对应的响应图, 提高目标定位和尺度估计的精度.自适应权重融合特征图的目标函数如下:

Qloctop(β)=-ξloctop{Rsβ}+σ(βs2+βd2), s.t.βs+βd=1, βs≥0, βd≥0.(4)

其中:Q表示损失函数; β 表示当前权重组合, 由β _d和β _s组成; σ 表示正则化参数; loc^top表示以权重组合β 融合后的响应图Rs_β 中最大响应值所在位置;

Rs_β =β _dRs_d+β _sRs_s, (5)

Rs_d表示深度特征响应图, Rs_s表示浅层特征响应图;

ξloctop{Rs_β }= minloc( Rsβ(loctop)-Rsβ(loc)Δ(loc-loctop)), (6)

loc为Rs_β 中元素的坐标, 上式中分母表示距离相关的权重,

Δ (ρ )=1-exp(- k2|ρ |²),

ρ 表示距离, k为固定常数.

关于式(4)目标函数的优化求解, 若直接求解涉及到β 和loc^top的同时优化, 需要在这两个变量各自的搜索空间中进行迭代求解, 复杂耗时.本文考虑到β 的搜索空间较小(β ∈ [0, 1]), 为标量, 因此, 使用穷举法直接以0.01为步长在β 的搜索空间中搜索使式(4)中目标函数 Qloctop(β )值最小的β , 找到的最小β 即为式(4)的解.

算法 多空间分辨率自适应特征融合的相关滤波

算法

输入 视频帧I_t, 上一帧目标位置p_t-1,

目标尺度s_t-1, 滤波器θ _t-1

输出 当前帧目标位置p_t, 目标尺度s_t,

滤波器θ _t

step 1 依据上一帧目标位置p_t-1和目标尺度s_t-1, 从I_t中分割不同尺度的图像块x_t, 分别从较大和较小的图像块中提取深度特征和浅层特征, 利用式(2)求得响应图.

step 2 使用式(5)所示自适应策略融合响应图后, 根据文献[23], 从多尺度的响应图中确定当前帧目标位置p_t和目标尺度s_t.

step 3 依据目标位置p_t和目标尺度s_t再次从I_t中分割不同尺度的图像块x_t, 分别提取深度特征和浅层特征后, 利用滤波器θ _t-1和交替方向乘子法(Alternating Direction Method of Multipilers, ADMM)学习滤波器θ _t.

step 4 根据滤波器θ _t, 使用式(3)求解滤波器θ _t.

为了验证本文算法的有效性, 在OTB-100^[25]、TC-128^[26]、UAV-123^[27] 、VOT2018^[28]数据集上进行对比实验.参与对比实验的算法包括:ECO(Effici-ent Convolution Operators for Tracking)^[29], BACF(Background-Aware Correlation Filters)^[30], STRC-F^[17], CSRDCF^[16], Staple(Sum of Template and Pixel-Wise Learners)^[31], SRDCF^[14], STAPLE_CA(Context-Aware Correlation Filter Tracking)^[32], CCOT(Lear-ning Continuous Convolution Operators for Visual Tra-cking)^[33], DSST^[13], SAMF^[12], DRT(Correlation Tra-cking via Joint Discrimination and Reliability Lear-ning)^[34]和LSART(Learning Spatial-Aware Regre-ssions for Visual Tracking)^[35].对比算法的实验结果均是使用原作者公开代码在相同环境下测试所得.

本文所用浅层特征包括HOG和CN特征, 而深度特征取已在IamgeNet中完成预训练的ResNet-50模型的第4个卷积块中第5个卷积层输出作为输入.实验中正则化参数σ =0.1, 针对目标尺度变化, 根据文献[23], 取尺度增长因子为1.01, 尺度数量为7.深度特征和浅层特征取值不同的参数设置如下:对于浅层特征, 正则化参数μ =12, 学习率η =0.6, 搜索区域为4.2倍目标图像块; 对于深度特征, μ =16, 学习率η =0.06, 搜索区域为4.4倍目标图像块.

本文算法在Matlab R2018a上编译.所有实验在配置为Intel i9 CPU 3.0 GHz, 16 GB内存和NVIDIA RTX2080Ti GPU的计算机上完成, 平均算法速度约为4帧/秒.

本文实验在OTB-100、TC-128、UAV-123数据集上展开, 采用评估标准为距离精度(Distance Preci-sion, DP)和成功率曲线下面积(AUC).DP表示实验所得目标位置与实际目标位置间欧氏距离小于阈值的视频帧占总帧数之比, 阈值一般为20.成功率为重叠率(Overlap, OP)大于指定阈值的视频帧占总帧数之比, 阈值一般取0.5, OP计算公式如下:

OP= Bcal⋂BgtBcal⋃Bgt,

其中, B_cal为跟踪算法预测的目标区域, B_gt为真实目标区域.但是, 此阈值取值不同易产生不同的实验结果, 带来不唯一性, 因此采用AUC能更好地体现算法性能.

在VOT2018数据集上使用的评估标准为失败次数(Failures), 精度(Accuracy)和期望平均重叠率(Expected Average Overlap, EAO), 其中, Failures

用于衡量算法鲁棒性, 值越小算法越鲁棒, Accuracy表示算法精度, EAO是对算法精度和鲁棒性的综合评价指标.

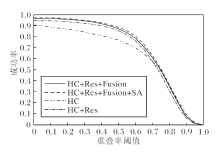
为了验证本文算法各个组分的有效性, 给出自对比的验证实验.图2为在OTB-100数据库上的实验结果, 其中HC表示仅使用浅层特征, Res表示使用ResNet-50提取深度特征, Fusion表示引入自适应融合方法, SA表示使用不同尺度搜索区域, 结合全部组分即为本文算法.由图可知, 算法在仅使用浅层特征的条件下取得63%的跟踪成功率, 主要是因为STRCF提出的时空正则化使滤波器更具鉴别、泛化性能.引入ResNet-50提取目标深度特征带来3.7%的性能提升, 这是因为深度特征包含的深层次语义信息提高特征的表示能力, 提高算法性能.在使用自适应融合策略后, 算法性能提升2.1%, 是由于自适应融合策略更好地利用浅层特征和深度特征的互补性.最后, 基于深度特征和浅层特征具有不同空间分辨率的事实, 采用区分搜索区域尺度的方式, 以更好的平衡应对特征的边界效应问题和训练样本数, 实验结果具有较理想的提升.上述实验结果表明, 本文算法的各个组分对于性能提升都有较大贡献, 同时也说明本文算法的有效性和优越性.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 OTB-100数据集上的消融实验结果Fig.2 Results of ablation experiment on OTB-100 dataset

另外, 本文深入研究本文算法中不同尺度的搜索区域和自适应特征融合部分.图3为在OTB-100数据集上使用不同尺度搜索区域组的实验结果.由图可知, 采用较浅层特征对应更大且适当的搜索区域以提取深度特征, 可以带来算法性能的提升.

图3

Fig.3

	Figure Option ViewDownloadNew Window
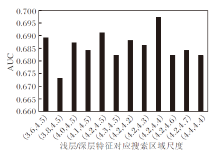	图3 OTB-100数据集上使用不同尺度搜索区域组的实验结果Fig.3 Experimental results of different search area groups with different scales on OTB-100 dataset

图4为Skating 2-1视频序列中不同场景下自适应特征融合的实验结果.(a)中场景未发生外观变化, 浅层特征的权重较大.(b)中目标被严重遮挡且变形严重, 深度特征权重更高.(c)中目标虽然存在轻微的遮挡和变形, 但整体上清晰, 浅层特征权重高于深度特征.由图可知, 自适应特征融合策略的引入能够更充分地利用深度特征和浅层特征的互补特性, 提高算法性能.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 Skating 2-1视频序列在不同场景下的自适应融合结果Fig.4 Adaptive fusion results of Skating 2-1 video sequence in different scenarios

为了更好地证实本文算法的优越性, 进行大量的对比实验.表1为各算法在OTB-100、TC-128和UAV-123数据集上的实验结果, 表2为各算法在VOT 2018数据集上的实验结果, 每项评估标准的最优结果使用黑体数字表示.

表1

Table 1

表1(Table 1)

表1 各算法在3个数据集上的实验结果 Table 1 Experimental results of different algorithms on 3 datasets 算法 OTB-100 TC-128 UAV-123 AUC DP AUC DP AUC DP DSST 0.520 0.693 0.378 0.540 0.358 0.590 SAMF 0.541 0.752 0.465 0.637 0.398 0.599 SRDCF 0.594 0.780 0.481 0.651 0.459 0.665 Staple 0.579 0.784 0.502 0.673 0.445 0.657 CSRDCF 0.579 0.802 0.475 0.673 0.430 0.665 STAPLE_CA 0.598 0.810 0.505 0.675 0.449 0.661 BACF 0.615 0.816 0.495 0.660 0.458 0.657 STRCF 0.675 0.880 0.587 0.788 0.510 0.708 CCOT 0.673 0.903 0.573 0.788 0.503 0.717 ECO 0.691 0.910 0.577 0.780 0.528 0.747 本文算法 0.698 0.937 0.579 0.799 0.541 0.775

表1 各算法在3个数据集上的实验结果 Table 1 Experimental results of different algorithms on 3 datasets

表2

Table 2

表2(Table 2)

表2 各算法在VOT2018数据集上的实验结果 Table 2 Experimental results of different algorithms on VOT2018 dataset ECO LSART STRCF DRT 本文算法 EAO 0.280 0.323 0.345 0.356 0.352 Accuracy 0.484 0.495 0.523 0.519 0.540 Failures 17.7 12.8 13.1 12.8 13.2

表2 各算法在VOT2018数据集上的实验结果 Table 2 Experimental results of different algorithms on VOT2018 dataset

OTB-100数据集是目前目标跟踪领域通用的数据集之一, 包含100个视频序列.由表1可知, 相比其它算法, 本文算法在OTB-100数据集上具有最优的跟踪精度(93.7%)和成功率(69.8%).相比次优的ECO, 本文算法在跟踪精度和成功率上分别有2.7%和0.7%的提高.相比STRCF, 本文算法分别有5.7%和2.4%的提高.

为了更清晰直观地展现算法性能, 图5给出9种算法在Shaking、Skating 2-1、Matrix、MotorRolling和Box等具有挑战性的视频序列上的跟踪结果.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各算法在6组视频上的跟踪结果Fig.5 Tracking results of different algorithms on 6 videos

由图5可见, 本文算法在复杂的环境下依然保持稳定跟踪效果和较高精度, 这是由于其使用由ResNet-50网络提取的更具语义信息的深度特征.同时, 自适应融合策略能更好地挖掘各类特征的表示能力, 提升跟踪算法应对复杂场景的鲁棒性.

TC-128数据集包含128个彩色视频序列的标准视频数据集.如表1所示, 本文算法在此数据集上跟踪精度和成功率分别为79.9%和58.7%.在跟踪精度上比STRCF仅降低0.8%, 但是, 本文算法具有最优的跟踪精度, 相比STRCF提高1.1%.

UAV-123数据集包含123个由无人机拍摄的视频序列.观察表1可知, 本文算法在此数据集上分别具有77.5%的跟踪精度和54.1%的成功率, 为本次实验中的最优算法.相比次优的ECO, 本文算法分别有2.8%和1.3%的提高.相比STRCF, 本文算法在跟踪成功率上提高3.1%, 而在跟踪精度上提高6.7%, 充分体现本文算法改进的有效性.

VOT 2018数据集由60个极具挑战性的视频序列组成.如表2所示, 本文算法具有最优的跟踪精度(0.540).此外, 本文算法在EAO指标上的结果为0.352, 仅次于DRT, Failures指标结果为13.2, 与该项指标的最优算法相近.相比STRCF, 本文算法具有近乎相同的鲁棒性, 但在Accuracy指标上, 相比STRCF, 本文算法有1.7%的提升, 在VOT最主要的评价指标EAO上也有一定提升, 这表明本文算法改进的有效性.