
张志鹏,博士,讲师,主要研究方向为数据挖掘、推荐系统.E-mail:zhipengzhang@lnnu.edu.cn.
作者简介:

任永功,博士,教授,主要研究方向为人工智能、数据挖掘.E-mail:jsj_paper@163.com.

石佳鑫,硕士研究生,主要研究方向为人工智能、数据挖掘.E-mail:934713390@qq.com.
针对新物品缺乏(非完全冷启动)或没有(完全冷启动)评分信息,协同过滤无法为新物品进行个性化推荐的问题,文中提出融合关系挖掘与协同过滤的推荐算法.首先,利用关系挖掘提取物品关系特征,根据属性之间的多种二元关系构建关系属性,丰富可用属性信息.然后,提出基于关系挖掘的近邻选取方法,增加邻近物品的多样性.最后,融合协同过滤方法,同时解决完全和非完全新物品冷启动问题,实现新物品的个性化推荐.在两个真实数据集上的实验表明,文中方法可以系统解决推荐系统中新物品的冷启动问题.
ZHANG Zhipeng, Ph.D., lecturer. His research interests include data mining and recommender system.
AboutAuthor:
REN Yonggong, Ph.D., professor. His research interests include artificial intelligence and data mining.
SHI Jiaxin, master student. Her research interests include artificial intelligence and data mining.
Collaborative filtering cannot provide personalized recommendation of new items due to the lack of scoring information for incomplete cold start(ICS) or the absence of scoring information for complete cold start(CCS). To address this problem, a recommendation algorithm combing interrelationship mining and collaborative filtering(CF) is proposed. Firstly, relationship features of items are extracted by using interrelationship mining, and the number of available attributes is expanded according to multiple binary relations between attributes. A neighbor selection approach based on interrelationship mining is proposed to increase the diversity of neighboring items. Finally, CF is integrated to solve CCS and ICS problems and then personalized recommendation of new items is realized. The experiments on two real world datasets indicate that the proposed algorithm solves the new item cold start problems of recommender systems effectively.
本文责任编委 张燕平
Recommended by Associate Editor ZHANG Yanping
推荐系统(Recommender System, RS)[1]根据目标用户的历史信息分析用户偏好, 为用户推荐可能喜欢的物品[2].RS能有效解决信息过载问题, 为用户提供个性化的服务, 在海量大数据时代得到广泛应用[3].
目前, 根据对用户信息的不同处理手段, RS中的推荐方法主要分为协同过滤(Collaborative Filter-ing, CF), 基于内容(Content Based, CB)过滤和混合过滤[4].CF是目前较成功的推荐技术之一[5], 主要利用用户的评分数据构建评分矩阵, 计算用户之间或物品之间的相似度, 预测用户未评分物品, 根据预测评分对目标用户进行推荐.CF依赖用户和物品之间的关系, 即用户对物品的评分, 不需要分析物品的内容及物品本身属性.
然而, CF存在冷启动(Cold Start, CS)问题, 根据评分记录的数量是否为零分为完全冷启动(Complete CS, CCS)问题和非完全冷启动(Incomplete CS, ICS)问题[6].CF需要用户或物品的大量评分以获得有效推荐, 系统中可用的评分较少, 甚至没有, 严重影响RS的质量.
CB可有效解决CF中的冷启动问题.CB依赖于用户偏好和新物品的特征信息, 不需要新物品的评分记录[7].Alharthi等[8]使用外部知识源增加RS中物品的内容, 实验表明, 使用CB的推荐效果优于CF.但CB只能处理内容丰富的物品.文献[9]方法在处理新物品时, 根据物品内容相似性寻找新物品所在的分组, 再根据组内物品受欢迎度进行排序并推荐.但是CB推荐只依赖于用户过去对某些物品的喜好, 无法推荐差异性物品.虽然CB有效解决CS, 但在现实推荐系统中, 物品的可用属性通常稀少.
混合过滤方法结合CB和CF, 研究人员通过引入额外信息解决CS问题, 在一定程度上取得较好的推荐结果.Cui等[10]融合用户上传照片和偏好照片作为混合偏好, 用于研究用户的特征, 利用超图模型从用户社交网络和多模态内容共同捕获异构高阶关系信息.混合过滤虽然能解决CS问题, 但获取信息的过程复杂, 容易产生对用户偏好的错误判断.刘华锋等[11]综述基于矩阵分解的社交推荐模型, 社交关系中的用户之间在一定程度上具有相似的偏好, 因此融合社交信息的推荐模型在一定程度上解决CS问题, 但属性特征提取困难, 额外信息也常不完整, 因此无法同时解决CCS问题和ICS问题.
基于目前各方法存在的问题, 本文提出融合关系挖掘与协同过滤的推荐算法(Interrelationship Mining Based CF, IMCF).采用关系挖掘理论提取每个物品属性与属性之间隐含的关系, 形成一个新的关系属性, 丰富可用属性信息.针对ICS问题, 引入调节参数, 充分利用用户-物品间少量历史评分数据对ICS中的新物品产生高质量推荐.实验表明, 本文算法可以同时解决CCS问题和ICS问题, 产生高精度和多样化的推荐.
本文算法旨在利用关系挖掘的丰富理论, 结合协同过滤的算法特性, 整体解决物品冷启动中的CCS问题和ICS问题.重点分析和研究如下3个问题:
1)物品可用属性信息较少, 不同物品间的区分度较低.
2)目标物品的邻近物品选取单一.
3)只可单方面解决CCS问题或ICS问题, 无法同时解决两者.
针对问题1), 本文利用关系挖掘(Interrela-tionship Mining)提取物品关系特征, 计算属性间多种二元关系, 将物品的现有属性扩展为新的“ 关系属性” , 丰富目标物品的可用属性信息.
针对问题2), 本文将通过属性关系挖掘提取的关系属性融入目标物品的邻近物品选取过程中, 提出基于关系挖掘的近邻选取方法(Interrelationship Mining Based Neighbor Selection, IMNS), 细化属性分类, 增加邻近物品的多样性.
针对问题3), 本文提出IMCF, 结合IMNS与CF, 引入调节参数进行寻优, 同时解决ICS问题和CCS问题.
粗糙集理论描述属性值组合的特征, 但提取的方法几乎都是基于同一属性值之间的对比.本文应用相互关系挖掘的概念[12], 根据不同属性值之间的对比提取特征.关系挖掘的一个主要思想是基于不同属性值之间的对比, 通过称为关系属性的新属性表示特性[13], 即可通过属性值的对比考虑属性之间的相互关系.
假设物品-属性信息表TIA={I, C, V}.I={Ii}为物品集, i=1, 2, …, g, g为物品的总数目, j∈ i但j≠ i.C={Cn}为属性集, n=1, 2, …, e, e为属性的总数目, f∈ n但f≠ n.V={1, 0}, 当V=1时表示该物品具有此属性, 当V=0时表示该物品不具有此属性.
Va为a∈ C的非空值集合,
RMC={{RMa}|a∈ C}
为在每个Va上定义的一组二元关系族{RMa}, ρ ∶ I× C→ V, 为一个信息函数, 将属性a∈ C的值 ρ (Ii, a)∈ Va分配给每个对象Ii∈ I, Va为C中所有属性的值集.每个属性a∈ C的二元关系族{RMa}可以包含各种二元关系.
令c=attribute, 并且a∈ attribute, b∈ attribute分别为值集Va、Vb的两个属性, RM⊆Va× Vb为从Va到Vb的二元关系.当且仅当存在对象Ii∈ I, 使
(ρ (Ii, a), ρ (Ii, b))∈ RM
成立时, 称属性a、b由RM相互关联, 表示属性a、b的值满足关系RM的对象集合如下:
RM(a, b)={Ii∈ I|(ρ (Ii, a), ρ (Ii, b))∈ RM},
集合RM(a, b)表示为a和b之间相互关系的支持集.
属性关系函数定义如下:
ρ int(Ii, c)=
其中:aRb为相互关联的属性, 称为关系属性, 表示每个对象Ii∈ I是否通过二元关系RM⊆
一般信息表都假设二元关系仅由等价关系“ 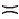
属性Practice和Exam之间的3种相互关系如表1所示, 属性Practice和Exam的范围相同, 可以将偏好关系≻Exam视为定义在VPractice× VExam上的一个二元关系≻P× E.
| 表1 属性关系举例 Table 1 Example of attribute interrelationship |
≻Exam的偏好关系定义如下:
outstanding≻good≻pass≻fail.
进一步构造3个关系属性P≻E, P 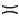
≻P× E(P, E)={S2, S3, S4},
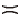
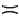
采用式(1)计算得到Practice和Exam属性关系函数值:
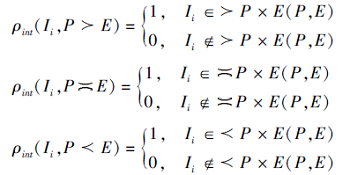
由表1可看出, Boarder和Poverty属性范围也相同.因此, 可以将偏好关系≻Boarder视为定义在VBoarder× VPoverty上的一个二元关系≻B× P.
≻Boarder的偏好关系定义如下:
≻Boarder∶ yes≻no.
下面构造3个关系属性B≻P, B 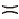
≻B× P(B, P)={S1, S3, S6},
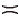
≺B× P(B, P)={S5}.
采用式(1)计算得到Boarder和Poverty属性关系函数值:
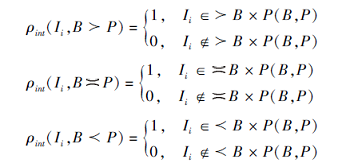
经过属性关系挖掘后产生关系属性如表2所示.
| 表2 关系属性表 Table 2 Interrelationship attribute table |
由于RS中每个物品的可用属性数量非常有限, 甚至只有一到两个, 所以无法有效区分系统中拥有庞大数量的物品, 因此需要挖掘物品属性间关系, 扩展可用属性的数量, 使物品间产生较大的差异度, 提高系统的推荐质量.
在CF中, 邻近物品的选取直接影响最终的推荐结果.基于物品的CF算法只根据用户的共同评分进行计算, 由于新物品缺少或没有评分信息, 常无法获得满意的推荐结果.
基于物品的CF算法中对相似度的计算都侧重于用户对物品的评分, 忽略不同商品在类别上的相关性.大部分用户都是通过属性选择自己喜欢的物品, 因此可能出现如下情况:系统给用户推荐高评分的物品, 但这并不是用户喜欢的类型.
针对此问题, 本文采用属性区分物品, 对于同类物品, 对其的定义一样, 而且一种物品可以有多种属性.一般来说, 同一类别的物品相似性高于不同类别的物品, 用户喜欢同类物品的概率较大.
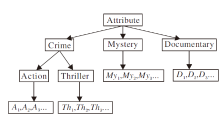
图1具体描述电影属性分类.显然My1和My2之间的相似度高于My1和Th1, 因为My1和My2同时属于Mystery, 而My1和Th1分别属于Mystery和Crime、Thriller, 则Th1和A1之间的相似度高于Th1和My1, 因为Th1和A1有一个共同的类别Crime.因此在计算物品相似性时, 需要考虑使用物品属性进行计算.
表3为系统中物品属性表.
| 表3 物品属性表 Table 3 Item attribute table |
Ix中C1值为1, 表示Ix具有C1属性, 否则, 值为0, 表示不具有C1属性.由此计算Ix和Iy之间的相似度[14]:
simJ(Ix, Iy)=
两个物品间共同拥有的属性越多, 相似度的值越大; 否则, 相似度值越小.
现有方法一般直接采用物品的属性计算相似度, 但是存在邻近物品选取不准确等问题.例如, 每个物品都有C1属性, 使用C1区分物品的能力较低, 一味地将具有C1属性的物品作为目标物品的邻近物品存在片面性.因此本文提出IMNS, 在邻近物品的选取中融入关系挖掘, 采用扩展属性数量后的“ 关系属性” 进行计算:
IMNS(Ii, Ij)=
其中
p=ρ int(Ii, ch), q=ρ int(Ij, ch), 1≤ h≤ m, c={c1, c2, …, cm},
m为关系属性的总数量,
m=
本文考虑3种属性关系, 因此系数选定为3.m恒大于e, 随着e的增加, m远大于e, 因此, 本文算法丰富目标物品的可用属性信息.
表4中有7个物品, 其中2个为目标物品, C1、C2、C3表示物品的3个属性, 根据式(2)计算得出目标物品2与物品3的相似度:
simJ(目标物品2, 物品3)=
利用IMNS计算目标物品2与物品3的相似度:
IMNS(目标物品2, 物品3)=
这与只用属性计算相似度的结果相差很大, 利用IMNS的计算结果表明两个物品并不相似.
| 表4 物品-属性示例 Table 4 Item attribute examples |
目标物品2和物品3都具有C1属性, 但只单独考虑C1而忽略C2、C3, 未整体分析所有属性隐含的关系.
对于物品3,
Ii∈ 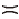
即具有C1的同时具有C3而不具有C2.
对于目标物品2,
Ii∈ 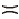
即具有C1的同时具有C2而不具有C3.
上述说明只利用两个物品共同拥有的属性计算相似度不够准确, 导致推荐结果准确度较低.
表5是表4中物品的用户评分矩阵, 用户4表示目标用户.用户评分值在1~5之间, 评分越高表示用户越喜欢此物品, * 表示用户没有评分.如果采用基于物品的CF算法进行计算, 当邻近物品为3时即与目标物品1相似度最高的前3个物品, 可得出目标物品1的邻近物品集
M1={物品1, 物品2, 物品5},
目标物品2的邻近物品集
M2={物品1, 物品2, 物品5},
即M1=M2, 导致两个目标物品具有相同的邻近物品.邻近物品的选取单一, 影响推荐结果的多样性.
| 表5 用户-物品评分矩阵 Table 5 User-item scoring matrix |
本文在邻居选取阶段挖掘物品属性之间的相互关系, 可从一定程度上分析物品与物品之间的关系, 更准确地找到目标物品的邻近物品, 利用IMNS得出目标物品1的邻近物品集
IMNS1={物品2, 物品4, 物品5},
目标物品2的邻近物品集
IMNS2={物品1, 物品2, 物品5}.
相比CF, 本文在邻近物品的选取上更多样化.
推荐系统中有很多ICS物品只具有少量评分信息, 现有的一些文献忽略这些评分数据.本文认为虽然物品评分信息量很小, 但也有存在的价值, 因此提出IMCF, 充分考虑评分信息.
CF中计算物品间相似度的方法很多, 本文以余弦相似度为例, 具体如下:
simR(Ii, Ij)=
其中,
引入调节参数结合二者:
sims'(Ii, Ij)=∂ IMNS(Ii, Ij)+(1-∂ )simR(Ii, Ij), (5)
其中, ∂ 为调节参数, 取值范围为[0, 1], 当∂ =1时, 表示只使用IMNS解决物品CCS问题, 当∂ 取值为0~1之间时, 解决物品ICS问题.
本文算法具体步骤如下, 其中:
算法 IMCF
输入 物品-用户评分矩阵R, 物品属性矩阵AM
输出 目标用户u推荐的N个物品
for n=1 to card(e) do
for f=1 to card(e) do
n≠ f
计算每两个属性的关系属性
end for
end for
for i=1 to card(g) do
for j=1 to card(g) do
j≠ i
利用式(3)计算IMNS
利用式(4)计算simR
利用式(5)计算sims'
end for
end for
for ∀ Ii∈
计算物品Ii的k个邻近物品集
for ∀ Ij∈
end for
end for
推荐前N个具有最高
本文算法与基于物品的CF算法在相似度计算上存在不同之处, 因此在对比时间复杂度时对比相似度算法即可.假设系统中有g个物品, e种属性, CF的计算物品相似度的时间复杂度为O(g2).本文算法的时间复杂度主要取决于属性集的长度, 计算属性关系相似度最坏时的时间复杂度为
O(gm)+O(g2),
关系属性数量
m=
属性数量远小于系统中物品数量, 而现实中m值也不大, 因此本文算法时间复杂度为O(g2), 在CF的基础上并未产生更高的消耗.
本文选取经典的评估推荐系统的MovieLens100K、MovieLens10M数据集进行实验.
MovieLens100K数据集包含100 000条评分记录, 943名用户, 1 682部电影.MovieLens10M数据集包含10 000 054条评分记录, 71 567名用户, 10 681部电影.
每个评分的取值范围为1~5, 包含电影的18个基本属性, 1表示电影属于该类型, 0表示不属于, 一部电影可以同时使用多种类型.
选取评分数量小于15%的物品作为CS物品, 并将数据集中80%的数据作为训练集, 20%的数据作为测试集.采用交叉验证法.邻近物品集取值为20, 30, 40, 50, 60.推荐物品长度为20.θ 为评分阈值, 当θ > 3时为用户喜欢的物品.
对于每名目标用户, 只考虑用户在测试集中已评过分的电影.首先, 假设目标电影没有被目标用户评过分, 再使用本文算法, 利用属性和其余电影获得的信息预测每个目标电影的评分.最后, 对比测试集里的原始数据与预测的电影评分.
对于CS物品推荐的多样性, 本文采用平均个性度(Mean Personality, MP)[15]和覆盖率[16]衡量:
MP(T)=1-
其中, T为推荐的电影数量, #u为目标用户总数.将每名目标用户的预测评分按照降序排序, 提取排在前T部的电影, 记为集合Ω (Τ ).对于2名目标用户u、v, 计算前T部电影集Ω u(T)、Ω v(T)共同拥有的电影数量, 进一步归一量化, 得到2部电影集的重叠程度, 将MP定义为1减去每2名用户之间的平均重叠程度.
本文采用平均新颖度(Mean Novelty, MN)[15]衡量CS物品的新颖性:
MN(T)=-
其中,
本文采用平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE)衡量CS物品的预测精度:
MAE=
RMSE=
其中
Ou={Ii∈ I|
|
本文采用精确率(Precision)衡量CS物品的分类精度:
Precision=
其中Zu表示向用户推荐的N个物品的推荐集.
为了验证IMCF的性能, 选取如下4种算法作为对比算法:
1)基于物品的协同过滤算法(Item Based Colla-borative Filtering, IBCF)[17].
2)基于Jaccard的评分算法(Jaccard Based Ra-ting, JacRA)[18].使用物品属性信息, 是在Jaccard基础上提出的相似度计算方法, 用于解决冷启动问题.
3)考虑用户、标签与项目属性的个性化推荐算法(Consider User, Tag and Item-Attribute Persona-
lized Recommendation Algorithm, CUTA)[19].综合考虑用户、标签与属性信息计算预测评分值, 是解决冷启动问题的代表性算法.
4)基于关联的物品类型与导演相似度算法(Correlation-Based Item Similarity-Genre and Director, CIS-GD)[20].首先结合电影属性与导演, 再与评分进行加权处理以解决冷启动问题, 提高系统的准确性.
本文在IMCF中引入调节参数∂ , 合适的∂ 值能大幅提高推荐系统的准确率, 因此, 本节就∂ 的不同取值进行对比实验.
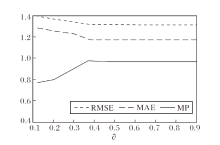
选取推荐物品长度为20, 邻近物品为20, ∂ 的变化趋势如图2所示.
由图2可看出, 随着∂ 值的增大, MP值也随之增加, 当∂ =0.4时, MP值达到峰值, 之后不再变化, 趋向平稳.同理, MAE、RMSE的值也是在∂ =0.4时达到最优.
表6为∂ 变化对Precision的影响.由表6可看出, 随着∂ 值的增大, Precision值也在增加, 当∂ =0.4时, Precision值达到最大.之后, Precision值越来越小.对实验数据的分析结果表明, 当∂ =0.4时, 算法的准确率最高, 说明该指标能影响推荐系统的性能.因此, 本文将∂ 的最优值定为0.4.
| 表6 $\partial$对Precision的影响 Table 6 Effect of $\partial$ on precision |
为了验证CS物品的推荐性能, 从如下4方面进行评估:多样性、新颖性、分类精度和预测精度.评价CS物品推荐的多样性采用MP和覆盖率进行计算, 评价CS物品的新颖性采用Coverage进行计算, 评价CS物品的分类精度采用Precision进行计算, 评价CS物品预测精度采用MAE和RMSE进行计算.
在2个数据集上, 各算法在邻近物品集为20~60, 推荐物品数为2~12时的Precision值对比如表7和表8所示.通过实验可看出, 在大部分情况下本文算法Precision值最高.
| 表7 各算法在MovieLens100K数据集上的Precision值对比 Table 7 Comparison of precision values of different algorithms on MovieLens100K dataset |
| 表8 各算法在MovieLens10M数据集上的Precision值对比 Table 8 Comparison of precision values of different algorithms on MovieLens10M dataset |
各算法在2个数据集上的预测精度如图3和图4所示.
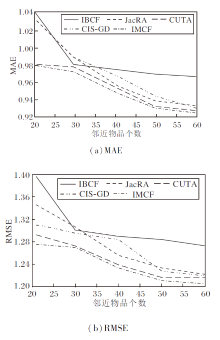 | 图3 各算法在MovieLens100K数据集上预测精度对比Fig.3 Comparison of prediction accuracy of different algorithms on MovieLens100K dataset |
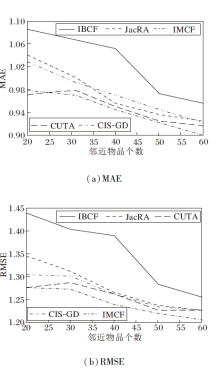 | 图4 各算法在MovieLens10M数据集上预测精度对比Fig.4 Comparison of prediction accuracy of different algorithms on MovieLens10M dataset |
由图3和图4可直观看出, IMCF的误差趋势明显最低.
各算法在2个数据集上的多样性如图5和图6所示.由图可知, 采用IMCF进行推荐时, 多样性和覆盖率都呈稳定上升趋势.
 | 图5 各算法在MovieLens100K数据集上的多样性对比Fig.5 Diversity comparison of different algorithms on MovieLens100K dataset |
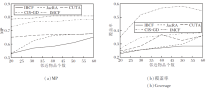 | 图6 各算法在MovieLens10M数据集上的多样性对比Fig.6 Diversity comparison of different algorithms on MovieLens10M dataset |
各算法在2个数据集上的新颖性如图7所示.由图可看出, 在MovieLens100K数据集上, IMCF在邻近物品数为40时开始优于其它方法并呈稳定上升趋势.
在MovieLens10M数据集上, IMCF在邻近物品数为30时开始优于其它方法.
对于新物品而言, 没有用户对其评分或者评分很少, 使用传统的方法不能准确找到它的邻近物品, 导致RS的准确度不高.而且, 对于新物品来说, 不能对它进行预测评分以及推荐, 就不能作为推荐物品推荐给用户, 这是CF存在的CS问题.新物品不能被推荐, 推荐的都是流行的常用物品, 导致RS的物品多样性不高.
本文采用物品属性进行相似度计算, 能有效缓解上述问题.因为每个物品都有对应的属性值, 本文在物品属性相似度的基础上, 增加属性关系挖掘, 进一步探讨属性与属性之间存在的关系, 挖掘隐含涵义, 扩展属性数量, 增加物品之间的区分度.实验显示, 本文算法在邻近物品的选取上更多样化, 不拘泥于流行的物品, 增加其它物品被推荐的机会, 因此推荐的物品多样性较高.实验显示, 本文算法在邻近物品提取上较准确, 因此推荐的准确度也较高, 可以同时解决物品CCS问题和ICS问题.
本文在RS广泛应用的背景下, 提出融合关系挖掘与CF的物品推荐算法, 解决新物品CCS和ICS的推荐问题.结合物品的属性关系与CF, 属性关系挖掘负责物品内容特征的提取与分析, CF负责预测未知的评分.在MovieLens 100K、MovieLens 10M数据集上进行大量实验对比和交叉验证, 用于评估算法性能, 结果表明, 本文算法不仅有效解决新物品冷启动问题, 推荐的多样性和准确度也较高.本文算法在一定范围内提高RS的质量, 但也有许多待改进的地方, 今后将继续深入探索物品的多元属性值对物品相似度和推荐结果的影响.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|




 E
E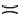 P
P