引用本文
于欢, 张孙贤, 刘子昂, 王志晓. 基于先验估计的传播中心溯源算法. 模式识别与人工智能, 2020,33(1): 86-92
YU Huan, ZHANG Sunxian, LIU Ziang, WANG Zhixiao. Propagation Source Tracing Algorithm Based on Priori Estimation. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2020,33(1): 86-92.  
Doi: 10.16451/j.cnki.issn1003-6059.202001010
Permissions
Copyright©2020, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于先验估计的传播中心溯源算法
于欢1, 张孙贤1, 刘子昂1, 王志晓1
1.中国矿业大学 计算机科学与技术学院 徐州 221116
通讯作者：

王志晓,博士,教授,主要研究方向为数据挖掘、社交网络分析.E-mail:zhxwang@cumt.edu.cn.

作者简介：

于 欢,硕士研究生,主要研究方向为社交网络溯源.E-mail:2537901129@qq.com.

张孙贤,硕士研究生,主要研究方向为社交网络分解.E-mail:ts18170033A31@cumt.edu.cn.

刘子昂,硕士研究生,主要研究方向为社交网络分析.E-mail:634551802@qq.com.

收稿日期: 2019-06-10 接受日期: 2019-10-15
资助项目: 国家自然科学基金项目(No.61876186,61976217)资助
摘要

针对多数信息传播溯源算法未考虑先验估计对溯源的作用和价值,造成溯源检测率较低、错误距离较大等问题,文中利用易感-感染模型(SI)模拟信息在加权网络上的传播过程,提出基于先验估计的传播中心溯源算法.算法综合考虑邻居节点中感染节点和未被感染节点,根据它们的数量关系作为源节点先验估计值,有效弥补现有溯源算法先验估计不足的缺陷.在人工网络和真实网络上的实验表明,文中算法检测率较高、错误距离较小、真实源节点排名精确度较高.

关键词: 传播溯源; 易感-感染模型(SI); 先验估计; 感染节点; 未感染节点
中图分类号:TP 391
Propagation Source Tracing Algorithm Based on Priori Estimation
YU Huan1, ZHANG Sunxian1, LIU Ziang1, WANG Zhixiao1
1. School of Computer Science and Technology, China University of Mining and Technology, Xuzhou 221116
Corresponding author：

WANG Zhixiao, Ph.D., professor. His research interests include data mining and social network analysis.

AboutAuthor：

YU Huan, master student. His research interests include social network source detection.
ZHANG Sunxian, master student. His research interests include network dismantling.

LIU Ziang, master student. His research interests include social network analysis.

Fund:National Natural Science Foundation of China(No.61876186,61976217)
Abstract

The deficiencies of most existing spreading source detection methods are low detection rate and large error distance due to the disregard of priori estimation of source node. The infection model, susceptible-infected(SI), is utilized to simulate the propagation process of information in weighed social networks, and a spreading source tracing algorithm based on priori estimation is proposed. Both infected and uninfected nodes of neighborhood are considered, and priori estimations are assigned to the source node according to the number relationship between infected nodes and uninfected nodes. Experiments on artificial and real networks indicate that the proposed algorithm achieves a high detection rate, a small error distance and a high accuracy of real source node ranking.

Key words: Key Words Spreading Source Tracing; Susceptible-Infected(SI) Model; Priori Estimation; Infected Node; Uninfected Node

本文责任编委 于剑

Recommended by Associate Editor YU Jian

随着社交网络[1]的发展, 信息源检测[2]、信息传播分析[3]等研究日益受到关注.信息传播溯源是根据某一时刻网络节点状态信息寻找信息扩散源节点的模型, 被广泛应用于现实生活中.例如:当疫情发生时, 快速推断疾病起源, 有利于疾病防控; 当计算机病毒在网络中爆发时, 准确找出病毒源, 有效维护网络安全.

现有信息传播溯源算法大致分为3类:基于传播源中心性的溯源算法、基于置信传播的溯源算法和基于蒙特克洛模拟的溯源算法.

传播源中心性算法主要包括传播中心性(Rumor Centrality, RC)[4]、距离中心性(Distance Cen-trality, DC)[5]和Jorden 中心性 (Jorden Centrality, JC)[6].RC认为感染子图中某个节点是传播源的概率和信息与从该节点出发感染其它节点的所有可能顺序的计数呈正比[2].DC认为源节点到其余感染节点的距离之和最小.为了降低计算的复杂度, 定义类似Jordan中心性的Jordan感染中心, 认为源节点到其它感染节点的最大距离最小.此类算法只考虑感染节点, 忽略未被感染节点, 认为感染节点作为源节点的先验估计值相等.

基于置信度传播的溯源算法主要包括动态消息传递算法(Dynamic Message-Passing, DMP)[7]和置信传播算法(Belief Propagation, BP)[8].DMP计算每个节点在t时刻的各状态概率, 时间复杂度较高.BP基于因子图所得的传播源后验概率, 真实源能在所有节点中取得最大值[2].

基于蒙特卡洛模拟的溯源算法主要是k最小距离溯源算法(k-Minimum Distance Rumor Source De-tection, k-MDSRD)[9]. k-MDRSD对观察到的感染节点采用蒙特卡洛模型模拟信息反向传播过程, 根据模拟效果计算k个候选节点, 通过这些节点以最小的询问代价找到源节点, 但时间复杂度较高.

Jiang等[10]将溯源运用到时序网络中.计算每个节点在每时刻各状态概率, 取与观察到状态一致且概率较高的节点为源节点.Zhou等[11]在易感-曝光-感染-恢复模型(Susceptible-Exposed-Infected-Recover-ed, SEIR)上提出基于最优感染过程(Opti-mal Infection Process, OP)的溯源算法, 通过寻找最优感染过程进行溯源.Pan 等[12]提出基于摄动的单源溯源算法(Perturbation-Based Single Source Identi-fication, PSSI), 将感染网络转化为非回溯矩阵(Nonbacktracking Matrix), 计算得到主特征值下降量, 取下降量最大的节点作为源节点.此方法更适合于环结构较多的网络.

目前, 大多数信息传播溯源算法忽略先验估计的作用和价值, Chang等[13]提出基于贪婪近似搜索和传播中心性的溯源算法(Greedy Search Bound Approximation-Rumor Centrality, GSBA-RC), 虽然考虑先验估计的重要性, 但仅以RC作为先验估计存在一定缺陷.针对上述问题, 本文综合考虑邻居节点中感染节点和未被感染节点, 根据它们的数量关系作为源节点先验估计值, 提出基于先验估计的传播中心溯源算法(Propagation Source Tracing Algorithm Based on Priori Estimation, PSTPE).实验表明, 本文算法在检测率、错误距离、真实源节点排名精度等方面的性能都较优, 在不同规模、不同结构的网络中表现较强的适应性.

1 基于先验估计的传播中心溯源算法
1.1 问题定义

使用G(V, E, A)表示无向加权网络, 其中, V为节点集, E为边集, A=[aij], aij∈ [0, 1]为节点i和j之间的信息传播概率.在网络上利用易感-感染(Susceptible-Infected, SI)模型进行信息扩散, 每个节点有两种可能的状态:未被感染、感染.一旦节点i被感染, 它将保持感染状态, 不再恢复.同时节点i尝试将信息传播到未被感染的邻居节点j, 节点j被感染概率为aij.

随机选择一个节点作为传播源, 当N个节点被感染后停止传播.感染节点集合使用VI表示, EI 为感染节点VI存在的边集, GI(VI, EI)为由VI和EI组成的感染子图, 该子图相互连通, 因为每个未被感染节点只能被其邻居感染.

溯源问题是指:在已知感染子图GI的前提下, 计算v* 作为源节点的可能性, 表示为P(v* =v|GI), 取度量值最大的节点作为源节点,

v^=arg maxv∈GIP(v* =v|GI).(1)

基于贝叶斯理论, 可以把溯源问题写成先验估计与后验估计的乘积形式:

P(v* =v|GI)= P(v* =v)P(GI|v* =v)P(GI)∝ P(v* =v)P(GI|* =v),

其中, P(v* =v)表示v* 节点作为源节点的先验估计, P(GI |v* =v)表示当v* 作为源节点时能观察到GI的后验估计.

1.2 源节点先验估计

本文从感染时间的角度出发, 认为源节点参与感染时间最长, 对邻居节点感染时间也最长, 其邻居中被感染的比例应该最大.以v节点邻居中的感染节点与邻居节点数量比值的N次方作为v节点的先验估计:

P(v* =v)=(vnivn)N, (2)

其中, vni表示节点v邻居中感染节点的数量, vn表示节点v邻居数量, N表示感染节点数量.

图1为网络节点状态快照, 观察图可发现, 节点2邻居全被感染, 节点4邻居部分被感染, 节点2作为源节点的先验估计应高于4.若以RC作为先验估计, 节点2的RC值和节点4相等.以本文方法作为先验, 节点2的先验估计值

P(v* =2)=(33)6,

节点4的先验估计值

P(v* =4)=(37)6,

节点2的值远高于节点4.由此可见, 本文算法的先验估计更符合实际情况.

图1 网络节点状态快照Fig.1 Snapshot of network node status

1.3 传播中心性

传播中心性R(v, GI)[4]是从节点v出发感染其它节点的所有可能顺序的计数, 在本文中作为节点v的后验估计.R(v, GI)认为信息扩散后, 会生成一个感染节点序列:

σ = {v1, v2, …, vN}, 1≤ i≤ N,

其中vi∈ VI为第i个感染节点, 即σ (i) = vi.这个序列按照感染时间进行排序, 称为允许排列.它和网络结构统一.例如, 在图1中{1, 2, 3, 4, 5, 6}是允许排列, 但{1, 3, 2, 4, 5, 6}不是允许排列, 因为节点3不是节点1的邻居, 不可能直接被节点1感染.

若GI是树结构, R(v, GI)定义如下:

R(v, GI)=N! ∏u∈GI1Tuv,

其中, u为GI的某个节点, Tuv为GI中以节点u为源节点、向远离节点v的方向展开的子树中的节点数量[2], N为感染节点数量.

如果GI 是非树结构, 则先以v为根节点, 构建宽度优先搜索树, 使用符号 Tbfs(v)表示, 再使用 Tbfs(v)代替GI进行计算.

1.4 算法步骤

本文算法思想描述如下:根据感染节点集合VI生成感染子图GI.再根据感染子图GI, 构建以v为根节点的宽度优先搜索树 Tbfs(v), 计算R(v, Tbfs(v)), 同时遍历节点v的邻居状态, 求出先验估计P(v* =v).最后根据式(1)计算v作为源节点的度量, 选择度量值最大的节点.具体算法步骤如下.

算法 PSTPE

输入 网络G, 感染节点集合VI

输出 检测源节点 v^

GI= GetSubGraph(G, VI);

/* 根据网络、感染节点得到感染子图GI* /

for v∈ VI do

Tbfs(v)= GenerateBFS(GI, v);

/* 根据GI, 构建以v为根节点的宽度优先搜索树* /

P(GI|v* =v)= CalRC(v, Tbfs(v));

/* 计算v节点的传播中心性值* /

P(v* =v)= CalPrior(v, VI);

/* 根据式(2)计算v节点的先验值* /

P(v* =v|GI)= P(GI|v* =v)P(v* =v)

Select v^according to Eq.(1)

Return v^

2 实验及结果分析

实验数据集包括2类:人工网络SCALE-FREE和真实网络POWER-GRID[14]、WIKI-VOTE[15]、CA-ASTROH[16].

人工网络利用Barabá si-Albert模型[7]生成.POWER-GRID为美国电力网络, WIKI-VOTE为Wikipedia上的一个投票网络, CA-ASTROPH为一个协作网络.实验中所用网络的信息如表1所示.

表1 实验数据集 Table 1 Information of datasets

本文选取5种具有代表性的信息传播溯源算法, 从不同角度对比算法性能.对比算法包括:RC、JC、DC、GSBA-RC和PSSI.

RC的时间复杂度为O(|V2|2).DC和JC的时间复杂度为

O(|E2||V2|).

GSBA-RC的时间复杂度为O(C|V2|2), 其中C表示网络的平均度值.PSSI的时间复杂度为O(|V2|).PSTPE的时间复杂度为O(|V2|2).

本文采用3个指标[2, 5, 18]评价溯源算法性能的好坏.

1)检测率(Detection Rate).又称准确率, 定义如下:

Detection Rate= MTM,

其中, M表示实验的总次数, MT表示检测的源节点正确的次数.

2)错误距离(Error Hops).表示检测源节点到真正源节点的最短距离.

3)标准化排名(Normalized Ranking).根据算法计算各节点是源节点的估量值, 对这些值进行降序排列, 求真正的源节点在排列中的百分比, 定义如下:

Normalized Ranking= Ranking(v* )-1N,

其中, v* 表示真正源节点, N表示感染节点数量, Ranking(v* )表示v* 在排序列表中的名次.

检测率在一定程度上反映算法找到源节点的准确程度.错误距离显示检测到的源节点与真实源节点的最短距离.标准化排名可以验证算法对真实源节点排序的精度.检测率越大, 对应算法性能越好, 但错误距离和标准化排名相反, 值越小表示对应算法性能越好.

为了分析感染节点与未感染节点数量关系的重要性, 在SCALE-FREE网络上对比GSBA-RC与PSTPE的性能.GSBA-RC同时考虑感染节点和未感染节点, PSTPE不仅考虑感染节点和未感染节点, 而且考虑它们之间的数量关系.

表2显示一组实验中GSBA-RC和PSTPE源节点估计值前10%节点的编号, 其中真实源节点编号为92.GSBA-RC得到的前10%的估计源节点到真实源节点92的距离分别为2、0、2、2、2.PSTPE计算的前10%的估计源节点到真实源节点92的距离分别为0、2、2、1、1.对比两种结果发现, 虽然都能在估计值前10%的节点内找到真实源节点, 但PSTPE中估计值靠前的节点距离真实源节点更近, 从侧面表明感染节点和未感染节点数量关系的重要性.

表2 2种算法源节点估计值前10%节点的编号 Table 2 Node number of top 10% of source node estimation for 2 algorithms

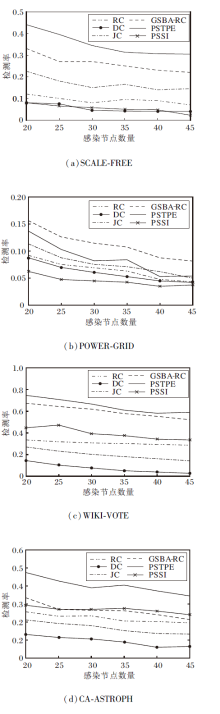
图2为6种信息传播溯源算法在4个网络上检测率随感染节点数量增多而变化的情况.

图2 各算法在4个网络上的检测率Fig.2 Detection rate of different methods on 4 networks

由图2可看出, 当感染节点增多时, 6种算法的检测率呈现下降趋势.在人工网络SCALE-FREE中, PSTPE检测率最高, 效果最优.在真实网络POWER-GRID中, PSTPE检测率仅次于GSBA-RC, 高于其它对比算法, 但相比其它3个网络, 所有算法检测率都不高, 原因是:POWER-GRID网络较稀疏, 在感染一定数量的节点的前提下, 信息传播范围较大, 溯源难度较高; 其次, GSBA-RC的后验估计是通过前i-1个节点计算第i个感染节点的概率, 当网络稀疏时, 每轮感染节点数量更少, 更贴合方法思想, 所以实验效果较好.而PSTPE先验估计与邻居节点中感染节点和未感染节点数量关系相关, 当网络稀疏时, 先验估计趋向于1或0的概率较大, 效果不佳, 因此该模型更适合于非稀疏网络.在WIKI-VOTE和CA-ASTROPH网络上, PSTPE效果最优, 特别在CA-ASTROPH网络上, PSTPE比排名第二的算法检测率高出15%左右.

实验分析表明, 在实验所选4个网络上, PSTPE在3个网络上性能最优, 在POWER-GRID网络上的性能仅次于GSBA-RC.

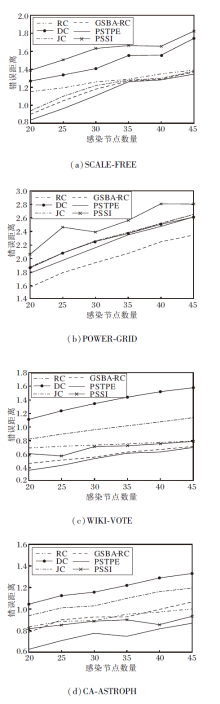
图3为6种信息传播溯源算法错误距离的折线图, 错误距离越短, 表示检测的源节点越靠近真实的源节点, 算法效果越优.此组实验结果与图2类似, 在此就不再赘述.

图3 各算法在4个网络上的错误距离Fig.3 Error distance of different methods on 4 networks

表3为6种信息传播溯源算法标准化排名随感染节点数量的变化情况.由表可看出, 标准化排名出现一种反常情况:前两种评价指标都是随着感染节点的增多, 效果变差, 部分溯源算法对源节点的排名精确度有所提升.分析原因是:标准化排名是一个比值, 随着感染节点数量的增加, 排名名次变大, 但变化幅度低于分母感染节点数量的变化幅度, 所以值变小, 效果变佳.其余结果与图2类似, 在此不再赘述.

表3 各算法的标准化排名 Table 3 Normalized ranking of different methods
3 结束语

针对大多数信息传播溯源算法因缺失先验估计造成溯源检测率不高、错误距离较大等问题, 本文通过考虑邻居节点的感染状态, 提出基于先验估计的传播中心溯源算法.

在人工网络和真实网络上的结果表明:本文算法具有检测率较高、错误距离较小、真实源节点排名精确度较高等优势, 具有较强的适应性, 在不同规模、不同结构的网络上表现稳定.

未来工作主要从两方面展开:

1)本文算法基于SI信息传播模型, 考虑到感染节点可能会恢复成健康状态, 下一步将算法推广到易感-感染-恢复(Susceptible-Infected-Recovered, SIR)等模型.

2)本文算法主要针对单源溯源问题, 现实中会出现多个传播源同时传播信息的情况, 因此有必要将本文算法扩展至多源溯源中.

参考文献
[1] LIU Q, XIANG B, YUAN N J, et al. An Influence Propagation View of PageRank. ACM Transactions on Knowledge Discovery from Data, 2017, 11(3). DOI: DOI:10.1145/3046941. [本文引用:1]
[2] 黄春林, 刘兴武, 邓明华, 等. 复杂网络上疾病传播溯源算法综述. 计算机学报, 2018, 41(6): 1376-1399.
(HUANG C L, LIU X W, DENG M H, et al. A Survey on Algorithms for Epidemic Source Identification on Complex Networks. Chinese Journal of Computers, 2018, 41(6): 1376-1399. ) [本文引用:5]
[3] 郭琛. 社交网络分析与信息传播研究. 硕士学位论文. 上海: 复旦大学, 2012.
(GUO C. Research on Social Network Analysis and Information Dissemination. Master Dissertation. Shanghai, China: Fudan University, 2012. ) [本文引用:1]
[4] SHAH D, ZAMAN T. Rumors in a Network: Who's the Culprit? IEEE Transactions on Information Theory, 2009, 57(8): 5163-5181. [本文引用:2]
[5] SHAH D, ZAMAN T. Detecting Sources of Computer Viruses in Net-works. ACM SIGMETRICS Performance Evaluation Review, 2010, 38(1): 203-214. [本文引用:2]
[6] ZHU K, YING L. Information Source Detection in the SIR Model: A Sample Path Based Approach. IEEE/ACM Transactions on Networking, 2016, 24(1): 408-421. [本文引用:1]
[7] LOKHOV A Y, MEZARD M, OHTA H, et al. Inferring the Origin of an Epidemic with a Dynamic Message-Passing Algorithm. Physical Review E, 2013, 90(1). DOI: DOI:10.1103/PhysRevE.90.012801. [本文引用:2]
[8] ALTARELLI F, BRAUNSTEIN A, DALL'ASTA L, et al. Bayesian Inference of Epidemics on Networks via Belief Propagation. Physical Review Letters, 2013, 112(11): 118701-118706. [本文引用:1]
[9] LIM S, HAO J, LU Z X, et al. Approximating the k-Minimum Distance Rumor Source Detection in Online Social Networks // Proc of the 27th International Conference on Computer Communication and Networks. Washington, USA: IEEE, 2018. DOI: DOI:10.1109/ICCCN.2018.8487400. [本文引用:1]
[10] JIANG J J, WEN S, YU S, et al. Rumor Source Identification in Social Networks with Time-Varying Topology. IEEE Transactions on Dependable and Secure Computing, 2018, 15(1): 166-179. [本文引用:1]
[11] ZHOU Y S, WU C J, ZHU Q Y, et al. Rumor Source Detection in Networks Based on the SEIR Model. IEEE Access, 2019, 7: 45240-45258. [本文引用:1]
[12] PAN J C, ZHANG W Y. Identifying Rumor Source Using Dominant Eigenvalue of Nonbacktracking Matrix // Proc of the IEEE Global Conference on Signal and Information Processing. Washington, USA: IEEE, 2018, 748-752. [本文引用:1]
[13] CHANG B, CHEN E H, ZHU F D, et al. Maximum a Posteriori>Estimation for Information Source Detection. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2018. DOI: DOI:10.1109/TSMC.2018.2811410. [本文引用:1]
[14] WATTS D J, STROGATZ S H. Collective Dynamics of 'Small-World' Networks. Nature, 1998, 393: 440-442. [本文引用:1]
[15] LESKOVEC J, HHTTENLOCHER D, KLEINBERG J. Predicting Positive and Negative Links in Online Social Networks // Proc of the 19th International Conference on World Wide Web. New York, USA: ACM, 2010: 641-650. [本文引用:1]
[16] LESKOVEC J, KLEINIBER J, FALOUTSOS C. Graph Evolution: Densification and Shrinking Diameters. ACM Transactions on Knowledge Discovery from Data, 2007, 1(1). DOI: DOI:10.1145/1217299.1217301. [本文引用:1]
[17] BARABÁSI A L, ALBERT R. Emergence of Scaling in Rand om Networks. Science, 1999, 286(5439): 509-512 [本文引用:1]
[18] NGUYEN D T, NGUYEN N P, THAI M T. Sources of Misinformation in Online Social Networks: Who to Suspect? // Proc of the IEEE Military Communications Conference. Washington, USA: IEEE, 2013. DOI . DOI:10.1109/MILCOM.2012.6415780. [本文引用:1]