基于局部曲面特征直方图的点云识别

引用本文

陆军, 华博文, 朱波. 基于局部曲面特征直方图的点云识别. 模式识别与人工智能, 2020,33(10): 934-943
LU Jun, HUA Bowen, ZHU Bo. Point Cloud Recognition Based on Local Surface Feature Histogram. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2020,33(10): 934-943. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202010008
Permissions

《模式识别与人工智能》编辑部

基于局部曲面特征直方图的点云识别

陆军¹, 华博文¹, 朱波¹

1.哈尔滨工程大学智能科学与工程学院哈尔滨 150001

通讯作者:

陆军,博士,教授,主要研究方向为计算机视觉、智能控制.E-mail:lujun0260@sina.com.

作者简介:

华博文,硕士研究生,主要研究方向为计算机视觉.E-mail:1041893894@qq.com.

朱波,硕士研究生,主要研究方向为计算机视觉.E-mail:2205252739@qq.com.

收稿日期: 2020-06-22 接受日期: 2020-10-26

摘要

针对三维点云的快速识别问题,文中提出基于局部曲面特征直方图的点云识别算法.首先,采用循环体素滤波算法,将不同分辨率的点云滤波至指定分辨率.再基于邻域曲率均值最大的关键点查找算法选取点云局部特征较明显的点作为关键点,根据关键点邻域内点云重心与邻域曲面内各点的法线和距离的关系计算关键点的特征描述符.然后,根据临近关键点间的空间关系和特征描述符欧氏距离进行特征匹配.最后,采用多线程识别框架,加快在线识别速度.实验表明文中算法识别速度较快.

关键词: 三维点云; 特征描述符; 配准; 识别

中图分类号:TP391.4

Point Cloud Recognition Based on Local Surface Feature Histogram

LU Jun¹, HUA Bowen¹, ZHU Bo¹

1.College of Intelligent Systems Science and Engineering, Harbin Engineering University, Harbin 150001

Corresponding author:
LU Jun, Ph.D., professor. His research interests include computer vision and intelligent control.

AboutAuthor:
HUA Bowen, master student. His research interests include computer vision.
ZHU Bo, master student. His research interests include computer vision.

Abstract

Aiming at fast recognition of 3D point clouds, a point cloud recognition algorithm based on local surface feature histogram is proposed. Firstly, the cyclic voxel filtering algorithm is applied to filter the point clouds with different resolutions to the specified resolution. Secondly, the points with obvious local characteristics are selected as the key points based on the key point search algorithm with the maximum mean curvature of the neighborhood. The feature descriptor of the key point is calculated according to the relationship between the center of gravity of the point clouds in the neighborhood and the normal and distance of each point in the neighborhood surface. Then, the features are matched according to the spatial relationship between the adjacent key points and the Euclidean distance of the feature descriptor. Finally, the multithread recognition framework is adopted to speed up the online recognition. The experimental results show that the recognition speed is high.

Key words: Key Words 3D Point Cloud; Feature Descriptor; Registration; Recognition

文章图片

本文责任编委汪增福

Recommended by Associate Editor WANG Zengfu

目标识别是计算机视觉领域研究的热点问题之一, 主要应用领域包括监视器^[1]、生物特征识别^[2]、工业检查、场景理解和机器人自动行走^{[3, 4]}.针对二维识别, 现存的方法主要分为特征提取^{[5, 6]}、机器学习^{[7, 8]}、仿射变换技术^{[9, 10]}.然而, 由于二维识别算法需要将点云由三维空间投影至二维空间, 图像丢失物体的深度信息, 造成识别算法对光照、姿态、遮挡较敏感, 所以近年来越来越多的学者开始关注使用三维点云数据识别对象.

由于点云数据的无序性、易变性和数据量较大的特点, 点云识别算法又可分为基于模型的方法、基于外观的方法、基于图匹配的方法、基于统计学的方法和基于降维的方法.

基于模型的点云识别算法通过关键点与模型匹配以识别整体^{[11, 12]}, 需要在离线阶段生成各类别的模型点云、关键点、特征描述符.在在线识别阶段, 需要在场景点云中提取关键点, 使用局部特征描述关键点的局部邻域, 并与已离线好的模型库匹配.基于模型的物体识别无需对单目标点云进行分割, 关键点和特征描述符直接影响识别算法的最终性能.

Shah等^[13]提出基于3D形状的对象识别系统, 可同时识别场景中多个对象.识别系统使用旋转图像描述符匹配点和表面, 由于该描述符包含关键点邻域的统计信息, 故抗旋转性较好, 缺点是只能处理分布较均匀的点云.Sales等^[14]提出在3D模型和对象局部视图上检测特征丰富关键点的算法, 关键点在对象的部分视图之间具有较高的可重复性, 采用主成分分析计算关键点的局部坐标系, 通过协方差矩阵计算点云姿态, 直接在识别搜索表中搜索该参数值, 避免只根据法线识别导致识别方位模糊的问题.由于算法容易受到噪声、非均匀点云的影响, 特征描述的鲁棒性较差.Guo等^[15]提出高度独特的局部表面特征, 称为TriSI(Tri-Spin-Image)特征, 用于在杂波和遮挡时识别3D对象.对于一个特征点, 首先使用相邻三角形面的隐式几何信息构造一个唯一、可重复的局部参考系(Local Reference Frame, LRF).然后基于LRF的3个正交坐标轴生成3个签名, 连接这3个签名并将它们压缩为TriSI功能.最后, 提出基于层次特征匹配的有效3D对象识别算法, 并测试多个特征描述符在噪声、遮挡、分辨率等多方面干扰下的性能.张哲等^[16]提出快速点特征直方图, 通过简化的点特征直方图(Point Feature Histograms, PFH)实现算法加速.尽管这类算法的识别性能不断提高, 但由于点云数据的计算复杂度较高, 识别时间仍较长, 自动化程度较低.

针对上述问题, 本文提出基于局部曲面特征直方图的点云识别算法.算法主要由循环体素滤波算法、基于局部曲率均值的关键点查找算法、基于局部曲面直方图的特征描述符、基于关键点间空间位置关系的特征匹配算法和多线程识别框架组成.算法可根据点云尺度自动设置滤波后场景点云和目标点云的分辨率大小、邻域尺寸大小和对应点最大距离等相关参数, 整个识别过程不需要人工参与设定参数, 识别精度和计算效率都较高.

1 基于局部曲面特征直方图的点云识别算法

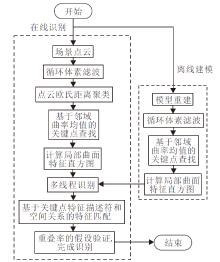
基于局部曲面特征直方图的点云识别算法主要包括离线建模和在线识别两部分, 算法流程图如图1所示.在对物体场景点云进行在线识别之前, 需要先通过离线建模建立一个完整的点云模型库, 包含物体的模型点云、关键点和特征描述符.

	Figure Option View Download New Window
	图1 本文算法流程图Fig.1 Flowchart of the proposed algorithm

离线建模首先通过模型重建构建物体的一个完整的三维模型点云.再通过循环体素滤波算法将模型点云滤波到指定分辨率, 为在线识别做准备.最后基于邻域曲率均值查找模型点云的关键点, 计算得到的模型点云关键点的局部曲面特征直方图作为特征描述符, 并将得到的三维模型点云、模型点云的关键点和特征描述符加入模型库中完成离线建模.

在线识别首先通过循环体素滤波将场景点云滤波到模型点云的分辨率, 目的是为了使用预先建立的离线模型库.再基于邻域曲率均值查找聚类后场景点云的关键点, 计算场景点云关键点的局部曲面特征直方图, 作为特征描述符.然后采用多线程识别框架, 对模型库中的模型点云都开启一个线程.最后根据关键点特征描述符和空间关系进行特征匹配, 计算重叠率, 识别对象.

1.1 在线识别

1.1.1 循环体素滤波算法

由于点云采集设备的不同及与物体间距离的远近不同, 采集到的点云分辨率存在较大的差异, 导致在识别过程中需要人工设置多个参数.为了减少手动设置算法参数的工作量, 实现点云自动快速识别, 首先需要计算点云中点与点的平均距离, 即点云分辨率s:

s= $\frac{1}{n} \overset{n}{\sum_{i = 1}}$ ‖ p_i-p'_i‖ ₂,

其中, p_i为点云中的第i个点, p'_i为其最近邻点, n为点云中点的数量.

通过循环体素滤波算法将点云滤波到统一分辨率s_target, 具体步骤如下.

算法1 循环体素滤波算法

step 1 计算当前点云分辨率s_now.

step 2 如果1.02s_now小于设定值s_target, 继续对当前点云进行体素滤波, 体素大小

s_loop=s_target+0.2(s_target-s_now);

如果1.02s_now大于等于设定值s_target, 转入step 4.

step 3 重新计算一轮循环后的点云分辨率, 并将其赋于s_now, 重复step 2.

step 4 结束滤波.

为了将s_now与s_target的误差控制在2%以内, 在循环体素滤波算法设置参数1.02和0.2, 其中0.2为一个经验参数, 取值范围可在0~1之间.

通过多次循环体素滤波, 将点云分辨率逼近到设定分辨率, 便于后续查找关键点和计算特征描述符.

1.1.2 基于邻域曲率均值的关键点查找算法

点云滤波后, 点数仍旧较多, 大部分点位于平面等局部特征不明显的区域.为了加快识别速度, 需要查找点云的关键点以减少计算量.经典算法通常根据点云中单个点的属性查找关键点, 对噪声较敏感.为了提高算法的抗噪性和快速性, 本文提出基于邻域曲率均值最大的关键点查找算法, 主要包括预关键点查找算法、局部曲率均值计算和非极大值抑制.

1)预关键点查找算法.由于平面特征较少, 选取大于一定曲率的点云作为关键点可有效降低关键点数量.大量实验表明, 选取曲率c_th=0.02可有效去除平面上的点被选作关键点, 并保留曲面点, 在曲率大于c_th的点中寻找关键点, 可加快关键点查找速度.建立n维列向量pre存储点云中的点是否为预关键点, 向量初始值设为0.pre_i=0, i=1, 2, …, n, 表示第i个点不是预关键点, pre_i=1, i=1, 2, …, n, 表示第i个点是预关键点, 如果第i个点的曲率大于c_th, 将pre_i设置为1, 作为预关键点.

2)局部曲率均值计算.建立n维列向量ac_i表示第i个点邻域内所有点的曲率均值:

ac_i= $\frac{1}{m} \overset{m}{\sum_{a = 1}} c_{i}^{a}$ ,

其中, $c_{i}^{a}$ 为点p_i的邻域点 $p_{i}^{a}$ 的曲率, m为邻域点数.

初始值ac_i=0, i=1, 2, …, n, 邻域大小r=5s_target.若点p_i不是预关键点, 邻域曲率均值ac_i=0.若点p_i是预关键点, 计算ac_i邻域内的点表示为 $p_{i}^{a}$ 均值.

3)非极大值抑制.当判定一预关键点是其邻域内曲率均值最大的点时, 将属于该预关键点邻域内的其它预关键点的标志置1, 否则, 将该预关键点的标志置0.进一步减少预关键点数量, 实现算法加速, 并确保邻域内具有代表性的点被选作关键点.

经过上述3个过程, 最后将预关键点标志为1的点作为最终的关键点p_k.关键点查找流程如图2所示, 图中pr $e_{i}^{a}$ 为点p_i的邻域点 $p_{i}^{a}$ 的预关键点标志.

	Figure Option View Download New Window
	图2 关键点查找流程图Fig.2 Flowchart of key point search algorithm

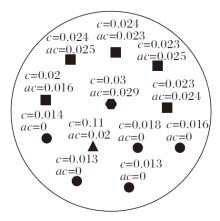
关键点查找算法抗噪原理如图3所示, 曲率阈值c_th=0.02, 由于曲率小于曲率阈值, 圆形点为非预关键点, 直接令其邻域曲率均值为0.正方形点的曲率大于曲率阈值, 但其邻域曲率均值并非邻域内最大值, 为预关键点.三角形点曲率值异常, 曲率大于曲率阈值, 为噪声点.六边形点曲率大于曲率阈值, 其邻域曲率均值为自身邻域内最大值, 为关键点.

	Figure Option View Download New Window
	图3 关键点查找算法抗噪声示意图Fig.3 Anti-noise diagram of key point search algorithm

在计算邻域曲率均值时, 以及噪声点周围的邻域点计算自身的邻域曲率均值时, 都是使用该噪声点的异常曲率.异常曲率对其邻域内所有点的曲率均值造成相同影响, 所以噪声点的曲率异常对寻找关键点的影响较小.

1.1.3 局部曲面特征直方图

经典点云特征描述符依赖于关键点与其邻域点属性的关系, 描述以关键点为基准的邻域信息, 当误将噪声作为关键点时, 由于噪声点信息异常, 导致特征描述符无法正确描述关键点邻域的几何特征.为此根据关键点邻域内点云重心与邻域曲面内各点的法线和距离的关系计算关键点的特征描述符, 通过直方图的方法进行统计, 并把此特征描述符命名为局部曲面特征直方图.该特征描述符将局部点云作为整体描述, 可有效克服关键点噪声的影响.

首先需要确定关键点p_k的邻域, 邻域半径r=5s_target.然后计算该邻域点集的重心 ${\overset{̅}{p}}_{k}$ 和邻域点 $p_{k}^{a}$ 到重心 ${\overset{̅}{p}}_{k}$ 的距离d_a, 将最近距离记作d_min, 最远距离记作d_max.把最远距离到最近距离的差平均分为15份, 如图4所示, 其中每份距离

d_res= $\frac{d_{\max} - d_{\min}}{15}$ .

	Figure Option View Download New Window
	图4 距离分组示意图Fig.4 Illustration of distance grouping

计算邻域点 $p_{k}^{a}$ 所属的距离分组:

bi $n_{d}^{a}$ =「 $\frac{d_{a} - d_{\min}}{d_{res}}$ ⌉∈ [1, 15],

其中「⌉为向上取整.

同理, 计算邻域点 $p_{k}^{a}$ 的法线和该点与重心 ${\overset{̅}{p}}_{k}$ 连线的夹角angle_a∈ (0, 180^°), 将夹角平均分为18份, 每份10° , 得到邻域点 $p_{k}^{a}$ 所属的余弦值分组:

bi $n_{angle}^{a}$ =「 $\frac{angl e_{a}}{angl e_{res}}$ ⌉∈ (1, 18),

其中angle_res=10.

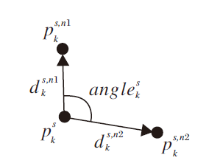
当误将噪声计算为关键点时, 由于特征描述符计算关键点邻域重心与其邻域内其它点的几何关系, 可缩小特征描述符误差.距离分组抗噪原理如图5所示, 其中, p_k为正确关键点, p'_k为噪声点, p_k对应的重心点为 ${\overset{̅}{p}}_{k}$ , p'_k对应的重心点为 $\overset{̅}{p}$ '_k.

	Figure Option View Download New Window
	图5 距离分组抗噪示意图Fig.5 Illustration of anti-noise distance grouping

由图5可看出, 当误将噪声点作为关键点时, 产生的邻域重心误差较小, 由错误重心计算的邻域点 $p_{k}^{a}$ 在分组位置bi $n_{d}^{a}$ 的误差较小, 计算的特征描述符仍可正确描述该邻域.

给关键点p_k建立初始值全为0的33维列向量F, 用于存储邻域信息, 其中前15维用于存储邻域点落在每个距离分组的点数, 后18维用于存储邻域点落在每个角度分组的点数.计算每个邻域点 $p_{k}^{a}$ 的bi $n_{d}^{a}$ 和bi $n_{angle}^{a}$ , 在F的相应位置加一计数.

由于点云表面的弯曲程度不同, 尽管分辨率和邻域半径相同, 邻域点数也不相同, 为了便于度量特征描述符的差异, 需对特征描述符进行归一化处理, 将每个特征描述符的每一维除以该关键点的邻域点数.

1.1.4 基于关键点特征描述符和空间关系的特征匹配算法

常见特征匹配通常基于关键点特征描述符的欧氏距离度量特征差异, 通过查找特征描述符的最近点作为对应关系, 但由于点云中某些关键点的邻域信息相似, 造成大量匹配, 若匹配关系错误过多, 造成最终配准失败.为此, 本文从全局出发, 提出基于关键点复合特征的特征匹配算法, 有效利用关键点间空间位置关系和关键点的特征描述符进行精确匹配.

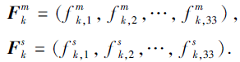
设模型点云关键点 $p_{k}^{m}$ 的特征向量为 $F_{k}^{m}$ , 场景点云关键点 $p_{k}^{s}$ 的特征向量为 $F_{k}^{s}$ :

计算特征向量 $F_{k}^{m}$ 与 $F_{k}^{s}$ 的欧氏距离:

d( $F_{k}^{m}$ , $F_{k}^{s}$ )= $\sqrt[]{\overset{33}{\sum_{j = 1}} (f_{k, j}^{m} - f_{k, j}^{s})^{2}}$ .

对于场景点云的关键点 $p_{k}^{s}$ , 根据特征描述符, 在模型点云中建立KD-tree, 搜索模型点云中与该关键点特征描述符的10个近邻点, 并按照这些特征描述符与关键点 $p_{k}^{s}$ 描述符的欧氏距离从小到大排序 $p_{k}^{m, j}$ , j=1, 2, …, 10, $p_{k}^{m, j}$ 表示场景点云关键点 $p_{k}^{s}$ 在模型点云关键点中按照特征描述符欧氏距离从小到大排序的第j个近邻.若最近邻 $p_{k}^{m, 1}$ 的特征描述符与关键点 $p_{k}^{s}$ 的特征描述符的欧氏距离小于次近邻 $p_{k}^{m, 2}$ 的特征描述符与关键点 $p_{k}^{s}$ 的特征描述符欧氏距离的一半, 则将该最近邻 $p_{k}^{m, 1}$ 作为该场景点云关键点 $p_{k}^{s}$ 的对应点, 组成一组对应关系.否则, 查找场景点云关键点 $p_{k}^{s}$ 在场景点云关键点中按照空间坐标欧氏距离的最近邻点 $p_{k}^{s, n 1}$ 和次近邻点 $p_{k}^{s, n 2}$ , 并计算点 $p_{k}^{s}$ 分别与点 $p_{k}^{s, n 1}$ 和点 $p_{k}^{s, n 2}$ 的空间距离 $d_{k}^{s, n 1}$ 和欧氏距离 $d_{k}^{s, n 2}$ , 计算场景点云关键点 $p_{k}^{s}$ 与场景点云关键点最近邻 $p_{k}^{s, n 1}$ 的连线和场景点云关键点 $p_{k}^{s}$ 与次近邻 $p_{k}^{s, n 2}$ 连线的夹角angl $e_{k}^{s}$ , 如图6所示.

	Figure Option View Download New Window
	图6 关键点空间关系示意图Fig.6 Spatial relationship of key points

按照空间距离, 依次计算点 $p_{k}^{m, j}$ , j=1, 2, …, 10在模型点云关键点中的最近邻 $p_{k}^{m, j, n 1}$ 和它们之间的空间距离 $d_{k}^{m, j, n 1}$ 、次近邻 $p_{k}^{m, j, n 2}$ 及其与 $p_{k}^{m, j}$ 的空间距离 $d_{k}^{m, j, n 2}$ , 计算模型点云关键点 $p_{k}^{m, j}$ 与模型点云关键点中的最近邻 $p_{k}^{m, j, n 1}$ 的连线与模型点云关键点中的次近邻 $p_{k}^{m, j, n 2}$ 连线的夹角angl $e_{k}^{m, j}$ .按照 $p_{k}^{m, j}$ , j=1, 2, …, 10的顺序, 依次计算 $d_{k}^{s, n 1}$ 与 $d_{k}^{m, j, n 1}$ 的差值d₁和特征描述符差值d_F₁、 $d_{k}^{s, n 2}$ 与 $d_{k}^{m, j, n 2}$ 的差值d₂和特征描述符差值d_F₂、夹角angl $e_{k}^{s}$ 和夹角angl $e_{k}^{m, j}$ 的差值angle.当d₁与d₂小于3s_now、d_F₁和d_F₂小于0.2、夹角差值angle小于10° 时, 将 $p_{k}^{m, j}$ 作为该场景点云关键点 $p_{k}^{s}$ 的对应点, 将 $p_{k}^{m, j, n 1}$ 作为 $p_{k}^{s, n 1}$ 的对应点, 将 $p_{k}^{m, j, n 2}$ 作为 $p_{k}^{s, n 2}$ 的对应点, 组成3组对应关系.

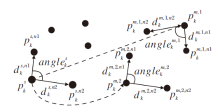基于关键点特征描述符和空间关系的特征匹配算法可在有多个目标点云关键点的特征描述符与场景点云关键点的特征描述符相近时, 查找关键点间的相互关系, 得到正确的匹配关系, 如图7所示.由于模型点云中 $p_{k}^{m, 1}$ 与 $p_{k}^{m, 2}$ 的邻域形状相似, 造成 $p_{k}^{m, 1}$ 与 $p_{k}^{m, 2}$ 的特征描述符相近, 但是由于 $p_{k}^{m, 1}$ 与 $p_{k}^{s}$ 的复合特征不同, 可有效排除 $p_{k}^{m, 1}$ , 从而找到正确的对应点 $p_{k}^{m, 2}$ .

	Figure Option View Download New Window
	图7 关键点空间关系特征匹配算法抗噪示意图Fig.7 Anti-noise diagram of feature matching algorithm of key point spatial relation

1.1.5 多线程识别框架

由于在识别过程中, 有多个类别的模型点云需要对比, 但配准结果互不影响, 为此使用多线程在线识别框架.聚类后, 对每类开启一个线程, 对其滤波, 查找关键点和计算特征描述符.在特征匹配过程中, 由于有多个模型点云需要匹配, 在每个线程中为每个模型点云开启线程, 通过关键点特征描述符和空间关系的特征匹配, 并结合精简ICP(Iterative Closest Point)算法计算模型点云到场景点云的旋转平移变换矩阵, 进行位姿估计.最后, 计算重叠率, 并将重叠率最高且重叠率大于80%的模型点云作为识别结果.

1.2 离线建模

1.2.1 模型重建

在对物体场景点云进行在线识别之前, 需要先建立一个完整的点云模型库, 模型库中包含物体的模型点云、关键点和特征描述符.图1中的模型重建是为了构建物体一个完整的三维模型点云, 采集物体在多个角度下的片状点云, 并将物体的片状点云进行拼接, 组成物体完整的三维模型点云.

1.2.2 离线建模与在线识别间的联系

如图1所示, 离线建模与在线识别都包含循环体素滤波、基于曲率均值提取关键点和计算局部曲面特征直方图, 在处理点云数据时的方法和参数均相同.不同之处在于离线建模处理的点云数据是模型点云, 而在线识别处理的点云数据是待识别的场景点云.在离线建模中, 这3种算法的作用是为了查找拼接好的模型点云的关键点并计算特征描述符.最后将得到的三维模型点云、模型点云的关键点和特征描述符加入模型库中, 完成离线建模.

在整个算法流程中, 离线建模在先, 在线识别在后.在线识别基于曲率均值提取关键点算法, 查找待识别场景点云的关键点, 然后计算关键点局部曲面特征直方图, 作为关键点的特征描述符.基于关键点特征描述符和空间关系的特征匹配算法对在线识别中得到的场景点云关键点特征描述符和在离线模型中得到的模型点云关键点特征描述符进行特征匹配, 目的是为了寻找场景点云和模型点云中对应的关键点对, 为重叠率的计算做准备.

2 实验及结果分析

实验使用Microsoft Visual Studio 2017编译环境, 在Windows 10操作系统上实现, PC机配置为Intel(R)Core(TM)i5-4210M CPU@2.6 MHz处理器, 8.00 GB的物理内存.实验中使用点云模型数据如图8所示, 包含16种类别, 同时包含各模型的场景点云及场景点云组合.通过对比实验验证本文算法的可行性和有效性.

	Figure Option View Download New Window
	图8 点云识别模型Fig.8 Point cloud recognition model

由于点云采集设备的不同, 与物体间距离的远近不同, 使采集到的点云分辨率存在较大差异.为此本文经过多次循环体素滤波算法, 将点云自动调整至指定分辨率, 免除人工手动试凑, 自动适应识别场景中不同设备、目标的远近程度.其中dragon和cheff的模型点云与场景点云的滤波过程如表1所示.

表1 循环体素滤波算法的滤波过程及相关数据 Table 1 Filtering process and related data of cyclic voxel filtering algorithm

本文采用绝对重复性、相对重复性评价关键点性能.绝对重复性是指在场景点云与模型点云中检测的可正确匹配的关键点数目, 相对重复性是指正确匹配的关键点数目与场景点云关键点数目的比值.通过添加不同倍分辨率的高斯噪声, 即σ =0.1, 0.2, …, 0.5, 测试关键点查找算法的抗噪能力, 在此阶段调节各算法的邻域半径, 控制各算法关键点点数在200左右.本文算法在不同高斯噪声下的关键点分布如图9所示.

	Figure Option View Download New Window
	图9 本文算法在不同高斯噪声下的关键点分布Fig.9 Distribution of key points with different Gaussian noises

图10分别为关键点的绝对重复性和相对重复性, 当无噪声时, 法线对齐的径向特征(Normal Aligned Radial Feature, NARF)、尺度不变特征变换(Scale-Invariant Feature Transform, SIFT)、Harris、邻域法线方差算法、邻域曲率均值算法的关键点匹配点数相似, 绝对重复性和相对重复性大致相等.当噪声较小时, NARF、SIFT、Harris、邻域法线方差算法、邻域曲率均值算法的关键点匹配点数相似, 绝对重复性和相对重复性大致相等.

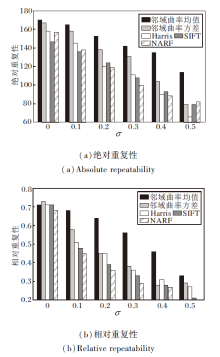	Figure Option View Download New Window
	图10 σ 不同时各算法的关键点重复性对比Fig.10 Comparison of key point repeatability of algorithms with different Gaussian noises

当高斯噪声参数σ =0.3时, 基于邻域曲率均值算法的绝对重复性和相对重复性最高, 这是由于噪声增大时, NARF、SIFT、Harris查找的关键点受到噪声影响, 正确匹配点数降低, 造成绝对重复性和相对重复性下降较快.而邻域法线方差算法、邻域曲率均值算法由于采用非极大值抑制, 随着噪声增大, 关键点位置较稳定, 导致绝对重复性和相对重复性下降较慢.当高斯噪声参数σ =0.5时, 由于点云混乱程度过大, 算法性能都开始大幅下降.

在不同邻域半径下, 300个特征描述符的计算耗时如表2所示.当邻域半径较大时, PFH、快速点特征直方图(Fast Point Feature Histograms, FPFH)计算耗时大幅增加, SHOT(Signature of Histogram of Orientation)和本文的局部曲面特征直方图缓慢增加.局部曲面特征直方图耗时较短, 这是由于PFH、FPFH随着邻域点数增加, 计算量呈指数增加, SHOT、局部曲面特征直方图随着邻域点数增加, 计算量呈线性增长.相比其它算法, 局部曲面特征直方图计算时间较短.

表2 在不同邻域半径下各描述符的计算耗时 Table 2 Calculation time of different descriptors in different neighborhood radia

图11为模型点云与场景点云的匹配对应关系.(a)为单目标对应关系, 即场景中只有一个待识别点云对象.(b)为多目标对应关系, 即场景中有多个待识别点云对象.

	Figure Option View Download New Window
	图11 模型点云与场景点云的匹配对应关系Fig.11 Matching correspondence between model point cloud and scene point cloud

基于局部曲面直方图、关键点空间关系特征匹配算法可寻找大量有效的对应关系, 提高识别算法的稳健性.通过精简的ICP并结合局部曲面特征描述符和关键点空间关系特征匹配进行位姿估计(即计算模型点云到场景点云的坐标变换矩阵), 其中精简ICP的滤波体素为10倍分辨率, 精度为0.1倍分辨率, 最大对应点距离为5倍分辨率.多目标位姿估计结果如下所示.cheff位姿估计结果为

$[\begin{array}{l} 0.989049 & - 0.138996 & 0.0496107 & 27.3924 \\ 0.144757 & 0.979135 & - 0.142619 & - 6.70272 \\ - 0.0287521 & 0.148239 & 0.988534 & 19.0237 \\ 0 & 0 & 0 & 1 \end{array}]$ ,

chicken位姿估计结果为

$[\begin{array}{l} 0.954526 & - 0.174576 & - 0.241668 & - 2.8341 \\ 0.230389 & 0.946418 & 0.226303 & 21.4457 \\ 0.189212 & - 0.27169 & 0.943601 & - 27.9953 \\ 0 & 0 & 0 & 1 \end{array}]$ ,

dragon位姿估计结果为

$[\begin{array}{l} 0.952959 & - 0.246095 & - 0.176935 & - 11.104 \\ 0.259859 & 0.963843 & 0.0589951 & - 7.2534 \\ 0.156019 & - 0.102198 & 0.982453 & - 24.1411 \\ 0 & 0 & 0 & 1 \end{array}]$ ,

根据位姿估计结果将模型点云旋转平移至场景点云中, 并把模型点云与场景点云中重叠率大于80%的类作为识别结果, 识别结果如图12所示, 其中模型点云与场景点云中对象基本重合, 表明识别结果的准确性.

	Figure Option View Download New Window
	图12 本文算法的识别结果Fig.12 Recognition results of the proposed algorithm

表3为各算法在cheff、dragon、armadillo、bunny、chicken目标点云下的识别时间.由表可看出, 本文局部曲面特征直方图的识别时间约为0.3 s, SHOT的识别时间约为0.6 s, FPFH的识别时间约为1.5 s, PFH的识别时间约为3 s.显然, 局部曲面特征直方图识别速度更快.

表3 目标点云在各算法下的识别时间 Table 3 Recognition time of target point cloud of different algorithms ms

表4为本文算法的实验数据, 单目标识别时间约为0.3 s, 三目标识别时间约为0.6 s, 识别速度更快.

表4 本文识别算法的实验数据及结果 Table 4 Experimental data and results of the proposed algorithm

综上所述, 本文算法将点云自动调整到指定分辨率, 免除人工手动试凑参数, 可自动适应识别场景中不同设备、目标的远近程度.关键点和特征描述符的抗噪性较强, 特征描述符的计算时间较短, 目标点云的识别速度较快.

3 结束语

本文提出基于局部曲面特征直方图的点云识别算法.循环体素滤波算法精简点云, 方便不同分辨率下的点云自动识别, 基于邻域曲率均值的关键点查找算法加快执行时间和提高关键点查找性能, 局部特征描述符提高抗噪声能力和计算性能, 基于关键点空间关系的特征匹配算法提高匹配关系的准确性.设计多线程框架, 将识别分成离线模型库生成和在线识别两部分, 利用硬件设备加速识别过程.实验结果验证本文算法抗噪性较好, 识别速度较快.随着模型库中模型点云数量的增加, 目标点云与各个模型点云的匹配时间大幅增加, 造成识别速度下降.因此, 如何提高场景点云与模型点云的匹配速度将是今后需要研究的关键问题.

参考文献

文献选项

[1]	NGUYEN X S, MOUADDIB A I, PHUONG T, et al. Action Recog-nition in Depth Videos Using Hierarchical Gaussian Descriptor. Multimedia Tools and Applications, 2018, 77(12): 21617-21652. [本文引用:1]
[2]	YAO H X, JIANG X H, SUN T F, et al. 3D Human Action Recognition Based on the Spatial-Temporal Moving Skeleton Descriptor // Proc of the IEEE International Conference on Multimedia and Expo. Washington, USA: IEEE, 2017: 937-942. [本文引用:1]
[3]	GUO Y L, BENNAMOUN M, SOHEL F, et al. An Integrated Framework for 3-D Modeling, Object Detection, and Pose Estimation from Point-Clouds. IEEE Transactions on Instrumentation and Measurement, 2015, 64(3): 683-693. [本文引用:1]
[4]	LIE Y J, GUO Y L, HAYAT M, et al. A Two-Phase Weighted Co-llaborative Representation for 3D Partial Face Recognition with Single Sample. Pattern Recognition, 2016, 52: 218-237. [本文引用:1]
[5]	TIAN C W, ZHANG Q, ZHANG J, et al. 2D-PCA Representation and Sparse Representation for Image Recognition. Journal of Computational and Theoretical Nanoscience, 2017, 14(1): 829-834. [本文引用:1]
[6]	FAN Z, LI Z X, LI W J, et al. A Combined Texture-Shape Global 3D Feature Descriptor for Object Recognition and Grasping // Proc of the International Conference on Industrial Informatics-Computing Technology, Intelligent Technology, Industrial Information Integration. Washington, USA: IEEE, 2017: 47-54. [本文引用:1]
[7]	REN S Q, HE K M, GIRSHICK R, et al. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(6): 1137-1149. [本文引用:1]
[8]	LI R F, LU W C, LIANG H Y, et al. Multiple Features with Extreme Learning Machines for Clothing Image Recognition. IEEE Access, 2018, 6: 36283-36294. [本文引用:1]
[9]	LU T T, HU W D, LIU C, et al. Relative Pose Estimation of a Land er Using Crater Detection and Matching. Optical Engineering, 2016, 55(2). DOI: DOI:10.1117/1.OE.55.2.023102. [本文引用:1]
[10]	YANG J Q, XIAO Y, CAO Z G. Toward the Repeatability and Robustness of the Local Reference Frame for 3D Shape Matching: An Evaluation. IEEE Transactions on Image Processing, 2018, 27(8): 3766-3781. [本文引用:1]
[11]	GUO Y L, BENNAMOUN M, SOHEL F, et al. 3D Object Recognition in Cluttered Scenes with Local Surface Features: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11): 2270-2287. [本文引用:1]
[12]	KECHAGIAS-STAMATIS O, AOUF N, CHERMAK L. B-HoD: A Lightweight and Fast Binary Descriptor for 3D Object Recognition and Registration // Proc of the 14th IEEE International Conference on Networking, Sensing and Control. Washington, USA: IEEE, 2017. DOI: DOI:10.1109/ICNSC.2017.8000064. [本文引用:1]
[13]	SHAH S A A, BENNAMOUN M, BOUSSAID F. A Novel Feature Representation for Automatic 3D Object Recognition in Cluttered Scenes. Neurocomputing, 2016, 205: 1-15. [本文引用:1]
[14]	SALES D O, AMARO J, OSÓRIO F S. 3D Shape Descriptor for Objects Recognition // Proc of the Latin American Robotics Symposium(LARS) and Brazilian Symposium on Robotics(SBR). Washington, USA: IEEE, 2017. DOI: DOI:10.1109/SBR-LARS-R.2017.8215285. [本文引用:1]
[15]	GUO Y L, SOHEL F, BENNAMOUN M, et al. A Novel Local Surface Feature for 3D Object Recognition under Clutter and Occlusion. Information Sciences, 2015, 293: 196-213. [本文引用:1]
[16]	张哲, 许宏丽, 尹辉. 一种基于关键点选择的快速点云配准算法. 激光与光电子学进展, 2017, 54(12): 121002-1-121002-9. (ZHANG Z, XU H L, YI H. A Fast Point Cloud Registration Algorithm Based on Key Point Selection. Laser and Optoelectronics Progress, 2017, 54(12): 149-157. ) [本文引用:1]

2018

0.0

... 目标识别是计算机视觉领域研究的热点问题之一,主要应用领域包括监视器^[1]、生物特征识别^[2]、工业检查、场景理解和机器人自动行走^[3,4] ...

2017

0.0

... 目标识别是计算机视觉领域研究的热点问题之一,主要应用领域包括监视器^[1]、生物特征识别^[2]、工业检查、场景理解和机器人自动行走^[3,4] ...

2015

0.0

... 目标识别是计算机视觉领域研究的热点问题之一,主要应用领域包括监视器^[1]、生物特征识别^[2]、工业检查、场景理解和机器人自动行走^[3,4] ...

2016

0.0

... 目标识别是计算机视觉领域研究的热点问题之一,主要应用领域包括监视器^[1]、生物特征识别^[2]、工业检查、场景理解和机器人自动行走^[3,4] ...

2017

0.0