深度多网络嵌入聚类

引用本文

陈锐, 唐永强, 张彩霞, 张文生, 郝志峰. 深度多网络嵌入聚类. 模式识别与人工智能, ,34(1): 14-24
CHEN Rui, TANG Yongqiang, ZHANG Caixia, ZHANG Wensheng, HAO Zhifeng. Deep Multi-network Embedded Clustering. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,34(1): 14-24. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202101002
Permissions

《模式识别与人工智能》编辑部所有

深度多网络嵌入聚类

陈锐^1,^2,³, 唐永强², 张彩霞^1,³, 张文生², 郝志峰¹

1.佛山科学技术学院机电工程与自动化学院佛山 528225

2.中国科学院自动化研究所精密感知与控制研究中心北京 100190

3.广东省工程技术研究中心广东省智慧城市基础设施健康监测与评估工程技术研究中心佛山 528000

通信作者：张彩霞,博士,教授,主要研究方向为人工智能、机器学习、数据挖掘.E-mail: zh_caixia@163.com.

作者简介: 陈锐,硕士研究生,主要研究方向为机器学习、数据挖掘、计算机视觉.E-mail:chenrui_1216@163.com.

唐永强,博士,助理研究员,主要研究方向为机器学习、数据挖掘、计算机视觉.E-mail:yongqiang.tang@ia.ac.cn.

张文生,博士,教授,主要研究方向为人工智能、机器学习、数据挖掘.E-mail:zhangwenshengia@hotmail.com.

郝志峰,博士,教授,主要研究方向为人工智能、机器学习、数据挖掘.E-mail: 2297278685@qq.com.

收稿日期: 2020-09-02 接受日期: 2020-11-23

资助项目: 国家自然科学基金青年基金项目(No.61803087); 广东省教育厅特色创新项目(No.2019KTSCX192); 广东省基础与应用基础研究基金粤港澳应用数学中心项目(No.2020B1515310003); 佛山核心技术攻关项目(No.1920001001367)资助

摘要

现有的深度无监督聚类方法通常局限于单网络结构设计,无法充分利用多种异构网络提取特征中蕴含的互补信息,制约深度聚类方法性能的进一步提升.为此,文中提出深度多网络嵌入聚类算法(DMNEC).首先,以端到端的方式预训练多个异构网络分支,获取各网络的初始化参数.在此基础上,定义多网络软分配,借助多网络辅助目标分布建立面向聚类的KL散度损失.与此同时,利用样本重建损失对预训练阶段的解码网络进行微调,保留数据的局部结构性质,避免特征空间发生扭曲.通过随机梯度下降与反向传播优化重建损失与聚类损失的加权和,联合学习多网络表征及其簇分配.在4个公开图像数据集上的实验验证文中算法的优越性.

关键词: 深度无监督聚类; 数据表征; 多网络分支; 互补信息; 局部结构保留

Deep Multi-network Embedded Clustering

CHEN Rui^1,^2,³, TANG Yongqiang², ZHANG Caixia^1,³, ZHANG Wensheng², HAO Zhifeng¹

1.School of Mechatronic Engineering and Automation, Foshan University, Foshan 528225

2.Research Center of Precision Sensing and Control, Institute of Automation, Chinese Academy of Sciences, Beijing 100190

3.Guangdong Province Smart City Infrastructure Health Monitoring and Evaluation Engineering Technology Research Center, Guangdong Engineering Technology Research Center, Foshan 528000

Corresponding author: ZHANG Caixia, Ph.D., professor. Her research interests include artificial intelligence, machine learning and data mining.

About the Author:CHEN Rui, master student. His research interests include machine learning, data mi-ning and computer vision.

TANG Yongqiang, Ph.D., assistant professor. His research interests include machine learning, data mining and computer vision.

ZHANG Wensheng, Ph.D., professor. His research interests include artificial intelligence, machine learning and data mining.

HAO Zhifeng, Ph.D., professor. His research interests include artificial intelligence, machine learning and data mining.

Fund:Supported by Youth Program of National Natural Science Foundation of China(No.61803087); Feature Innovation Project of Guangdong Province Department of Education(No.2019KTSCX192); Guangdong-Hong Kong-Macao Applied Mathematics Center Project of Guangdong Basic and Applied Basic Research Fund(No.2020B1515310003); Foshan Core Technology Research Project(No.1920001001367)

Abstract

Existing deep unsupervised clustering methods cannot make full use of the complementary information between the extracted features of different network structures due to the single network structure in them, and thus the clustering performance is restricted. A deep multi-network embedded clustering(DMNEC) algorithm is proposed to solve this problem. Firstly, the initialization parameters of each network are obtained by pretraining multi-network branches in an end-to-end manner. On this basis, the multi-network soft assignment is defined, then the clustering-oriented Kullback-Leibler divergence loss is established with the help of the multi-network auxiliary target distribution. The decoding network in the pretraining stage is finetuned via reconstruction loss to preserve the local structure and avoid the distortion of feature space. The weighted sum of reconstruction loss and clustering loss is optimized by stochastic gradient descent(SGD) and back propagation(BP) to jointly learn multi-network representation and cluster assignment. Experiments on four public image datasets demonstrate the superiority of the proposed algorithm.

Key words: Key Words Deep Unsupervised Clustering; Data Representation; Multi-network Branches; Complementary Information; Local Structure Preservation

文章图片

无监督聚类^[1]旨在对无标注数据的潜在分布结构进行分析, 进而将相似样本划分至同一簇内, 是数据科学和机器学习领域中的一个重要研究课题, 已成功在图像分类^{[2, 3, 4]}、数据可视化^[5]等众多现实场景中得到广泛应用.无监督聚类方法的性能很大程度上取决于数据的表征, 例如, 对于传统聚类方法K-均值(K-means, KM)^[6]或高斯混合模型(Gaussian Mixture Model, GMM)^[7]而言, 随着数据表征维度的升高, 相似性度量不再可靠, 致使聚类变得无效.针对这一问题, 一种直观的解决方案是首先利用降维技术, 如主成分分析(Principal Component Analysis, PCA)^[8]、非负矩阵分解(Non-negative Matrix Factoriza-tion, NMF)^[9]、多维缩放(Multiple Dimensional Sca-ling, MDS)^[10]等, 将数据从高维空间转至低维空间, 再对降维后的数据进行聚类.然而, 典型的PCA、NMF、MDS等降维方法本质上属于线性模型, 难以深刻描述实际数据中蕴含的复杂分布结构.

深度神经网络作为一种非线性关系建模的有力工具, 可对输入的原始数据进行连续、非线性变换, 从而获得高质量的数据表征.其中, 自动编码器(Autoencoder, AE)^[11]是深度神经网络的一种特殊形式, 以完全无监督的方式学习数据表征.AE基本原理为:首先将原始数据嵌入低维表征空间, 基于此空间重建原始数据.尽管AE在数据表征的非线性提取方面优势明显, 但其学习到的表征往往难以与数据的聚类结构相适配.

针对这一问题, 近年来, 学者们相继提出一系列深度无监督聚类方法, 旨在利用深度神经网络同时学习原始数据的表征及其对应的簇分配.Yang等^[12]提出联合无监督学习(Joint Unsupervised Lear-ning, JULE), 结合卷积神经网络(Convolutional Neural Network, CNN)^[13]的表征学习与层次聚类, 基于统一权重的三元组损失进行优化, 取得较优的聚类表现, 但计算复杂度较高.Xie等^[14]提出深度嵌入聚类算法(Deep Embedded Clustering, DEC), 预训练自动编码器, 学习原始数据的低维表征, 在自学习辅助目标分布的帮助下迭代优化基于KL散度的聚类损失.Guo等^[15]提出改进的深度嵌入聚类算法(Improved DEC, IDEC), 在DEC损失函数中加入重建项, 用于保留特征空间属性.Li等^[16]提出判别性提升聚类(Discriminatively Boosted Clustering, DBC), 将DEC的预训练网络置换为CNN, 提取包含像素空间信息的高质量特征, 提升整体聚类性能.Yang等^[17]提出深度聚类网络(Deep Clustering Network, DCN), 利用深度神经网络进行数据降维, 学习一个与KM算法相适配的潜在表征空间, 在此空间中交替优化网络参数、簇质心、簇分配.Fard等^[18]提出深度K-均值 (Deep K-means, DKM), 对数据表征、簇质心及簇分配进行连续的端到端联合学习.Guo等^[19]提出自适应自步聚类(Adaptive Self-paced Clustering, ASPC), 借鉴自步学习(Self-paced Lear-ning, SPL)思想, 优先利用高置信度样本训练聚类网络, 消除聚类边界样本的负面影响.Peng等^[20]提出深度子空间聚类(Deep Subspace Clustering, DSC), 计算样本的稀疏重构关系, 保留样本的局部性子空间结构和全局性子空间结构.Chang等^[21]提出深度自适应聚类(Deep Adaptive Clustering, DAC), 假设成对图像为二进制关系, 将聚类目标转化为二值成对分类问题.Bo等^[22]提出结构化深度聚类网络(Structural Deep Clustering Network, SD-CN), 将图卷积网络融入聚类网络中, 旨在捕捉数据的结构化信息, 获取更具判别性的数据表征, 提升模型聚类性能.有关更多方法的介绍可参考文献[23]、文献[24].

尽管上述深度方法显著提升聚类性能, 但均运行于单网络结构环境下.DEC借助有效的辅助目标分布指导聚类, 取得良好的性能.但是, 基于单网络结构设计提取的表征质量不高, 导致初始化表现不理想, 经常出现数值不稳定情况, 最终难以获得优越的聚类表现.

众所周知, 同个网络结构的不同层提取的特征存在互补性:低层包含较多细节信息, 但是语义性较低; 高层具有较强的语义信息, 但是分辨率较低, 对细节感知能力较差.受此启发, 本文提出深度多网络嵌入聚类算法(Deep Multi-network Embedded Clus-tering, DMNEC), 旨在将DEC从单网络结构扩展至多网络, 捕获包含多种异构网络互补信息的高质量表征, 解决由DEC基于单网络结构设计引起的聚类性能不佳问题.同时, 为了避免特征空间扭曲, 进一步引入局部结构保留(Local Structure Preservation, LSP)机制.通过优化多网络表征与相应簇质心, 达成聚类目的.在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]基准图像数据集上的实验验证本文算法的有效性和优越性.

1 相关工作

1.1 深度嵌入聚类

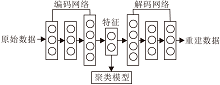
深度嵌入聚类(DEC)^[14]框图如图1所示.

	Figure Option View Download New Window
	图1 DEC框图Fig.1 Framework of DEC

DEC包含两个阶段:参数初始化阶段与联合学习阶段.在参数初始化阶段, DEC首先使用3个去噪自动编码器(Denoising Autoencoder, DAE)进行逐层贪婪训练(Greedy Layer-Wise Training), 将编码层按顺序连接, 解码层按逆序连接, 形成一个堆栈式自动编码器(Stacked Autoencoder, SAE).然后, 以SAE作为基础模型, 将原始数据x_i∈ R^D映射至潜在特征空间, 用于学习低维表征z_i∈ R^d, 再基于表征

Z={z₁, z₂, …, z_n}∈ R^d^×ⁿ

执行KM算法, 获取初始化簇质心μ _j.在联合学习阶段, DEC移除SAE的解码网络g_{θ '}(· ), 仅保留编码网络f_θ(· ), 其中θ 表示编码网络的参数集.在t分布随机邻域嵌入(t-Distributed Stochastic Neighbour Embedding, t-SNE)^[5]的启发下, DEC采用学生t分布(Student's t-Distribution)作为软分配, 度量低维表征z_i=f_θ(x_i)与簇质心μ _j之间的相似性:

q_ij= $\frac{{(1 + \frac{{(z_{i} - μ_{j})}^{2}}{α})}^{- \frac{α + 1}{2}}}{\sum_{j'} (1 + \frac{{(z_{i} - μ_{j'})}^{2}}{α})^{- \frac{α + 1}{2}}}$ ,

其中, α 表示学生t分布的自由度, 通常取值为1.q_ij被称为软分配, 是因为它可解释为模型将第i个样本分配给第j个簇的概率.由于无监督任务中原始数据是未标注的, 所以DEC借助辅助目标分布p_ij, 通过提高软分配的高置信度以指导聚类.辅助目标分布的定义为

p_ij= $\frac{q_{ij}^{2}}{\sum_{i} q_{ij}} [\sum_{j'} [\frac{q_{ij'}^{2}}{\sum_{i} q_{ij'}}]]$ ^-1.

利用上述软分配q_ij和辅助目标分布p_ij, DEC优化如下基于KL散度的聚类目标:

L(z_i, μ _j)= $\sum_{i} \sum_{j}$ p_ijln $[\frac{p_{ij}}{q_{ij}}]$ .

采用随机梯度下降(Stochastic Gradient Descent, SGD)与反向传播(Back Propagation, BP)迭代更新低维表征z_i和簇质心μ _j:

z_i=z_i-λ $\frac{\partial L}{\partial z_{i}}$ , μ _j=μ _j-λ $\frac{\partial L}{\partial μ_{j}}$ ,

其中λ 表示学习率.网络训练结束后, 未标注数据的簇分配为

s_i=arg $\max_{j}$ q_ij.

1.2 基于局部结构保留的深度嵌入聚类

相比DEC, 改进的深度嵌入聚类算法(IDEC)^[15]保留数据的局部结构, 框图如图2所示.

	Figure Option View Download New Window
	图2 IDEC框图Fig.2 Framework of IDEC

为了实现这个目的, IDEC保留解码网络, 目标函数为

L(z_i, μ _j)= $\overset{n}{\sum_{i}} {(x_{i} - g_{θ'} (f_{θ} (x_{i})))}_{2}^{2}$ +γ $\sum_{i} \sum_{j}$ p_ijln $[\frac{p_{ij}}{q_{ij}}]$ ,

其中γ ≥ 0用于权衡重建损失与聚类损失的重要性.将重建损失加入目标函数中可避免嵌入空间出现大范围的扭曲, 较好地保留数据局部结构与特征属性.

2 深度多网络嵌入聚类

为了解决DEC基于单网络结构设计引起的聚类性能不佳问题, 本文提出深度多网络嵌入聚类算法(DMNEC), 旨在将DEC扩展为多网络结构设计, 提升聚类性能.与DEC相似, DMNEC也包含特征提取阶段和网络微调阶段.具体而言, 在特征提取阶段, 首先以不同结构的自动编码器作为多网络分支, 预训练多网络分支, 提取每个网络分支的潜在表示.再将潜在表示进行拼接融合, 得到包含互补信息的完备融合表示.基于融合表示执行KM算法, 得到初始化簇质心.在网络微调阶段, 引入多网络软分配及其辅助目标分布, 保留多网络分支的解码网络.基于聚类损失和多网络分支重建损失微调网络, 实现多网络分支特征和簇质心的联合学习.DMNEC框图如图3所示.

	Figure Option View Download New Window
	图3 DMNEC框图Fig.3 Framework of the proposed DMNEC

2.1 特征提取

给定原始数据集

X={x₁, x₂, …, x_n}∈ R^D^×ⁿ,

DMNEC使用多个非线性编码映射建模x_i∈ R^D与其潜在表示 $z_{i}^{(v)}$ ∈ R^d^×^v之间的关系, 再使用同等数量的非线性解码映射建模 $z_{i}^{(v)}$ 与其重建数据x'_i∈ R^D之间的关系:

$z_{i}^{(v)}$ =f $_{θ}^{(v)}$ (x_i), x'_i= $g_{θ'}^{(v)}$ ( $z_{i}^{(v)}$ ),

其中, f $_{θ}^{(v)}$ (· )表示多网络编码映射, $g_{θ'}^{(v)}$ (· )表示解码映射, v表示多网络索引, θ 表示编码参数集, θ '表示解码参数集.由于不同网络结构f⁽^v⁾→ g⁽^v⁾提取的特征具有不同特性, 为了捕获这种异构互补信息, DMNEC通过最小化如下重建损失提取每个网络分支的低维特征:

$L_{(r)}^{(v)}$ = $\overset{n}{\sum_{i}} {(x_{i} - g_{θ'}^{(v)} (f_{θ}^{(v)} (x_{i})))}_{2}^{2}$ . (1)

2.2 网络微调

特征提取工作完成, 将多个低维特征 $z_{i}^{(v)}$ 进行拼接融合, 此种融合机制可最大限度地保留每种特征的独有属性.通过执行KM算法获取初始化簇质心 $μ_{j}^{(v)}$ , 以学生t分布衡量 $z_{i}^{(v)}$ 与 $μ_{j}^{(v)}$ 的相似度, 引出多网络软分配:

q_ij= $\frac{\sum_{v} (1 + \frac{{(z_{i}^{(v)} - μ_{j}^{(v)})}^{2}}{α})^{- \frac{α + 1}{2}}}{\sum_{j'} \sum_{v'} {(1 + \frac{{(z_{i}^{(v')} - μ_{j}^{(v')})}^{2}}{α})}^{- \frac{α + 1}{2}}}$ ,

其中α =1表示学生t分布的自由度.由q_ij可推导对应辅助目标分布:

p_ij= $\frac{q_{ij}^{2}}{\sum_{i} q_{ij}} [\sum_{j'} [\frac{q_{ij'}^{2}}{\sum_{i} q_{ij'}}]]$ ^-1. (2)

基于上述多网络软分配Q和辅助目标分布P, 以 KL(P‖ Q)作为聚类约束:

L_c= $\sum_{i} \sum_{j}$ p_ijln $[\frac{p_{ij}}{q_{ij}}]$ .

受IDEC^[11]启发, 进一步保留各个分支对应的解码网络, 保留数据特征属性.因此, DMNEC的损失函数如下:

L( $z_{i}^{(v)}$ , $μ_{j}^{(v)}$ )=L_r+γ L_c,

其中, γ ≥ 0用于平衡多网络分支重建损失与聚类损失.

基于上述损失微调网络, 可最大限度地避免扭曲特征空间, 最终实现对多网络分支特征和簇质心的联合学习.

2.3 模型优化

通过随机梯度下降和反向传播优化L( $z_{i}^{(v)}$ , $μ_{j}^{(v)}$ ), 有3种参数需要优化:簇质心 $μ_{j}^{(v)}$ 、编码网络参数θ 、解码网络参数θ '.由于α =1, 为了简化符号, 在此定义:

$d_{ij}^{(v)}$ = ${(z_{i}^{(v)} - μ_{j}^{(v)})}^{2}$ , U= $\sum_{j'} \sum_{v'}$ (1+ $d_{ij}^{(v')}$ )^-1.

因此, 聚类损失L_c关于多网络分支特征 $z_{i}^{(v)}$ 、簇质心 $μ_{j}^{(v)}$ 的梯度如下:

$\frac{\partial L_{c}}{\partial z_{i}^{(v)}}$ =2 $\sum_{j} \frac{\partial L_{c}}{\partial d_{ij}^{(v)}}$ ( $z_{i}^{(v)}$ - $μ_{j}^{(v)}$ ), $\frac{\partial L_{c}}{\partial μ_{j}^{(v)}}$ =-2 $\sum_{j} \frac{\partial L_{c}}{\partial d_{ij}^{(v)}}$ ( $z_{i}^{(v)}$ - $μ_{j}^{(v)}$ ),

推导可得

$\frac{\partial L_{c}}{\partial d_{ij}^{(v)}}$ =- $\sum_{t}$ p_it $\frac{\partial \ln q_{it}}{\partial d_{ij}^{(v)}}$ =- $\sum_{t}$ p_it $\frac{\partial (\ln q_{it} U - \ln U)}{\partial d_{ij}^{(v)}}$ =- $\sum_{t}$ p_it $[\frac{1}{q_{it} U} \frac{\partial q_{it} U}{\partial d_{ij}^{(v)}} - \frac{1}{U} \frac{\partial U}{\partial d_{ij}^{(v)}}]$ =- $\sum_{t}$ i_t $[\frac{1}{q_{it}} \frac{\partial (\sum_{v'} (1 + d_{ij'}^{(v')})^{- 1})}{\partial d_{ij}^{(v)}} - \frac{1}{U} \frac{\partial (\sum_{j'} \sum_{v'} (1 + d_{ij'}^{(v')})^{- 1})}{\partial d_{ij}^{(v)}}]$ pij $\frac{1}{q_{ij} U} (1 + d_{ij}^{(v)})^{- 2}$ - $\frac{1}{U} (1 + d_{ij}^{(v)})^{- 2}$ ( $\frac{(1 + d_{ij}^{(v)})^{- 2}}{q_{ij} U}$ ij_-_qij_).

在学习率λ 下, 簇质心 $μ_{j}^{(v)}$ 、编码参数θ 、解码参数θ '更新如下:

$μ_{j}^{(v)}$ = $μ_{j}^{(v)}$ -λ $\frac{\partial L_{c}}{\partial μ_{j}^{(v)}}$ , (3)

θ =θ -λ $[\frac{\partial L_{r}}{\partial θ} + γ \frac{\partial L_{c}}{\partial θ}]$ , (4)

θ '=θ '-λ $\frac{\partial L_{r}}{\partial θ'}$ . (5)

待所有参数优化完毕, 无标签样本的预测标签为

s_i=arg $\max_{j}$ q_ij. (6)

DMNEC步骤如算法1所示.

算法 1 DMNEC

输入数据集X, 簇数量K, 平衡系数γ ,

收敛阈值δ , 最大迭代次数T

输出簇分配S

// 多网络分支预训练

for v={1, 2, …, n} do

根据式 (1) 初始化θ 、θ ', 获取低维表征

Z⁽^v⁾=f $_{θ}^{(v)}$ (X)

end for

// 质心初始化

基于Z⁽^v⁾执行KM算法以获取簇质心M⁽^v⁾

// 网络微调

for t={1, 2, …, T} do

根据式(2)更新辅助目标分布P

根据式(6)更新簇分配S

根据式(3)~式(5)更新簇质心 $μ_{j}^{(v)}$ 、编码参数

θ 、解码参数θ '

if 1- $\frac{1}{n} \sum_{i} s_{ij}^{t} s_{ij}^{t - 1}$ < δ then

满足收敛判别准则, 停止迭代

end if

end for

3 实验及结果分析

3.1 实验环境

本文实验环境如下:操作系统为Linux.硬件平台为Intel(R) Xeon(R) E5-2640 v4@2.40 GHz CPU, 120 GB内存, 11 GB高速缓存, NVIDIA GeForce GTX 1080 Ti GPU.编程环境为Python 3.7.深度学习框架为Tensorflow 2.0.0-beta0.

在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]图像数据集上评估DMNEC.MNIST数据集为经典手写数字识别库, 包含70 000个样本, 类别总数为10类, 图像大小为28× 28, 每幅图像中的数字都是居中状态, 已标准化处理.其中训练集包含60 000个样本, 测试集包含10 000个样本.USPS数据集包含9 298幅来自10个类别的灰度手写数字图像, 图像大小为16× 16.FMNIST数据集涵盖70 000幅来自10种类别的时尚产品正面图像, 图像大小、格式、训练/测试划分比例与MNIST数据集完全一致.COIL20数据集包含1 440幅来自20个类别的灰度实体图像, 图像大小为128× 128, 实验中将尺寸重置为32× 32.

上述图像数据集的属性描述如表1所示.特别说明, 对于已被划分为训练集和测试集的数据集, 合并后再进行实验.另外, 所有数据集的图像像素值都被缩放至数值区间[-1, 1], 以便神经网络更好地训练.

实验选用的对比算法如下:

1)传统聚类算法:KM^[6]、GMM^[7]、谱聚类(Spectral Clustering, SC)^[34].

2)基于表征的聚类算法:SAE+KM、变分自动编码器(Variational Autoencoder, VAE)+KM、卷积自动编码器(Convolutional Autoencoder, CAE)+KM.

3)深度聚类算法:DEC^[14]、IDEC^[15]、DCN^[17]、DKM^[18]、ASPC^[19]、SDCN^[22]、深度散度聚类(Deep Divergence-Based Clustering, DDC)^[35]、深度张量核聚类(Deep Tensor Kernel Clustering, DTKC)^[36]、深度堆栈式稀疏嵌入聚类(Deep Stacked Sparse Embedded Clustering, DSSEC)^[37].

表1 实验数据集 Table 1 Experimental datasets

3.2 评价指标

为了衡量算法的聚类性能, 采用如下3个聚类评价指标:聚类精度(Clustering Accuracy, ACC)^[29]、归一化互信息(Normalized Mutual Information, NMI)^[30]和调整兰德指数(Adjusted Rand Index, ARI)^[31].

ACC计算如下:

ACC= $\max_{m} \frac{1}{n} \overset{n}{\sum_{i}}$ 1{l_i=map(c_i)},

其中, n为样本数量, l_i为真实标签, c_i为模型产生的预测标签, map(c_i)为映射函数, 包含预测标签与真实标签之间所有可能的一对一映射.匈牙利算法(Hungarian Algorithm)^[32]可有效计算最佳映射.

NMI是衡量2个聚类之间共享信息量的信息论度量, 较可靠地评价不平衡数据集聚类效果.NMI计算如下:

NMI= $\frac{I (l; c)}{\max {H (l), H (c)}}$ ,

其中, I(l; c)表示l和c之间的互信息, H(l)表示的熵值, H(c)表示c的熵值.

ARI是兰德指数(Rand Index, RI)^[33]的修正版本, 计算如下:

ARI= $\frac{RI - E (RI)}{\max (RI) - E (RI)}$ ,

其中E(RI)表示RI的数学期望.

总体而言, 上述3种指标是评价聚类性能较常用的度量, 各有利弊, 将它们综合起来可更客观地说明聚类算法的有效性.ACC、NMI在[0, 1]内取值, 数值越大表示聚类性能越优; ARI在[-1, 1]内取值, 1表示最优的聚类表现, -1表示最差的聚类表现.

3.3 实验设置

DMNEC设置3个多网络分支, 分别为堆栈式自动编码器(SAE)、变分自动编码器(VAE)和卷积自动编码器(CAE).对于第1个网络分支SAE, 编码网络结构为配备全连接层 (Fully Connected Layer) 的多层感知机 (Multi-layer Perceptron, MLP), 前向网络维度变化为

D→ 500→ 500→ 2000→ 10,

其中D表示输入数据的原始维度.对于第2个网络分支VAE, 编码网络结构为

con $v_{6}^{2}$ → con $v_{20}^{3}$ → con $v_{60}^{3}$ → fc256→ fc10.

其中:con $v_{n}^{k}$ 表示配置n个过滤器、过滤器尺寸为k× k、卷积步长为2的卷积层; fcn表示包含n个结点的全连接层.对于第3个网络分支CAE, 编码网络结构为

con $v_{32}^{5}$ → con $v_{64}^{5}$ → con $v_{128}^{3}$ → fc10.

解码网络均为编码网络的镜像版本, 将编码网络置于解码网络顶部, 形成端到端连接的3个异构深度神经网络, 除了输入层、瓶颈层和输出层之外, 其它层均使用修正线性单元(Rectified Linear Unit, ReLU)进行非线性数值转换.

对上述3个多网络分支分别进行端到端的预训练, 次数分别为200、400、600, 采用自适应矩估计(Adaptive Moment Estimation, Adam)优化器(初始学习率为0.001)优化对应分支的网络参数, 批量大小设置为256.在后续微调网络过程中, 采用自适应梯度(Adaptive Gradient, Adagrad)优化器, 初始学习率设置为0.000 1, 批量大小设置为256, 平衡系数γ =0.1, 最大迭代次数设置为20 000.当满足收敛判别准则δ =0.001时, 停止迭代.

此外, 为了公平起见, 在4个图像数据集上对DMNEC进行10次随机重启, 求取各个指标的平均值, 将其作为最终实验结果.

3.4 方法对比

各算法在4个数据集上的指标值对比如表2所示, 其中, 黑体数字表示最优结果, 斜体数字表示次优结果, -表示没有结果.

为了说明局部结构保留的重要性, 表2中也给出DMNEC在网络微调阶段的多分支解码网络移除后所得算法(简称为DMNEC w/o LSP)的结果.

由表可知:DMNEC在3个聚类评价指标上最优.特别地, 在MNIST数据集上, 相比ASPC、DSS-EC, DMNEC的ACC值分别提升7.5%、5.7%, 达到93.4%, 这表明DMNEC的优越性.在USPS数据集上, 相比SDCN, DMNEC的ACC值、NMI值、ARI值分别提升0.6%、3.4%、3.3%, 达到78.7%、82.9%、75.1%, 表明DMNEC性能较优.另外, 在小型数据集COIL20上, 相比ASPC, DMNEC的NMI值分别提升5.3%, 达到79.6%, 这表明DMNEC具备良好的泛化性能.

由表2可看出, DMNEC w/o LSP在4个数据集上均取得较优的聚类表现, 表明DMNEC在预训练阶段使用多网络分支, 可有效挖掘多种网络结构特征之间的互补信息, 学习更高质量的嵌入特征, 更好地衔接后续的聚类任务.此外, 在大多数数据集上, DMNEC性能优于DMNEC w/o LSP, 表明DMNEC在网络微调阶段保留的解码网络可一定程度上避免特征空间扭曲, 最大限度保留数据局部结构, 提升最终聚类性能.

表2 各算法在4个图像数据集上的指标值对比 Table 2 Comparison of metric values of different algorithms on 4 image datasets

图4为DMNEC、DEC在MNIST数据集上的部分聚类结果, 随机筛选每簇中的10个图像样本进行可视化, 每行对应一个簇.

	Figure Option View Download New Window
	图4 各算法在MNIST数据集上的部分聚类结果Fig.4 Some clustering results of different algorithms on MNIST dataset

由图4可清晰地观察到, DEC经常混淆数字4、9, 说明DEC倾向于将手写数字集合聚为9类, 与实际类别数(10类)矛盾.而这一现象在图4(a)中未出现, 说明DMNEC可准确地将手写数字集合聚为10类, 反映DMNEC在聚类任务中表现更出色.

3.5 消融实验

由于本文算法包含多个异构网络分支, 因此探究每个网络分支对最终聚类结果的影响.DMNEC配备3个网络分支:Net 1(SAE)、Net 2(VAE)、Net 3(CAE).图5为在USPS数据集上算法只考虑单个网络与同时考虑3个网络的ACC、ARI指标随迭代次数的变化情况.

由图5可观察到, 在迭代过程的各个阶段, 多网络模型的聚类性能明显优于任何单网络模型, 表明预训练阶段使用多网络结构, 可获取包含互补信息的高质量特征, 进而更好地衔接后续的聚类任务.

	Figure Option View Download New Window
	图5 网络数量不同时指标值随迭代次数的变化情况Fig.5 Metric values variation with iteration times with different numbers of networks

为了更直观的理解, 在此将预训练阶段使用单网络提取的特征和使用多网络提取的特征进行可视化, 如图6所示.由图可看出, 相比使用单网络提取的特征, 使用多网络提取的特征表现更佳的团簇结构, 说明多网络模型可捕获不同网络结构特征之间的互补信息, 充分反映数据潜在的聚类结构.

	Figure Option View Download New Window
	图6 基于MNIST子集的异构网络特征鲁棒性可视化结果Fig.6 Visualization results of robustness of heterogeneous network features based on a subset of MNIST

在FMNIST、COIL20数据集上的实验结果如表3所示, 这也验证上述结论.

表3 DMNEC在2个数据集上的消融实验结果 Table 3 Results of ablation experiment of DMNEC on 2 datasets

3.6 收敛性分析

本节分析DMNEC的收敛情况.首先使用t-SNE^[5]对DMNEC在MNIST子集 (包含1 000个样本) 上的聚类过程进行可视化, 完整的聚类过程如图7所示.

由图7可看出, 原始数据点分布高度重叠, 这意味着聚类任务的艰巨.簇质心初始化后, 相比原始数据点, 预训练多网络分支提取的融合特征点更容易被分离, 但仍存在许多边缘样本点.随着微调网络的进行, 如在第140次迭代时, 同个簇中的大多数数据点都聚集在一起, 只有少数未被较好地分离.迭代过程继续进行, 当满足收敛判定准则时, 训练进程终止, 此时数据点分布已达到稳定状态, 较好地分离数据点, 簇内元素高度集中, 簇间间隔尤其明显.

	Figure Option View Download New Window
	图7 DMNEC在MNIST子集上不同阶段的可视化Fig.7 Visualization of DMNEC on a subset of MNIST at different phases

图8为DMNEC在MNIST、USPS数据集上的聚类指标随迭代次数的变化情况.

由图8可看出, 指标数值在最初的几轮迭代不断升高, 最后趋于稳定.

综上所述, DMNEC在通常情况下都可在一个较理想的局部极小值处收敛.

	Figure Option View Download New Window
	图8 DMNEC在2个数据集上的指标值随迭代次数的变化情况Fig.8 Variation of metric values of DMNEC with iteration times on 2 datasets

3.7 复杂度分析

考虑到对深度模型的复杂度理论分析较困难, 在此采纳模型在某个数据集上的训练时长, 用于评价模型的复杂度.

表4为不同聚类算法在USPS数据集上的耗时与性能情况, 由表可看出, KM算法效率较高但性能较差.DEC、IDEC由于只涉及单个网络的预训练, 效率可观, 性能良好.特别地, DMNEC耗时为DEC和IDEC的8倍多, 这也反映DMNEC虽然性能优越, 但是多网络分支的预训练过程及解码网络的微调过程较耗时, 导致效率并不理想.

在今后的研究工作中, 将致力于改进模型的训练效率.

表4 各算法在USPS数据集上的耗时与指标值对比 Table 4 Comparison of time consumption and metric values of different algorithms on USPS dataset

4 结束语

本文提出深度多网络嵌入聚类算法(DMNEC), 可联合学习包含互补信息的多网络特征及其簇分配.DMNEC包含2个阶段:第1阶段通过端到端地预训练多网络分支, 获取完备的鲁棒低维表征; 第2阶段定义多网络软分配, 借助多网络辅助目标分布建立面向聚类的KL散度损失.同时, 保留编码器的解码网络以保留数据局部结构, 最大程度地避免特征空间扭曲.最后基于多网络分支重建损失和聚类损失微调网络.在4个公开的图像数据集上的实验表明, DMNEC具有较优的聚类性能与良好的泛化性能.今后将会探究更有效的特征融合机制, 用于挖掘多网络特征之间更深层次的互补信息, 尝试在大型三通道场景数据集上进行实验, 探索更先进的深度多网络聚类算法.

参考文献

文献选项

[1]	孙吉贵, 刘杰, 赵连宇. 聚类算法研究. 软件学报, 2008, 19(1): 48-61. (SUN J G, LIU J, ZHAO L Y. Clustering Algorithms Research. Journal of Software, 2008, 19(1): 48-61. ) [本文引用:1]
[2]	SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[C/OL]. [2020-08-24]. https://arxiv.org/pdf/1409.1556.pdf. [本文引用:1]
[3]	SZEGEDY C, LIU W, JIA Y Q, et al. Going Deeper with Convolutions // Proc of the IEEE Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2015. DOI: 10.1109/CVPR.2015.7298594. [本文引用:1]
[4]	HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:1]
[5]	VAN DER MAATEN L, HINTON G. Visualizing Data Using t-SNE. Journal of Machine Learning Research, 2008, 9: 2579-2605. [本文引用:3]
[6]	MACQUEEN J. Some Methods for Classification and Analysis of Multivariate Observations // Proc of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, USA: University of California Press, 1967: 281-297. [本文引用:2]
[7]	BISHOP C. Pattern Recognition and Machine Learning. Berlin, Ger-many: Springer, 2006. [本文引用:2]
[8]	WOLD S, ESBENSEN K, GELADI P. Principal Component Analysis. Chemometrics and Intelligent Laboratory Systems, 1987, 2: 37-52. [本文引用:1]
[9]	XU W, LIU X, GONG Y H. Document Clustering Based on Non-negative Matrix Factorization // Proc of the 26th Annual Internatio-nal ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2003: 267-273. [本文引用:1]
[10]	COX M A A, COX T F. Multidimensional Scaling // CHEN C H, HÄRDLE W, UNWIN A, eds. Hand Book of Data Visualization. Berlin, Germany: Springer, 2008: 315-347. [本文引用:1]
[11]	贾文娟, 张煜东. 自编码器理论与方法综述. 计算机系统应用, 2018, 27(5): 1-9. (JIA W J, ZHANG Y D. Survey on Theories and Methods of Autoencoder. Computer Systems and Applications, 2018, 27(5): 1-9. ) [本文引用:2]
[12]	YANG J W, PARIKH D, BATRA D. Joint Unsupervised Learning of Deep Representations and Image Clusters // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 5147-5156. [本文引用:1]
[13]	周飞燕, 金林鹏, 董军. 卷积神经网络研究综述. 计算机学报, 2017, 40(6): 1229-1251. (ZHOU F Y, JIN L P, DONG J. Review of Convolutional Neural Network. Chinese Journal of Computers, 2017, 40(6): 1229-1251. ) [本文引用:1]
[14]	XIE J Y, GIRSHICK R, FARHADI A. Unsupervised Deep Embedding for Clustering Analysis // Proc of the 33rd International Conference on Machine Learning. New York, USA: ACM, 2016: 478-487. [本文引用:3]
[15]	GUO X F, GAO L, LIU X W, et al. Improved Deep Embedded Clustering with Local Structure Preservation // Proc of the 26th International Joint Conference on Artificial Intelligence. San Francisco, USA: Morgan Kaufmann, 2017: 1753-1759. [本文引用:3]
[16]	LI F F, QIAO H, ZHANG B, et al. Discriminatively Boosted Image Clustering with Fully Convolutional Auto-Encoders. Pattern Recognition, 2018, 83: 161-173. [本文引用:1]
[17]	YANG B, FU X, SIDIROPOULOS N, et al. Towards k-means-Friendly Spaces: Simultaneous Deep Learning and Clustering // Proc of the 34th International Conference on Machine Learning. New York, USA: ACM, 2017: 3861-3870. [本文引用:2]
[18]	FARD M M, THONET T, GAUSSIER E. Deep k-means: Jointly Clustering with k-means and Learning Representations. Pattern Recognition Letters, 2020, 138: 185-192. [本文引用:2]
[19]	GUO X F, LIU X W, ZHU E, et al. Adaptive Self-paced Deep Clustering with Data Augmentation. IEEE Transactions on Know-ledge and Data Engineering, 2020, 32(9): 1680-1693. [本文引用:2]
[20]	PENG X, XIAO S J, FENG J S, et al. Deep Subspace Clustering with Sparsity Prior // Proc of the 25th International Joint Confe-rence on Artificial Intelligence. San Francisco, USA: Morgan Kaufmann, 2016: 1925-1931. [本文引用:1]
[21]	CHANG J L, WANG L F, MENG G F, et al. Deep Adaptive Image Clustering // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 5880-5888. [本文引用:1]
[22]	BO D Y, WANG X, SHI C, et al. Structural Deep Clustering Network // Proc of the International World Wide Web Conference. New York, USA: ACM, 2020: 1400-1410. [本文引用:2]
[23]	ALJALBOUT E, GOLKOV V, SIDDIQUI Y, et al. Clustering with Deep Learning: Taxonomy and New Methods[C/OL]. [2020-08-24]. https://arxiv.org/pdf/1801.07648.pdf. [本文引用:1]
[24]	MIN E X, GUO X F, LIU Q, et al. A Survey of Clustering with Deep Learning: From the Perspective of Network Architecture. IEEE Access, 2018, 6: 39501-39514. [本文引用:1]
[25]	LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-Based Lear-ning Applied to Document Recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. [本文引用:2]
[26]	HULL J J. A Database for Hand written Text Recognition Research. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 550-554. [本文引用:2]
[27]	HAN X, RASUL K, VOLLGRAF R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms[C/OL]. [2020-08-24]. https://arxiv.org/pdf/1708.07747.pdf. [本文引用:2]
[28]	NENE S A, NAYAR S K, MURASE H. Columbia Object Image Library(COIL-20). Technical Report, CUCS-006-96. New York, USA: Columbia University, 1996. [本文引用:2]
[29]	LI T, DING C. The Relationships among Various Nonnegative Matrix Factorization Methods for Clustering // Proc of the 6th IEEE International Conference on Data Mining. Washington, USA: IEEE, 2006. DOI: 10.1109/ICDM.2006.160. [本文引用:1]
[30]	STREHL A, GHOSH J. Cluster Ensembles-A Knowledge Reuse Framework for Combining Multiple Partitions. Journal of Machine Learning Research, 2002, 3: 583-617. [本文引用:1]
[31]	HUBERT L, ARABIE P. Comparing Partitions. Journal of Classification, 1985, 2(1): 193-218. [本文引用:1]
[32]	KUHN H W. The Hungarian Method for the Assignment Problem. Naval Research Logistics Quarterly, 1955, 2(1): 83-97. [本文引用:1]
[33]	RAND W M. Objective Criteria for the Evaluation of Clustering Methods. Journal of the American Statistical Association, 1971, 66(336): 846-850. [本文引用:1]
[34]	SHI J B, MALIK J. Normalized Cuts and Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905. [本文引用:1]
[35]	KAMPFFMEYER M, LOKSE S, BIANCHI F M, et al. Deep Divergence-Based Approach to Clustering. Neural Networks, 2019, 113: 91-101. [本文引用:1]
[36]	TROSTEN D J, KAMPFFMEYER M C, JENSSEN R. Deep Image Clustering with Tensor Kernels and Unsupervised Companion Objectives[C/OL]. [2020-08-24]. https://arxiv.org/pdf/2001.07026.pdf. [本文引用:1]
[37]	CAI J Y, WANG S P, GUO W Z. Stacked Sparse Auto-Encoder for Deep Clustering // Proc of the IEEE International Conference on Parallel and Distributed Processing with Applications , Big Data and Cloud Computing, Sustainable Computing and Communications, Social Computing and Networking. Washington, USA: IEEE, 2019: 1532-1538. [本文引用:1]

2008

0.0

... 无监督聚类^[1]旨在对无标注数据的潜在分布结构进行分析,进而将相似样本划分至同一簇内,是数据科学和机器学习领域中的一个重要研究课题,已成功在图像分类^[2,3,4]、数据可视化^[5]等众多现实场景中得到广泛应用 ...

0.0

2015

0.0

2016

0.0

2008

0.0

... 在t分布随机邻域嵌入(t-Distributed Stochastic Neighbour Embedding, t-SNE)^[5]的启发下,DEC采用学生t分布(Student's t-Distribution)作为软分配,度量低维表征z_i=f_{#cod#x003b8 ...}

... 首先使用t-SNE^[5]对DMNEC在MNIST子集 (包含1 000个样本) 上的聚类过程进行可视化,完整的聚类过程如图7所示 ...

1967

0.0

... 无监督聚类方法的性能很大程度上取决于数据的表征,例如,对于传统聚类方法K-均值(K-means, KM)^[6]或高斯混合模型(Gaussian Mixture Model, GMM)^[7]而言,随着数据表征维度的升高,相似性度量不再可靠,致使聚类变得无效 ...

... 1)传统聚类算法:KM^[6]、GMM^[7]、谱聚类(Spectral Clustering, SC)^[34] ...

2006

0.0

... 1)传统聚类算法:KM^[6]、GMM^[7]、谱聚类(Spectral Clustering, SC)^[34] ...

1987

0.0

... 针对这一问题,一种直观的解决方案是首先利用降维技术,如主成分分析(Principal Component Analysis, PCA)^[8]、非负矩阵分解(Non-negative Matrix Factoriza-tion, NMF)^[9]、多维缩放(Multiple Dimensional Sca-ling, MDS)^[10]等,将数据从高维空间转至低维空间,再对降维后的数据进行聚类 ...

2003

0.0

2008

0.0

2018

0.0

... 其中,自动编码器(Autoencoder, AE)^[11]是深度神经网络的一种特殊形式,以完全无监督的方式学习数据表征 ...

... 受IDEC^[11]启发,进一步保留各个分支对应的解码网络,保留数据特征属性 ...

2016

0.0

... Yang等^[12]提出联合无监督学习(Joint Unsupervised Lear-ning, JULE),结合卷积神经网络(Convolutional Neural Network, CNN)^[13]的表征学习与层次聚类,基于统一权重的三元组损失进行优化,取得较优的聚类表现,但计算复杂度较高 ...

2017

0.0

2016

0.0

... Xie等^[14]提出深度嵌入聚类算法(Deep Embedded Clustering, DEC),预训练自动编码器,学习原始数据的低维表征,在自学习辅助目标分布的帮助下迭代优化基于KL散度的聚类损失 ...

... 1 深度嵌入聚类深度嵌入聚类(DEC)^[14]框图如图1所示 ...

... 3)深度聚类算法:DEC^[14]、IDEC^[15]、DCN^[17]、DKM^[18]、ASPC^[19]、SDCN^[22]、深度散度聚类(Deep Divergence-Based Clustering, DDC)^[35]、深度张量核聚类(Deep Tensor Kernel Clustering, DTKC)^[36]、深度堆栈式稀疏嵌入聚类(Deep Stacked Sparse Embedded Clustering, DSSEC)^[37] ...

2017

0.0

... Guo等^[15]提出改进的深度嵌入聚类算法(Improved DEC, IDEC),在DEC损失函数中加入重建项,用于保留特征空间属性 ...

... 2 基于局部结构保留的深度嵌入聚类相比DEC,改进的深度嵌入聚类算法(IDEC)^[15]保留数据的局部结构,框图如图2所示 ...

2018

0.0

... Li等^[16]提出判别性提升聚类(Discriminatively Boosted Clustering, DBC),将DEC的预训练网络置换为CNN,提取包含像素空间信息的高质量特征,提升整体聚类性能 ...

2017

0.0

... Yang等^[17]提出深度聚类网络(Deep Clustering Network, DCN),利用深度神经网络进行数据降维,学习一个与KM算法相适配的潜在表征空间,在此空间中交替优化网络参数、簇质心、簇分配 ...

2020

0.0

... Fard等^[18]提出深度K-均值 (Deep K-means, DKM),对数据表征、簇质心及簇分配进行连续的端到端联合学习 ...

2020

0.0

... Guo等^[19]提出自适应自步聚类(Adaptive Self-paced Clustering, ASPC),借鉴自步学习(Self-paced Lear-ning, SPL)思想,优先利用高置信度样本训练聚类网络,消除聚类边界样本的负面影响 ...

2016

0.0

... Peng等^[20]提出深度子空间聚类(Deep Subspace Clustering, DSC),计算样本的稀疏重构关系,保留样本的局部性子空间结构和全局性子空间结构 ...

2017

0.0

... Chang等^[21]提出深度自适应聚类(Deep Adaptive Clustering, DAC),假设成对图像为二进制关系,将聚类目标转化为二值成对分类问题 ...

2020

0.0

... Bo等^[22]提出结构化深度聚类网络(Structural Deep Clustering Network, SD-CN),将图卷积网络融入聚类网络中,旨在捕捉数据的结构化信息,获取更具判别性的数据表征,提升模型聚类性能 ...

0.0

... 有关更多方法的介绍可参考文献[23]、文献[24] ...

2018

0.0

... 有关更多方法的介绍可参考文献[23]、文献[24] ...

1998

0.0

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]基准图像数据集上的实验验证本文算法的有效性和优越性 ...

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]图像数据集上评估DMNEC ...

1994

0.0

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]基准图像数据集上的实验验证本文算法的有效性和优越性 ...

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]图像数据集上评估DMNEC ...

0.0

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]基准图像数据集上的实验验证本文算法的有效性和优越性 ...

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]图像数据集上评估DMNEC ...

1996

0.0

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]基准图像数据集上的实验验证本文算法的有效性和优越性 ...

... 在MNIST^[25]、USPS^[26]、FMNIST^[27]、COIL20^[28]图像数据集上评估DMNEC ...

2006

0.0

... 2 评价指标为了衡量算法的聚类性能,采用如下3个聚类评价指标:聚类精度(Clustering Accuracy, ACC)^[29]、归一化互信息(Normalized Mutual Information, NMI)^[30]和调整兰德指数(Adjusted Rand Index, ARI)^[31] ...

2002

0.0

1985

0.0

1955

0.0

... 匈牙利算法(Hungarian Algorithm)^[32]可有效计算最佳映射 ...

1971

0.0

... ARI是兰德指数(Rand Index, RI)^[33]的修正版本,计算如下: ...

2000

0.0

... 1)传统聚类算法:KM^[6]、GMM^[7]、谱聚类(Spectral Clustering, SC)^[34] ...

2019

0.0

2019

0.0