引用本文
曲军谊, 鲍蕾, 陶卿. 非光滑凸问题投影型对偶平均优化方法的个体收敛性. 模式识别与人工智能, ,34(1): 25-32
QU Junyi, BAO Lei, TAO Qing. Individual Convergence of Projected Dual Averaging Methods in Nonsmooth Convex Cases. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,34(1): 25-32.  
Doi: 10.16451/j.cnki.issn1003-6059.202101003
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部 所有
非光滑凸问题投影型对偶平均优化方法的个体收敛性
曲军谊1, 鲍蕾1, 陶卿1
1.中国人民解放军陆军炮兵防空兵学院 信息工程系 合肥 230031

通信作者：陶卿,博士,教授,主要研究方向为模式识别、机器学习、应用数学.E-mail:qing.tao@ia.ac.cn.

作者简介：曲军谊,硕士研究生,主要研究方向为机器学习中凸优化算法及其应用.E-mail:qjy15056933890@163.com.

鲍蕾,博士研究生,主要研究方向为机器学习中凸优化算法及其应用.E-mail:baolei1219@sina.cn.

收稿日期: 2020-08-17 接受日期: 2020-11-17
资助项目: 国家自然科学基金项目(No.61673394); 国家自然科学基金项目(No.620706252)、安徽省自然科学基金项目(No.1908085MF193)资助; 安徽省自然科学基金项目(No.1908085MF193)资助
摘要

对于一般凸问题,对偶平均方法的收敛性分析需要在对偶空间进行转换,难以得到个体收敛性结果.对此,文中首先给出对偶平均方法的简单收敛性分析,证明对偶平均方法具有与梯度下降法相同的最优个体收敛速率 Ο(lnt/ $\sqrt{t}$).不同于梯度下降法,讨论2种典型的步长策略,验证对偶平均方法在个体收敛分析中具有步长策略灵活的特性.进一步,将个体收敛结果推广至随机形式,确保对偶平均方法可有效处理大规模机器学习问题.最后,在L1范数约束的hinge损失问题上验证理论分析的正确性.

关键词: 对偶平均; 个体收敛速率; 稀疏性; 非光滑
Individual Convergence of Projected Dual Averaging Methods in Nonsmooth Convex Cases
QU Junyi1, BAO Lei1, TAO Qing1
1.Department of Information Engineering, Chinese Academy of People's Liberation Army Artillery Air Defense Academy,Hefei 230031
Corresponding author: TAO Qing, Ph.D. professor. His research interests include pa-ttern recognition, machine learning and applied mathematics.

About the Author: QU Junyi, master student. His research interests include convex optimization algorithm and its application in machine lear-ning.

BAO Lei, Ph.D. candidate. Her research interests include convex optimization algorithm and its application in machine learning.

Fund:Supported by National Natural Science Foundation of China(No.61673394); Supported by National Natural Science Foundation of China(No.620706252); Natural Science Foundation of Anhui Province(No.1908085MF193)
Abstract

For convex problems, since the convergence analysis of DA(dual averaging) needs to be transformed in dual space, it is difficult to gain individual convergence. In this paper, a simple convergence analysis of DA is presented, and then it is proved that DA can attain the same optimal Ο(lnt/ $\sqrt{t}$) individual convergence rate as gradient descent(GD). Different from GD, the individual convergence of DA is proved to be step-size flexible by analyzing two typical step-size strategies. Furthermore, the stochastic version of the derived convergence is extended to solve large-scale machine learning problems. Experiments on L1-norm constrained hinge loss problems verify the correctness of the theoretical analysis.

Key words: Key Words Dual Averaging; Individual Convergence Rate; Sparsity; Nonsmooth

对偶平均方法(Dual Averaging, DA)是Nesterov[1]提出的一阶梯度优化方法.特别是在非光滑凸问题中, DA克服梯度下降法由于引入衰减步长而导致的固有弊端, 具有步长策略灵活的特点, 同时, 由于每次迭代都利用过往梯度的信息, 目标函数值在迭代过程中不会出现剧烈震荡, 算法具有较好的收敛稳定性.

Xiao[2]提出正则化对偶平均方法(Regularized DA, RDA), 将DA推广到正则化随机学习和在线优化问题, 证明DA比梯度下降法能更有效地利用问题结构, 特别是在使用L1正则化项的情况下, 可提升特征权重的稀疏性.然而遗憾的是, RDA沿用DA的收敛性分析方法, 需使用对偶空间及函数的共轭等概念和性质[1], 仅能得到最优平均收敛性, 而以平均形式的输出结果在一定程度上破坏原有的稀疏性.

为了解决这一问题, 学者们尝试改变DA的算法结构.Chen等[3]提出最优正则化对偶平均方法(Optimal RDA, ORDA), 在DA每步迭代中添加一步子优化问题求解, 对一般凸、强凸及光滑问题, 均得到Ο (1/ $\sqrt{t}$)的最优个体收敛速率.Nesterov等[4]在DA的基础上添加线性插值策略, 也得到一般凸问题Ο (1/ $\sqrt{t}$)的最优个体收敛速率.

但仔细分析可发现, 文献[3]中采用添加子优化问题求解的方法会直接导致收敛的不稳定性, 对DA改动较大, 难以将其推广应用.文献[4]尽管对算法的改动极小, 具有较好的收敛稳定性, 但插值累积作为最终输出, 却破坏个体输出方式极力想要保持的稀疏性[5].

考虑到DA作为梯度下降法的一种变形, 在特定情况下可等价于梯度下降法, 但反观梯度下降法在非光滑凸问题中的个体收敛性已有全面的进展.Shamir[6]提出梯度下降法最优个体收敛速率的开放性问题.Shamir等[7]提出由平均收敛速率直接得到个体收敛速率的一般技巧, 得到非光滑条件下强凸问题Ο (lnt/t)和一般凸问题Ο (lnt/ $\sqrt{t}$)的个体收敛速率, 相比强凸问题Ο (1/t)和一般凸问题Ο (1/ $\sqrt{t}$)的最优平均收敛速率, 仅相差一个对数因子.Harvey等[8]证明这个对数因子是必不可少的, 即梯度下降法关于一般凸问题和强凸问题的最优个体收敛速率就是Ο (lnt/ $\sqrt{t}$)和Ο (lnt/t).随后, 陶蔚等[9]和程禹嘉等[10]分别采用Nesterov步长策略和heavy-ball动量技巧将梯度下降法在一般凸问题上的个体收敛速率加速到Ο (1/ $\sqrt{t}$).Tao等[11]又采用Nesterov步长策略将梯度下降法在强凸问题上的个体收敛速率加速到Ο (1/t).

基于上述分析.本文给出DA对于一般凸问题一种简单的收敛性分析方法, 并在此基础上证明DA具有Ο (lnt/ $\sqrt{t}$)的最优个体收敛速率, 选取2种典型的步长策略, 验证DA在得到个体收敛性的同时, 仍具有步长策略灵活的特性.典型的L1范数约束的hinge损失函数实验验证理论分析的正确性.

1 对偶平均方法及其收敛性

考虑有约束优化问题:

minw∈Qf(w), (1)

其中, f(w)为Q上的凸函数, Q∈ Rn为有界闭凸集.记w* 为式(1)的一个最优解, 通常平均收敛速率是指f( w^t)-f(w* )的收敛速率, 其中

w^t=$\frac{1}{t}\sum^{t}_{k=1}$ wk,

而个体收敛速率是指f(wt)-f(w* )的收敛速率.

对于问题(1), 批处理形式的DA迭代步骤

wt+1=arg minw∈Q∑k=0tαkf(wk), w+γtd(w), (2)

其中, α t为迭代步长, γ t为控制参数, f(wt)为f(w)在wt处的次梯度, d(w)为定义域Q上具有强凸性质的近似函数, 满足

d(y)≥ d(x)+< d(x), y-x> + 12‖ y-x‖ 2, x∈ Q, y∈ Q.

并存在一个最小点w0, 使d(w0)=0.其中, d(w)一种最简单取法为

d(w)= 12‖ w-w0‖ 2.

Neserov[1]给出DA加权平均形式的收敛界:

1At$\sum^{t}_{k=0}$α k f(wk)-f(w* )≤ γtAt(w* )+$\frac{1}{A_{t}}\sum^{t}_{k=0}$ αk22γk-1f(wk)‖ 2,

其中

At= $\sum^{t}_{k=0}$α k.

同时给出一系列步长策略, 即当

α t=(t+1)p, γ t=c(t+1)p+0.5, p> -0.5,

可得到阶为

Ο max1, 1p+0.5p+1k+1

的收敛速率.这表明当p取有限值时, 均可得到最优平均收敛速率[1].

但是DA的收敛性分析是建立在对偶空间及函数的共轭等概念和性质上, 个体收敛性难以得到稳定的稀疏解, 特别是对于正则化形式的RDA, 在令正则化项

ψ (w)=λ ‖ w‖ 1, d(w)= 12‖ w ‖22

时, 可得到特征权重在各个维度上的解析解:

wt+1(i)= 0, g¯t(i)≤λ-tγ(g¯t(i)-λsgn(g¯t(i))), g¯t(i)> λ

其中,

i=1, 2, …, n, γ t=γ $\sqrt{t}$, g¯t= 1t$\sum^{t}_{k=1}$f(wk),

wt+1(i)为wt+1在第i维上的数值.

这一结果超过当时在稀疏性方法处于领先地位的前向后向切分(Forward-Backward Splitting, FOB-OS)[12], 但是RDA最终平均形式的输出结果还是破坏原有的稀疏性.

2 对偶平均方法的个体收敛性分析

Shamir等[7]给出梯度下降法得到个体收敛速率的技巧, 其中引入后缀平均项:

Sj= 1j+1 $\sum^{t}_{k=t-j}$f(wk), j=0, 1, …, t.

通过巧妙设置步长, 成功构建平均收敛速率与个体收敛速率之间的关键联系:

f(wt)-f( w^t)≤ Ο (lnt/ $\sqrt{t}$).

在此基础上, 再与平均收敛速率

f( w^t)-f(w* )≤ Ο (1/ $\sqrt{t}$)

进行简单叠加, 得到期待的个体收敛速率

f(wt)-f(w* )≤ Ο (lnt/ $\sqrt{t}$).

引理 1 假设f为下半连续的凸函数, wt+1满足式(2)的迭代关系, 则有如下不等式成立:

< $\sum^{t}_{k=0}$α kf(wk), w> +γ td(w)≥ < $\sum^{t}_{k=0}$α kf(wk), wt+1> +γ td(wt+1)+ γt2‖ w-wt+1‖ 2,

相关详细内容及证明过程可参见文献[13]附录A.

引理 2 假设Q为有界闭凸集, 对∀ x∈ Q, ∀ y∈ Q, 均有

‖ x-y‖ ≤ F.

相关证明可参见文献[14].

假设 1 ∃G> 0, 使∀ w∈ Q, 均有

‖ f(w)‖ ≤ G.

依据引理1可得到如下定理1.

定理 1 设f为Q上的一般凸函数, wt由式(2)产生, 取j=0, 1, …, t, 则有

$\sum^{t}_{k=t-j}α_{k}f(w_{k})$-$\sum^{t}_{k=t-j}$α k f(wt-j)≤ (γ t-γ t-j-1)d(wt-j)+ $\sum^{t}_{k=t-j}$ 22γk-1▽f(wk)‖ 2.

此处提出DA可得到个体收敛速率的一种简单收敛性分析方法, 其中当j=t时, 可得到DA的加权平均收敛界.

证明 由凸性可得

$\sum^{t}_{k=t-j}$α k f(wk)- $\sum^{t}_{k=t-j}$α k f(wt-j)≤ $\sum^{t}_{k=t-j}$< α kf(wk), wk-wt-j> , $\sum^{t}_{k=t-j}$α k f(wk)- $\sum^{t}_{k=t-j}$α k f(wt-j)≤ $\sum^{t}_{k=0}$< α kf(wk), wk-wt-j> - $\sum^{t-j-1}_{k=0}$< α kf(wk), wk-wt-j> .

根据引理1可得

$\sum^{t}_{k=t-j}$α k f(wk)- $\sum^{t}_{k=t-j}$α k f(wt-j)≤ $\sum^{t}_{k=0}$< α kf(wk), wk-wt+1> -γ td(wt+1)- γt2‖wt-j-wt+1‖2+γ td(wt-j)- $\sum^{t-j-1}_{k=0}$< α kf(wk), wk-wt-j> .

根据引理1可得

$\sum^{t}_{k=0}$< α kf(wk), wk-wt+1> -γ td(wt+1)≤ $\sum^{t-1}_{k=0}$< α kf(wk), wk-wt> -γ t-1d(wt)- γt-12‖wt-wt+1‖2+< α tf(wt), wt-wt+1> -γ td(wt+1)+γ t-1d(wt+1).

根据γ t系数的递增性质, 可得

$\sum^{t}_{k=0}$< α kf(wk), wk-wt+1> -γ td(wt+1)≤ $\sum^{t-1}_{k=0}$< α kf(wk), wk-wt> -γ t-1d(wt)- γt-12‖ wt-wt+1‖ 2+ < α tf(wt), wt-wt+1> ≤

$\sum^{t-1}_{k=0}$< α kf(wk), wk-wt> -γ t-1d(wt)+ αt22γt-1‖ f(wt)‖ 2.

对上式进行j次递归, 可得

$\sum^{t}_{k=0}$< α kf(wk), wk-wt+1> -γ td(wt+1)≤ $\sum^{t-j-1}_{k=0}$< α kf(wk), wk-wt-j> -γ t-j-1d(wt-j)+ $\sum^{t}_{k=t-j}$ αk22γk-1‖ f(wk)‖ 2.

综上可得

$\sum^{t}_{k=t-j}$α k f(wk)- $\sum^{t}_{k=t-j}$α k f(wt-j)≤ (γ t-γ t-j-1)d(wt-j)+$\sum^{t}_{k=t-j}$ αk22γk-1‖ f(wk)‖ 2. (3)

考虑到DA作为一种步长策略灵活的算法, 即取α t=1和α t=t这2种典型的步长选取策略, 与之对应的

γ t=c $\sqrt{t}$, γ t=c(t+1) $\sqrt{t}$,

由此可得到推论1和推论2.

推论 1 在定理1的基础上, 取

α t=1, γ t=c $\sqrt{t}$,

则有

f(wt)-f(w* )≤ G2c+cF222+lntt.

证明 令

γ t=c $\sqrt{t}$, α t=1, d(w)= w-w0‖22,

代入式(3)可得

$\sum^{t}_{k=t-j}$f(wk)-(j+1)f(wt-j)≤ c(t-t-j-1)2‖ wt-j-w0‖ 2+$\sum^{t}_{k=t-j}$ 12ck-1‖ f(wk)‖ 2. (4)

根据引理2和假设1, 令

‖ wt-w0‖ ≤ F, ‖ f(wt)‖ ≤ G,

代入式(4),

$\sum^{t}_{k=t-j}$f(wk)-(j+1)f(wt-j)≤ c(t-t-j-1)2F2+$\sum^{t}_{k=t-j}$ 12ck-1G2.

由于

$\sum^{t}_{k=t-j}$ 1k-1≤ 2( $\sqrt{t}$- t-j-1),

可得

$\sum^{t}_{k=t-j}$f(wk)-(j+1)f(wt-j)≤ c(t-t-j-1)2F2+ t-t-j-1cG2≤ cF22+G2cj+1t,

不等式两侧同时除以j+1,

$\frac{1}{j+1}\sum^{t}_{k=t-j}$ f(wk)-f(wt-j)≤ cF22+G2c1t.

令

Sj=$\frac{1}{j+1}\sum^{t}_{k=t-j}$f(wk),

可得

-f(wt-j)≤ -Sj+ cF22+G2c1t.

由Sj定义可得

jSj-1=(j+1)Sj-f(wt-j)≤ (j+1)Sj-Sj+ cF22+G2c1tjSj+ cF22+G2c1t

不等式两侧同时除以j,

Sj-1≤ Sj+ cF22+G22c1jt.

递归可得

f(wt)=S0≤ St+ 1tcF22+G2c $\sum^{t}_{k=1}\frac{1}{k}$ ≤ St+ 1tcF22+G2c+lnt), f(wt)-St≤ 1tcF22+G2c(1+lnt).

已知DA的平均收敛界, 即

$\sum^{t}_{k=0}$α k f(wk)- $\sum^{t}_{k=0}$α k f(w* )≤ $\sum^{t}_{k=0}$ αk22γk-1‖ f(wk)‖ 2+γ td(w* ), (5)

将

γ t=c $\sqrt{t}$, t≥ 1, γ -1=γ 0=γ 1, α t=1, d(w)= w-w0‖22

代入式(5),

$\sum^{t}_{k=0}$f(wk)- $\sum^{t}_{k=0}$f(w* )≤ $\frac{1}{c}$F2+ $\sum^{t}_{k=2}$ 12ck-1F2+ ctG22≤ G2c+cF22t，St -f(w* )≤ 1tG2c+cF22.

综上可得

f(wt)-f(w* )≤ G2c+cF222+lntt.

推论 2 在定理1的基础上, 取

γ t=c(t+1) $\sqrt{t}$, α t=t,

则有

f(wt)-f(w* )≤ G2c+cF222+lntt.

证明 由定理1可知,

$\sum^{t}_{k=t-j}$α k f(wk)- $\sum^{t}_{k=t-j}$α k f(wt-j)≤ (γ t-γ t-j-1)d(wt-j)+$\sum^{t}_{k=t-j}$ αk22γk-1‖ ▽f(wk)‖ 2.

取

γ t=c(t+1) $\sqrt{t}$, α t=t, d(w)= w-w0‖22, γ t-γ t-j-1=(t+1) $\sqrt{t}$-(t-j) t-j-1= (t-j)( $\sqrt{t}$- t-j-1)+(1+j) $\sqrt{t}$≤ (1+j)(2t-j)t,

$\sum^{t}_{k=t-j}$ αk22γk-1=$\sum^{t}_{k=t-j}$ 12k-1≤ $\sqrt{t}$- t-j-1≤ j+1t, $\sum^{t}_{k=t-j}$α k= (j+1)(2t-j)2.

根据引理2和假设1, 令

‖ wt-w0‖ ≤ F, ‖ f(wt)‖ ≤ G,

整理可得

$\sum^{t}_{k=t-j}$kf(wk)- (j+1)(2t-j)2f(wt-j)≤ c(1+j)(2t-j)2tF2+ (j+1)ctG2,

$\frac{\sum^{t}_{k=t-j}kf(w_{k})} {sum^{t}_{k=t-j}k}$-f(wt-j)≤ ctF2+ 2ct(2t-j)G2≤ ctF2+ 2cttG2.

令

Sj=$(\sum^{t}_{k=t-j}k)^{-1} sum^{t}_{k=t-j}$kf(wk),

可得

-f(wt-j)≤ -Sj+ ctF2+ 2cttG2.

由Sj定义可得

$\sum^{t}_{k=t-j+1}$ kSj-1≤ $\sum^{t}_{k=t-j}$ kSj-(t-j)Sj+(t-j) ctF2+2cttG2≤

$\sum^{t}_{k=t-j+1}$ kSj+(t-j) (ctF2+ 2cttG2), Sj-1≤ Sj+ 2(t-j)j(2t-j+1)( ctF2+ 2cttG2)≤

Sj+ 1jctF2+2cttG2.

递归可得

f(wt)=S0≤ St+ ctF2+2cttG2$\sum^{t}_{k=1} \frac{1}{k}$ ≤ St+ ctF2+2cttG2(1+lnt).

已知DA的平均收敛界:

$\sum^{t}_{k=0}$α k f(wk)- $\sum^{t}_{k=0}$α k f(w* )≤ $\sum^{t}_{k=0}$ αk22γk-1‖ f(wk)‖ 2+γ td(w* ).

取

γ t=c(t+1) $\sqrt{t}$, t≥ 1, γ -1=γ 0=γ 1, α t=t, d(w)= w-w0‖22

代入式(5), 可得

$\sum^{t}_{k=0}$ kf(wk)- $\sum^{t}_{k=0}$ kf(w* )≤ 14cF2+$\sum^{t}_{k=2}$ 12ck-1F2+ c(1+t)tG22≤ G2tc+ c(1+t)tF22,

St-f(w* )≤ 2G2c(1+t)t+ cF2t≤ 2G2ctt+ cF2t.

综上可得

f(wt)-f(w* )≤ 2G2ct+cF22+lntt.

由此, 得到非光滑条件下DA的最优个体收敛速率, 并验证在选取不同阶的步长策略时仍能得到最优个体收敛速率.推论1的证明与梯度下降法对应部分的证明基本相似.推论2使用变步长, 在证明的难度上提升一个维度, 但结果依然能得到最优个体收敛速率.

为了便于理解, 上述论述得到的结果均是在批处理的情形下, 但批处理不适合处理大规模数据, 因此, 需要将上述结果推广至随机形式以求解机器学习问题.

考虑最基本的二分类问题, 假设训练样本集:

S={(xi, yi)|i=1, 2, …, m}Rn× {1, -1},

其中(xi, yi)为独立同分布.

考虑非光滑稀疏学习问题hinge损失函数:

fi(w)=max{0, 1-yi< w, xi> }.

优化目标函数:

minw∈Qf(w)=$\frac{1}{m}\sum^{m}_{i=1}$ fi(w).

约束情况下随机形式的DA迭代步骤如下:

wt+1=arg minw∈Q{< $\sum^{t}_{k=0}$α k▽fi(wk), w> +γ td(w)}, (6)

其中i为迭代到第t步时随机抽取的样本序号.

随机形式的不同之处在于迭代步骤中的fi(wt)为fi(w)在wt处的次梯度, 由于hinge损失函数的次梯度有多种计算方式, 这里采用文献[15]的方式进行计算, 即

▽fi(wt)=$\frac{1}{m} \sum^{}_{(x_{i}, y_{i})∈A^{+}_{t}}$ yixi, (7)

其中,

At$\subseteq$ S, At+={(xi, yi)∈ At∶ yi< w, xi> < 1},

并设置|At|$\subseteq$1.

算法 1 随机DA算法

输入 循环次数t

输出 wt+1

初始化 向量w0=0

For k=0 to t

更新γ k=c k, α k=1;

随机选取i=1, 2, …, m;

由式(7)计算fi(wk);

由式(6)计算wk+1;

End For

假设样本点满足独立同分布条件, 采取随机抽取样本方式计算得到fi(wt)为f(w)在wt处次梯度的无偏估计.而随机算法就是将批处理形式的目标函数梯度换成无偏估计, 所以文献[16]给出将批处理算法收敛界转换为随机算法收敛界的技巧, 同样适用于推论1和推论2.进而可将定理1与推论1结合推广至随机形式, 得到定理2; 将定理1与推论2结合推广至随机形式得到定理3.

定理 2 设f为一般凸函数, wt由式(6)产生, 取

γ t=c $\sqrt{t}$, α t=1,

则有

E[f(wt)-f(w* )]≤ G2c+cF222+lntt.

定理 3 设f为一般凸函数, wt由式(6)产生, 取

γ t=c(t+1) $\sqrt{t}$, α t=t,

则有

E[f(wt)-f(w* )]≤ 2G2ct+cF22+lntt.

3 实验及结果分析

实验主要目的是验证算法1的个体收敛速率的理论分析.主要采用来源于台湾大学林志仁LIBSVM网站中属于分类问题的6个常用标准数据集.表1详细介绍这6个数据集.

表1 标准数据集 Table 1 Standard datasets

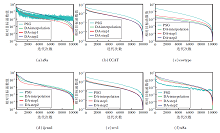
实验选取如下4种个体输出方式的随机优化方法进行对比:投影次梯度方法(Projected Subgradient, PSG)[14], 线性插值DA(简记为DA-interpolation)[4], 2种步长策略的DA(简记为DA-step1, DA-step2).2种步长策略的DA分别对应本文定理2和定理3.

为了体现实验的客观性, 最后输出的结果均采用各方法在每个数据集上运行10次后的平均值, 同时取迭代次数t=10 000.在实验中, 对于有约束条件下的投影计算, 调用高效投影稀疏学习(Sparse Learning with Efficient Projections, SLEP)工具箱的函数[17], 其中PQ为l1范数球{w∶ ‖ w‖ 1≤ z}上的投影算子, z的取值随数据集的改变而不同, 同个数据集条件下各方法均取相同的约束参数.

在收敛速率方面, 对于非光滑凸问题, 理论上梯度下降法和DA仅能得到Ο (lnt/ $\sqrt{t}$)的个体收敛速率, 而线性插值DA是对标准算法进行修改, 可得到

Ο (1/ $\sqrt{t}$)的最优个体收敛速率.在收敛稳定性方面, DA每步迭代都使用所有过往梯度的平均值, 而线性插值DA对梯度和特征权重都使用平均值, 所以线性插值DA的收敛稳定性最高, DA次之.

图1给出各方法在6个数据集上的收敛速率对比, 纵轴取对数坐标, 表示当前目标函数值与目标函数最优值之差(即收敛精度), 4种方法在6个数据集上迭代运算达到9 000步时, 2种步长策略的DA和梯度下降法均可达到

f(wt)-f(w* )≤ 9× 10-2

的收敛精度, 而线性插值DA可达到

f(wt)-f(w* )≤ 10-2

的收敛精度, 这在一定程度上验证DA个体收敛性分析的正确性.同时, 从图中曲线的震荡程度上看, DA的波动幅度普遍小于梯度下降法, 这也说明DA在收敛稳定性上具有一定的优势.

图1 各方法在6个数据集上的收敛速率对比Fig.1 Comparison of convergence rates of different methods on 6 datasets

4 结束语

本文在给出DA一种简单收敛分析的基础上, 证明其在一般凸问题上可得到与梯度下降法同样的最优个体收敛速率, 但比梯度下降法更具有收敛的稳定性, 同时讨论2种典型的步长策略, 证明DA在泛化能力上优于梯度下降法.今后将考虑DA在正则化和强凸条件下的最优个体收敛速率, 同时还会考虑改变算法, 特别是运用动量技巧, 尝试实现DA在个体收敛性上的加速.

参考文献
[1] NESEROV Y. Primal-Dual Subgradient Methods for Convex Pro-blems. Mathematical Programming, 2009, 120(1): 221-259. [本文引用:4]
[2] XIAO L. Dual Averaging Methods for Regularized Stochastic Lear-ning and Online Optimization. Journal of Machine Learning Research, 2010, 11: 2543-2596. [本文引用:1]
[3] CHEN X, LIN Q H, PEÑA J. Optimal Regularized Dual Averaging Methods for Stochastic Optimization // Proc of the 25th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2012, I: 295-403. [本文引用:2]
[4] NESTEROV Y, SHIKHMAN V. Quasi-Monotone Subgradient Me-thods for Nonsmooth Convex Minimization. Journal of Optimization Theory and Applications, 2015, 165(3): 917-940. [本文引用:3]
[5] 陶卿, 马坡, 张梦晗, 等. 机器学习随机优化方法的个体收敛性研究综述. 数据采集与处理, 2017, 32(1): 17-25.
(TAO Q, MA P, ZHANG M H, et al. Individual Convergence of Stochastic Optimization Methods in Machine Learning. Journal of Data Acquisition. Individual Convergence of Stochastic Optimization Methods in Machine Learning. Journal of Data Acquisition and Processing, 2017, 32(1): 17-25). [本文引用:1]
[6] SHAMIR O. Open Problem: Is Averaging Needed for Strongly Convex Stochastic Gradient Descent? // Proc of the 25th Annual Conference on Learning Theory. New York, USA: ACM, 2012: 47. 1-47. 3. [本文引用:1]
[7] SHAMIR O, ZHANG T. Stochastic Gradient Descent for Nonsmoo-th Optimization: Convergence Results and Optimal Averaging Schemes // Proc of the 30th International Conference on Machine Learning. New York, USA: ACM, 2013: 71-79. [本文引用:2]
[8] HARVEY N J A, LIAW C, PLAN Y, et al. Tight Analyses for Non-smooth Stochastic Gradient Descent // Proc of the 32nd Annual Conference on Learning Theory. New York, USA; ACM, 2019: 1579-1613. [本文引用:1]
[9] 陶蔚, 潘志松, 储德军, 等. 使用Nesterov 步长策略投影次梯度方法的个体收敛性. 计算机学报, 2018, 41(1): 164-176.
(TAO W, PAN Z S, CHU D J, et al. The Individual Convergence of Projected Subgradient Methods Using the Nesterov's Step-Size Strategy. Chinese Journal of Computers, 2018, 41(1): 164-176. ) [本文引用:1]
[10] 程禹嘉, 陶蔚, 刘宇翔, 等. Heavy-ball型动量方法的最优个体收敛速率. 计算机研究与发展, 2019, 56(8): 1686-1694.
(CHENG Y J, TAO W, LIU Y X, et al. Optimal Individual Convergence Rate of the Heavy-Ball-Based Momentum Methods. Journal of Computer Research and Development, 2019, 56(8): 1686-1694. ) [本文引用:1]
[11] TAO W, PAN Z S, WU G W, et al. The Strength of Nesterov's Extrapolation in the Individual Convergence of Nonsmooth Optimization. IEEE Transactions on Neural Networks and Learning Sys-tems, 2020, 31(7): 2557-2568. [本文引用:1]
[12] DUCHI J, SINGER Y. Efficient Online and Batch Learning Using forward Backward Splitting. Journal of Machine Learning Research, 2009, 10: 2899-2934. [本文引用:1]
[13] TSENG P. Approximation Accuracy, Gradient Methods, and Error Bound for Structured Convex Optimization. Mathematical Progra-mming, 2010, 125(2): 263-295. [本文引用:1]
[14] BERTSEKAS D P, NÉDICA A, OZDAGLAR A E. Convex Analysis and Optimization. Belmont, USA: Athena Scientific, 2003. [本文引用:2]
[15] SHALEV-SHWARTZ S, SINGER Y, SREBRO N, et al. PeGa-sos: Primal Estimated Sub-gradient Solver for SVM. Mathematical Programming, 2011, 127(1): 3-30. [本文引用:1]
[16] RAKHLIN A, SHAMIR O, SRIDHARAN K. Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization // Proc of the 29th International Conference on Machine Learning. New York, USA: ACM, 2012: 1571-1578. [本文引用:1]
[17] LIU J, JI S W, YE J P. SLEP: Sparse Learning with Efficient Projections[CB/OL]. [2020-08-08]. http://citeseer.ist.psu.edu/viewdoc/download;jsessionid=23332E4606BC9D0D84E693C2FF63ADB6?doi=10.1.1.214.1045&rep=rep1&type=pdf. [本文引用:1]