局部协同视角下的鲁棒标记分布学习

引用本文

徐苏平, 商琳, 周宇杰. 局部协同视角下的鲁棒标记分布学习. 模式识别与人工智能, ,34(1): 44-57
XU Suping, SHANG Lin, ZHOU Yujie. Robust Label Distribution Learning from a Perspective of Local Collaboration. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,34(1): 44-57. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202101005
Permissions

《模式识别与人工智能》编辑部所有

局部协同视角下的鲁棒标记分布学习

徐苏平^1,², 商琳^1,², 周宇杰^1,²

1.南京大学计算机科学与技术系南京 210023

2.南京大学计算机软件新技术国家重点实验室南京 210023

通信作者：商琳,博士,副教授,主要研究方向为机器学习、数据挖掘、计算智能等.E-mail:shanglin@nju.edu.cn.

作者简介:徐苏平,博士研究生,主要研究方向为机器学习、数据挖掘、计算智能等.E-mail:supingxu@smail.nju.edu.cn.

周宇杰,硕士研究生,主要研究方向为深度学习、图像描述、图像分类等.E-mail:yujiezhou@smail.nju.edu.cn.

收稿日期: 2020-06-15 接受日期: 2020-10-09

资助项目: 国家自然科学基金项目(No.61672276)资助; 国家自然科学基金项目(No.51975294)资助; 国家自然科学基金项目(No.62006128)资助; 国家自然科学基金项目(No.62076111)资助

摘要

已有标记分布学习(LDL)算法在一定程度上破坏不同标记间的关联性及标记分布的整体结构,同时,大多仅以提升标记分布的预测性能为目的,忽略计算代价和噪声鲁棒性在实际应用中的重要性.为了缓解上述不足,文中提出基于局部协同表达的标记分布学习算法(LCR-LDL).在LCR-LDL中,一个未标记样本可被视作由该未标记样本邻域构建的局部字典的协同表达,表达系数中的鉴别信息可用于重构未标记样本的标记分布.在15个真实的LDL数据集上的实验表明,LCR-LDL不仅可有效提升LDL的预测性能,而且具有较强的鲁棒性和轻量级的计算开销.

关键词: 标记分布学习(LDL); 多标记学习; 标记多义性; 稀疏字典学习; 鲁棒性

Robust Label Distribution Learning from a Perspective of Local Collaboration

XU Suping^1,², SHANG Lin^1,², ZHOU Yujie^1,²

1.Department of Computer Science and Technology, Nanjing University, Nanjing 210023

2.State Key Laboratory for Novel Software Technology, Nanjing University, Nanjing 210023

Corresponding author: SHANG Lin, Ph.D., associate professor. Her research interests include machine learning, data mining and computational intelligence.

About the Author: XU Suping, Ph.D. candidate. His research interests include machine learning, data mi-ning and computational intelligence.)

ZHOU Yujie, master student. His research interests include deep learning, image caption and image classification.)

Fund:Supported by National Natural Science Foundation of China(No.61672276); Supported by National Natural Science Foundation of China(No.51975294); Supported by National Natural Science Foundation of China(No.62006128); Supported by National Natural Science Foundation of China(No.62076111)

Abstract

In the most of label distribution learning(LDL)algorithms, the correlations among different labels and the overall structure of label distribution are destroyed to a certain extent. Moreover, most existing LDL algorithms mainly focus on improving the predictive performance of label distribution, while ignoring the significance of computational cost and noise robustness in practical applications. To tackle these issues, a local collaborative representation based label distribution learning algorithm (LCR-LDL) is proposed. In LCR-LDL, an unlabeled sample is treated as a collaborative representation of the local dictionary constructed by the neighborhood of the unlabeled sample, and the discriminating information of representation coefficients is utilized to reconstruct the label distribution of unlabeled sample. Experimental results on 15 real-world LDL datasets show that LCR-LDL effectively improves the predictive performance for LDL tasks with a better robustness and low computational cost.

Key words: Key Words Label Distribution Learning(LDL); Multi-label Learning; Label Ambiguity; Sparse Dictionary Learning; Robustness

文章图片

在机器学习^{[1, 2]}与数据挖掘^{[3, 4]}的研究中, 标记多义性问题受到广泛关注, 多标记学习(Multi-Label Learning, MLL)^{[2, 5, 6, 7]}为处理一个样本可能同时属于多个标记这一多义性问题提供一种有效的技术手段.然而, 在MLL框架下, 与样本关联的所有标记都被视为同等重要.而在很多现实的应用中, 人们常期望获得描述某个特定样本时各个标记的相对重要性程度(标记集合上的一个分布).例如:在面部表情的情感分析^{[8, 9]}中, 一个面部表情通常是由多种基本情感构成, 即愤怒、厌恶、恐惧、喜悦、悲伤和惊讶等.每种基本情感为构建面部表情做出不同程度的贡献, 所有基本情感下的贡献程度形成一个面部表情的情感分布.在电影评级预测^{[10, 11]}中, 如果存在一个系统能够在电影上映前就准确预测电影评级的分布情况, 不仅有助于观众选择性地观看其最喜欢的电影, 而且可降低制片方的投资风险和时间成本.

尽管可通过设定一个较高(最高)的标记阈值, 将上述标记(情感、评级)分布问题转化入MLL框架, 甚至是单标记学习(Single-Label Learning, SLL)框架, 但这将丢失相关标记的相对重要的信息.Geng等^{[12, 13]}提出标记分布学习(Label Distribution Lear-ning, LDL), 用于处理进一步的标记多义性问题.考虑到每个相关标记对样本的不同描述程度, 相比SLL和MLL, LDL可被视为一种更泛化的机器学习框架.

如今LDL大体上可分为3类:算法适应方法、问题转化方法和专门设计的方法.

算法适应方法直接修改一些约束条件, 用于扩展已有的SLL和MLL, 使其可处理标记分布问题, 如AA-kNN(Algorithm Adaptation: k-Nearest Neigh-bor)^{[12, 13, 14]}和AA-BP(Algorithm Adaptation: BackPropagation)^{[12, 13, 15]}.

问题转化方法将LDL任务转换成多个SLL任务, 基于概率或置信度的SLL处理这些任务.例如, 将一个标记的描述度作为采样权值从原始的LDL数据中进行采样后, SLL中常见的基学习器朴素贝叶斯(Naive Bayes, NB)和支持向量机(Support Vector Machine, SVM), 分别被用于生成有代表性的问题转换方法PT-Bayes(Problem Transformation:Bayes)^{[12, 13]}和PT-SVM(Problem Transformation:SVM)^{[12, 13]}.

专门设计的方法使预测的标记分布和真实的标记分布之间的相似度最大化, 直接聚焦标记分布的预测问题.SA-IIS(Specialized Algorithm:Improved Iterative Scaling)^{[14, 15]}和SA-BFGS(Specialized Algo-rithm:Broyden-Fletcher-Goldfarb-Shanno)^{[12, 15]}都是以Kullback-Leibler散度为目标函数, 构造最大熵模型, 分别采用改进迭代缩放(Improved Iterative Scaling, IIS)^[16]和拟牛顿法BFGS^[17]实施优化.LDLogitBoost(LogitBoost Based LDL)^[18]采用Boosting策略, 借助数量递增的加权回归器(加权回归树)处理LDL任务.LSM-LDL(Least Square Method Based LDL)利用变换矩阵将每个标记视为样本特征的线性组合, 通过最小二乘法建立优化模型.现有的研究结果^{[11, 12]}表明, 相比算法适应方法和问题转化方法, 专门设计的方法能更有效地处理真实的LDL任务.

尽管上述专门设计的方法在处理LDL任务中的标记多义性方面提升改进的性能, 却在一定程度上破坏不同标记间的关联性.保持标记分布的整体结构, 完整地保留标记间的关联性可能是一种提升LDL系统性能的有效方式.此外, 目前针对LDL开展的研究工作中, 很少有研究人员关注到LDL的计算代价及噪声破坏环境下的鲁棒性问题.

基于上述原因, 受到稀疏字典学习中表达/重构概念的启发, 本文提出基于局部协同表达的标记分布学习算法(Local Collaborative Representation Based LDL, LCR-LDL), 首先借助最近邻(k-Nearest Neigh-bor, kNN)规则搜索某一未标记样本的局部邻域空间, 再在l₂范数的约束下, 使用邻域空间内全部样本构建的局部字典对未标记样本进行协同表达, 其中, 具有正表达系数的样本与未标记样本间存在正相关性, 它们的表达系数可直接被视为重构标记分布时的鉴别信息.然后, 引入映射函数ϕ (· , · ), 分别获得各个标记对该未标记样本的描述程度.最后, 采用归一化, 获得未标记样本的标记分布.在15个真实的LDL数据集上的实验表明, LCR-LDL不仅可有效提升对LDL任务的预测性能, 而且具有较强的鲁棒性和较优的计算效率.

1 基础知识

1.1 标记分布学习框架

从某种程度上讲, LDL是SLL和MLL的一种泛化形式.在SLL和MLL中, 对于一个给定样本, 全部可能的标记集合中的每个元素要么与其关联, 要么与其无关, 即学习系统建立在由“ 硬的” 1/0标识预定义的标记集合上, 1表示样本具有该标记, 0表示样本不具有该标记.特别地, 在SLL中预定义的标记是互斥的, 即每个样本仅能与单一标记关联.因此, 假设学习系统中存在p种可能的标记, 对于MLL, 共存在2^p-1种可能的输出结果, 对于SLL, 共存在p种可能的输出结果.相比SLL和MLL, LDL拥有更丰富的标记形式, 即LDL可能的输出结果不再是一个标记集合, 而是所有p种可能的标记对应的多个实值描述程度, 反映全部标记在描述一个样本时的相对重要程度.

LDL的形式化描述如下.令X=R^m为m维的样本空间, Y={y₁, y₂, …, y_p}为由全部p种标记构成的有限集合,

T={(x_i, d_i)|i=1, 2, …, n}

为由n个已标记样本构成的LDL训练集.其中:样本

x_i=[ $x_{i}^{1}$ , $x_{i}^{2}$ , …, $x_{i}^{m}$ ]∈ X⊂X,

表示为一个m维的特征向量;

d_i=[ $d_{x_{i}}^{y_{1}}$ , $d_{x_{i}}^{y_{2}}$ , …, $d_{x_{i}}^{y_{p}}$ ]

是与x_i关联的标记分布, $d_{x_{i}}^{y_{j}}$ 表示标记y_j(j=1, 2, …, p)对x_i的描述程度.对于每个x_i, 有

∀ $d_{x_{i}}^{y_{j}}$ ∈ [0, 1], $\sum^{p}_{j=1}$ $d_{x_{i}}^{y_{j}}$ =1

成立, 这意味着所有标记能够完全描述x_i.

值得注意的是, 对于一给定样本x_i, d_i中的所有元素 $d_{x_{i}}^{y_{j}}$ 形成一个概率单纯形, 每个 $d_{x_{i}}^{y_{j}}$ 并不是y_j正确标记x_i的概率, 而是y_j在完全描述x_i中所占的比例^[12].所有非零的 $d_{x_{i}}^{y_{j}}$ 对应的标记y_j实际上都可描述x_i, 相对重要性由 $d_{x_{i}}^{y_{j}}$ 进行度量.

由上述形式化定义可知, SLL和MLL可视作LDL的特殊情形.图1分别展示SLL、MLL和 LDL的标记分布示意图.SLL中x_i仅与标记y₂关联, 即y₂可完全描述x_i, 则有 $d_{x_{i}}^{y_{2}}$ =1.MLL中x_i同时与标记y₂、y_?关联, 重要性相等, 则有 $d_{x_{i}}^{y_{2}}$ = $d_{x_{i}}^{y_{?}}$ =0.5.LDL中全部标记y₁, y₂, …, y_p共同描述x_i, 具有

$d_{x_{i}}^{y_{1}}$ =0.1, $d_{x_{i}}^{y_{2}}$ =0.5, $d_{x_{i}}^{y_{3}}$ =0.05, $d_{x_{i}}^{y_{?}}$ 0.2, $d_{x_{i}}^{y_{p}}$ 0.15,

满足

∀ $d_{x_{i}}^{y_{j}}$ ∈ [0, 1], $\sum^{p}_{j=1}$ $d_{x_{i}}^{y_{j}}$ =1.

	Figure Option View Download New Window
	图1 SLL、MLL和LDL的标记分布示意图Fig.1 Label distribution of SLL, MLL and LDL

1.2 稀疏表达和协同表达

在稀疏字典学习中, 一个过完备字典

X= $[x_{1}, x_{2}, \dots, x_{n}]^{T}$ ∈ Rⁿ^×^m, n> m

能由训练样本集合T构建.给定一个未标记样本x'_i, 稀疏表达(Sparse Representation, SR)试图通过解决如下l₀范数最小化问题, 获得一组表达系数:

${\hat{α}}_{0}$ =arg $\min_{α}$ ‖ α ‖ ₀, s.t. ‖ x'i_-α X‖ 2_≤ε , (1)

其中, ε > 0 为误差容忍程度, ‖ · ‖ ₀为一个给定向量中非零元素的个数.然而, 在大多数实际应用问题中, 式(1)构建一个欠定系统, 这意味着获得式(1)的精确解是一个NP难问题, 甚至很难被近似求解^{[19, 20]}.已有的研究工作^{[21, 22]}表明, 如果表达系数 ${\hat{α}}_{0}$ 足够稀疏, 使用l₁范数约束代替l₀范数约束, 可获得一个闭式解, 由l₁范数约束近似:

${\hat{α}}_{1}$ =arg $\min_{α}$ ‖ α ‖ ₁, s.t ‖ x'_i-α X‖ ₂≤ ε .

上式可视为经典的凸优化问题, 可被转换成一个由l₁范数约束的最小二乘问题:

${\hat{α}}_{1}$ =arg $\min_{α}$ ‖ x'_i-α X $‖_{2}^{2}$ +λ ‖ α ‖ ₁, (2)

其中, λ > 0为正则化参数, 目的是平衡表达误差和α 的稀疏性.

Zhang等^[23]研究表明, 不是l₁范数最小化基于的稀疏性假设, 而是协同表达机制, 使SR在学习任务中变得有效.所有样本都应对表达一个未标记样本做出贡献.因此, 采用l₂范数约束代替l₁范数约束, 提出协同表达(Collaborative Representation, CR)^{[23, 24]}, 式(2)演变成:

${\hat{α}}_{2}$ =arg $\min_{α}$ ‖ x'_i-α X $‖_{2}^{2}$ +λ ‖ α $‖_{2}^{2}$ ,

其中λ > 0为正则化参数.由上式能推导出

${\hat{α}}_{2}$ =x'_iX^T(XX^T+λ I)^-1, (3)

其中I为单位矩阵.

2 局部协同表达的标记分布学习算法

在标记分布学习框架下, 一个标记分布信息矩阵

D= $[d_{1}, d_{2}, \dots, d_{n}]^{T}$ ∈ Rⁿ^×^p

可由训练样本集T构建.给定一个未标记样本x'_i∈ X, 通过kNN规则生成包含x'_i的k个邻居的相似空间δ (x'_i).

在相似空间δ (x'_i)中, 由式(3)获得一组表达系数

$\hat{α}$ =[ ${\hat{α}}_{1}$ , ${\hat{α}}_{2}$ , …, ${\hat{α}}_{k}$ ],

其中, ${\hat{α}}_{μ}$ (μ =1, 2, …, k)表示δ (x'_i)中的第μ 个样本对表达x'_i的贡献程度.

正的表达系数对应的样本与未标记样本x'_i有正的关联性, 这些正的系数可直接视为重构x'_i标记分布的鉴别信息.

根据鉴别信息和标记分布信息矩阵D, 可引入映射函数ϕ (x'_i, y_j), 获得y_j(j=1, 2, …, p)对未标记样本x'_i的描述程度, 映射函数

ϕ (x'_i, y_j)= $\sum^{k}_{μ=1}$ β _μ $d_{δ (x'_{i})_{μ}}^{y_{j}}$ , (4)

其中

β _μ= $\{\begin{array}{l} {\hat{α}}_{μ}, & {\hat{α}}_{μ} > 0 \\ 0, & {\hat{α}}_{μ} \leq 0 \end{array}$

δ $(x'_{i})_{μ}$ 为δ (x'_i)中第μ 个样本的特征向量.

根据假设“ 所有的标记能够完全地描述给定的样本” , 对全部标记的描述程度进行归一化操作.由上述分析可知, 基于局部协同表达的标记分布学习算法(LCR-LDL)包含4个主要步骤.首先, kNN规则被用于构建包含未标记样本的k个邻居的相似空间.再在相似空间内, 可通过协同机制计算得出一组表达系数, 并获得相似空间内的每个样本对于未标记样本表达的贡献程度.然后, 抽取重构未标记样本的标记分布过程中的鉴别信息, 获得每个标记对未标记样本的描述程度.最后, 执行归一化操作, 获得未标记样本预测的标记分布.LCR-LDL具体步骤如下所示.

算法 1 LCR-LDL

输入过完备词典X= $[x_{1}, x_{2}, \dots, x_{n}]^{T}$ ,

标记分布信息矩阵D= $[d_{1}, d_{2}, \dots, d_{n}]^{T}$ ,

邻域尺寸k, 未标记样本x'_i∈ X

输出预测x'_i的标记分布d'_i

step 1 采用l₂范数对X的每行进行归一化.

step 2 根据kNN规则, 从X中找出未标记样本x'_i的k个邻居.

step 3 在δ (x'_i)上对x'_i进行编码:

$\hat{α}$ =x'_iδ $(x'_{i})^{T}$ (δ (x'_i)δ $(x'_{i})^{T} {+ λI)}^{- 1}$ ,

其中, δ (x'_i)∈ R^k^×^m是由x'_i的k个邻居在X上抽取的数据矩阵.

step 4 由式(4)计算y_j(j=1, 2, …, p)对x'_i的描述程度ϕ (x'_i, y_j).

step 5 归一化ϕ (x'_i, y_j), 获得预测的标记分布:

d'_i= $[\frac{ϕ (x'_{i}, y_{1})}{\overset{p}{\sum_{j}} ϕ (x'_{i}, y_{j})}, \frac{ϕ (x'_{i}, y_{2})}{\overset{p}{\sum_{j}} ϕ (x'_{i}, y_{j})}, \dots, \frac{ϕ (x'_{i}, y_{p})}{\overset{p}{\sum_{j}} ϕ (x'_{i}, y_{j})}]$ .

值得注意的是, 并没有声称kNN规则是部署局部策略最佳的方式.实际上, 相似空间δ (x'_i)可通过其它的方式构建, 如采用聚类分析技术(k均值(k-means)、层次聚类分析(Hierarchical Clustering Analysis, HCA)、模糊C均值(Fuzzy C-means, FCM)等)识别与x'_i属于同一类簇的相似样本.尽管如此, LCR-LDL采用最简单的局部策略也获得具有竞争力的预测性能.

LCR-LDL计算复杂度集中在step 3, 计算表达系数

$\hat{α}$ =x'_iδ (x'_i)^T(δ (x'_i)δ (x'_i)^T+λ I)^-1,

其中,

B=δ (x'_i)δ (x'_i)^T

的计算复杂度为O(mk²),

W=(B+λ I)^-1

的计算复杂度为O(k³).此外, x'_iδ (x'_i)^TW的计算复杂度为O(mk²)+O(mk).因此, LCR-LDL的总体计算复杂度是

O(k³)+O(mk²)+O(mk).

k被推荐设定为原始样本数量的1%~10%, 因此, 通常mk≪mk²成立, 可认为LCR-LDL的计算复杂度为O(k³)+O(mk²).相比其它最小二乘的LDL的计算复杂度O(n³)+O(mn²), 当k为n的1%~10%时, 显著降低LCR-LDL的计算代价.

3 实验及结果分析

3.1 实验环境

为了评估LCR-LDL的有效性, 在15个真实的LDL数据集上进行实验分析, 它们源于LDL网站(http://ldl.herokuapp.com/download).表1 汇总实验数据集的基本信息.这15个数据集选自5种不同的实际应用领域:生物信息学、医学诊断、自然场景识别、面部表情识别和电影评级.

表1 实验数据集 Table 1 Experimental datasets

由于每个样本同时与多个具有不同描述程度的标记关联, 相比SLL和MLL, 有关LDL学习器的性能评估更复杂.实验中使用如下6种标记分布评估度量^[12]:切比雪夫距离(Chebyshev Distance)、克拉克距离(Clark Distance)、堪培拉测度(Canberra Metric)、KL散度(Kullback-Leibler Divergence)、余弦系数(Cosine Coefficient)、相交相似度(Intersection Simi-larity).

给定一个未标记样本x'_i∈ X, 假设预测的标记分布

d'_i=[ $d_{x'_{i}}^{y_{1}}$ , $d_{x'_{i}}^{y_{2}}$ , …, $d_{x'_{i}}^{y_{p}}$ ],

而真实的标记分布

$\overset{_{i}}{d'}$ = $[\bar{d_{x'_{i}}^{y_{1}}}, \bar{d_{x'_{i}}^{y_{2}}}, \dots, \bar{d_{x'_{i}}^{y_{p}}}],]$

6种评估指标的详情如下.

1)Chebyshev distance:

Chebyshev distance=max_j $|\bar{d_{x'_{i}}^{y_{j}}} - d_{x'_{i}}^{y_{j}}|$ .

2)Clark distance:

Clark distance= $\sqrt[]{\overset{p}{\sum_{j}} \frac{(\bar{d_{x'_{i}}^{y_{j}}} - d_{x'_{i}}^{y_{j}})^{2}}{(\bar{d_{x'_{i}}^{y_{j}}} + d_{x'_{i}}^{y_{j}})^{2}}}$ .

3)Canberra metric:

Canberra metric= $\sum^{p}_{j=1}$ $\frac{| \bar{d_{x'_{i}}^{y_{j}}} - d_{x'_{i}}^{y_{j}} |}{\bar{d_{x'_{i}}^{y_{j}}} + d_{x'_{i}}^{y_{j}}}$ .

4)Kullback-Leibler divergence:

Kullback-Leibler divergence=$\sum^{p}_{j=1}$ $\bar{d_{x'_{i}}^{y_{j}}}$ ln $(\frac{\bar{d_{x'_{i}}^{y_{j}}}}{d_{x'_{i}}^{y_{j}}})$ .

5)Cosine coefficient:

Cosine coefficient= $\frac{\sum_{j=1} p \bar{d_{x'_{i}}^{y_{j}}} d_{x'_{i}}^{y_{j}}}{\sqrt[]{\overset{p}{\sum_{j=1}} (d_{\overset{_{i}}{x'}}^{y_{j}})^{2}} \sqrt[]{\overset{p}{\sum_{j=1}} (d_{x'_{i}}^{y_{j}})^{2}}}$ ,

6)Intersection similarity:

Intersection similarity= $\sum^{p}_{j=1}$ min $(\bar{d_{x'_{i}}^{y_{j}}}, d_{x'_{i}}^{y_{j}})$ .

前4种度量从距离的角度评估LDL的性能, 值越小, 性能越优.后2种度量从相似度的角度评估LDL的性能.

在实验中, 选用如下7种主流的LDL进行对比分析:PT-Bayes、PT-SVM、AA-kNN、AA-BP、SA-IIS、SABFGS、LSM-LDL.所有对比算法的代码均由原作者分享.按照原作者建议, 在PT-Bayes中, 最大似然估计被用于估计高斯类条件概率密度函数.在PT-SVM中, 选用LIBSVM工具包中的C-SVC类型, 同时设定核函数为径向基函数(Radial Basis Function, RBF)核, C = 1.0.在AA-kNN中邻居数量k=4.在AA-BP中, 隐层神经元的数量设定为60.对于SA-IIS和SA-BFGS, 设定所有的初始化参数为默认值.此外, 为了获得较优的预测性能, 通过经验估计, 将LSM-LDL和LCR-LDL中的正则化参数均设定为λ =0.01.

值得注意的是, 在一些基于邻域的分类学习方法中, 鲜有文献报道有关邻域尺寸k设定的理论依据, 最佳的k值取决于数据集本身的特性.在大多数情况下, 较优的邻域尺寸k可通过调节训练样本的百分比决定, 本文称为邻域参数w.因此, 在实验中, 将在1%~20%内以1%为间隔, 依次调节邻域参数w, 测试邻域尺寸对LCR-LDL的性能影响.

实验在配置为Intel Core i7-6850K, 3.60 GHz处理器和32.00 GB内存的工作站上进行, 编程环境为Matlab R2017b.

3.2 邻域尺寸对预测性能的影响

本文在不同的邻域尺寸下评估LCR-LDL的预测性能.采用训练样本的百分比(邻域参数w)描述邻域尺寸, 在不同的邻域参数w下进行实验.在每个w下, 进行10折交叉验证, 记录10次实验结果的均值.

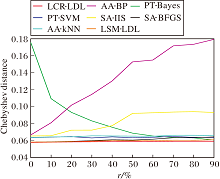
由于篇幅限制, 仅展示表1中7个LDL数据集上的Chebyshev distance指标值, 反映LCR-LDL随邻域尺寸变化时预测性能的变化趋势, 具体如图2所示.对于未显示的Yeast-cdc、Yeast-cold、Yeast-diau、Yeast-dtt、Yeast-elu、Yeast-heat、Yeast-spo、Human Gene数据集上的实验结果, 它们的预测性能的变化趋势与 Yeast-alpha数据集上的变化趋势相似.

由图2可见, 在Chebyshev distance指标上, 随着邻域参数w的增大, LCR-LDL的预测性能大体上先保持上升趋势, 再逐渐下降.特别地, 当w在[1%, 10%]内时, LCR-LDL可获得最好或是几乎最好的预测性能.主要原因如下:如果邻域尺寸设置过小, 所选邻域空间内样本数量会出现不充足的情况, 使LCR-LDL无法表达未标记样本.随着邻域尺寸的增长, 越来越多的信息可被用于表达未标记样本, LCR-LDL的预测性能呈现上升趋势.

然而, 如果邻域尺寸大于一个特定的值, 字典中大量较低相似度的噪声样本会落入未标记样本的邻域空间中, 这对以局部方式表达未标记样本造成干扰, 致使LCR-LDL的预测性能下降.

	Figure Option View Download New Window
	图2 w不同时LCR-LDL的Chebyshev distance值对比Fig.2 Chebyshev distance value comparison of LCR-LDL with different w

3.3 各算法性能对比

将LCR-LDL的预测性能与7种LDL进行对比分析.对于每种评估度量, 使用10折交叉验证, 评估不同算法的有效性, 分别记录10次实验结果的均值和方差.值得注意的是, 如图2所示, 从Yeast-alpha数据集到Human Gene数据集(表1第1行~11行), 当邻域参数w在10%附近时, LCR-LDL获得较优的预测性能.然而, 从Natural Scene数据集到Movie数据集(表1第12行~15行), 当邻域参数w在1%附近时, LCR-LDL可获得较优的预测性能.因此, 在前11个数据集和后4个数据集上, 分别在w = 10%和w = 1%下评估各算法的预测性能.

各算法针对6种评估指标的预测性能的对比结果如表2~表7所示, 对于每种评估指标, 最优预测性能由黑体数字表示.

针对Chebyshev distance和Cosine coefficient指标, LCR-LDL获得较令人满意的预测结果.基于Kullback-Leibler divergence、Intersection similarity指标, LCR-LDL在14个LDL数据集上获得最优的预测性能.在S-JAFFE、Movie数据集上, LCR-LDL的预测性能不是最优, 但与最优值接近.对于Clark distance、Canberra metric指标, LCR-LDL在12个LDL数据集上的预测性能显著最优, 在另外3个数据集上, LCR-LDL的预测性能与AA-kNN、SA-BFGS、AA-BP相当.综合上述实验结果可发现, LCR-LDL的预测性能明显优于其它对比算法, 主要原因如下:消除一些较低相似度样本, 局部邻域搜索策略可有效降低噪声对分类学习的影响, 协同机制可完整保持标记间的相关性及不同标记的相对重要性, 最终使标记分布学习系统的性能得到较大幅度提升.

从整体上看, 在全部预测性能的结果中, LSM-LDL和SA-BFGS排在第二位的情形分别占据53.33%和57.78%, 排在第三位的情形分别占据33.33%和20.00%, 排在第四至第八位的情形均很少.因此, LSM-LDL和SA-BFGS的预测性能也较显著, 然而, LSM-LDL和SA-BFGS存在如下不足:1)在LSM-LDL中, 当探索每维特征和每个标记的描述度之间的相关性时, 训练样本中可能存在噪声数据, 导致由训练样本的特征和对应的标记分布构造的转换矩阵在一定程度上遭到破坏.2)SA-BFGS的设计过程中同样未考虑噪声的干扰, 当处理真实的LDL任务时, 面对密集的特征噪声, 在原始特征空间上, 基于最大熵模型的各个标记下的个体学习器效果并不理想.对于AA-kNN和AA-BP, 预测性能位于第一名、第二名或第三名的情况仅占18.89%, 这意味着直接修改SLL和MLL中的一些约束条件, 对于LDL任务而言并不是最好的选择.

此外, 对于PT-SVM、SA-IIS和PT-Bayes, 它们的预测性能都排在第四至第八位之间, 不存在排名位于前三位的情况, 主要原因如下:LDL会破坏不同标记的内在关联性, 因此, PT-SVM和PT-Bayes不能获得令人满意的预测结果.

为了更完善地对比预测性能, 进一步采用Friedman检验^[25], 它是一种在多个数据集上对比两种以上算法的统计学检验方法^[26].假设存在s种待对比算法, N种实验数据集, r^j_i表示第j种算法在第i个数据集上预测性能排名, 第j种算法在全部数据集上的平均排名为

R_j= $\frac{1}{N}$ $\sum^{N}_{i=1}$ r^j_i.

在原假设下, Friedman统计量F_F符合一个自由度为(s - 1)和(s - 1)(N - 1)的Fisher分布:

F_F= $\frac{(N - 1) χ_{F}^{2}}{N (s - 1) - χ_{F}^{2}}$ , $χ_{F}^{2}$ = $\frac{12 N}{s (s + 1)} (\overset{s}{\sum_{j=1}} R_{j}^{2} - \frac{s {(s + 1)}^{2}}{4})$

表2 各算法在15个LDL数据集上的Chebyshev distance值对比 Table 2 Chebyshev distance value comparison of different algorithms on 15 LDL datasets

数据集	PT-Bayes	PT-SVM	AA-kNN	AA-BP	SA-IIS	SA-BFGS	LSM-LDL	LCR-LDL
Yeast-alpha	0.09957 (± 0.10929)	0.01389 (± 0.00619)	0.01467 (± 0.00674)	0.03634 (± 0.01899)	0.02021 (± 0.00868)	0.01342 (± 0.00641)	0.01342 (± 0.00641)	0.01334 (± 0.00641)
Yeast-cdc	0.10706 (± 0.11263)	0.01703 (± 0.00838)	0.01756 (± 0.00805)	0.03851 (± 0.02095	0.02329 (± 0.01056)	0.01621 (± 0.00817)	0.01621 (± 0.00817)	0.01613 (± 0.00812)
Yeast-cold	0.17746 (± 0.13015)	0.05735 (± 0.02975)	0.05513 (± 0.02953)	0.05855 (± 0.03201)	0.06163 (± 0.03263)	0.05118 (± 0.02809)	0.05118 (± 0.02809)	0.05046 (± 0.02810)
Yeast-diau	0.15418 (± 0.13184)	0.04616 (± 0.01910)	0.03895 (± 0.01967)	0.04831 (± 0.02346)	0.04541 (± 0.02027)	0.03698 (± 0.01813)	0.03695 (± 0.01813)	0.03625 (± 0.01792)
Yeast-dtt	0.17768 (± 0.14419)	0.03865 (± 0.02151)	0.03909 (± 0.02223)	0.04354 (± 0.02567)	0.04920 (± 0.02826)	0.03601 (± 0.02119)	0.03601 (± 0.02119)	0.03540 (± 0.02122)
Yeast-elu	0.11101 (± 0.11765)	0.01697 (± 0.00722)	0.01760 (± 0.00762)	0.03693 (± 0.02013)	0.02396 (± 0.01064)	0.01630 (± 0.00748)	0.01629 (± 0.00748)	0.01608 (± 0.00743)
Yeast-heat	0.17518 (± 0.13098)	0.04422 (± 0.02069)	0.04459 (± 0.02086)	0.05298 (± 0.02558)	0.05255 (± 0.02274)	0.04224 (± 0.01986)	0.04227 (± 0.01986)	0.04130 (± 0.01949)
Yeast-spo	0.17566 (± 0.13207)	0.06356 (± 0.03539)	0.06368 (± 0.03603)	0.06666 (± 0.03394)	0.06543 (± 0.03219)	0.05837 (± 0.03140)	0.05837 (± 0.03141)	0.05783 (± 0.03165)
Yeast-spo5	0.20392 (± 0.14321)	0.09321 (± 0.05751)	0.09549 (± 0.06188)	0.09330 (± 0.05713)	0.09704 (± 0.05961)	0.09141 (± 0.05670)	0.09142 (± 0.05670)	0.08939 (± 0.05492)
Yeast-spoem	0.17717 (± 0.14073)	0.09119 (± 0.07397)	0.09124 (± 0.07087)	-	0.09279 (± 0.06867)	0.08679 (± 0.06469)	0.08679 (± 0.06470)	0.08501 (± 0.06357)
Human Gene	0.18354 (± 0.20344)	-	0.06449 (± 0.07674)	0.05995 (± 0.07533)	0.05343 (± 0.07797)	0.05330 (± 0.07797)	0.05327 (± 0.07797)	0.05319 (± 0.07793)
Natural Scene	0.66227 (± 0.29842)	0.42515 (± 0.25147)	0.29346 (± 0.19879)	0.32871 (± 0.20504)	0.35141 (± 0.23707)	-	0.31278 (± 0.17968)	0.27339 (± 0.17776)
S-JAFFE	0.12037 (± 0.05803)	0.12675 (± 0.05978)	0.08975 (± 0.05364)	0.11553 (± 0.05656)	0.12549 (± 0.05905)	0.15616 (± 0.07972)	0.14008 (± 0.05906)	0.08414 (± 0.05932)
S-BU_3DFE	0.66405 (± 0.18453)	0.14077 (± 0.07649)	0.09944 (± 0.06017)	0.12742 (± 0.06740)	0.13551 (± 0.07293)	-	0.10864 (± 0.04921)	0.09887 (± 0.05347)
Movie	0.20016 (± 0.11220)	0.22969 (± 0.06816)	0.12368 (± 0.07195)	0.12321 (± 0.07056)	0.14637 (± 0.07236)	0.12593 (± 0.07341)	0.12634 (± 0.07223)	0.12300 (± 0.06680)

表2 各算法在15个LDL数据集上的Chebyshev distance值对比 Table 2 Chebyshev distance value comparison of different algorithms on 15 LDL datasets

表3 各算法在15个LDL数据集上的Clark distance值对比 Table 3 Clark distance value comparison of different algorithms on 15 LDL datasets

数据集	PT-Bayes	PT-SVM	AA-kNN	AA-BP	SA-IIS	SA-BFGS	LSM-LDL	LCR-LDL
Yeast-alpha	1.17066 (± 0.74048)	0.22072 (± 0.08036)	0.23142 (± 0.08256)	0.72361 (± 0.42337)	0.30338 (± 0.09420)	0.20987 (± 0.08244)	0.20987 (± 0.08243)	0.20874 (± 0.08225)
Yeast-cdc	1.06245 (± 0.66499)	0.22521 (± 0.10068)	0.23661 (± 0.09786)	0.58602 (± 0.34851)	0.29256 (± 0.10571)	0.21586 (± 0.09891)	0.21586 (± 0.09891)	0.21476 (± 0.09854)
Yeast-cold	0.48275 (± 0.33809)	0.15505 (± 0.08246)	0.15011 (± 0.08199)	0.15983 (± 0.08907)	0.16512 (± 0.08700)	0.13970 (± 0.07966)	0.13971 (± 0.07967)	0.13779 (± 0.07936)
Yeast-diau	0.72941 (± 0.45314)	0.24820 (± 0.10648)	0.21091 (± 0.10906)	0.26495 (± 0.13470)	0.24186 (± 0.10564)	0.20071 (± 0.10343)	0.20053 (± 0.10343)	0.19669 (± 0.10178)
Yeast-dtt	0.48143 (± 0.35661)	0.10499 (± 0.06241)	0.10623 (± 0.06473)	0.11837 (± 0.07365)	0.13126 (± 0.07535)	0.09824 (± 0.06213)	0.09823 (± 0.06213)	0.09651 (± 0.06225)
Yeast-elu	1.03471 (± 0.65579)	0.21087 (± 0.07734)	0.21770 (± 0.08161)	0.50907 (± 0.30067)	0.27564 (± 0.09150)	0.19894 (± 0.07818)	0.19893 (± 0.07817)	0.19721 (± 0.07842)
Yeast-heat	0.68591 (± 0.40737)	0.19050 (± 0.08633)	0.19364 (± 0.08624)	0.23397 (± 0.11828)	0.22394 (± 0.09065)	0.18266 (± 0.08326)	0.18275 (± 0.08325)	0.17889 (± 0.08262)
Yeast-spo	0.69063 (± 0.41312)	0.26870 (± 0.13318)	0.26892 (± 0.13772)	0.29018 (± 0.14011)	0.27863 (± 0.12639)	0.24984 (± 0.12702)	0.24983 (± 0.12703)	0.24748 (± 0.12732)
Yeast-spo5	0.42572 (± 0.30532)	0.18764 (± 0.12457)	0.19175 (± 0.12801)	0.18787 (± 0.12385)	0.19427 (± 0.12566)	0.18424 (± 0.12361)	0.18428 (± 0.12360)	0.18065 (± 0.11989)
Yeast-spoem	0.29356 (± 0.25529)	0.13465 (± 0.11715)	0.13577 (± 0.11105)	-	0.13738 (± 0.11018)	0.12918 (± 0.10541)	0.12918 (± 0.10542)	0.12672 (± 0.10403)
Human Gene	4.60810 (± 1.19775)	-	2.37670 (± 1.11276)	3.35112 (± 0.85015)	2.12773 (± 1.23981)	2.10832 (± 1.24589)	2.10990 (± 1.24571)	2.10142 (± 1.24603)
Natural Scene	2.85884 (± 0.14870)	2.57619 (± 0.26247)	1.69678 (± 0.58254)	2.46253 (± 0.29503)	2.46803 (± 0.31561)	-	2.44442 (± 0.28518)	2.07832 (± 0.45056)
S-JAFFE	0.42923 (± 0.12312)	0.46070 (± 0.13918)	0.31976 (± 0.14369)	0.41600 (± 0.12617)	0.45774 (± 0.12890)	0.62974 (± 0.23732)	0.70791 (± 0.27018)	0.30227 (± 0.17408)
S-BU_3DFE	2.09374 (± 0.23069)	0.43346 (± 0.16270)	0.31715 (± 0.15482)	0.39910 (± 0.15022)	0.41895 (± 0.15354)	-	0.39620 (± 0.15101)	0.31247 (± 0.13142)
Movie	0.80319 (± 0.34100)	0.83257 (± 0.24116)	0.54736 (± 0.28364)	0.55895 (± 0.27083)	0.57946 (± 0.25616)	0.54910 (± 0.28200)	0.59086 (± 0.29592)	0.55930 (± 0.27388)

表3 各算法在15个LDL数据集上的Clark distance值对比 Table 3 Clark distance value comparison of different algorithms on 15 LDL datasets

表4 各算法在15个LDL数据集上的Canberra metric值对比 Table 4 Canberra metric value comparison of different algorithms on 15 LDL datasets

数据集	PT-Bayes	PT-SVM	AA-kNN	AA-BP	SA-IIS	SA-BFGS	LSM-LDL	LCR-LDL
Yeast-alpha	4.18970 (± 2.86247)	0.72035 (± 0.25309)	0.75662 (± 0.25957)	2.38559 (± 1.37766)	1.01402 (± 0.32073)	0.68161 (± 0.26062)	0.68161 (± 0.26061)	0.67811 (± 0.25920)
Yeast-cdc	3.48168 (± 2.34120)	0.67497 (± 0.28069)	0.71565 (± 0.27639)	1.77360 (± 1.03966)	0.89760 (± 0.31282)	0.64733 (± 0.27240)	0.64733 (± 0.27240)	0.64413 (± 0.27076)
Yeast-cold	0.84300 (± 0.61488)	0.26703 (± 0.14112)	0.25998 (± 0.14094)	0.27543 (± 0.15271)	0.28613 (± 0.15217)	0.24046 (± 0.13594)	0.24047 (± 0.13595)	0.23744 (± 0.13562)
Yeast-diau	1.65489 (± 1.11493)	0.53610 (± 0.21852)	0.45421 (± 0.23172)	0.56992 (± 0.28114)	0.52830 (± 0.22625)	0.43075 (± 0.21505)	0.43038 (± 0.21501)	0.42205 (± 0.21136)
Yeast-dtt	0.84346 (± 0.66032)	0.17991 (± 0.10249)	0.18248 (± 0.10716)	0.20357 (± 0.12160)	0.22824 (± 0.12959)	0.16905 (± 0.10170)	0.16904 (± 0.10171)	0.16581 (± 0.10171)
Yeast-elu	3.28111 (± 2.24167)	0.62293 (± 0.21248)	0.64384 (± 0.22967)	1.49812 (± 0.85029)	0.82408 (± 0.27107)	0.58250 (± 0.21335)	0.58249 (± 0.21334)	0.57775 (± 0.21409)
Yeast-heat	1.44460 (± 0.92074)	0.37993 (± 0.16473)	0.38919 (± 0.16781)	0.46980 (± 0.23193)	0.45502 (± 0.18107)	0.36433 (± 0.15823)	0.36448 (± 0.15819)	0.35650 (± 0.15691)
Yeast-spo	1.46019 (± 0.92642)	0.55362 (± 0.28010)	0.55407 (± 0.28624)	0.59494 (± 0.28533)	0.57328 (± 0.25877)	0.51347 (± 0.25976)	0.51345 (± 0.25977)	0.50820 (± 0.26013)
Yeast-spo5	0.66049 (± 0.48796)	0.28817 (± 0.18581)	0.29504 (± 0.19418)	0.28866 (± 0.18470)	0.29922 (± 0.18971)	0.28300 (± 0.18405)	0.28305 (± 0.18404)	0.27718 (± 0.17840)
Yeast-spoem	0.39554 (± 0.33316)	0.18777 (± 0.15967)	0.18890 (± 0.15153)	-	0.19142 (± 0.14951)	0.17970 (± 0.14233)	0.17971 (± 0.14233)	0.17620 (± 0.14028)
Human Gene	33.6387 (± 10.8906)	-	16.1936 (± 8.81004)	22.8328 (± 7.03316)	14.5776 (± 9.77926)	14.4323 (± 9.82037)	14.4402 (± 9.81933)	14.3799 (± 9.81818)
Natural Scene	8.41427 (± 0.62078)	7.30224 (± 1.10443)	3.87866 (± 1.67883)	6.77910 (± 1.23866)	6.80025 (± 1.35251)	-	6.69993 (± 1.19621)	5.16965 (± 1.60060)
S-JAFFE	0.90045 (± 0.28681)	0.95854 (± 0.30349)	0.65727 (± 0.30291)	0.86488 (± 0.28107)	0.94598 (± 0.28476)	1.30704 (± 0.52409)	1.39522 (± 0.54244	0.61328 (± 0.35771)
S-BU_3DFE	4.91216 (± 0.73096)	0.91919 (± 0.35932)	0.64841 (± 0.32494)	0.85271 (± 0.34524)	0.90527 (± 0.36119)	-	0.81282 (± 0.30614)	0.65716 (± 0.29175)
Movie	1.55564 (± 0.74128)	1.60936 (± 0.51369)	1.05184 (± 0.58326)	1.06282 (± 0.55186)	1.11350 (± 0.52580)	1.05714 (± 0.58408)	1.11540 (± 0.59635)	1.06383 (± 0.55226)

表4 各算法在15个LDL数据集上的Canberra metric值对比 Table 4 Canberra metric value comparison of different algorithms on 15 LDL datasets

表5 各算法在15个LDL数据集上的Kullback-Leibler divergence值对比 Table 5 Kullback-Leibler divergence value comparison of different algorithms on 15 LDL datasets

数据集	PT-Bayes	PT-SVM	AA-kNN	AA-BP	SA-IIS	SA-BFGS	LSM-LDL	LCR-LDL
Yeast-alpha	0.28201 (± 0.48230)	0.00594 (± 0.00418)	0.00658 (± 0.00467)	0.08409 (± 0.10818)	0.01145 (± 0.00676)	0.00548 (± 0.00416)	0.00548 (± 0.00416)	0.00542 (± 0.00414)
Yeast-cdc	0.27003 (± 0.43545)	0.00759 (± 0.00648)	0.00822 (± 0.00644)	0.06540 (± 0.09111)	0.01276 (± 0.00860)	0.00696 (± 0.00603)	0.00696 (± 0.00603)	0.00689 (± 0.00600)
Yeast-cold	0.21033 (± 0.38195)	0.01463 (± 0.01613)	0.01387 (± 0.01527)	0.01594 (± 0.01887)	0.01689 (± 0.01816)	0.01208 (± 0.01424)	0.01208 (± 0.01424)	0.01180 (± 0.01405)
Yeast-diau	0.26766 (± 0.48380)	0.01911 (± 0.01540)	0.01484 (± 0.01537)	0.02414 (± 0.03447)	0.01871 (± 0.01552)	0.01306 (± 0.01293)	0.01304 (± 0.01292)	0.01258 (± 0.01256)
Yeast-dtt	0.21651 (± 0.41130)	0.00684 (± 0.00883)	0.00716 (± 0.00968)	0.00912 (± 0.01345)	0.01105 (± 0.01325)	0.00615 (± 0.00897)	0.00615 (± 0.00897)	0.00599 (± 0.00887)
Yeast-elu	0.27975 (± 0.47287)	0.00681 (± 0.00478)	0.00737 (± 0.00535)	0.05222 (± 0.07538)	0.01209 (± 0.00779)	0.00615 (± 0.00466)	0.00615 (± 0.00466)	0.00607 (± 0.00464)
Yeast-heat	0.26405 (± 0.45340)	0.01375 (± 0.01186)	0.01423 (± 0.01243)	0.02231 (± 0.03227)	0.01898 (± 0.01462)	0.01257 (± 0.01096)	0.01258 (± 0.01097)	0.01206 (± 0.01064)
Yeast-spo	0.26998 (± 0.42546)	0.02937 (± 0.02950)	0.02958 (± 0.03160)	0.03339 (± 0.03537)	0.02999 (± 0.02606)	0.02456 (± 0.02386)	0.02456 (± 0.02387)	0.02422 (± 0.02390)
Yeast-spo5	0.21621 (± 0.39814)	0.03022 (± 0.03560)	0.03289 (± 0.04425)	0.03016 (± 0.03524)	0.03252 (± 0.03814)	0.02918 (± 0.03448)	0.02919 (± 0.03448)	0.02779 (± 0.03338)
Yeast-spoem	0.16780 (± 0.36870)	0.02835 (± 0.04841)	0.02778 (± 0.04252)	-	0.02748 (± 0.04195)	0.02426 (± 0.03664)	0.02426 (± 0.03665)	0.02334 (± 0.03551)
Human Gene	1.76286 (± 3.14382)	-	0.29804 (± 0.37999)	0.50021 (± 0.40103)	0.23831 (± 0.36340)	0.23586 (± 0.36242)	0.23605 (± 0.36250)	0.23415 (± 0.36082)
Natural Scene	11.3119 (± 6.07276)	1.56049 (± 0.93447)	1.13042 (± 1.35052)	0.86688 (± 0.50318)	0.91746 (± 0.46429)	-	0.81706 (± 0.53138)	0.72646 (± 0.69691)
S-JAFFE	0.07379 (± 0.04660)	0.08696 (± 0.05969)	0.04569 (± 0.04796)	0.06902 (± 0.04559)	0.08517 (± 0.05408)	0.15358 (± 0.11984)	0.18847 (± 0.16629)	0.04636 (± 0.06169)
S-BU_3DFE	5.39918 (± 2.75621)	0.09364 (± 0.07746)	0.05090 (± 0.05533)	0.07541 (± 0.06023)	0.08411 (± 0.06185)	-	0.06549 (± 0.05434)	0.04583 (± 0.04028)
Movie	0.69671 (± 2.46474)	0.29038 (± 0.16432)	0.11621 (± 0.13947)	0.11093 (± 0.12015)	0.12941 (± 0.12609)	0.11708 (± 0.14162)	0.13159 (± 0.16194)	0.10942 (± 0.11533)

表5 各算法在15个LDL数据集上的Kullback-Leibler divergence值对比 Table 5 Kullback-Leibler divergence value comparison of different algorithms on 15 LDL datasets

表6 各算法在15个LDL数据集上的Cosine coefficient值对比 Table 6 Cosine coefficient value comparison of different algorithms on 15 LDL datasets

数据集	PT-Bayes	PT-SVM	AA-kNN	AA-BP	SA-IIS	SA-BFGS	LSM-LDL	LCR-LDL
Yeast-alpha	0.84865 (± 0.15336)	0.99416 (± 0.00408)	0.99352 (± 0.00459)	0.94873 (± 0.04636)	0.98812 (± 0.00726)	0.99461 (± 0.00408)	0.99461 (± 0.00408)	0.99466 (± 0.00405)
Yeast-cdc	0.85341 (± 0.14774)	0.99268 (± 0.00595)	0.99206 (± 0.00593)	0.95719 (± 0.04166)	0.98705 (± 0.00875)	0.99330 (± 0.00548)	0.99330 (± 0.00548)	0.99337 (± 0.00545)
Yeast-cold	0.89646 (± 0.10729)	0.98598 (± 0.01470)	0.98679 (± 0.01386)	0.98498 (± 0.01669)	0.98365 (± 0.01726)	0.98852 (± 0.01290)	0.98852 (± 0.01290)	0.98878 (± 0.01273)
Yeast-diau	0.86820 (± 0.13000)	0.98212 (± 0.01318)	0.98628 (± 0.01364)	0.97911 (± 0.02024)	0.98207 (± 0.01437)	0.98793 (± 0.01127)	0.98795 (± 0.01126)	0.98838 (± 0.01089)
Yeast-dtt	0.89757 (± 0.11271)	0.99339 (± 0.00786)	0.99311 (± 0.00861)	0.99136 (± 0.01103)	0.98912 (± 0.01254)	0.99408 (± 0.00782)	0.99408 (± 0.00782)	0.99424 (± 0.00774)
Yeast-elu	0.85457 (± 0.14771)	0.99339 (± 0.00442)	0.99285 (± 0.00501)	0.96378 (± 0.03549)	0.98762 (± 0.00817)	0.99404 (± 0.00432)	0.99404 (± 0.00432)	0.99413 (± 0.00429)
Yeast-heat	0.86499 (± 0.12072)	0.98682 (± 0.01089)	0.98639 (± 0.01149)	0.98019 (± 0.02041)	0.98133 (± 0.01430)	0.98798 (± 0.01005)	0.98797 (± 0.01005)	0.98848 (± 0.00971)
Yeast-spo	0.85928 (± 0.13060)	0.97234 (± 0.02651)	0.97213 (± 0.02840)	0.96958 (± 0.02746)	0.97139 (± 0.02368)	0.97692 (± 0.02096)	0.97692 (± 0.02096)	0.97726 (± 0.02102)
Yeast-spo5	0.89546 (± 0.11322)	0.97312 (± 0.02890)	0.97075 (± 0.03676)	0.97315 (± 0.02887)	0.97082 (± 0.03189)	0.97409 (± 0.02792)	0.97408 (± 0.02792)	0.97537 (± 0.02700)
Yeast-spoem	0.92248 (± 0.10083)	0.97544 (± 0.03627)	0.97584 (± 0.03354)	-	0.97611 (± 0.03098)	0.97904 (± 0.02670)	0.97904 (± 0.02671)	0.97987 (± 0.02582)
Human Gene	0.46948 (± 0.18641)	-	0.76972 (± 0.18731)	0.72336 (± 0.16314)	0.83293 (± 0.17671)	0.83478 (± 0.17682)	0.83485 (± 0.17675)	0.83587 (± 0.17601)
Natural Scene	0.47432 (± 0.29104)	0.45893 (± 0.25503)	0.73287 (± 0.23036)	0.70332 (± 0.18359)	0.67461 (± 0.15105)	-	0.72985 (± 0.18708)	0.77143 (± 0.19746)
S-JAFFE	0.93040 (± 0.04458)	0.91906 (± 0.05450)	0.95633 (± 0.04426)	0.93502 (± 0.04356)	0.91978 (± 0.05113)	0.88207 (± 0.09205)	0.89268 (± 0.07860)	0.95655 (± 0.05386)
S-BU_3DFE	0.47328 (± 0.18705)	0.90997 (± 0.07097)	0.94946 (± 0.05273)	0.92712 (± 0.05285)	0.91826 (± 0.05757)	-	0.94104 (± 0.04462)	0.95439 (± 0.03936)
Movie	0.84975 (± 0.07857)	0.78278 (± 0.10771)	0.92299 (± 0.08675)	0.92748 (± 0.07643)	0.90915 (± 0.08408)	0.92412 (± 0.08530)	0.92303 (± 0.08507)	0.92795 (± 0.07351)

表6 各算法在15个LDL数据集上的Cosine coefficient值对比 Table 6 Cosine coefficient value comparison of different algorithms on 15 LDL datasets

表7 各算法在15个LDL数据集上的Intersection similarity值对比 Table 7 Intersection similarity value comparison of different algorithms on 15 LDL datasets

数据集	PT-Bayes	PT-SVM	AA-kNN	AA-BP	SA-IIS	SA-BFGS	LSM-LDL	LCR-LDL
Yeast-alpha	0.77284 (± 0.15095)	0.96023 (± 0.01380)	0.95817 (± 0.01427)	0.87565 (± 0.06638)	0.94281 (± 0.01833)	0.96237 (± 0.01424)	0.96237 (± 0.01424)	0.96257 (± 0.01416)
Yeast-cdc	0.77442 (± 0.14813)	0.95555 (± 0.01810)	0.95287 (± 0.01784)	0.88799 (± 0.06111)	0.93970 (± 0.02104)	0.95741 (± 0.01748)	0.95741 (± 0.01748)	0.95762 (± 0.01737)
Yeast-cold	0.80146 (± 0.13563)	0.93390 (± 0.03393)	0.93586 (± 0.03388)	0.93210 (± 0.03679)	0.92878 (± 0.03746)	0.94075 (± 0.03244)	0.94075 (± 0.03244)	0.94151 (± 0.03238)
Yeast-diau	0.77549 (± 0.14607)	0.92510 (± 0.02882)	0.93691 (± 0.03156)	0.92103 (± 0.03747)	0.92560 (± 0.03098)	0.94030 (± 0.02869)	0.94035 (± 0.02869)	0.94152 (± 0.02819)
Yeast-dtt	0.80274 (± 0.14658)	0.95556 (± 0.02396)	0.95495 (± 0.02522)	0.94975 (± 0.02872)	0.94304 (± 0.03179)	0.95829 (± 0.02372)	0.95829 (± 0.02372)	0.95910 (± 0.02372)
Yeast-elu	0.77329 (± 0.15049)	0.95601 (± 0.01467)	0.95456 (± 0.01601)	0.89768 (± 0.05402)	0.94057 (± 0.01984)	0.95891 (± 0.01477)	0.95891 (± 0.01477)	0.95925 (± 0.01482)
Yeast-heat	0.76983 (± 0.13853)	0.93754 (± 0.02640)	0.93611 (± 0.02706)	0.92322 (± 0.03638)	0.92420 (± 0.03004)	0.94021 (± 0.02529)	0.94018 (± 0.02528)	0.94154 (± 0.02503)
Yeast-spo	0.76603 (± 0.14172)	0.90843 (± 0.04608)	0.90854 (± 0.04700)	0.90235 (± 0.04573)	0.90494 (± 0.04214)	0.91547 (± 0.04151)	0.91548 (± 0.04151)	0.91638 (± 0.04158)
Yeast-spo5	0.79608 (± 0.14321)	0.90679 (± 0.05751)	0.90451 (± 0.06188)	0.90670 (± 0.05713)	0.90296 (± 0.05961)	0.90859 (± 0.05670)	0.90858 (± 0.05670)	0.91061 (± 0.05492)
Yeast-spoem	0.82283 (± 0.14073)	0.90881 (± 0.07397)	0.90876 (± 0.07087)	-	0.90721 (± 0.06867)	0.91321 (± 0.06469)	0.91321 (± 0.06470)	0.91499 (± 0.06357)
Human Gene	0.48266 (± 0.16197)	-	0.74332 (± 0.13848)	0.66979 (± 0.11855)	0.78237 (± 0.14622)	0.78462 (± 0.14679)	0.78460 (± 0.14677)	0.78547 (± 0.14655)
Natural Scene	0.31780 (± 0.28429)	0.35695 (± 0.20038)	0.59697 (± 0.21398)	0.50416 (± 0.16980)	0.46880 (± 0.18030)	-	0.53544 (± 0.16096)	0.60983 (± 0.18887)
S-JAFFE	0.84664 (± 0.05381)	0.83582 (± 0.05732)	0.88668 (± 0.05590)	0.85266 (± 0.05251)	0.83674 (± 0.05426)	0.78984 (± 0.08674)	0.79518 (± 0.08069)	0.89390 (± 0.06533)
S-BU_3DFE	0.29295 (± 0.13803)	0.83350 (± 0.07131)	0.88182 (± 0.06306)	0.84750 (± 0.06474)	0.83764 (± 0.06864)	-	0.86024 (± 0.05434)	0.88184 (± 0.05502)
Movie	0.72345 (± 0.10717)	0.69017 (± 0.09933)	0.82307 (± 0.10381)	0.82428 (± 0.09551)	0.80451 (± 0.09563)	0.82308 (± 0.10339)	0.82017 (± 0.10318)	0.82320 (± 0.09354)

表7 各算法在15个LDL数据集上的Intersection similarity值对比 Table 7 Intersection similarity value comparison of different algorithms on 15 LDL datasets

当s = 8, N = 15时, 6种评估度量下的Fried-man统计量F_F如下:Chebyshev distance为25.211 6, Clark distance为21.646 0, Canberra metric为20.852 5, Kullback-Leibler divergence为22.704 1, Cosine coeffi-cient为24.701 2, Intersection similarity为24.414 6, 对应的临界值为2.104 4.

对于每种评估度量, 在α =0.05显著性水平下的Friedman检验都拒绝“ 全部对比的算法具有相等的预测性能” 这一原假设.

进一步采用Post-hoc检验(本文采用Nemenyi检验)分析算法是否具有显著的差异.在全部数据集上, 如果2种对比算法预测性能的平均排序的差值大于1个临界差异(Critical Difference, CD), 称这两种算法是显著不同的.CD定义如下:

CD=q_α $\sqrt[]{\frac{s (s + 1)}{6 N}}$ ,

其中, 临界值q_α源于Studentized Range统计量除以 $\sqrt[]{2}$ .在显著性水平α =0.05时, 有

q_α=3.031, CD=2.7110,

其中s = 8, N = 15.

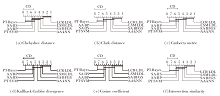
为了可视化地展示各算法在预测性能上的实际差异性, 绘制不同评估指标下的CD图^[26], 如图3所示, 每种对比的LDL算法的预测性能的平均排序沿着横轴标注, 排名靠前的位于坐标轴右侧.

在图3每幅子图中, 如果一组算法在Nemenyi检验下无显著的差异性, 使用一条粗线连接它们.同时, 每种评估度量下的CD显示在对应的坐标横轴上方.

	Figure Option View Download New Window
	图3 各算法在不同评估指标上的CD图Fig.3 CD diagrams of different algorithms on different evaluation metrics

由图3可得如下结论:1)在Chebyshev distance指标上, 相比SA-BFGS、AA-kNN、PT-SVM、AA-BP、SA-IIS、PT-Bayes, LCR-LDL获得统计上优异的预测性能; 2)在Clark distance、Kullback-Leibler divergence、Cosine coefficient、Intersection similarity指标上, 无明确的证据表明LCR-LDL、LSM-LDL、SA-BFGS的预测性能存在显著的差异; 3)在Canberra metric指标上, LCR-LDL的预测性能与LSM-LDL、SA-BFGS、AA-kNN相当, 都明显优于PT-Bayes.

从整体上看, 在全部预测性能的对比结果上, LCR-LDL仅在28.57%的情况下获得统计上可比的预测性能, 具体包括:在全部6种评估度量上与LSM-LDL的对比; 在Clark distance、Canberra metric、Kullback-Leibler divergence、Cosine coefficient和Inter-section similarity指标上与SA-BFGS的对比; 在 Canberra metric指标上与AA-kNN的对比.在其它71.43%的情况下, LCR-LDL获得统上优越的预测性能, 并且没有算法的预测性能优于LCR-LDL.由此可见, 相比其它主流的LDL, LCR-LDL在预测性能上具有优越性.

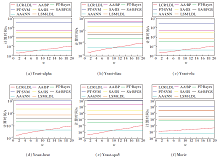
在6个LDL数据集上对比8种算法的计算时间, 结果如图4所示, 其中图4的纵坐标以常用对数刻度为单位(以10为底的log函数).

由图4可知, 随着邻域尺寸的增加, LCR-LDL的计算时间呈现逐步上升的趋势, 主要原因如下:字典中越来越多的样本可被用于对未标记样本进行表达重构, 从而导致LCR-LDL中step 3的计算效率降低.

	Figure Option View Download New Window
	图4 各算法在6个LDL数据集上的计算时间对比Fig.4 Computational time comparison of different algorithms on LDL datasets

然而, 当w在[1%, 10%]内时, 局部邻域搜索策略将产生较优异的计算效率.从整体上来讲, 在图4中, 8种LDL算法在6个LDL数据集上的计算效率的排名基本一致, 即

AA-kNN和LCR-LDL< PT-Bayes< SA-BFGS和LSM-LDL< SA-IIS< AA-BP< PT-Bayes.

由于没有显式的训练过程, AA-kNN和LCR-LDL在处理LDL任务时都获得较高的计算效率.特别地, 相比AA-kNN, LCR-LDL具有更显著的预测性能.

3.4 噪声扰动下的鲁棒性

为了验证LCR-LDL对噪声干扰的鲁棒性, 在特征噪声干扰的LDL数据集上, 对比分析各算法的预测性能.具体而言, 在每个未标记样本中, 随机选择一定比例的特征进行干扰, 即使用从均匀分布中产生的独立同分布的噪声替代被选特征值.对于每个未标记样本, 被干扰的特征随机确定, 被干扰特征的百分比(噪声率r)在0%~90%内以步长10%递增.在每种噪声水平下, 实验均采用十折交叉验证的方式, 10次预测结果的均值作为最终的实验结果.

由于篇幅的限制, 仅展示Yeast-spo 数据集上, 各算法在不同随机特征噪声干扰水平下的Chebyshev distance指标值, 结果如图5所示.

	Figure Option View Download New Window
	图5 r不同时各算法的Chebyshev distance值对比Fig.5 Chebyshev distance value comparison of different algorithms with different r

由图5不难发现, 相比AA-kNN、PT-SVM、SA-BFGS、LSM-LDL、LCR-LDL, PT-Bayes、AA-BP和SA-IIS明显具有较差的抗噪声性能.

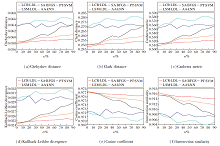
为了更详细地刻画5种较鲁棒的LDL算法(AA-kNN、PT-SVM、SA-BFGS、LSM-LDL和LCR-LDL)间抗噪声性能的差异性, 进一步绘制它们在全部6种评估指标下的抗噪声性能对比, 如图6所示.

在6种评估指标上, 5种较鲁棒的LDL算法抗噪声性能的排名一致, 即

LCR-LDL< LSM-LDL< SA-BFGS< PT-SVM< AA-kNN.

综上所述, 随着噪声率的增长, LCR-LDL在全部对比的LDL算法中获得最显著的抗噪声性能, 另外7种LDL算法的预测性能明显减弱.

	Figure Option View Download New Window
	图6 r不同时5种较鲁棒的LDL的预测性能对比Fig.6 Predictive performance comparison of 5 robust LDL algorithms with different r

4 结束语

标记分布学习是处理标记多义性的有效手段, 它考虑相关标记对样本的不同描述程度.现有的LDL不仅破坏不同标记间的关联性和标记分布的整体结构, 还忽略现实应用中的计算代价和噪声鲁棒性问题.为了缓解这些不足, 本文提出基于局部协同表达的标记分布学习算法(LCR-LDL).首先借助kNN规则为每个未标记样本构建局部字典, 再将未标记样本视作局部字典对其的协同表达.通过l₂范数约束的最小化, 获得一组表达系数, 它们的鉴别信息能与标记分布信息矩阵联合, 生成未标记样本的预测标记分布.在15个真实LDL数据集上的实验表明, LCR-LDL可达到较好的预测性能和抗噪优势, 同时具有轻量级的计算代价.在一些现实场景中, 由于数据采集器精度和可靠性的限制, LDL任务可能存在冗余和无关的特征, 及不完备的数据表示.今后将对LDL任务进行特征选择或构建一个潜在语义特征空间, 进一步提升LDL算法的泛化性能.

参考文献

文献选项

[1]	LI J, XU D, GAO W. Removing Label Ambiguity in Learning-Based Visual Saliency Estimation. IEEE Transactions on Image Processing, 2012, 21(4): 1513-1525. [本文引用:1]
[2]	XU S P, YANG X B, YU H L, et al. Multi-label Learning with Label-Specific Feature Reduction. Knowledge-Based Systems, 2016, 104: 52-61. [本文引用:2]
[3]	GAN W S, LIN J C, CHAO H C, et al. Data Mining in Distributed Environment: A Survey. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2017, 7(6). DOI: DOI:10.1002/widm.121. [本文引用:1]
[4]	GAN W S, LIN J C, FOURNIER-VIGER P, et al. Extracting Recent Weighted-Based Patterns from Uncertain Temporal Databases. Engineering Applications of Artificial Intelligence, 2017, 61: 161-172. [本文引用:1]
[5]	GIBAJA E, VENTURA S. Multi-label Learning: A Review of the State of the Art and Ongoing Research. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2014, 4(6): 411-444. [本文引用:1]
[6]	ZHANG M L, LI Y K Y, LIU X, et al. Binary Relevance for Multi-label Learning: An Overview. Frontiers of Computer Science, 2018, 12(2): 191-202. [本文引用:1]
[7]	ZHANG M L, ZHOU Z H. A Review on Multi-label Learning Algorithms. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819-1837. [本文引用:1]
[8]	LYONS M, AKAMATSU S, KAMACHI M, et al. Coding Facial Expressions with Gabor Wavelets // Proc of the 3rd IEEE International Conference on Automatic Face and Gesture Recognition. Washington, USA: IEEE, 1998: 200-205. [本文引用:1]
[9]	ZHOU Y, XUE H, GENG X. Emotion Distribution Recognition from Facial Expressions // Proc of the 23rd ACM International Conference on Multimedia. New York, USA: ACM, 2015: 1247-1250. [本文引用:1]
[10]	GENG X, HOU P. Pre-release Prediction of Crowd Opinion on Movies by Label Distribution Learning // Proc of the 24th International Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2015: 3511-3517. [本文引用:1]
[11]	SHEN W, ZHAO K, GUO Y L, et al. Label Distribution Learning Forests // GUYON I, LUXBURG U V, BENGIO S, et al. , eds. Advances in Neural Information Processing Systems 30. Cambridge, USA: The MIT Press, 2017: 834-843. [本文引用:2]
[12]	GENG X. Label Distribution Learning. IEEE Transactions on Know-ledge and Data Engineering, 2016, 28(7): 1734-1748. [本文引用:9]
[13]	GENG X, JI R. Label Distribution Learning // Proc of the 13th IEEE International Conference on Data Mining Workshops. Wa-shington, USA: IEEE, 2013: 377-383. [本文引用:5]
[14]	GENG X, SMITH-MILES K, ZHOU Z H. Facial Age Estimation by Learning from Label Distributions // Proc of the 24th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2010: 451-456. [本文引用:2]
[15]	GENG X, YIN C, ZHOU Z H. Facial Age Estimation by Learning from Label Distributions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(10): 2401-2412. [本文引用:3]
[16]	PIETRA S D, PIETRA V D, LAFFERTY J. Inducing Features of Rand om Fields. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(4): 380-393. [本文引用:1]
[17]	NOCEDAL J, WRIGHT S. Numerical Optimization. 2nd Edition. Berlin, Germany: Springer, 2006. [本文引用:1]
[18]	XING C, GENG X, XUE H. Logistic Boosting Regression for Label Distribution Learning // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 4489-4497. [本文引用:1]
[19]	AMALDI F, KANN V. On the Approximability of Minimizing Nonzero Variables or Unsatisfied Relations in Linear Systems. Theoretical Computer Science, 1998, 209(1/2): 237-260. [本文引用:1]
[20]	HUANG S, YANG Y, YANG D, et al. Class Specific Sparse Re-presentation for Classification. Signal Processing, 2015, 116: 38-42. [本文引用:1]
[21]	LU C Y, MIN H, GUI J, et al. Face Recognition via Weighted Sparse Representation. Journal of Visual Communication and Image Representation, 2013, 24(2): 111-116. [本文引用:1]
[22]	WRIGHT J, YANG A Y, GANESH A, et al. Robust Face Recognition via Sparse Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. [本文引用:1]
[23]	ZHANG L, YANG M, FENG X C. Sparse Representation or Co-llaborative Representation: Which Helps Face Recognition? // Proc of the International Conference on Computer Vision. Washington, USA: IEEE, 2011: 471-478. [本文引用:2]
[24]	SHAO C B, SONG X N, FENG Z H, et al. Dynamic Dictionary Optimization for Sparse-Representation-Based Face Classification Using Local Difference Images. Information Sciences, 2017, 393: 1-14. [本文引用:1]
[25]	FRIEDMAN M. A Comparison of Alternative Tests of Significance for the Problem of m Rankings. Annals of Mathematical Statistics, 1940, 11(1): 86-92. [本文引用:1]
[26]	DEMSAR J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research, 2016, 7: 1-30. [本文引用:2]

2012

0.0

... 在机器学习^[1,2]与数据挖掘^[3,4]的研究中,标记多义性问题受到广泛关注,多标记学习(Multi-Label Learning, MLL)^[2,5,6,7]为处理一个样本可能同时属于多个标记这一多义性问题提供一种有效的技术手段 ...

2016

0.0

2017

0.0

2017

0.0

2014

0.0

2018

0.0

2014

0.0

1998

0.0

... 例如:在面部表情的情感分析^[8,9]中,一个面部表情通常是由多种基本情感构成,即愤怒、厌恶、恐惧、喜悦、悲伤和惊讶等 ...

2015

0.0

... 例如:在面部表情的情感分析^[8,9]中,一个面部表情通常是由多种基本情感构成,即愤怒、厌恶、恐惧、喜悦、悲伤和惊讶等 ...

2015

0.0

... 在电影评级预测^[10,11]中,如果存在一个系统能够在电影上映前就准确预测电影评级的分布情况,不仅有助于观众选择性地观看其最喜欢的电影,而且可降低制片方的投资风险和时间成本 ...

2017

0.0

... 现有的研究结果^[11,12]表明,相比算法适应方法和问题转化方法,专门设计的方法能更有效地处理真实的LDL任务 ...

2016

0.0

... Geng等^[12,13]提出标记分布学习(Label Distribution Lear-ning, LDL),用于处理进一步的标记多义性问题 ...

... 算法适应方法直接修改一些约束条件,用于扩展已有的SLL和MLL,使其可处理标记分布问题,如AA-kNN(Algorithm Adaptation: k-Nearest Neigh-bor)^[12,13,14]和AA-BP(Algorithm Adaptation: BackPropagation)^[12,13,15] ...

... 例如,将一个标记的描述度作为采样权值从原始的LDL数据中进行采样后,SLL中常见的基学习器朴素贝叶斯(Naive Bayes, NB)和支持向量机(Support Vector Machine, SVM),分别被用于生成有代表性的问题转换方法PT-Bayes(Problem Transformation:Bayes)^[12,13]和PT-SVM(Problem Transformation:SVM)^[12,13] ...

... SA-IIS(Specialized Algorithm:Improved Iterative Scaling)^[14,15]和SA-BFGS(Specialized Algo-rithm:Broyden-Fletcher-Goldfarb-Shanno)^[12,15]都是以Kullback-Leibler散度为目标函数,构造最大熵模型,分别采用改进迭代缩放(Improved Iterative Scaling, IIS)^[16]和拟牛顿法BFGS^[17]实施优化 ...

... 现有的研究结果^[11,12]表明,相比算法适应方法和问题转化方法,专门设计的方法能更有效地处理真实的LDL任务 ...

... 值得注意的是,对于一给定样本x_i,d_i中的所有元素 dxiyj形成一个概率单纯形,每个 dxiyj并不是y_j正确标记x_i的概率,而是y_j在完全描述x_i中所占的比例^[12] ...

... 实验中使用如下6种标记分布评估度量^[12]:切比雪夫距离(Chebyshev Distance)、克拉克距离(Clark Distance)、堪培拉测度(Canberra Metric)、KL散度(Kullback-Leibler Divergence)、余弦系数(Cosine Coefficient)、相交相似度(Intersection Simi-larity) ...

2013

0.0

... Geng等^[12,13]提出标记分布学习(Label Distribution Lear-ning, LDL),用于处理进一步的标记多义性问题 ...

2010

0.0

2013

0.0

1997

0.0

2006

0.0

2016

0.0

... LDLogitBoost(LogitBoost Based LDL)^[18]采用Boosting策略,借助数量递增的加权回归器(加权回归树)处理LDL任务 ...

1998

0.0

... 然而,在大多数实际应用问题中,式(1)构建一个欠定系统,这意味着获得式(1)的精确解是一个NP难问题,甚至很难被近似求解^[19,20] ...

2015

0.0

... 然而,在大多数实际应用问题中,式(1)构建一个欠定系统,这意味着获得式(1)的精确解是一个NP难问题,甚至很难被近似求解^[19,20] ...

2013

0.0

... 已有的研究工作^[21,22]表明,如果表达系数 α^0足够稀疏,使用l₁范数约束代替l₀范数约束,可获得一个闭式解,由l₁范数约束近似: ...

2009

0.0

... 已有的研究工作^[21,22]表明,如果表达系数 α^0足够稀疏,使用l₁范数约束代替l₀范数约束,可获得一个闭式解,由l₁范数约束近似: ...

2011

0.0

... Zhang等^[23]研究表明,不是l₁范数最小化基于的稀疏性假设,而是协同表达机制,使SR在学习任务中变得有效 ...

... 因此,采用l₂范数约束代替l₁范数约束,提出协同表达(Collaborative Representation, CR)^[23,24],式(2)演变成: ...

2017

0.0

... 因此,采用l₂范数约束代替l₁范数约束,提出协同表达(Collaborative Representation, CR)^[23,24],式(2)演变成: ...

1940

0.0

... 为了更完善地对比预测性能,进一步采用Friedman检验^[25],它是一种在多个数据集上对比两种以上算法的统计学检验方法^[26] ...

2016

0.0

... 为了更完善地对比预测性能,进一步采用Friedman检验^[25],它是一种在多个数据集上对比两种以上算法的统计学检验方法^[26] ...

... 为了可视化地展示各算法在预测性能上的实际差异性,绘制不同评估指标下的CD图^[26],如图3所示,每种对比的LDL算法的预测性能的平均排序沿着横轴标注,排名靠前的位于坐标轴右侧 ...