引用本文
卞则康, 张进, 王士同. 基于类标感知的KNN分类算法. 模式识别与人工智能, 2021,34(10): 873-884
BIAN Zekang, ZHANG Jin, WANG Shitong. Class-Aware Based KNN Classification Method. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(10): 873-884.  
Doi: 10.16451/j.cnki.issn1003-6059.202110001
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于类标感知的KNN分类算法
卞则康1, 张进1, 王士同1,2
1.江南大学 人工智能与计算机学院 无锡 214122
2.无锡太湖学院 江苏省物联网应用技术重点建设实验室 无锡 214064
通讯作者:

王士同,硕士,教授,主要研究方向为人工智能、模式识别.E-mail:wxwangst@aliyun.com.

作者简介:

卞则康,博士研究生,主要研究方向为人工智能、模式识别.E-mail:bianzekang@163.com.

张 进,博士研究生,主要研究方向为人工智能、模式识别.E-mail:jin.zhang.jnu@gmail.com.

收稿日期: 2021-06-21 接受日期: 2021-10-26
资助项目: 国家自然科学基金项目(No.61972181,61772198)、江苏省自然科学基金项目(No.BK20191331)、江苏省物联网应用技术重点建设实验室2020年度开放课题(No.WXWL01)资助
摘要

许多传统分类算法都以训练数据和测试数据具有相同或至少非常相似的分布为前提,但是在实际应用中,该前提很难得到保证,这降低支持向量机等传统分类算法的分类精度.因此,文中提出基于类标感知的KNN分类算法(CA-KNN).CA-KNN给出稀疏表示模型,基于任何测试数据都可使用训练数据集进行稀疏表示的假设.CA-KNN可有效利用数据集上的类标信息,提升稀疏表示的准确性.引入KNN的最近邻分类思想,进一步提升CA-KNN的泛化能力,并且从理论上证明CA-KNN分类器与最小误差的Bayes决策规则关联.实验和理论分析的结果表明,CA-KNN具有较好的分类性能.

关键词: 类标感知; 稀疏表示; K近邻分类; 最小误差的Bayes决策规则
中图分类号:TP181
Class-Aware Based KNN Classification Method
BIAN Zekang1, ZHANG Jin1, WANG Shitong1,2
1. School of Artificial Intelligence and Computer Science, Jiangnan University, Wuxi 214122
2. Jiangsu Key Construction Laboratory of Internet of Things App-lication Technology, Wuxi Taihu University, Wuxi 214064
Corresponding author:
WANG Shitong, master, professor. His research interests include artificial intelligence and pattern recognition.

About Author:
BIAN Zekang, Ph.D. candidate. His research interests include artificial intelligence and pattern recognition.
ZHANG Jin, Ph.D. candidate. His research interests include artificial intelligence and pattern recognition.

Fund:National Natural Science Foundation of China(No.61972181,61772198), Natural Science Foundation of Jiangsu Province(No.BK20191331), Internet of Things Application of Jiangsu Province Key Construction Laboratory 2020 Open Project(No.WXWL01)
Abstract

Many conventional classification methods start with the hypothesis that the distribution of training samples is same as or at least similar to that of testing samples. In many practical applications, it is difficult to agree with the above hypothesis. And thus the classification performance of some traditional methods, such as support vector machine, is reduced. Therefore, a class-aware based KNN classification method(CA-KNN) is proposed. A sparse representation model is proposed based on the assumption that any testing sample can be represented sparsely by the training samples. The class label information is utilized effectively by CA-KNN to improve the accuracy of the sparse representation. The idea of nearest neighbor classification of KNN is introduced to improve the generalization capability of CA-KNN . And it is proved in theory that CA-KNN classifier is directly related to Bayes decision rule for the minimum error. The experimental and theoretical results show that CA-KNN generates better classification performance.

Key words: Key Words Class-Aware; Sparse Representation; K Nearest Neighbor Classification; Bayes Decision Rule for Minimum Error

本文责任编委 高 阳

Recommended by Associate Editor GAO Yang

分类分析作为一种常用的机器学习算法, 在人工智能与模式识别、图像和文本挖掘等领域具有广泛的应用价值.分类分析实际上是一种数据分类过程, 在这个过程中, 数据点被识别、区分和理解.一般来说, 传统的分类算法以训练数据和测试数据具有相同或至少非常相似的分布为基本前提.分类可分为两个步骤:首先使用训练数据得到分类器模型, 然后使用测试数据检验分类器模型的性能.传统的分类算法包括支持向量机(Support Vector Machine, SVM)[1]、贝叶斯分类算法[2]和模糊分类[3, 4, 5].然而, 在对象识别[6, 7, 8, 9]和图像处理[10, 11, 12, 13]等实际应用场景中, 上述算法的基本前提很难得到保证, 即训练图像和测试图像往往不具有相同的数据分布, 这在某种程度上限制传统分类技术的适用性.

针对上述问题, 学者们相继提出许多算法解决此问题[6, 7, 8, 14, 15, 16, 17, 18].K近邻(K Nearest Neighbor, KNN)分类算法[6]是一种较好的选择, 它的分类思想是根据数据点近邻的主要若干数据点投票判别该数据点的归属, 即测试数据点的类标是由数据集上某些训练样本决定, 而不是由所有的训练样本决定.相比传统分类算法, KNN分类算法不需要利用训练数据集训练模型, 因此, 较好地规避训练数据与测试数据同分布的限制.

然而, 对于高维数据集(如文本和图像), KNN分类算法的分类性能严重下降.这是因为KNN分类算法使用距离度量寻找测试数据点的最近邻点, 然而某些距离度量已被证实不适用于高维数据集, 例如, 欧氏距离已被证实可导致“ 同簇” 现象[19, 20].因此, 如何提高分类算法在高维数据集上的分类性能成为一个重要的研究方向.

近年来, 基于稀疏表示(编码)的分类算法[8, 11, 12]已被证明能有效提高在高维数据集上的分类性能, 它的主要思想是利用训练数据训练稀疏表示(特征表示)或字典, 然后基于求解的稀疏表示或字典对测试数据进行分类.由于高效的分类性能和简单的分类思想, 基于稀疏表示的分类算法已被应用到机器学习的许多领域, 如目标识别[15, 21, 22, 23]和图像识别[24, 25, 26, 27, 28]等.然而, 作为一种基于全局特征的稀疏表示算法, 基于稀疏表示的分类算法需要花费时间和资源训练判别字典和分类未知数据点.此外, 经过训练的字典可能会非常庞大, 导致字典冗余.因此, Wang等[28]提出局部线性约束编码算法(Loca-lity-Constrained Linear Coding, LLC), Yang等[29]提出基于字典的算法, 都是基于局部特征的稀疏表示算法, 可解决字典冗余的问题.上述算法基于数据集的局部特征对测试数据集进行稀疏表示, 在一定程度上减少相应字典的大小, 提高算法的有效性.但是, 这些操作不免增加算法的复杂性, 即需要消耗过多的时间和资源学习判别字典.

为了避免过多地依赖判别字典并节省学习判别字典的时间, Lasso及其延伸的算法[14, 30]将测试数据点直接表示为训练数据点的线性组合.在不使用任何字典的情况下, 建立测试数据点和训练数据点之间的直接关联, 然后根据求解的稀疏表示分类测试数据点.在Lasso的基础上, 为了进一步提高算法的分类性能, 研究人员提出弹性网络(Elastic Net)[7, 31], 不仅保持Lasso的稀疏性, 而且求解得到的稀疏表示具有集群效应.然而, 尽管Lasso和弹性网络能取得较好的分类性能, 但仍具有改进空间.例如:上述两种算法在学习稀疏表示时, 都未利用数据集的类标信息.

为了有效利用数据集的类标信息和提高算法的分类性能, 本文提出基于类标感知的KNN分类算法(Class-Aware Based KNN Classification Method, CA-KNN), 该算法是基于稀疏表示的分类算法.相比常见的基于稀疏表示的分类算法, CA-KNN在保持高度稀疏和集群效应的基础上, 有效利用训练数据集的类标信息, 提高求解得到的稀疏表示的准确性.在此基础上, 参考KNN的最近邻分类思想, 即测试点的类别由其最近邻的主要若干训练数据点投票决定, CA-KNN分类器根据若干最大的稀疏表示系数对应的若干训练数据点的类别, 投票决定测试点的类别, 提升算法的泛化性能.在UCI数据集和常用的文本数据集上的实验表明, CA-KNN具有较好的分类性能, 尤其是在高维数据集和文本数据集上.此外, 理论分析的结果也证明CA-KNN的优越性.

1 相关工作

稀疏学习作为一种高效的学习方法, 是基于稀疏学习分类算法的核心, 它的主要思想可简述如下.

假设

Y=[y1, y2, …, ym]∈ Rd× m

是一组具有m个已知标签样本的训练数据集(字典集), x∈ Rd为一个测试数据, x可由所有训练数据集Y线性表示, 即x=Yv, 其中

v=[v1, v2, …, vm]T∈ Rm.

稀疏学习的最终目标是寻找一个最优的稀疏向量v, 使其大多数元素的值为0或接近0.一个典型的稀疏学习的目标公式如下:

minv‖x-Yv ‖22+λ g(v).

其中:第1项为重构项, 反映测试数据点x的重构误差; 第2项为正则化项, 保证v的稀疏性; 参数λ用于控制这两项之间的权衡.很显然, 稀疏学习的核心是如何确定非零元素及其值.根据不同的正则化项g(v), 学者们提出多种实用的稀疏学习的算法[7, 14, 28, 30, 32, 33, 34].下面简要介绍3种典型的基于稀疏学习的分类算法.

1.1 局部线性约束编码

Wang等[28]提出局部线性约束编码(LLC), 它的目标函数如下:

minv‖x-Yv ‖22+α‖d* v ‖22, s.t. 1Tv=1, (1)

其中, d=[d1, d2, …, dm]T∈ Rm, di表示x与yi之间的距离, * 表示点乘运算符, 参数α控制l2正则化的权重.式(1)中第2项为l2正则化项, 能增强同类的系数权重.由于使用l2范数而不是l1范数, LLC不能保证学习得到的v拥有足够的稀疏性.

1.2 Lasso算法和弹性网络

为了使求解得到的v具有较高的稀疏性, Tibshirani等[30]提出利用l1范数作为正则化项的算法, 称为Lasso, 其目标函数为

minv‖x-Yv ‖22+λ‖v‖ 1, (2)

其中λ控制l1正则项的权重.

由式(2)可看出, Lasso的目标函数是由一个重构项和l1正则化项构成.尽管l1正则化项确实提升v的稀疏性, 但忽略特征之间的高度相关性, 因为它倾向于只选择其中一个[15], 因此不具备集群效应.这在一定程度上造成求解得到的稀疏表示不稳定, 难以解释[31].

因此, 为了解决上述问题, Zou等[7]提出Elastic Net.与Lasso不同的是, 弹性网络使用l1正则化项以保证稀疏性, 同时使用l2正则化项以实现集群效应, 其目标函数如下所示:

minv‖x-Yv ‖22+λ‖v‖ 1+α‖v ‖22.(3)

实验结果表明, 弹性网络的分类性能优于LLC和Lasso.而且, 经过弹性网络求解得到的稀疏表示在具有高度稀疏性的同时, 也具有一定的集群效应[7].

尽管基于稀疏表示的分类算法能有效提升高维数据集的分类精度, 但是也忽略一个事实, 即测试数据点通常与同类中的训练数据点高度相关, 即集群效应不能完全反映训练数据集中所有类别信息, 同时也不能扩大已知类之间的差异.

2 基于类标感知的KNN分类算法
2.1 目标函数

从第1节的描述中可看出, 基于稀疏表示的分类算法能有效克服训练数据集与测试数据集难以同分布这一问题.在此基础上, 本文同时考虑数据集中的类标信息对于分类性能的影响, 提出基于类标感知的KNN分类算法(CA-KNN), CA-KNN基于如下3点可靠的考虑.

1)CA-KNN是基于弹性网络的稀疏表示模型, 继承弹性网络的高度稀疏性和集群效应.

2)在弹性网络的基础上, CA-KNN改进l2正则化项.新的l2正则化项不仅具有集群效应, 而且考虑训练集上类标信息的影响, 通过在新的l2正则项中增加类标信息, 提高稀疏表示的准确性, 进一步提升算法的分类性能.

3)传统的基于稀疏表示算法在对测试样本进行分类时, 首先计算每类中所有训练样本对应的稀疏系数之和, 然后对比所有类的稀疏系数之和的大小, 测试样本会划分到稀疏系数之和最大的类.为了进一步提升泛化性能, 参考KNN的最近邻分类思想, 即测试样本的类标主要是由与其最近的k个训练样本的类标决定.引入KNN的最近邻分类思想可有效减少边缘点对于样本的影响, 提高算法的泛化性能.因此, CA-KNN分类器只考虑每类中最大的k个稀疏系数的训练样本对于测试样本的影响, 从而提升CA-KNN分类器的泛化性能.有关CA-KNN的详细描述如下所示.

假设

x=(x1, x2, …, xd)T∈ Rd

为一个测试数据,

Y=[y1, y2, …, ym]∈ Rd× m

为所有的训练数据集.参考文献[31]中的数据处理方法, 需要使用l2范式对x进行归一化, 即‖x‖ 2=1.依据线性表示的原理[35, 36], x可被m个训练数据线性表示为

x=v1y1+v2y2+…+vmym, (4)

其中

v=[v1, v2, …, vm]T∈ Rm

为稀疏表示向量.

在式(4)中, x可通过对比稀疏表示向量v中每类的系数之和进行分类, 即x归属于系数之和最大的那个类.

当训练数据集的类标信息已知时, 假设训练数据有c类, 可将表示向量分为c块.这样, 就可将式(4)重写为

x=∑j=1cYjv'j,

其中Yj表示第j块的训练数据, v'j表示第j块稀疏表示向量.因此, 可重新划分训练数据

Y=[Y1, Y2, …, Yc]

和稀疏表示向量

v=[v1, v2, …, vm]T=[v'1, v'2, …, v'c]T.

基于上述3点可靠的考虑, CA-KNN的目标函数表示如下:

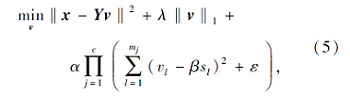
其中, c表示训练数据的类别数, mj表示第j类训练数据数, ε表示一个极小常量, 用于控制式(5)的第3项不为0, λ、α、β都是预设参数, 用于控制权重,

s=[s1, s2, …, sm]T∈ Rm

用于衡量测试数据x与所有m个训练数据之间的相似度, 每个元素

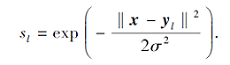
与上述一样, s也被分为c块, 即

s=[s'1, s'2, …, s'c]T∈ Rm,

其中s'j表示第j块相似度向量, 表示x与mj块训练数据之间的相似度.

从CA-KNN的目标函数可看出, 相比LLC, CA-KNN学习的稀疏表示具有较好的稀疏性.相比Lasso, CA-KNN同时保持集群效应.相比弹性网络, CA-KNN使用数据集上的类别信息, 进一步加强集群效应, 即加强同类之间的联系, 扩大不同类之间的差别.

相比式(1)~式(3)可看出, 式(5)主要的不同在于第3个正则化项

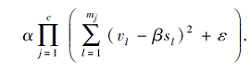
显然, 由于使用 ∑l=1mj(vl-β sl)2, 优化得到的稀疏表示具有集群效应, 当考虑到训练数据集上的类别信息时, 这种正则化项更符合集群效应和类标感知的思想.

通过对式(5)进行优化, 可得到一个优化的稀疏表示v, 然后利用CA-KNN分类器对x进行分类, CA-KNN分类器的定义如下:

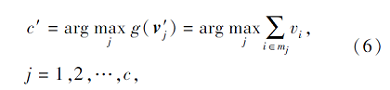
其中, c表示样本类别数, mj表示第j块训练数据, g(v'j)表示第j块稀疏表示向量中的系数之和.

为了进一步提升CA-KNN分类器的泛化性能, 参考KNN的最近邻分类思想, 本文定义参数k, 用于控制选取的每类中系数个数, 所以式(6)进一步转化为

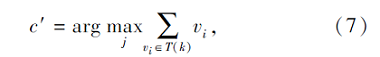
其中, T(k)表示每类中的最大前k个系数, 即测试数据点x可仅由ck(ck≤m)个训练数据点而不是m个训练数据点表示.通过这些操作, 不仅简化分类器分类的过程, 而且减少边缘点的影响, 提升CA-KNN分类器的泛化能力.

2.2 与最小误差的Bayes决策规则的理论联系

为了证明CA-KNN分类器与最小误差的Bayes决策规则相关联, 首先需要对优化得到的v进行转换, 这种转化不影响最后的分类结果, 具体转化如下:

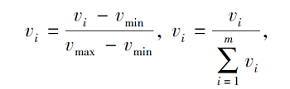
其中vmin、vmax分别表示稀疏表示向量v中元素的最小值和最大值.CA-KNN分类器与最小误差Bayes决策规则的理论联系如定理1所示.

定理1 给定一个测试数据x和使用CA-KNN优化得到的稀疏表示向量v, 如果训练数据中的每类的先验分布p(j), j=1, 2, …, c都相同, CA-KNN分类器与最小误差的Bayes决策可表示为

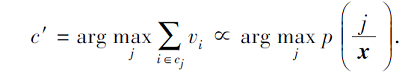
证明 首先, 定义如下函数:

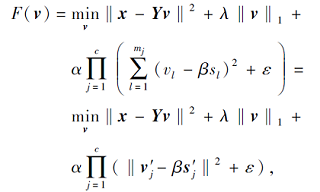
其中, v表示由CA-KNN优化得到的稀疏表示向量, v'j表示第j块稀疏表示向量, s'j表示第j块相似度向量.当v=0时, 这是一个极限情况, 即训练集上所有样本都不能用于稀疏表示测试样本x, 此时的目标函数值为F(0).本文算法研究测试样本可由训练数据集稀疏表示, 即至少有一个训练样本可用于稀疏表示测试样本x, 所以F(v)≤F(0).因此, 可得

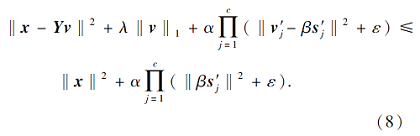
由于本文的数据使用l2范数进行归一化(‖x‖ 2=1), 因此, 式(8)可转化为

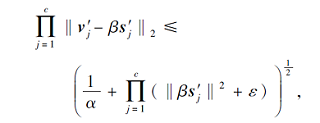
其中

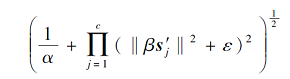
为一个正数常量, 即

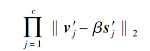
理论上可由一个正数常量限定上界.

下面使用传统数学归纳原理证明上述理论, 要证明上述理论, 即证明第j块的稀疏表示向量系数可由mj个正数常量构成的向量constj约束, 即

v'j≈β s'j+constj.

首先当 c=1时, 式(8)转化为

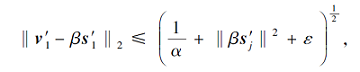
上式由一个正数常量向量限定上界.所以可得到

v'≈β s'+const1.

当c=c'时, 式(8)转化为

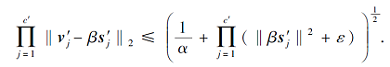
假设上式也由一个正数常量向量限定, 即

(v'1, v'2, …, v'c')≈β(s'1, s'2, …, s'c')+constc'.

由此可得

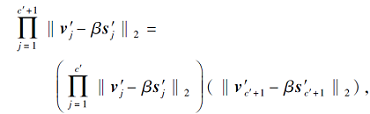
可看出上式也是由2个正数常量限定上界.因此可得

(v'1, v'2, …, v'c', v'c'+1)≈ β(s'1, s'2, …, s'c', s'c'+1)+constc'+1.

根据传统的数学归纳原理, 可得

v'j≈β s'j+const, j=1, 2, …, c,

即上述理论得证.

从上述证明中, 可得到

v'j≈β s'j+const.

进而由式(6)进一步转化为

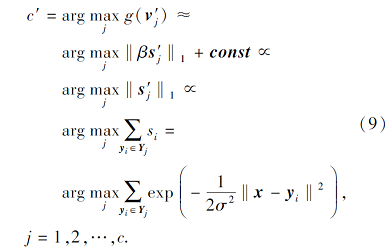
定义nj为第j类训练数据的数量, 定义q为固定参数, 控制所有类的平滑度, 并考虑零均值和单位方差的高斯核, 因此, 式(9)近似地表示为条件概率的核密度估计p(x|j), 形式如下:

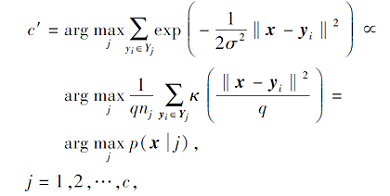
其中κ(· )为标准高斯核函数(零均值和单位方差), 定义为

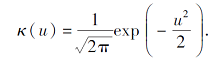
由此可知, 如果训练数据每类数据具有相同的先验概率p(j), CA-KNN分类器可近似于转化为如下形式:

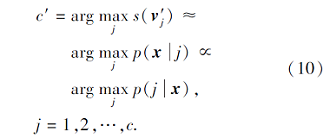
从式(10)的转化过程可看出, CA-KNN分类器与最小误差的Bayes决策规则相关联.

2.3 优化目标函数

对于CA-KNN的目标函数式(5)的优化, 本文提出基于交替优化策略[33]的优化算法求解稀疏表示向量.

首先将式(5)的第1项改写为每个元素之和的形式:

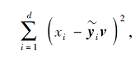
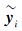
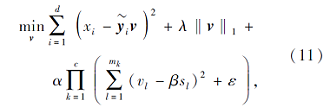
其中 为Y的第i行.因此, 式(5)可以转化为

令

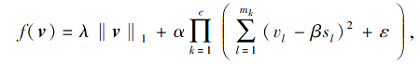
其中ε为一个极小的正数(ε=10e-6).所以式(11)进一步转化为

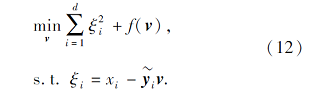
根据统计学习理论[37], 可将式(11)转化为一个重加权的最小二乘支持向量机模型.首先令

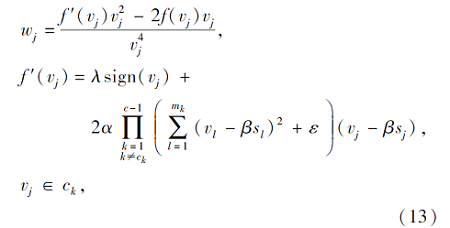
其中vj≠ 0.然后式(12)可转化为

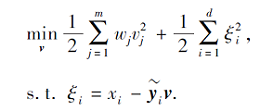
为了优化上式, 首先得到它的拉格朗日函数:

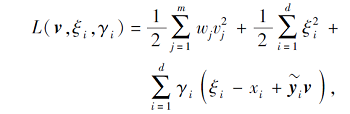
其中γ i为拉格朗日乘子.上式的KKT条件为

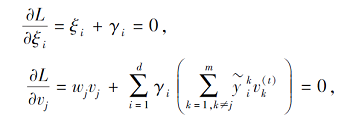
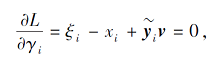
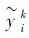
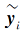
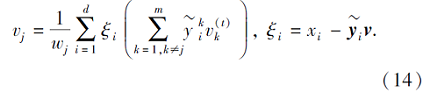
其中 为 中第k个元素.进而可得到

对于一个给定稀疏表示向量

vt=[ v1t, v2t, …, vmt]T,

其中t表示迭代t次, 可通过计算式(13)得到 wjt, j=1, 2, …, m.进而可通过式(14)求解得到 ξit, 然后更新

vt+1=[ v1t+1, v2t+1, …, vmt+1]T.

详细过程如算法1所示.

算法1 优化求解v

输入 测试数据x=(x1, x2, …, xd)T∈ Rd,

训练数据Y=[y1, y2, …, ym]∈ Rd× m,

训练数据类别数c, 已知的类别信息,

最大迭代次数Tmax=300,

λ, α, β, σ, k, ε=10e-6, θ=e-10.

输出 稀疏表示向量v和测试数据x的类标

step 1 初始化v1 和t=1.

step 2 重复 t<Tmax

如果 vjt=0, 则 vjt+1=0,

如果 vjt≠ 0, 则通过式(14)求解vj.

step 3 通过式(13)计算 wj, j=1, 2, …, m.

step 4 计算ξ(t)=[ ξ1(t), ξ2(t), …, ξd(t)]T,

ξi(t)=xi- y˙iv(t).

step 5 计算

γ(t)=[ γ1(t), γ2(t), …, γd(t)]T=-ξ(t).

step 6 计算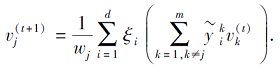

step 7 设置t=t+1.

step 8 直至‖v(t+1)-v(t)‖ ≤θ或t>Tmax.

step 9 使用式(10)中的CA-KNN分类器预测x.

step 10 输出最优v和x的类标.

2.4 时间复杂度分析

本节逐步分析算法1的时间复杂度.算法1的时间复杂度主要集中在迭代过程中, 即step 3~step 6.从算法1的过程易知, step 3~step 6的时间复杂度分别为O(m3d)、O(dm2)、O(d)、O(dm2).在step 9中, 采用CA-KNN分类器预测类标的时间复杂度为O(md).

因此, 算法1中迭代所需总的时间复杂度为

O(Tmax(md2+d+m3d+dm2))=O(Tmaxm3d).

此外, 在算法1之前的数据预处理时, 计算测试数据与每个训练数据的距离度量, 需要的时间复杂度为O(Nmd), 其中N为测试数据集的样本数.

所以, 对于N个测试样本, 算法1总的时间复杂度为O(Nmd+NTmaxm3d).从上述描述可看出, 算法1的时间复杂度与测试样本数N、训练数据个数m和维度d有直接联系.

3 实验及结果分析
3.1 实验环境

为了评估CA-KNN的分类性能, 选取13个常用的UCI数据集作为实验数据集, 详细信息如表1所示.由表1可看出, 13个数据集包括4个二类数据集和9个多类数据集.

表1 UCI数据集的详细信息 Table 1 Details of UCI datasets

除此以外, 为了进一步评估CA-KNN的分类性能, 本文选取20Newsgroups文本数据集作为实验数据集.20Newsgroups是一个广泛使用的数据集, 收集大约20 000份新闻组文档, 划分为20个不同的新闻组.实验中使用4个父类数据集comp、rec、sci、talk, 其中每个父类数据集分别包含四到五个子数据集.作为一个稀疏的数据集, 20个新闻组数据集的维数从63到229不等.因此, 本文在实验数据中添加零值, 将低维数据扩展到高维数据.表2中列出20 Newsgroups具体组合情况.

表2 20 Newsgroups数据组合情况 Table 2 Combinations of 20 Newsgroups datasets

本文选取3种基于稀疏表示的分类算法:基于稀疏表示的分类算法(Sparse Representation Classi-fication Method, SRC)[15]、Elastic Net[7]、局部线性KNN分类算法(Locally Linear KNN Classification Method, LLKc)[12]作为对比算法.除此以外, 也选取常用的基于字典学习的分类算法Fisher判别词典学习算法(Fisher Discrimination Dictionary Lear-ning Method, FDDL)[23]作为对比算法.

对于CA-KNN, 需要设置5个参数:λ, α, β, σ, k.参数λ和α对于稀疏表示具有重要作用, 然而, 目前为止还没有精确的准则确定这两个参数的值, 而且对于不同的数据集, 参数设置也不相同.因此, 本文使用网格搜索确定参数λ和α的值.根据参考文献[6, 7, 12], 本文设置λ=10-5, 10-4, 10-3, 10-2, 10-1, 100, α=10-4, 10-3, 10-2, 10-1, 100, 101.为了公平对比, 在对比算法Elastic Net和LLKc中, 也使用相同的寻参范围.

在CA-KNN和LLKc中, 参数σ是高斯核的宽度, 依据斯科特法则[38], 设置σ=5s n-1d+4, 其中, s为数据集的标准差, n为数据集的大小, d为数据集的维度.在本文的实验中, 简单设置寻参范围σ=0.1, 0.5, 1, 1.5, 2.参数β控制着相似度的权重, 设置寻参范围β=10-3, 10-2, 10-1, 100.

对于CA-KNN和LLKc中的参数k, 参考文献[12], 本文设置寻参范围k=2, 3, …, 10.

本文的实验数据集均需要使用l2范式对每个样本进行归一化.为了评估算法的分类性能, 选择分类准确度(Accuracy, ACC)[39]作为实验的评价指标.

实验平台为Matlab2019b, 实验环境为Windows操作系统, 计算机处理器为AMD Ryzen 9 3900 12-Core Processor CPU, 内存为64 GB.

3.2 UCI数据集上的实验结果

在本次实验中, 选取13个UCI数据集作为实验数据集.正如2.4节中指出, CA-KNN的运行速率受到训练样本个数的影响较大.因此, 考虑本文算法的运行速率, 对每个数据集随机选取40%的数据作为训练数据集, 余下的数据作为测试数据集.每种算法运行20次, 实验结果选取其平均值, 如表3所示, 表中黑体数字表示最优结果.

表3 各算法在UCI数据集上的ACC值 Table 3 ACC values of different algorithms on UCI datasets

由表3可看出, CA-KNN具有更好的分类精度.相比FDDL, CA-KNN能有效挖掘数据之间的联系, 即由CA-KNN优化得到的稀疏表示能更有效描述不同样本之间的联系, 因此具有更好的分类性能.相比SRC、Elastic Net、LLKc, CA-KNN不仅保持稀疏表示的优点, 即能有效描述样本之间的联系, 而且由于CA-KNN在优化过程中有效利用数据集上的类别信息, 通过新的约束项, 强化类别信息的重要性, 使优化得到的稀疏表示更准确, 因此CA-KNN具有更高的分类性能.

由表3也可得到如下结论:相比基于稀疏表示的算法, 基于字典的算法的分类精度主要受字典的影响, 字典的准确性受到训练数据集的影响, 而稀疏表示的算法直接建立测试数据与训练数据集之间的联系, 减少由于字典的差异对分类精度的影响.因此, 相比Elastic Net、LLKc、CA-KNN, FDDL的分类性能较低.尽管SRC也是基于稀疏表示的算法, 但是相比Elastic Net、LLKc、CA-KNN, SRC未考虑训练数据点之间的联系, 因此分类性能较低.Elastic Net和LLKc都考虑到同类样本之间的联系, 即集群效应, 因此具有较好的分类性能, 但是相比Elastic Net, LLKc进一步加强集群效应, 因此具有较好的分类精度.

3.3 20Newsgroups数据集上的实验结果

为了进一步评估CA-KNN的实用性, 选取常用的稀疏高维度数据集20Newsgroups文本数据集作为本次实验的数据集.相比UCI数据集, 20News-groups数据集具有更多的样本和更高的维度.与前面的实验类似, 考虑到数据集数据量的增加对于算法运行速率的影响, 对于每个数据集, 随机选取30%的数据作为训练数据集, 余下的数据作为测试数据集.每种算法运行20次, 实验结果取均值, 如表4所示, 表中黑体数字表示最优结果.由表4可看出, CA-KNN在文本数据集上具有更好的分类性能.这是因为随着数据集维度的增加, 数据集的信息更复杂, 类之间和类之内的区别较少, 这在一定程度上降低分类算法的精度.相比FDDL、SRC、Elastic Net、LLKc, CA-KNN能有效利用数据集的类标信息, 使优化得到的稀疏表示能更准确地反映数据集的分布, 提升算法的分类性能.

表4 各算法在20Newsgroups数据集上的ACC值 Table 4 ACC values of different algorithms on 20 Newsgroups datasets
3.4 运行时间分析

在本次实验中, 对比5种算法在13个UCI数据集上的运行时间, 评估各算法的运行速率.由于本文算法需要进行寻参操作, 因此每种算法运行20次, 结果取均值, 如表5所示.

表5 各算法在12个UCI数据集上的运行时间 Table 5 Running time of 5 algorithms on 12 UCI datasets s

由表5可看出, 基于字典的FDDL具有最多的时间消耗.这是因为FDDL需要花费大量的时间学习字典, 而且随着数据的样本量和维度的增加, 字典规模也在增加, 所以FDDL需要最多的时间.基于稀疏表示的算法直接建立测试样本与训练样本之间的联系, 减少花费在字典学习上的时间.相比SRC, Elasitc Net和LLKc由于采用快速迭代收缩阈值算法(Fast Iterative Shrinkage-Thresholding Algorithm, FISTA)进行优化, 因此具有较少的时间消耗.CA-KNN由于不仅考虑集群效应, 而且充分利用数据集的类别信息, 因此相比SRC、Elasitc Net、LLKc, 具有较多的时间消耗, 但是相比FDDL, 运行速度较快.综合考虑, 就算法的分类性能而言, CA-KNN的时间消耗是可接受的.

3.5 参数敏感性分析

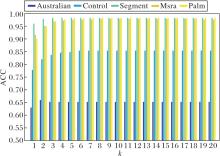
参数k对于CA-KNN的分类性能具有重要影响, 为了评估CA-KNN的分类性能随k值的变化过程, 在本次实验中, 选取Australian、Control、Seg-ment、Msra、Palm数据集作为实验数据集.为了更好地评估k值的影响, 设置k值的寻参范围为k=1, 2, …, 15, 其它参数λ=0.001, α=0.01, β=0.01, σ=1.5.k不同时CA-KNN的ACC值如图1所示.

图1 k不同时CA-KNN的ACC值Fig.1 ACC values of CA-KNN with different k values

由图1可看出, 随着k值的提升, CA-KNN的分类精度首先呈现增加的趋势, 最后趋于稳定.这是因为随着k值的增加, 测试数据点周围的训练样本数也随之增加, 即可用来表示测试数据点的训练样本数量增加, CA-KNN的表达能力也随之增加, 所以ACC值会出现增加的趋势.当测试样本周围的训练样本达到一定量时, 算法的表达能力达到最大值, 增加其周围训练样本的数量对算法的表达能力不会再产生影响, 此时CA-KNN的ACC值也不会再变化, 呈现稳定的状态.由此可看出, 对于测试数据点的表达, CA-KNN只需要其周围的一些数量的训练样本就可得到最好的分类精度.从另一个方面来说, k值可避免一些不重要的训练样本或偏远样本对于测试样本的影响.

3.6 统计分析

为了进一步评估CA-KNN的优越性, 本次实验采用两种统计方法:Friedman检验结合Holm后续检验法[40]及成对t检验[40].

Friedman检验结合Holm后续检验法是一种常用的统计学习算法, 能有效检验算法之间是否存在显著的统计差异, 从而进一步检验算法的优越性.本次实验是基于CA-KNN与所有对比算法在13个UCI数据集上分类精度的统计分析.各算法在Friedman检验中的排名如下:FDDL为3.923 1, SRC为4.923 1, Elastic Net为2.923 1, LLKc为1.846 2, CA-KNN为1.384 6.排名值越低, 说明算法的性能越优.由此可知, CA-KNN具有较好的分类性能.

表6为各算法的Holm后续检验结果.为了更好地理解Holm后续检验结果, 首先介绍空假设的定义.空假设定义为算法之间无显著的统计差异, 如果两种算法的Holm后续检验结果p< 0.05, 则两种算法之间具有显著的统计差异, 此时空假设被拒绝, 否则, 空假设不被拒绝.由表6可看出, CA-KNN与SRC、FDDL、Elastic Net之间具有显著的统计差异.尽管CA-KNN与LLKc之间无显著的统计差异, 但是结合表3中实验结果可看出, CA-KNN还是具有一定优势.

表6 各算法的Holm后续检验结果 Table 6 Results of different algorithms by post-Holm test

为了进一步验证CA-KNN与每种对比算法的差异性, 基于13个UCI数据集上运行20次的ACC值, 将CA-KNN和其它对比算法进行成对t检验, 检验结果如表7所示, 表中p=0表示p值小于0.000 1.成对t检验也是根据p值的大小判断空假设拒绝与否.当p< 0.05时, 表示两种算法之间存在明显的统计差异, 即空假设被拒绝.

表7 各算法的成对t检验结果(p值) Table 7 Results (p) of different methods by paired t-test

由表7可看出, 在所有13个UCI数据集上, 相比FDDL和SRC, CA-KNN具有显著差异.在大多数数据集上, 相比Elastic Net和LLKc, CA-KNN也具有显著差异.

总之, 通过上述的统计分析结果可知, CA-KNN在采用的数据集上, 相比对比算法, 具有较显著的优势.

4 结束语

针对实际应用中测试数据点和训练数据点不同分布的问题, 本文提出基于类标感知的KNN分类算法(CA-KNN).相比传统的基于稀疏表示的分类算法, CA-KNN不仅能有效利用训练数据点线性表示测试数据点, 而且能有效利用训练数据集中的类标信息, 使优化得到的稀疏表示不仅具有集群效应, 还能有效反映数据集的类别信息, 提升稀疏表示的准确性, 提高CA-KNN的分类性能.除此之外, 引入KNN的最近邻分类思想, 进一步提升CA-KNN分类器的泛化性能.而且, CA-KNN分类器可从理论上证明其与最小误差的Bayes决策规则相关联.实验和理论分析表明, CA-KNN具有较好的分类性能.

CA-KNN具有很大的后续研究空间.例如, 基于交替优化的优化算法使CA-KNN运行非常缓慢, 不适用于数据量较大的数据集.因此, 在后续的研究中会努力寻找一个快速的优化算法代替本文优化算法.另外, 交替优化算法求得的解是局部最优, 并不稳定, 这也是一个需要解决的问题.

参考文献
[1] CHEN S H, GAO C H. Linear Priors Mined and Integrated for Transparency of Blast Furnace Black-Box SVM Model. IEEE Transactions on Industrial Informatics, 2020, 16(6): 3862-3870. [本文引用:1]
[2] LU Y, CHEUNG Y M, TANG Y Y. Bayes Imbalance Impact Index: A Measure of Class Imbalanced Data Set for Classification Problem. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(9): 3525-3539. [本文引用:1]
[3] LIU H Y, ZHU T W, SHANG F H, et al. Deep Fuzzy Graph Con-volutional Networks for PolSAR Imagery Pixelwise Classification. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14(1): 504-514. [本文引用:1]
[4] ES-SABERY F, HAIR A, QADIR J, et al. Sentence-Level Classification Using Parallel Fuzzy Deep Learning Classifier. IEEE Access, 2021, 9(1): 17943-17985. [本文引用:1]
[5] FENG S, CHEN C L P, ZHANG C Y. A Fuzzy Deep Model Based on Fuzzy Restricted Boltzmann Machines for High-Dimensional Data Classification. IEEE Transactions on Fuzzy Systems, 2020, 28(7): 1344-1355. [本文引用:1]
[6] ZHANG M L, ZHOU Z H. ML-KNN: A Lazy Learning Approach to Multi-label Learning. Pattern Recognition, 2007, 40(7): 2038-2048. [本文引用:4]
[7] ZOU H, HASTIE T. Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society(Statistical Metho-dology), 2005, 67(2): 301-320. [本文引用:8]
[8] GONG F K, ZHANG S S, HE Q. Sparse Bayesian Learning for Distributed Passive Radar Imaging via Covariance Sparse Representation // Proc of the 6th Asia-Pacific Conference on Synthetic Aperture Radar. Berlin, Germany: Springer, 2019. DOI: DOI:10.1109/APSAR46974.2019.9048544. [本文引用:3]
[9] LI C L, SUN X, WANG X, et al. Grayscale-Thermal Object Tracking via Multitask Laplacian Sparse Representation. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2017, 47(4): 673-681. [本文引用:1]
[10] DAI B W, LI H H, WEI L. Image Processing Unit for General-Purpose Representation and Association System for Recognizing Low-Resolution Digits with Visual Information Variability. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2018, 48(3): 317-328. [本文引用:1]
[11] WANG S S, TAN S, GAO Y, et al. Learning Joint-Sparse Codes for Calibration-Free Parallel MR Imaging. IEEE Transactions on Medical Imaging, 2018, 37(1): 251-261. [本文引用:2]
[12] LIU Q F, LIU C J. A Novel Locally Linear KNN Method with Applications to Visual Recognition. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(9): 2010-2021. [本文引用:5]
[13] SHAFIEE M J, HAIDER S A, WONG A, et al. Apparent Ultra-High b-Value Diffusion-Weighted Image Reconstruction via Hidden Conditional Rand om Fields. IEEE Transactions on Medical Imaging, 2015, 34(5): 1111-1124. [本文引用:1]
[14] TIBSHIRANI R, SAUNDERS M, ROSSET S, et al. Sparsity and Smoothness via the Fused Lasso. Journal of the Royal Statistical Society(Statistical Methodology), 2005, 67(1): 91-108. [本文引用:3]
[15] WRIGHT J, YANG A Y, GANESH A, et al. Robust Face Recognition via Sparse Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. [本文引用:4]
[16] WANG J, ZHANG H Q, WANG J Z, et al. Feature Selection Using a Neural Network with Group Lasso Regularization and Controlled Redundancy. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(3): 1110-1123. [本文引用:1]
[17] ZHANG S R, ZHU Z B, ZHANG B X, et al. Fused Group Lasso: A New EEG Classification Model with Spatial Smooth Constraint for Motor Imagery-Based Brain-Computer Interface. IEEE Sensors Journal, 2021, 21(2): 1764-1778. [本文引用:1]
[18] SUN H, LI S Y, ZHENG X T, et al. Remote Sensing Scene Classification by Gated Bidirectional Network. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 82-96. [本文引用:1]
[19] FRANCE S, CARROLL D. Is the Distance Compression Effect Overstated? Some Theory and Experimentation // Proc of the International Workshop on Machine Learning and Data Mining. Berlin, Germany: Springer, 2009: 280-294. [本文引用:1]
[20] BIAN Z K, ISHIBUCHI H, WANG S T. Joint Learning of Spectral Clustering Structure and Fuzzy Similarity Matrix of Data. IEEE Transactions on Fuzzy Systems, 2019, 27(1): 31-44. [本文引用:1]
[21] ZHANG T, ZHENG W M, CUI Z, et al. Spatial-Temporal Recurrent Neural Network for Emotion Recognition. IEEE Transactions on Cybernetics, 2019, 49(3): 839-847. [本文引用:1]
[22] LEE S J, LEE S, CHO S I, et al. Object Detection-Based Video Retargeting with Spatial-Temporal Consistency. IEEE Transactions on Circuits and Systems for Video Technology, 2020, 30(12): 4434-4439. [本文引用:1]
[23] YANG M, ZHANG L, FENG X C, et al. Sparse Representation Based Fisher Discrimination Dictionary Learning for Image Classification. International Journal of Computer Vision, 2014, 109(3): 209-232. [本文引用:2]
[24] BI P F, DU X. Application of Locally Invariant Robust PCA for Underwater Image Recognition. IEEE Access, 2021, 9(1): 29470-29481. [本文引用:1]
[25] CHEN X, LUO X Z, WENG J, et al. Multi-view Gait Image Generation for Cross-View Gait Recognition. IEEE Transactions on Image Processing, 2021, 30: 3041-3055. [本文引用:1]
[26] XU Y W, GAO X T, LIN S, et al. Automatic Grading of Nuclear Cataracts from Slit-Lamp Lens Images Using Group Sparsity Regression // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2013: 468-475. [本文引用:1]
[27] CHENG J, YIN F S, WONG D W K, et al. Sparse Dissimilarity-Constrained Coding for Glaucoma Screening. IEEE Transactions on Biomedical Engineering, 2015, 62(5): 1395-1403. [本文引用:1]
[28] WANG J J, YANG J C, YU K, et al. Locality-Constrained Linear Coding for Image Classification // Proc of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2010: 3360-3367. [本文引用:4]
[29] YANG J C, YU K, GONG Y H, et al. Linear Spatial Pyramid Matching Using Sparse Coding for Image Classification // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2009: 1974-1801. [本文引用:1]
[30] TIBSHIRANI R. Regression Shrinkage and Selection via the Lasso: A Retrospective. Journal of the Royal Statistical Society (Statistical Methodology), 2011, 73(3): 273-282. [本文引用:3]
[31] ZHONG L W, KWOK J T. Efficient Sparse Modeling with Automatic Feature Grouping. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(9): 1436-1447. [本文引用:3]
[32] WRIGHT J, MA Y, MAIRAL J, et al. Sparse Representation for Computer Vision and Pattern Recognition. Proceedings of the IEEE, 2010, 98(6): 1031-1044. [本文引用:1]
[33] YANG W H, LIU J Y, YANG S, et al. Image Super-Resolution via Nonlocal Similarity and Group Structured Sparse Representation // Proc of the IEEE Conference on Visual Communications and Image Processing. Washington, USA: IEEE, 2015. DOI: DOI:10.1109/VCIP.2015.7457822. [本文引用:]
[34] ARGYRIOU A, EVGENIOU T, PONTIL M. Convex Multi-task Fea-ture Learning. Machine Learning, 2008, 73(3): 243-272. [本文引用:]
[35] SHAN H M, ZHANG J P, KRUGER U. Learning Linear Representation of Space Partitioning Trees Based on Unsupervised Kernel Dimension Reduction. IEEE Transactions on Cybernetics, 2016, 46(12): 3427-3438. [本文引用:]
[36] DUMONT C, KLUYSKENS V, DEHEZ B. Linear State-Space Re-presentation of Heteropolar Electrodynamic Bearings with Radial Magnetic Field. IEEE Transactions on Magnetics, 2016, 52(1): 1-9. [本文引用:]
[37] MARONNA R A, MARTIN D R, YOHAI V J. Robust Statistics: Theory and Methods. New York, USA: John Wiley & Son, 2006. [本文引用:]
[38] SCOTT D W. Multivariate Density Estimation: Theory, Practice, and Visualization. New York, USA: John Wiley & Son, 2008. [本文引用:]
[39] FAWCETT T. An Introduction to ROC Analysis. Pattern Recognition Letters, 2006, 27(8): 861-874. [本文引用:]
[40] DEMSAR J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research, 2006, 7: 1-30. [本文引用:]