MMTSSVM是解决极度不平衡分类问题的有效的两阶段算法.首先, 在特征空间中构造一个将负类数据包含在内的小超球体, 再根据最大间隔原则求得另一个大的同心球, 将所有的正类点排除在外.具体公式如下:

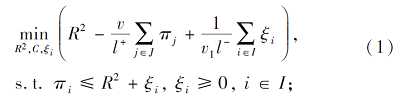
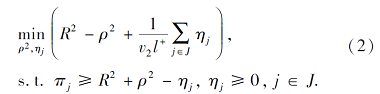
其中:v、v₁、v₂表示权衡参数, R表示高维特征空间中小超球体的半径, ρ表示两同心球之间的间隔, C表示特征空间中超球体的球心.

在目标函数(1)中, 第1项R²意味着极小化小超球体的体积, 第2项表示极大化所有正类点离球心的距离, 最后一项是损失函数, 将所有负类点限制在小超球体内部.在目标函数(2)中, -ρ²的极小化意味着极大化两个同心球之间的间隔, 同样地, 最后一项是损失函数, 目的是将所有正类点排除在大超球体之外.

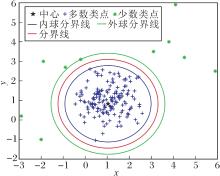
线性MMTSSVM在二维数据上的分类原理如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 线性MMTSSVM在二维数据上的分类Fig.1 Classification of linear MMTSVM on two-dimensional data

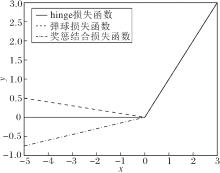
hinge损失函数^[19](如图2所示)与样本集合间的最小距离有关, 常被用于“ 最大间隔” 的分类任务, 定义如下:

L_hinge(u)=max{0, u}, ∀u∈ R.

然而对于所给的训练集T, MMTSSVM中hinge损失函数会使模型忽略满足π _i-R²< 0(∀i∈I)(即小球内的负类)和R²+ρ²-π _j< 0(∀j∈J)(即大球外的正类)的数据点的贡献, 即hinge损失函数仅考虑小部分数据以构造决策超球面, 使其对重采样不稳定, 对噪声值异常敏感, 尤其是分类边界附近的噪声.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 3种常见损失函数Fig.2 Three common loss functions

弹球损失函数^[20](如图2所示)是回归中常用的一种损失函数, 近年常用于分类模型, 使用分位数距离度量经验损失, 定义如下:∀u∈R,

Lpinτ(u)=u, u≥0-τu, u< 0

其中τ> 0.

对于训练集T, 使用弹球损失函数的最大间隔支持向量机(Maximum Margin of Twin Spheres Machine with Pinball Loss, Pin-MMTSM)^[21]定义如下:

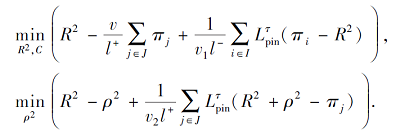
相比hinge损失函数, 弹球损失函数惩罚训练集上的每个点, 即使分类正确的点也给予惩罚, 通过参数τ控制惩罚的大小.Pin-MMTSM在构造分类器时充分利用所有数据, 对决策边界附近的噪声具有很强的抗干扰性.但是, 弹球损失函数在惩罚分类正确的数据提高模型稳定性的同时, 也牺牲一定的分类准确性.

奖励机制在强化学习中被广泛应用^[22], 在最初未知的环境中识别奖励最大化的行为.随后又被应用于深度神经网络, 实现奖励与重构损失联合优化.但强化学习和神经网络都需要大量数据, 在可用数据集数量有限时, SVM是一种有效的分类算法.基于奖惩结合损失函数的支持向量机(Reward Cum Penalty Loss Function Based SVM, RP-SVM)^[23]使用奖惩结合的损失函数(如图2)衡量经验风险项, 所用的损失函数定义如下:∀u∈R,

L(τ1, τ2)(u)=max{τ₁u, τ₂u},

其中τ₂>τ₁> 0.损失函数 L(τ1, τ2)(u)既可取正值又可取负值, 通过 L(τ1, τ2)(u)的正负分别对目标函数给予惩罚和奖励.

对于所给的训练集T, RP-SVM求解的问题可写为

minw, b12(‖w‖ ²+ \sum _{i\in M}L(τ1, τ2)(1-y_i(w^Tx_i+b))).

RP-SVM使用奖惩结合的损失函数奖励满足y_i(w^Tx_i+b)> 1的点, 惩罚满足y_i(w^Tx_i+b)≤ 1的点.充分利用数据隐含的信息, 使落入w^Tx+b=1和w^Tx+b=-1之间的数据点更少, 即难分的样本个数减少, 有效提高SVM的分类精度.另外, 区别于传统的损失函数仅使用小部分数据构造决策函数的特点, 奖惩结合损失函数利用所有可用数据, 使模型对决策边界附近噪声的敏感性降低.

负类样本:对落入小球之外的负类样本给予惩罚, 惩罚力度与样本和小球的间距呈正比; 对落入小球之内的负类样本, 尤其是靠近小球边界附近的点, 根据距离给予适当的奖励, 这将忽视边界附近的负类噪声点, 使小球更紧凑; 离小球面较远的样本点却容易被识别, 因此奖励将随距离的增加而趋于稳定.

正类样本:对落入到大球内部的正类点接受惩罚, 同样, 惩罚与样本和大球的间距呈正比; 给予落入大球外部的正类点一定的奖励, 这是模型的目标.另外, 正类点在问题中占有更重要的地位, 需更重视正类样本点携带的信息, 因此加大正类对应的奖励和惩罚.

根据2.1节提出的准则设计一个光滑损失函数, 以处理极度不均衡分类问题:∀u∈ R,

L(u)=γu, u≥0γ(expu-1), u< 0(3)

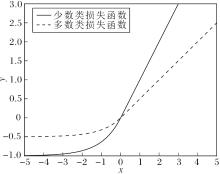
其中γ用于控制对两类样本集的不同重视程度.通常多数类的损失函数中的参数γ更小, 即0<γ_maj<γ_min.

如图3所示:当u≥ 0时, 损失函数L(u)取正值, 作惩罚功能; 否则, 损失函数L(u)取负数, 极小化此损失函数等价于极大化-L(u), 作奖励功能.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 光滑有下界的奖惩结合损失函数Fig.3 Smooth reward-penalty loss function with lower bound

对比图2和图3, 相比hinge损失函数和弹球损失函数, SRPB函数可取负值, 在充分利用全部数据信息的同时保证分类精度.相比RP-SVM的奖惩结合损失函数, SRPB函数在负值部分逐渐趋于平缓, 即远离决策边界的样本点给予相同的奖励.由于远离决策边界的数据点特征明显, 属于容易分类样本, 因此趋于平缓的奖励策略更恰当.并且SRPB函数将多数类和少数类的经验风险区别处理, 具有针对性, 更适合于极度不均衡分类问题.此外, 相比1.2节的损失函数, SRPB函数是光滑的, 在某些情况下性质更优.

对于训练集T, 使用SRPB函数衡量MMTSSVM的经验风险.由于SRPB函数中要求0<γ_maj<γ_min, 不妨将γ_min固定为1, 而0<γ_maj< 1, 记作γ γ_maj.

对于负类:u_i=π _i-R², i∈I,

L(u_i)=γ(πi-R2), πi≥R2γ(exp(πi-R2)-1), πi< R2(4)

对于正类:u_j=R²+ρ²-π _j, j∈J,

L(u_j)=R2+ρ2-πj, πj≤R2+ρ2exp(R2+ρ2-πj)-1, πj> R2+ρ2(5)

SRPB函数惩罚满足约束π _i≥R²(i∈I)和π _j≤R²+ρ²(j∈J)的数据点, 奖励满足约束π _i<R²(i∈I)和π _j>R²+ρ²(j∈J)的数据点.另外, 根据图3可得出, 不论是奖励还是惩罚, 正类都要大于负类, 这也符合本文的设计理念.

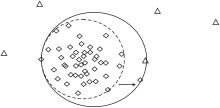
使用一个简单的图解阐述SRPB函数的工作原理, 图中包含多数类和极少量的少数类样本(不一定是训练集中的真实样本), 使用实线和虚线分别表示SRPB函数使用前后MMTSSVM的分类效果, 如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 2种函数的线性分类器Fig.4 Linear classifiers of 2 functions

图4中使用SRPB函数后, 模型重新寻找超球体的球心和半径, 新超球体的体积小于旧模型, 抛弃多余的空隙, 提高正确检测少数类点的概率.这是由于SRPB函数使模型以全部样本表示决策边界, 不易受到边界附近噪声的干扰, 决策超球面更紧凑, 有效提高边界附近少数类样本的检测准确率.

为了方便叙述, 这里先简要说明本节中使用的符号和基本概念.样本集T选自概率分布p, 分类的目标是构建一个具有最小误分率的决策函数f:X→Y, 误分率由函数R(f)衡量, 定义为

R(f)=∫_{X× Y}Γ _{y≠ f(x)}dp=∫_Xp(y≠f(x)|x)dρ,

其中, Γ表示指示函数, ρ表示在集合X上间隔的分布, p(y|x)表示p在x处的条件分布, 为一个二值分布函数, 取值P(y=1|x)与P(y=-1|x).贝叶斯分类器定义为

f_B(x)=-1, P(y=-1|x)≥P(y=1|x)1, P(y=-1|x)< P(y=1|x)

因此, f_B极小化误分率, 即

f_B=arg minf∶X→YR(f).

实际上, 本文寻找实值函数f:X→R, 并使用它的符号函数构建二值分类器, 则误分率

∫_{X× Y}Γ _{y≠ sign(f)(x)}dp=∫_{X× Y}L_mis(yf(x))dp,

其中, L_mis(u)表示损失函数,

L_mis(u)=0, u≥01, u< 0

因此, 极小化关于实值函数的误分率可生成贝叶斯分类器f_B.

定义1^[25] 已知f为决策函数, L((x_i, y_i), f(· ))为预先选定的损失函数, f_L为模型找到的最优分类器.若f_L(x)=f_B(x), 则损失函数L是Fisher一致的且分类器f_L符合贝叶斯决策规则.

根据定义1, 可判断损失函数L((x_i, y_i), f(· ))满足Fisher一致性, 同时也说明使用SRPB函数构建的模型能找到最优解, 下文证明使用SRPB函数也可生成贝叶斯分类器.

对任意损失L, 可测函数f:X→ R的期望风险如下:

R_{L, p}(f)=∫_{X× Y}L(1-yf(x))dp,

最小化所有可测函数的期望风险, 可得

f_{L, p}=arg mint∫_YL(1-y(x)t)dp(y|x), ∀x∈X.(6)

则对SRPB函数L_γ , 有如下定理.

定理1 设函数 fLγ, p使所有可测函数f:X→R的L_γ 期望风险最小化, 此函数等价于贝叶斯分类器, 即

fLγ, p(x)=f_B(x), ∀x∈X.

证明 将式(3)代入式(6)的右侧, 有

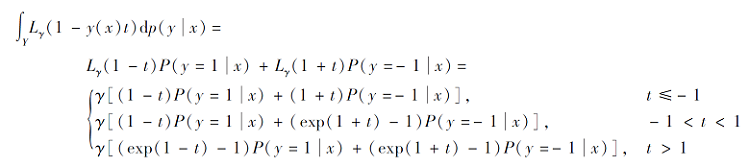
因此, 当

P(y=1|x)> P(y=-1|x)时,

在t=1处取得最小值, 值为2γ P(y=-1|x); 当

P(y=1|x)< P(y=-1|x)时,

在t=-1处取得最小值, 值为2γ P(y=1|x); 当

P(y=1|x)=P(y=-1|x)时,

在任意t∈ [-1, 1]处取得最小值, 值为1.故当由 fLγ, p极小化L_γ 衡量的经验风险时, 有

fLγ, p(x)=1, P(y=1|x)≥P(y=-1|x)-1, P(y=1|x)< P(y=-1|x)

等价于 fLγ, p(x)=f_B(x).根据定义1, SRPB函数L_γ 是Fisher一致的, fLγ, p符合贝叶斯决策规则.

使用式(4)和式(5)分别替换式(1)和式(2)中的hinge损失函数, 得

RPMMTS1:

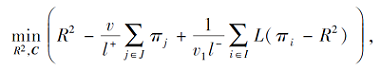
RPMMTS2:

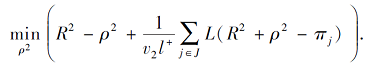
其中:v、v₁、v₂表示预先选定的参数, R表示高维空间中小超球体的半径, ρ表示高维空间中两个同心球体之间的间隔.

RPMMTS1中极小化R²意味着使高维特征空间中包含负类样本的小超球体尽量小, 第2项使正类样本尽量远离球心C, 第3项是损失项, 使小超球体尽可能地覆盖所有负类样本.若L(· )> 0, 表示负类数据点落到小球外, 给予目标函数惩罚; 否则, 负类样本点落入小球之内, 极小化L(· )等价于极大化|L(· )|, 即给目标函数一个奖励.在RPMMTS2中, R²和C已知, 根据最大间隔原则极小化-ρ², 即极大化两个同心球之间的间隔.第3项为损失函数项, 使正类样本尽可能地被排除在大超球体外部, 奖惩原理与RPMMTS1中类似.不同于MMTSSVM使用的损失函数, SRPB函数具有光滑性, 根据数据点的位置给予奖励或惩罚, 使模型能更充分地利用数据集内部的信息, 避免小球边界附近噪声样本的干扰.

光滑牛顿算法或半光滑牛顿算法是无约束优化中重要的方法, 具有二次收敛速度, 通过求解牛顿方程, 迭代更新当前的解.无约束问题RPMMTS1中使用的损失函数属于光滑损失函数, 因此考虑使用牛顿法进行求解.

根据表示定理^[26], 存在向量α, 使

C=\sum _{i\in M}α _iϕ(x_i)

表示RPMMTS1的最优解.

将C代入RPMMTS1, 有

π _i=‖ϕ(x_i)-C‖ ²=K_ii-2 KTiMα+α^TKα, i∈M.

于是可将RPMMTS1在再生核希尔伯特空间中转化为如下不含隐式映射ϕ(x)的模型:

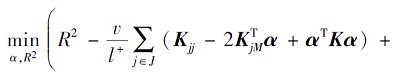
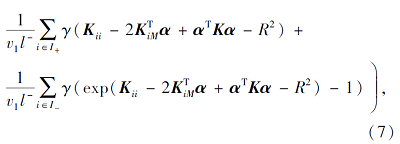
其中,

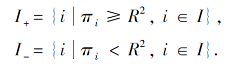
去掉常数项后, 问题(7)改写为如下矩阵形式:

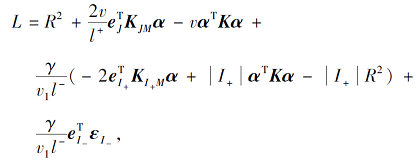
其中

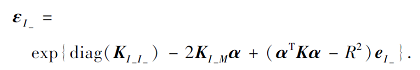
具体地, 令

c₁=γv1l-, δ=2vl+KTJMe_J,

使用牛顿方向 d¯更新

z^(t+1)=z^(t)+θ d¯,

而步长θ通过回溯Armijo搜索^[27]确定.则指标集通过迭代更新:

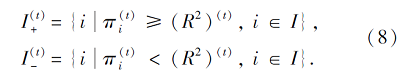
其中

πi(t)=K_ii-2 KTiMα^(t)+(α^(t))^TKα^(t).

因此, 问题(7)的梯度g^(t)和海森矩阵H^(t)表示为

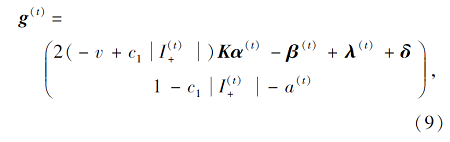
其中

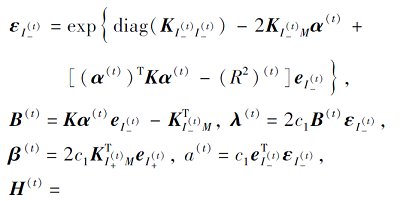
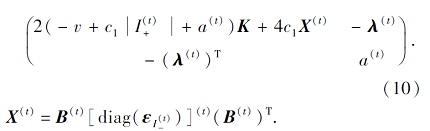
根据上述分析, 建立RPMMTS1的求解算法, 如下所示.

算法 RPMMTS1求解算法

输入 训练集T={(x_i, y_i) }i=1l, 核函数K(x, z),

参数v> 0, v₁> 0, v₂> 0, 0<γ< 1,

精度eps> 0, 最大迭代步数N

输出 α, R²

step 1 取初始点z⁽¹⁾=[α⁽¹⁾, (R²)⁽¹⁾]^T; 置t=1; 计算c₁, δ .

step 2 按式(8)计算指标集 I+(1)和 I-(1), 按式(9)计算g⁽¹⁾.

step 3 若‖g⁽¹⁾‖ <eps, 停止计算, 得到RP-MMTS1的近似解z⁽¹⁾.

step 4 按式(10)计算H^(t).

step 5 根据牛顿方程H^(t)d=-g^(t)计算牛顿方向 d¯.

step 6 使用回溯Armijo法确定搜索步长θ, 并更新z^(t+1)=z^(t)+θ d¯.

step 7 按式(8)计算指标集 I+(t+1)和 I-(t+1), 按式(9)计算g^(t+1).

step 8 若‖g^(t+1)‖ <eps或t>N, 停止计算, 得到RPMMTS1的近似解z^(t+1).

step 9 置t=t+1, 转step 4.

在第1阶段, RPMMTS1解得α和R²后, 记

c₂=1v2l+, ε _j=exp(R²-π _j), j∈J,

第2阶段的RPMMTS2简化为关于单个变量ρ²的凸函数:

c₂ \sum _{j\in J_{-}}ε _jexp(ρ²)+(-1+c₂|J₊|)ρ²+(1+c₂|J₊|(R²-π _j)-c₂|J_-|),

其中,

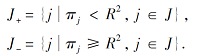
则RPMMTS2的解析解为

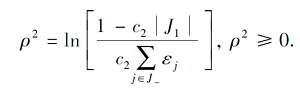
因此, 对一个测试点x_t, 仅需对比它在核空间中距超球体中心C的距离‖ϕ(x_t)-C‖ 和分类超球面的半径((R+ R2+ρ2)/2), 得到如下的分类准则:

y_t=-1, ϕ(xt)-C≤R+R2+ρ221, ϕ(xt)-C> R+R2+ρ22

其中, -1表示预测的结果为负(多数)类, 1表示预测的结果为正(少数)类.

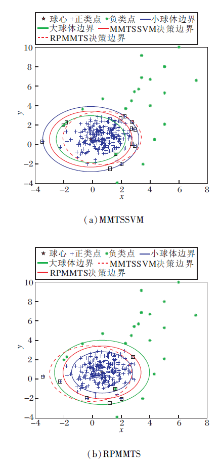
随机生成两组二维不平衡数据点, 用于模拟少数类样本极少、不具有代表性的极度不均衡数据集.在人工数据集中, 230个负类点来自分布N(1, 1), 并在负类数据边界附近随机添加8个负类噪声点.18个正类数据在负类数据外围随机产生, 并在负类边界附近随机添加3个正类噪声点.在此数据集上, MMTSSVM和RPMMTS在线性情况下的分类结果如图5所示.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 两种方法在人工数据集上的分类结果Fig.5 Classification results of 2 methods on artificial datasets

对比图5(a)、(b), MMTSSVM构造的球心位于所有负类样本的中心, RPMMTS构造的球心位于负类样本密集处的中心.观察可得MMTSSVM中有3个正类点和10个负类点被误分, 误分率分别为14.29%和4.2%, 而RPMMTS中有1个正类点和5个负类点被误分, 误分率仅为4.76%和2.1%.上述情况说明RPMMTS提高分类的准确性, 尤其是在识别少数类点方面.这是由于在SRPB函数中, 即使分类正确的点也被用于构造决策超球面, 避免在决策边界附近一些噪声的干扰.换言之, 在构造同心球时, SRPB函数使用所有可用数据点, 避免模型在构造小超球体时为尽量将负类数据包含而过大, 在构造大超球体时为尽量将正类数据排除而过小.因此, SRPB函数使包围负类样本的小超球体更紧凑, 降低错分正类点的概率, 同时放大大超球体的半径, 有利于正确识别决策边界附近的样本点.因此, 根据图5结果, 本文模型在分类过程中能有效抵抗决策边界附近噪声的干扰, 提高决策边界附近样本点的分类正确率.

本节利用UCI数据集上的实验研究本文模型的性能, 并对比RPMMTS与基于核的不均衡算法.具体地, 对比RPMMTS和4个基于间隔的球形分类器的算法:SVDD、SSLM、SVM-SVDD、MMTSSVM.也对比RPMMTS与常见的两个处理不平衡问题的算法:代价敏感支持向量机(Cost-Sensitive SVM, CS-SVM)^[28]和基于亲和力与类概率的模糊支持向量机(Affinity and Class Probability-Based Fuzzy SVM, ACFSVM)^[29].

4.2.1 数据集选择

首先, 使用UCI数据集上的10个数据集评估方法的有效性, 表1给出数据集的统计特性, 所有特征都归到[0, 1]内.表1中除Shuttle、Spambase、Minist、Vechile为多类数据集以外, 其余6个数据集均为二类数据集.而多分类问题可转化为多个二分类问题求解, 仅需分别识别其中每个类和其余所有类构成的不均衡问题.

表1

Table 1

表1(Table 1)

表1 UCI数据集基本信息 Table 1 Basic information of UCI datasets 名称 原总数据个数 训练集数据个数 测试集数据个数 特征个数 负 正 负 正 负 正 Shuttle 34108 9392 27287 28 6821 9364 9 Svmguide1 2000 1089 1600 5 400 1084 4 Cod-rna 39690 19845 31752 32 7938 19813 8 IJCNN 45137 4853 36110 37 9027 4816 22 Mushrooms 4208 3916 3367 5 841 3911 111 Phishing 6157 4898 4926 10 1231 4888 68 Spambase 2788 1813 2231 5 557 1808 57 Adult 24720 7841 19776 20 4944 7821 123 Minist8 54149 5851 43320 44 10829 5807 784 Vechile 39439 39384 31552 32 7887 39352 100

表1 UCI数据集基本信息 Table 1 Basic information of UCI datasets

在本次实验中:Shuttle、Spambase数据集将类1视作正类, 其余所有类视作负类; Minist8数据集将类8视为正类, 其余所有类视为负类; Vechile数据集将类3视为正类, 其余所有类视为负类.另外, 对每个数据集, 随机取全部负类数据的80%和小部分正类数据用于训练, 使构造的训练集中负类和正类占比约为1 000:1, 剩余的全部数据用于测试.由此构造一个包含大量负类数据和极少量正类数据的训练集, 模拟训练集中少数类极少、甚至无法代表数据结构的特点.

4.2.2 性能评估和参数设置

本文使用正负两类数据分类准确率的几何平均值(Geometric Mean, Gm)作为衡量算法分类性能的标准:

Gm=a+·a-,

其中, a^-表示负类的分类准确率, a⁺表示正类的分类准确率.在处理不平衡数据集时, 广泛使用Gm标准^{[12, 13, 14, 15, 16, 17, 18]}, 并同时反映多数类和少数类的分类结果.

在CS-SVM、SVDD、ACFSVM中, 参数均选自{1e-4, 1e-3, …, 1e+7, 1e+8}.SSLM的参数v在{10, 20, …, 90}中选取, 参数v₁和v₂在{1e-4, 1e-3, 1e-2, 1e-1}中选择.SVM-SVDD的参数v在{0.1, 0.2, …, 0.9}中选取, v₁和v₂在{1e-3, 1e-2, …, 1e+2, 1e+3}中选取.在MMTSSVM、RPMMTS中, 参数v和v₁在{0.1, 0.2, …, 0.9, 1}中选取.

在实验中, 为了减小参数选择的复杂度, 令SSLM、SVM-SVDD、MMTSSVM、RPMMTS中v₁=v₂.所有算法均使用高斯核函数

K(x_i, x_j)=exp(-h‖x_i-x_j‖ ),

h在{2^-10, 2^-9, …, 2⁶}中选取.

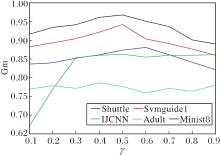
SRPB函数中γ对模型的分类性能具有较大影响.随机选取5个数据集讨论γ取值的影响, γ在{0.1, 0.2, …, 0.9}中选择, 实验结果如图6所示.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 γ不同时5个数据集上的Gm值的变化Fig.6 Gm value variation with different γ on 5 datasets

由图6可知, Adult数据集上Gm值曲线波动不大, 随γ变化呈平缓态势, 说明此数据集上γ对模型效果影响不大.在Shuttle、Svmguide1、Minist8数据集上Gm值随γ先增大后减小.在IJCNN上Gm值随γ先增大后稳定在最高值附近.总之, 所有数据集Gm值都在γ=0.5附近达到最高, 这表明并不是奖惩的程度越大越好.因此, 为了使模型有更好的分类性能, 所有实验中γ取值均在0.5附近.

在研究参数h时, 表2列举各算法在各数据集上的最优高斯核参数h时, 异于最后一列(固定值)使用黑体数字表示.由表2可知, 同个数据集上不同算法的最优高斯核参数波动不大, 都在某一个固定值附近小幅度波动, 尤其当h较大时, 波动更小.因此, 在同个数据集上, 高斯核参数变化不明显, 固定每个数据集的最优高斯核参数进行后续实验.

表2

Table 2

表2(Table 2)

表2 各算法在10个数据集上的最优高斯核参数h对比 Table 2 Comparison of optimal Gaussian kernel parameter h of different algorithms on 10 datasets 数据集 CS-SVM SVDD SSLM SVM-SVDD ACFSVM MMTSSVM RPMMTS 固定值 Shuttle 2-4 2-4 2-5 2-4 2-3 2-4 2-4 2-4 Svmguide1 2-1 2-2 2-2 2-2 2-2 2-2 2-2 2-2 Cod-rna 2-9 2-9 2-8 2-4 2-9 2-9 2-9 2-9 IJCNN 21 20 20 20 20 20 20 20 Mushrooms 2-1 2-2 2-1 2-1 2-1 20 2-1 2-1 Phishing 2-2 2-2 2-2 2-3 2-2 2-2 2-2 2-2 Spambase 2-2 2-2 2-2 2-2 2-2 2-2 2-2 2-2 Adult 2-6 2-6 2-6 2-6 2-5 2-6 2-5 2-6 Minist8 2-5 2-6 2-6 2-6 2-6 2-8 2-6 2-6 Vechile 2-3 2-2 2-2 2-2 2-2 2-2 2-2 2-2

表2 各算法在10个数据集上的最优高斯核参数h对比 Table 2 Comparison of optimal Gaussian kernel parameter h of different algorithms on 10 datasets

注意, 当研究γ和h影响时, 其它参数通过交叉验证选择最优.

4.2.3 实验结果

为了验证RPMMTS在处理极度不平衡问题上的有效性, 在10个基准数据集上对比各算法.Gm值对比如表3所示, 最优参数对比如表4所示.

表3

Table 3

表3(Table 3)

表3 各算法在不平衡数据集上的Gm值对比 Table 3 Gm value comparison of different algorithms on unbalanced datasets % 数据集 CS-SVM SVDD SSLM SVM-SVDD ACFSVM MMTSSVM RPMMTS Shuttle 85.76± 1.35 73.41± 0.60 75.36± 0.00 85.77± 1.91 83.79± 0.67 80.40± .0.98 87.37± 0.22 Svmguide1 81.39± 1.92 77.86± 0.39 93.01± 0.37 89.96± 0.42 82.73± 1.23 90.38± 3.10 94.21± 0.39 Cod-rna 56.29± 2.99 62.93± 1.19 59.34± 3.78 52.65± 1.81 56.60± 3.87 58.63± 2.17 63.08± 2.63 IJCNN 88.46± 4.65 75.06± 4.57 87.60± 0.73 86.54± 0.61 85.97± 3.14 84.75± 1.73 87.29± 2.04 Mushrooms 68.63± 3.46 64.39± 1.76 65.46± 1.00 68.28± 1.35 68.83± 2.77 71.35± 1.21 72.03± 1.28 Phishing 54.57± 3.35 59.85± 0.24 57.89± 1.85 59.75± 1.77 59.16± 2.31 60.74± 2.04 62.92± 1.74 Spambase 40.72± 3.76 61.44± 0.84 64.59± 1.56 56.90± 0.38 49.11± 0.00 62.59± 0.67 63.64± 0.28 Adult 68.25± 2.54 69.27± 1.31 72.29± 1.15 69.22± 1.37 69.98± 0.38 76.84± 0.00 77.67± 0.56 Minist8 95.84± 0.41 93.11± 0.67 96.36± 0.89 95.00± 0.12 95.59± 0.89 95.94± 0.13 96.78± 0.22 Vechile 46.98± 5.32 57.63± 2.39 67.63± 0.78 53.07± 6.28 44.56± 3.72 68.23± 5.21 65.61± 2.16

表3 各算法在不平衡数据集上的Gm值对比 Table 3 Gm value comparison of different algorithms on unbalanced datasets %

表4

Table 4

表4(Table 4)

表4 各算法在不平衡数据集上的最优参数对比 Table 4 Comparison of optimal parameters of different algorithms on unbalanced datasets 数据集 CS-SVM SVDD SSLM SVM-SVDD ACFSVM MMTSSVM RPMMTS c1 c2 v1 v2 v v1 v v1 c1 c2 v v1 v v1 Shuttle 10-1 100 103 10-1 20 10-1 0.6 100 100 100 0.9 0.7 0.1 0.3 Svmguide1 10-3 10-2 106 10-2 50 10-3 0.3 102 0.3 100 0.9 0.3 0.6 0.9 Cod-rna 10-1 105 103 100 30 10-2 0.4 10-1 103 103 0.9 0.4 0.6 0.8 IJCNN 10-2 102 104 103 40 10-3 0.6 102 100 101 0.1 0.1 0.7 0.9 Mushrooms 10-2 101 102 10-2 30 10-3 0.3 100 103 102 0.7 0.1 0.3 0.9 Phishing 100 103 103 10-1 50 10-2 0.7 101 105 102 0.2 0.2 0.8 0.8 Spambase 10-1 10-2 104 10-2 70 10-3 0.5 102 105 103 0.9 0.4 0.8 0.9 Adult 10-1 100 102 102 70 10-3 0.8 102 100 102 0.7 0.4 0.9 0.6 Minist8 101 103 103 100 90 10-2 0.3 10-1 103 103 0.9 0.1 0.1 0.8 Vechile 102 104 105 10-3 30 10-1 0.7 102 101 103 0.1 0.4 0.8 0.5

表4 各算法在不平衡数据集上的最优参数对比 Table 4 Comparison of optimal parameters of different algorithms on unbalanced datasets

由表3和表4可知, 从Gm值的角度分析, RPM-MTS在大多数数据集上具有更高的测试精度.在IJCNN、Spambase数据集上, RPMMTS的Gm值虽不是最高(略低于最高值, 在IJCNN数据集上降低1.17%, 在Spambase数据集上降低0.95%), 但高于其它5种算法.RPMMTS在Vechile数据集上的Gm值低于SSLM和MMTSSVM, 但明显高于其它4种算法.

特别地, 观察表2中最后两列, 除了Vechile数据集以外, 在所有的数据集上RPMMTS的分类效果都要优于MMTSSVM.这是由于极度不平衡问题中正类只占训练样本的极少数, RPMMTS将正负两类样本分两阶段处理, 在确定负类边界后, 再极大化和正类样本之间的间隔, 能保证正类样本在训练分类器时得到充分重视.相比MMTSSVM, RPMMTS引入奖励策略, 可充分挖掘负类训练样本中隐含的信息, 避免决策边界附近噪声的干扰.因此, RPMMTS更适用于极度不平衡问题.

为了进一步说明RPMMTS的性能, 选取模型分类性能最佳的4个数据集:Shuttle、Svmguide1、IJCNN、Minist8.文献[14]将训练集中的正类占比按从1‰ 到20‰ 递增, 划分为5个等级进行实验, 对比RPMMTS和MMTSSVM的性能.具体地, 如在Minist8数据集上, 1‰ 表示所有的正类样本(5 851)中仅1‰ 的数据被用于5折交叉验证的训练过程, 20‰ 表示20‰ 的正类样本被用于训练.RPMMTS和MMTSSVM在各个正类样本占比不同的训练集上的Gm值对比如图7所示.

图7

Fig.7

	Figure Option ViewDownloadNew Window
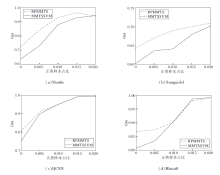	图7 正类样本占比不同时2种方法在4个数据集上的Gm值对比Fig.7 Gm value comparison of 2 algorithms with different proportions of positive samples on 4 datasets

由图7可知, 在正类样本占比1‰ 到20‰ 的4个数据集上, 随着正类样本占比的增大, RPMMTS的Gm值与MMTSVM差距减小, 尤其在正类样本占比极低的的情况下, RPMMTS的Gm值明显高于MMTSSVM, 这说明RPMMTS在不平衡程度更高的数据集上的分类性能更优.另外, 在15‰ 和20‰ 的Minist8数据集上, RPMMTS的分类性能略逊于MMTSSVM, 但相差不大.总之, RPMMTS的Gm值在所有数据集上均高于MMTSSVM, 这表明即使在不平衡程度较低的问题上, SRPB函数依然能使原模型的性能得到改进, 只是改进效果略有减弱.