引用本文
刘鑫, 周凯锐, 何玉琳, 景丽萍, 于剑. 基于度量的小样本分类方法研究综述. 模式识别与人工智能, 2021,34(10): 909-923
LIU Xin, ZHOU Kairui, He Yulin, JING Liping, YU Jian. Survey of Metric-Based Few-Shot Classification. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(10): 909-923.  
Doi: 10.16451/j.cnki.issn1003-6059.202110004
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于度量的小样本分类方法研究综述
刘鑫1,2, 周凯锐1,2, 何玉琳3, 景丽萍1,2, 于剑1,2
1.北京交通大学 交通数据分析与挖掘北京市重点实验室 北京 100044
2.北京交通大学 计算机与信息技术学院 北京 100044
3.北京新纽科技有限公司 北京 100083
通讯作者:

景丽萍,博士,教授,主要研究方向为机器学习、高维数据表示及其在人工智能领域中的应用.E-mail:lpjing@bjtu.edu.cn.

作者简介:

刘 鑫,博士研究生,主要研究方向为机器学习、度量学习、小样本学习.E-mail:xin.liu@bjtu.edu.cn.

周凯锐,硕士研究生,主要研究方向为机器学习、小样本学习.E-mail:20120460@bjtu.edu.cn.

何玉琳,博士,主要研究方向为企业级架构设计、高性能分布式交易系统、离线及实时大数据分析等.E-mail:heyl@xnewtech.com.

于 剑,博士,教授,主要研究方向为人工智能、机器学习.E-mail:jianyu@bjtu.edu.cn.

收稿日期: 2021-04-28 接受日期: 2021-09-13
资助项目: 国家自然科学基金项目(No.61632004)、基本科研业务费研究生创新项目(No.2021YJS031)、北京市自然科学基金项目(No.Z180006)、中央高校基本科研业务费专项项目(No.2019JBZ110)资助
摘要

小样本学习旨在让机器像人类一样通过对少量样本的学习达到对事物认知和概括的能力.基于度量的小样本学习方法希望学习一个低维嵌入空间,直接对比查询集合和支持类之间的相似性,分类测试样本.文中针对基于度量的小样本学习方法,尝试从这类方法需要解决的关键问题、类表示学习和相似性度量入手,梳理相关文献.与已有相关综述不同,文中只针对基于度量的小样本学习方法进行更详尽全面的分类,而且从关键问题角度进行分类.最后总结目前代表性工作在常用的图像分类任务数据集上的实验结果,分析现有方法存在的问题,并展望未来工作.

关键词: 小样本学习; 基于度量的小样本学习; 类表示; 相似性学习; 图像分类
中图分类号:TP391
Survey of Metric-Based Few-Shot Classification
LIU Xin1,2, ZHOU Kairui1,2, He Yulin3, JING Liping1,2, YU Jian1,2
1. Beijing Key Laboratory of Traffic Data Analysis and Mining, Beijing Jiaotong University, Beijing 100044
2. School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044
3. Beijing Newlink Technology Co., Ltd., Beijing 100083
Corresponding author:
JING Liping, Ph.D., professor. Her research interests include machine learning, high-dimensional representation lear-ning and its application in artificial intelligence fields.

About Author:
LIU Xin, Ph.D. candidate. Her research interests include machine learning, metric learning and few-shot learning.
ZHOU Kairui, master student. His research interests include machine learning and few-shot learning.
HE Yulin, Ph.D. His research interests include enterprise architecture design, high-performance distributed trading system, offline and real-time big data analysis.
YU Jian, Ph.D., professor. His research interests include artificial intelligence and machine learning.

Fund:National Natural Science Foundation of China(No.61632004), Fundamental Research Funds for Graduate Student Innovation Project(No.2021YJS031), Beijing Natural Science Foundation(No.Z180006), Fundamental Research Funds for the Central Universities(No.2019JBZ110)
Abstract

Few-shot learning aims to make machines recognize and summarize things by learning from a small number of samples like humans. The metric-based few-shot learning method is designed to learn a low-dimensional embedding space and query samples can be classified based on a distance between the query samples and the class embeddings in this space. In this paper, the key issues, class representation learning and similarity learning , are discussed to sort out the relevant literature. Only metric-based few-shot learning methods are classified in a detailed and comprehensive way, and they are classified from the perspective of key issues. Finally, the experimental results of current representative research on commonly used image classification datasets are summarized, the problems of the existing methods are analyzed, and the future research is prospected.

Key words: Key Words Few-Shot Learning; Metric-Based Few-Shot Learning; Class Representation; Similarity Learning; Image Classification

本文责任编委 王士同

Recommended by Associate Editor WANG Shitong

大数据时代人类搜集、存储、传输和管理数据的能力日益提高, 积累大量的数据资源, 如何快速有效分析海量数据成为难点问题[1].在此背景下, 深度学习由于强大的特征提取能力得到学术界和工业界的广泛关注, 并在图像分类[2, 3]、人脸识别[4, 5]等任务上取得较大成功.然而深度学习需要依靠大量的标签数据, 在实际生活中, 有些领域有标签的数据却很难获得或获取成本非常高, 如医学、金融等.相比计算机, 人们不仅可从大量数据中挖掘知识, 也可从很少的数据中进行学习, 这就是机器学习和人类学习之间存在的差距.受人类学习观点的启发, 如何让机器模仿人类, 对于新的事物, 只需要少量样本就可以进行学习, 由此产生的小样本学习成为一个研究热点.

小样本学习最早兴起于计算机视觉领域[6], 近年来在其它领域, 如自然语言处理[7], 也受到学者们的关注, 并在图像分类[8, 9, 10, 11]、文本分类[12, 13, 14]等任务上取得不错的成绩.小样本学习的难点是容易过拟合.为了解决这一问题, 常用的方法是数据扩充[15]和知识迁移[16].数据扩充是对数据集中样本或特征进行变换(如旋转[17]、裁剪[18]、缩放[19]等), 增加样本量, 避免过拟合, 但数据扩充的方式很大程度上取决于数据集, 在某个数据集上有效的数据扩充方式不一定对另一个数据集有效[20].因此, 可以把数据扩充作为数据预处理手段与知识迁移的方法一起使用.

知识迁移是将在大量非目标数据集上学到的知识迁移到目标数据集上.在小样本学习中, 常用的知识迁移技术是元学习[17, 21, 22], 在一系列小样本任务上学习, 得到解决这类任务的元知识, 再将元知识迁移到只有少量有标记样本的目标任务上.根据要迁移的元知识, 小样本学习方法大致可分为基于微调的小样本学习方法[23, 24, 25, 26, 27, 28, 29, 30, 31]和基于度量的小样本学习方法[8, 9, 32, 33, 34, 35, 36, 37, 38, 39, 40].基于微调的小样本学习方法学到的元知识通常是一个好的初始点, 当一个新的任务到来时, 利用新任务中的少量支持集样本调整模型参数, 可快速收敛到新任务的最优点.基于度量的小样本学习方法学到的元知识是一个低维嵌入空间, 直接对比新任务中查询集合和支持集之间的相似性, 以此分类测试样本.关于小样本学习方法的相关综述可见文献[41]~文献[43].

相比基于微调的小样本学习方法, 基于度量的小样本学习方法简单有效, 是小样本学习中的重要分支.例如, 在文献[41]中的小样本学习发展图中, 基于度量的小样本学习方法与所有基于深度学习代表方法数量的比值为1/2.在文献[42]中的典型方法分类图中, 基于度量的方法占9/26.文献[43]中基于度量的分类方法与所有方法的占比为9/29.因此, 本文决定详述基于度量的小样本学习方法.

本文首先简要介绍小样本学习任务和基于度量的小样本学习方法, 分析基于度量的小样本学习方法的难点及优势, 并根据这类方法要解决的问题将基于度量的小样本学习方法分类为类表示学习方法和相似性学习方法.在实际数据上进行实验对比, 分析近年基于度量的小样本学习方法的差异.再分析现有基于度量的小样本学习方法的不足, 包括方法训练依赖于非目标数据集、泛化能力难以保证、训练机制和优化过程有待改进、模型缺乏可解释性和理论保证.针对上述问题, 提出可能的解决思路, 展望未来的研究方向.

1 问题定义及分类
1.1 N-way K-shot任务和元学习训练机制

小样本学习是指利用少量样本对事物进行认知的过程.为了方便对比不同方法, 在N-way K-shot任务上进行测试, 认为如果一个方法可在N-way K-shot任务上取得好的结果, 该方法就具备小样本学习能力.

N-way K-shot任务通常包括两部分数据:支持集(Support Set)和查询集(Query Set).支持集包括N×K个样本, 其中N为需要学习的类的数目, 每类包含K个样本, 通常设为1或5.查询集包括N×Q个样本, 来自支持集中的N类, 每类Q个样本, 用于验证方法通过支持集样本对N类的认知能力.

然而, 只利用N×K个样本学习容易导致过拟合, 为了解决此问题, 常借助其它有大量标签的非目标数据集A, 利用元学习的技术进行知识迁移.具体地, 在非目标数据集A上构造一系列N-way K-shot任务(通常称为Episode), 在这一系列任务上学习解决这类任务的元知识, 再将元知识迁移到只有少量有标记样本的目标任务上进行测试.

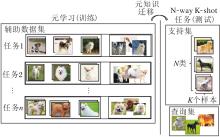
基于元学习训练机制的小样本学习方法如图1所示.由图可看出, 基于元学习的小样本学习方法的关键是元知识的迁移, 只有学到迁移性较强的元知识, 才能在测试时的小样本数据集上取得较优结果.

图1 N-way K-shot任务和基于元学习训练机制Fig.1 N-way K-shot task and meta-learning training mechanism

1.2 基于度量的小样本学习方法的分类

基于度量的小样本学习方法需要学习的元知识是一个嵌入空间(Embedding Space), 在该空间中同类样本的距离更近, 不同类样本的距离更远.由于基于度量的小样本学习方法将样本投影到一个更低维的空间, 所以训练时需要的样本量会下降[43, 44].在测试时, 计算查询样本和支持集中各个类的相似性, 分类查询样本.

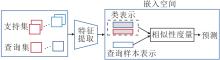
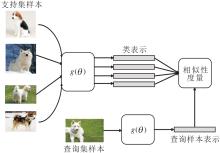
基于度量的小样本学习方法一般框架如图2所示.由图可看出, 基于度量的小样本学习方法与人类认知事物的思路一致.在对查询样本进行分类时, 依据该样本与类之间的相似性进行判断.例如, 机器学习公理化[45]中提出归类原则:归哪类, 像哪类, 像哪类, 归哪类.根据归类原则可知, 在进行归类时包括2个关键问题:类表示和相似性度量.只有将这两个问题学习好, 才能根据归类原则正确查询到样本归类.因此, 本文主要从两个问题上对基于度量学习的小样本学习方法进行综述.事实上, 任何一种方法都会涉及到这两个关键问题, 只不过在方法设计时, 通常主要解决其中一个问题.

图2 基于度量的小样本学习方法框图Fig.2 Framework of metric learning based few-shot learning methods

在类表示的方法中, 本文依据认知科学中概念表示的不同理论将类表示学习分为基于原型的类表示学习方法、基于样例的类表示学习方法和基于任务的类表示学习方法.在相似性学习方法中, 本文依据相似性计算的方式将方法分为特征独立的距离度量、特征相关的距离度量和自适应距离学习.此外, 还可依据表示形式将类表示方法分为基于向量表示的方法、基于张量表示的方法和基于图表示的方法.在相似性学习方法中, 可依据相似性计算的对象分为基于特征的相似性计算和基于关系的相似性计算, 但目前大部分文献的表示形式都是采用向量, 相似性计算方式都是基于特征.

本文与其它小样本学习综述的区别如下.

1)本文只针对于基于度量的小样本学习方法.虽然目前有一些关于小样本学习的研究综述, 但均是对小样本学习相关的所有论文进行分类, 而本文只强调基于度量的小样本学习方法, 对该类方法进行更详尽的分类.

2)本文基于关键问题进行分类, 而不是根据方法类型进行分类.从问题出发对方法进行分类更容易让初学者了解不同方法设计的初衷及现有方法存在的问题和改进空间.

3)本文在分类时结合人类认知理论和机器学习公理化中的相关内容, 基于小样本学习方法的出发点, 让机器模仿人类认知的联系更紧密.

2 类表示学习方法

小样本学习中首要解决的问题是如何从数据中学习概念(类).机器学习的基本任务是获取知识, 最终输出结果为知识.机器学习公理化[45]中指出, 知识由各种概念组成, 概念是构成人类认知世界的最小单元.因此, 机器学习首先要解决如何从数据中学习概念(类).同样, 在小样本学习中首要解决的问题也是如何从数据中学习概念, 由于小样本学习中数据不充分, 概念的学习更困难.

在1953年前, 人们通常认为概念是可精确定义的, 所有目前不能准确定义的概念仅是因为受限于目前的认知水平.按照这样信念得到的概念的定义叫作经典定义.Wittgenstein[46]通过研究“ 游戏” 这个概念, 对于概念是否一定存在精确定义提出质疑.现代认知科学的发展支持这一看法, 明确指出, 各种概念, 如人、猫、狗等, 都不一定存在经典的内涵表示.现代认知科学已提出新型的概念内涵表示理论, 如原型理论、样例理论和知识理论[47].基于上述理论, 本文将小样本类表示学习方法分为3种:基于原型理论的类表示学习方法、基于样例的类表示学习方法和基于任务的类表示学习方法.

2.1 基于原型理论的类表示学习方法

原型理论认为一个概念可由一个原型表示, 一个原型可以是一个实际或虚拟的对象样例, 通常假设为概念的最理想代表.

最早的基于类原型理论的小样本学习方法是类原型网络[8], 将每类样本在嵌入空间表示的均值作为该类的类原型, 通过对比查询样本与类原型间的距离将查询样本进行分类.

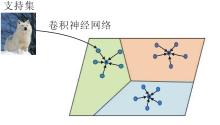
类原型网络示意图如图3所示, 图中彩色圆圈表示不同类样本在嵌入空间的表示, 黑色圆圈表示类原型, 由各类样本在嵌入空间中的特征求均值得到.此方法简单有效, 是基于度量的小样本分类方法中代表性研究之一.

图3 类原型网络Fig.3 Prototype network

虽然文献[8]证明在一个特定的空间点集中, 不论样本点满足何种概率分布时, 这些点的平均点是这个空间的最小平均距离.但是小样本学习中每类样本量太少, 难以满足任何概率分布, 即小样本学习中的每类样本只是该类所有样本中非常小的一部分, 难以代表该类的分布.

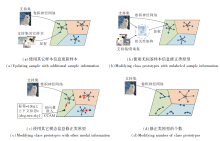
此外, 小样本学习中的另一个问题是类内方差较大.因此, 简单采用样本均值作为该类的类原型可能是有偏的.为了解决这一问题, 学者们提出类原型计算方法.这些方法的基本思想是利用一些其它信息以修正类原型, 如图4(a)所示.

图4 不同类型的类原型修正Fig.4 Different types of class prototype modification

Zheng等[48]提出主要特性网络(Principal Cha-racteristic Networks, PCN), 采用绝对差之和(Sum of Absolute Difference, SAD)衡量每个样本的重要性, 由于类原型是由样本计算得到, 如果能给具有代表性的样本更大的权重就会得到更好的原型.在小样本学习中, 样本的重要性尤为重要.Zheng等[48]根据每个样本与其它样本的差异作为自身的重要性, 并对样本进行加权, 得到最终的类原型表示.每个样本在隐空间的SAD如下所示:

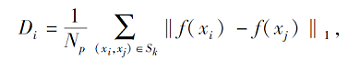
其中, f(xi)表示第i个样本在嵌入空间的表示, Sk表示支持集中样本集合, Np表示第i个样本所在类的支持集中样本对的个数.可以看出, 样本与该类其它样本之间的差异越大, SAD值越大.在此基础上, 类原型表示为

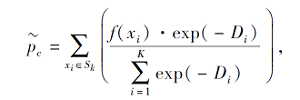
其中K表示某类支持集中样本个数.可以看出, 上式中的类原型是通过对支持集中样本加权求均值得到的.样本与类内其它样本的差异越大, 该样本的权重越小.因此, 此方法可降低异常点对类原型计算的干扰.

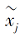
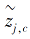
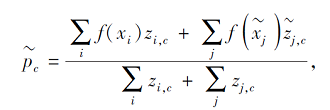
Ren等[49]引入无标签样本, 增加样本数量, 避免小样本原型学习不准确的问题.计算无标签样本 和类原型pc的距离, 得到无标签样本属于该类的置信度 , 再以置信度作为权重, 将无标签样本加入类原型学习中, 具体公式如下:

置信度

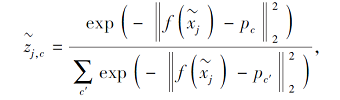
其中c'表示所有类原型.可以看出, 无标签样本与某类初始类原型的距离越近, 该样本属于该类的置信度越大.此外, 针对更复杂的实际情况, Ren等[49]设计另外两种引入无标签数据的策略以更新类原型, 共设计3种半监督小样本学习方法.

虽然Ren等[49]引入未标记样本, 可对类原型进行更新, 但将监督的小样本学习方式转换成半监督学习方法.Hou等[32]提出交叉注意力网络(Cross Attention Network, CAN), 只利用每个任务中给定的部分未标记样本, 通过均值得到的类原型和查询样本的相关性作为权重以更新类原型.具体地, 先通过简单求均值得到一个初始的类原型, 再计算查询样本和初始类原型的相关性矩阵, 最后基于相关性矩阵更新初始类原型的表示.

Liu等[50]提出消除偏见-基于余弦相似性的原型网络(Bias Diminishing-Cosine Similarity Based Prototypical Network, BD-CSPN), 也是利用查询样本(Query)修正类原型, 但同时考虑类间偏差的影响.先采用伪标签生成策略为查询样本预测类别, 根据查询样本与原始类中心直接的相似性得到查询样本属于每个类的概率w:

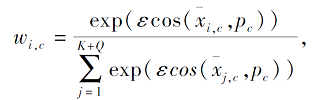
其中, ε表示一个标量参数, xi, c表示第c类的第i个样本, x̅i, c表示标准化的xi, c, K表示每类中支持集的样本个数, Q表示每类中查询集的样本个数.

将查询样本也加入到类原型的计算中:

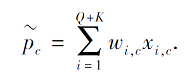
然后为标准化的类原型引入偏移项, 消除类和类之间的偏差.偏移项的定义如下:

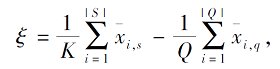
其中, x̅i, s、 x̅i, q分别表示来自支持集和查询集标准化后的样本表示.

除了利用已(未)标记样本信息对类原型进行修正以外, 学者们还利用其它额外信息, 如文本信息、修正类原型.Xing等[33]提出自适应模态混合机制(Adaptive Modality Mixture Mechanism, AM3), 引入类别的词向量表示, 使用多模态信息(文本信息和图像信息)进行类原型学习.当图像提供的信息难以进行分类时, 由于文本信息包含丰富的语义信息, 可利用文本信息辅助学习.因此, Xing等[33]提出自适应融合视觉类原型和文本类原型的方法, 融合后的类原型表示为

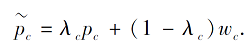
其中:pc表示视觉类原型, 即对类内样本的图像表示求均值得到的类原型;wc表示文本类原型, 通过对类别的词向量表示进行映射得到;λ c表示视觉类原型的权重, 通过自适应机制学习得到.类似地, Fortin等[51]引入上下文信息, 基于注意力机制学习为每类学习一个上下文表示, 作为文本信息的类原型, 再将文本类原型和视觉类原型自适应融合, 得到最终的类原型.

上述方法中假设每类只有一个类原型, 当数据分布较简单时, 用一个类原型就可较好地表示该类.但是针对类别分布较复杂的情况, 如果每类只学习一个类原型, 就难以有效地对该类进行表示.于是, Allen等[52]提出无限混合原型学习(Infinite Mixture Prototypes Learning, IMP), 可自适应地为不同类学习不同数目的类原型.分布复杂的类学习多个类原型, 分布简单的类学习一个类原型.

总之, 基于原型理论的类表示学习方法的关键是如何得到更好的类原型, 使类原型可更好地代表这个类, 包括样本修正、类原型计算方式和数目修正.

2.2 基于样例的类表示学习方法

样例理论认为, 人们主要根据新样例与记忆中存储先前碰到的一个或多个实例的相似程度对新样例的范畴隶属进行判别, 所以样例理论中的类表示为单个或多个样本.

小样本学习中基于样例理论进行类表示学习的最早的方法是匹配网络(Matching Network)[39].该方法结合注意力机制, 计算查询样本与支持集中每类样本之间的相似性, 作为查询样本属于该类的概率:

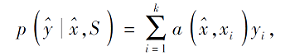
其中, a表示通过注意力机制学到的权重, x^表示任务中的查询样本, xi表示任务中的支持样本, yi表示样本i的标签, S表示支持集样本集合.文献[39]将元学习机制引入小样本学习中, 并结合非参学习, 具体框图如图5所示.

图5 匹配网络框图Fig.5 Sketch map of matching network

但匹配网络是为单样本(One-Shot)学习设计的, 在单样本学习的情况下, 每类只有一个样本, 因此, 使用唯一的样本表示每类.分类时, 对比查询样本和每类的唯一样本, 得到最终分类结果.事实上, 所有的单样本学习的模型都是基于样例理论表示类, 因为每类只有一个样本, 如果不进行数据扩充等操作, 该类只能由这唯一的样本表示.在分类时, 查询样本也只是和每类唯一的样本进行对比.

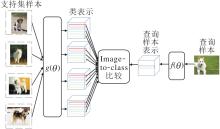
对于每类样本不止一个的小样本学习方法, 典型的基于样例理论进行类表示学习的方法为深度近邻网络(Deep Nearest Neighbor Neural Network, DN4)[35].DN4框图如图6所示.

图6 DN4框图Fig.6 Sketch map of DN4

与样例理论中近邻方法相似, DN4的类由所有样本表示, 在进行分类预测时, 计算查询样本与其近邻的距离作为样本与类的距离.此外, 与一般的小样本类表示不同, DN4中类表示是基于局部信息进行表示的.较早的小样本学习中通常将类表示为一个向量, 表示这类的全局信息, 但对于小样本学习, 由于样本量太少, 一些局部信息可能更有用.实际上, 人类在进行分类时, 当样本量不充足时, 更关注的也是具有判别性的局部信息.因此, DN4将类表示成为一个张量x∈ Rc× w× h, c表示网络的通道数, w表示高度, h表示宽度, 更好地捕捉类的局部判别信息.在计算相似性时, DN4计算查询样本中所有特征图(Feature Map)xi与某个类中最近k个特征图距离的均值, 以此作为查询样本与该类的相似性:

其中, xi表示查询样本的第i个特征图, x^ij表示xi第j个最近邻的特征图, NS表示支持集样本个数.

目前小样本学习中大部分的类表示都是基于原型理论.由于基于样例的方法需要储存多个样本, 占用更多的储存空间, 时间复杂度更高, 所以这类方法相对较少.

2.3 基于任务的类表示学习方法

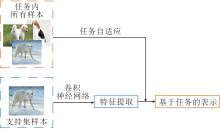
认知理论中的知识理论认为, 概念是特定知识框架(文明)的一个组成部分.类似地, 在基于度量的小样本学习中, 类(样本)的表示也不能独立于任务而存在.本文把在小样本学习中这种基于知识的概念表示学习方法称为基于知识(任务)的类表示学习方法.这类方法的关键是如何利用任务信息对表示(样本表示)进行调整, 生成基于任务的表示, 一般框架如图7所示.

图7 基于任务的类表示学习方法框图Fig.7 Framework class representation of knowledge-based learning

在对类(样本)表示进行调整时, 一种策略是利用类似条件批正则化[53]或面向特征的仿射变换(Feature-Wise Linear Modulation, FiLm)[54]的方式对卷积神经网络(Convolutional Neural Network, CNN)中每层隐表示都进行调整.Oreshkin等[36]提出任务相关自适应度量(Task Dependent Adaptive Metric, TADAM), 将所有类的均值作为任务表示, 将任务表示输入2个残差网络, 学习缩放系数γ和平移系数β, 通过对CNN中样本的每层隐表示进行缩放和平移, 得到基于任务的表示:

hl+1=γ☉hl+β,

其中, hl表示特征学习网络中第l层的表示, ☉表示对应元素的积运算.Bateni等[37]提出简单的基于类协方差矩阵的距离度量(Simple Class-Covariance-Based Distance Metric, Simple CNAPS), 利用类似上述机制生成基于任务的表示.此外, 除学习基于任务的表示, 在进行相似性计算时也采用基于任务的马氏距离作为度量函数.

另一种策略是直接对经过CNN学习的高层特征表示进行调整.Wang等[38]将所有类的属性信息作为任务表示, 放入多个网络中生成多个权重Wi, 得到基于任务的表示:

xi+1=Wixi+b.

Li等[55]拼接任务内所有样本, 通过网络学习可体现任务内共性和类间差异的一个掩膜 p, 再将掩膜作用到样本表示上, 生成基于任务的样本表示:

x=x☉p.

Ye等[56]为了避免任务之间类别的顺序对基于任务的表示造成负面影响, 提出使用集合到集合类型的映射, 学习不同分类任务之间的相关性, 通过集合自适应的方法, 适配特征提取方法, 学习与目标任务相关的特征, 适应到不同的分类任务中.

基于任务的类表示方法由于考虑不同任务的差异性, 会得到更稳定的类表示, 是近年来研究较多的方向.

3 基于相似性的学习方法

基于度量的小样本分类方法的第2个关键问题是如何计算查询样本与类的相似性.机器学习公理化[45]指出人类进行分类的原则就是“ 归哪类, 像哪类, 像哪类, 归哪类” .同样, 在基于度量的小样本分类任务中, 也是依据查询样本和类表示的相似性对查询样本进行分类.因此, 如何度量测试样本和类表示之间的相似性成为基于度量的小样本分类任务中的关键问题.根据相似性学习的方式, 本文将小样本学习分为3类:特征独立的距离度量、特征相关的距离度量和自适应距离学习.

特征独立的距离度量是指在计算查询样本和类表示时采用的距离函数假定任务特征之间是独立的, 如欧氏距离、余弦距离等.代表性的原型网络和匹配网络采用特征独立的距离函数.然而在实际应用中, 在没有强加正交约束下很难保证特征之间是独立的, 因此, Bateni等[37]提出使用马氏距离作为距离函数.马氏距离可学习不同特征之间的相关性, 更好地计算样本之间的相似性.然而马氏距离计算向量之间的距离, 考虑向量中特征之间的相关性.在类表示学习中, 为了更好地捕获数据的局部信息, 有学者将类表示成张量.因此, Zhang等[11]采用推土机距离(Earth Mover's Distance, EMD), 考虑两个张量之间的相关性, 结合深度学习, 提出DeepEMD, 更好地学习张量间的相似性.具体地, DeepEMD将查询集和支持集样本表示成张量, 张量中不同的向量表示图像的不同部分, 计算两者之间的最佳匹配代价, 表示得到二者之间的相似程度.当每类样本数目为1时, 查询集的类表示为该样本表示, 当样本数目大于1时, 如果通过简单求均值的方式计算类原型, 会忽略不同图像中目标物体可能出现在不同位置的问题, 因此通过学习的方法得到基于张量的类原型.

虽然马氏距离和EMD可考虑特征间的相关性, 但只能衡量特征间较简单的相关性.例如, 2个样本点x和y之间的马氏距离表示为

dM=(x-y)TM-1(x-y)　,

其中M为特征之间的相关性矩阵.从公式可看出, dM在计算时只考虑特征间一层相关性.

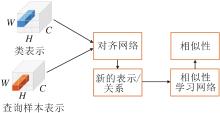
受神经网络可提取数据间复杂关系的启发, Sung等[9]提出使用神经网络代替距离函数, 自适应地学习样本间的相似性.关系网络(Relation Net-work)[9]是小样本学习中代表性工作, 框图如图8所示.Sung等[9]指出想要学习一个可迁移的距离度量, 而不是采用固定的距离函数, 又由于神经网络可较好地学习数据的非线性结构, 因此, 将类原型和查询样本拼接后放入一个神经网络中, 自适应地学习它们之间的相似性.

图8 关系网络框图Fig.8 Sketch map of relation network

在关系网络中, 网络输入类表示和查询样本拼接后的向量.有学者指出针对小样本学习的相似性问题, 采用张量计算更好[11, 32, 34, 35, 57].因为张量体现样本的局部信息, 在进行小样本分类时, 局部信息可能会提供更具有判别性的信息.

将关系网络中的向量表示拓展到张量上, 首先将类表示和查询样本表示成张量, 拼接后放到一个网络中, 学习对应局部信息的相关性, 大致框图如图9所示.

图9 基于张量表示的相似性计算框图Fig.9 Framework of similarity calculation based on tensor representation

由于目标物体通常出现在图像的不同位置, 直接将特征图拼接后放入网络中, 学习相关性未考虑到类和查询样本的位置对齐和语义对齐, 需要将类和查询样本对齐后再计算相似性.

为了解决这一问题, Hou等[32]通过注意力机制, 先修正类表示和测试样本, 再进行语义对齐, 修正后的类表示和测试样本拼接后放到网络中学习相似性.

上述方法都是计算特征之间的相似性.在小样本学习中, 特征之间的相似性关系因位置不同等原因可能并不是很稳定, 于是增加相对位置之间的相似性计算, 同时计算相对位置和特征之间的相似性[16, 18, 57].Hao等[40]提出语义对齐的度量学习(Semantic Alignment Metric Learning, SAML), 先计算类表示的每个特征图和查询样本每个特征图之间的距离, 得到一个相似性矩阵:

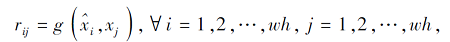
其中, 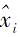表示查询样本的第i个特征图, xj表示类表示的第j个特征图.增强相似性矩阵中的关键部位的相关性, 减弱无关部位的相关性, 进行语义对齐, 将语义对齐后的相似性矩阵放入网络中, 学习最终的相似性.Wu等[57]提出考虑位置的关系网络(Posi-tion-Aware Relation Networks, PARN), 利用注意力机制, 不仅考虑类表示和查询样本之间的相关性矩阵, 还考虑类表示和查询样本的自相关性矩阵, 将所有的相关性矩阵拼接后放入网络中, 学习最终的相似性.Cao等[34]构造两项损失函数, 同时学习特征表示的相似性和相对位置之间的相似性.

相似性学习虽然已有很多成果, 但仍是一个难点问题.因为相似性学习与任务和数据密不可分, 独立于任务和数据的相似性计算函数并无实际意义, 因此, 如何结合小样本分类任务的特性及数据的表现形式, 更好地度量数据之间的相似性仍值得研究.

4 其它基于度量的小样本学习方法

除了上述主流方法以外, 还有一些其它的基于度量的小样本学习方法.

在类表示时, 上述方法都是将类表示成向量或张量.还有一些学者将类表示成图(Graph), 更好地挖掘样本之间的关系.Garcia等[58]将图卷积神经网络应用到小样本图像分类任务上, 将每个样本视为图中的一个节点, 通过图卷积网络学习样本的表示.Kim等[59]在构建图时不仅利用节点信息, 还利用边的连接信息, 使网络可直接利用类内相似性和类间不相似性指导表示的学习.Cheng等[60]在图卷积网络构建时, 引入注意力机制, 包括节点自注意力(Node Self-Attention)、邻居注意力(Neighborhood Attention)、层间记忆注意力(Layer Memory Atten-tion), 提高方法泛化能力.Shi等[61]在构建图时, 不仅考虑新类的关系, 同时考虑新类和基类的关系, 在原型网络的基础上, 提出广义的小样本学习方法(Graph-Convolutional Global Prototypical Networks, GcGPN), 不仅可对新类分类, 还可以对基类分类.Zhang等[62]提出自适应聚合图卷积的方法, 减小数据集中噪声(不相关的图像)的影响.

在相似性学习时, 上述方法都是为了设计更好的相似性计算方式.还有学者引入间隔(Margin)和度量学习的思想, 设计更好的损失函数以更好地学习相似性.Oreshkin等[36]和Zhang等[63]提出使用可学习的温度参数以调整距离度量, 在普通的交叉熵损失中引入调整机制, 并从理论上分析调整的作用.Li等[64]指出使用自适应的间隔损失函数替换交叉熵损失函数, 更好地区分类间距离, 并利用类别的语义信息提出任务相关的自适应间隔学习方法.Li等[65]借鉴度量学习中的N对损失[66], 提出K元组损失函数, 利用样本间的关系, 更好地学习度量空间.

已有很多学者研究关于间隔和度量学习[67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77], 怎样更好地将这些工作与小样本学习结合, 也是一个值得思考的问题.

此外, 随着自监督学习的发展, 利用自监督技术更好地帮助小样本学习的方法也得到广泛关注.Su等[78]和Li等[79]通过在预训练过程中引入自监督损失(旋转损失或位置预测损失), 提取更鲁棒的表示.

5 实验及结果对比
5.1 实验数据集

在小样本图像分类任务中, 不同文献中标准数据集使用都是一致的.常用的数据集包括Omniglot[80]、miniImageNet[81]、tieredImageNet[48]数据集.此外还有一些细粒度数据集, 如CUB数据集[82].

Omniglot数据集由来自50种不同语言的1 623个手写字符构成, 每个字符都是由20个不同的人通过亚马逊的Mechanical Turk在线绘制.数据集样本类别很多(1 623种), 但每种类别的样本数量较少(20个).在实验中通常选择1 200种字符作为训练集, 剩余的423种字符作为测试集.

MiniImageNet数据集是ImageNet数据集的一个子集, 共有60 000幅图像, 100类, 每类有600幅图像, 每幅图像的尺寸为84× 84.实验中通常选择其中80类作为训练集, 剩余的20类作为测试集.也有的实验选择64类作为训练集, 16类作为验证集, 剩余的20类作为测试集.

TieredImageNet数据集也是ImageNet数据集的一个子集, 具有层级结构, 包含34个大类(Cate-gories), 每个大类又包含10~30个小类(Classes), 每类的图像数量不等, 共608个类别, 779 165幅图像.实验中通常选择20个大类作为训练集, 6个大类作为验证集, 剩余的8个大类作为测试集.

CUB-200数据集的全称为Caltech-UCSD Birds-200-2011数据集, 是由加利福尼亚理工学院提供的鸟类数据库, 共包含200种鸟类的11 788幅图像, 每幅图像的尺寸也统一裁剪为84× 84.使用中通常选择100类作为训练集, 50类作为验证集, 剩余的50类作为测试集.

5.2 实验结果对比

为了更好地对比现有方法以进行后续研究, 本文整理一些典型的基于元学习训练机制模型的实验结果, 具体如表1和表2所示.

表1 基于度量的小样本学习方法特点 Table 1 Characteristics of metric-based few-shot learning methods
表2 基于度量的小样本学习方法在4个数据集上的精确度对比 Table 2 Accuracy comparison of metric based few-shot learning methods on 4 datasets %

由表1和表2可看出, 早期方法都在Omniglot、miniImagnet数据集上进行验证.不同方法在不同数据集上的表现相似.由于Omniglot数据集较简单, 精度接近100%, 提升空间很小, 因此, 后期方法大都在miniImagnet、tieredImageNet数据集上进行验证.随着近几年小样本学习的发展, 不论是1个样本任务还是5个样本任务, 在各数据集上的精度都有较大提升, 但仍有很大的提升空间.

由于本文只是整理不同方法的实验结果, 而不同方法采用的数据预处理及网络框架等设置并不相同, 所以很难对比不同方法真正的优势.从表1可大致得出以下结论.在类表示方法上, 目前大部分的方法都是基于原型的方法, 基于样例的方法很少, 基于知识的方法最近开始受到学者们的关注.较早的论文大部分都采用基于向量的表示形式, 最近基于张量的方法逐渐增加.在相似性学习上, 近期都采用自适应学习的方法.在网络架构上, ResNet-12[2]被广泛使用.从实验精度上看, 基于原型的方法和基于知识的方法优于基于样例的方法.

6 问题与展望
6.1 存在问题及挑战

尽管近年来基于度量的小样本学习已得到深入研究, 取得一定进展, 但仍然存在一些问题.

1)泛化性难以保证.目前基于度量的小样本学习方法都是基于迁移学习的方法, 需要在大量的非目标数据集上进行预训练, 如果目标数据集与非目标数据集差异较大, 难以保证迁移的效果.虽然最近有些学者[83, 84, 85, 86, 87]提出在预训练时使用自监督的技术, 可提高方法的泛化能力, 但这些方法只能部分解决该问题.如何只利用目标数据集上的少量样本, 实现真正意义上的小样本学习仍是一个难点问题.

2)训练机制有待优化.目前基于度量的小样本学习方法均采用元学习的训练机制, 构建一系列小样本任务, 学习解决这类问题的元知识, 但在构造不同任务时都是随机的, 未考虑任务的重要性和任务之间的关系.从理论上来说, 任务的构建和学习中任务的先后对方法的优化和泛化能力具有重要影响.因此, 之后的小样本学习方法不应只关注单个任务上的学习性能, 更应关注整体的训练和学习.

3)缺乏可解释性.虽然基于度量学习的小样本学习方法可从人类认知的角度进行分类, 分类时也是利用查询样本与类表示之间的相似性, 依据“ 归哪类像哪类” 的原则, 有一定的可解释性, 但分类是在由深度网络得到的嵌入空间上进行, 而嵌入空间中特征的含义难以解释, 导致这类方法仍不具备可以让人类能理解的解释性.

4)设计缺乏理论指导.虽然近年来小样本学习受到学者们广泛关注, 并取得不错的成果, 但是关于小样本学习的理论研究却很少.大部分方法设计的初衷都是来源于人类认知过程中的启发或猜测, 并无理论保证或指导.

6.2 展望

通过对当前基于度量的小样本学习研究方法的梳理及目前基于度量的小样本学习难点的分析, 可以展望未来小样本学习的发展方向.

1)多模态小样本学习.小样本学习的难点是样本量少, 难以学到类的正确表示.如果可以将其它模态信息加以利用, 就可得到更丰富的信息, 这有利于小样本学习, 尤其是认知视觉上较相近的类.事实上, 人类在对小样本进行认知时, 多模态信息也会发挥重要的作用.除了音频、文本等其它模态信息也可提供丰富且重要的信息.目前已有一些多模态小样本学习文献, 但大都只利用标签的文本信息.此外, 虽然多模态信息可带来更多信息, 但也可能会引入噪音和信息冗余.如何充分合理利用多模态信息, 既考虑不同信息源的一致性, 又考虑它们直接的互补性, 同时消除多源信息的冗余性, 弥补小样本数据匮乏的问题是一个值得研究的方向.

2)可解释小样本学习.已有多数小样本学习方法仅提供分类预测的准确率, 而对于为什么这么分类的解释却很少.虽然原型理论、样例理论和知识理论可部分解释为什么将查询样本分为某类, 但具体依据哪些特点(如形状或颜色)却并不知道.人类在对小样本分类时, 不仅可给出分类时依靠的理论, 还可给出分类时具体依据的特征.因此, 如何设计可解释小样本学习方法, 如通过特征解耦或部分原型学习的方法, 使学到的特征具有解释性, 更好地让机器像人一样学习是未来值得研究的问题.

3)因果小样本学习.目前的小样本学习主要依靠元知识的迁移, 要求目标域与训练时的非目标数据集相差不大, 如果相差太大, 就难以将元知识迁移到目标数据中.不仅如此, 在非目标数据集上进行训练, 还可能导致负迁移.出现这种情况的主要原因是方法在学习时未学到变量间的因果关系, 只学习相关关系.

为了解决这一问题, Yue等[88]提出因果小样本学习方法.在已有模型上引入因果机制, 可让已有方法得到更优的泛化能力.这虽然在一定程度上解决预训练带来的虚假因果关系, 但在设计时需要提前假设混淆因子是什么.在实际应用中, 可能只知道部分混淆因子或根本不知道混淆因子.Yue等[88]提出可混合一些补丁, 如使图像变得更多样化, 再通过对比损失进行学习, 使一些简单的关联不再有效, 学习一些真正的规则.上述方法只是对因果小样本学习的初探.如何设计更好的因果小样本学习方法, 提高小样本学习的泛化性能, 仍是一个值得研究的方向.

4)小样本学习的优化和理论.目前大部分小样本学习都是基于元学习的训练机制, 文献[89]~文献[93]中关于元学习的理论已很多, 但基于元学习训练的小样本学习方法的相关理论文献却很少[94, 95].如何结合元学习理论, 设计更好的优化方法, 加速模型的优化过程, 使小样本学习可真正应用到实际场景中也是今后关注的问题.

参考文献
[1] LEE J G, KANG M. Geospatial Big Data: Challenges and Opportunities. Big Data Research, 2015, 2(2): 74-81. [本文引用:1]
[2] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:2]
[3] SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1409.1556.pdf. [本文引用:1]
[4] SUN Y, CHEN Y H, WANG X G, et al. Deep Learning Face Re-presentation by Joint Identifcation-Verifcation // Proc of the 27th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2014: 1988-1996. [本文引用:1]
[5] TAIGMAN Y, YANG M, RANZATO M A, et al. Deepface: Clo-sing the Gap to Human-Level Performance in Face Verification // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2014: 1701-1708. [本文引用:1]
[6] 杨军, 刘妍丽. 基于图像的单样本人脸识别研究进展. 西华大学学报(自然科学版), 2014, 33(4): 1-5, 10.
(YANG J, LIU Y L. The Latest Advances in Face Recognition with Single Training Sample. Journal of Xihua University(Natural Science), 2014, 33(4): 1-5, 10. ) [本文引用:1]
[7] MANNING C, SCHUTZE H. Foundations of Statistical Natural Language Processing. Cambridge, USA: The MIT Press, 1999. [本文引用:1]
[8] SNELL J, SWERSKY K, ZEMEL R S. Prototypical Networks for Few-Shot Learning // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 4080-4090. [本文引用:4]
[9] SUNG F, YANG Y X, ZHANG L, et al. Learning to Compare: Relation Network for Few-Shot Learning // Proc of the IEEE Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 1199-1208. [本文引用:5]
[10] CHEN W Y, LIU Y C, KIRA Z, et al. A Closer Look at Few-Shot Classification // Proc of the International Conference on Learning Representations[C/OL]. [2021-03-21]. https://openreview.net/pdf?id=HkxLXnAcFQ. [本文引用:1]
[11] ZHANG C, CAI Y J, LIN G S, et al. DeepEMD: Few-Shot Image Classification with Differentiable Earth Mover's Distance and Structured Classifiers // Proc of the IEEE/CVF Conference on Compu-ter Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 12203-12213. [本文引用:3]
[12] RIOS A, KAVULURU R. Few-Shot and Zero-Shot Multi-label Lear-ning for Structured Label Spaces // Proc of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, USA: ACL, 2018: 3132-3142. [本文引用:1]
[13] GENG R Y, LI B H, LI Y B, et al. Induction Networks for Few-Shot Text Classification[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1902.10482.pdf. [本文引用:1]
[14] LYU C, LIU W J, WANG P. Few-Shot Text Classification with Edge-Labeling Graph Neural Network-Based Prototypical Network // Proc of the 28th International Conference on Computational Linguistics. New York, USA: ACM, 2020: 5547-5552. [本文引用:1]
[15] TANNER M A, WONG W H. The Calculation of Posterior Distributions by Data Augmentation. Journal of the American Statistical Association, 1987, 82(398): 528-540. [本文引用:1]
[16] PAN S J, YANG Q. A Survey on Transfer Learning. IEEE Tran-sactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. [本文引用:2]
[17] SANTORO A, BARTUNOV S, BOTVINICK M, et al. Meta-Lear-ning with Memory-Augmented Neural Networks // Proc of the 33rd International Conference on Machine Learning. Cambridge, USA: The MIT Press, 2016: 1842-1850. [本文引用:2]
[18] QI H, BROWN M, LOWE D G. Low-Shot Learning with Imprinted Weights // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 5822-5830. [本文引用:2]
[19] ZHANG Y B, TANG H, JIA K. Fine-Grained Visual Categorization Using Meta-Learning Optimization with Sample Selection of Auxiliary Data // Proc of the European Conference on Computer Vision. Berlin, German: Springer , 2018: 233-248. [本文引用:1]
[20] CUBUK E D, ZOPH B, MANE D, et al. Autoaugment: Learning Augmentation Policies from Data[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1805.09501v3.pdf. [本文引用:1]
[21] RAVI S, LAROCHELLE H. Optimization as a Model for Few-Shot Learning // Proc of the International Conference on Learning Re-presentations[C/OL]. [2021-03-21]. https://openreview.net/pdf?id=rJY0-Kcll. [本文引用:1]
[22] FINN C, ABBEEL P, LEVINE S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks // Proc of the 34th International Conference on Machine Learning. New York, USA: ACM 2017: 1126-1135. [本文引用:1]
[23] SANTORO A, BARTUNOV S, BOTVINICK M, et al. One-Shot Learning with Memory-Augmented Neural Networks[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1605.06065.pdf. [本文引用:1]
[24] LI Z G, ZHOU F W, CHEN F, et al. Meta-SGD: Learning to Learn Quickly for Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1707.09835.pdf. [本文引用:1]
[25] ZHOU F W, WU B, LI Z G. Deep Meta-Learning: Learning to Learn in the Concept Space[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1802.03596.pdf. [本文引用:1]
[26] SCHWARTZ E, KARLINSKY L, SHTOK J, et al. Delta-Encoder: An Effective Sample Synthesis Method for Few-Shot Object Reco-gnition // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018. 2850-2860. [本文引用:1]
[27] JAMAL M A, QI G J. Task Agnostic Meta-Learning for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 11711-11719. [本文引用:1]
[28] SUN Q R, LIU Y Y, CHUA T S, et al. Meta-Transfer Learning for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 403-412. [本文引用:1]
[29] YOON J, KIM T, DIA O, et al. Bayesian Model-Agnostic Meta-Learning // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 7343-7353. [本文引用:1]
[30] BERTINETTO L, HENRIQUES J F, VALMADRE J, et al. Lear-ning Feed-Forward One-Shot Learners // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 523-531. [本文引用:1]
[31] COLLINS L, MOKHTARI A, SHAKKOTTAI S. Task-Robust Mo-del-Agnostic Meta-Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2002.04766v2.pdf. [本文引用:1]
[32] HOU R B, CHANG H, MA B P, et al. Cross Attention Network for Few-Shot Classification // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2019: 4003-4014. [本文引用:4]
[33] XING C, ROSTAMZADEH N, ORESHKIN B N, et al. Adaptive Cross-Modal Few-Shot Learning // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2019: 4847-4857. [本文引用:3]
[34] CAO C Q, ZHANG Y N. Learning to Compare Relation: Semantic Alignment for Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2003.00210v1.pdf. [本文引用:3]
[35] LI W B, WANG L, XU J L, et al. Revisiting Local Descriptor Based Image-to-Class Measure for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 7253-7260. [本文引用:3]
[36] ORESHKIN B N, RODRIGUEZ P, LACOSTE A. TADAM: Task Dependent Adaptive Metric for Improved Few-Shot Learning // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 719-729. [本文引用:3]
[37] BATENI P, GOYAL R, MASRANI V, et al. Improved Few-Shot Visual Classification // Proc of the IEEE/CVF Conference on Com-puter Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 14481-14490. [本文引用:3]
[38] WANG X, YU F, WANG R, et al. TAFE-Net: Task-Aware Feature Embeddings for Low Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 1831-1840. [本文引用:2]
[39] VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching Networks for One Shot Learning // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 3637-3645. [本文引用:3]
[40] HAO F S, HE F X, CHENG J, et al. Collect and Select: Semantic Alignment Metric Learning for Few-Shot Learning // Proc of the IEEE/CVF International Conference on Computer Vision. Wa-shington, USA: IEEE, 2019: 8459-8468. [本文引用:2]
[41] LU J, GONG P, YE J P, et al. Learning from Very Few Samples: A Survey[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2009.02653v1.pdf. [本文引用:2]
[42] BENDRE N, MARÍN H T, NAJAFIRAD P. Learning from Few Samples: A Survey[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2007.15484.pdf. [本文引用:1]
[43] WANG Y Q, YAO Q M, KWOK J T, et al. Generalizing from a Few Examples: A Survey on Few-Shot Learning. ACM Computing Surveys, 2020, 53(3): 1-34. [本文引用:3]
[44] 赵凯琳, 靳小龙, 王元卓. 小样本学习研究综述. 软件学报, 2021, 32(2): 349-369.
(ZHAO K L, JIN X L, WANG Y Z. Survey on Few-Shot Lear-ning. Journal of Software, 2021, 32(2): 349-369. ) [本文引用:1]
[45] 于剑. 机器学习: 从公理到算法. 北京: 清华大学出版社, 2017.
(YU J. Machine Learning: From Axioms to Algorithms. Beijing, China: Tsinghua University Press, 2017.) [本文引用:3]
[46] WITTGENSTEIN L. Philosophical Investigations. New York, USA: John Wiley & Sons, 2010. [本文引用:1]
[47] MURPHY G L. The Big Book of Concepts. Cambridge, USA: The MIT Press, 2004. [本文引用:1]
[48] ZHENG Y, WANG R G, YANG J, et al. Principal Characteristic Networks for Few-Shot Learning. Journal of Visual Communication and Image Representation, 2019, 59: 563-573. [本文引用:3]
[49] REN M Y, TRIANTAFILLOU E, RAVI S, et al. Meta-Learning for Semi-supervised Few-Shot Classification[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1803.00676.pdf. [本文引用:3]
[50] LIU J L, SONG L, QIN Y Q. Prototype Rectification for Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1911.10713.pdf. [本文引用:1]
[51] FORTIN M P, CHAIB-DRAA B. Few-Shot Learning with Contextual Cueing for Object Recognition in Complex Scenes[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1912.06679.pdf. [本文引用:1]
[52] ALLEN K R, SHELHAMER E, SHIN H, et al. Infinite Mixture Prototypes for Few-Shot Learning // Proc of the 36th International Conference on Machine Learning. New York, USA: ACM, 2019: 232-241. [本文引用:1]
[53] DE VRIES H, STRUB F, MARY J, et al. Modulating Early Vi-sual Processing by Language // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 6597-6607. [本文引用:1]
[54] PEREZ E, STRUB F, DE VRIES H, et al. FiLM: Visual Reaso-ning with a General Conditioning Layer[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1709.07871.pdf. [本文引用:1]
[55] LI H Y, EIGEN D, DODGE S, et al. Finding Task-Relevant Features for Few-Shot Learning by Category Traversal // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019. DOI: DOI:10.1109/CVPR.2019.00009. [本文引用:1]
[56] YE H J, HU H X, ZHAN D C, et al. Few-Shot Learning via Embedding Adaptation with Set-to-Set Functions // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 8805-8814. [本文引用:1]
[57] WU Z Y, LI Y W, GUO L H, et al. PARN: Position-Aware Relation Networks for Few-Shot Learning // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 6659-6667. [本文引用:3]
[58] GARCIA V, BRUNA J. Few-Shot Learning with Graph Neural Net-works[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1711.04043.pdf. [本文引用:1]
[59] KIM J, KIM T, KIM S, et al. Edge-Labeling Graph Neural Network for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 11-20 [本文引用:1]
[60] CHENG H, ZHOU J T, TAY W P, et al. Attentive Graph Neural Networks for Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2007.06878.pdf. [本文引用:1]
[61] SHI X H, SALEWSKI L, SCHIEGG M, et al. Relational Genera-lized Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1907.09557.pdf. [本文引用:1]
[62] ZHANG J H, ZHANG M L, LU Z W, et al. ADARGCN: Adaptive Aggregation GCN for Few-Shot Learning // Proc of the IEEE Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2021: 3482-3491. [本文引用:1]
[63] ZHANG X, YU F X, KARAMAN S, et al. Heated-up Softmax Embedding[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1809.04157.pdf. [本文引用:1]
[64] LI A X, HUANG W R, LAN X, et al. Boosting Few-Shot Lear-ning with Adaptive Margin Loss // Proc of the IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 12576-12584. [本文引用:1]
[65] LI X M, YU L Q, FU C W, et al. Revisiting Metric Learning for Few-Shot Image Classification. Neurocomputing, 2020, 406: 49-58. [本文引用:1]
[66] SOHN K. Improved Deep Metric Learning with Multi-class n-Pair Loss Objective // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 1857-1865. [本文引用:1]
[67] LIU W Y, WEN Y D, YU Z D, et al. Large-Margin Softmax Loss for Convolutional Neural Networks // Proc of the 33rd International Conference on Machine Learning. New York, USA: ACM, 2016: 507-516. [本文引用:1]
[68] LIU W Y, WEN Y D, YU Z D, et al. SphereFace: Deep Hypersphere Embedding for Face Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 212-220. [本文引用:1]
[69] WANG F, CHENG J, LIU W Y, et al. Additive Margin Softmax for Face Verification. IEEE Signal Processing Letters, 2018, 25(7): 926-930. [本文引用:1]
[70] WANG H, WANG Y T, ZHOU Z, et al. CosFace: Large Margin Cosine Loss for Deep Face Recognition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 5265-5274. [本文引用:1]
[71] DENG J K, GUO J, XUE N N, et al. ArcFace: Additive Angular Margin Loss for Deep Face Recognition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4685-4694. [本文引用:1]
[72] LIU H, ZHU X Y, LEI Z, et al. AdaptiveFace: Adaptive Margin and Sampling for Face Recognition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 11939-11948. [本文引用:1]
[73] SCHROFF F, KALENICHENKO D, PHILBIN J. FaceNet: A Unified Embedding for Face Recognition and Clustering // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 815-823. [本文引用:1]
[74] SONG H O, XIANG Y, JEGELKA S, et al. Deep Metric Learning via Lifted Structured Feature Embedding // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 4004-4012. [本文引用:1]
[75] GE W F, HUANG W L, DONG D K, et al. Deep Metric Learning with Hierarchical Triplet Loss // Proc of the European Conference on Computer Vision. Berlin, German: Springer, 2018: 272-288. [本文引用:1]
[76] ZHENG W Z, LU J W, ZHOU J. Hardness-Aware Deep Metric Learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(9): 3214-3228. [本文引用:1]
[77] WANG X S, HUA Y, KODIROV E, et al. Ranked List Loss for Deep Metric Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 5202-5211. [本文引用:1]
[78] SU J C, MAJI S, HARIHARAN B. Boosting Supervision with Self-supervision for Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1906.07079v1.pdf. [本文引用:1]
[79] LI H N, TAO R S, LI J, et al. Multi-pretext Attention Network for Few-shot Learning with Self-supervision[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2103.05985.pdf. [本文引用:1]
[80] LAKE B M, SALAKHUTDINOV R, TENENBAUM J B. Human-Level Concept Learning through Probabilistic Program Induction. Science, 2015, 350(6266): 1332-1338. [本文引用:1]
[81] MALALUR P, JAAKKOLA T. Alignment Based Matching Networks for One-Shot Classification and Open-Set Recognition[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1903.06538.pdf. [本文引用:1]
[82] CUI Y, ZHOU F, LIN Y Q, et al. Fine-Grained Categorization and Dataset Bootstrapping Using Deep Metric Learning with Humans in the Loop // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1153-1162 [本文引用:1]
[83] RIZVE M N, KHAN S, KHAN F S, et al. Exploring Complementary Strengths of Invariant and Equivariant Representations for Few-Shot Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 10836-10846. [本文引用:1]
[84] GIDARIS S, BURSUC A, KOMODAKIS N, et al. Boosting Few-Shot Visual Learning with Self-Supervision // Proc of the IEEE/CVF International Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2019: 8058-8067. [本文引用:1]
[85] PHOO C P, HARIHARAN B. Self-training for Few-Shot Transfer across Extreme Task Differences[C/OL]. [2021-03-21]. https://openreview.net/pdf?id=O3Y56aqpChA. [本文引用:1]
[86] FEI N Y, LU Z W, XIANG T, et al. MELR: Meta-Learning via Modeling Episode-Level Relationships for Few-Shot Learning[C/OL]. [2021-03-21]. https://openreview.net/pdf?id=D3PcGLdMx0. [本文引用:1]
[87] ZHANG M L, ZHANG J H, LU Z W, et al. IEPT: Instance-Level and Episode-Level Pretext Tasks for Few-Shot Learning[C/OL]. [2021-03-21]. https://openreview.net/pdf?id=xzqLpqRzxLq. [本文引用:1]
[88] YUE Z Q, ZHANG H W, SUN Q R, et al. Interventional Few-Shot Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2009.13000.pdf. [本文引用:2]
[89] MAURER A. Algorithmic Stability and Meta-Learning. Journal of Machine Learning Research, 2005, 6: 967-994. [本文引用:1]
[90] WANG H X, SUN R Y, LI B. Global Convergence and Induced Kernels of Gradient-Based Meta-Learning with Neural Nets[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2006.14606.pdf. [本文引用:1]
[91] COLLINS L, MOKHTARI A, SHAKKOTTAI S. Task-Robust Mo-del-Agnostic Meta-Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2002.04766.pdf. [本文引用:1]
[92] DENEVI G, PONTIL M, CILIBERTO C. The Advantage of Conditional Meta-Learning for Biased Regularization and Fine Tuning[C/OL]. [2021-03-21]. https://export.arxiv.org/pdf/2008.10857. [本文引用:1]
[93] GAO K, SENER O. Modeling and Optimization Trade-Off in Meta-Learning[C/OL]. [2021-03-21]. https://arxiv.org/pdf/2010.12916.pdf. [本文引用:1]
[94] CAO T S, LAW M T, FIDLER S. A Theoretical Analysis of the Number of Shots in Few-Shot Learning[C/OL]. [2021-03-21]. https://openreview.net/pdf?id=HkgB2TNYPS. [本文引用:1]
[95] RAGHU A, RAGHU M, BENGIO S, et al. Rapid Learning or Feature Reuse?Towards Understand ing the Effectiveness of Maml[C/OL]. [2021-03-21]. https://arxiv.org/pdf/1909.09157v1.pdf. [本文引用:1]