引用本文
张玉红, 余道远, 胡学钢. 领域自适应任务中的动态参数调整方法. 模式识别与人工智能, 2021,34(10): 924-931
ZHANG Yuhong, YU Daoyuan, HU Xuegang. Dynamic Parameter Setting Method for Domain Adaptation. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(10): 924-931.  
Doi: 10.16451/j.cnki.issn1003-6059.202110005
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
领域自适应任务中的动态参数调整方法
张玉红1,2, 余道远1,2, 胡学钢1,2
1.合肥工业大学 计算机与信息学院 合肥 230601
2.合肥工业大学 教育部大数据知识工程重点实验室 合肥 230601
通讯作者:

张玉红,博士,副教授,主要研究方向为迁移学习、机器学习.E-mail:zhangyh@hfut.edu.cn.

作者简介:

余道远,硕士研究生,主要研究方向为领域自适应、机器学习.E-mail:807342680@qq.com.

胡学钢,博士,教授,主要研究方向为数据挖掘、Web挖掘、机器学习等.E-mail:Jsjxhuxg@hfut.edu.cn.

收稿日期: 2021-05-07 接受日期: 2021-07-19
资助项目: 国家自然科学基金项目(No.61976077,62076087,62076085)资助
摘要

领域自适应方法在特征变换过程中对多个度量大多采取静态权重设置,导致方法在不同任务上效果差异较大.为此,文中提出领域自适应任务中的动态参数调整方法.基于再生希尔伯特空间模型,最小化域间可区分性联合概率分布差异,求解域间不变特征空间.在此过程中,依据 A-距离计算域间差异中同类标签和不同类标签分布差异的占比,并以此动态调整可区分性和可迁移性的权重参数,从而达到最优的自适应效果.在3个图像分类数据集上的实验表明文中方法的有效性.

关键词: 领域自适应; 联合概率分布; 动态参数调整; A-距离
中图分类号:TP391
Dynamic Parameter Setting Method for Domain Adaptation
ZHANG Yuhong1,2, YU Daoyuan1,2, HU Xuegang1,2
1. School of Computer Science and Information Engineering, Hefei University of Technology, Hefei 230601
2. Key Laboratory of Knowledge Engineering with Big Data, Mi-nistry of Education, Hefei University of Technology, Hefei 230601
Corresponding author:
ZHANG Yuhong, Ph.D., associate professor. Her research interests include transfer learning and machine learning.

About Author:
YU Daoyuan, master student. His research interests include domain adaptation and machine learning.
HU Xuegang, Ph.D., professor. His research interests include data mining, Web mining and machine learning.

Fund:National Natural Science Foundation of China(No.61976077,62076087,62076085)
Abstract

The performance of domain adaptation methods for different tasks is unstable due to its static weight settings for multiple measures during feature shift process. Therefore, a dynamic parameter setting method for domain adaption is proposed. Reproducing Kernel Hilbert space is introduced to learn the invariant space by minimizing the distance between both domains according to the discriminative joint probability distribution. In this process, A-distance is employed to measure the discrepancy ratio of the same labels to the different labels, and this ratio is utilized to adjust the proportion of transferability and discriminability distributions dynamically. With this dynamic parameter settings, better performance is obtained. Experimental results on three image classification datasets show the effectiveness of the proposed method.

Key words: Key Words Domain Adaptation; Joint Probability Distribution; Dynamic Parameter Setting; A-distance

本文责任编委 苗夺谦

Recommended by Associate Editor MIAO Duoqian

实际应用中标签信息的不足及领域间的分布差异促进领域自适应学习的广泛研究.领域自适应[1, 2, 3]将从标记源域学习到的知识用于辅助不同分布的未标记或部分标记的目标域学习, 广泛应用在图像分类、情绪识别等领域.

领域自适应的核心问题在于如何减少源域和目标域之间的分布差异[4, 5], 其中, 基于特征表示的方法取得较优效果, 这些方法可分为浅层学习和深层学习两类.

浅层学习方法主要使用结构对应学习, 利用源域和目标域间的轴特征提取非轴特征和轴特征之间的潜在关系.Sun等[6]对齐源和目标分布的二阶统计信息, 最大限度地减少域移动, 不需要任何目标域的标签.Chen等[7]提出无监督的领域自适应算法, 将最大平均值差异(Maximum Mean Discrepancy, MMD)引入极端学习机框架中, 保留目标领域的鉴别信息.Gong等[8]基于测地线核方法(Geodesic Flow Kernel, GFK), 构造一条测地线, 使源域靠近目标域.

深度学习方法是基于深度模型和对抗模型以学习域间不变的特征表示.

基于对抗模型的领域自适应方法多通过特征生成器和判别器间的对抗完成特征表示学习.Ganin等[9]提出基于反向传播的无监督领域适应方法(Unsupervised Domain Adaptation by Backpropaga-tion, UDAB), 通过领域分类器和特征抽取器间的博弈学习域不变特征.Glinchant等[10]提出无监督的正则化转移学习方法, 避免过度拟合.Long等[11]设计条件域对抗网络(Conditional Domain Adversarial Networks, CDAN), 根据分类器预测的鉴别信息调整对抗域自适应模型, 通过多线性条件化和分类器预测之间的互协方差提高可分辨性.

基于深度模型的领域自适应方法多基于一个度量标准, 通过域间分布差异的最小化学习不变特征, 完成领域适应.Zhu等[12]提出叠层重构独立分量分析方法(Stacked Reconstruction Independent Com-ponent Analysis, SRICA), 通过KL散度度量域间特征空间分布差异, 并采用softmax回归对源域中数据的标签进行编码.Shen等[13]利用神经网络估计源样本和目标样本间的经验Wasserstein距离, 优化特征提取网络, 使估计的Wasserstein距离达到最优值.Long等[14]提出深度自适应网络, 在再生核希伯尔空间(Reproducing Kernel Hilbert Space, RKHS)中, 基于多核MMD距离, 采用最优多核选择方法进行均值嵌入匹配, 增强特定任务中的特征可传递性, 进一步减小域差异.Deng等[15]提出基于注意力机制的领域适应, 结合鉴别器的概率确定性, 考虑不同区域的概率确定性估计, 获得更好适应的区域.Pan等[16]提出迁移成分分析方法(Transfer Component Analysis, TCA), 使用MMD最小化源域和目标域之间的边缘分布, 减小差异.

此外, 有学者提出多角度结合的域间差异度量方法.Wang等[17]提出多重嵌入式分布比对方法(Manifold Embedded Distribution Alignment, MEDA), 在Grassmann流形中, 基于MMD度量域间边缘和条件联合概率分布的差异, 根据结构风险最小化进行动态分布对齐, 实现领域适应.Long等[18]提出联合最大均方差(Joint MMD, JMMD), 度量联合分布之间的关系, 推广深度神经网络的转移学习能力, 适应不同领域的数据分布.与文献[18]相似, Long等[19]提出联合分布自适应方法(Joint Distribution Adaptation, JDA), 度量边缘分布和条件分布的联合MMD分布差异.随后, Zhang等[20]提出联合概率分布的领域适应方法(Joint Probability Domain Adap-tation, JDPA), 在考虑边缘分布和条件分布迁移性的同时, 利用与标签空间的联合概率分布进行域间差异度量, 进一步提高特征空间的类别区分性.

上述方法在学习领域不变的特征空间过程中大多基于特征空间[4, 12]和标签空间[21], 从边缘分布、条件分布等多个角度, 基于MMD和协方差关系对齐(Correlation Alignment, CORAL)[6]等指标, 使域间差异最小.

然而, 上述方法在考虑多项相似度度量时, 对各项的权重采取静态权重, 而在实际领域自适应任务中, 域间差异性体现在各项度量上的表现是不同的, 静态参数的设置使方法在不同任务上的表现差异较大.因此, 需要考虑多个度量间的动态参数调整策略方法.在已有的工作中, Wang等[22]提出平衡分布适应方法(Balanced Distribution Adaptation, BDA), 强调权重动态调整的重要性, 但仅利用实验中的交叉验证得到最优值, MEDA基于A-距离[16]对边缘分布和条件分布的权重进行动态调整, 未考虑域间可区分性[23]的度量, 在领域差异较大任务中, 适应效果不理想.

在实际应用中, 域间差异性较小, 主要表现为同类标签条件下特征分布不同, 因此, 在这类领域自适应任务中, 需要更多地考虑域间的特征可迁移性表示学习.当域间差异性较大时, 主要表现为不同类标签间的特征分布不相似, 因此领域自适应过程应更多地关注类间的可区分性特征表示学习.

为此, 本文认为领域自适应过程中特征的可迁移性与可区分性的权重与域间的差异性有关, 并基于可区分联合分布的领域自适应框架[20], 设计领域自适应任务中的动态参数调整方法(Dynamic Para-meter Setting Method for Domain Adaptation, DPDA), 动态调整联合概率分布表示中的域间可迁移性与模型可区分性的权重, 实现域间的特征空间动态对齐.在3个图像分类数据集上实验验证本文方法的有效性.

1 领域自适应任务中的动态参数调整方法

给定标记的数据源域Ds和未标记的目标域Dt, 领域自适应的目的是将源领域Ds数据Xs和标签Ys跨领域地使用在目标域中Dt的数据Xt上, 为目标域学习一个高性能的分类器.本文方法综合考虑类间可区分性与域间可迁移性表示, 通过最小化域间分布差异进行领域自适应.在此基础上, 进一步引入自适应参数计算方法, 动态调整类间可区分性与域间可迁移性的权重μ, 使方法在不同任务上都能达到较优效果.

1.1 可区分联合概率分布

基于边缘和条件概率分布度量的领域自适应方法仅考虑域间的可迁移性, 忽略类间的可区分性.而可区分联合概率分布综合类间可区分性和域间可迁移性, 具体表示为

d(Ds, Dt)=Mt-Md,

其中, Mt表示域间可迁移性, Md表示类间可区分性.Mt旨在求解领域间的不变特征表示, 通过最小化两个领域间同类标签的特征分布差异求解表示, 而Md旨在求解更具有类别区分力的特征表示, 提高分类器在目标域的分类性能, 可通过最大化域间不同类标签之间的特征分布距离进行求解.

Mt具体表示为

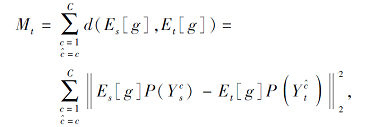
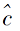
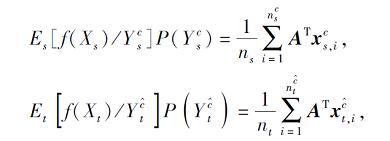
其中, c=1, 2, …, C为源域标签, =1, 2, …, C为目标域标签.设P(Y/X)为类条件概率, P(X)为类先验概率, 则

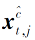
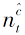
其中, 为源域中同类的特征向量, 为源域中同类的样本数量, 为目标域中同类的特征向量, 为目标域中同类的样本数量, A为对角域指示矩阵,

P(Y sc)=nsc/ns.

由此可得, Mt可表示为

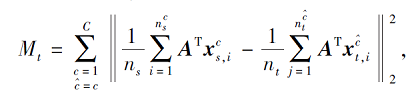
同理可得

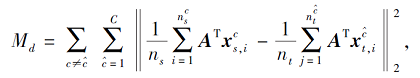
相比MMD, 可直接从数据中计算联合概率分布中的各项, 无需取近似值, 将可区分性纳入差异统计中, 提高迁移的精确性.

1.2 动态的参数自适应计算

可区分联合概率分布在自适应过程中综合考虑同类的可迁移性和类间的可区分性两个度量.面向不同任务时, 自适应任务可根据具体任务的域间分布差异情况, 定量估计每个分布度量的相对重要性, 实现动态调整参数, 达到一个相对较优的结果.

为此, 本文在可区分性联合概率分布基础上, 引入一个自适应因子μ, 权衡类间可区分性Md和域间可迁移性Mt在域间分布差异中所占的权重, 实现自适应动态调整, 即

d(Ds, Dt)=(1-μ)Mt-μ Md.

权重因子μ表示域间可区分性占域间整体分布差异的比例.A-距离[16]是一种广为接受的域间距离的指标, 利用A-距离分别度量两个领域间的同类标签的特征分布和不同类标签的特征分布, 在一定程度上反映域间可迁移性和可区分性差异在整个域间分布差异中的占比.为此, 本文基于A-距离计算权值, 能够在自适应过程中对差异较大的分布进行更多关注和训练, 提高自适应效果.

可迁移性表示源域和目标域中具有相同类标签的数据分布距离, 具体计算过程是将源域和目标域按照标签划分成多个子域, 计算各个子域间的分布差异, 完成不同域条件下相同类标签的特征分布差异, 从而完成域间可迁移性的度量, 计算方法可表示为

Dt(c)=DA(Ds(c), Dt(c)).

这里的域间距离采用A-距离测算.A-距离被定义为建立一个线性分类器以区分两个数据领域的hinge损失.由于目标域是未标记的, 这里使用当前分类器进行预标记, 并以预标记的数据进行相同标签的特征分布差异计算.

而域间总体分布差异的度量表示源域和目标域所有数据之间的A-距离条件分布:

D=DA(Ds, Dt)=2(1-ε(h)),

其中ε(h)为线性分类的hinge损失.因此, 类间可区分性在整个数据分布中的占比可表示为

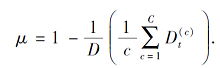
当源域数据和目标域数据总体差异较小, 此时域间的差异更多地表现为同类标签条件下样本的特征表示存在较大差异, 因此在自适应过程中应更多地关注域间同一标签样本的特征表示学习, 即更多地关注域间可迁移性, 此时, 应适当降低μ值.否则, 域间差异较大, 差异性更多地表现为不同类标签的区分差异时, 应更多地关注特征表示的类别区分能力, 适当增大μ值.因此, μ可依据域间分布差异性进行自适应计算.

2 实验及结果分析
2.1 实验环境

本文采用如下3个图像公共数据集进行实验.1)Office-Caltech10数据集[24].包含来自Office环境中Amazon(A)、Webcam(W)、DSLR(D)和Caltech256(C)图像域中的10个对象类别, 每个类别有8~151个样品, 共有2 533幅图像.2)MultiPIE数据集[25].包含68名不同人的41 368幅32× 32人脸图像, 有5个子集:左姿势(C05)、向上姿势(C07)、向下姿势(C09)、正面姿势(C27)、右姿势(C29).在每个子集合(姿势)中, 人脸图像都是在不同的光线、照明和表情下拍摄.随机选择2个子集(姿势), 分别作为源域和目标域, 得到5× 4=20个不同的跨域转移任务.3)COIL数据集.由Xu等[26]发布的随机抽取1 800幅图像的USPS数据集和抽取2 000幅图像的MNIST数据集组成.每个数据集都有10类不同分布的数字数据集.

本文采用如下对比方法.

1)TCA[16].使用MMD在再生核Hilbert空间中学习一些跨域的迁移成分, 利用该子空间中的新表示, 训练源域的分类器并在目标域中使用.

2)JDA[19].经典的联合概率分布算法, 使用静态的联合概率测量两个域的分布差异.

3)BDA[22].对边缘分布和条件分布进行动态处理, 在不同领域中效果更佳.

4)JDPA[20].使用区分性联合概率MMD(Dis-criminative Joint Probability MMD, DJP-MMD)代替域自适应中常用的联合MMD.

5)联合部分优化传输领域适应方法(Joint Partial Optimal Transport for Domain Adaption, JPOT)[26].提出联合部分最优传输, 充分利用标记源域的信息, 还充分利用目标域中未知类的区别性表示.

文中所有对比方法都采用原文献中的方法及参数设置.本文方法(DPDA)采用与JDA、JDPA相同的RKHS及参数设置.子空间维数p=100, 迭代次数T=10.此外, 在Office数据集上, 采用线性内核, 正则化参数λ=1, 而在原始内核(Primal Kernel)数据集MultiPIE和COIL上, 采用原始内核, 正则化参数λ=0.1.所有方法采用1-近邻分类器进行目标域的分类.

另外, 对于Office数据集中的样本向量表示, 首先提取加速健壮特征(Speeded Up Robust Features, SURF)并量化为一个800-bin的直方图, 再通过Z-score进行标准化.对COIL、MultiPIE数据集上的样本向量采用原始特征表示.

2.2 分类精度对比

各方法在3个数据集上的准确率对比如表1~表3所示, 表中黑体数字表示最优结果.

表1 各方法在MultiPIE数据集上的准确率对比 Table 1 Accuracy comparison of different methods on MultiPIE dataset
表2 各方法在Office-Caltech10数据集上的准确率对比 Table 2 Accuracy comparison of different methods on Office-Caltech10 dataset
表3 各方法在COIL数据集上的准确率对比 Table 3 Accuracy comparison of different methods on COIL dataset

由表1~表3可看出, JDA采用边缘条件联合概率分布, DPDA和JDPA采用可区分联合概率分布.相比JDA, DPDA和JDPA的准确率优势表明可区分的联合分布模型比一般的边缘、条件概率联合分布更有利于域自适应任务.相比JDPA, DPDA的平均准确率有所提高, 表明引入动态的自适应参数计算比静态参数设置更有效.相比BDA, 表明动态调整可区分性和可迁移性的方法在准确率上比只考虑可迁移性的算法有所提高.

同时, DPDA在Office-Caltech10数据集上的总体表现差于其余两个数据集.DPDA在Office-Caltech10数据集上有7个任务表现最优, 提升幅度在[0.34%, 8.56%], 5个任务略差, 低于最优效果[0.62%, 1.78%].总之, DPDA在Office-Caltech10数据集上是有效的.对照各个数据集可见, DPDA在MultiPIE数据集上的优势较明显, 而在Office-Caltech10数据集的部分任务上效果不明显.

为了进一步分析原因, 选取Office-Caltech10数据集上性能较差的Caltech 256-Amazon任务和MultiPIE性能较优的C05-C07进行可视化, 结果如图1和图2所示.

图1 各方法在MultiPIE数据集C05~C07任务上的可视化结果Fig.1 Visualization of different methods for C05~C07 on MultiPIE dataset

图2 各方法在office-Caltech10数据集Caltech 256-Amazon任务上的可视化结果Fig.2 Visualization of different methods for Caltech 256-Amazon on office-Caltech10 dataset

由图1和图2可得如下结论.在两个任务中, JPDA和DPDA都能学习到较好的特征表示以进行领域适应.具体地, 相比原始特征空间, JPDA和DPDA学习后的特征空间中源域和目标域的特征表示趋向重叠, 表明可迁移性特征表示学习具有一定效果.同时, 两种方法自适应后的特征空间不同类标签的分布距离较远, 表明可区分性表示学习的有效性.图2中Office-Caltech10数据集的Caltech 256-Amazon任务原始特征空间中各类标签之间的区分不明显, DPDA在进行类区分力的调整时难以较好地计算相应的域间距离和有效的动态调整, 导致性能略差于静态的JPDA.同时, 这也是DPDA在Office-Caltech10数据集上效果不如MultiPIE数据集效果的原因.

2.3 自适应参数计算的有效性

领域差异较大和较小的领域自适应任务效果随μ值的变化情况如图3所示.由图可见, 分类精度随μ的不同而变化, μ=0时, 表示领域自适应过程仅关注域间可迁移性而不关注类内可区分性, 随着μ值增大, 准确率有所提升, 但μ值过大时, 表示领域适应过程过于关注类内可区分性而忽略域间可迁移性, 准确率随之下降.

图3 域间差异不同时准确率随μ值的变化曲线Fig.3 Curve of accuracy changing with μ under different distances between domains

DPDA根据域间差异自适应计算μ值, 计算结果接近手动调参的最优值.如(b)中COIL2-COIL1任务, DPDA计算的μ值为0.16, 与最优调参结果0.2较接近, 准确率也接近最优值.

由此可见, DPDA依据域间差异性自适应计算参数是有效的.

在域间差异较大, 多表现为类间可区分性差异时, DPDA中μ> 0.2; 而在域间差异较小, 多表现为域间可迁移性差异时, DPDA中μ∈ [0.1, 0.2].由此可见, 域间差异较大时, 应更关注类内可区分性, 而域间差异较小时, 应更关注域间可迁移性.由此验证DPDA的有效性.

3 结束语

本文提出领域自适应的动态参数调整方法.基于区分性联合概率分布, 考虑不同领域适应任务的差异性, 提出依据领域差异动态调整区分性联合概率分布中的域间可迁移性和类内可区分性的比例, 进一步提高域自适应的性能.在图像数据集上证实本文方法的有效性.今后将进一步研究适应于对抗学习模型的度量方法以获得更佳的参数调整效果.

参考文献
[1] TAN C Q, SUN F C, KONG T, et al. A Survey on Deep Transfer Learning // Proc of the 27th International Conference on Artificial Networks. Berlin, Germany: Springer, 2018: 270-279. [本文引用:1]
[2] PAN S J, YANG Q. A Survey on Transfer Learning. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. [本文引用:1]
[3] 庄福振, 罗平, 何清, 等. 迁移学习研究进展. 软件学报, 2015, 26(1): 26-39.
(ZHUANG F Z, LUO P, HE Q, et al. Survey on Transfer Learning Research. Journal of Software, 2015, 26(1): 26-39). [本文引用:1]
[4] TZENG E, HOFFMAN J, SAENKO K, et al. Adversarial Discriminative Domain Adaptation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 2962-2971. [本文引用:2]
[5] LONG M S, WANG J M, DING G G, et al. Adaptation Regularization: A General Framework for Transfer Learning. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1076-1089. [本文引用:1]
[6] SUN B C, FENG J S, SAENKO K. Return of Frustratingly Easy Domain Adaptation // Proc of the 30th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2016: 2058-2065. [本文引用:2]
[7] CHEN Y M, SONG S J, LI S, et al. Domain Space Transfer Extreme Learning Machine for Domain Adaptation. IEEE Transactions on Cybernetics, 2019, 49(5): 1909-1922. [本文引用:1]
[8] GONG B Q, SHI Y, SHA F, et al. Geodesic Flow Kernel for Unsupervised Domain Adaptation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2012: 2066-2073. [本文引用:1]
[9] GANIN Y, LEMPITSKY V. Unsupervised Domain Adaptation by Backpropagation // Proc of the 32nd International Conference on Machine Learning. New York, USA: ACM, 2015: 1180-1189. [本文引用:1]
[10] CLINCHANT S, CSURKA G, CHIDLOVSKII B. A Domain Adaptation Regularization for Denoising Autoencoders // Proc of the 54th Annual Meeting of the Association for Computational Linguistics(Short Papers). Stroudsburg, USA: ACL, 2016, II: 26-31. [本文引用:1]
[11] LONG M S, CAO Z J, WANG J M, et al. Conditional Adversarial Domain Adaptation // Proc of the 32nd Annual Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 1647-1657. [本文引用:1]
[12] ZHU Y, HU X G, ZHANG Y H, et al. Transfer Learning with Stacked Reconstruction Independent Component Analysis. Know-ledge-Based Systems, 2018, 152: 100-106. [本文引用:2]
[13] SHEN J, QU Y R, ZHANG W N, et al. Wasserstein Distance Guided Representation Learning for Domain Adaptation[C/OL]. [2021-04-12]. https://export.arxiv.org/pdf/1707.01217 [本文引用:1]
[14] LONG M S, CAO Y, CAO Z J, et al. Transferable Representation Learning with Deep Adaptation Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(12): 3071-3085. [本文引用:1]
[15] DENG H L, ZHANG L, SHU X. Feature Memory-Based Deep Recurrent Neural Network for Language Modeling. Applied Soft Computing, 2018, 68: 432-446. [本文引用:1]
[16] PAN S J, TSANG I W, KWOK J T, et al. Domain Adaptation via Transfer Component Analysis. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210. [本文引用:4]
[17] WANG J D, FENG W J, CHEN Y Q, et al. Visual Domain Adaptation with Manifold Embedded Distribution Alignment // Proc of the 26th ACM International Conference on Multimedia. New York, USA: ACM, 2018: 402-410. [本文引用:1]
[18] LONG M S, ZHU H, WANG J M, et al. Deep Transfer Learning with Joint Adaptation Networks // Proc of the 34th International Conference on Machine Learning. New York, USA: ACM, 2017: 2208-2217. [本文引用:]
[19] LONG M S, WANG J M, DING G G, et al. Transfer Feature Learning with Joint Distribution Adaptation // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2013: 2200-2207. [本文引用:2]
[20] ZHANG W, WU D R. Discriminative Joint Probability Maximum Mean Discrepancy(DJP-MMD) for Domain Adaptation [C/OL]. [2021-04-12]. https://arxiv.org/pdf/1912.00320.pdf [本文引用:]
[21] 应文豪, 王士同, 邓赵红, 等. 基于类分布的领域自适应支持向量机. 自动化学报, 2013, 39(8): 1273-1288.
(YING W H, WANG S T, DENG Z H, et al. Support Vector Machine for Domain Adaptation Based on Class Distribution. Acta Automatica Sinica, 2013, 39(8): 1273-1288. ) [本文引用:]
[22] WANG J D, CHEN Y Q, HAO S J, et al. Balanced Distribution Adaptation for Transfer Learning // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2017: 1129-1134. [本文引用:]
[23] KURMI V K, KUMAR S, NAMBOODIRI V P. Attending to Discriminative Certainty for Domain Adaptation // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 491-500. [本文引用:]
[24] GRIFFIN G, HOLUB A, PERONA P. Caltech-256 Object Category Dataset[DB/OL]. [2021-04-12]. https://authors.library.caltech.edu/7694/1/CNS-TR-2007-001.pdf [本文引用:]
[25] GROSS R, MATTHEWS I, COHN J F, et al. Multi-PIE // Proc of the 8th IEEE International Conference on Automatic Face and Gesture Recognition. Washington, USA: IEEE, 2008. DOI: DOI:10.1109/AFGR.2008.4813399. [本文引用:]
[26] XU R J, LIU P L, ZHANG Y, et al. Joint Partial Optimal Transport for Open Set Domain Adaptation // Proc of the 29th International Joint Conference on Artificial Intelligence. Cambridge, USA: Morgan Kaufmann, 2020: 2540-2546. [本文引用:]