张 永,博士,教授,主要研究方向为数据挖掘、智能计算.E-mail:zhyong@lnnu.edu.cn.
作者简介:

夏天琦,硕士研究生,主要研究方向为机器学习、智能计算.E-mail:tancy_x@163.com.

黄 丹,博士,讲师,主要研究方向为数据挖掘、模式识别.E-mail:hdsy@sina.com.
当域之间差异较大时,域适应的迁移效果较差.缩小域差可改善迁移效果,但却忽略后期分类时的可区分性.因此,文中提出基于无监督域适应的可区分联合匹配算法,根据域间类别的不同进行差异化处理,并结合特征匹配和实例重加权提高迁移效果.使用联合概率分布作为域之间数据分布差异的度量,缩小相同类域之间的距离,提高迁移性;扩大不同类域之间的距离,提高区分性.在特征降维的过程中联合特征匹配和实例重加权,共同构造特征变换矩阵.实验表明,文中算法在18组任务上的分类效果较优.
ZHANG Yong, Ph.D., professor. His research interests include data mining and intelligent computing.
About Author:
XIA Tianqi, master student. Her research interests include machine learning and intelligent computing
HUANG Dan, Ph.D., lecturer. Her research interests include data mining and pa-ttern recognition.
The transfer effect of domain adaption is poor due to the large differences between domains. It can be improved by reducing the domain difference. However, the discriminability of later classification is ignored. A discriminative joint matching algorithm is proposed to handle this problem. Differentiation treatments are conducted according to different categories between domains. Feature matching and instance reweighting are combined to improve the migration effect. The joint probability distribution is employed to measure the difference of data distribution between domains. The transferability is enhanced by reducing the distance between the same domains. The discriminability is improved by expanding the distance between different domains. Feature matching and instance weighting are combined in the process of feature dimensionality reduction to jointly construct a feature transformation matrix. The experimental results show that the classification result of the proposed algorithm on 18 tasks is better.
本文责任编委 高 阳
Recommended by Associate Editor GAO Yang
传统的机器学习技术已取得较大成功, 但对于某些现实世界的场景仍存在一定局限性[1].例如, 随着网络的迅速发展, 在线图像和视频呈指数级增长, 对图像和其它多媒体数据的自动识别及分析技术产生巨大需求.然而, 在新的视觉领域中有标签的图像数量仍较稀少, 获取足够的有标签的数据以训练机器学习模型通常是昂贵、耗时的, 甚至是不现实的[2].迁移学习(Transfer Learning, TL)就是在这种情况下产生的.TL利用一些已有、拥有丰富标签的源域样本帮助新的目标域学习, 是一种解决跨领域学习的有效方法, 已广泛应用于医学图像处理[3]、情感识别[4]、脑机接口[5]等领域.
由于来自不同的领域, 源域数据和目标域数据的概率分布往往不同.因此, 现有的迁移学习方法主要集中于如何减少域之间数据分布的差异, 即域适应(Domain Adaptation, DA)[1, 6]方法.现有的域适应方法主要分为2类:特征匹配和实例重加权.
特征匹配的目的是发现一种共享的特征子空间, 可在减少域间不同分布差异的同时保留数据的重要属性, 一般最小化不同域的边缘概率分布[7]、条件概率分布[8]、联合概率分布[9, 10]之间的最大均值差异(Maximum Mean Discrepancy, MMD)[11], 或利用几何结构在子空间中实现分布对齐[2].Pan等[7]提出缩小边缘概率分布的迁移成分分析方法(Transfer Component Analysis, TCA).Long等[8]结合边缘概率分布和条件概率分布, 提出联合分布自适应方法(Joint Distribution Adaptation, JDA).JDA广泛应用于后期DA的改进中, 如对不同概率分布的权重进行自调整的均衡分布自适应方法(Balanced Distribution Adaptation, BDA)[12], 分开考虑类间及类内分布的联合概率分布自适应方法(Joint Proba-bility Distribution Adaptation, JPDA)[9].
实例重加权是根据某种技术对源域的实例重新赋予权重, 利用加权后的源域实例训练分类器以实现最小化分布差异, 通常使用核均值匹配(Kernel Mean Matching, KMM)[13]、KL重要性估计过程(Kullback-Leibler Importance Estimation Procedure, KLIEP)[14]等估计源域实例在损失函数中的权重, 或通过迭代机制调整负迁移实例权重[15].然而, 基于单一的特征匹配或实例重加权方法, 当面临两个域之间的差异较大时, 迁移效果不够理想.因此, Long等[16]联合特征匹配和实例重加权两种方法, 提出迁移联合匹配(Transfer Joint Matching, TJM), 仅考虑数据在边缘概率上的分布, 忽略数据类别的不同, 导致对于边缘概率相差不大的任务, 迁移效果不佳.
为了更好地结合特征匹配与实例重加权, 本文提出基于无监督域适应的可区分联合匹配算法(Discriminative Joint Matching for Unsupervised Do-main Adaption, DJM).使用联合概率分布作为域之间数据分布差异的度量, 减少不同域中相同类别的分布距离, 提高域的迁移性.增加不同域中不同类别的分布距离, 提高后期分类时的区分性, 并在寻找共享特征时结合l2, 1范式进行实例重加权.在USPS、MNIST、Semeion、Office、Caltech、COIL20数据集上构建18组跨领域迁移任务, 实验表明, DJM的分类准确率有所提高.
本文工作涉及特征匹配和重加权两方面.在特征匹配中, 如何有效地度量域之间的分布差异一直是个重要问题, 两个域之间的差异通常使用联合概率分布P(X, Y)或P(Y|X)P(X)、P(X|Y)P(Y)表示, 而度量方法通常采用MMD[11]:
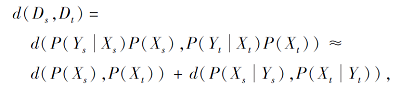
其中, Ds表示源域, Dt表示目标域, d表示MMD度量.
MMD将联合概率分为P(X|Y)+P(X), 使用类条件分布P(X|Y)预估后验概率分布P(Y|X), 忽略P(Y|X)、P(X)之间的依赖性, 造成多次近似估计.因此, Zhang等[17]提出联合概率判别MMD(Discriminative Joint Probability MMD, DJP-MMD), 利用P(X|Y)P(Y)联合概率分布直接进行计算, 将数据分为相同类和不同类:
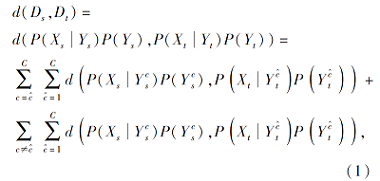
其中, c表示源域类别,
重加权方法一般分为两类:对相关特征的重新加权[18]和对源域实例的重新加权[19].特征加权通常和特征匹配结合, 在降维过程中联合执行, 而在训练分类器时使用较多的实例重加权.TJM[16]将特征选择用于实例重加权, 实现与特征匹配结合.
给定源域
Ds={(xs, 1, ys, 1), (xs, 2, ys, 2), …, (xs, n, ys, n)},
有n个带标签的源域样本xs, 目标域
Dt={xt, 1, xt, 2, …, xt, m}
有m个不带标签的样本xt, x∈X, y∈Y, X为一个特征空间, Y为一个标签空间.假设源域和目标域的特征空间和标签空间相同, 即Xs=Xt, Ys=Yt, 属于同质迁移学习, 但它们的边缘、条件及联合概率分布都不同.迁移学习的目标是利用源域Ds为目标域Dt学习标签yt.
迁移学习的域适应方法通常是将源域和目标域映射到一个相同的子空间内, 利用降维的方法学习它们的特征变换矩阵, 常用的降维方法是主成分分析(Principal Component Analysis, PCA)[20].假设
X=[xs, xt]
为由源域和目标域数据组成的输入矩阵, I∈ R(n+m)× (n+m)为单位矩阵,
H=I-
为中心矩阵, 协方差矩阵可表示为XHXT.PCA的目标是通过
找到一个正交变换矩阵A∈ R(n+m)× k, 使数据在降维过程中的方差最大, 从而保留更多的数据信息.其中, k为降维后的维度, tr(· )为矩阵的迹.
本文提出基于无监督域适应的可区分联合匹配算法(DJM).首先最小化源域与目标域的相同类的类内距离, 提高域的可迁移性, 完成跨域特征匹配.然后最大化不同类的类间距离, 提高分类时的可区分性.最后通过结构化稀疏性对源域实例进行重加权.目标函数如下:
其中, μ> 0, λ> 0, 为2个权重参数, ‖ · ‖ 2, 1为l2, 1范式, dT为相同类之间的距离, dF为不同类之间的距离, A为特征变换矩阵.通过降维使源域和目标域的特征更匹配.
2.4.1 类内距离
在传统的迁移学习中, 常用MMD测量两个域之间的分布差异, 采用的分布一般是边缘分布和条件分布的近似结合.本文采用基于DJP-MMD[17]的联合概率分布, 这样两个域之间的距离可根据式(1)表示为
d(Ds, Dt)=d(P(xs|ys)P(ys), P(xt|yt)P(yt)),
相同类之间的距离表示为
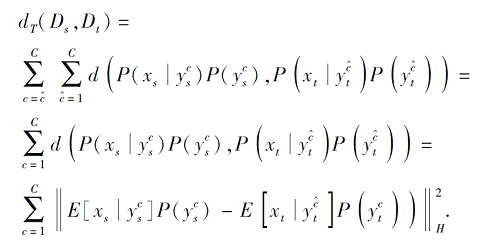
其中:c=1, 2, …, C为源域的标签集合, 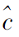
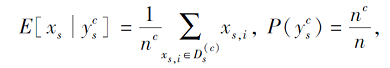
xs, i表示源域的第i个样本,
表示源域中c类样本的集合, nc=|
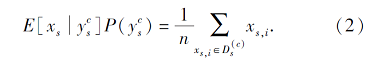
同样, 目标域部分可表示为
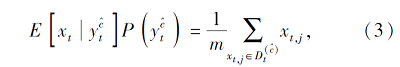
其中, xt, j表示目标域的j个样本,
表示目标域中c类样本集合.
整合式(2)和式(3)可得到dT, 再利用PCA[20]对其进行矩阵化, 可得

其中,
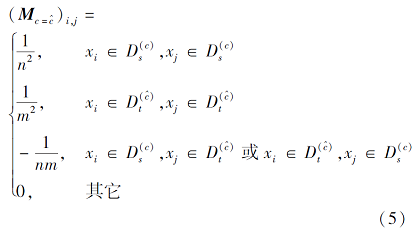
2.4.2 类间距离
源域和目标域中不同类之间的距离dF根据DJP-MMD可表示为
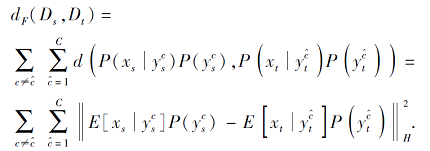
与dT类似, 将上式拆解后整理, 可得到新的dF计算方法, 再利用矩阵技巧对其进行变化, 可得
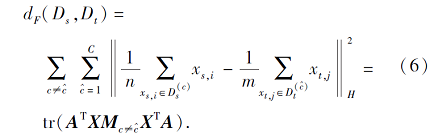
和式(4)类似, 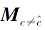
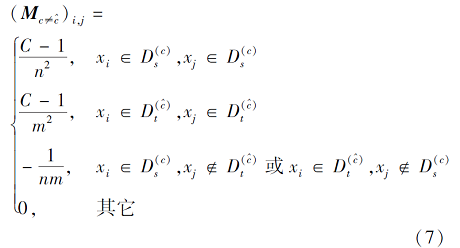
常见的实例重加权方法包括核均值匹配[13]、样本选取[19]和对负迁移实例重加权[15].但这些方法仅是单纯的实例重加权, 如何将它们与特征匹配统一以获得更优性能还没有一个较好的解决方案.本文对变换矩阵A使用l2, 1-norm结构稀疏正则化器[21], 将行稀疏性引入变换矩阵A中, 因为矩阵的每行都对应一个实例, 因此行稀疏性从本质上实现实例重加权, 其表现形式如下:
‖As‖ 2, 1+‖At‖ .(8)
值得注意的是:1)本文只针对源域的实例进行重加权, 对于目标域的实例采用正则化处理; 2)为了提高目标域伪标签的准确性, 本文采用迭代优化操作.具体地说, 就是在每次迭代中执行DJM.再利用特征转换过的实例Z=ATX训练分类器, 基于训练好的分类器更新目标域的伪标签.然后, 使用更新后的伪标签重复执行DJM, 直至收敛.在这个过程中, 特征转换矩阵A在不断地变化, ‖As‖ 2, 1+‖At‖ 也随之变化.利用这种正则化形式, DJM对相关实例的迁移更高效, 对不相关实例引起的域差异更鲁棒.
本文算法有3个目标:1)最小化源域与目标域中相同类之间的距离; 2)最大化源域和目标域中不同类之间的距离; 3)对变换矩阵进行实例重加权.根据上述分析, 本文结合式(4)、式(6)和式(8), 得到DJM的目标函数:
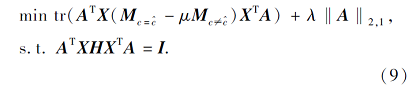
上式利用拉格朗日乘子法进行优化, 可得
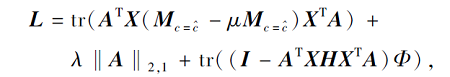
其中Φ={φ1, φ2, …, φ k}为拉格朗日乘子.
对L求偏导, 并令∂L/∂A=0, 优化问题可转换成一个求广义特征值分解问题:
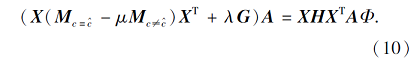
求解式(10), 可得到特征变换矩阵A和k个特征向量.在式(10)中, G为一个单位对角矩阵, 由 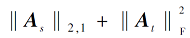
gii=
当xi∈Dt时, 保持单位对角矩阵不变[16].
对非线性情况, 可将核映射ψ:x|→ψ(x)应用到X上, 表示为
K=ψ(X)Tψ(X)∈ R(n+m)× (n+m),
核映射可利用线性核或高斯核构造.目标函数(9)可改写为
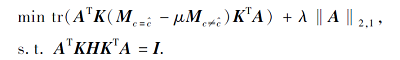
优化方法类似.
本文算法步骤如下.
算法1 DJM
输入 源域特征矩阵Xs, 目标域特征矩阵Xt,
源域标签ys, 子空间维度k, 权衡参数μ,
正则化参数λ, 迭代次数T
输出 特征转换矩阵A, 分类器f在基分类器上训练Xs, 并用于预测Xt得到伪标签 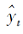
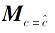
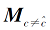
Repeat
求解式(10)中的广义特征值分解问题, 并采用k
个特征向量构建矩阵A
利用{ATXs, ys}训练分类器f
更新目标域的伪标签 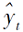
利用式(5)、式(7)和式(11)更新矩阵 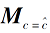
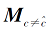
Until 收敛
Return 分类器f
本文使用6个广泛应用的数据集USPS、MNIST、Semeion[22]、Office[23]、Caltech、COIL20, 构造18组不同的迁移任务, 数据集的具体描述如表1所示.
| 表1 实验数据集 Table 1 Experimental datasets |
USPS、MNIST、Semeion为3个通用的手写体识别数据集, 广泛应用于机器学习算法评测的各方面.USPS数据集包括7 291幅训练图像和2 007幅测试图像, 图像大小为16× 16.MNIST数据集包括60 000幅训练图像和10 000幅测试图像, 图像大小为28× 28.Semeion数据集包括1 593幅图像, 图像大小为16× 16.3个数据集分别服从不同的概率分布, 包含10个类别, 每个类别是1~10之间的某个数.本文选取USPS中任意1 800幅图像、MNIST中任意2 000幅图像和Semeion中全部图像进行实验.
Office数据集由3个现实世界的对象域组成:Amazon, Webcam, DSLR, 包含4 652幅图像和31个类别.Caltech数据集是用于对象识别的标准数据库, 包含30 607幅图像和256个类别.Office、Caltech数据集上有10个通用的类别, 因为Office、Caltech数据集上对象遵循不同的分布, 可用领域自适应实现跨域识别.本文采用Office-10+Caltech-10的数据集进行实验.
COIL20数据集包含20个对象类别, 共1 440幅图像, 每个对象类别包括72幅图像, 每幅图像拍摄时对象水平旋转5° (共360° ).每幅图像大小为32× 32, 表征为1 024维的向量.实验中将该数据集划分为2个不相交的子集COIL1和COIL2.COIL1数据集包括位于拍摄角度为[0° , 85° ]∪ [180° , 265° ](第一、三象限)的所有图像, COIL2包括拍摄角度为[90° , 175° ]∪ [270° , 355° ](第二、四象限)的所有图像.子集COIL1、COIL2的图像因为拍摄角度不同服从不同的概率分布.
本文采用如下7种对比算法:1 Nearest Neighbor Classifier(1NN), Transfer Component Ana-lysis(TCA)+1NN, Transfer Joint Matching(TJM)+1NN, JDA+1NN, BDA+1NN, Easy Transfer Learning(EasyTL), JPDA+1NN.
1NN为传统机器学习中常用算法, 除了EasyTL[24], 其它算法都是基于1NN进行分类.EasyTL不使用通用分类器, 根据数据到类中心点的距离进行分类, BDA[12]、EasyTL[24]、JPDA[9]都是近期提出的迁移学习算法.
为了更公平合理地进行对比, 实验中TCA、JDA、BDA的最优参数根据文献[12]设置, TJM、JPDA的参数根据文献[9]和文献[16]设置, EasyTL无需设置参数.
实验涉及到的参数如下:降维后的特征维度k, 类内距离和类间距离之间的权衡参数μ, 实例重加权的权重参数λ .在本文实验中, 都使用线性核函数, 迭代次数T=10, 其中Office-10+Caltech-10数据集上参数设置为k=30, λ=1, μ=0.3.USPS+MNIST、USPS+Semeion、COIL2数据集上参数设置为k=30, λ=1, μ=0.05.
本文将分类器对目标域Dt分类的准确率作为评价标准:
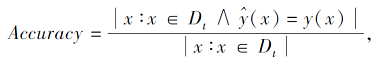
其中, 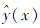
根据表1, 本文构造18组学习任务.根据数据集的不同属性, 划分为3类:1~4组学习任务基于手写数字数据集; 5~6组学习任务基于COIL20数据集; 7~18组学习任务基于Office数据集.
各算法在18组学习任务上的迁移准确率如表2所示, 表中黑体数字表示最优结果.由表可知, DJM在大部分任务上准确率最优, 平均准确率达到58.13%, 比传统机器学习算法(1NN)提高15.75%, 比BDA提高4.43%.
| 表2 各算法在18组任务上的迁移准确率 Table 2 Transfer accuracy of different algorithms on 18 tasks % |
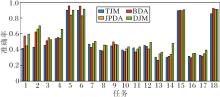
为了更直观地进行观察, 将TJM、BDA、JPDA、DJM在18组任务上的结果进行可视化处理(TCA、JDA可看成特殊的BDA), 结果如图1所示.
在18组任务上, DJM在11组任务上最优, 在剩余7组任务上虽未取得最优效果, 但也有较好表现.COIL20数据集为分割图像, 无法获取整幅图像完整的信息, 使用联合概率分布则显劣势, 故使用联合概率分布的JPDA与DJM在此表现都不突出, 但相比JPDA, DJM结合实例重加权, 在另一方面弥补不足, 迁移效果相对较佳.由此可看出DJM在各类图像数据集上的有效性和鲁棒性.
相比同样进行实例重加权的TJM, DJM在所有任务上的表现更佳.针对领域自适应问题, TJM仅考虑减少两个域之间的边缘概率分布, 而不考虑条件概率分布和联合概率分布的情况, 所以在一些边缘分布相差不大, 而条件分布有显著差异的数据集上, TJM并不能获得较好结果.
与之不同的是, DJM不仅考虑边缘和条件结合的联合概率分布情况, 还更分开处理相同类别和不同类别的联合概率分布.由实验结果可看出, 在域自适应时, 考虑联合概率分布优于仅考虑边缘概率分布.
BDA和JPDA在18组任务上的表现基本相当, 但不如DJM.BDA减少源域和目标域之间的边缘概率分布和条件概率分布的差异, 实现领域自适应; JPDA减少相同类(增加不同类)联合概率分布, 实现领域自适应.
不同于BDA和JPDA, DJM不仅综合考虑源域和目标域之间的分布不同, 更对源域实例进行重加权, 提高对不相关实例迁移的鲁棒性.
为了进一步验证DJM的优越性, 引入弗里德曼检验(Friedman Test)方法[25].该方法通过重复测量ANOVA的非参数等价物, 对不同算法在同个数据集上的结果进行排序, 最后得到不同算法在所有数据集上的平均等级.取值越低, 等级越高.Fried-man检验结果如下:1NN为6.83, TCA为4.86, TJM为4.92, JDA为4.64, BDA为4.17, EasyTL为5.08, JPDA为3.58, DJM为1.92.由此可知, DJM数值最低, 等级最高.
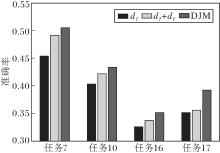
DJM主要涉及3部分:相同类分布dT、不同类分布dF、实例重加权.为了验证各部分的重要性, 随机选取4组任务进行消融实验, 结果如图2所示.仅考虑dT部分的准确率最低, 随着dF和实例重加权的加入, 每个任务的准确率逐步递增.以任务7和任务17为例, 可明显看出dF和实例重加权的重要性, 都能大幅提升DJM的准确率.由此证实3部分在DJM中都必不可少.
本文选用任务7~任务9、任务14、任务15、任务18共6组迁移任务, 验证T, k, λ, μ在DJM中的敏感性.
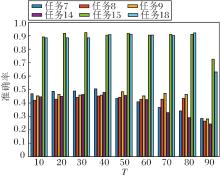
首先是对于算法收敛性的分析.保持其它参数值不变, 令T=1, 2, …, 20.T对准确率的影响如图3所示.由图3可看出, 算法的收敛速度很快, 在大部分任务上, 仅迭代5次, 准确率就趋于稳定.但在任务9上有轻微浮动.
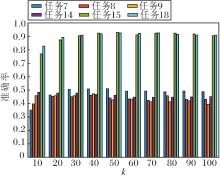
再分析特征变换矩阵A的维度k.令k=10, 20, …, 100, k对准确率的影响如图4所示.任务9和任务14在维度较低时表现较优, 维度越大反而结果越差.任务8受维度影响明显, 而其它任务在低维时的表现都较差, 维度较大时趋于稳定.当k=30, 40时, 所有任务表现都较优, 由此可看出变换矩阵A的重要性.
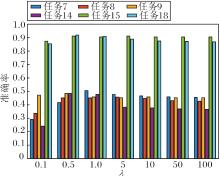
权重参数λ对准确率的影响如图5所示.λ∈ [0.5, 1]时效果最佳.当λ< 0.5时, 实例重加权在迁移时的效果很弱, 由此得到的结果也不令人满意.当λ> 1时, 实例重加权的权重过大, 特征迁移的效果较弱.从λ的变化可明显看出, 只有当特征迁移与实例重加权重要性相当时才能得到最佳结果.
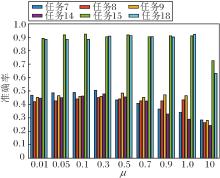
μ表示增强分类时的可区分性的权重参数, μ对准确率的影响如图6所示.由图可看出, μ∈ [0.01, 0.7], DJM较鲁棒, 当μ> 1时, 准确率开始明显下降, 故在实验中不能仅单一增强可区分性, 还应注意与迁移性的平衡.
本文提出基于无监督域适应的可区分联合匹配算法(DJM).算法不仅将特征匹配和实例重加权在降维过程中联合匹配, 还分开考虑迁移过程中相同类和不同类的迁移措施, 减少相同类之间的距离, 提高迁移性, 增加不同类之间的距离, 提高区分性.在多个任务上的实验表明, DJM在迁移效果和分类准确性上较优, 参数在一定范围之内较鲁棒.如何针对不同的任务自适应调整参数的取值及如何将其扩展到多源, 从而进一步应用于别的研究领域, 是下一步需要研究的方向.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|