引用本文
代磊超, 冯林, 尚兴林, 苏菡, 龚勋. 基于深度网络的快速少样本学习算法. 模式识别与人工智能, 2021,34(10): 941-956
DAI Leichao, FENG Lin, SHANG Xinglin, SU Han, GONG Xun. Fast Few-Shot Learning Algorithm Based on Deep Network. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(10): 941-956.  
Doi: 10.16451/j.cnki.issn1003-6059.202110007
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于深度网络的快速少样本学习算法
代磊超1, 冯林1, 尚兴林1, 苏菡1, 龚勋2
1.四川师范大学 计算机科学学院 成都 610101
2.西南交通大学 计算机与人工智能学院 成都 611756
通讯作者:

冯 林,博士,教授,主要研究方向为机器学习、数据挖掘.E-mail:fenglin@sicnu.edu.cn.

作者简介:

代磊超,硕士研究生,主要研究方向为计算机视觉、模式识别.E-mail:daileichao@gmail.com.

尚兴林,硕士研究生,主要研究方向为机器学习.E-mail:1250919363@qq.com.

苏 菡,博士,教授,主要研究方向为模式识别、图像处理.E-mail:jkxy_sh@sicnu.edu.cn.

龚 勋,博士,教授,主要研究方向为计算机视觉、模式识别、医学图像处理.E-mail:xgong@swjtu.edu.cn.

收稿日期: 2021-07-26 接受日期: 2021-10-19
资助项目: 国家自然科学基金项目(No.61876158)、中央高校基本科研业务费科技创新项目(No.2682021ZTPY030)资助
摘要

少样本学习方法模拟人类从少量样本中学习的认知过程,已成为机器学习研究领域的热点.针对目前少样本学习迭代过程的任务量较大、过拟合现象严重等问题,文中提出基于深度网络的快速少样本学习算法.首先,利用核密度估计和图像滤波方法向训练集加入多种类型的随机噪声,生成支持集和查询集.再利用原型网络提取支持集和查询集图像特征,并根据Bregman散度,以每类支持集支持样本的中心点作为类原型.然后,使用L2范数度量支持集与查询图像的距离,利用交叉熵反馈损失,生成多个异构的基分类器.最后,采用投票机制融合基分类器的非线性分类结果.实验表明,文中算法能加快少样本学习收敛速度,分类准确率较高,鲁棒性较强.

关键词: 深度网络; 少样本学习; Bregman散度; 度量学习
中图分类号:TP391.4
Fast Few-Shot Learning Algorithm Based on Deep Network
DAI Leichao1, FENG Lin1, SHANG Xinglin1, SU Han1, GONG Xun2
1. College of Computer Science, Sichuan Normal University, Chengdu 610101
2. School of Computing and Artificial Intelligence, Southwest Jiaotong University, Chengdu 611756
Corresponding author:
FENG Lin, Ph.D., professor. His research interests include machine learning and data mining.

About Author:
DAI Leichao, master student. His research interests include computer vision and pattern recognition. SHANG Xinglin, master student. Her research interests include machine learning.
SU Han, Ph.D., professor. Her research interests include pattern recognition and image processing.
GONG Xun, Ph.D., professor. His research interests include computer vision, pa-ttern recognition and medical image proce-ssing.

Fund:National Natural Science Foundation of China(No.61876158), Fundamental Research Funds for the Central Universities(No.2682021ZTPY030)
Abstract

The cognitive process of the few-shot learning method simulating human learning from a small number of samples is one of the hotspots in the machine learning field. To solve the problems of large task volume and serious overfitting in the iterative process of the current few-shot learning methods, a fast few-shot learning algorithm based on deep network is proposed. Firstly, the kernel density estimation and image filtering methods are utilized to add multiple types of random noise to the training set to generate support sets and query sets. Then, the prototype network is applied to extract the image features of the support set and query set. According to the Bregman divergence, the center point of the support sample of each type of support set is employed as the class prototype. Then, the L2 norm is utilized to measure the distance between the support set and the query image. Multiple heterogeneous base classifiers are generated using cross-entropy feedback loss. Finally, the voting mechanism is introduced to fuse the nonlinear classification results of the base classifiers. Experiments show that the proposed algorithm speeds up the convergence of few-shot learning with higher classification accuracy and strong robustness.

Key words: Key Words Deep Network; Few-Shot Learning; Bregman Divergence; Metric Learning

本文责任编委 杨明

Recommended by Associate Editor YANG Ming

近年来, 大量标记数据用于机器学习的训练以及强大的硬件提供计算资源, 使机器学习尤其是深度学习领域发展迅速.然而, 数据样本的搜集、处理和标注过程耗费众多的人力物力, 这些问题限制机器学习良好的发展态势.因此, 只需少量标记样本就能达到较优的识别效果, 并且可在很少的训练迭代次数下, 快速学习并达到较高识别率的少样本学习(Few-Shot Learning)[1]越来越受到人们的关注.

少样本学习发展到现在, 已取得许多研究成果.现有的基于深度神经网络的少样本学习算法主要分为基于元学习(Meta-Learning)的少样本学习算法、基于数据增强学习(Data Augmentation)的少样本学习算法和基于度量学习(Metric Learning)的少样本学习算法.

基于元学习的少样本学习算法目标是训练元模型, 使其可在多种不同学习任务上达到较好表现.Finn等[2]提出模型无关元学习(Model-Agnostic Meta-Learning, MAML), 迭代步骤较少、泛化性能较优, 模型简单, 无需关心模型形式, 直接利用梯度下降就可训练.Li等[3]提出元随机梯度下降优化器(Meta-stochastic Gradient Descent, Meta-SGD), 可学习更新方向和学习速率, 在每个任务中进行有效学习.Liu等[4]提出传导传播网络(Transductive Propagation Network, TPN), 利用标签传播应对数据较少的问题.

基于数据增强学习的少样本学习算法是对数据集采取平移、旋转等操作, 或利用生成模型生成更大的数据集参与训练.Zhang等[5]提出元生成对抗网络(Meta Generative Adversarial Network, MetaGAN), 为特定任务生成样本, 增加训练数据.

基于度量学习的少样本学习算法模拟样本之间距离分布, 度量样本之间的相似性, 达到分类目的.Gregory等[6]提出卷积孪生网络(Convolutional Siamese Nets), 由两个结构相同且权值共享的子网络组成, 使用两个输入映射的特征向量之间的“ 距离” 作为判别差异的表示, 每次需要输入两个样本作为样本对, 计算损失.匹配网络(Matching Net-work)通过端到端地学习最近邻(K-Nearest Neigh-bor, KNN)分类器, 直接训练并一次性学习.建模过程利用注意力机制和外部存储的网络, 实现快速学习, 训练过程保持与测试过程一致, 达到较优的测试结果[7].Sung等[8]定义由卷积模块和关系模块组成的关系网络(Relation Network, R-Net).Cai等[9]提出记忆匹配网络(Memory Matching Networks, MM-Net), 是对匹配网络的改进, 与匹配网络的外部存储不同, MM-Net利用内存将上下文信息集成到深度嵌入架构, 达到增强学习的目的.蒋留兵等[10]提出改进匹配网络的学习模型, 分别采用双向长短时记忆网络(Long Short Term Memory Networks, LSTM)和注意力长短时记忆网络对训练样本和测试样本进行编码, 并利用L2范数进行度量.Snell等[11]提出原型网络(Prototypical Networks, Pro-Net), 将输入样本通过神经网络进行嵌入, 计算输入的支持集平均值, 找到原型, 计算查询值与原型的距离, 达到分类目的.Ren等[12]提出元学习半监督少样本学习(Meta Semi-supervised Few-Shot Learning, Meta SSL), 利用半监督的方法改进Pro-Net.Garcia等[13]利用图神经网络(Graph Neural Network, GNN), 通过度量学习进行分类.

上述算法是在无噪声、图像特征清晰的环境下训练模型, 但在现实生活中, 因为天气、物理设备、物体遮挡等原因, 人眼看到的图像往往存在各种噪声, 在这种情况下, 模型泛化能力往往较弱.从众多实验中可看出, 在图像清晰、特征明显的环境中, 模型往往过拟合严重, 造成分类准确率下降, 并且少样本学习为了模拟人眼辨认物体, 传统的模型训练往往需要经过多达上万次的迭代, 训练时间较长.

模型过拟合和训练时间较长是少样本学习需要解决的问题.增加训练样本、优化网络结构及限制训练时间提前停止训练都是用于防止过拟合、加快训练速度的常用方法, 但少样本学习每轮的支持样本有限, 网络结构相对简单, 上述方法此时并不适用.而在网络输入时增加噪声, 噪声会随着网络传播, 在输出中生成干扰项.训练时按照权值的平方放大, 并传播到输出层, 对误差产生影响, 达到减小误差的目的, 同时也会对噪声产生的干扰项进行惩罚, 减小权值的平方.在输出时融合多种模型的方法可减小误差对损失的影响, 提升模型准确率, 减小过拟合.

为了使少样本学习过程更快速, 并且具有更好的鲁棒性和可扩展性, 本文提出基于深度网络的快速少样本学习算法(Fast Few-Shot Learning Algorithm Based on Deep Network, Fast-FSL).首先, 利用核密度估计和图像滤波方法, 向训练集加入多种类型的随机噪声, 生成支持集和查询集.再利用原型网络提取支持集和查询集图像特征, 并根据Bregman散度, 以每类支持集支持样本的中心点作为类原型.然后, 使用L2范数度量支持集与查询图像的距离, 利用交叉熵反馈损失, 生成多个异构的基分类器.最后, 采用投票机制融合基分类器的非线性分类结果.实验表明, 本文算法能加快少样本学习收敛速度, 分类准确率较高, 鲁棒性较强.

1 问题定义

为了方便叙述, 归纳总结现有少样本学习的相关问题定义, 并使用形式化数学的方法定义少样本学习的相关基本概念[4, 6, 7, 8, 11].

定义1 少样本数据集 设数据集D为一个二元组D=(X, Y), 其中:

X为某输入空间的子集, 由|X|个输入实例{x1, x2, …, x|X|}构成.文中∀xi∈X, xi表示输入的图像实例.

Y为某输出空间的子集, 由|Y|个类标签{y1, y2, …, y|Y|}构成.

g:X→Y为一未知标号的待求解信息函数, 指定X中每个输入实例的类别标签值, 即∀xi∈X, ∃yj∈Y, 有g(xi)=yj成立.

∀yj∈Y, 若

g-1(yj)={xi∈X|g(xi)= yj},

称g-1(yj)为类标签yj的实例集.

特别地, 如果

|Y|=C, |g-1(yj) |=K,

通常当K较小时, 称D为C-way, K-shot少样本数据集, 其中, |· |为集合的势, i=1, 2, …, |X|, j=1, 2, …, |Y|.

在少样本学习中, 需要在一个大的源域数据集Ds=(Xs, Ys)上按一定方法抽样生成多个C-way, K-shot少样本数据集, 然后在这些小样本数据集上训练分类模型, 并把分类模型较好地迁移到目标域数据Dt=(Xt, Yt)上, Ds与Dt需满足Ys∩Yt=Ø .

定义2 C-way, K-shot少样本训练任务、支持集与查询集 给定数集

Ds=(Xs, Ys), Str=(XS, YS), Qtr=(XQ, YQ),

从YS中随机抽取C类{yj|j=1, 2, …, C}, 一个C-way, K-shot少样本训练任务定义在T=(Str, Qtr)上, 满足

1)YS=YQ={yj|j=1, 2, …, C},

2)∀ym∈YS, |g-1(ym) |=K,

3)∀yn∈YQ, |g-1(yn) |=q,

4)XS∩XQ=Ø,

其中, Str为训练任务支持集, Qtr为查询集.

定义3 C-way, K-shot少样本测试任务、支持集与查询集 给定数据集

Dt=(Xt, Yt), Ste=(Xe, Ye), Qte=(Xh, Yh),

从Yt中随机抽取C类{yj|j=1, 2, …, C}, 一个C-way, K-shot少样本测试任务定义在R=(Ste, Qte)上, 满足

1)Ye=Yh={yj|j=1, 2, …, C},

2)∀ym∈Ye, |g-1(ym) |=K,

3)∀yn∈Yh, |g-1(yn) |=p,

4)Se∩Qh=Ø,

其中, Ste为测试任务支持集, Qte为查询集.

定义4 C-way, K-shot少样本学习 给定训练任务集合Tasks={(Str, Qtr)}、测试任务集合T={(Ste, Qte)}, C-way, K-shot少样本学习任务是在多个训练任务的数据集上, 学习一个分类函数F* , 并在测试任务的支持集Ste上, 学习分类函数f* =F* (Ste), 使f* 完成对测试任务中查询集的分类.学习过程如下.

1)训练阶段.定义一组学习分类函数F及F的损失函数L, 对于每个训练任务k∈T, 利用支持集Str, 生成fk=F(Str), 并在查询集Qtr上计算fk的损失lk.再计算训练任务集合上的损失函数

L(F)=∑k=1|Tasks|lk,

并最小化L(F), 生成训练任务集合上的分类模型

F* =arg minFL(F).

2)测试阶段.对于测试任务集的测试任务, 利用支持集Ste, 生成分类模型f* =F* (Ste), 再使用查询集Qte完成对f* 的评估.

特别地, 在训练F* 的过程中, 如果涉及模型超参数的调整, 也可把训练任务集再划分为训练任务集与验证任务集.

对于定义4中少样本的定义, 存在两种特殊的情况.当K=1时称此任务为单样本学习, 每次训练只给出一个类的单幅图像作为支持集, 剩下的图像作为查询集.少样本学习另一种特殊情况为零样本学习, 零样本学习并不是完全不需要训练样本, 而是研究当特定类训练样本缺失时, 利用训练集样本和样本对应辅助文本描述、属性特征信息对模型进行训练[14, 15, 16, 17, 18].

2 基于深度网络的快速少样本学习算法

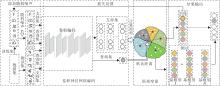
本文提出基于深度网络的快速少样本学习算法(Fast-FSL), 总体架构如图1所示.

图1 Fast-FSL流程图Fig.1 Flow chart of Fast-FSL

2.1 深度卷积神经网络

卷积神经网络(Convolutional Neural Networks, CNN)[19]是目前深度学习中具有代表性的网络架构, 在图像特征提取和模式识别领域获得重要应用.CNN主要特征为采用局部感受野和权值共享的处理方式, 即神经元仅与其上一层的相邻神经元相连, 学习局部特征, 最后综合为全局特征.同一卷积核在对不同局部提取特征时, 权值参数是共享的, 这样可减少权值更新计算量.具体网络层可分为输入层、卷积层、池化层、激活层、批量归一化、全连接和输出层.

卷积层是CNN最重要的一个层次, 卷积层的两个关键操作是:1)局部关联, 每个神经元为一个滤波器, 利用核函数进行滤波操作; 2)窗口滑动, 计算局部数据.卷积层最重要的超参数是要确定的深度、滑动窗口的步长和填充值(Padding).卷积公式如下:

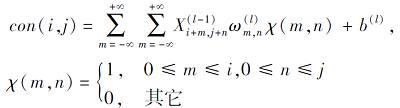
其中, ∀i∈ [0, k), ∀j∈ [0, l), Xi, jl-1为l-1层大小为k×l的输入矩阵元素, ωm, n(l)为m×n的卷积核, b(l)为偏置单元, χ(m, n)为当卷积核超出卷积边界时的填充值.

池化层用于压缩数据, 减少参数量, 具有特征不变性、特征降维的性质和作用, 可在一定程度上防止过拟合.CNN中主要有最大池化(Max Pooling)和平均池化(Average Pooling)两种方式, 最大池化是应用最多的池化方式.最大池化公式如下:

p(i, j)=maxm, n(X(i-m, j-n)),

其中, ∀i∈ [0, k), ∀j∈ [0, l), X(k, l)为大小为k×l的输入矩阵元素.

激活层用于将卷积层的输出结果进行非线性映射, 运行时激活层可将某一部分神经元的激活信息向后传入下一层神经网络.激活函数加入的非线性因素弥补线性模型的表达力, 解决神经网络非线性问题.CNN激活函数一般为ReLU函数, 特点是收敛较快, 梯度求解简单, 一定程度上避免梯度消失问题.ReLU激活函数如下:

R(i)=0, i≤0i, i> 0

其中i为卷积层输出值.

2.2 随机噪声的添加

在模型输入中增加随机噪声, 会使噪声随着网络传播按照权值的平方放大, 并一直传播至输出层, 从而对损失产生影响, 是防止过拟合的一种有效方法.添加噪声后模型的输出如下:

ynoisy=∑iwixi+ ∑iwiε i,

其中ε i为来自N(0, σi2)的样本.

对期望的影响如下:

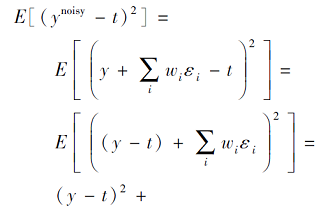
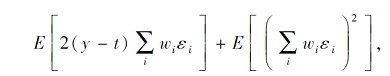
因为ε i独立于ε j和(y-t),

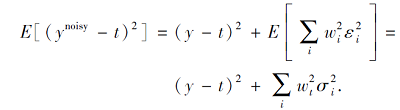
因此输入中增加噪声, 会在输出中生成 ∑iwt2σi2的干扰项.在训练时, 减小误差, 同时也会对噪声产生的干扰项 σi2进行惩罚, 达到减小权值的平方的目的.

在模型训练阶段, 采用非参数估计法的核密度估计法与滤波操作, 为训练集添加随机噪声.

核密度估计的噪声添加过程如下.首先, 读取训练集样本图像, 获取像素矩阵.再选择不同核函数K(· ), 利用平均积分平方误差(Mean Integrated Squared Error, MISE)计算核函数带宽h.然后, 利用该核函数对像素矩阵进行核密度估计(Kernel Density Estimation, KDE)运算, 筛选相应像素值.最后, 将计算后矩阵还原为图像并输出.平均积分平方误差如下:

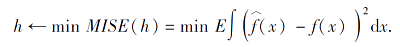
其中:MISE(· )为平均积分平方误差; 对于核函数K(· )≥ 0且积分为1, f(x)为任一给定样本点的概率密度; 为拟合后的核计算概率密度值.核密度估计公式如下:

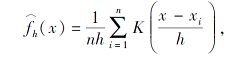
其中, n为样本容量, x1, x2, …, xn为样本点, h为核函数带宽, K(x)≥ 0,

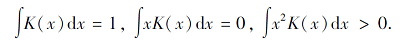
图像滤波(Image Filtering)操作过程如下.区别于CNN的卷积操作, 图像滤波技术是为了利用满足不同分布的滤波器对图像矩阵进行卷积操作.首先, 读取样本图像, 得到样本图像像素矩阵.再选定满足不同分布的滤波器作为核函数, 并定义卷积核大小.然后, 对每个像素点, 将其邻域像素与滤波器对应的元素进行乘积运算, 相加后作为该像素位置的值.最后, 还原矩阵为样本图像.图像滤波公式如下:

其中, X(i, j)为图像像素矩阵元素, (i, j)为像素在图像中的位置, K(m, n)为核函数, (m, n)为卷积核中的位置, X(i+m, j+n)为核函数与图像对应像素值.

实验对比同种核函数但不同参数的gaussian核密度估计及不同参数的bilateralFilter图像双边滤波, 发现核函数分布相同但参数不同的情况对实验准确度和融合效果影响较小, 因此实验时采用不同类型的噪声参与训练, 噪声类型有:Gaussian、bila-teralFilter、blur、localvar、medianBlur、speckle、salt、sharpening、pepper、S& P、poisson等.

2.3 距离度量

神经网络通过嵌入函数fϕ :RD→ RM和可通过学习进行更新的参数ϕ计算每类M维原型ck∈ RM, 每个原型为其类支持图像嵌入向量的均值, 原型

(1)

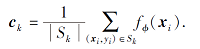距离度量算法采用Bregman散度的平方欧几里得距离‖z-z'‖ 2, 对具有指数族密度的支持集进行混合密度估计, 对于Legendre型可微凸函数φ, 有Bregman散度

(2)

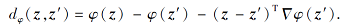原型的计算按照式(1), 在支持集上通过类似于聚类的方式实现, 每个支持样本分配给对应类别集群.对于Bregman散度, 达到指定点最小距离的代表点为集群的均值[20].因此, 式(1)对于原型的计算在给定的支持集情况下产生集群的代表点.正则Bregman散度可唯一确定一个含有参数θ和函数ψ的正则指数簇分布:

pψ (z|θ)=exp{zTθ-ψ(θ)-gψ (z)}= exp(-dφ (z, μ(θ))-gφ (z)).

参数Γ={θ k, π k} k=1K的正则指数簇混合模型为

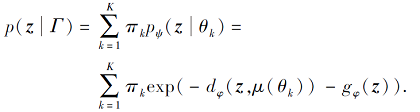
通过未标记点z推断标签:

(3)

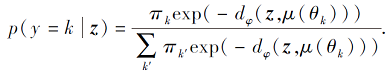对于每类一个簇的等权混合模型, 式(3)与式(4)(其中fϕ (X)=z, ck=μ(θ k))等价, 在此情况下可有效进行混合密度估计, 指数簇分布由dφ 确定.

2.4 损失函数和优化方法

模型训练阶段采用softmax函数, 利用自适应矩估计(Adaptive Moment Estimation, Adam)优化器优化网络, 学习率为0.001, 计算并学习最小化损失, 反馈网络, 更新参数进行训练.

具体地, 给定距离度量函数

d:RM× RM→ [0, +¥),

查询集样本通过嵌入生成嵌入空间矩阵, 计算与原型距离的softmax值, 生成查询点x的分布:

pϕ (y=k|x)=exp(-dφ(fϕ(x), ck))∑k'exp(-dφ(fϕ(x), ck')).(4)

利用式(4), 最小化预测类与真实类的负对数概率值

L(ϕ)=-ln pϕ (y=k|x),

学习并更新参数.

2.5 原型网络

原型网络(Pro-Net)[11]是基于CNN的度量学习模型.首先, 通过CNN将样本集和查询集样本图像映射投影至同一空间.再根据Bregman散度分别对每类样本集样本计算提取其中心点作为类原型.然后, 使用L2范数作为度量, 训练使查询集样本能靠近自己所在类别而疏远其它类别, 从而达到分类目的.最后, 计算查询集中各类样本的损失, 得到所有样本的平均损失, 采用损失函数优化基于度量的原型网络样本间的距离分布, 并反馈损失以优化整个网络.嵌入网络为一组四层的CNN, 每层含有64个滤波器, 每个滤波器利用3× 3的卷积核进行卷积操作, 再对卷积后的数据进行批处理归一化, 利用ReLU作为激活函数, 防止数据过大而导致网络不稳定, 最后利用2× 2的最大池化提取重要特征信息, 去除不重要信息, 减少计算开销.

具体描述如下.首先, 将支持集图像与查询集图像通过CNN卷积操作提取图像特征XS与XQ.再利用式(1)函数fϕ , 以XS中每类的支持点xi的均值作为其类的原型点ck.然后, 根据式(2)计算查询集Qtr中查询样本Qki与原型点ck的距离dφ .最后, 通过梯度下降算法, 计算其交叉熵损失, 更新训练网络.

2.6 融合网络

在机器学习领域, 学习目标是得到一个稳定且各方面表现良好的模型, 但有时实际情况往往不甚理想.集成学习的思想是通过一定训练方式训练得到某些方面的偏好模型, 通过组合以期望得到更优表现, 并在某分类器得到错误预测的情况下, 其它分类器可纠正错误.集成学习方法可达到减小方差、偏差或改进预测的效果, 在机器学习领域受到越来越多的关注.

训练多个模型, 以模型的平均输出作为结果:

y̅=<yi>i=1N∑i=1Nyi,

其中i为N个模型的索引.

模型平均输出的期望误差如下:

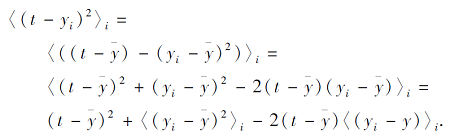
最终, -2(t- y̅)< (yi- y̅)>i项随着训练的进行而消失.

尽管原型网络分类效果较优, 但仍存在一些局限性, 一个突出的问题是模型使用平均值确定中心, 忽略支持数据集的方差, 阻碍当图像存在噪声时模型的分类能力.而Fast-FSL给训练集添加不同类型随机噪声, 即在噪声的环境下进行训练, 得到不同噪声环境的基模型, 再通过相对多数投票的方式, 将异构模型融合成为强分类模型, 既减小方差, 又增强模型的鲁棒性和分类效果.

Fast-FSL解决多分类问题, 模型融合阶段对基分类器最末层Softmax结果采取相对多数投票(Plurality Voting)的方法得到最终结果.具体地:首先, 求得异构基分类器的预测结果向量p的和作为最终预测输入.然后, 选择后验概率相对最大的类别结果作为最终预测结果.相对多数投票法表示如下:

(5)

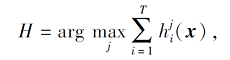其中, ∀i=1, 2, …, N, ∀j=1, 2, …, C, hij(x)∈ [0, 1]为基分类器输出, T为基分类器个数, x为单个基分类器的结果向量, H为投票后结果, 若同时存在多个得票相同者, 随机选择其一作为最终结果.

2.7 训练策略

Fast-FSL的训练过程如下.首先, 将数据集划分为训练集和测试集.再建立多个并行子任务, 为每个子任务的训练集添加不同类型随机噪声, 根据定义2随机抽取每轮迭代的C个类数据集, 形成支持集和查询集.然后, 并行训练基模型, 根据式(1)提取每个类别支持集特征向量均值作为原型, 利用L2范数作为度量计算查询集与原型距离, 利用交叉熵损失调整网络, 通过Adam对网络进行优化, 得到模型Ω1, Ω2, …, Ω N.最后, 将基模型最后的softmax概率结果进行融合作为最终结果, 输出Ω .

算法1 训练策略

输入 数据集D={X, Y, f}, 分类种类C,

测试集分类种类C_test,

每类所取支持集样本数K, 集成规模N,

训练次数(Episodes)为1 000

输出 少样本学习模型Ω

step 1 根据定义1, 划分数据集D为训练集Ds和测试集Dt

For i in |Ds| //选择训练集样本

Xi=random_noise(Xi) //为图像矩阵添加噪声

End For

step 2 Parallel Training step2 to step4//并行训练模型1~N

If Episodes=1000

Init_weight //初始化网络权重

Init_loss=0 //初始化损失

Best_loss=1 //初始化最优损失

Patient=200

//初始化提前停止(Early Stop)训练参数为200次, 超过200次未更新停止运行

Init_lr=10-3//初始化学习率

End If

根据定义2, T←Random({1, K}, C), T=(Str, Qtr)

//随机选择每次迭代所需训练子集并分为支持集和查询集, C为子集类数.Random(a, b)表示从集合a中均匀随机选择b个元素的集合, 训练时分类类别数为C, 测试时分类类别数为C_test

For k in(1, C)

Sk←Random(Str, K) //Sk表示从Str中随机选择的支持样本

Qk←Random(Str/Sk, q) //Qk表示从Str中随机选择的查询样本

Sk、Qk输入CNN, 得到支持样本与查询样本特征

xi, Qki

For convolution in (1, 4)

BatchNormal()

ReLU()

Maxpooling()

End For

根据式(1), 计算原型点ck← 1NC∑(xi, yi)∈Skfϕ (xi)

End For

step 3 根据式(2), Dist=Euclidean(Qki, ck)

//计算预测值与原点欧氏距离

根据式(4), L=log_softmax(-Dist) //计算损失L

计算预测类与真实类的交叉熵损失的负对数概率值并更新

L=L+ 1NCNq[Dist(fϕ (x), ck)+ln ∑k'exp(-Dist(fϕ (x), ck))].

If L<Best_loss

Best_loss=L

End If

If Patient=0 or Episodes=0

输出当前模型Ω N

End If

Break //如果超过Early Stop阈值, 训练停止, 输出基模型

step 4

If(loss> 0 and Episodes> 0) //Episodes为迭代次数

Backforward //利用梯度下降反馈网络修改参数

Episodes=Episodes-1

End If

Patient=Patient-1

step 5 根据式(5), 采用相对多数投票, 融合基网络模型Ω1, Ω2, …, Ω N, 得到少样本模型Ω .

step 6 输出模型Ω, 算法结束.

3 实验及结果分析
3.1 实验环境

本文在Omniglot[21]、miniImageNet数据集上进行实验.Omniglot数据集包含50个字母表, 共1 623类手写体字符, 每类包含20个不同人手绘的20个样本.类别较多、每类样本较少的特征使此数据集适合作为少样本学习.实验采用与文献[11]相同的分割方式, 选择1 200种字符作为训练集, 图像大小调整为28× 28, 施加旋转90° 、180° 、270° , 增加训练字符, 训练集共4 800个类.miniImageNet数据集由60 000幅彩色图像组成, 包含100类, 每类包含600个示例, 每类之间的差异性很大.实验使用文献[11]的分割方式, 将彩图调整为84× 84, 将100类分为64个训练类、16个验证类和20个测试类, 16个验证类用于监控泛化性能.

实验参照文献[11]算法与参数设置, 在Omnig-lot数据集上共进行5-way 1-shot、5-way 5-shot、10-way 1-shot、10-way 5-shot、20-way 1-shot、20-way 5-shot实验.5-way 1-shot采用的查询集批次为19(batch), 5-way 5-shot的查询集批次为15, 10-way 1-shot查询集批次为15, 10-way 5-shot查询集批次为10, 20-way 1-shot查询集批次为10, 20-way 5-shot查询集批次为5.每次迭代共需N·batch+k·N幅图像, 如5-way 1-shot实验, 需要5× 19+1× 5= 100幅图像.

为了进行对比, 参照文献[11]采用两种训练方式:1)模仿测试时的分类方式, 训练时采用和测试同way(same-way)同shot的样本选取方式进行训练; 2)进行高way同shot的训练测试方式, 即在训练时设置60-way, 测试时设置为5-way、10-way、15-way, 而shot值保持一致.测试集测试次数与对比实验相同, 均为1 000个随机产生的子集.

同样, 在miniImageNet数据集上进行5-way 1-shot、5-way 5-shot实验, 也分为同way同shot和高way同shot的训练测试方式, 1-shot和5-shot训练分别采用同way同shot及训练时30-way、20-way同shot训练测试方式, 每个模型训练200个迭代周期, 每个迭代周期迭代100次.

实验系统为Linux系统, 实验语言为Python语言, 借助Pytorch深度学习框架和NVIDIA Tesla V100 GPU算力加速实验.

3.2 分类效果对比

为了验证Fast-FSL的有效性, 在Omniglot、miniImageNet数据集上进行测试.并选用如下对比算法:MAML[2]、Meta-SGD[3]、TPN[4]、Convolutional Siamese Nets[6]、Matching Network[7]、R-Net[8]、Pro-Net[11]、Meta SSL[12]、GNN[13]、Siamese Nets with Me-mory[22].具体参数设置与文献[11]相同.mini-ImageNet数据集实验分为5-way 1-shot、5-way 5-shot任务, Omniglot数据集上增加10-way 1-shot、10-way 5-shot任务及难度较大的20-way 1-shot、20-way 5-shot任务.

实验步骤如下所示.

step 1 设置N=10, C=5, 10, 20, C_test=5, 10, 20, 分别输出当K=1, 5时, Omniglot数据集上训练模型Ω1、Ω2、Ω3、Ω4、Ω5、Ω6.

step 2 设置N=10, C=60, C_test=5, 10, 20, 分别输出当K=1, 5时, Omniglot数据集上训练模型Ω7、Ω8、Ω9、Ω10、Ω11、Ω12.

step 3 利用Omniglot数据集随机产生的测试集对模型Ω1~Ω12测试1 000个迭代周期, 计算模型Ω1~Ω12的识别率作为最终的测试结果.

step 4 设置N=10, C=5, C_test=5, 分别输出当K=1, 5时, miniImageNet数据集上训练模型Ω13、Ω14.

step 5 设置N=10, C=30, 20, C_test=5, 分别输出当K=1, 5时, miniImageNet数据集上训练模型Ω15、Ω16.

step 6 利用miniImageNet数据集随机产生的测试集对模型Ω13~Ω16测试600个迭代周期, 计算模型Ω13~Ω16的识别率作为最终结果.

各算法在Omniglot、miniImageNet数据集上的具体准确率对比如表1和表2所示, 表中黑体数字表示最优结果.

表1 各算法在Omniglot数据集上的准确率对比 Table 1 Accuracy comparison of different methods on Omniglot dataset %
表2 各算法在miniImageNet数据集上的准确率对比 Table 2 Accuracy comparison of different methods on miniImageNet dataset %

按照文献[11]算法和参数设置, Omniglot数据集上进行same-way Training和high-way Training, 增加10-way任务的实验.在实验中, same-way Training即训练和测试采用相同设置, 训练和测试采用相同way数和shot数, 旨在训练时模拟测试, 得到更优的训练效果.在实验中发现训练和测试采用相同shot数时, 使用high-way Training更利于分类.60-way Training即训练和测试时保持shot相同, 训练way数为60, 测试way数依次为5、10、20.同样, miniImage-Net数据集上也采用high-way Training和same-way Training, 在1-shot和5-shot任务上采用30-way 1-shot和20-way 1-shot的设置, 验证和测试时采用5-way 1-shot和5-way 5-shot的设置.另一种训练方式是在两个实验上训练和测试时均采用5-way 1-shot和5-way 5-shot的设置.

由表1可看出, Fast-FSL分类效果较优.在same-way Training实验中, Fast-FSL在5-shot任务上提升较小, 但准确率均已达到99%左右, 在1-shot任务上提升较大, 尤其是分类难度较大的20-way 1-shot任务, 比Pro-Net提升1.45%, 相比同样采用L2范数度量的Match Network(Squared Euclidean), 提升2.22%.在high-way Training实验中, Fast-FSL在5-shot任务上准确率均已超过99%.在分类难度较高的20-way 1-shot任务上, 相比Pro-Net, 准确率提升1.51%, 相比Match Network(Squared Euclidean), 准确率提升3.17%.

由表2可看出, 相对原改进模型, 在same-way Trai-ning实验中, Fast-FSL在5-way 1-shot任务上准确率提升0.9%, 而在5-way 5-shot任务上, 准确率提升2.49%.在high-way Training实验中, Fast-FSL在5-way 1-shot任务上准确率提升3.04%, 在5-way 5-shot任务上表现更优, 准确率提升3.89%.相比灰度图像的Omniglot数据集, Fast-FSL在彩色图像上表现更佳.

由表1和表2可看出, Fast-FSL可有效提升模型分类效果, 是一种有效的改进方式.相比其它算法, Fast-FSL分类结果方差更小, 说明分类更稳定, 鲁棒性更好.同时, 相比same-way Training, high-way Trai-ning训练的模型分类准确率均有较大提升.mini-ImageNet数据集上5-way 1-shot任务有3.89%的提升, Omniglot数据集上5-way 1-shot任务也有2.02%的提升.这是因为模型采用Bregman散度, 类原型采用支持点嵌入的均值作为代表点, 充分考虑相同类无限接近, 而未考虑不同类充分远离.因此在利用high-way Training时, high-way分类难度的提高有助于网络更好地泛化, 迫使模型做出更细粒度的决策, 而shot数设置相同, 是控制模型完成1-shot和5-shot的任务.这种思想对今后类似少样本学习起到一定的迁移和启发作用, 或许可将类似训练方式用于其它少样本学习任务中.

3.3 集成规模参数分析

为了确定集成规模参数, 探究其对模型最终分类效果的关系, 下面对集成规模进行实验, 每次实验控制K不变, N从1逐渐增加至10, 在Omniglot、miniIma-geNet数据集上进行研究.

具体实验步骤如下所示.

step 1 当i=1, 2, …, 10.

step 1.1 设置N=i, C=5, 10, 20, C_test=5, 10, 20, 分别输出K=1, 5时Omniglot数据集上训练模型Ω1~Ω6.

step 1.2 设置N=i, C=5, 10, 20, C_test=5, 10, 20.

step 1.2.1 如果N=1, 不为图像矩阵增加噪声.

step 1.2.2 分别输出当K=1, 5时Omniglot数据集上训练模型Ω7~Ω12.

step 2 设C=60, 重复step 1, 输出Omniglot数据集上训练模型Ω13~Ω24.

step 3 设置C=5, C_test=5, 重复step 1, 分别输出当K=1, 5时miniImageNet数据集上训练模型Ω25~Ω28.

step 4 设置C=30, 20, C_test=5, 重复step 1, 分别输出当K=1, 5时miniImageNe数据集上训练模型Ω29~Ω32.

step 5 利用Omniglot数据集随机产生的测试集对模型进行测试, 每次重复1 000个迭代周期, 计算模型Ω1~Ω24的准确率作为最终结果.利用miniImageNet数据集随机产生的测试集对模型进行测试, 每次重复600个迭代周期, 计算模型Ω25~Ω32的准确率作为最终结果.

实验按照same-way Training和high-way Trai-ning进行可视化, 结果如表3、表4和图2所示.表3和图2(a)为训练和测试时采用相同way数和shot数进行训练的集成规模结果, 表4和图2(b)为训练时, Omniglot数据集采用60-way, miniImageNet数据集5-way 1-shot任务采用30-way, 5-way 5-shot任务采用20-way, 测试时采用对应任务way数, shot数保持相同的集成规模实验结果, prototype对应N=1时模型为Pro-Net, 在此基础上逐渐增加异构模型规模, 对应的way数和shot数为其对应的分类任务.

表3 same-way Training时Fast-FSL在Omniglot数据集上分类效果与N的关系 Table 3 Relationship between classification effect of Fast-FSL on Omniglot dataset and N in same-way training
表4 60-way Training时Fast-FSL在Omniglot数据集上分类效果与N的关系 Table 4 Relationship between classification effect of Fast-FSL on Omniglot dataset and N in 60-way training

图2 Fast-FSL在miniImageNet数据集上分类效果与N的关系Fig.2 Relationship between Fast-FSL classification effect on miniImageNet dataset and N

从表3和表4可看出, 无论是same-way Training还是60-way Training, 都会从N=4开始收敛, 达到最高分类准确率.而且1-shot收敛速度快于5-shot, 因为5-shot本身已接近99%的准确率, 提升难度较大, 而1-shot实验提升更明显.从图2可看出, 1-shot在N=6时算法开始收敛, 并有上下波动的趋势, 5-shot在N=5时算法开始收敛, 逐渐接近于固定值.较特殊的是图2(a)中1-shot无prototype实验, 算法在起初提升后开始接近固定值并有下降趋势, 而prototype 1-shot实验在N=5时达到最高值, 然后开始震荡, 可能的原因是本身准确度太低, 集成效果不明显, 甚至出现拉低整体准确率的现象.上述现象说明随机噪声的模型训练方式对形成异构基模型的有效性, 及Fast-FSL对提升分类效果的有效性.

图2中算法最终收敛于固定值附近并上下震荡, 说明算法分类能力已达极限, 集成器并非越多越好.算法准确率最终收敛, 说明随机噪声的种类只影响出现收敛的时间, 最终都会收敛, 因此N对应添加的不同类型噪声训练的基模型对最终收敛影响较小, 可不予考虑先后顺序.

实验验证原型网络在不同参数核的多个Gaussian核密度估计及不同参数的bilateralFilter图像双边滤波下, 发现核函数分布相同但参数不同对实验准确度和融合效果影响较小, 结果几乎不变, 因此实验时可考虑采用不同类型的噪声参与训练和融合.

3.4 性能分析

为了探究噪声及high-way Training对算法收敛性、准确率和泛化性能的影响, 本节对采用same-way Training和high-way Training的算法训练、验证时的错误率、损失及集成测试结果进行可视化展示.针对Omniglot、miniImageNet数据集的训练集和验证集在加入椒盐噪声(图中使用S& P表示)前后进行可视化展示, 在Omniglot数据集的测试集上对分类难度最大的20-way 1-shot任务进行可视化展示, 在miniImageNet数据集的测试集上对5-way 1-shot任务进行可视化展示.

实验步骤如下所示.

step 1 按照算法1步骤, 设置C=20, 60, C_test=20, K=1, 迭代次数为200, 不向图像矩阵添加噪声.输出Omniglot数据集上训练集错误率和损失值及验证集错误率和损失.

step 2 按照算法1步骤, 设置C=20, 60, C_test=20, K=1, 迭代次数为200, 向Omniglot数据集训练集添加椒盐噪声(S& P), 输出训练集错误率和损失值及验证集错误率和损失.

step 3 按照算法1步骤, 设置C=5, 30, C_test=5, K=1, 迭代次数为200, 不向图像矩阵添加噪声.输出miniImageNet数据集上训练集错误率和损失值及验证集错误率和损失.

step 4 按照算法1步骤, 设置C=5, 30, C_test=5, K=1, 迭代次数为200, 向miniImageNet数据集训练集添加椒盐噪声(S& P), 输出训练集错误率和损失值及验证集错误率填空和损失.

step 5 设置N=10, C=20, 60, C_test=20, 输出当K=1时Omniglot数据集上训练模型Ω1、Ω2.

step 6 利用Omniglot数据集随机产生测试集, 对模型Ω1、Ω2测试1 000个迭代周期, 输出模型Ω1、Ω2的错误率和损失.

step 7 设置N=10, C=5, 30, C_test=5, 输出当K=1时miniImageNet数据集上训练模型Ω3和Ω4.

step 8 利用miniImageNet数据集随机产生测试集, 对模型Ω3、Ω4测试600个迭代周期, 输出模型Ω3、Ω4的错误率和损失.

加入椒盐噪声前后Fast-FSL在Omniglot、miniImageNet数据集上5-way 1-shot任务的训练错误率和损失函数值如图3和图4所示.在图中:same-way Training为训练和测试采用相同way数训练的准确率和损失; same-way Training with S& P为训练和测试采用相同way数训练, 并在训练时加入椒盐噪声的准确率和损失; 60-way Training为训练时采用60-way和测试时采用任务way数训练的准确率和损失; 60-way Training with S& P为训练时采用60-way和测试时采用任务way数训练, 并在训练时加入椒盐噪声的准确率和损失; 30-way Training为训练时采用30-way和测试时采用任务way数训练的准确率和损失; 30-way Training with S& P为训练时采用30-way和测试时采用任务way数训练, 并在训练时加入椒盐噪声的的准确率和损失.

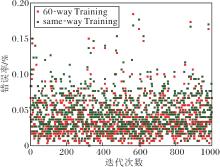
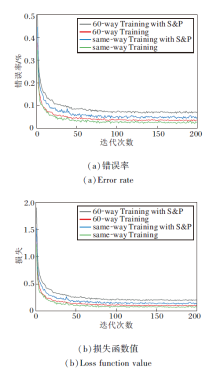图3 加入椒盐噪声前后Fast-FSL在Omniglot数据集上 20-way 1-shot的训练错误率和损失函数值Fig.3 Training error rate and loss function value of Fast-FSL with and without S& P noise for 20-way 1-shot on Omniglot dataset

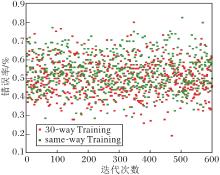
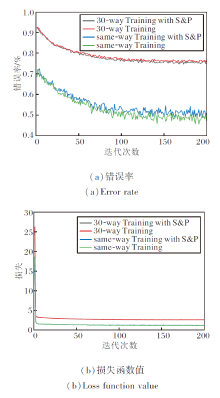图4 加入椒盐噪声前后Fast-FSL在miniImageNet数据集上5-way 1-shot的训练错误率和损失函数值Fig.4 Training error rate and loss function value of Fast-FSL with and without S& P noise for 5-way 1-shot on miniImageNet dataset

由图3可看出, 随着训练的增多, 算法损失逐渐降低, 错误率逐渐降低, 准确率不断提高.在20-way 1-shot任务中分类错误率仍然较高, 说明只给一个样本时的分类任务仍是一个具有挑战性的任务, 分类难度较大, 噪声加入在一定程度上降低算法的准确率.

由图4可看出, 随着训练次数的增加, 算法损失迅速收敛, 对应的错误率逐渐降低, 准确率逐渐提高.添加噪声的算法的损失略高于未添加噪声, 对应的错误率也较高, 这是由于噪声对特征的模糊影响, 造成准确率降低.对比两种不同way训练方式, 相比high-way Training, same-way Training损失更低, 错误率也更低, 这是由于训练集分类按照对应way数进行分类, 因此错误率和损失较高.

在Omniglot数据集上两种训练方式下每种任务迭代次数如图5所示, 图中Pro-Net为原模型训练时验证损失达到最小值时的迭代次数, 噪声训练模型为加入噪声(N=10)后不同任务训练时验证损失达到最小值时的平均迭代次数.

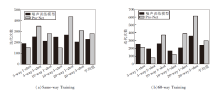图5 在Omniglot数据集上两种训练方式下的迭代次数对比Fig.5 Statistics on the number of iterations of two training methods for each task on Omniglot dataset

结合图4损失值拟合结果可看出, 加入噪声后, 算法仍可迅速收敛, 并且可更迅速收敛到稳定值, 对比5-way任务和20-way任务, 发现way数越高, 效果越明显.same-way Training平均迭代次数为229次, 相比Pro-Net的279次, 提前51次完成训练, 提升率为18%.60-way Training平均迭代次数为239次, 相比Pro-Net的297次, 提前58次完成训练, 提升率达到20%.

由于算法为并行训练, 需要更多的存储和计算开销, 但噪声的加入在整体上促进算法提前收敛, 减少时间成本, 是一种更快速的学习方法, 而高way的训练方式并未使训练时间变化太多, 只增加10步左右, 这同样表明算法的有效性.

在Omniglot数据集上, 各算法加入噪声(N=10)后不同任务训练时验证损失达到最小值时的平均迭代次数对比如表5所示, 表中数字为算法按照对应模型结构和参数复现的结果.

表5 在Omniglot数据集上采用噪声前后算法迭代次数 对比 Table 5 Comparison of the number of iterations for 3 algorithms before and after using noise on Omniglot dataset

首先, MAML的原始训练次数均值为34 000, 采用噪声进行训练后的平均迭代次数为31 250, 提升8.09%.R-Net对应迭代次数分别为60 700和53 200, 提升12.36%.

此外, MAML和R-Net结构比Pro-Net更复杂, 当采用相同的硬件和环境时, MAML训练基模型的平均时间由大约15 h减少到大约11 h, R-Net由大约70 h减少到57 h, Pro-Net由大约8 h减少到5 h(由于噪声类型的不同, 训练时间会上下略微浮动).

通过对比可发现, Fast-FSL的训练方法在基于优化的少样本学习方法MAML和同样基于度量的学习方法R-Net上同样有效.

加入椒盐噪声前后Fast-FSL在Omniglot、mini-ImageNet数据集上20-way 1-shot任务的验证错误率和损失如图6和图7所示.由图可看出, 随着训练继续, 损失逐渐减小, 验证损失也逐渐减小, 错误率逐渐降低, 准确率逐渐提高.

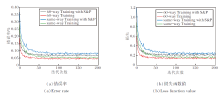图6 加入椒盐噪声前后Fast-FSL在Omniglot数据集上20-way 1-shot的验证错误率和损失函数值Fig.6 Validation error rate and loss function value of Fast-FSL with and without S& P noise for 20-way 1-shot on Omniglot dataset

图7 加入椒盐噪声前后Fast-FSL在miniImageNet数据集上5-way 1-shot的验证错误率和损失函数值Fig.7 Validation error rate and loss function value of Fast-FSL with and without S& P noise for 5-way 1-shot on miniImageNet dataset

在Omniglot数据集上, 对于60-way Training加入椒盐噪音的20-way 1-shot任务, 训练集错误率最低为6.06%, 准确率最高为93.94%, 验证集错误率最低为5.89%, 准确率最高为94.11%, 而在测试集任务上错误率为5.77%, 准确率高达94.23%.

在miniImageNet数据集上, 对于30-way Training加入椒盐噪音的5-way 1-shot任务, 虽然训练集错误率高达为74.62%, 准确率最高仅为25.38%, 但是验证集错误率最低可达到46.45%, 准确率最高为53.55%, 而在测试集任务上错误率最高也能达到48.99%, 准确率高达51.01%.通过上述分析可看出, 通过验证集可有效提升算法泛化性能, 提升准确率.

在same-way Training和high-way Training两种训练方式下, Fast-FSL在Omniglot、miniImageNet数据集上的测试错误率如图8和图9所示.

图8 Omniglot数据集上20-way 1-shot的测试错误率Fig.8 Test error rate of 20-way 1-shot on Omniglot dataset

图9 miniImageNet数据集上5-way 1-shot的测试错误率Fig.9 Test error rate of 5-way 1-shot on miniImageNet dataset

由图8可看出, 20-way 1-shot任务难度较大, 但Fast-FSL平均错误率仍小于4.58%, 平均准确率可达到95.42%, 比Pro-Net(93.97%)提升1.45%, 结合表1可更清晰看出, FAST-FSL具有更好的识别效果.而采用high-way Training能更好提升算法准确率, 尤其是在5-way 1-shot任务中, high-way Training的准确率比same-way Training提高2%, 相对20-way 1-shot任务的0.95%更明显.而high-way Training的平均准确率方差(0.06)小于same-way Training(0.07), 说明离散度更低、更稳定.

由图9可看出, Fast-FSL在minimageNet这种分类难度较大的数据集上, 平均准确率仍可达到47.3%, 相比Pro-Net(46.4%)提高0.9%, 提升虽然较小, 但结合表1的high-way Training可看出, 相比Pro-Net, Fast-FSL有3.04%的提升.Fast-FSL的优势更是体现在5-way 5-shot任务中, 无论是same-way Training还是high-way Training, 提升都较大.这说明Fast-FSL的有效性及high-way Training对于原型网络的有效性.从离散度的角度上看, high-way Training方差(0.17)略高于same-way Training(0.12), 离散度相对高一点, 这说明算法在数据集上牺牲一定的稳定性, 达到更高的准确率.

4 结束语

近年来, 少样本学习因其需要的标记样本较少而越来越受到行业的关注, 但现有的少样本学习算法过拟合问题严重, 造成在新域分类准确率较低, 泛化能力较差, 训练均需大量的迭代过程, 造成时间和人力成本上升.本文首先利用形式化数学定义方法描述少样本的相关概念, 运用随机噪声技术有效生成多个异构基分类器, 提出基于深度网络的快速少样本学习算法(Fast-FSL).同时, 针对Bregman散度的度量分类类内聚类良好、类间差异性较差的问题, 进行高way同shot的少样本训练方式.实验表明, Fast-FSL能有效促进算法快速收敛, 是一种快速学习的少样本学习方式, 有效提升算法准确率, 加入噪声的训练鲁棒性更强.实验采用网络更深或特征提取利用方式更细的类似更细粒度的学习方式, 结果表明粒度越细, 模型过拟合越严重, 可能并不适用于少样本学习.此外, 高way同shot的少样本训练方式强制算法增加类间距离和差异, 可提升Bregman散度度量的多分类问题准确率.今后可将方法迁移至其它同类少样本问题, 并考虑将Fast-FSL应用于数据自动标注问题.

参考文献
[1] LI F F, FERGUS R, PERONA P. One-Shot Learning of Object Ca-tegories. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(4): 594-611. [本文引用:1]
[2] FINN C, ABBEEL P, LEVINE S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks // Proc of the 34th International Conference on Machine Learning. New York, USA: ACM, 2017: 1126-1135. [本文引用:2]
[3] LI Z G, ZHOU F W, CHEN F, et al. Meta-SGD: Learning to Learn Quickly for Few-Shot Learning[C/OL]. [2021-06-15]. https://arxiv.org/pdf/1707.09835.pdf. [本文引用:2]
[4] LIU Y B, LEE J, PARK M, et al. Learning to Propagate Labels: Transductive Propagation Network for Few-Shot Learning[C/OL]. [2021-06-15]. https://openreview.net/pdf?id=SyVuRiC5K7. [本文引用:3]
[5] ZHANG R X, CHE T, GHAHRAMANI Z, et al. MetaGAN: An Adversarial Approach to Few-Shot Learning // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 2371-2380. [本文引用:1]
[6] GREGORY K, RICHARD Z, RUSLAN S. Siamese Neural Networks for One-Shot Image Recognition[C/OL]. [2021-06-15]. http://www.cs.utoronto.ca/~rsalakhu/papers/oneshot1.pdf. [本文引用:3]
[7] VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching Networks for One Shot Learning // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 3637-3645. [本文引用:3]
[8] SUNG F, YANG Y X, ZHANG L, et al. Learning to Compare: Relation Network for Few-Shot Learning // Proc of the IEEE Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 1199-1208. [本文引用:3]
[9] CAI Q, PAN Y W, YAO T, et al. Memory Matching Networks for One-Shot Image Recognition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 4080-4088. [本文引用:1]
[10] 蒋留兵, 周小龙, 姜风伟, 等. 基于改进匹配网络的单样本学习. 系统工程与电子技术, 2019, 41(6): 1210-1217.
(JIANG L B, ZHOU X L, JIANG F W, et al. One-Shot Learning Based on Improved Matching Network. Systems Engineering and Electronics, 2019, 41(6): 1210-1217. ) [本文引用:1]
[11] SNELL J, SWERSKY K, ZEMEL R S. Prototypical Networks for Few-Shot Learning // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 4077-4087. [本文引用:10]
[12] REN M Y, TRIANTAFILLOU E, RAVI S, et al. Meta-Learning for Semi-supervised Few-Shot Classification[C/OL]. [2021-06-15]. https://arxiv.org/pdf/1803.00676.pdf. [本文引用:2]
[13] GARCIA V, BRUNA J. Few-Shot Learning with Graph Neural Network[C/OL]. [2021-06-15]. https://arxiv.org/pdf/1711.04043.pdf. [本文引用:2]
[14] 张鲁宁, 左信, 刘建伟. 零样本学习研究进展. 自动化学报, 2020, 46(1): 1-23.
(ZHANG L N, ZUO X, LIU J W. Research and Development on Zero-Shot Learning. Acta Automatica Sinica, 2020, 46(1): 1-23. ) [本文引用:1]
[15] ANTOL S, ZITNICK C. L, PARIKH D. Zero-Shot Learning via Visual Abstraction // Proc of the European Conference on Compu-ter Vision. Berlin, Germany: Springer, 2014: 401-416. [本文引用:1]
[16] ROBYNS P, MARIN E, LAMOTTE W, et al. Physical-Layer Fingerprinting of LoRa Devices Using Supervised and Zero-Shot Lear-ning // Proc of the 10th ACM Conference on Security and Privacy in Wireless and Mobile Networks. New York, USA: ACM, 2017: 58-63. [本文引用:1]
[17] YANG Y, LUO Y D, CHEN W L, et al. Zero-Shot Hashing via Transferring Supervised Knowledge // Proc of the 24th ACM International Conference on Multimedia. New York, USA: ACM, 2016: 1286-1295. [本文引用:1]
[18] 林克正, 李昊天, 白婧轩, 等. 语义自编码结合关系网络的零样本图像识别算法. 模式识别与人工智能, 2019, 32(3): 214-224.
(LIN K Z, LI H T, BAI J X, et al. Zero-Shot Image Recognition Algorithm via Semantic Auto-Encoder Combining Relation Network. Pattern Recognition and Artificial Intelligence, 2019, 32(3): 214-224. ) [本文引用:1]
[19] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet Cla-ssification with Deep Convolutional Neural Networks. Communications of the ACM, 2017, 60(6): 84-90. [本文引用:1]
[20] BANERJEE A, MERUGU S, DHILLON I S, et al. Clustering with Bregman Divergences. Journal of Machine Learning Research, 2005, 6: 1705-1749. [本文引用:1]
[21] LAKE B, SALAKHATDINOV R, GROSS J, et al. One Shot Lear-ning of Simple Visual Concepts[C/OL]. [2021-06-15]. https://web.mit.edu/jgross/Public/lake_etal_cogsci2011.pdf. [本文引用:1]
[22] KAISER Ł, NACHUM O, ROY A, et al. Learning to Remember Rare Events[C/OL]. [2021-06-15]. https://arxiv.org/pdf/1703.03129v1.pdf. [本文引用:]