自适应Rulkov神经元聚类算法

引用本文

廖云荣, 任海鹏. 自适应Rulkov神经元聚类算法. 模式识别与人工智能, 2021,34(10): 957-968
LIAO Yunrong, REN Haipeng. Adaptive Rulkov Neuron Clustering Algorithm. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(10): 957-968. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202110008
Permissions

《模式识别与人工智能》编辑部

自适应Rulkov神经元聚类算法

廖云荣¹, 任海鹏¹

1.西安工业大学兵器科学与技术学院西安 710021

通讯作者:

任海鹏,博士,教授,主要研究方向为复杂系统控制、智能信息处理.E-mail:renhaipeng@xaut.edu.cn.

作者简介:

廖云荣,硕士研究生,主要研究方向为计算机视觉、数字图像处理算法硬件实现.E-mail:lyr_0517@163.com.

收稿日期: 2021-04-12 接受日期: 2021-07-27

摘要

针对类间间距较小、可分性较差的样本数据聚类问题,文中提出自适应Rulkov神经元聚类算法.首先,构建基于自适应距离和共享近邻的相似度矩阵,将样本构成的无向图的最优分割问题转化为拉普拉斯矩阵的谱分解问题,并按特征值大小选取拉普拉斯矩阵的特征向量作为新的样本特征,增大样本类间间距,减小类内间距.然后,将样本根据新特征映射为神经元,样本特征距离决定神经元之间的耦合权值,通过耦合强度自学习进一步提升样本可分性.最后,通过强连通分量实现样本聚类.在多个合成数据集和真实数据集上的实验表明文中算法获得较优的聚类效果.

关键词: 共享近邻; 相似度矩阵; Rulkov神经元; 自适应学习

中图分类号:TP391

Adaptive Rulkov Neuron Clustering Algorithm

LIAO Yunrong¹, REN Haipeng¹

1. College of Armament Science and Technology, Xi'an Technological University, Xi'an 710021

Corresponding author:
REN Haipeng, Ph.D., professor. His research interests include complex system control and intelligent information processing.

About Author:
LIAO Yunrong, master student. Her research interests include computer vision and hardware implementation of digital image processing algorithm.

Abstract

Aiming at the clustering of sample datasets with small inter-class distance and poor separability, an adaptive Rulkov neuron clustering algorithm is proposed. Firstly, a similarity matrix based on adaptive distance and shared nearest neighbor is constructed. Secondly, the optimal segmentation of the undirected graph consisting of samples is replaced by the Laplace spectral decomposition of the matrix according to the similarity matrix, and the eigen vectors of Laplacian matrix with larger eigen values are selected as new features of the samples. Thus, the inter-class distance is increased and the intra-class spacing of the samples is reduced. Then, the samples are mapped to the neurons with the mutual coupling strength determined by the distance of the samples. The separability of the different clusters is improved by the self-learning of the mutual coupling strength. Finally, the strong coupled subset in the neural network is utilized as clustering result. The comparative experiments are conducted on synthetic and real datasets. The results show that the proposed algorithm achieves better clustering performance.

Key words: Key Words Shared Nearest Neighbor; Similarity Matrix; Rulkov Neuron; Adaptive Learning

文章图片

本文责任编委于剑

Recommended by Associate Editor YU Jian

聚类分析在人工智能、图像分割、大数据处理和模式识别等领域得到广泛应用, 这也是模式识别领域热门问题之一.聚类作为一种无监督学习方法, 根据样本间相似性, 将样本划分至不同子集, 使子集内样本相似性较大、子集间样本相似性较小.

根据算法适用的样本分布不同, 聚类算法可分为仅适用于球形结构样本空间的聚类算法和适用于任意结构样本空间的聚类算法两种.

适用于球形结构样本空间的聚类算法主要包含K均值聚类算法(K-means Clustering Algorithm, K-means)^[1]、模糊C均值聚类算法(Fuzzy C-means Clustering Algorithm, FCM)^[2]和K中心点聚类算法(K-medoids Clustering Algorithm, K-medoids)^[3]等.这类算法受初始聚类中心选择影响较大, 当初始聚类中心选择不当时, 聚类效果较差.针对初始聚类中心选择困难的问题, 学者们提出改进算法^{[4, 5, 6]}, 但这些改进算法大多仍建立在球形结构样本空间假设基础之上, 当样本空间非凸时, 聚类效果依然较差.

适用于任意结构样本空间的聚类算法大致分为基于层次的聚类算法^[7]、基于网格的聚类算法^[8]、基于密度的聚类算法^{[9, 10, 11]}和基于谱的聚类算法^{[12, 13]}等.基于谱的聚类算法是现在通用聚类算法之一^[14], 其中经典方法为基于规范化拉普拉斯矩阵的谱聚类算法^[15].在该算法中将每个样本看作无向图中的节点, 样本间相似性看作无向图中节点间边的权重, 将聚类问题转化为无向图最优分割问题, 再利用拉普拉斯矩阵的谱分解求解无向图的最优分割问题, 提高样本特征的可分性.基于规范化拉普拉斯矩阵的谱聚类算法在构建相似度矩阵时, 需人为给定尺度参数, 当尺度参数选择不当时, 无法正确反映样本分布, 导致聚类效果较差.同时, 基于规范化拉普拉斯矩阵的谱聚类算法在相似度矩阵的基础上, 直接使用K-means算法对所得样本特征进行聚类, 未进一步改进样本特征, 当样本特征的类间区分度不足时, 聚类效果欠佳.此外, 该算法中采用的K-means也存在初始聚类中心选择的问题, 当初始聚类中心选择不当时, 影响聚类效果.

Rulkov神经元模型^{[16, 17]}可模拟大脑皮层的神经元系统的动态行为.Held等^[18]将Rulkov神经元模型用于聚类, 提出基于Rulkov神经元的赫布学习聚类算法(Rulkov-Hebbian-Learning Clustering, RHLC), 将每个样本看作一个Rulkov神经元, 利用样本间距离构建Rulkov神经元网络.再根据神经元之间耦合强度的分布情况, 不断更新Rulkov神经元网络中的耦合权值, 实现样本的自适应聚类.RHLC适用于任意样本空间及高维数据的聚类问题, 具有较优的聚类性能, 但对可分性较差的数据集, 容易将类间间距较小的不同类别误分为同一类.

本文针对RHLC存在的问题, 提出自适应Rulkov神经元聚类算法(Adaptive Rulkov Neuron Clustering Algorithm, ARNC).首先, 提出基于自适应距离和共享近邻的相似度矩阵构建方法, 利用该方法构建的拉普拉斯矩阵经谱分解后得到可分性更好的样本特征.然后, 结合可分性更好的样本特征, 引入Rulkov神经元模型, 自适应学习样本间相似性, 实现样本聚类, 提高聚类性能.ARNC在不显著增加计算量的同时, 可获得较优的聚类性能.对比实验也验证ARNC的有效性和优越性.

1 相关算法

1.1 基于规范化拉普拉斯矩阵的谱聚类算法

将每个样本映射为无向图中节点, 样本间相似度对应无向图中节点间边的权重, 以此构建样本的无向图.然后, 以类内间距较小、类间间距较大为目标, 将无向图划分为不同的子图.具体方法如下.

1)计算相似度矩阵.样本集表示为

V={v₁, v₂, …, v_n}∈ R^dim^×ⁿ,

其中, 样本数为n, 样本特征维度为dim.然后, 根据样本间欧氏距离构建相似度矩阵W=[w_ij]∈ Rⁿ^×ⁿ,

w_ij= $\{\begin{array}{l} \exp (- \frac{dis t^{2} (v_{i}, v_{j})}{2 σ_{r}^{2}}), & i \neq j \\ 0, & i = j \end{array}$

其中, w_ij表示样本v_i、v_j的相似度, dist(v_i, v_j)表示样本v_i、v_j间的欧氏距离, σ _r表示尺度参数.根据相似度矩阵W, 计算对角矩阵

D∈ Rⁿ^×ⁿ, d_ii= $∑ j = 1 n$ w_ij.

2)构建样本特征矩阵.为了提取可分性较好的样本特征, 利用标准割(Normalized Cut, Ncut)^[19]将1)中构建的无向图A划分为K个子图A₁, A₂, …, A_K.具体方法如下:

(1)

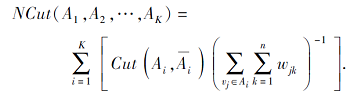其中:

Cut(A_i, A_j)= $\underset{v_{j} \in A_{j}}{\sum_{v_{i}}}$ w_ij

表示子图A_i、A_j间的相似性, Cut值越小, 子图A_i、A_j间的差异性越大; ${\bar{A}}_{i}$ 表示除子图A_i以外的所有子图.

为了使子图间差异性尽可能大, 应最小化式(1)中的NCut值.利用规范化拉普拉斯矩阵的性质^[20], 可将NCut最小化问题转化如下优化问题:

$\min_{Z \in R^{n \times K}}$ tr(Z^T(I-D^-1^/²WD^-1^/²)Z), s.t. ZT^Z=I.(2)

根据Rayleigh-Ritz原理^[21], 拉普拉斯矩阵L=D^-1^/²WD^-1^/²的前K个最大特征值对应的特征向量(列向量z_i, i=1, 2, …, K)构成的矩阵

Z=[z₁, z₂, …, z_K]∈ Rⁿ^×^K

为式(2)中最小化问题的解.若样本集的类别数已知, K为类别数; 若类别数未知, 可给定一个大于2的常数K完成类似功能.对矩阵Z按行进行规范化:

H∈ Rⁿ^×^K, h_ij=z_ij( $∑ j = 1 K z_{ij}^{2}$ ) $^{- \frac{1}{2}}$ ,

获得新的样本特征矩阵U=H^T∈ R^K^×ⁿ.

3)K-means聚类.对于样本特征矩阵

U=[u₁, u₂, …, u_n]∈ R^K^×ⁿ,

使用K-means将所有样本聚类成K个子类, 完成聚类过程.

1.2 基于Rulkov神经元的赫布学习聚类算法

基于Rulkov神经元的赫布学习聚类算法将每个样本映射为一个Rulkov神经元, 任意神经元可与其近邻神经元相互耦合, 耦合强度由相邻神经元表示的样本间距离决定, 按照这一原则构建Rulkov神经元网络.定义神经元之间的同步度与其耦合强度相关, 根据神经元间同步度对耦合强度进行学习, 增加具有高同步度神经元之间的耦合强度, 减小具有低同步度神经元之间的耦合强度.该操作可减小类间相似性, 增大类内相似性.最后, 根据样本间的耦合强度连接关系, 将同个强连通分量的样本划分为一类, 实现样本的自适应聚类.具体步骤如下.

1)构建Rulkov神经元网络.通过Rulkov神经元模型建立耦合神经元网络, 神经元v_i具有2个状态变量:快变量x_i_,_t和慢变量y_i_,_t.不同神经元之间状态变量相互耦合, 则

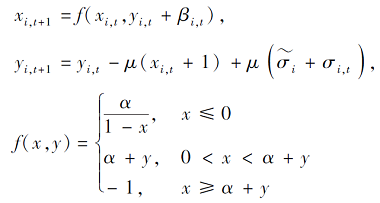
其中:β _i_,_t、σ _i_,_t均为电流变量, 可增强神经元之间的交流及同步, 获得更大的耦合强度, 耦合方程

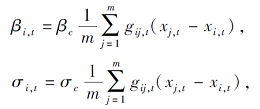
β _c、σ _c均为常数, 分别用于衡量耦合作用对电流变量β _i_,_t、σ _i_,_t的影响程度;μ表示快变量x_i_,_t对慢变量y_i_,_t的影响程度;

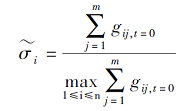
用于驱动未耦合神经元的恒定输入电流;α为快变量的演变控制参数, 决定神经元处于放电状态还是静息状态.

根据样本间距离定义神经元的耦合强度矩阵G_t=[g_ij_,_t]_n_×_n∈ Rⁿ^×ⁿ, 初始值如下:

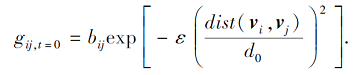
其中:g_ij_,_t₌₀表示t=0时神经元v_i、v_j间的初始耦合强度;B=[b_ij]_n_×_n∈ Rⁿ^×ⁿ表示邻接矩阵, 若v_j属于v_i的m近邻, b_ij=1, 否则b_ij=0;ε表示耦合参数;

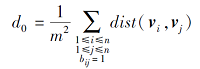
表示所有m近邻样本间的平均距离.

2)更新Rulkov神经元网络权值.神经元间的耦合强度由神经元间同步度确定, Rulkov神经元网络权值(耦合强度)更新步骤如下.

(1)根据Pearson相关系数^[22]定义神经元之间的同步度矩阵S_t∈ Rⁿ^×ⁿ,

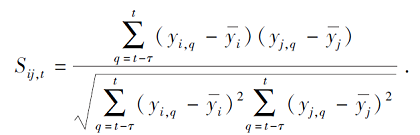
其中:S_ij_,_t表示t时刻, 神经元v_i、v_j间的同步度, 即两个变量一起增大或一起减小的可能性;τ为慢变量同步测量所需的最短时间;

${\bar{y}}_{i}$ = $\frac{1}{τ} ∑ q = t - τ t$ y_i_,_q

表示慢变量在τ内的均值.

(2)两个神经元之间的耦合强度变化取决于其相对于近邻神经元平均同步度的大小, 高同步度神经元之间耦合强度增加, 低同步度神经元之间耦合强度减小.耦合强度矩阵G_t的更新规则如下:

g_ij_,_t₊₁=g_ij_,_t+ $\frac{τ}{t}$ (c₁S_ij_,_t-c₂ ${\bar{S}}_{i, t}$ ),

其中, c₁用于控制高同步度神经元之间耦合强度增加量的系数, c₂用于控制低同步度神经元之间耦合强度减小量的系数,

${\bar{S}}_{i, t}$ = $\frac{1}{m} ∑ j = 1 m$ S_ij_,_t,

为神经元v_i的m近邻神经元在t时刻的平均同步度.

3)耦合强度学习停止条件.当Rulkov神经元网络中强连接数不再发生显著变化时, 停止学习, 耦合强度学习停止条件如下:

$\frac{n_{l}}{n_{s}}$ ≤ω .(3)

其中:n_l为正在学习的连接数, 即当前G_t中介于弱耦合度阈值θ₁和强耦合度阈值θ₂之间的元素个数;n_s为强连接数, 即G_t中大于等于θ₂的元素个数;ω为设定常数.

4)样本聚类.将耦合强度矩阵G_t中大于或等于θ₂的元素值对应的样本间连接保留, 否则, 去除样本间连接, 得到一个新的有向图.再利用Tarjan算法^[23], 寻找有向图中的强连通分量, 每个强连通分量对应一个类别, 从而实现样本聚类.

2 自适应Rulkov神经元聚类算法

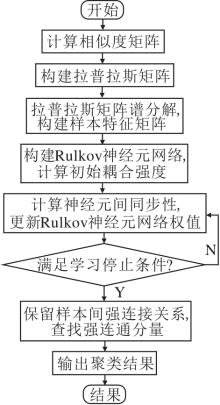
本文提出自适应Rulkov神经元聚类算法(ARNC), 采用基于自适应距离和共享近邻构建相似度矩阵, 可避免基于规范化拉普拉斯矩阵的谱聚类算法中尺度参数选择困难的问题.本文使用Rulkov神经元聚类算法进行聚类, 进一步学习样本间相似性, 提升样本的类间间距, 避免基于规范化拉普拉斯矩阵的谱聚类算法使用K-means时存在初始聚类中心的选择不当, 导致算法聚类效果较差的问题.采用拉普拉斯矩阵的特征向量作为样本新特征, 提高样本可分性, 避免原Rulkov神经元聚类算法在处理可分性较差的样本的聚类时造成的误分类问题.ARNC流程图如图1所示.

	Figure Option View Download New Window
	图1 ARNC流程图Fig.1 Flowchart of ARNC

ARNC可分为如下两个阶段.

1)样本特征提取.将样本映射到无向图中, 根据自适应距离和共享近邻构建相似度矩阵, 利用拉普拉斯矩阵谱分解方法, 获得样本特征矩阵, 提高样本可分性.

本文提出基于自适应距离和共享近邻的相似度矩阵构建方法, 相似度矩阵W元素表示如下:

w_ij= $\{\begin{array}{l} \exp (- \frac{dis t^{2} (v_{i}, v_{j})}{{\bar{λ}}_{i} {\bar{λ}}_{j} (SNN (v_{i}, v_{j}) + 1)}), & i \neq j \\ 0, & i = j \end{array}$

其中:N(v_i)为样本v_i的近邻集合, 每个样本的近邻数采用文献[24]方法确定, 该方法确定的每个样本近邻数可能各不相同.样本v_i、v_j的共享近邻数

SNN(v_i, v_j)=|N(v_i)∩N(v_j)|;

${\bar{λ}}_{i}$ 表示样本v_i到其近邻集合N(v_i)中所有样本的平均距离, ${\bar{λ}}_{i}$ =0时, 取距离样本v_i为非0的最近邻居v_j∈N(v_i)对应的 ${\bar{λ}}_{j}$ 代替.

近邻集合中样本的平均距离及不同共享近邻数的引入可适应样本的不同分布, 使样本与其近邻样本之间的相似度较高, 与非相邻样本之间的相似度较低, 便于后续使用Rulkov神经元进行聚类.

获得无向图后, 根据2.1节中的拉普拉斯矩阵谱分解方法, 得到样本特征矩阵

U=[u₁, u₂, …, u_n]∈ R^K^×ⁿ.

2)自适应Rulkov神经元聚类.引入Rulkov神经元模型, 建立根据新的样本特征u_i间距离确定的神经元耦合关系.再利用迭代方式增强具有较高相似度神经元之间的耦合强度.最终, 根据耦合强度矩阵中的强连接关系查找强连通分量, 实现样本的自适应聚类.

ARNC步骤如下所示.

算法 ARNC

输入数据集V={v₁, v₂, …, v_n}∈ R^dim^×ⁿ

输出数据集样本标签

step 1 计算样本间的相似度矩阵W;

step 2 利用相似度矩阵构造拉普拉斯矩阵L;

step 3 根据拉普拉斯矩阵L的前K个最大特征向量, 构建新的样本特征矩阵U;

step 4 根据特征矩阵U, 构建Rulkov神经元网络, 计算耦合强度矩阵G_t的初始值;

step 5 根据神经元间同步度S_t, 更新耦合矩阵G_t;

step 6 当G_t满足停止条件式(3)时, 停止学习, 转step 7, 否则, 转step 5;

step 7 应用Tarjan算法, 实现类的划分, 输出数据集样本标签.

神经元的初始点随机分布在

{x_i_,_t₌₀, y_i_,_t₌₀}={-1, -3},

ARNC相对该初始点是稳定的.原则上可使用的参数范围如表1所示.

表1 ARNC中参数及其范围 Table 1 Parameters and their ranges in ARNC

3 实验及结果分析

3.1 实验数据集及评价指标

本文实验选用部分合成数据集、UCI数据集^[25]和LFW数据集^[26].UCI数据集的具体信息如表2所示.LFW数据集共有1 000多类, 从中随机选取30个类别作为本文实验的部分数据集, LFW数据集是由VGGFace网络中第一个全连接层的4 096维特征构成, 样本总数为645, 样本特征数为4 069, 样本类别数为30, 类别分布属性如下:10/10/17/55/12/21/42/12/21/24/20/11/13/11/53/17/19/17/31/11/17/19/23/28/19/15/60/12/14/11.

表2 实验所用UCI数据集 Table 2 UCI datasets used in experiment

为了评估算法的聚类效果, 本文采用常用的兰德指数(Rand Index, RI)^[27]和F1值(F1-measure, F1)^[28]聚类评价指标进行评价, 2个指标的取值范围均为[0, 1], 指标值越大, 算法聚类效果越优.

兰德指数定义如下:

RI= $\frac{2 (a_{1} + a_{2})}{n (n - 1)}$ .

为了方便描述, 将样本v_i的真实标签记为l_i, 将算法的聚类结果标签记为l'_i, {v_i, v_j}表示样本对, i=1, 2, …, n, j=1, 2, …, n, i≠j.a₁表示数据中真实标签相等(l_i=l_j)且对应的聚类结果标签也相等(l'_i=l'_j)的样本对数;a₂表示数据中真实标签不相等(l_i≠l_j)且对应的聚类结果标签也不相等(l'_i≠l'_j)的样本对数.

F1值定义如下:

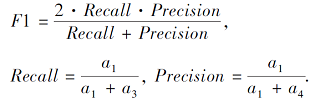
其中:a₃表示数据集中真实标签相等(l_i=l_j), 但对应的聚类结果标签不相等(l'_i≠l'_j)的样本对数;a₄表示数据集中真实标签不相等(l_i≠l_j), 但对应的聚类结果标签相等(l'_i=l'_j)的样本对数.

3.2 对比算法

为了验证ARNC的聚类性能, 选择如下对比算法.基于动态共享最近邻的平均密集谱聚类算法(Spectral Averagely-Dense Clustering Based on Dy-namic Shared Nearest Neighbors, DSNN-SAC)^[24]、自适应谱聚类算法(Self-Tuning Spectral Cluste-ring, STSC)^[29]、基于k质心初始化的聚类算法(Proposed k-Centroid Initialization Algorithm, PkCIA)^[30]、基于间隙的中心自动检测密度峰值聚类算法(Density Peaks Clustering with Gap-Based Automatic Center Detection, GB-DPC)^[31]、RHLC^[18].

STSC针对基于规范化拉普拉斯矩阵的谱聚类算法尺度参数的选择问题, 提出基于第l近邻的确定方法, l通常取7.DSNN-SAC在STSC的相似度矩阵基础上引入共享近邻数, 提高聚类性能.PkCIA针对K-means的初始聚类中心的选择问题进行改进, 在一定程度上提高聚类效果.GB-DPC为基于密度峰值的快速聚类算法的改进算法, 建立在2个假设基础上:1)样本聚类中心点密度较大, 且被一些密度较低的点围绕.2)聚类中心点彼此距离较远.RHLC属于Rulkov神经元聚类算法, 可发现任意结构样本空间的类.

由于DSNN-SAC和STSC计算结果具有不确定性, 将DSNN-SAC和STSC分别执行50次, 取50次实验结果的RI、F1的均值及标准差作为评价指标.由于GB-DPC结果受截断距离参数影响较大, 使用文献[9]方法确定截断距离的取值, 近邻数取值范围为[1, $\sqrt[]{n}$ ], 使用该范围内求得的截断距离参数进行遍历, 取得最好的RI、F1值作为评价指标.由于ARNC、PkCIA和RHLC的计算结果不存在随机性, 故采用单次执行的RI、F1值作为评价指标.

3.3 合成数据集上的实验结果

首先使用同心圆形、双月牙形、火焰形、条形4种合成数据集进行实验, 合成数据集均为2维数据.各算法的RI、F1值如表3和表4所示, 表中黑体数字表示最优结果.

表3 各算法在合成数据集上的RI值对比 Table 3 RI value comparison of different algorithms on synthetic datasets

表4 各算法在合成数据集上的F1值对比 Table 4 F1 value comparison of different algorithms on synthetic datasets

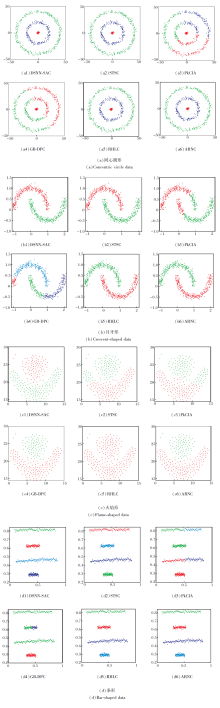
为了直观地观察6种算法, 图2给出6种算法对于合成数据集的聚类结果.由于DSNN-SAC和STSC结果具有不确定性, 图2中给出的均为DSNN-SAC和STSC执行50次后效果最优的结果图.

由表3和表4可看出, DSNN-SAC对于火焰形和条形数据的RI、F1值均低于ARNC, 故DSNN-SAC对于4种合成数据集聚类效果略差于ARNC.虽然DSNN-SAC引入动态共享最近邻, 但直接使用拉普拉斯矩阵谱分解后的样本特征进行聚类, 并未对样本间相似性进一步学习, 当样本特征可分性欠佳时, 聚类效果欠佳.结合表3和表4及图2可看出, STSC对于同心圆形和火焰形数据效果较差, RI、F1值均低于ARNC.主要原因是当初始中心点选择不当时, STSC聚类效果较差.

	Figure Option View Download New Window
	图2 各算法在合成数据集上的聚类结果Fig.2 Clustering results of different algorithms on synthetic datasets

PkCIA将距离较近的样本点划分为一类, 对4种合成数据的评价指标较低, 聚类效果都较差.虽然PkCIA对K-means的初始中心点的选择进行优化, 但依然建立在样本空间为球形域的假设基础上, 当数据不满足该假设条件时(如同心圆形数据和月牙形数据), PkCIA聚类效果较差.

GB-DPC对于同心圆形、月牙形和条形三种合成数据较差, 主要原因是GB-DPC假设聚类中心彼此间距离较远, 聚类中心密度较大且由一些密度较低的点围绕.这三种数据均不满足其假设条件, 故聚类效果较差.

RHLC对于火焰形数据的RI、F1值与ARNC分别相差0.434 6和0.299, 根本原因是RHLC主要通过相邻样本间的耦合作用进行相似性学习, 对于样本特征可分性较差、类间间距较小的不同类, RHLC会将其划分为一类.如火焰形数据所示, 不同类别的相邻样本被划分为同一类, 导致最终聚类效果较差.

综上所述, 对于合成数据集, ARNC性能最优.

3.4 真实数据集上的实验结果

下面在UCI、LFW数据集的8种真实数据上检验各算法的聚类性能.各算法的RI、F1值分别如表5和表6所示, 表中黑体数字表示最优结果.由表5和表6可看出, 在wine、wdbc、ionosphere、breasttissue、LFW上, ARNC的RI值均最高.在seeds、wine、wdbc、ionosphere、breasttissue、LFW上, ARNC的F1值均最高.主要原因是ARNC引入基于自适应距离和共享近邻的相似度矩阵, 增加相邻样本间的相似性, 减小非相邻样本间的相似性.其次, ARNC利用拉普拉斯矩阵的谱分解提取可分性更强的样本特征.再者, ARNC引入Rulkov神经元模型, 实现样本的自适应聚类.上述3个操作均能提高样本的可分性, 获得更优的聚类效果.综上所述, ARNC具有一定的优越性.

表5 各算法在真实数据集上的RI值对比 Table 5 RI value comparison of different algorithms on real datasets

表6 各算法在真实数据集上的F1值对比 Table 6 F1 value comparison of different algorithms on real datasets

在如下实验中, 以UCI数据集中的wine数据为例, 说明ARNC的迭代过程, 实验的可视化^[32]结果如图3所示.图3(a)中给出wine数据的真实类别标签, 图中方框为两个类别的临界区域, 可看出类别间无明显界限, 影响样本的聚类效果.(b)为ARNC第1次迭代的聚类结果, wine数据被分为24类, 由于ARNC中引入自适应距离和共享近邻, 增大样本类间间距, 可看出方框内样本多数被单独分为一类.随着迭代次数的增加, 方框内不同类别不断被合并, ARNC的最终聚类结果如(c)所示.由(c)可看出, ARNC将wine数据最终聚类为3个类别, 并接近于(a)中真实类别标签.

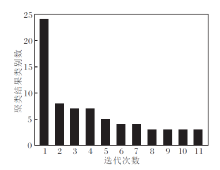
	Figure Option View Download New Window
	图3 ARNC在wine数据集上的可视化结果Fig.3 Visualization results of ARNC on wine dataset

同时, 图4给出ARNC对于wine数据的类别数随迭代次数的变化曲线, 随着迭代次数的增加及不同类的合并, 类别数不断减少.ARNC仅迭代11次即可获得准确类别数, 具有较快的类别迭代收敛速度.

	Figure Option View Download New Window
	图4 ARNC中类别数随迭代次数的变化曲线Fig.4 Curve of category number changing with the iteration number of ARNC

3.5 相似度矩阵的有效性验证

本文的基于自适应距离和共享近邻的相似度矩阵构建方法可避免基于规范化拉普拉斯矩阵的谱聚类算法中尺度参数选择困难的问题, 性能较优.为了验证方法的优越性, 下面将对比两种相似度矩阵构建方法.为了保证对比的公平性, 仅对比相似度矩阵产生的影响, 分别将STSC^[29]中的相似度矩阵构建方法和基于局部标准差谱聚类算法(Local Standard Deviation Spectral Clustering, SDSC)^[33]中的相似度矩阵构建方法替换ARNC中的相似度矩阵构建方法并进行对比.利用8种真实数据进行实验, 得到的对比相似度矩阵聚类效果如表7所示, 表中黑体数字表示最优结果.ST-RNC表示将ARNC中的相似度矩阵替换为STSC中的相似度矩阵后得到的算法.SD-RNC表示将ARNC中的相似度矩阵替换为SDSC中的相似度矩阵后得到的算法, 最近邻参数设置为10.

表7 各算法在真实数据集上的RI、F1值对比 Table 7 RI and F1 value comparison of different algorithms on real datasets

观察表7中ST-RNC和ARNC的评价指标可发现, ARNC的RI指标在iris、zoo、wdbc、ionosphere、LFW数据上均高于ST-RNC.在seeds、iris、zoo、wdbc、ionosphere、LFW数据上ARNC的F1值均高于ST-RNC.故ARNC可获得比ST-RNC更优的聚类效果, 即本文相似度矩阵可获得比STSC中相似度矩阵更优的聚类效果.

观察表7中SD-RNC和ARNC的评价指标可发现, 在iris、zoo、wdbc、LFW数据上, ARNC的RI值均高于SD-RNC.在seeds、iris、zoo、wdbc、breasttissue、LFW数据上, ARNC的F1值均高于SD-RNC.故本文的相似度矩阵可获得比SDSC中相似度矩阵更优的聚类效果.

综上所述, 本文算法能获得比传统相似度矩阵构建算法更优的聚类效果.

3.6 算法复杂度分析

ARNC计算时间主要包括4部分:相似度矩阵W的构建、拉普拉斯矩阵L的谱分解、耦合强度矩阵G_t的学习、强连通分量的查找.各部分的时间复杂度分别为O(n²)、O(n³)、O((r+τ)n)、O(n+e), 其中, r为耦合强度矩阵G_t学习所需的迭代次数, e为G_t学习完成后的强耦合边数.综上所述, 在n较大时, ARNC的时间复杂度为O(n³).DSNN-SAC、STSC、PkCIA的时间复杂度为O(n³), GB-DPC、RHLC的时间复杂度为O(n²).由于ARNC需求解矩阵的特征值及特征向量, 该部分的时间复杂度较高, 所以ARNC与DSNN-SAC、STSC、PkCIA复杂度相当, 但高于DB-DPC和RHLC的时间复杂度.

4 结束语

本文提出自适应Rulkov神经元聚类算法(ARNC).首先引入基于自适应距离和共享近邻的相似度矩阵, 通过拉普拉斯矩阵的谱分解得到大特征值对应的特征向量, 构成新的样本特征, 提高样本的可分性.再将样本看作Rulkov神经元, 根据神经元之间的同步度改变神经元间耦合强度, 进行样本的自适应聚类.分别在合成数据集和真实数据集上对ARNC进行实验验证, 同时与其它算法进行对比分析.实验表明ARNC具有较优的聚类性能, 结果验证ARNC的有效性和优越性.由于ARNC需要进行矩阵的谱分解, 导致算法的复杂度较高, 如何在保证算法性能的前提下, 降低时间复杂度以获得更高的运行效率是后续值得研究的方向.

参考文献

文献选项

[1]	LI J T, LIU Y H, HAO Y. The Improvement and Application of a K-means Clustering Algorithm // Proc of the IEEE International Conference on Cloud Computing and Big Data Analysis. Washington, USA: IEEE, 2016: 93-96. [本文引用:1]
[2]	YANG M M, HUANG Q X, GAO Y F, et al. Dynamic Equivalent Research Based on Fuzzy C-means // Proc of the IEEE Asia Power and Energy Engineering Conference. Washington, USA: IEEE, 2019: 156-160. [本文引用:1]
[3]	SUNGE A S, HERYADI Y, RELIGIA Y, et al. Comparison of Distance Function to Performance of K-medoids Algorithm for Clustering // Proc of the International Conference on Smart Technology and Applications. Washington, USA: IEEE, 2020. DOI: DOI:10.1109/ICoSTA48221.2020.1570615793. [本文引用:1]
[4]	LI Y T, CAI J H, YANG H F, et al. A Novel Algorithm for Initial Cluster Center Selection. IEEE Access, 2019, 7: 74683-74693. [本文引用:1]
[5]	张鑫涛, 马福民, 曹杰, 等. 基于混合度量与类簇自适应调整的粗糙模糊 K-means聚类算法. 模式识别与人工智能, 2019, 32(12): 1141-1150. (ZHANG X T, MA F M, CAO J, et al. Rough Fuzzy K-means Clustering Algorithm Based on Mixed Metrics and Cluster Adaptive Adjustment. Pattern Recognition and Artificial Intelligence, 2019, 32(12): 1141-1150. ) [本文引用:1]
[6]	ZHANG D D, LIU X Y, ZHAO Y Z. Improved K-medoids Clus-tering Algorithm for a Class of P Systems // Proc of the 10th International Conference on Information Technology in Medicine and Education. Washington, USA: IEEE, 2019: 674-678. [本文引用:1]
[7]	ZHANG Y R, DING S F, WANG L J, et al. Chameleon Algorithm Based on Mutual k-Nearest Neighbors. Applied Intelligence, 2020, 51: 2031-2044. [本文引用:1]
[8]	LI X L, LUO M. An Improved Wave Cluster Algorithm Based on ICA // Proc of the 5th International Conference on Wireless Communications, Networking and Mobile Computing. Washington, USA: IEEE, 2009. DOI: DOI:10.1109/WICOM.2009.5302493. [本文引用:1]
[9]	FANG F, QIU L, YUAN S F. Adaptive Core Fusion-Based Density Peak Clustering for Complex Data with Arbitrary Shapes and Densities. Pattern Recognition, 2020, 107. DOI: DOI:10.1016/j.patcog.2020.107452. [本文引用:2]
[10]	王万良, 吴菲, 吕闯. 自动确定聚类中心的快速搜索和发现密度峰值的聚类算法. 模式识别与人工智能, 2019, 32(11): 1032-1041. (WANG W L, WU F, LÜ C. Automatic Determination of Clus-tering Center for Clustering by Fast Search and Find of Density Peaks. Pattern Recognition and Artificial Intelligence, 2019, 32(11): 1032-1041. ) [本文引用:1]
[11]	LI H, LIU X J, LI T, et al. A Novel Density-Based Clustering Algorithm Using Nearest Neighbor Graph. Pattern Recognition, 2020, 102. DOI: DOI:10.1016/j.patcog.2020.107206. [本文引用:1]
[12]	ALSHAMMARI M, STAVRAKAKIS J, TAKATSUKA M. Refining a k-nearest Neighbor Graph for a Computationally Efficient Spectral Clustering. Pattern Recognition, 2021, 114. DOI: DOI:10.1016/j.patcog.2021.107869. [本文引用:1]
[13]	HESS S, DUIVESTEIJN W, HONYSZ P, et al. The SpectACl of Nonconvex Clustering: A Spectral Approach to Density-Based Clustering // Proc of the 33rd AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2019: 3788-3795. [本文引用:1]
[14]	VON LUXBURG U. A Tutorial on Spectral Clustering. Statistics and Computing, 2007, 17(4): 395-416. [本文引用:1]
[15]	NG A Y, JORDAN M I, WEISS Y. On Spectral Clustering: Ana-lysis and an Algorithm // Proc of the 14th International Conference on Neural Information Processing Systems: Natural and Syrithetic. Cambridge, USA: The MIT Press, 2002: 849-856. [本文引用:1]
[16]	RULKOV N F. Modeling of Spiking-Bursting Neural Behavior Using Two-Dimensional Map. Physical Review E, 2002, 65(4). DOI: DOI:10.1103/PhysRevE.65.041922. [本文引用:1]
[17]	SHILNIKOV A L, RULKOV N F. Origin of Chaos in a Two-Dimensional Map Modeling Spiking-Bursting Neural Activity. International Journal of Bifurcation and Chaos, 2003, 13(11): 3325-3340. [本文引用:1]
[18]	HELD J, LORIMER T, ALBERT C, et al. Hebbian Learning Clustering with Rulkov Neurons // Proc of the 13th International Conference on Nonlinear Dynamics of Electronic Systems. Berlin, Germany: Springer, 2017: 127-141. [本文引用:2]
[19]	TAO W B, JIN H, ZHANG Y M. Color Image Segmentation Based on Mean Shift and Normalized Cuts. IEEE Transactions on Systems, Man, and Cybernetics(Cybernetics), 2007, 37(5): 1382-1389. [本文引用:1]
[20]	ZHANG L, WANG D, ZHANG X Q, et al. Simultaneous Learning of Affinity Matrix and Laplacian Regularized Least Squares for Semi-supervised Classification // Proc of the IEEE International Confe-rence on Image Processing. Washington, USA: IEEE, 2018: 1633-1637. [本文引用:1]
[21]	YIN G J. A Contour-Integral Based Method with Schur-Rayleigh-Ritz Procedure for Generalized Eigenvalue Problems. Journal of Scientific Computing, 2019, 81(1): 252-270. [本文引用:1]
[22]	WANG S, ZHANG L. A Supervised Correlation Coefficient Me-thod: Detection of Different Correlation // Proc of the 12th International Conference on Advanced Computational Intelligence. Washington, USA: IEEE, 2020: 408-411. [本文引用:1]
[23]	LOWE G. Concurrent Depth-First Search Algorithms Based on Tarjan's Algorithm. International Journal on Software Tools for Technology Transfer, 2016, 18(2): 129-147. [本文引用:1]
[24]	YUAN C Y, ZHANG L S. Spectral Averagely-Dense Clustering Based on Dynamic Shared Nearest Neighbors // Proc of the 5th International Conference on Computational Intelligence and Applications. Washington, USA: IEEE, 2020: 138-144. [本文引用:2]
[25]	SUN C, YUE S H, LI Q. Clustering Characteristics of UCI Dataset // Proc of the 39th Chinese Control Conference. Washington, USA: IEEE, 2020: 6301-6306. [本文引用:1]
[26]	KAYAL S. Face Verification Experiments on the LFW Database with Simple Features, Metrics and Classifiers // Proc of the 8th International Workshop on Multidimensional Systems. Washington USA: IEEE, 2013: 205-210. [本文引用:1]
[27]	YEH C C, YANG M S. Evaluation Measures for Cluster Ensembles Based on a Fuzzy Generalized Rand Index. Applied Soft Computing, 2017, 57: 225-234. [本文引用:1]
[28]	XIONG H, WU J J, CHEN J. K-means Clustering Versus Validation Measures: A Data-Distribution Perspective. IEEE Transactions on Systems, Man, and Cybernetics (Cybernetics), 2009, 39(2): 318-331. [本文引用:1]
[29]	ZELNIK-MANOR L, PERONA P. Self-tuning Spectral Clustering // Proc of the 17th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2004: 1601-1608. [本文引用:2]
[30]	MANOCHANDAR S, PUNNIYAMOORTHY M, JEYACHITRA R K. Development of New Seed with Modified Validity Measures for k-means Clustering. Computers and Industrial Engineering, 2020, 141. DOI: DOI:10.1016/j.cie.2020.106290. [本文引用:1]
[31]	FLORES K G, GARZA S E. Density Peaks Clustering with Gap-Based Automatic Center Detection. Knowledge-Based Systems, 2020, 206. DOI: DOI:10.1016/j.knosys.2020.106350. [本文引用:1]
[32]	VAN DER MAATEN L, HINTON G. Visualizing Data Using t-SNE. Journal of Machine Learning Research, 2008, 9: 2579-2605. [本文引用:1]
[33]	XIE J Y, ZHOU Y, DING L J. Local Stand ard Deviation Spectral Clustering // Proc of the IEEE International Conference on Big Data and Smart Computing. Washington, USA: IEEE, 2018: 242-250. [本文引用:1]

2016

0.0

... 适用于球形结构样本空间的聚类算法主要包含K均值聚类算法(K-means Clustering Algorithm, K-means)^[1]、模糊C均值聚类算法(Fuzzy C-means Clustering Algorithm, FCM)^[2]和K中心点聚类算法(K-medoids Clustering Algorithm, K-medoids)^[3]等 ...

2019

0.0

2020

0.0

2019

0.0

... 针对初始聚类中心选择困难的问题,学者们提出改进算法^[4,5,6],但这些改进算法大多仍建立在球形结构样本空间假设基础之上,当样本空间非凸时,聚类效果依然较差 ...

2019

0.0

2019

0.0

2020

0.0

... 适用于任意结构样本空间的聚类算法大致分为基于层次的聚类算法^[7]、基于网格的聚类算法^[8]、基于密度的聚类算法^[9,10,11]和基于谱的聚类算法^[12,13]等 ...

2009

0.0

2020

0.0

... 由于GB-DPC结果受截断距离参数影响较大,使用文献[9]方法确定截断距离的取值,近邻数取值范围为[1,n],使用该范围内求得的截断距离参数进行遍历,取得最好的RI、F1值作为评价指标 ...

2019

0.0

2020

0.0

2021

0.0

2019

0.0

2007

0.0

... 基于谱的聚类算法是现在通用聚类算法之一^[14],其中经典方法为基于规范化拉普拉斯矩阵的谱聚类算法^[15] ...

2002

0.0

... 基于谱的聚类算法是现在通用聚类算法之一^[14],其中经典方法为基于规范化拉普拉斯矩阵的谱聚类算法^[15] ...

2002

0.0

... Rulkov神经元模型^[16,17]可模拟大脑皮层的神经元系统的动态行为 ...

2003

0.0

... Rulkov神经元模型^[16,17]可模拟大脑皮层的神经元系统的动态行为 ...

2017

0.0

... Held等^[18]将Rulkov神经元模型用于聚类,提出基于Rulkov神经元的赫布学习聚类算法(Rulkov-Hebbian-Learning Clustering, RHLC),将每个样本看作一个Rulkov神经元,利用样本间距离构建Rulkov神经元网络 ...

... 基于动态共享最近邻的平均密集谱聚类算法(Spectral Averagely-Dense Clustering Based on Dy-namic Shared Nearest Neighbors, DSNN-SAC)^[24]、自适应谱聚类算法(Self-Tuning Spectral Cluste-ring, STSC)^[29]、基于k质心初始化的聚类算法(Proposed k-Centroid Initialization Algorithm, PkCIA)^[30]、基于间隙的中心自动检测密度峰值聚类算法(Density Peaks Clustering with Gap-Based Automatic Center Detection, GB-DPC)^[31]、RHLC^[18] ...

2007

0.0

... 为了提取可分性较好的样本特征,利用标准割(Normalized Cut, Ncut)^[19]将1)中构建的无向图A划分为K个子图A₁,A₂,…,A_K ...

2018

0.0

... 利用规范化拉普拉斯矩阵的性质^[20],可将NCut最小化问题转化如下优化问题: ...

2019

0.0

... 根据Rayleigh-Ritz原理^[21],拉普拉斯矩阵L=D^-1^/²WD^-1^/²的前K个最大特征值对应的特征向量(列向量z_i,i=1,2,…,K)构成的矩阵 ...

2020

0.0

... (1)根据Pearson相关系数^[22]定义神经元之间的同步度矩阵S_t#cod#x02208 ...

2016

0.0

... 再利用Tarjan算法^[23],寻找有向图中的强连通分量,每个强连通分量对应一个类别,从而实现样本聚类 ...

2020

0.0

... 其中:N(v_i)为样本v_i的近邻集合,每个样本的近邻数采用文献[24]方法确定,该方法确定的每个样本近邻数可能各不相同 ...

2020

0.0

... 1 实验数据集及评价指标本文实验选用部分合成数据集、UCI数据集^[25]和LFW数据集^[26] ...

2013

0.0

... 1 实验数据集及评价指标本文实验选用部分合成数据集、UCI数据集^[25]和LFW数据集^[26] ...

2017

0.0

... 为了评估算法的聚类效果,本文采用常用的兰德指数(Rand Index, RI)^[27]和F1值(F1-measure, F1)^[28]聚类评价指标进行评价,2个指标的取值范围均为[0,1],指标值越大,算法聚类效果越优 ...

2009

0.0

2004

0.0

... 为了保证对比的公平性,仅对比相似度矩阵产生的影响,分别将STSC^[29]中的相似度矩阵构建方法和基于局部标准差谱聚类算法(Local Standard Deviation Spectral Clustering, SDSC)^[33]中的相似度矩阵构建方法替换ARNC中的相似度矩阵构建方法并进行对比 ...

2020

0.0

2020

0.0

2008

0.0

... 在如下实验中,以UCI数据集中的wine数据为例,说明ARNC的迭代过程,实验的可视化^[32]结果如图3所示 ...

2018

0.0