基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake

引用本文

李豪, 袁广林, 李从利, 秦晓燕, 朱虹. 基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake. 模式识别与人工智能, 2021,34(11): 1004-1016
LI Hao, YUAN Guanglin, LI Congli, QIN Xiaoyan, ZHU Hong. Deep Snake with 2D-Circular Convolution and Difficulty Sensitive Contour-IoU Loss. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(11): 1004-1016. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202111004
Permissions

《模式识别与人工智能》编辑部

基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake

李豪¹, 袁广林¹, 李从利², 秦晓燕¹, 朱虹¹

1.中国人民解放军陆军炮兵防空兵学院信息工程系合肥 230031

2.中国人民解放军陆军炮兵防空兵学院兵器工程系合肥 230031

通讯作者:

袁广林,博士,副教授,主要研究方向为计算机视觉、机器学习及其应用.E-mail:1183212999@qq.com.

作者简介:

李豪,硕士研究生,主要研究方向为实例分割、目标跟踪、目标检测.E-mail:HaoLi086@163.com.

李从利,硕士,教授,主要研究方向为计算机视觉.E-mail:lcliqa@163.com.

秦晓燕,硕士,副教授,主要研究方向为目标检测、机器学习及其应用.E-mail:70853559@qq.com.

朱虹,硕士,讲师,主要研究方向为图像处理、计算机视觉.E-mail:729039126@qq.com.

收稿日期: 2021-07-08 接受日期: 2021-09-03

资助项目: 安徽省自然科学基金项目(No.2008085QF325)资助

摘要

Deep Snake端到端地变形初始目标框到目标轮廓,能提升实例分割的性能,但存在对初始目标框敏感和轮廓参数独立回归的问题.因此文中提出基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake.首先,基于轮廓的空间上下文信息设计2D循环卷积,解决对初始目标框敏感的问题.然后,基于定积分的几何意义与样本难易度提出难度敏感轮廓交并比损失函数,将轮廓参数进行整体回归.最后,利用2D循环卷积和难度敏感轮廓交并比损失函数完成实例分割.在Cityscapes、Kins、Sbd数据集上的实验证明文中方法的实例分割精度较优.

关键词: 实例分割; 深度主动轮廓; 循环卷积; 难度敏感; 轮廓交并比损失

中图分类号:TP391.41

Deep Snake with 2D-Circular Convolution and Difficulty Sensitive Contour-IoU Loss

LI Hao¹, YUAN Guanglin¹, LI Congli², QIN Xiaoyan¹, ZHU Hong¹

1. Department of Information Engineering, Army Academy of Artillery and Air Defense of People's Liberation Army of China, Hefei 230031

2. Department of Ordnance Engineering, Army Academy of Artillery and Air Defense of People's Liberation Army of China, Hefei 230031

Corresponding author:
YUAN Guanglin, Ph.D., associate professor. His research interests include computer vision, machine learning and its application.

About Author:
LI Hao, master student. His research interests include instance segmentation, object tracking and object detection.
LI Congli, master, professor. His research interests include image computer vision.
QIN Xiaoyan, master, associate professor. Her research interests include object detection, machine learning and its application.
ZHU Hong, master, lecturer. Her research interests include image processing and computer vision.

Fund:Natural Science Foundation of Anhui Province(No.2008085QF325)

Abstract

The initial bounding box is deformed to the object contour end-to-end by Deep Snake, and the performance of instance segmentation is significantly improved. However, the problems of sensitivity to the initial bounding box and independent regression of contour parameters emerge. To address these issues, Deep Snake with 2D-circular convolution and difficulty sensitive intersection over union(contour-IoU) loss is proposed. Firstly, 2D-circular convolution is designed based on the spatial context information of the contour to solve the problem of sensitivity to the initial bounding box. Secondly, difficulty sensitive contour-IoU loss function is proposed according to the geometric meaning of the definite integral and the difficulty of the sample to regress the contour parameters as a whole unit. Finally, instance segmentation is accomplished by the proposed 2D-circular convolution and difficulty sensitive contour-IoU loss function. Experiments on Cityscapes, Kins and Sbd datasets show that the proposed method achieves better segmentation accuracy.

Key words: Key Words Instance Segmentation; Deep Active Contour; Circular Convolution; Difficulty Sensitive; Contour-Intersection over Union Loss

文章图片

本文责任编委黄华

Recommended by Associate Editor HUANG Hua

实例分割是计算机视觉的基本任务之一, 其目标是预测图像中每个实例的位置和掩膜, 在视频分析、自动驾驶和机器人抓取等方面具有广阔的应用前景.相比计算机视觉中图像分类和目标检测等其它任务, 实例分割更具挑战性.近年来, 得益于深度学习的进步, 实例分割取得较快发展, 已涌现许多方法.目前, 实例分割方法主要有区域实例分割方法^{[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}和轮廓实例分割方法^{[11, 12, 13, 14, 15, 16, 17, 18, 19]}两类.

区域实例分割方法有两阶段区域实例分割方法^{[1, 2, 3, 4]}和一阶段区域实例分割方法^{[5, 6, 7, 8, 9, 10]}.Li等^[1]提出FCIS(Fully Convolutional Instance-Aware Semantic Segmentation), 是两阶段区域实例分割方法的早期工作, 该方法同时检测和分割对象实例, 但对物体重叠区域的分割效果不佳.He等^[2]提出Mask R-CNN(Mask Region-Based Convolutional Neural Network), 在Faster-RCNN(Faster Region-Based Convolutional Neural Network)^[20]上增加一个掩膜分支网络, 提高实例分割的精度.Liu等^[3]在Mask R-CNN的基础上聚合底层特征和高层特征, 提出PANet(Path Aggregation Network), 进一步提升实例分割的性能.Zhang等^[4]提出Mask SSD(An Effective Single-Stage Approach to Object Instance Segmentation), 检测子网络和实例分割子网络, 预测目标检测框和分割掩膜, 取得较优的实例分割效果.上述两阶段区域实例分割方法的局限性在于容易受到检测框精度的影响, 速度较慢.

为了提高实例分割的速度, 学者们提出一阶段区域实例分割方法.Dai等^[5]提出InstanceFCN(Instance-Sensitive Fully Convolutional Networks), 利用全卷积网络以滑动窗口的方式生成敏感实例分割建议, 实现一阶段区域实例分割.Liang等^[6]提出PFN(Proposal-Free Network), 利用无建议网络, 提高一阶段实例分割的精度.基于语义像素的实例隶属关系, Liu等^[7]和Gao等^[8]设计端到端的一阶段区域实例分割方法, 提高实例分割的速度.Neven等^[9]提出聚类损失函数, 进一步提升一阶段区域实例分割的性能.Chen等^[10]提出TensorMask(A Foundation for Dense Object Segmentation)通用框架, 将密集实例分割建模为4D张量上的Mask预测任务, 取得与Mask R-CNN相当的结果.总之, 相比两阶段区域实例分割方法, 虽然一阶段区域实例分割方法提升实例分割的速度, 但分割精度较低.

轮廓是目标表示的另一种重要方式, 相比区域表示, 轮廓表示参数较少、较简洁.为了提取目标轮廓, Kass等^[11]提出主动轮廓模型(Snake), 得到广泛关注^{[12, 13, 14]}.方法优化由手工特征定义的能量函数入手, 将初始轮廓迭代变形为目标边界, 然而手工设计的能量函数是非凸的, 容易陷入局部最优解.受到深度学习在目标检测中应用的启发, 学者们提出基于深度学习的轮廓实例分割方法^{[15, 16, 17, 18, 19]}.Jetley等^[15]提出Straight to Shapes(STS), 使用数据驱动的能量函数用于实例分割, 取得较优的实例分割效果.Zhang等^[16]和Yang等^[17]提出直接从RGB图像中回归目标边界点的实例分割方法, 打破通过优化能量函数寻找目标轮廓的思路.Xie等^[18]提出单阶段实例分割框架PolarMask(Single Shot Instance Segmentation with Polar Representation), 使用极坐标系建模轮廓, 将实例分割形式化为实例中心点的分类和密集距离回归问题, 实现高效实例分割.针对区域实例分割方法速度较慢的问题, Peng等^[19]在文献[21]的基础上提出基于深度学习的主动轮廓模型(Deep Snake), 根据轮廓的循环拓扑结构设计1D循环卷积, 用于目标轮廓结构化特征学习, 并以此为基础提出快速准确的轮廓实例分割方法.

综上所述, Deep Snake虽提升实例分割性能, 但存在对初始目标框敏感和轮廓参数独立回归的问题, 降低实例分割的精度.对初始目标框敏感也就是实例分割的精度依赖于目标检测框的准度, 即当目标检测框较准时, 实例分割的精度较高, 反之亦然.Deep Snake使用1D循环卷积进行特征学习, 利用的目标轮廓信息较少, 是对初始目标框敏感的原因之一, 另一方面, Deep Snake利用若干个离散变量描述目标轮廓, 使用Smooth_L₁损失函数^[19]回归目标的轮廓参数.由文献[18]可知:Smooth_L₁损失函数未利用轮廓的整体结构, 造成轮廓回归不准确.

为此, 本文提出基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake.基于轮廓的空间上下文信息设计2D循环卷积, 解决Deep Snake对初始目标框敏感的问题.基于定积分的几何意义和样本难易度提出难度敏感轮廓交并比损失函数, 利用轮廓点的相关性和样本的难易属性将轮廓参数进行整体回归.最后, 结合2D循环卷积和难度敏感轮廓交并比损失函数, 实现实例分割.在Cityscapes、Kins、Sbd数据集上的实验证实本文方法达到预期的分割效果, 整体性能优于Deep Snake.

1 嘻2D循环卷积

目标轮廓是图像上一组有序点V= ${x_{i}}_{i = 1}^{N}$ 的集合, 其中, x_i=(x_i, y_i)为点的坐标, N为点的个数.点x_i的特征f_i=[F(x_i); x'_i], 其中, F(x_i)为点x_i在F上的双线性插值, F为原始输入图像通过卷积神经网络得到的特征图, x'_i=(x_i-x_min, y_i-y_min)为x_i的平移不变坐标,

x_min=min ${x_{i}}_{i = 1}^{N}$ , y_min=min ${y_{i}}_{i = 1}^{N}$ .

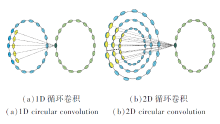
如图1所示, 蓝点表示轮廓上点的特征, 黄点表示核函数, 绿点表示卷积结果, 深绿点表示黄色卷积核与对应的轮廓点进行循环卷积得到的特征.Deep Snake^[19]将轮廓上点的特征向量看作周期信号 $(f_{N})_{i}$ f_i_mod_N, 并定义1D循环卷积如下:

$(f_{N} {* k)}_{i}$ = $\overset{r}{\sum_{j = - r}}$ (f_N)_i₊_jk_j,

	Figure Option View Download New Window
	图1 循环卷积Fig.1 Circular convolution

其中, k为1D卷积核, * 为1D卷积操作.

Deep Snake使用1D循环卷积学习轮廓特征, 未利用轮廓周围点的特征信息, 导致对初始目标框较敏感.轮廓周围点的特征信息也就是轮廓的空间上下文信息, 为此, 本文基于轮廓的空间上下文信息设计2D循环卷积, 用于轮廓特征学习.如图1(b)所示, 轮廓及其上下文信息可构成二维周期信号

f'_N(t, i) f(t, i mod N).

根据1D循环卷积和2D卷积的定义, 本文提出2D循环卷积公式如下:

$(f'_{N} {* K)}_{i}$ = $\overset{d}{\sum_{t = - d}}$ $\overset{r}{\sum_{j = - r}}$ f'_N(t, i+j)K(t, j),

其中, K为2D卷积核, * 为2D卷积操作.

由图1可看出, 相比1D循环卷积, 2D循环卷积不仅利用轮廓的空间结构, 还利用轮廓的循环拓扑结构, 提高对初始目标框的鲁棒性.需要说明的是, 2D循环卷积会提升实例分割精度, 但不可避免地增加计算量, 使实例分割的速度有所下降, 但其速度仍能满足视频数据的实例分割需求.

2 难度敏感轮廓交并比损失函数

Deep Snake^[19]将实例分割转化为轮廓参数的回归问题, 使用的回归损失函数是Smoot ${h_{L 1}}^{[19]}$ .目前, 目标检测和实例分割使用的回归损失函数主要有Smooth _L₁和交并比(Intersection over Union, IoU)^[22].由文献[18]可知, Smooth _L₁损失函数独立回归目标参数, 精度较低, IoU损失函数将目标视为一个整体进行回归, 直接优化评价指标IoU, 具有较高的精度.显然, 利用IoU损失函数可提高轮廓回归的精度.在文献[18]的启发下, 本文提出轮廓交并比(Contour-IoU, C-IoU)计算方法, 如图2所示, 图中红线为标签轮廓, 红点为标签轮廓点x_i={x_i, y_i $}_{i = l}^{N}$ , 黑线为预测轮廓, 黑点为预测轮廓点

${\tilde{x}}_{i}$ ={ ${\tilde{x}}_{i}$ , ${\tilde{y}}_{i}}_{i = l}^{N}$ .

	Figure Option View Download New Window
	图2 轮廓交并比示意图Fig.2 Illustration of contour-IoU

交并比定义为标签轮廓内区域与预测轮廓内区域的交并比.

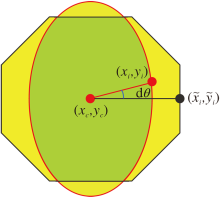
在此基础上定义难度敏感轮廓交并比(Difficulty Sensitive Contour-IoU, DSC-IoU)损失函数.假设x_i为标签轮廓点, ${\tilde{x}}_{i}$ 为预测轮廓点, (x_c, y_c)为实例质心, 质心计算方法与文献[18]相同.如图2所示, 基于定积分的几何意义, 轮廓交并比定义如下:

C-IoU= $\frac{\int_{0}^{2π} \frac{1}{2} \min [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}] d θ}{\int_{0}^{2π} \frac{1}{2} \max [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}] d θ}$ .

将上式转换成如下离散形式:

C-IoU=〔 $\lim_{N \to \infty} \frac{\overset{N}{\sum_{i = 1}} \frac{1}{2} \min [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}] Δθ}{\overset{N}{\sum_{i = 1}} \frac{1}{2} \max [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}] Δθ}$ 〕 .

当N趋于无穷时, 离散形式逼近连续形式.因轮廓各点均匀采样, 故具有同样的角度Δ θ = $\frac{2 π}{N}$ , 所以上式简化为

C-IoU= $\frac{\overset{N}{\sum_{i = 1}} \min [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}]}{\overset{N}{\sum_{i = 1}} \max [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}]}$ .

由文献[22]可知, 交并比损失函数可定义为交并比的负对数, 因此轮廓交并比损失函数可定义为

L_C-IoU=ln〔 $\frac{\overset{N}{\sum_{i = 1}} \max [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}]}{\overset{N}{\sum_{i = 1}} \min [(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}, ({\tilde{x}}_{i} - x_{c})^{2} + ({\tilde{y}}_{i} - y_{c})^{2}]}$ 〕 . (1)

通过复现文献[19]的实验发现:不规则轮廓样本较难回归, 规则轮廓样本较易回归.图3分别给出难样本和易样本示例.由于不规则轮廓样本的标签轮廓点与实例质心距离的标准差σ 较大, 而规则轮廓样本的标签轮廓点与实例质心距离的标准差σ 较小, 因此可使用标签轮廓点与实例质心距离的标准差σ 评价样本的难易程度, 即使用σ 作为样本损失权重λ 的初值.另一方面, 由文献[23]可知:在训练过程中, 需要关注误差较大的样本, 误差的大小可由交并比损失α =1-C-IoU自适应度量, 因此可利用交并比损失α 动态更新样本损失权重λ , 提高对难样本的学习性能.

	Figure Option View Download New Window
	图3 难样本与易样本示意图Fig.3 Illustration of hard and easy samples

由上述分析可知, 难度敏感轮廓交并比(DSC-IoU)损失函数可定义为L_DSC-IoU=λ L_C-IoU, 其中, λ =σ +α 为权重参数, 表示轮廓回归的难易程度,

α =1-C-IoU, σ = $\sqrt[]{\frac{1}{N} \overset{N}{\sum_{i = 1}} (d_{i} {- \bar{d})}^{2}}$ di=, $\sqrt[]{(x_{i} - x_{c})^{2} + (y_{i} - y_{c})^{2}}$ = $\bar{d}$ d $\frac{1}{N} \overset{N}{\sum_{i = 1}}$

实验中λ 在每批数据中进行归一化处理, 保证权重λ 在0和1之间.

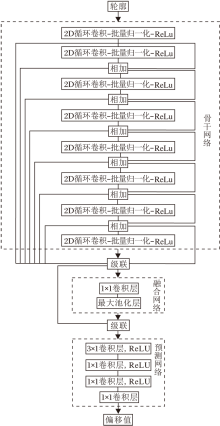
3 基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake

3.1 网络结构

本文设计基于2D循环卷积和难度敏感轮廓交并比损失的Deep Snake(简称为2D-Deep Snake), 网络结构如图4所示.网络由骨干网络、融合网络和预测网络组成.骨干网络由8个2D循环卷积-批量归一化-ReLU层组成, 所有层均使用残差连接.融合网络级联骨干网络中所有层的特征, 通过1× 1卷积层进行特征融合, 再进行最大池化, 最后融合特征与每点的特征级联, 得到最终特征.预测网络通过1个3× 1卷积层和3个1× 1卷积层输出轮廓点的偏移值.

	Figure Option View Download New Window
	图4 2D-Deep Snake网络结构Fig.4 2D-Deep Snake network structure

由图4可看出, 2D-Deep Snake与Deep Snake的主要区别在于本文骨干网络使用2D循环卷积进行特征学习, 以便利用更多的空间上下文信息.由于使用大小为(3, 9)的2D循环卷积核, 故在预测网络中增加一个3× 1的卷积层, 通过轮廓周围的特征信息得到轮廓的偏移值.

3.2 工作流程

由2D-Deep Snake网络结构可得如图5所示的框图, 包括CenterNet、初始轮廓建议和轮廓变形三部分.在损失函数方面, 由于在初始轮廓建议过程中无需计算交并比, 因此采用与Deep Snake相同的极值点预测损失函数, 即

L_ex= $\frac{1}{4} \overset{4}{\sum_{i = 1}}$ Smooth_L1( ${\tilde{x}}^{ex}_{i}$ - ${x^{ex}}_{i}$ ),

	Figure Option View Download New Window
	图5 2D-Deep Snake框图Fig.5 Framework of 2D-Deep Snake

其中, ${\tilde{x}}^{ex}_{i}$ 为极值点的预测坐标, ${x^{ex}}_{i}$ 为极值点的标注坐标.

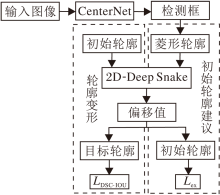
在轮廓变形过程中, 采用本文的难度敏感轮廓交并比损失函数L_DSC-IoU.2D-Deep Snake流程图如图6所示.首先, 输入图像通过CenterNet网络得到目标检测框; 再连接检测框各边的中点得到菱形轮廓; 然后, 菱形轮廓通过2D-Deep Snake得到极值点, 得到八边形轮廓; 最后, 八边形轮廓通过2D-Deep Snake迭代变形为目标轮廓.

	Figure Option View Download New Window
	图6 2D-Deep Snake流程图Fig.6 Flowc hart of 2D-Deep Snake

3.3 初始轮廓建议和轮廓变形

初始轮廓建议采用与文献[19]同样的方法, 即以八边形作为初始轮廓, 构造过程如图7所示.给定一个目标检测框, 首先取4条边的中点{ ${x^{bb}}_{i}$ |i=1, 2, 3, 4}, 连接这4个中点得到菱形轮廓.然后, 将菱形轮廓输入2D-Deep Snake, 得到4个极值点{ ${x^{ex}}_{i}$ |i=1, 2, 3, 4}.最后通过4个极值点构造八边形.

	Figure Option View Download New Window
	图7 八边形构造示意图Fig.7 Illustration of octagon construction

轮廓变形包括3步.首先, 从第1个极值点 ${x^{ex}}_{1}$ 开始在八边形上均匀采样N个点; 再将这N个点通过2D-Deep Snake得到坐标偏移值; 最后, 将N个点的坐标与其偏移值相加得到变形后的轮廓.上述过程迭代M次得到目标轮廓.对于超参数N与M的取值, 本文采用与Deep Snake相同的设置, 即N=128, M=3.

4 实验及结果分析

4.1 实验环境

在SYS-7048GR-TR台式机(CPU型号为Intel Xeon(R)ES-2630v4@2.20 GHz× 20, 内存为64 GB, GPU为RTX2080Ti 11G)上进行实验.软件环境为:Ubuntu 18.04、Python 3.7、torch 1.1.0、cuda10.0和cudnn7.5.考虑到基于34层DLA(Deep Layer Aggrega-tion-34)的CenterNet在检测速度和精度上具有较优的综合性能^[24], 本文所有实验均使用DLA-34作为目标检测器的骨干网络.

本文采用Cityscapes^[25]、Kins^[26]、Sbd^[27]数据集作为实验数据集.Cityscapes数据集包含8种目标, 由2 975幅训练图像、500幅验证图像和1 525幅测试图像组成.Kins数据集包含7种目标, 由7 474幅训练图像和7 517幅测试图像组成.Sbd数据集包含20种目标, 由5 623幅训练图像和5 732幅测试图像组成.

所有实验中均使用多尺度数据增强策略, 学习率初值设为1e^-4.评价指标与文献[19]相同, 即采用AP、AP₅₀、AP₇₀、AP_class、AP_vol、AP_Amodalseg、AP_detection指标, 这些指标的含义和计算方法如下.

对于一个目标, 当其分割掩膜与标注掩膜的 IoU大于阈值IoU_threshold时, 该目标为正样本, 否则为负样本.假设TP表示真正例数, FP表示假正例数, FN表示假反例数, 则某类目标的精度(Precision)和召回率(Recall)的定义如下:

Precision_class= $\frac{TP}{TP + FP}$ ,

Recall_class= $\frac{TP}{TP + FN}$ .

以某类目标的召回率Recall_class为横轴、精度Precision_class为纵轴做图, 得到的曲线称为PR曲线, PR曲线下面积定义为该类目标的平均精度AP_class, 则

AP_class= $\frac{1}{N_{pos}} \sum_{r \in {1 / N_{pos}, 2 / N_{pos}, \dots, N_{pos} / N_{pos}}}$ $\quad$P_interp(r),

其中N_pos为正样本的数量,

P_interp(r)= $\max_{\tilde{r} : \tilde{r} \geq r}$ P( $\tilde{r}$ ),

P( $\tilde{r}$ )为召回率为 $\tilde{r}$ 的精度.

利用AP_class定义一个数据集的平均精度如下:

AP_threshold= $\frac{1}{N_{class}} \overset{N_{class}}{\sum_{t = 1}}$ AP_class,

其中N_class为数据集上的类别数量.

IoU_threshold=0.5, 0.7, 利用AP_threshold得到平均精度AP₅₀和AP₇₀.

IoU_threshold=0.5, 0.55, …, 0.95, 利用AP_threshold得到

AP= $\frac{1}{10} \overset{9}{\sum_{i = 0}}$ AP₅₀₊₅_i.

IoU_threshold=0.1, 0.2, …, 0.9, 得

AP_vol= $\frac{1}{9} \overset{8}{\sum_{i = 0}}$ AP₁₀₊₁₀_i.

AP_Amodalseg为遮挡目标的平均精度, 计算方法与AP相同.AP_detection为检测器的平均精度, 计算方法与AP的区别在于:IoU的定义不同, AP_detection中IoU定义为检测矩形框与标注矩形框的交并比.

4.2 消融实验结果

在Sbd数据集上进行消融实验, 训练2D-Deep Snake共160个周期, 学习率在第80个和第120个周期下降一半.消融实验结果如表1所示.由表可看出, 将Deep Snake中1D循环卷积换为2D循环卷积后, AP_vol提高0.6%.将Deep Snake中轮廓变形阶段的损失函数由Smooth_L1损失函数换为DSC-IoU损失函数后, AP_vol提高0.9%.

表1 各方法的消融实验结果 Table 1 Results of ablation experiment of different methods

为了验证DSC-IoU损失函数的重要性, 对具有Smooth_L1损失函数和不同权重参数的DSC-IoU损失函数的实例分割方法在Sbd数据集上进行实验, 消融实验结果如表2所示, 表中黑体数字表示最优结果.由表可看出, 具有DSC-IoU损失函数的实例分割方法性能优于具有Smooth_L1损失函数的实例分割方法, σ +α 作为权重值时性能最优.

表2 损失函数不同时的消融实验结果 Table 2 Results of ablation experiment with different loss functions

DSC-IoU损失函数和Smooth_L1损失函数的实例分割错误率曲线如图8所示, 由图可看出:DSC-IoU损失函数的错误率下降快于Smooth_L1损失函数, 表明DSC-IoU损失函数具有较快的收敛性.而且DSC-IoU损失函数的错误率曲线平滑度与Smooth_L1损失函数的错误率曲线平滑度近似, 即两种损失函数的稳定性相当.

	Figure Option View Download New Window
	图8 损失函数不同时的错误率曲线Fig.8 Curves of miss rate with different loss functions

4.3 Cityscapes数据集上的实验结果

在Cityscapes数据集上选择如下对比方法:Mask R-CNN^[2]、PANet^[3]、 GMIS(Graph Merge for In- stance Segmentation)^[7]、Spatial(Instance Segmentation by Jointly Optimizing Spatial Embeddings and Clustering Bandwidth)^[9]、Deep Snake^[19]、SGN(Sequential Grouping Networks)^[28]、PolygonRNN++(Efficient In-teractive Annotation of Segmentation Datasets with Po-lygon-RNN++)^[29].采用与Deep Snake^[19]相同的训练策略和参数设置.首先在Cityscapes数据集上单独训练CenterNet网络140个周期, 在第80个和第120个周期学习率下降一半.再训练2D-Deep Snake共200个周期, 在第80个、120个、150个周期下降一半.对于Cityscapes数据集上存在的目标遮挡问题, 本文采用Deep Snake的多组件分割方法.

各方法的指标值对比如表3所示, 表中黑体数字表示最优结果, 对比方法的指标值取自原文献.由表可看出, 2D-Deep Snake的AP值比Deep Snake提高1.1%, AP₅₀值提高0.7%.

表3 各方法在Cityscapes数据集上的指标值对比 Table 3 Index value comparison of different methods on Cityscapes dataset

对于大部分类别, 2D-Deep Snake的AP值均优于Deep Snake, 但AP_truck值比Deep Snake低0.3%.其原因是:Deep Snake采用标注矩形框代替目标检测器输出的矩形框进行训练, 而2D-Deep Snake并未采用这一训练技巧.

2D-Deep Snake与Deep Snake在Cityscapes数据集上的分割结果对比如图9所示, 由图可看出, 2D-Deep Snake的分割精度优于Deep Snake.

	Figure Option View Download New Window
	图9 各方法在Cityscapes数据集上的分割结果Fig.9 Segmentation results of different methods on Cityscapes dataset

对比图9第1列可看出, 2D-Deep Snake对bus的分割精度高于Deep Snake, 且Deep Snake出现误检目标house.对比图9第2列可看出, 2D-Deep Snake对person和train的分割精度高于Deep Snake.对比图9第3列可看出, 2D-Deep Snake准确检测car和truck等目标, 并取得较高的分割精度, 而Deep Snake出现误检.

4.4 Kins数据集上的实验结果

在Kins数据集上选择如下对比方法:FCIS^[1]、Mask R-CNN^[2]、PANet^[3]、Deep Snake^[19]、MNC(Multi-task Network Cascades)^[30]、ORCNN(Occlusion Region-Based Convolutional Neural Network)^[31].采用与Deep Snake^[19]相同的训练策略和参数设置, 即在Kins数据集上训练2D-Deep Snake共150个周期, 分别在第80个和第120个周期学习率衰减为原来的一半和十分之一.

各方法的A ${P_{Amodal}}_{seg}$ 和AP_detection值对比如表4所示, 表中对比方法的指标值取自原文献.由表4可看出, 相比Deep Snake, 2D-Deep Snake的AP_detection值提高0.8%, A ${P_{Amodal}}_{seg}$ 值提高 0.9%.

表4 各方法在Kins数据集上的指标值对比 Table 4 Index value comparison of different methods on Kins dataset

方法	AP_detection	A ${P_{Amodal}}_{seg}$
MNC	20.9	18.5
FCIS	25.6	23.5
ORCNN	30.9	29.0
Mask R-CNN	31.3	29.3
PANet	32.3	30.4
Deep Snake	32.8	31.3
2D-Deep Snake	33.6	32.2

表4 各方法在Kins数据集上的指标值对比 Table 4 Index value comparison of different methods on Kins dataset

2D-Deep Snake和Deep Snake在Kins数据集上的分割结果对比如图10所示.对比图10可看出, 2D-Deep Snake对遮挡目标的分割结果较准确, 虚假目标较少, 即2D-Deep Snake性能优于Deep Snake.

	Figure Option View Download New Window
	图10 各方法在Kins数据集上的分割结果Fig.10 Segmentation results of different methods on Kins dataset

4.5 Sbd数据集上的实验结果

在Sbd数据集上选择如下方法:STS^[15]、Deep Snake^[19]、ESE-Seg(Explicit Shape Encoding for Real-Time Instance Segmentation)^[32].采用与Deep Sna-ke^[19]相同的训练策略和参数设置, 即在Sbd数据集上训练2D-Deep Snake共150个周期, 在第80个和第120个周期学习率下降一半.

各方法的AP_vol、AP₅₀和AP₇₀值对比如表5所示, 表中对比方法的指标值取自原文献, ESE-Sag(20)和ESE-Sag(50)中数字表示嵌入向量的维度.

表5 各方法在Sbd数据集上的指标值对比 Table 5 Index value comparison of different methods on Sbd dataset

由表5可看出, 2D-Deep Snake的AP_vol值比Deep Snake 提高1.5%, 并且高于其它基于轮廓的实例分割方法.

2D-Deep Snake与Deep Snake在Sbd数据集上的分割结果对比如图11所示, 图中蓝色虚线框为分割细节标识框.由对比图可看出, 相比Deep Snake, 2D-Deep Snake得到的目标轮廓更平滑、准确.

	Figure Option View Download New Window
	图11 各方法在Sbd数据集上的分割结果Fig.11 Segmentation results of different methods on Sbd dataset

4.6 特征图对比实验结果

为了验证2D-Deep Snake的轮廓分割能力, 将Deep Snake和2D-Deep Snake中CenterNet输出的特征图进行对比.2D-Deep Snake和Deep Snake在Sbd数据集一幅图像上的特征图对比如图12所示.对比图中灰度特征图和伪彩色特征图可看出, 2D-Deep Snake的平均特征图中目标轮廓较清晰.其原因在于, 2D-Deep Snake使用2D循环卷积和难度敏感轮廓交并比损失函数, 影响CenterNet网络权重参数的学习, 具有更高的轮廓分割精度.

	Figure Option View Download New Window
	图12 Deep Snake和2D-Deep Snake的特征图对比Fig.12 Feature map comparison of Deep Snake and 2D-Deep Snake

4.7 分割效率对比实验

为了验证2D-Deep Snake各组件对实例分割效率的影响, 在Sbd数据集(图像大小为512× 512)上对比运行时间, 结果如表6所示.

表6 各方法的运行时间对比 Table 6 Running time comparison of different methods

综合表1和表6可看出:2D循环卷积对实例分割精度有所提升, 但是降低速度; DSC-IoU损失函数提升实例分割的精度, 对实例分割的速度没有影响; 2D循环卷积和DSC-IoU损失函数共同作用会提升实例分割的精度, 同时降低实例分割的速度, 但仍具有实时性.

4.8 卷积核大小对比

本次实验中2D循环卷积核大小设置为(3, 9), 3为卷积核的宽度, 9为卷积核的长度.卷积核的宽度决定使用轮廓上下文信息的多少, 卷积核的长度决定使用轮廓点信息的数量.文献[19]表明:卷积核的长度设置为9较优.对于卷积核宽度的取值, 本文进行实验分析, 结果如表7所示.由表可看出, 综合速度和精度指标, 2D循环卷积核大小设置为(3, 9)较优.更大的卷积核会增大网络的参数量, 降低分割速度; 更小的卷积核不能精确提取物体特征, 降低分割精度.

表7 卷积核大小对指标值的影响 Table 7 Effect of convolution kernel size on index values

4.9 损失函数性能推广

需要说明的是, C-IoU损失函数不但可用于轮廓分割, 还可推广到目标检测中.本文将C-IoU损失函数应用于CenterNet, 即在CenterNet中加入C-IoU损失函数.其中C-IoU损失函数的计算方法如下.首先, 在数据准备阶段将标注矩形框拟合为与其等面积的椭圆作为标注值; 然后, 在训练阶段将CenterNet输出的目标矩形框也拟合为与其等面积的椭圆作为预测值; 最后, 在椭圆上均匀采样N个点, 利用式(1)计算C-IoU损失函数.

对加入C-IoU损失函数的CenterNet在COCO数据集上的实验结果如表8所示, N=128.由表可看出, C-IoU损失函数提升目标检测精度, 但对目标检测速度没有影响.

表8 COCO数据集上C-IoU的加入对结果的影响 Table 8 Effect of adding C-IoU into COCO dataset on results

5 结束语

针对Deep Snake存在的对初始目标框敏感和轮廓参数独立回归的问题, 本文提出基于2D循环卷积和难度敏感轮廓交并比损失函数的Deep Snake(简称为2D-Deep Snake).一方面, 使用2D循环卷积进行轮廓特征学习, 利用轮廓的空间上下文信息, 增强对初始目标框的鲁棒性.另一方面, 使用难度敏感轮廓交并比损失函数将轮廓参数进行整体回归, 利用轮廓点的相关性和样本的难易属性, 提升实例分割的精度.在Cityscapes、Kins、Sbd数据集上的实验结果表明, 相比Deep Snake, 2D-Deep Snake取得更好的实例分割效果.虽然本文方法在提升实例分割精度的同时对速度有所降低, 但仍具有实时性.

参考文献

文献选项

[1]	LI Y, QI H Z, DAI J F, et al. Fully Convolutional Instance-Aware Semantic Segmentation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 4438-4446. [本文引用:]
[2]	HE K M, GKIOXARI G, DOLLAR P, et al. Mask R-CNN // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 2980-2988. [本文引用:]
[3]	LIU S, QI L, QIN H F, et al. Path Aggregation Network for Instance Segmentation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8759-8768. [本文引用:]
[4]	ZHANG H, TIAN Y L, WANG K F, et al. Mask SSD: An Effective Single-Stage Approach to Object Instance Segmentation. IEEE Transactions on Image Processing, 2020, 29(1): 2078-2093. [本文引用:]
[5]	DAI J F, HE K M, LI Y, et al. Instance-Sensitive Fully Convolutional Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 534-549. [本文引用:]
[6]	LIANG X D, LIN L, WEI Y C, et al. Proposal-Free Network for Instance-Level Object Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(12): 2978-2991. [本文引用:]
[7]	LIU Y D, YANG S Y, LI B, et al. Affinity Derivation and Graph Merge for Instance Segmentation // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 708-724. [本文引用:]
[8]	GAO N Y, SHAN Y H, WANG Y P, et al. SSAP: Single-Shot Instance Segmentation with Affinity Pyramid. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(2): 661-673. [本文引用:]
[9]	NEVEN D, DE BRABANDERE B, PROESMANS M, et al. Instance Segmentation by Jointly Optimizing Spatial Embeddings and Clustering Band width // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 8829-8837. [本文引用:]
[10]	CHEN X L, GIRSHICK R, HE K M, et al. TensorMask: A Foundation for Dense Object Segmentation // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 2061-2069. [本文引用:]
[11]	KASS M, WITKIN A, TERZOPOULOS D. Snakes: Active Contour Models. International Journal of Computer Vision, 1988, 1(4): 321-331. [本文引用:]
[12]	周昌雄, 于盛林, 吴陈, 等. 基于先验知识和区域信息的Snake模型图像分割研究. 模式识别与人工智能, 2006, 19(2): 257-261. (ZHOU C X, YU S L, WU C, et al. Research on Image Segmentation Based on Snake Model of Previous Knowledge and Region Information. Pattern Recognition and Artificial Intelligence, 2006, 19(2): 257-261. ) [本文引用:]
[13]	李春明, 李玉山, 张大朴, 等. 基于PCA/Snake混合模型的运动目标外轮廓求解. 模式识别与人工智能, 2007, 20(3): 313-318. (LI C M, LI Y S, ZHANG D P, et al. Contour Extraction of Mo-ving Objects Based on PCA/Snake Mixture Model. Pattern Recognition and Artificial Intelligence, 2007, 20(3): 313-318. ) [本文引用:]
[14]	李敏, 梁久祯, 廖翠萃, 等. 基于聚类信息的活动轮廓图像分割模型. 模式识别与人工智能, 2015, 28(7): 665-672. (LI M, LIANG J Z, LIAO C C, et al. Active Contour Model for Image Segmentation Based on Clustering Information. Pattern Re-cognition and Artificial Intelligence, 2015, 28(7): 665-672. ) [本文引用:]
[15]	JETLEY S, SAPIENZA M, GOLODETZ S, et al. Straight to Shapes: Real-Time Detection of Encoded Shapes // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 4207-4216. [本文引用:]
[16]	ZHANG L S, BAI M, LIAO R J, et al. Learning Deep Structured Active Contours End-to-End // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8877-8885. [本文引用:]
[17]	YANG Z, XU Y H, XUE H, et al. Dense RepPoints: Representing Visual Objects with Dense Point Sets[C/OL]. [2021-06-26]. https://export.arxiv.org/pdf/1912.11473. [本文引用:]
[18]	XIE E Z, SUN P E, SONG X G, et al. PolarMask: Single Shot Instance Segmentation with Polar Representation // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 12190-12199. [本文引用:]
[19]	PENG S D, JIANG W, PI H J, et al. Deep Snake for Real-Time Instance Segmentation // Proc of the IEEE Conference on Compu-ter Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 8533-8542. [本文引用:]
[20]	REN S Q, HE K M, GIRSHICK R, et al. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. [本文引用:]
[21]	LING H, GAO J, KAR A, et al. Fast Interactive Object Annotation with Curve-GCN // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 5252-5261. [本文引用:]
[22]	YU J H, JIANG Y N, WANG Z Y, et al. UnitBox: An Advanced Object Detection Network // Proc of the 24th ACM International Conference on Multimedia. New York, USA: ACM, 2016: 516-520. [本文引用:]
[23]	FREUND Y, SCHAPIRE R E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. Journal of Computer and System Sciences, 1997, 55(1): 119-139. [本文引用:]
[24]	ZHOU X Y, WANG D Q, KRÄHENBÜHL P. Objects as Points[C/OL]. [2021-06-26]. https://arxiv.org/pdf/1904.07850.pdf. [本文引用:]
[25]	CORDTS M, OMRAN M, RAMOS S, et al. The Cityscapes Dataset for Semantic Urban Scene Understand ing // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 3213-3223. [本文引用:]
[26]	QI L, JIANG L, LIU S, et al. Amodal Instance Segmentation with Kins Dataset // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 3009-3018. [本文引用:]
[27]	HARIHARAN B, ARBELÁEZ P, BOURDEV L, et al. Semantic Contours from Inverse Detectors // Proc of the International Confe-rence on Computer Vision. Washington, USA: IEEE, 2011: 991-998. [本文引用:]
[28]	LIU S, JIA J Y, FIDLER S, et al. SGN: Sequential Grouping Networks for Instance Segmentation // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 3516-3524. [本文引用:]
[29]	ACUNA D, LING H, KAR A, et al. Efficient Interactive Annotation of Segmentation Datasets with Polygon-RNN++ // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 859-868. [本文引用:]
[30]	DAI J F, HE K M, SUN J. Instance-Aware Semantic Segmentation via Multi-task Network Cascades // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 3150-3158. [本文引用:]
[31]	FOLLMANN P, KONIG R, HÄRTINGER P, et al. Learning to See the Invisible: End-to-End Trainable Amodal Instance Segmentation // Proc of the IEEE Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2019: 1328-1336. [本文引用:]
[32]	XU W Q, WANG H Y, QI F B, et al. Explicit Shape Encoding for Real-Time Instance Segmentation // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 5168-5177. [本文引用:]