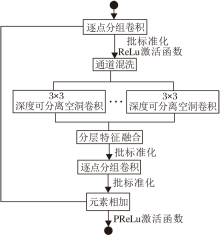
Dilated LightNet^[14]使用不同扩张率的空洞卷积多尺度地提取每个分组的信息, 基本单元如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 Dilated LightNet基本单元[14]Fig.1 Dilated LightNet unit[14]

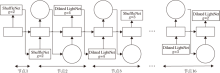
但是, 多层串联的Dilated LightNet单元会放大空洞卷积的网格效应.为了解决这一问题, 在网络架构上混合使用ShuffleNet单元与Dilated LightNet单元, 保证在提取多尺度特征的同时减少网格效应的负面影响.具体网络架构如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Dilated LightNet网络架构[14]Fig.2 Dilated LightNet architecture[14]

图2中的Dilated LightNet网络架构由人工设计得到, 为了避免次优问题, 本文通过神经网络结构搜索的方式搜索整体网络架构, 分组结构作为整体网络架构一部分可同时进行搜索.神经网络结构搜索主要分为控制器和生成器^[16].

控制器是一个长短期记忆网络(Long Short-Term Memory, LSTM), 以一定的概率对表示不同网络结构的子模型进行采样, 生成一串表示网络结构的序列.例如, Dilated LightNet网络需要搜索的部分共16层, 每层可选的单元包括不同分组的Shuffle-Net单元和Dilated LightNet单元共8种, LSTM由16个节点组成, 每个节点输出0~7之间的整数, 16个节点输出组成的序列表示采样的网络结构.LSTM通过Softmax分类器以自回归的方式对决策进行采样, 上一步的输出作为下一步的输入.

生成器部分是CNN, 本文使用Dilated LightNet网络, 根据控制器采样的网络结构, 即生成序列, 构建同样结构的网络, 在训练集上训练以收敛, 并在验证集上测试得到准确率.控制器使用策略梯度方法, 最大化生成器在验证集上获得准确率并更新控制器参数, 随着迭代次数的增加, 控制器生成更优的网络结构.

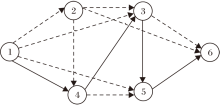
CANAS最终迭代的所有结构都可视为一个更大结构的子结构, 可使用一个有向无环图^[16]表示CANAS的搜素空间.图3为CANAS的有向无环图示例, 通过采样有向无环图的子图获得特定的网络结构, 实线连接的子图就是一种网络结构.简单来说, CANAS的有向无环图是所有可能的子模型在搜索空间中的叠加, 其中, 节点表示具体的单元, 边表示信息流向.CANAS保存每个节点单元的参数, 每次只更新被激活节点的参数, 保证每次采样完成后生成器不必重新训练, 只在之前训练的参数基础上更新, 因此所有子模型的参数共享.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 CANAS的有向无环图Fig.3 Direct acyclic graph of CANAS

根据搜索的目标不同, 有向无环图中节点的单元也有所变化.从全局尺度上看, 如果要搜索整体的网络结构, 则每个节点就应该是网络中完整的一层.从局部的尺度上看, 如果想要搜索用于搭建整体网络的具体单元, 那么每个节点应该是不同的计算操作, 如不同参数的卷积池化等操作.如果想要同时解决每层分组结构与卷积结构的问题, 每个节点应该是不同分组的ShuffleNet单元和Dilated LightNet单元.具体的搜索空间如图4所示, 图中g为分组数.根据图2中的网络架构, 搭建成图4中的搜索空间, 前两层和后两层保持不变, 中间16层中每层具体的单元需要通过搜索得到, 实线连接的结构表示控制器采样生成的网络架构.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 结合不同分组的搜索空间Fig.4 Search space consisting of different groups

在CANAS框架中, 有2个可学习的参数:控制器LSTM的参数θ 、子模型的共享参数ω .整体的训练过程由2个阶段交替进行, 第一阶段通过数据集训练子模型的共享参数ω , 梯度Δ _ω 使用标准的反向传播计算.第二阶段是对θ 进行固定步数的训练, 使用强化学习更新参数.

1)训练子模型的共享参数ω .首先固定控制器的策略π (m; θ ), 并对ω 使用随机梯度下降法(Sto-chastic Gradient Descent, SGD)最小化期望损失函数E_m~π [L(m; ω )], L(m; ω )为使用采样自π (m; θ )的子模型m在训练集上以minibatch方式计算的标准交叉熵损失.可通过蒙特卡洛估计得到梯度, 即

ΔωEm~π(m; θ)[L(m; ω )]≈ 1M∑i=1MΔ _ω L(m_i; ω ),

上式是梯度 ΔωEm~π(m; θ)[L(m; ω )]的一个无偏估计, 这个估计在m固定时方差大于标准SGD梯度.然而在实验中发现, M=1时也可取得较优效果, 即可使用从π (m; θ )采样的任何单一模型m的梯度以更新ω .

2)训练控制器参数θ .本文固定ω 更新θ , 目标是最大化期望奖励E_{m~π (m; θ )}[R(m, ω )].奖励R(m, ω )是在验证集上计算得到, 目的是鼓励CANAS选择泛化性更优的模型而不是过拟合训练集的模型.在图像分类实验中, 奖励函数是模型在验证集上的准确率.本文采用自适应矩估计(Adaptive Moment Estimation, Adam)优化器, 由强化学习算法计算得到梯度, 使用移动平均基线减少方差.

在强化学习计算梯度的过程中, 本文将控制器产生的序列看作是一系列的动作, 记做a_{1∶ G}, 这些序列表示生成的网络结构.将生成器在验证集上的准确率记作R, 为了找到最佳网络结构, CANAS要求控制器最大化其期望奖励, 重新表示为

J(θ )= EP(a1∶G; θ)[R].

由于奖励R不可微, 需使用策略梯度方法迭代更新θ .本文使用REINFORCE方法^[17], 梯度

Δ _θ J(θ )= ∑g=1GEP(a1∶G; θ)[Δ _θ ln P(a_g|a_{(g-1)∶ 1}; θ )R],

根据经验上式约等于

1N∑n=1N∑g=1GΔ _θ ln P(a_g|a_{(g-1)∶ 1}; θ )R_n,

其中, N为控制器在一个批次中采样的不同结构的数量, G为控制器设计网络结构时输出的序列长度.上式是对梯度的无偏估计, 但有相对较大的方差, 为了减少这一估计的方差, 采用基线函数:

1N∑n=1N∑g=1GΔ _θ ln P(a_g|a_{(g-1)∶ 1}; θ )(R_n-b). (1)

只要基线函数b不依赖于当前动作, 这仍是一个无偏梯度估计.此处, 基线b是之前网络结构准确率的指数移动平均值.

神经网络结构搜索算法只是将最大化准确率作为搜索目标, 然而在实际应用中通常还要考虑其它条件.例如, 本文的目标轻量化可使用浮点计算量进行量化表示.基于上述原因, 讨论神经网络结构搜索(Neural Architecture Search, NAS)的多目标优化问题, 为了在不同目标的权衡中选择理想的结果, 需要计算该问题的帕累托前沿, 即一组帕累托最优的网络结构.

对于NAS而言, 可能存在的结构数量非常多, 结构评估的成本很高, 因此较难准确高效地获得完整的帕累托前沿.关于多目标NAS的大多工作都依靠标量化的方式以近似帕累托前沿, 即通过加权和或乘积的方式将多个目标合为一个:

R(m)=Acc(m)· 〔flop(m)F〕α, α = -1, flops(m)> F0, flops(m)≤F(2)

此奖励函数是一种复杂的标量化方式, 其中, Acc表示模型m在验证集上的准确率, flops表示模型m的浮点计算量, F表示目标浮点计算量, 只有在模型浮点计算量高于目标计算量时, 函数右边才会变成一个小于1的惩罚项, 用于控制奖励函数的整体值.

然而, 为了获得多个帕累托最优解, 需要在不同目标计算量下多次运行NAS, 这会消耗大量的计算资源.为了准确高效地搜索整个帕累托前沿, 本文提出循环退火搜索策略(Cycle Annealing Search, CAS).不同于传统多目标NAS, 本文的奖励函数是非平稳的, 可随搜索进程的推进不断调整策略, 有效产生整个帕累托前沿, 奖励函数

R(m)=Acc(m)· exp〔- flops(m)-Fλ·δ〕. (3)

式(3)重点在于奖励函数的右半部分, CANAS将整个搜索过程分为加热和退火两个阶段, 退火阶段又分为慢退火和快退火两个阶段, 在不同阶段用于控制惩罚项参数λ · δ 发生变化.以外, 在退火阶段设F∈ [F_min, F_max].

由式(3)可见, 想要获得更高的奖励取决于模型的准确率和每秒浮点计算量(Floating Point Ope-rations per Second, FLOPs).如果θ 表示目标计算量为f时的最优控制器参数, 可认为f附近的目标计算量f'的最优控制器参数θ '也应接近θ .因此, 假设已知目标计算量f时的最佳控制器策略为π , 从已知的最优策略π 开始, 只需经过少量计算就可得到f附近目标计算量为f'的最佳控制器策略π '.

综上所述, 本文的循环退火搜索算法步骤如下.

算法 CAS

输入 数据集D, 目标计算量[F_min, F_max],

惩罚项参数δ _warm、δ _anneal, 循环周期T,

循环次数N_warm、N_{slow_anneal}、N_{fast_anneal}

输出 子模型结构及性能的集合

{m, flops(m), Acc_valid(m), Acc_test(m)}

1.随机初始化控制器参数θ

2.随机初始化子模型的共享参数ω

//加热阶段

3.设F=F_min, λ =1, δ =δ _warm

4.for step=1 to N_warmdo:

5. 控制器采样子模型m

6. 使用训练集D_train更新ω

7. 使用验证集D_valid的准确率, 根据式(3)计算奖

励r

8. 使用奖励r更新参数θ

9. 在测试集D_test评估模型m

10.end for

//慢退火阶段

11.设λ =1, δ =δ _anneal

12.for step=1 to N_{slow_anneal} do

13. 设

F=F_min+ Fmax-Fmin2·

(1-cos(2π · step·mod(T+1)T))

//mod为取模函数

14. 重复5~9

15. 更新m, flops(m), Acc_valid(m), Acc_test(m)

16.end for

//快退火阶段

17.设0< λ < 1, δ =δ _anneal

18.for step=1 to N_{fast_anneal}do

19. 设λ =λ ^(Ceil(step/T)) //Ceil为向上取整函数

20. 重复13~15

21.end for

CAS可细分为三个阶段.第一阶段为加热阶段, 在此阶段学习得到最小目标计算量F_min时的最优策略, 为后续的退火过程做准备, 此时的δ _warm为一个较大的值, 对奖励函数惩罚也相对较小.第二阶段为慢退火阶段, 此时引入参数循环周期T, 目标计算量F会在循环周期T内从F_min遍历至F_max.同时δ _anneal为一个更小的值, 意味着惩罚力度更大.第三阶段是快退火阶段, 相比慢退火阶段, 此时只有参数λ 发生变化, 设为一个0~1之间的小数, 随着循环次数的增加, λ 会越来越小, λ · δ 整体会变得更小, 这意味着随着循环次数的增加, 同时也是迭代次数的增加, 模型浮点计算量偏离目标计算量付出的代价也越来越大.

综上所述, CAS将在慢退火阶段和快退火阶段以不同的惩罚力度学习所有目标计算量时的最优策略, 在退火阶段结束时, 就可得到整个帕累托前沿.

本文实验使用MNIST^[18]、CIFAR-10、CIFAR-100^[19]数据集, 三者均为分类任务.MNIST数据集由0~9的手写数字组成, 图像大小为28× 28, 训练集包含60 000幅图像, 测试集包含10 000幅图像.CIFAR-10数据集包含10种类别, CIFAR-100数据集包含100种类别, 图像大小均为32× 32, 训练集包含50 000幅图像, 测试集包含10 000幅图像.

实验使用Pytorch深度学习框架, 全部实验均采用相同的软硬件和参数配置, CPU为Intel Broadwell E5-2620V4, GPU为GeForce RTX 2080 Ti, 显存大小为12 GB, 内存大小为128 GB, 操作系统为Ubuntu 16.04LTS, 开发语言为Python3.6.

实验分为2类:1)神经网络结构搜索实验, 用于搜索网络结构; 2)常规的模型训练测试实验, 用于验证模型的有效性.2类实验在训练时均采用相同的数据增强方法, 包括随机裁剪和几何翻转等.在神经网络结构搜索的训练中, 将CIFAR训练集再次划分, 其中45 000幅作为训练集, 剩下5 000幅作为验证集, MNIST训练集分为50 000幅和10 000幅.此外, 为了与ShuffleNet网络进行对比分析, 网络的输入图像分辨率大小为224× 224, 当与输入为224× 224的方法对比时, 数据集的图像都使用双线性插值法将原图像变为224× 224.当使用CIFAR数据集原图尺寸输入时, Dilated LightNet网络去除开始的卷积层和池化层.此外, 由于MNIST数据集较简单, Dilated LightNet网络去除池化层, 每个阶段只保留两层单元.

实验中参数涉及到CANAS的控制器和生成器参数及生成网络的实验参数, 大部分参数设置参考ENAS^[16].CANAS的控制器是一个16层的LSTM, 即式(1)中G=16, 采样数量N=10, 使用学习率为0.001的Adam优化器进行训练.为了防止过早收敛, 本文对控制器logits添加一个值为1.5的tanh常数, 将控制器的样本熵添加到奖励中, 权重为0.1.生成器是根据控制器生成的CNN, 初始学习率设为0.05.其它设置与生成网络的设置相同, 迭代次数为300.同时为了保证网络中每层的通道数能被不同的分组数整除, 本文设置阶段2、阶段3、阶段4的输出通道数分别为288、576、1 152.对于循环退火搜索算法中的参数, 由于该通道数下的生成网络最低计算量为83 M, 所以设F_min=8× 10⁷, 为了确保搜索到的网络计算量低于ShuffleNet网络的最低计算量136 M, 设F_max=1.2× 10⁸.由于搜索过程中的重点阶段是快退火阶段, 在该阶段不断更新帕累托前沿, 所以将总迭代次数中的较大部分分配给快退火阶段, 前两个阶段只要训练至接近收敛即可, 循环周期T=50, 因此

N_warm=50, N_{slow_anneal}=50, N_{fast_anneal}=200.

另外,

δ _warm= 12(F_max-F_min), δ _anneal= 12α(F_max-F_min),

其中, α 表示控制惩罚项的重要参数.α 不同时CANAS的准确率和计算量对比如图5所示.由图可知, α =2时效果最优.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 α 不同时CANAS的准确率和计算量Fig.5 Accuracy and FLOPs of CANAS with different α

对于生成网络的测试, 使用带动量的随机梯度下降法更新参数, 损失函数使用交叉熵损失, 动量设置为0.9, 权重衰减设置为0.000 25, 批大小设置为128, 迭代次数设置为300.初始学习率设置为0.02, 使用余弦退火学习率调整方法^[20], 循环周期设置为10, 最小学习率设置为0.000 5.

本文在3个数据集上所有实验的参数设置都保持一致.

本文将不同分组的ShuffleNet单元和Dilated LightNet单元作为搜索空间, 使用CANAS搜索新网络结构的Dilated LightNet(Dilated LightNet+CANAS).对搜索得到的Dilated LightNet网络的性能进行实验评价, 验证有效性.分别在3个数据集上进行神经网络结构搜索的实验, 控制器的输出如图6所示, 每个节点输出一层网络使用的单元.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 控制器的输出示意图Fig.6 Illustration of controller output

在CIFAR-10、CIFAR-100数据集上搜索的网络结构分布如图7所示.由图可见, 实验中有些网络结构在验证集上的准确率明显低于其它网络结构, 这是由于在搜索过程中, 神经网络结构搜索算法只能尽量靠近目标计算量, 并不能准确得到符合目标计算量的绝对最佳网络结构, 因此, 由于网络结构上的细微差异, 每次得到的网络计算量带有一定的随机性.可能在之后的循环中, 一些计算量下的网络结构不会被再次搜索到, 也就不可能更新参数获得更高的准确率, 所以在不丢弃这些网络结构的情况下, 其在图中表现为准确率较低的点.搜索的网络结构收敛在最小目标计算量与最大目标计算量之间, 选取空心点标注的准确率最高的网络结构用于之后的实验.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 在2个数据集上搜索的网络结构Fig.7 Network architecture searched on 2 datasets

搜索得到的网络结构在3个数据集上的指标值结果如表1所示, 在表中, CIFAR-10数据集上分组数为4, CIFAR-100数据集上ShuffleNet网络的分组数为8, Dilated LightNet网络的分组数为4.

表1

Table 1

表1(Table 1)

表1 各网络在2个数据集上的指标值结果 Table 1 Index values of different networks on 2 datasets 网络 CIAFR-10 CIFAR-100 准确率/% 计算量/M 参数量/M 准确率/% 计算量/M 参数量/M ShuffleNet 92.26 133 0.90 69.75 137 1.07 Dilated LightNet 93.63 134 0.90 72.15 134 1.00 Dilated LightNet+CANAS 93.49 88 0.55 72.36 99 0.71

表1 各网络在2个数据集上的指标值结果 Table 1 Index values of different networks on 2 datasets

ShuffleNet网络和Dilated LightNet网络均选择4种分组中准确率最高的结果, 在CIFAR-10数据集上, 相比ShuffleNet网络, Dilated LightNet+CANAS网络准确率增加1.23%, 计算量减少33.8%, 参数量减少38.8%.相比Dilated LightNet网络, Dilated Light-Net+CANAS网络的准确率基本保持一致, 但计算量只有原来的65.6%, 参数量只有原来的61.1%.Dilated LightNet+CANAS网络在CIFAR-100数据集上表现更佳.相比ShuffleNet网络, 计算量减少27.7%, 参数量减少33.6%, 准确率增加2.61%.相比Dilated LightNet网络, Dilated LightNet+CANAS网络的准确率略有提升, 计算量只有原来的73.8%, 参数量只有原来的71%.由此说明本文结合循环退火搜索策略的神经网络结构搜索算法的有效性, 也验证关于分组结构会影响模型表达的假设.

本文的循环退火搜索策略是为了解决神经网络结构搜索中的多目标优化问题, 当神经网络结构搜索只将准确率作为搜索目标时, 得到的网络往往为了准确率倾向于搜索到计算量更大的网络结构, 无法实现网络的轻量化.本节提出如下对比方法:直接使用ENAS、将离散的搜索空间松弛为可导的连续空间的可微架构搜索(Differentiable Architecture Search, DARTS)^[21]、在ENAS基础上使用标量化多目标优化的标量化多目标搜索(Scalar Multi-objec-tive Search, SMS)、使用循环退火搜索策略的CANAS.对比分析各方法性能, 验证CANAS中循环退火搜索策略的有效性.

SMS使用的奖励函数如式(2)所示, 目标浮点计算量F=1.4× 10⁸, 训练方法和参数设置与2.2节中本文方法相同.其它方法的参数设置与原文献完全一致, 实验中本文方法的参数设置也与2.2节保持一致, 实验结果如表2所示.

表2

Table 2

表2(Table 2)

表2 不同搜索算法得到的Dilated LightNet网络在2个数据集上的实验结果 Table 2 Experimental results of Dilated LightNet obtained by different search algorithms on 2 datasets 网络 CIAFR-10 CIFAR-100 准确率/% 计算量/M 参数量/M 准确率/% 计算量/M 参数量/M Dilated LightNet+ENAS 93.87 196 1.34 72.71 197 1.66 Dilated LightNet+DARTS 93.76 191 1.04 72.69 191 1.15 Dilated LightNet+SMS 93.41 102 0.61 72.46 133 1.03 Dilated LightNet+CANAS 93.49 88 0.55 72.36 99 0.71

表2 不同搜索算法得到的Dilated LightNet网络在2个数据集上的实验结果 Table 2 Experimental results of Dilated LightNet obtained by different search algorithms on 2 datasets

从CIFAR-10数据集上的实验结果可看出, Dilated LightNet+CANAS网络的计算量只有Dilated LightNet+ENAS网络的44.8%, 参数量也只有Dilated LightNet+ENAS网络的41%, 准确率比Dilated LightNet+ENAS网络下降0.38%.相比Dilated LightNet+DARTS网络, Dilated LightNet+CANAS网络结果也相似.进一步与Dilated LightNet+SMS网络对比, Dilated Light-Net+CANAS网络在准确率、计算量和参数量上都有更优表现.

在CIFAR-100数据集上, Dilated LightNet+CANAS网络在准确率基本保持不变的基础上:相比Dilated LightNet+ENAS网络, 计算量减少49.7%, 参数量减少57.2%; 相比Dilated LightNet+DARTS网络, 计算量减少48.1%, 参数量减少38.2%; 相比Dilated LightNet+SMS网络, 计算量减少25.5%, 参数量减少31%.

综合2个数据集的结果可见, 只使用准确率作为搜索目标时, 得到的是计算代价较高的网络结构, 无法兼顾轻量化, 即使使用标量化的多目标优化方法, 本文的循环退火搜索策略在神经网络结构搜索的多目标优化问题上也表现更优.

在网络轻量化的问题上, 有诸如紧凑网络、网络剪枝、低秩分解、参数量化等多种方法, 为了能全面客观地评价本文方法, 选择当前用于网络轻量化的一些先进方法进行对比分析:对ResNet-56使用基于几何中值剪枝的FPGM^[6]、将ResNet-56中空间卷积替换为移位操作且膨胀系数为6时的ShiftRes-Net^[12]、对ResNet-32进行软剪枝的SFP^[7]、对VGG-16剪枝的MFP^[8]、使用深度可分离卷积和逆残差结构的紧凑网络MobileNetV2^[9]、根据最终响应的重要性分数指导LeNet和ResNet-56剪枝的神经元重要性分数传播剪枝(Neuron Importance Score Propaga-tion, NISP)^[22]、使用生成对抗网络对LeNet和Res-Net-56剪枝的生成对抗剪枝(Generative Adversarial Learning, GAL)^[23]、对LeNet和ResNet-20进行结构稀疏化剪枝的结构稀疏化剪枝(Structured Sparsity Learning, SSL)^[24].NISP、GAL和SSL在MNIST数据集上对LeNet剪枝, 在CIFAR数据集上对ResNet剪枝.对比方法的参数设置与原文献完全一致, 本文方法的实验设置与2.1节相同, 实验结果如表3~表5所示, 表中黑体数字表示最优值.

表3

Table 3

表3(Table 3)

表3 各方法在CIFAR-10数据集上的指标值 Table 3 Index values of different methods on CIFAR-10 输入 方法 CIAFR-10 准确率/% 计算量/M 参数量/M 32× 32 FPGM 92.93 59 - ShiftResNet 92.69 102 0.58 SFP 92.08 40 - MFP 93.14 154 7.20 SSL 92.60 36 0.26 NISP 93.01 81 0.49 GAL 91.58 50 0.29 Dilated LightNet+ CANAS 93.21 45 0.95 224× 224 MobilenetV2 93.25 126 0.70 Dilated LightNet+ CANAS 93.49 88 0.55

表3 各方法在CIFAR-10数据集上的指标值 Table 3 Index values of different methods on CIFAR-10

表4

Table 4

表4(Table 4)

表4 各方法在CIFAR-100数据集上的指标值 Table 4 Index values of different methods on CIFAR-100 输入 方法 CIAFR-100 准确率/% 计算量/M 参数量/M 32× 32 FPGM 69.66 59 - ShiftResNet 72.13 102 0.58 SFP 68.37 40 - SSL 67.47 31 0.25 GAL 70.13 73 0.73 Dilated LightNet+ CANAS 72.72 52 1.19 224× 224 MobilenetV2 71.93 126 0.81 Dilated LightNet+ CANAS 72.36 99 0.71

表4 各方法在CIFAR-100数据集上的指标值 Table 4 Index values of different methods on CIFAR-100

表5

Table 5

表5(Table 5)

表5 各方法在MNIST数据集上的指标值 Table 5 Index values of different methods on MNIST 方法 MNIST 准确率/% 计算量/M 参数量/M SSL NISP GAL SOTA Dilated LightNet+CANAS 99.00 99.18 99.14 99.84 99.21 0.20 0.65 0.43 24 0.30 0.10 0.11 0.05 1.5 0.04

表5 各方法在MNIST数据集上的指标值 Table 5 Index values of different methods on MNIST

为了在相近的计算量下对比, 实验中使用缩放因子为0.5的MobileNetV2进行对比, 输入为32× 32时的Dilated LightNet网络宽度扩大为原来的4/3倍, 在MNIST数据集上宽度缩小为原来的1/6倍.在CIFAR-10数据集上, 本文方法准确率最佳时, 计算量少于其中大部分方法.输入为32× 32时, 相比准确率最高的MFP, 本文方法准确率只高出0.07%, 计算量却减少70.7%.相比计算量最低的SSL, 本文方法在计算量上略有增加, 但准确率提高0.61%.输入为224× 224时, 相比MobileNetV2, 本文方法在准确率、计算量、参数量上都表现更优.

CIFAR-100、CIFAR-10数据集上的图像均来自Tiny Images数据集, 但这2个数据集的类别互斥, 因此CIFAR-100数据集可作为CIFAR-10数据集的反例.CIFAR-100数据集上有100类图像, 每类包含600幅图像.CIFAR-10数据集上有10类图像, 每类包含6 000幅图像.因此CIFAR-100数据集上的训练图像少于CIFAR-10数据集, 任务难度更大, 分类效果下降更明显.由CIFAR-100数据集上的实验结果看出, 本文方法仍得到最高的识别准确率, 而计算量仍低于平均计算量.SSL虽然时间复杂度相对较低, 但识别准确率却下降5.25%.此外, 本文方法在输入为32× 32时表现优于224× 224, 计算量更少.这是因为224× 224的图像是通过插值得到, 信息量没有增加, 计算量却翻了数倍.

MNIST数据集上的结果也与CIFAR-10、CIFAR-100数据集基本保持一致, 本文方法在综合考虑性能与复杂度的情况下均最优.

从3个数据集的综合对比实验结果可看出, 本文方法在平衡识别性能和轻量化方面表现更优, 这表明方法的有效性.本文同时与MNIST的最高水平/最佳结果(State of the Art, SOTA)^[25]进行对比分析, 实验表明, 本文方法在识别准确率上已经接近胶囊网络方法^[25], 但在时间复杂度和空间复杂度上更优, 在平衡性能与时间空间复杂度方面, 本文方法更有优越性.