基于最优传输的层次化图核

引用本文

马凯, 黄硕, 张道强. 基于最优传输的层次化图核. 模式识别与人工智能, 2021,34(12): 1085-1092
MA Kai, HUANG Shuo, ZHANG Daoqiang. Optimal Transport Based Hierarchical Graph Kernel. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(12): 1085-1092. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202112002
Permissions

《模式识别与人工智能》编辑部

基于最优传输的层次化图核

马凯¹, 黄硕¹, 张道强¹

1.南京航空航天大学计算机科学与技术学院模式分析与机器智能工业和信息化部重点实验室南京 211100

通讯作者:

张道强,博士,教授,主要研究方向为机器学习、模式识别、医学图像分析.E-mail:dqzhang@nuaa.edu.cn.

作者简介:

马凯,博士研究生,主要研究方向为机器学习、医学图像分析.E-mail:kaim@nuaa.edu.cn.

黄硕,博士研究生,主要研究方向为机器学习、医学图像分析.E-mail:huangshuo@nuaa.edu.cn.

收稿日期: 2021-04-28 接受日期: 2021-07-04

资助项目: 国家重点研发计划项目(No.2018YFC2001600,2018YFC2001602,2018ZX10201002)、国家自然科学基金项目(No.61876082,61732006,61861130366)资助

摘要

已有的图核大多关注图的局部属性,利用局部的拓扑特征构建图的相似性度量,忽略图的层次结构信息.为了解决这个问题,文中提出基于最优传输的层次化图核.首先,将每个图表示成层次化的图结构.在层次化图结构构建过程中,利用 K-means聚类算法构造每层图的节点,节点间的概率连接作为图的边.然后,利用带有熵约束的最优传输计算两图的层次结构上每层图之间的最优传输距离.最后,基于最优传输距离计算基于最优传输的层次化图核.在6个真实图数据集上的实验表明,文中方法可提升分类性能.

关键词: 图核; 最优传输; 层次结构; 拓扑特征

中图分类号:TP 391

Optimal Transport Based Hierarchical Graph Kernel

MA Kai¹, HUANG Shuo¹, ZHANG Daoqiang¹

1. MIIT Key Laboratory of Pattern Analysis and Machine Intelligence, College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 211100

Corresponding author:
ZHANG Daoqiang, Ph.D., professor. His research in-terests include machine learning, pattern re-cognition and medical image analysis.

About Author:
MA Kai, Ph.D. candidate. His research interests include machine learning and medical image analysis.
HUANG Shuo, Ph.D. candidate. His research interests include machine learning and medical image analysis.

Fund:National Key Research and Development Program of China(No.2018YFC2001600,2018YFC2001602,2018ZX10201002), National Natural Science Foundation of China(No.61876082,61732006,61861130366)

Abstract

In the existing graph kernels, local attributes of graphs are concerned and local topological features are utilized to compute the similarity measurement of graphs. However, hierarchical structure information of the graph is ignored. To handle this problem, optimal transport based hierarchical graph kernel is proposed. Firstly, each graph is represented as a hierarchical graph structure. During the constructive process of hierarchical graph structure, K-means clustering algorithm is employed to construct new nodes and probabilities of connections between new nodes is regarded as edges of graph at each layer. Then, the optimal transport distance between paired graphs in the special hierarchical structure is calculated using optimal transport with entropic constraints. Finally, the optimal transport distance based hierarchical graph kernel is calculated. The experimental results on six graph datasets show that the classification performance is significantly improved by the proposed graph kernel.

Key words: Graph Kernel; Optimal Transport; Hierarchical Structure; Topological Feature

文章图片

本文责任编委于剑

Recommended by Associate Editor YU Jian

图结构数据广泛存在于真实世界中, 如生物网络^[1]、社交网络^[2]、引文网络^[3]等.在图结构数据分析任务中, 如何度量图的相似性是一项具有挑战性的任务.常规的处理图数据的方法是将图数据映射到向量空间, 例如, 利用图结构上的数据指标, 包括度^[4]、聚类系数^[5]等.在度量图相似性时, 需要将这些数据指标转换为向量, 再利用向量内积进行相似性度量.然而, 这类基于向量的图相似性度量方法忽视图的空间结构信息.图核作为一种图相似性度量方法, 广泛应用于图结构数据上^[6], 利用图数据特定的空间结构信息计算图的相似性, 在很多分类任务中取得较大成功.

学者们提出各种各样的图核, 利用不同的图结构信息度量图在空间结构上的相似性, 如最短路径图核(Shortest Path Kernel, SP)^[7], 环路图核^[8], 随机行走图核(Random Walk Kernel, RW)^[9], 返回概率图核^[10], 树模式图核^[11], Weisfeiler-Lehman图核^[12], 金字塔匹配(Pyramid Match Kernel, PM)图核^[13]等.这些图核利用特定的图结构(如最短路径、子树)表示图, 再在这些特定的结构上计算图的相似性.图上的这些特定结构反映图特定的结构属性.例如, 在最短路径图核中, 图上两节点间的最短路径反映图的路径属性.这些基于图的特定结构构建的图核关注图的局部属性, 忽视图的层次结构信息.

图的层次结构是将单个图表示为一个层次化图, 层次化图的每层是一个新的图结构.由于构建层次化图的策略不同, 图的层次结构表达的空间结构信息也会有所不同.Liu等^[14]利用图上节点标号信息的相似性构建层次化图结构.然而, 这种构建层次化图的方法忽视图本身的结构信息.Mousavi等^[15]利用谱聚类的方法构建图的层次化结构, 以原始图结构作为图层次结构的最底层图, 对底层图采用谱聚类的方法构建上一层图的结构, 依次类推, 构建具有层次结构的图.此方法有效利用图的结构信息构建层次化图结构.然而, 分析图的层次结构时, Mousavi等^[15]直接将层次结构上的图拉成向量, 再对所有的向量进行拼接.这种分析方法忽视层次结构图中每层图的全局结构信息.

在图的全局信息处理上, 最优传输(Optimal Transport, OT)理论^[16]表现出优越的性能.在最优传输理论中, 在地面距离(Ground Distance)给定的前提下, 最优传输距离被用于度量两个概率分布的相似性.最优传输距离可捕获潜在概率空间的几何信息.利用相关图嵌入算法, 图数据可被表示为概率分布.因此, 最优传输距离可应用于图数据的研究分析.Nikolentzos等^[13]利用最优传输距离度量图在向量空间的相似性, 在蛋白质和分子分类任务上取得较优性能.Togninalli等^[17]在图数据上将最优传输距离与Weisfeiler-Lehman结合, 提出Wasserstein Weis-feiler-Lehman图核, 并应用于属性图分类, 在分类结果上取得优越性能.然而, 上述基于最优传输的图方法都基于单层图, 忽视图的层次结构信息.

为了解决上述问题, 本文提出基于最优传输的层次化图核, 将最优传输理论与图的层次化结构结合, 充分利用层次结构上每层图的全局结构信息.利用K-means聚类算法构建层次化图结构, 将每个图转换为层次化图结构.在层次化图结构上计算最优传输距离, 并计算基于最优传输距离的层次化图核.最后, 在6个图数据集分类任务上验证本文方法的性能.

1 图核

图核是一类核函数, 用于度量成对图或网络之间的相似性.存在一个映射ϕ 将原始的图数据集G隐式地嵌入到希尔伯特空间Η , ϕ :G→ Η .在图数据集G中, 图核K:G× G→ R是一个与H有关的函数.给定2个图G₁和G₂, G₁∈ G, G₂∈ G, 图核K表示为高维空间H中的点积,

K(G₁, G₂)=< ϕ (G₁), ϕ (G₂)> _H.

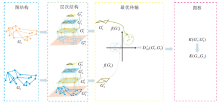
核函数K是对称的, 即K(G₁, G₂)=K(G₂, G₁).对于任意的图{G_i} $_{i = 1}^{N}$ , Gram矩阵K∈ R^N^×^N定义为K(i, j)=K(G_i, G_j), 如果K(i, j)是正定的, 则K(G_i, G_j)也是正定的.

2 基于最优传输的层次化图核

本文提出基于最优传输的层次化图核方法.方法由如下三部分组成:1)层次化图结构, 将每个图转换为层次化图结构; 2)图上的最优传输距离, 在层次化图结构上计算最优传输距离; 3)基于最优传输的层次化图核, 计算基于最优传输距离的图核.基于最优传输的层次化图核的框图如图1所示.

	Figure Option View Download New Window
	图1 基于最优传输的层次化图核框图Fig.1 Flow chart of optimal transport based hierarchical graph kernel

在介绍本文方法之前, 为正定化的最优传输图核提供相关定义和理论保证.

定义1最优传输图核给定图的集合G={G₁, G₂, …, G_N}和2个图之间的最优传输距离 D $_{OT}^{f}$ , N表示图的数量, f表示图嵌入函数, 将图转化为概率分布.最优传输图核定义如下:

K_OT(G_i, G_j)=exp(-γ D $_{OT}^{f}$ (G_i, G_j)),

其中, G_i、G_j为2个任意的图, G_i∈ G, G_j∈ G, γ > 0, D $_{OT}^{f}$ (G_i, G_j)为图最优传输距离, 用于度量图G_i、G_j之间的运输损失.

显然, 最优传输图核是基于拉普拉斯图核.这个图核可能不是正定的, 因为最优传输距离 D $_{OT}^{f}$ 是非等距的, 由它所诱导的度量空间依赖于测定距离.在这里为正定化的最优传输图核提供充要条件, 如定理1所示.

定理1 对于所有的γ > 0, 最优传输图核K_OT(G_i, G_j)为正定图核, 当且仅当最优传输距离 D $_{OT}^{f}$ (G_i, G_j)为条件负定.

证明最优传输距离 D $_{OT}^{f}$ (G_i, G_j)可被视为一个定义在图G_i、G_j之间的度量函数M.根据文献[18]中理论5.2和文献[19]中理论2, 核e^(-^{γ M}⁾为正定的, 当且仅当度量函数M为条件负定.因此, K_OT(G_i, G_j)为正定的, 当且仅当 D $_{OT}^{f}$ (G_i, G_j)为条件负定.

2.1 层次化图结构

目前, 已有的基于图的方法大多只关注单一尺度图结构上的信息, 忽视图的多个层次的结构信息.在本文方法中, 将每个图表示为一个层次化的图结构.

给定一个图G, 由节点和边的集合组成, 表示为G=(V, E).图G可使用邻接矩阵A∈ R^m^×^m表示, 则

A_ij= $\{\begin{array}{l} w, & e_{ij} \in E \\ 0, & 其它 \end{array}$

e_ij为连接节点i和节点j的边, w为边e_ij上的权值.

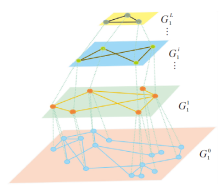
假设图G的层次化结构 G_H 由L层图构成, G_H={G⁰, G¹, …, G^L}, 如图2所示.

	Figure Option View Download New Window
	图2 图G的层次化图结构Fig.2 Hierarchical structure of graph G

G⁰为层次化结构的第0层图, 是图G本身, 即G⁰=G.第i层图Gⁱ由第i-1层图Gⁱ^-1构建, 构建步骤包括节点构建和边构建.

2.1.1 节点构建

第i层图Gⁱ的节点由第i-1层图Gⁱ^-1的节点通过聚类算法获得.受文献[15]和文献[20]的启发, 本文采用基于谱方法的K-means聚类算法对第i-1层图Gⁱ^-1的节点进行聚类, 将聚类后的集合作为第i层图的节点, 此方法又称为节点划分方法.

给定图Gⁱ^-1, i=1, 2, …, L, 表示为层次结构G_H的第i-1层图, 该图的节点集为Vⁱ^-1, 将其划分为k个子集, 每个子集由图Gⁱ^-1中的节点组成, 划分后的每个子集被视为第i层图Gⁱ中的节点, 如图2绿色虚线所示.这k个子集组成图Gⁱ的节点集

Vⁱ={V $_{1}^{i - 1}$ , V $_{2}^{i - 1}$ , …, V $_{k}^{i - 1}$ },

V $_{j}^{i - 1}$ (j=1, 2, …, k)为节点集Vⁱ^-1的第j个划分, 视为图Gⁱ的第j个节点.矩阵Π =[ $π_{v_{j}}$ ]为对应的节点划分矩阵, j=1, 2, …, k.图划分方法的目的是寻找到合适的矩阵Π , 使划分损失Cost(Vⁱ)最小:

Cost(Vⁱ)=1'_nAⁱ^-11_n-tr(Π 'Aⁱ^-1Π ), (1)

其中Aⁱ^-1为图Gⁱ^-1的邻接矩阵.此图划分方法可通过近似算法进行求解, 近似算法如下:

Π :=arg $\min_{Π}$ ‖ Π -UZ‖ _F,

其中, U为邻接矩阵Aⁱ^-1特征分析后的特征向量, Z为k× k的矩阵.

给定矩阵Z, 通过最小化式(1)求解Π 很明确, 因为

(Π '-Z'U')(Π -ZU)= Π 'Π +Z'Z-Z'U'Π -Π UZ, (2)

其中, $π_{v_{i}}$ 、 $u_{v_{i}}$ 表示n× k矩阵Π 和 $\bar{U}$ :=UZ的第v_i个条目, 则

‖ Π -UZ $‖_{F}^{^{2}}$ =n+‖ Z‖ _F+2tr(Z'U'Π )= n+‖ Z‖ _F+2 $\overset{k}{\sum_{i = 1}} \overset{n}{\sum_{v = 1}}$ i_v_πv_i,

i_v表示Π 的第v行条目的第i个索引, 则

‖ Π -UZ $‖_{F}^{^{2}}$ =n+‖ Z‖ _F-2 $\overset{n}{\sum_{v = 1}} u_{i_{v} v} π_{v i_{v}}$ .

Z可通过启发式搜索算法进行求解, 本文采用K-means算法.求解得到的矩阵Π 对应图Gⁱ^-1中节点的k个划分.

2.1.2 边构建

对第i-1层图Gⁱ^-1的节点集Vⁱ^-1进行k次划分后, 获得图Gⁱ的节点集Vⁱ.为了获得图Gⁱ的连接结构, 需要定义节点集Vⁱ中节点之间的连接边.

给定图G, 它的层次结构表示为G_H, Gⁱ^-1(i=1, 2, …, L)为层次结构G_H的第i-1层图, 该图的节点集为Vⁱ^-1.图Gⁱ的节点集为Vⁱ, 含有k个节点, 分别为V $_{1}^{i - 1}$ , V $_{2}^{i - 1}$ , …, V $_{k}^{i - 1}$ , 节点V $_{h}^{i - 1}$ , V $_{j}^{i - 1}$ (h=1, 2, …, k; j=1, 2, …, k)为图Gⁱ的第h个和第j个节点, 由图Gⁱ^-1的第h次和第j次划分获得.

假设V $_{h}^{i - 1}$ 和V $_{j}^{i - 1}$ 分别含有m个和n个来自于Vⁱ^-1的节点, 在图Gⁱ^-1中, m个节点和n个节点之间有N条边相连, 如果这些边有权重, 令这些边的权重和为W.在定义节点V $_{h}^{i - 1}$ 和V $_{j}^{i - 1}$ 之间的边时, 如果研究的图的边无权重, 利用V $_{h}^{i - 1}$ 和V $_{j}^{i - 1}$ 中来自Vⁱ^-1的节点之间真实边的数目与这些节点组成的完全二分图边的数目的比值(即 $\frac{N}{mn}$ )作为V $_{h}^{i - 1}$ 和V $_{j}^{i - 1}$ 之间是否有边的判别依据, 如果比值大于特定的阈值, 认为V $_{h}^{i - 1}$ 和V $_{j}^{i - 1}$ 之间有边, 否则, 它们之间无边.如果图Gⁱ^-1中边有权重信息, 则将 $\frac{W}{N}$ 作为节点V $_{h}^{i - 1}$ 和V $_{j}^{i - 1}$ 之间边的权重, 依此类推, 获得其它节点之间的边.

构建第i层图Gⁱ的节点和边后, 获得图Gⁱ的连接结构, 其它层的图构建依此类推.每层图构建完成后获得图G的层次化结构G_H, 如图2所示.

2.2 图上的最优传输距离

对给定的图构建完图的层次结构后, 需要计算基于层次结构的最优传输距离, 主要包括层次结构嵌入和最优传输距离计算.

2.2.1 层次结构嵌入

图层次结构的每层都是一个图结构, 将每层的图采用特征分解方法嵌入到向量空间, 获得图的向量表示.给定图G=(V, E), 它的层次结构中的第i层为图Gⁱ=(Vⁱ, Eⁱ), 假设Gⁱ有n个节点, 它的邻接矩阵为Aⁱ, 对邻接矩阵Aⁱ进行特征分解, 获得图Gⁱ在向量空间的节点表示.特征分解表示如下:

Aⁱ=UΛ U^T,

其中U的第j行u_j对应节点v $_{j}^{i}$ ∈ Vⁱ在向量空间中的嵌入.采用特征分解方法对图进行嵌入能获得图的全局属性, 为相关的机器学习任务提供灵活有力的机制保证^[13].

对图Gⁱ进行特征分解后, 可获得每个节点的向量表示, 所有节点向量表示的集合{u₁, u₂, …, u_n}作为图Gⁱ在向量空间的嵌入.对层次结构上的每层图进行嵌入操作, 可获得层次结构在向量空间的嵌入表示.

2.2.2 最优传输距离计算

获得图层次结构在向量空间的嵌入表示后, 需要计算两图之间的最优传输距离.最优传输起源于土堆的运输问题, 抽象成数学问题后, 被用于判断两个概率分布是否具有差异性.最优传输诱导的距离又叫作移土距离 (Mover's Distance)或Wasserstein距离.近期最优传输在影像处理、计算机视觉和图相似性度量方面取得较大成功.

最优传输距离在度量2个概率分布方面具有较优性能, 尤其是概率空间具有几何结构.给定2个概率分布r和c, 它们来自Σ _n和Σ _m,

Σ _n:={x∈ $R_{+}^{n}$ :x^T1_n=1}.

令Γ (r, c)为r和c之间所有运输计划的集合, Γ 为一个n× m的矩阵, 定义如下:

Γ (r, c):={P∈ $R^{n×m}_+$P1_m=r, P^T1_n=c}. (3)

给定n× m的损失矩阵M, 该矩阵是定义在地面距离d(x, y)之上, x∈ r, y∈ c.通过运输矩阵P将r映射到c, c的总损失表示为< P, M> .最优传输距离

d_OT(r, c):= $\min_{P \in Γ (r, c)}$ < P, M> . (4)

因为式(4)定义的最优传输距离依赖地面距离, 该最优传输距离是非等距的, 不能等距保持映射到L²范数空间, 因此, 定义在该距离上的图核是非正定的.为了获得正定的图核, 对式(3)定义的运输计划集合Γ (r, c)加入熵约束.新的运输计划集合定义如下:

Γ '(r, c):={P∈ Γ (r, c)|KL(P‖ rc^T)=0},

其中, KL表示Kullback-Leibler散度,

KL(P‖ rc^T)= $\sum_{ij}$ p_ijlog₂( $\frac{p_{ij}}{r_{i} c_{j}}$ ),

p_ij为P中的元素.

定理2 对任意p_ij, 矩阵P∈ Γ (r, c), Γ (r, c)包含(X, Y)中所有可能的联合概率分布, X、Y为2个概率分布.p(X=i, Y=j)=p_ij, 令

p(X=i)=r_i, p(Y=j)=c_j,

则有

KL(P‖ rc^T)= $\sum_{ij}$ i_jlog2_pi_j_- $\sum_{i}$ ilog2_ri_- $\sum_{j}$ jlog2_cj_.

证明根据最大熵原理, rc^T有熵,

E(rc^T)=E(r)+E(c), E(rcT⁾=- $\sum_{ij}$ i_cjlog2_ri_cj_,E(r)=-r $\sum_{i}$ _log2r_i, E(c)=-cj $\sum_{j}$ l_og2cj_-_ri $\sum_{ij}$ jl_og2ri_cj₌-ri $\sum_{i}$ o_g2ri-c_j $\sum_{j}$ o_g2cj, K_L(P‖ rcT)=pⁱj $\sum_{ij}$ o_g2=( $\frac{p_{ij}}{r_{i} c_{j}}$ )pij l $\sum_{ij}$ g_2pij-_ri_cj $\sum_{ij}$ o_g2_ricj=pij lo $\sum_{ij}$ 2_pij-r_i_log $\sum_{i}$ r_i-cj l_og $\sum_{j}$ c_j.

带有熵约束的最优传输距离定义如下:

d'_OT(r, c):= $\min_{P \in Γ' (r, c)}$ < P, M> .(5)

获得图的层次嵌入后, 使用式(5)定义图上的最优传输距离.

给定2个图G₁、G₂, f_eig为图嵌入函数,

f_eig:G₁→ R^m^×ⁿ, G₂→ R^m^×ⁿ,

将图G₁、G₂映射到向量空间.在本文中, 使用图的特征分解作为嵌入函数, 欧氏距离作为地面距离.图G₁、G₂层次图结构的第i层分别为G $_{1}^{i}$ 和G $_{2}^{i}$ , 经过特征分解嵌入后分别表示为f_eig(G $_{1}^{i}$ )和f_eig(G $_{2}^{i}$ ).使用式(5)计算图G $_{1}^{i}$ 和G $_{2}^{i}$ 之间的最优传输距离:

D $_{_{OT}}^{^{f_{eig}}}$ (G $_{1}^{i}$ , G $_{2}^{i}$ )=d'_OT(f_eig(G $_{1}^{i}$ ), f_eig(G $_{2}^{i}$ )). (6)

2.3 基于最优传输的层次化图核

给定图G₁、G₂, 计算它们第i层图之间的最优传输距离后, 定义图G₁、G₂层次结构第i层图之间的相似性度量函数, 即图核.该图核定义如下:

K(G $_{1}^{i}$ , G $_{2}^{i}$ )=exp(-γ D $_{_{OT}}^{^{f_{eig}}}$ (G $_{1}^{i}$ , G $_{2}^{i}$ )),

其中, G $_{1}^{i}$ 、G $_{2}^{i}$ 为图G₁、G₂层次结构第i层图, D $_{_{OT}}^{^{f_{eig}}}$ (G $_{1}^{i}$ , G $_{2}^{i}$ )为G $_{1}^{i}$ 、G $_{2}^{i}$ 之间的最优传输距离, 由式(6)定义.图G₁、G₂之间的基于最优传输的层次化图核定义如下:

K(G₁, G₂)= $\overset{L}{\sum_{i = 0}}$ K(G $_{1}^{i}$ , G $_{2}^{i}$ ),

其中L表示图层次结构的层数.

定理3 基于最优传输的层次化图核K(G₁, G₂)为正定的.

证明式(6)中的地面距离是欧氏距离.根据文献[21], d'_OT(r, c)为负定的, 因此, D $_{_{OT}}^{^{f_{eig}}}$ (G $_{1}^{i}$ , G $_{2}^{i}$ )是负定的.根据定理1, K(G $_{1}^{i}$ , G $_{2}^{i}$ )为正定的.因此, K(G₁, G₂)为正定的.

本文方法的复杂性主要受两方面的影响, 分别是层次结构构建和最优传输距离计算.在层次结构构建中, 复杂性由每层图的节点个数和聚类个数决定.假设层次结构有L层, 每层有k个聚类中心, N个节点, 复杂性为O(LkN).在最优传输距离计算中, 给定两个图的层次结构, 每层之间计算最优传输距离的复杂性为O(N²), 所有层之间的复杂性为O(LN²).计算基于最优传输的层次化图核的总的复杂性为O(LkN+LN²).在层次结构计算中, 从层次结构底部到顶部, 每层图的节点个数依次减少, 因此总的复杂性小于O(LkN+LN²).因为, L和k都小于N, 为常量, 最后总的时间复杂性要小于O(N+N²).

3 实验及结果分析

3.1 实验环境

本文在如下6个公开的生物信息数据集上进行分类实验:MUTAG、KKI、NCI109、PTC-MR、BZR、COX2.这些数据集由图数据构成, 可从在线数据库Bench-mark Data Sets for Graph Kernels(https://ls11-www.cs.tu-dortmund.de/staff/morris/graphkerneldatasets)下载得到.

MUTAG数据集包含188幅图.KKI数据集包含83幅图.NCI109数据集包含4 127幅图.PTC-MR数据集包含344幅图.BZR数据集包含405幅图.COX2数据集包含467幅图.KKI为脑网络数据集, 由功能磁共振影像数据构建.MUTAG、PTC-MR、NCI109数据集为分子化合物数据集.BZR、COX2数据集为化合物数据集.

实验中使用如下图核方法进行对比:最短路径图核(SP)^[7], 最优分配图核(Optimal Assignment Kernel, OA)^[22], Graphlet图核(Graphlet Kernel, GR)^[23], 随机行走图核(RW)^[9], 金字塔匹配图核(PM)^[13], GraphHopper图核(GraphHopper Kernel, GH)^[24], Gromov-Wasserstein图核(GW)^[17].方法参数通过在训练样本上执行交叉验证的方式确定.

支持向量机(SVM)作为最终的分类器, 用于分类实验.SVM中的参数C从{10^-3, 10^-2, …, 10³}中选择.在每个数据集上, 对每种方法进行10次10折交叉验证实验, 取这10次重复实验的平均值作为最终的实验结果.

3.2 分类结果

本节将各图核应用到MUTAG、KKI、NCI109、PTC-MR、BZR、COX2数据集的分类任务中, 所有图核都是基于无标记图, 即未考虑图数据中节点的标签信息, 分类结果如表1所示.

表1 各方法在6个数据集上的分类性能 Table 1 Classification performance of different methods on 6 datasets

由表1可发现, 在分类结果上, 本文方法的性能最优.在KKI数据集上, 本文方法分类精度比第二好的GraphHopper图核提高7.23%.在MUTSG、NC109、BZR数据集上, 本文方法分类精度比第二好的金字塔匹配图核和Gromov-Wasserstein图核稍好.在PTC-MR、COX2数据集上, 本文方法分类精度比第二好的Gromov-Wasserstein图核提高1.49%和1.97%.分类结果表明, 图的层次化结构有助于提高分类精度.

3.3 参数分析

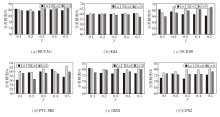
本文方法中包含参数γ 和L, γ 为核函数的超参数, L为层次结构的层数, 控制层次结构的规模.为了评价γ 和L对于最终分类结果的影响, 在6个数据集上分别测试使用不同γ 值(γ =0.1, 0.2, 0.3, 0.4, 0.5)及不同L值(L=1, 2, 3)时, 本文方法的分类能力.

图3图形化地显示在6个数据集上获得的分类结果.图中每种色柱表示固定L时, 图核随γ 变化获得的分类精度.

	Figure Option View Download New Window
	图3 γ 、L不同时本文方法的分类精度Fig.3 Classification accuracies of the proposed method with different γ and L

从图3和表1可看出, 随着γ 、L取值不同, 在大部分情况下本文方法分类效果都较优, 这进一步体现本文方法的有效性.

同时, 由图3可发现, 当L值固定时, 柱状图随γ 值变化较平滑, 这表明本文方法对于参数γ 的变化具有较好的鲁棒性.当固定γ 值时, 分类精度随L值变化较大, 这表明L值的选择很重要.

这一现象进一步表明L控制层次结构的规模, 因此网络的层次结构对度量两个网络的相似性具有深刻影响.

4 结束语

图的相似性度量是图数据分析中一个挑战性的问题.本文提出基于最优传输的层次化图核, 用于度量图的相似性.不同于已有的图核, 本文方法能充分利用图的层次结构信息和每层图的全局信息.在6个分子化合物数据集上进行分类实验, 结果表明, 本文方法的分类性能较优.今后将在更多的数据集上评价本文方法.

参考文献

文献选项

[1]	YOU J X, LIU B W, YING R, et al. Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 6412-6422. [本文引用:1]
[2]	XUE J L, YANG Z, YANG X Y, et al. VoteTrust: Leveraging Friend Invitation Graph to Defend against Social Network Sybils // Proc of IEEE INFOCOM. Washington, USA: IEEE, 2013: 2400-2408. [本文引用:1]
[3]	LEYDESDORFF L, WAGNER C S, BORNMANN L. Betweenness and Diversity in Journal Citation Networks as Measures of Interdisciplinarity-A Tribute to Eugene Garfield. Scientometrics, 2018, 114: 567-592. [本文引用:1]
[4]	LYNALL M E, BASSETT D S, KERWIN R, et al. Functional Connectivity and Brain Networks in Schizophrenia. The Journal of Neuroscience, 2010, 30(28): 9477-9487. [本文引用:1]
[5]	CHEN B, AKSHITA J, HAN P F, et al. Aberrancies of Brain Network Structures in Patients with Anosmia. Brain Topography, 2020, 33(3): 403-411. [本文引用:1]
[6]	VISHWANATHAN S V N, SCHRAUDOLPH N N, KONDOR R, et al. Graph Kernels. Journal of Machine Learning Research, 2010, 11(40): 1201-1242. [本文引用:1]
[7]	BORGWARDT K M, KRIEGEL H P. Shortest-Path Kernels on Graphs // Proc of the 5th IEEE International Conference on Data Mining. Washington, USA: IEEE, 2005. DOI: DOI:10.1109/ICDM.2005.132. [本文引用:2]
[8]	TAMAS H, THOMAS G S W. Cyclic Pattern Kernels for Predictive Graph Mining// Proc of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2004: 158-167. [本文引用:1]
[9]	KASHIMA H, TSUDA K, INOKUCHI A. Marginalized Kernels between Labeled Graphs// Proc of the 20th International Conference on Machine Learning. New York, USA: ACM, 2003: 321-328. [本文引用:2]
[10]	ZHANG Z, WANG M Z, XIANG Y J, et al. RetGk: Graph Kernels Based on Return Probabilities of Rand om Walks // Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2018: 3964-3974. [本文引用:1]
[11]	MAHÉ P, VERT J P. Graph Kernels Based on Tree Patterns for Molecules. Machine Learning, 2009, 75: 3-35. [本文引用:1]
[12]	SHERVASHIDZE N, SCHWEITZER P, VAN LEEUWEN E J, et al. Weisfeiler-Lehman Graph Kernels. Journal of Machine Lear-ning Research, 2011, 12: 2539-2561. [本文引用:1]
[13]	NIKOLENTZOS G, MELADIANOS P, VAZIRGIANNIS M. . Ma-tching Node Embeddings for Graph Similarity // Proc of the 31st AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2017: 2429-2435. [本文引用:4]
[14]	LIU J, LI M, LAN W, et al. Classification of Alzheimer's Disease Using Whole Brain Hierarchical Network. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2018, 15(2): 624-632. [本文引用:1]
[15]	MOUSAVI S F, SAFAYANI M, MIRZAEI A, et al. Hierarchical Graph Embedding in Vector Space by Graph Pyramid. Pattern Recognition, 2017, 61: 245-254. [本文引用:3]
[16]	FIGALLI A. Optimal Transport: Old and New. Berlin, Germany: Springer, 2009. [本文引用:1]
[17]	TOGNINALLI M, GHISU E, LLINARES-LOPEZ F, et al. Wasser-stein Weisfeiler-Lehman Graph Kernels // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2019: 6439-6449. [本文引用:2]
[18]	JAYASUMANA S, HARTLEY R, SALZMANN M, et al. Kernel Methods on Riemannian Manifolds with Gaussian RBF Kernels. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(12): 2464-2477. [本文引用:1]
[19]	KOLOURI S, ZOU Y, ROHDE G K. Sliced Wasserstein Kernels for Probability Distributions // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 5258-5267. [本文引用:1]
[20]	HESPANHA J P. An Efficient MATLAB Algorithm for Graph Partitioning[C/OL]. [2021-03-15]. https://web.ece.ucsb.edu/~hespanha/published/tr-ell-gp.pdf. [本文引用:1]
[21]	CUTURI M. Sinkhorn Distances: Lightspeed Computation of Optimal Transportation Distances // BURGES C J C, BOTTOU L, WELLING M, et al. , eds. Advances in Neural Information Processing Systems 26. Cambridge, USA: The MIT Press, 2013: 2292-2300. [本文引用:1]
[22]	JOHANSSON F D, DUBHASHI D. Learning with Similarity Functions on Graphs using Matchings of Geometric Embeddings// Proc of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2015: 467-476. [本文引用:1]
[23]	SHERVASHIDZE N, VISHWANATHAN S V N, PETRI T H, et al. Efficient Graphlet Kernels for Large Graph Comparison// Proc of the 20th International Conference on Artificial Intelligence and Statistics. New York, USA: ACM, 2009: 488-495. [本文引用:1]
[24]	FERAGEN A, KASENBURG N, PETERSEN J, et al. Scalable Kernels for Graphs with Continuous Attributes // BURGES C J C, BOTTOU L, WELLING M, et al. , eds. Advances in Neural Information Processing Systems 26. Cambridge, USA: The MIT Press, 2013: 216-224. [本文引用:1]

2018

0.0

... 图结构数据广泛存在于真实世界中,如生物网络^[1]、社交网络^[2]、引文网络^[3]等 ...

2013

0.0

... 图结构数据广泛存在于真实世界中,如生物网络^[1]、社交网络^[2]、引文网络^[3]等 ...

2018

0.0

... 图结构数据广泛存在于真实世界中,如生物网络^[1]、社交网络^[2]、引文网络^[3]等 ...

2010

0.0

... 常规的处理图数据的方法是将图数据映射到向量空间,例如,利用图结构上的数据指标,包括度^[4]、聚类系数^[5]等 ...

2020

0.0

... 常规的处理图数据的方法是将图数据映射到向量空间,例如,利用图结构上的数据指标,包括度^[4]、聚类系数^[5]等 ...

2010

0.0

... 图核作为一种图相似性度量方法,广泛应用于图结构数据上^[6],利用图数据特定的空间结构信息计算图的相似性,在很多分类任务中取得较大成功 ...

2005

0.0

... 学者们提出各种各样的图核,利用不同的图结构信息度量图在空间结构上的相似性,如最短路径图核(Shortest Path Kernel, SP)^[7],环路图核^[8],随机行走图核(Random Walk Kernel, RW)^[9],返回概率图核^[10],树模式图核^[11],Weisfeiler-Lehman图核^[12],金字塔匹配(Pyramid Match Kernel, PM)图核^[13]等 ...

... 实验中使用如下图核方法进行对比:最短路径图核(SP)^[7],最优分配图核(Optimal Assignment Kernel, OA)^[22],Graphlet图核(Graphlet Kernel, GR)^[23],随机行走图核(RW)^[9],金字塔匹配图核(PM)^[13],GraphHopper图核(GraphHopper Kernel, GH)^[24],Gromov-Wasserstein图核(GW)^[17] ...

2004

0.0

2003

0.0

2018

0.0

2009

0.0

2011

0.0

2017

0.0

... Nikolentzos等^[13]利用最优传输距离度量图在向量空间的相似性,在蛋白质和分子分类任务上取得较优性能 ...

... 采用特征分解方法对图进行嵌入能获得图的全局属性,为相关的机器学习任务提供灵活有力的机制保证^[13] ...

2018

0.0

... Liu等^[14]利用图上节点标号信息的相似性构建层次化图结构 ...

2017

0.0

... Mousavi等^[15]利用谱聚类的方法构建图的层次化结构,以原始图结构作为图层次结构的最底层图,对底层图采用谱聚类的方法构建上一层图的结构,依次类推,构建具有层次结构的图 ...

... 然而,分析图的层次结构时,Mousavi等^[15]直接将层次结构上的图拉成向量,再对所有的向量进行拼接 ...

... 受文献[15]和文献[20]的启发,本文采用基于谱方法的K-means聚类算法对第i-1层图Gⁱ^-1的节点进行聚类,将聚类后的集合作为第i层图的节点,此方法又称为节点划分方法 ...

2009

0.0

... 在图的全局信息处理上,最优传输(Optimal Transport, OT)理论^[16]表现出优越的性能 ...

2019

0.0

... Togninalli等^[17]在图数据上将最优传输距离与Weisfeiler-Lehman结合,提出Wasserstein Weis-feiler-Lehman图核,并应用于属性图分类,在分类结果上取得优越性能 ...

2015

0.0

... 根据文献[18]中理论5 ...

2016

0.0

... 2和文献[19]中理论2,核e^(-^{#cod#x003b3 ...}

2021

0.0

2013

0.0

... 根据文献[21], d'_OT(r,c)为负定的,因此,DOTfeig(G1i,G2i)是负定的 ...

2015

0.0

2009

0.0

2013

0.0