基于最大决策边界的局部在线流特征选择

引用本文

孙世明, 邓安生. 基于最大决策边界的局部在线流特征选择. 模式识别与人工智能, 2021,34(12): 1131-1142
SUN Shiming, DENG Ansheng. Local Online Streaming Feature Selection Based on Max-Decision Boundary. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(12): 1131-1142. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202112006
Permissions

《模式识别与人工智能》编辑部

基于最大决策边界的局部在线流特征选择

孙世明¹, 邓安生¹

1.大连海事大学信息科学技术学院大连 116026

通讯作者:

邓安生,博士,教授,主要研究方向为人工智能、自动推理.E-mail:ashdeng@dlmu.edu.cn.

作者简介:

孙世明,硕士研究生,主要研究方向为机器学习、数据挖掘.E-mail:sunshming@163.com.

收稿日期: 2021-06-07 接受日期: 2021-10-14

摘要

现有的在线流特征选择算法通常选择一个最优的全局特征子集,并假设该子集适用于样本空间的所有区域.但是,样本空间的每个区域都使用独有的特征子集进行准确描述,这些特征子集的特征和大小可能有所不同.因此,文中提出基于最大决策边界的局部在线流特征选择算法.引入局部特征选择,在充分利用局部信息的基础上,设计基于最大决策边界的特征衡量标准,尽可能分开同类样本和不同类样本.同时,使用最大化平均决策边界、最大化决策边界和最小化冗余3种策略选择合适的特征.针对局部区域选择最优的特征子集,然后使用类相似度测量方法进行分类.在14个数据集上的实验结果和统计假设检验验证文中算法的分类有效性和稳定性.

关键词: 特征选择; 流特征; 局部特征选择; 最大决策边界

中图分类号:TP 18

Local Online Streaming Feature Selection Based on Max-Decision Boundary

SUN Shiming¹, DENG Ansheng¹

1. School of Information Science and Technology, Dalian Maritime University, Dalian 116026

Corresponding author:
DENG Ansheng, Ph.D., professor. His research interests include artificial intelligence and automatic reasoning.

About Author:
SUN Shiming, master student. His research interests include machine learning and data mining.

Abstract

The existing online streaming feature selection algorithms usually select the optimal global feature subset, and it is assumed that this subset adapts to all regions of the sample space. However, each region of the sample space is characterized accurately by its own distinct feature subsets. The feature subsets are likely to be different in feature and size. Therefore, an algorithm of local online streaming feature selection based on max-decision boundary is proposed. The local feature selection is introduced. With the full usage of local information, feature measurement standards based on max-decision boundary are designed to separate samples of the same class from samples of different classes as far as possible. Meanwhile, three strategies, maximizing average decision boundary, maximizing decision boundary and minimizing redundancy, are employed to select appropriate features. The class similarity measurement method is applied after the optimal feature subset is selected for the local regions. Experimental results and statistical hypothesis tests on fourteen datasets demonstrate the effectiveness and stability of the proposed algorithm.

Key words: Feature Selection; Streaming Feature; Local Feature Selection; Max-Decision Boundary

文章图片

本文责任编委杨明

Recommended by Associate Editor YANG Ming

特征选择在大数据问题中具有重要作用^{[1, 2]}.传统的特征选择方法^{[3, 4, 5]}选择在整个样本空间中通用的特征子集.但是, 这种方案会限制算法适应样本空间变化的能力, 可能会影响分类性能.因此, 选择适应样本空间局部区域变化的特征具有重要的研究意义.

随着数据量和维数的增加, 传统的特征选择算法在效率上已不能满足需求.在现实应用中, 由于特征空间的动态性, 在特征选择之前不一定能全部获取训练数据的全部特征, 从而造成特征空间是动态、未知的, 如火星陨石坑的高分辨率探测行星的图像^[6]、新浪微博中热门话题榜单的变动^[7]及环境监测和分析^[8]等.流特征是随着时间推移一个接一个出现的特征, 而训练样本的数量是固定的^[6].传统的特征选择算法无法处理流特征场景, 因此, 能处理动态流特征的在线流特征选择算法受到广泛关注^[9].

为了快速高效地选择高质量的特征子集, 学者们提出基于统计策略或优化的在线流特征选择算法.Zhou等^[9]提出基于流回归的在线特征选择(Streamwise Feature Selection, α -Investing), 不需要一个全局模型, 但是需要特征空间结构的先验知识, 并对初始特征进行变换.Wu等^[6]提出在线流特征选择(Online Streaming Feature Selection, OSFS), 主要分为在线相关性分析和在线冗余分析2步, 使用条件独立性测试进行特征选择, 需要大量的训练实例.当选择的特征子集非常大时, 时间复杂度会较大, 表现不佳.因此, Wu等^[6]又提出快速的在线流特征选择(Fast OSFS, FOSFS), 改进在线冗余分析阶段, 降低时间复杂度.在大数据的应用中, Yu等^[7]提出可扩展、准确的在线特征选择算法(Scalable and Accurate Online Approach for Feature Selection, SAOLA), 用于超高维数据集.SAOLA采用在线成对比较方法, 主要通过在线方式建立随时间推移的简洁模型.但是, 上述算法只判断在单个条件下是否冗余, 无法去除全部的冗余特征.尤殿龙等^[10]提出采用互信息和条件独立性的在线流特征选择方法(Online Feature Selection Method Using Mutual Information and Conditional Independence), 采用四层过滤方法处理冗余特征和不相关特征.吴中华等^[11]提出基于l_{2, 1}范数的在线流特征选择算法(Online Streaming Feature Selection Algorithm Regularized by l_{2, 1}Norm, sfs_l21), 相比l₀范数和l₁范数, sfs_l21对噪声不敏感, 具有行稀疏性质.

此外, 粗糙集和模糊互信息也广泛应用于流特征选择^{[12, 13, 14, 15]}.Zhou等^[12]提出基于自适应邻域粗糙集的在线流特征选择算法(Online Streaming Feature Selection Using Adapted Neighborhood Rough Set, A3M), 基于自适应的邻域粗糙集, 通过最大依赖度、最大相关性和最大显著性评价标准, 可筛选高质量的特征子集.Zhou等^[13]还利用邻域样本的密度信息, 设计不需要预先指定任何参数的自适应邻域关系, 并提出基于自适应密度邻域关系的在线流特征选择方法(Online Streaming Feature Selection Method Based on Adaptive Density Neighborhood Rela-tion, OFS-Density), 通过模糊等式约束, 可考虑更多特征, 获得低冗余度的特征子集.

上述流特征选择算法选择单个公共特征子集作为样本空间所有区域的最优特征集, 但是, 公共特征子集并不能适应局部区域的变化.所以, 针对上述问题, 本文将局部特征选择^[16]扩展到流特征选择, 并使用最大决策边界作为选择特征的标准, 使每个局部区域决策边界最大的特征子集尽可能分开同类样本和不同类样本.根据利用局部信息方式的不同, 使用两种不同的方式计算局部区域的决策边界, 提出基于最大决策边界的局部在线流特征选择算法(Local Online Streaming Feature Selection Based on Max-Decision Boundary, LOFS).相比传统的流特征选择算法, LOFS可充分利用局部信息, 适应局部区域的变化, 在分类时较准确.在多个数据集上的实验表明, 本文算法分类性能得到明显提高.

1 局部特征选择

1.1 基本概念

假定一个分类问题有N个训练样本

{(x_i, y_i) $}_{i = 1}^{N}$ ⊂R^M× Y,

其中, x_i表示第i个样本, y_i∈ Y表示样本对应的标签, Y={Y₁, Y₂, …, Y_c}表示类标签的集合.为了实现局部特征选择, 需要将每个训练样本x_i看作它周围局部区域的代表点, 并且对应一个M维的指示向量f⁽ⁱ⁾∈ {0, 1}^M, 用于说明哪些特征有利于增大决策边界.如果f $_{m}^{(i)}$ =1, 说明样本x_i选择第m个特征, 否则, 未选择.

定义1^[16] 设 $x_{i}^{p}$ 是任意样本x_i在对应的指示向量f⁽ⁱ⁾上的投影:

$x_{i}^{p}$ =x_i$\otimes$f⁽ⁱ⁾, i=1, 2, …, N,

其中, $\otimes$表示向量元素积, $x_{i}^{p}$ 表示M维向量.

在 $x_{i}^{p}$ 的邻域内, 为了寻找一个最优的特征子集f⁽ⁱ⁾, 在f⁽ⁱ⁾对应的局部坐标系统中, 需要满足如下2个目标:

1)邻域中同类样本尽可能靠近 $x_{i}^{p}$ ,

2)邻域中不同类样本尽可能远离 $x_{i}^{p}$ .

定义2^[16] 为了实现上述目标, 需要定义N-1个目标函数, 目标函数分别是样本间的类内加权距离和类间加权距离:

$\min_{f^{(i)}}$ $w_{j}^{i}$ ‖ $x_{i}^{p}$ - $x_{j}^{p}$ ‖ ₂, j∈ C⁽ⁱ⁾, j≠ i, $\max_{f^{(i)}} w_{j}^{i} x_{i}^{p} x_{j}^{p}$ 2_,j∉C⁽ⁱ⁾^,

其中, C⁽ⁱ⁾表示类标签为y_i的训练样本的集合, $w_{j}^{i}$ 表示第i个样本与第j个样本之间距离的权重.距离与权重呈反比关系, 距离越小, 权重越大.距离计算使用欧氏距离.在特征空间f⁽ⁱ⁾下, 权重

$w_{j}^{i}$ =exp(-(d_ij- $d_{ij}^{\min}$ )), (1)

其中

d_ij=‖ $x_{i}^{p}$ - $x_{j}^{p}$ ‖ ₂, $d_{ij}^{\min} \{\begin{array}{l} \min_{v \in C^{(i)}} d_{iv}, & y_{j} = y_{i} \\ \min_{v \notin C^{(i)}} d_{iv}, & y_{j} \neq y_{i} \end{array}$

1.2 类相似度测量

由于每个样本选择一个特征子集, 不能使用传统的分类方法.因此, 采用类相似度测量方法^[16]进行分类.假设样本空间中包含N个区域, 每个区域都有一个代表点 $x_{i}^{p}$ , 标签y_i和最优特征子集Sⁱ.在Sⁱ约束的坐标系中, 将局部区域定义为以 $x_{i}^{p}$ 为中心的超球体Qⁱ.使用不纯度γ 确定Qⁱ的半径, 不纯度是不同类样本数目与同类样本数目的比值, γ 默认为0.2.

给定单个测试样本x_q, 定义二元函数s_i(x_q).如果x_q∈ Qⁱ, 并且x_q最近邻样本的类标签为y_i, s_i(x_q)=1; 否则, s_i(x_q)=0.x_q与类标签Y_l的相似度定义如下:

Si $m_{Y_{l}}$ (x_q)= $\frac{1}{n_{l}} \sum_{i \in Y_{l}}$ s_i(x_q),

其中, Y_l表示所有类标签为Y_l区域的集合, Y_l基数为n_l.计算与所有类标签的相似度后, 将相似度最大的类标签作为x_q的预测标签.

2 局部在线流特征选择算法

2.1 在线流特征选择的定义

给定OSFS=(U, A, D, T), 表示一个在线流特征选择决策系统, 其中, U为一个非空有限的样本集合, A为条件特征集合, D为决策属性, T为时间序列.时刻t-1的特征子集为S_t_-1⊆A.假设在时刻t, 新流进的特征为f_t, 目标是在特征集合S_t_-1∪ f_t中选择分类能力较强的子集.

2.2 评价指标

为了给不同局部区域选择最优的特征子集, 根据利用局部信息方式的不同, 提出2种评价指标:基于加权距离的m_weighted(D)和基于局部密度的m_density(D).

定义3 给定x_i∈ U, 在特征空间f下, x_i与其它样本的平均类内加权距离 $a_{i}^{f}$ _weighted和平均类间加权距离 $b_{i}^{f}$ _weighted定义如下:

$a_{i}^{f}$ _weighted= $\frac{1}{n_{(i)} - 1} (\underset{j \neq i}{\sum_{j \in C^{(i)}}} w_{j}^{i}$ ‖ x_i-x_j‖ ₂), $b_{i}^{f}$ weighted= $\frac{1}{n - n_{(i)}}$ ( $\sum_{j \notin C^{(i)}} w_{j}^{i}$ xi_-xj_‖2)

其中, n₍_i₎表示和x_i同类的样本数量, C⁽ⁱ⁾表示和x_i同类的样本下标集合, $w_{j}^{i}$ 表示x_i和x_j之间的权重.距离越小, 权重越大, 使用式(1)可将权重约束在区间(0, 1]内.加权的目的是为了利用局部信息, 关注邻近的样本.

由于特征的平均类内距离和平均类间距离使用加权, 加权后的类内距离和类间距离相差较小, 因此通过比值计算两者之间的差距.

定义4 在得到平均类内加权距离 $a_{i}^{f}$ _weighted和平均类间加权距离 $b_{i}^{f}$ _weighted后, 评价特征f好坏的标准为

$m_{f}^{i}$ _weighted(D)= $\frac{b_{i}^{f}_weig h ted}{a_{i}^{f}_weig h ted + b}$ , (2)

其中, b> 0为平衡项, 默认为1, 避免分母为0.值越大说明特征f在样本x_i的局部空间中决策边界越大, 越有助于分类.

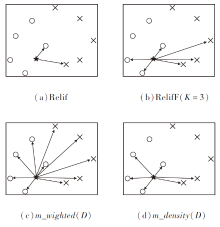
如图1所示, 4幅子图中都有2类样本, 其中, ★和○属于同类.

	Figure Option View Download New Window
	图1 4种算法的数据分布图Fig.1 Data distribution of 4 algorithms

图1为4种算法以★为中心, 选择局部样本的数据分布图.ReliefF^[3]会分别选择同类和不同类最近的K个样本, 而Relief是K=1的特例.由图可看出, m_weighted(D)选择全部样本, 并通过加权关注邻近的样本, 减少远距离样本对目标函数的影响.相比Relief和ReliefF, m_weighted(D)计算的决策边界会更准确.

定义5 设N_B(x_i)表示在给定特征子集B下, x_i与其它样本的距离从近到远的排序:

N_B(x_i)={x₍_i_{, 1)}, x₍_i_{, 2)}, …, x₍_i_,_j₎, …, x₍_i_,_n_-1)},

其中

Δ (x_i, x₍_i_{, 1)})≤ Δ (x_i, x₍_i_{, 2)})≤ …≤ Δ (x_i, x₍_i_,_n_-1)),

Δ (x, y)表示样本x、y之间的欧氏距离.x_i与x₍_i_,_k₎之间的密度定义简写为

d_i(k)= $\frac{1}{k}$ Δ (x_i, x₍_i_,_k₎).

定义6 给定特征子集B, 对于目标x_i, N_B(x_i)表示x_i从近到远的样本集合,

Density_B(x_i)={d_i(1), d_i(2), …, d_i(n-1)}

表示对应的样本密度集合.从第1个样本开始, 如果存在一个样本x_k(k> 1), 使d_i(k)> d_i(k-1)成立, 那么局部密度区域的样本就定义如下:

Local_B(x_i)={x₍_i_{, 1)}, x₍_i_{, 2)}, …, x₍_i_,_k_-1)}.

定义7 给定x_i∈ U, 在特征空间f下, x_i与其它样本的平均类内距离 $a_{i}^{f}$ _density和平均类间距离 $b_{i}^{f}$ _density表示如下:

$a_{i}^{f}$ _density= $\frac{1}{n_{intra_L_{f} (x_{i})}}$ ( $\sum_{j \in intra_L_{f} (x_{i})}$ ‖ x_i-x_j‖ ₂), $b_{i}^{f}$ density= $\frac{1}{n_{inter_L_{f} (x_{i})}}$ ( $\sum_{j \in inter_L_{f} (x_{i})}$ xi_-xj_‖2)

其中, intra_L_f(x_i)表示在与x_i同类的样本集合中计算的局部密度区域, inter_L_f(x_i)表示在与x_i不同类的样本集合中计算的局部密度区域, $n_{intra_L_{f} (x_{i})}$ 、 $n_{inter_L_{f} (x_{i})}$ 表示局部密度区域中样本的数量.

定义8 在得到平均类内距离 $a_{i}^{f}$ _density和平均类间距离 $b_{i}^{f}$ _density后, 评价特征f的衡量标准为

$m_{f}^{i}$ _density(D)= $b_{i}^{f}$ _density- $a_{i}^{f}$ _density.(3)

与定义4的计算方式不同, m_density(D)的平均类内距离和平均类间距离相差较大, 使用差值计算可清晰显示两者之间的差距, 值越大说明特征f的决策边界越大.m_density(D)未通过加权关注局部样本, 而是选择局部密度区域中的样本, 因此, 花费的时间较少.m_weighted(D)的优点在于考虑全部样本, 计算的决策边界会更准确.

如图1所示, m_density(D)会根据密度自适应地选择局部样本, 比使用Relief计算的决策边界更准确, 相比ReliefF, m_density(D)的优点是不用指定参数.

2.3 三种在线评估准则

对于在线流特征选择, 在时刻t, 给定样本x_i和已选择的特征集S_t_-1, 为了快速决定特征f_t是保留还是抛弃, 以及获得最大决策边界的特征子集, 本节提出3种评估特征子集的准则, 具体如下.

1)最大化平均决策边界.为了给特征集S_t选择区分能力较强的特征, 首先需要使S_t中的每个特征都具有较大的决策边界.因此, 通过最大化平均决策边界策略, 选择决策边界大于当前平均决策边界的特征, 这样才能最大化S_t的平均决策边界.特征f_t的衡量指标简写为 $m_{f_{t}}^{i}$ (D), 平均决策边界

Mea $n_{S^{i - 1}}$ = $\frac{1}{|S^{i - 1}|} \sum_{f \in S^{i - 1}} m_{f}^{i}$ (D).

对于每个特征f, 使用式(2)或式(3)计算m_f(D), 如果

m_f(D)> Mea $n_{S^{i - 1}}$ ,

特征f才会进行下一步的筛选.

2)最大化决策边界.算法的最终目标是最大化决策边界S_t, 因此新的特征f_t要能增大当前特征子集的决策边界.对于已选择的特征集S_t_-1:如果新的特征f_t满足

$m_{S_{t - 1} ⋃ f_{t}}$ (D)> $m_{S_{t - 1}}$ (D),

直接选择特征f_t; 否则, 不选择.其中, S_t_-1∪ f_t表示将特征f_t加入S_t_-1, $m_{S_{t - 1} ⋃ f_{t}}$ (D)表示对应子集的决策边界.在x_i代表的局部区域内, 通过选择增大决策边界的特征, 可使分类更准确.

3)最小化冗余.给定已选择的特征子集S_t, 决策属性D, 对于特征f_t, 重要度

sig(f_t, S_t, D)= $m_{S_{t}}$ (D)- $m_{S_{t} - f}$ (D).

如果仅使用前两种评估准则, 特征子集中仍会存在冗余特征.因此, 为了得到低冗余度的特征子集, 需要使S_t的平均重要度最大.但是, 在真实数据集中, 很少出现 $m_{S_{t - 1} ⋃ f_{t}}$ (D)恰好等于 $m_{S_{t - 1}}$ (D)的情况.所以, 本文采用文献[13]中的模糊等式约束替代相等约束.冗余分析的条件设置为

| $m_{S_{t - 1} ⋃ f}$ (D)- $m_{S_{t - 1}}$ (D)|≤ λ $m_{S_{t - 1}}$ (D).

模糊等式约束会选择可能表现较好的特征进行冗余分析, 因此, 冗余分析的次数会增多, 冗余度也会降低.参数λ 并不会太大, 默认设为0.05.

2.4 算法步骤

基于最大决策边界的局部在线流特征选择算法(LOFS)步骤如算法1所示.根据2种评价指标 $m_{f}^{i}$ _weighted(D)和 $m_{f}^{i}$ _density(D), 提出对应的算法LOFS-Weighted和LOFS-Density.由于2种算法只有评价指标不同, 因此简写为LOFS.

算法1 LOFS

输入 OSFS=(U, A, D)

输出所有样本的特征子集集合S

1.初始化特征子集Sⁱ=Ø , 决策边界 $M_{S^{i}}$ =0,

平均决策边界Mea $n_{S^{i}}$ =0, i=1, 2, …, N,

S={S¹, S², …, S^N}

2.循环等待新的特征到来

3.在时刻t到达的特征f_t

4.FOR each x_i in U

5. 计算特征f_t的决策边界 $m_{f_{t}}^{i}$ (D);

6. IF $m_{f_{t}}^{i}$ (D)< Mea $n_{S^{i}}$

7. Discard f_t;

8. END IF

9. IF $m_{S^{i} ⋃ f_{t}}^{i}$ (D)> $M_{S^{i}}$

10. Sⁱ=Sⁱ∪ f_t, $M_{S^{i}}$ = $m_{S^{i}}^{i}$ (D);

11. Mea $n_{S^{i}}$ = $\frac{1}{|S^{i}|} \sum_{f \in S^{i}} m_{f}^{i}$ (D);

12. ELSE

13. IF | $m_{S^{i} ⋃ f_{i}}^{i}$ (D)- $M_{S^{i}}$ |≤ λ $M_{S^{i}}$

14. Sⁱ=Sⁱ∪ f_t;

15. FOR each f in Sⁱ

16. 计算特征f的重要度sig(f, Sⁱ, D);

17. IF sig(f, Sⁱ, D)≤ 0

18. Sⁱ=Sⁱ-f;

19. END IF

20. END FOR

21. END IF

22. END IF

23.END FOR

24.直到没有新特征流入, 返回特征子集集合S.

在算法1中, 当新的特征f_t到来后, 以样本x_i为目标进行特征选择.首先, 在第5步中使用式(2)或式(3)计算在样本x_i下特征的决策边界.之后, 在第6步判断特征的决策边界是否大于平均决策边界, 如果大于, 继续, 否则, 抛弃当前特征.在第11步判断子集Sⁱ∪ f_t的决策边界是否大于Sⁱ的决策边界:如果大于, 说明当前特征f_t有助于增大决策边界, 选择这个特征; 否则, 再判断Sⁱ∪ f_t和Sⁱ的决策边界差距是否小于Sⁱ决策边界的λ 倍.如果满足, 进行冗余分析, 冗余分析会抛弃重要度小于或等于0的特征.经过3种在线评估策略的特征筛选, 最终获得决策边界最优的特征子集.

算法1的时间复杂度主要依赖于样本决策边界的计算.假设样本个数为N, 特征个数为F, 已选特征子集的数量为|S|.在算法中, 需要对每个样本都进行特征选择, 单个样本的同类样本数量和不同类样本数量的最大值为V, 最外层循环为N.LOFS-Weighted使用加权计算单个样本的决策边界, 时间复杂度为O(N), 所以, LOFS-Weighted总体的时间复杂度为O(F|S|N²), 最坏时间复杂度为O(F²N²).LOFS-Density使用密度计算单个样本的决策边界, 时间复杂度为O(V log₂V), LOFS-Density总体的时间复杂度为O(F|S|NV log₂V), 最坏时间复杂度为O(F²N²log₂N).

3 实验及结果分析

3.1 实验设置

本文在14个数据集上进行实验, 包括来自于UCI的数据集IONOSPHERE、SONAR、LSTV、ISOLET, 来自DNA microarray的数据集^{[17, 18]}COLON、LUNG2、LYMPHOMA、DLBCL、ALLAML、LEUKEMIA、GLI85, 来自Agnostic Learning vs. Prior Knowledge Challenge的数据集^[19]ADA、GINA, 来自NIPS 2003的数据集^[6]ARCENE.数据集的信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

所有的实验均在Windows 10 PC, Intel(R) Core(TM) i5-6500 CPU @3.20 GHz, 16 GB RAM环境中进行, 采用Matlab R2015b实现LOFS.实验前对数据集进行标准化处理.实验结果为10次10折交叉验证的平均值.

3.2 参数敏感度分析

本节主要分析λ 对LOFS-Weighted和LOFS-Density的影响.λ 是用于控制进行冗余分析的次数.λ 越小, 说明对特征的要求越严格; λ 越大, 说明对特征的要求越宽松, 进行冗余分析的次数也越多.因此, 在实验中将λ 设置为0, 0.01, 0.05, 0.1, 依次增大.λ =0表示相等约束, 并以此作为对照, 观察λ 对算法性能的影响.

两种算法在λ 不同时分类精度、选择特征数量和运行时间对比如表2~表4所示.由表可得, λ 不同时分类精度无显著差异, λ =0.1时取得最优表现.随着λ 的增大, 算法的运行时间增加, 主要原因是λ 越大, 算法的冗余度分析次数越多.同时, 选择特征数量也会减少, 反之亦然.总之, 增大λ 可去除更多的冗余特征, 提高分类精度, 但是λ 并不是越大越好, 为了平衡候选特征数量和运行时间, 实验中将λ 默认设置为0.05.

表2 λ 对LOFS-Weighted和LOFS-Density分类精度的影响 Table 2 Influence of λ on classification accuracy of LOFS-Weighted and LOFS-Density

表3 λ 对LOFS-Weighted和LOFS-Density选择特征数量的影响 Table 3 Influence of λ on the number of selected features of LOFS-Weighted and LOFS-Density

表4 λ 对LOFS-Weighted和LOFS-Density运行时间的影响 Table 4 Influence of λ on running time of LOFS-Weighted and LOFS-Density s

3.3 对比算法实验结果

为了评估本文算法的有效性, 选择如下具有代表性的流特征选择算法进行对比:α -Investing、OSFS、FOSFS、SAOLA、A3M、OFS-Density.α -Investing、OSFS、FOSFS、SAOLA均来自文献[20]中提供的在线流特征选择算法, A3M、OFS-Density来自文献[21]提供的源码.按原文献的实验设计为每种算法设置默认参数.LOFS设置参数λ =0.05.在对比算法特征选择完成后, 采用分类回归树(Classification and Regression Tree, CART)、K近邻(K Nearest Neighbor, KNN)(K=1)和线性支持向量机(Linear Support Vector Machine, LSVM)分类器对选定的特征子集进行评估.LOFS特征选择完成后, 采用1.2节的类相似度测量方法进行分类.

3.3.1 分类精度对比

针对CART、KNN、LSVM分类器, 各算法在14个数据集上的分类精度对比如表5~表7所示, 表中黑体数字表示该行的最优值.

表5 各算法在CART分类器上的分类精度对比 Table 5 Comparison of classification accuracy of different algorithms on CART classifier

表6 各算法在KNN分类器上的分类精度对比 Table 6 Comparison of classification accuracy of different algorithms on KNN classifier

表7 各算法在SVM分类器上的分类精度对比 Table 7 Comparison of classification accuracy of different algorithms on SVM classifier

由表5~表7可知, 在3个分类器上, 各算法在SVM分类器上的分类精度最高, LOFS-Weighed的平均分类精度最高.LOFS-Weighed、LOFS-Density、A3M整体的分类性能明显优于α -Investing和OSFS, 并且在ISOLET数据集上, α -Investing分类精度明显高于其它对比算法.在ADA、GINA数据集上, LOFS-Weighted和LOFS-Density分类精度略低于其它算法.这是因为对于样本数量较多的数据集, 本文算法给样本选择的局部区域会发生重叠, 影响分类精度.由于LOFS-Weighted考虑全部样本, 而LOFS-Density考虑部分样本, 因此, LOFS-Weighted的分类性能略高于LOFS-Density.在其它数据集上, LOFS-Weighted和LOFS-Density的分类精度略高于SAOLA、FOSFS、A3M.

表8为各算法在9个数据集(二分类)上的接收者特征曲线下面积(Area under Curve, AUC)值^[22]对比, 表中黑体数字表示该行的最优结果.由表可知, LOFS-Weighted、LOFS-Density、OFS-Density、A3M的AUC值高于其它对比算法, 在IONOSPHERE、LSTV、DLBCL、GLI85数据集上, LOFS-Density的AUC值明显高于α -Investing和A3M.

表8 各算法在SVM分类器上的AUC值对比 Table 8 AUC value comparison of different algorithms on SVM classifier

在14个数据集上各种分类器的对比中, LOFS-Weighted和LOFS-Density在总体上能在提高已有算法分类精度的基础上保持稳定的分类性能, 特别地, 在小样本的高维数据集上表现较优.

3.3.2 选择特征数量对比

由于LOFS的特殊性, 每个样本选择一个特征集合.所以, 本文将每个样本选择的特征子集的基数相加, 然后将总的特征数量除以样本个数作为算法选择特征数量.

各算法选择的候选特征数量对比如表9所示, 表中黑体数字表示该行的最优结果.由表可见, 选择特征数量最少的是OSFS, 最多的是A3M.LOFS-Weighted、LOFS-Density、SAOLA和OFS-Density选择的特征数量相差不大.在保持高精度的前提下, LOFS-Weighted选择特征的数量少于LOFS-Density, 原因是LOFS-Weighted使用加权方式利用局部信息, 会考虑所有样本, 而LOFS-Density只考虑一部分样本.因此, 在计算特征的决策边界时, LOFS-Weighted选择的特征会更少、更准确.

表9 各算法的选择特征数量对比 Table 9 The number of selected features of different algorithms

3.3.3 运行时间对比

各算法在14个数据集上的运行时间对比如表10所示, 表中黑体数字表示该行的最优结果.由表可见, 在所有数据集中, α -Investing、SAOLA、FOSFS明显快于其它算法.运行时间最短的是α -Investing, 最长的是A3M, LOFS-Weighed和LOFS-Density的运行时间与OFS-Density相差不大, 低于A3M.由于LOFS-Weighed会计算所有样本的平均加权距离, 不同特征的决策边界相差不大, 因此会进行更多的冗余分析, 选择的特征更少.所以, LOFS-Weighed的运行时间略长于LOFS-Density.

表10 各算法的运行时间对比 Table 10 Running time comparison of different algorithms s

3.4 算法有效性统计性假设检验

为了更直观地对比各算法之间分类性能的差异, 显著性水平α =0.05, 采用Friedman检验^[23]和Nemenyi后续检验^[23], 并假设所有算法的性能无明显差异.

首先进行Friedman检验, 给定k种算法, N个数据集, 计算数据集的平均序值.在原假设下, 通常使用变量F_F进行统计比较, 结果如表11所示.由表可看出, F_F大于显著性水平α =0.05的临界值, 因此拒绝原假设.

表11 不同实验下的Friedman统计F_F Table 11 Friedman statistics F_F in different experiments

之后, 通过Nemenyi检验准确对比不同算法之间的差异性, 计算平均序值差别的临界值域CD, 通过q_α₌₀_.₀₅=2.949, 计算CD=2.4073(k=7, N=14), CD=2.7158(k=7, N=11)(平均序值和临界值域CD的计算可参考文献[23]).

根据算法的平均序值绘制的性能差异图如图2和图3所示.排名高的算法在右边, 如果两种算法的平均排名之差大于CD, 则这两种算法的性能将显著不同.

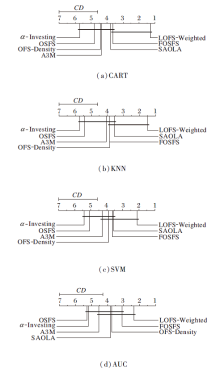	Figure Option View Download New Window
	图2 使用Nemenyi检验对比LOFS-Weighted与其它算法的性能差异Fig.2 Performance difference comparison of LOFS-Weighted and other algorithms in Nemenyi test

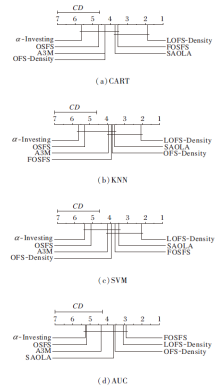	Figure Option View Download New Window
	图3 使用Nemenyi检验对比LOFS-Density与其它算法的性能差异Fig.3 Performance difference comparison of LOFS-Density and other algorithms in Nemenyi test

由图2和图3可看出, 在CART、KNN、SVM分类器上, LOFS-Weighted和LOFS-Density的准确率高于对比算法, 在AUC指标上也有较高的排名, 并且LOFS-Weighted在AUC指标上略高于LOFS-Density.

4 结束语

针对流特征场景下的在线特征选择问题, 为了选择适应样本局部空间变化的特征, 本文将局部特征选择应用到流特征选择问题中, 提出基于最大决策边界的局部在线流特征选择算法(LOFS).给每个样本的局部区域选择决策边界最大的特征子集, 可将局部区域中同类样本和不同类样本尽可能分开, 有效解决在线流特征选择问题.在实验中, 首先分析参数λ 对算法的影响, λ 会影响候选特征数量和分类精度, 但算法总体对参数不敏感.在大部分数据集上, 本文算法能达到更高的分类精度.最后, 使用统计性假设检验证实本文算法与其它算法在分类性能上有明显不同, 并优于大部分算法.

虽然LOSF在大部分数据集上提高分类性能, 但是对于样本较多的数据集, 分类精度有所下降.因此, 下一步工作是改进算法的运行效率及研究适合样本数多的局部在线流特征选择算法.

参考文献

文献选项

[1]	ARMANFARD N, REILLY J P, KOMEILI M. Logistic Localized Modeling of the Sample Space for Feature Selection and Classification. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(5): 1396-1413. [本文引用:1]
[2]	WANG Y X, JAN KLIJN J G, ZHANG Y, et al. Gene-Expression Profiles to Predict Distant Metastasis of Lymph-Node-Negative Primary Breast Cancer. The Lancet, 2005, 365(9460): 671-679. [本文引用:1]
[3]	URBANOWICZ R J, MELISSA M, CAVA W L, et al. Relief-Based Feature Selection: Introduction and Review. Journal of Biomedical Informatics, 2018, 85: 189-203. [本文引用:2]
[4]	GU Q Q, LI Z H, HAN J W. Generalized Fisher Score for Feature Selection // Proc of the 27th Conference on Uncertainty in Artificial Intelligence. Virginia, USA: AUAI Press, 2011: 266-273. [本文引用:1]
[5]	VERGARA J R, ESTÉVEZ P A. A Review of Feature Selection Methods Based on Mutual Information. Neural Computing and Applications, 2014, 24: 175-186. [本文引用:1]
[6]	WU X D, YU K, DING W, et al. Online Feature Selection with Streaming Features. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(5): 1178-1192. [本文引用:5]
[7]	YU K, WU X D, DING W, et al. Scalable and Accurate Online Feature Selection for Big Data. ACM Transactions on Knowledge Discovery from Data, 2016, 11(2): 1-39. [本文引用:2]
[8]	WU X D, ZHU X Q, WU G Q, et al. Data Mining with Big Data. IEEE Transactions on Knowledge and Data Engineering, 2013, 26(1): 97-107. [本文引用:1]
[9]	ZHOU J, FOSTER D P, STINE R A, et al. Streamwise Feature Selection. Journal of Machine Learning Research, 2006, 7: 1861-1885. [本文引用:2]
[10]	尤殿龙, 郭松, 赵春慧, 等. 面向分类的流特征在线特征选择算法. 电子学报, 2020, 48(2): 321-332. (YOU D L, GUO S, ZHAO C H, et al. Online Feature Selection with Streaming Features for Classification. Acta Electronica Sinica, 2020, 48(2): 321-332. ) [本文引用:1]
[11]	吴中华, 郑玮. 基于 l_{2, 1}范数的在线流特征选择算法. 计算机与数字工程, 2019, 47(6): 1306-1313. (WU Z H, ZHENG W. Online Streaming Feature Selection Algorithm Regularized by l_{2, 1}-norm. Computer and Digital Enginee-ring, 2019, 47(6): 1306-1313. ) [本文引用:1]
[12]	ZHOU P, HU X G, LI P P, et al. Online Streaming Feature Selection Using Adapted Neighborhood Rough Set. Information Sciences, 2019, 481: 258-279. [本文引用:2]
[13]	ZHOU P, HU X G, LI P P, et al. OFS-Density: A Novel Online Streaming Feature Selection Method. Pattern Recognition, 2019, 86: 48-61. [本文引用:3]
[14]	陈祥焰, 林耀进, 王晨曦. 基于邻域粗糙集的高维类不平衡数据在线流特征选择. 模式识别与人工智能, 2019, 32(8): 726-735. (CHEN X Y, LIN Y J, WANG C X. Online Streaming Feature Selection for High-Dimensional and Class-Imbalanced Data Based on Neighborhood Rough Set. Pattern Recognition and Artificial Intelligence, 2019, 32(8): 726-735. ) [本文引用:1]
[15]	程玉胜, 李雨, 王一宾, 等. 结合滑动窗口与模糊互信息的多标记流特征选择. 小型微型计算机系统, 2019, 40(2): 320-327. (CHENG Y S, LI Y, WANG Y B, et al. Multi-label Streaming Feature Selection Combining Sliding Window and Fuzzy Mutual Information. Journal of Chinese Computer Systems, 2019, 40(2): 320-327. ) [本文引用:1]
[16]	ARMANFARD N, REILLY J P, KOMEILI M. Local Feature Selection for Data Classification. IEEE Transactions on Pattern Ana-lysis and Machine Intelligence, 2015, 38(6): 1217-1227. [本文引用:4]
[17]	YANG K, CAI Z P, LI J Z, et al. A Stable Gene Selection in Microarray Data Analysis. BMC Bioinformatics, 2006, 7(1). DOI: DOI:10.1186/1471-2105-7-228. [本文引用:1]
[18]	YU L, DING C, LOSCALZO S. Stable Feature Selection via Dense Feature Groups // Proc of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2008: 803-811. [本文引用:1]
[19]	GUYON I, SAFFARI A, DROR G, et al. Agnostic Learning vs. Prior Knowledge Challenge // Proc of the International Joint Conference on Neural Networks. Washington, USA: IEEE, 2007: 829-834. [本文引用:1]
[20]	YU K, DING W, WU X D. LOFS: A Library of Online Streaming Feature Selection. Knowledge-Based Systems, 2016, 113: 1-3. [本文引用:1]
[21]	ZHOU P. Online Streaming Feature Selection Algorithms Source Code[DB/OL]. [2021-05-15]. https://github.com/doodzhou/OSFS. [本文引用:1]
[22]	BAGHERI A, SOFOTASIOS P C, TSIFTSIS T A, et al. Area under ROC Curve of Energy Detection over Generalized Fading Cha-nnels // Proc of the 26th IEEE Annual International Symposium on Personal, Indoor, and Mobile Radio Communications. Washington, USA: IEEE, 2015: 656-661. [本文引用:1]
[23]	DEMŠAR J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research, 2006, 7: 1-30. [本文引用:3]

2018

0.0

... 特征选择在大数据问题中具有重要作用^[1,2] ...

2005

0.0

... 特征选择在大数据问题中具有重要作用^[1,2] ...

2018

0.0

... 传统的特征选择方法^[3,4,5]选择在整个样本空间中通用的特征子集 ...

... ReliefF^[3]会分别选择同类和不同类最近的K个样本,而Relief是K=1的特例 ...

2011

0.0

... 传统的特征选择方法^[3,4,5]选择在整个样本空间中通用的特征子集 ...

2014

0.0

... 传统的特征选择方法^[3,4,5]选择在整个样本空间中通用的特征子集 ...

2013

0.0

... 在现实应用中,由于特征空间的动态性,在特征选择之前不一定能全部获取训练数据的全部特征,从而造成特征空间是动态、未知的,如火星陨石坑的高分辨率探测行星的图像^[6]、新浪微博中热门话题榜单的变动^[7]及环境监测和分析^[8]等 ...

... 流特征是随着时间推移一个接一个出现的特征,而训练样本的数量是固定的^[6] ...

... Wu等^[6]提出在线流特征选择(Online Streaming Feature Selection, OSFS),主要分为在线相关性分析和在线冗余分析2步,使用条件独立性测试进行特征选择,需要大量的训练实例 ...

... 因此,Wu等^[6]又提出快速的在线流特征选择(Fast OSFS, FOSFS),改进在线冗余分析阶段,降低时间复杂度 ...

... Prior Knowledge Challenge的数据集^[19]ADA、GINA,来自NIPS 2003的数据集^[6]ARCENE ...

2016

0.0

... 在大数据的应用中,Yu等^[7]提出可扩展、准确的在线特征选择算法(Scalable and Accurate Online Approach for Feature Selection, SAOLA),用于超高维数据集 ...

2013

0.0

2006

0.0

... 传统的特征选择算法无法处理流特征场景,因此,能处理动态流特征的在线流特征选择算法受到广泛关注^[9] ...

... Zhou等^[9]提出基于流回归的在线特征选择(Streamwise Feature Selection, #cod#x003b1 ...

2020

0.0

... 尤殿龙等^[10]提出采用互信息和条件独立性的在线流特征选择方法(Online Feature Selection Method Using Mutual Information and Conditional Independence),采用四层过滤方法处理冗余特征和不相关特征 ...

2019

0.0

... 吴中华等^[11]提出基于l_2,1范数的在线流特征选择算法(Online Streaming Feature Selection Algorithm Regularized by l_2,1Norm, sfs_l21),相比l₀范数和l₁范数,sfs_l21对噪声不敏感,具有行稀疏性质 ...

2019

0.0

... 此外,粗糙集和模糊互信息也广泛应用于流特征选择^{[12,13,14,15]} ...

... Zhou等^[12]提出基于自适应邻域粗糙集的在线流特征选择算法(Online Streaming Feature Selection Using Adapted Neighborhood Rough Set, A3M),基于自适应的邻域粗糙集,通过最大依赖度、最大相关性和最大显著性评价标准,可筛选高质量的特征子集 ...

2019

0.0

... 此外,粗糙集和模糊互信息也广泛应用于流特征选择^{[12,13,14,15]} ...

... Zhou等^[13]还利用邻域样本的密度信息,设计不需要预先指定任何参数的自适应邻域关系,并提出基于自适应密度邻域关系的在线流特征选择方法(Online Streaming Feature Selection Method Based on Adaptive Density Neighborhood Rela-tion, OFS-Density),通过模糊等式约束,可考虑更多特征,获得低冗余度的特征子集 ...

... 所以,本文采用文献[13]中的模糊等式约束替代相等约束 ...

2019

0.0

... 此外,粗糙集和模糊互信息也广泛应用于流特征选择^{[12,13,14,15]} ...

2019

0.0

... 此外,粗糙集和模糊互信息也广泛应用于流特征选择^{[12,13,14,15]} ...

2015

0.0

... 所以,针对上述问题,本文将局部特征选择^[16]扩展到流特征选择,并使用最大决策边界作为选择特征的标准,使每个局部区域决策边界最大的特征子集尽可能分开同类样本和不同类样本 ...

... 定义1^[16] 设 xip是任意样本x_i在对应的指示向量f⁽ⁱ⁾上的投影: ...

... 定义2^[16] 为了实现上述目标,需要定义N-1个目标函数,目标函数分别是样本间的类内加权距离和类间加权距离: ...

... 因此,采用类相似度测量方法^[16]进行分类 ...

2006

0.0

... 1 实验设置本文在14个数据集上进行实验,包括来自于UCI的数据集IONOSPHERE、SONAR、LSTV、ISOLET,来自DNA microarray的数据集^[17,18]COLON、LUNG2、LYMPHOMA、DLBCL、ALLAML、LEUKEMIA、GLI85,来自Agnostic Learning vs ...

2008

0.0

2007

0.0

... Prior Knowledge Challenge的数据集^[19]ADA、GINA,来自NIPS 2003的数据集^[6]ARCENE ...

2016

0.0

... -Investing、OSFS、FOSFS、SAOLA均来自文献[20]中提供的在线流特征选择算法,A3M、OFS-Density来自文献[21]提供的源码 ...

2021

0.0

... -Investing、OSFS、FOSFS、SAOLA均来自文献[20]中提供的在线流特征选择算法,A3M、OFS-Density来自文献[21]提供的源码 ...

2015

0.0

... 表8为各算法在9个数据集(二分类)上的接收者特征曲线下面积(Area under Curve, AUC)值^[22]对比,表中黑体数字表示该行的最优结果 ...

2006

0.0

... 05,采用Friedman检验^[23]和Nemenyi后续检验^[23],并假设所有算法的性能无明显差异 ...

... 7158(k=7,N=11)(平均序值和临界值域CD的计算可参考文献[23]) ...