引用本文
吕君环, 许柯, 王东. 基于指数移动平均知识蒸馏的神经网络低比特量化方法. 模式识别与人工智能, 2021,34(6): 1143-1151
LÜ Junhuan, XU Ke, WANG Dong. Low-Bit Quantization of Neural Network Based on Exponential Moving Average Knowledge Distillation. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(6): 1143-1151.  
Doi: 10.16451/j.cnki.issn1003-6059.202112007
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于指数移动平均知识蒸馏的神经网络低比特量化方法
吕君环1,2, 许柯1,2, 王东1,2
1.北京交通大学 信息科学研究所 北京 100044
2.北京交通大学 现代信息科学与网络技术北京市重点实验室 北京 100044
通讯作者:

王 东,博士,教授,主要研究方向为图像处理、模型压缩、芯片设计等.E-mail:wangdong@bjtu.edu.cn.

作者简介:

吕君环,硕士研究生,主要研究方向为神经网络量化、模型压缩等.E-mail:lvjunhuan@bjtu.edu.cn.

许 柯,博士研究生,主要研究方向为神经网络模型剪枝、量化、模型压缩等.E-mail:xuke225@bjtu.edu.cn.

收稿日期: 2021-04-20 接受日期: 2021-08-25
资助项目: 国家重点研发计划项目(No.2019YFB2204200)、中央高校基本科研业务费项目(No.2020JBM020)、北京市自然科学基金项目(No.4202063)资助
摘要

目前存储和计算成本严重阻碍深度神经网络应用和推广,而神经网络量化是一种有效的压缩方法.神经网络低比特量化存在的显著困难是量化比特数越低,网络分类精度也越低.为了解决这一问题,文中提出基于指数移动平均知识蒸馏的神经网络低比特量化方法.首先利用少量图像进行自适应初始化,训练激活和权重的量化步长,加快量化网络收敛.再引入指数移动平均(EMA)知识蒸馏的思想,利用EMA对蒸馏损失和任务损失进行归一化,指导量化网络训练.在ImageNet、CIFAR-10数据集上的分类任务表明,文中方法可获得接近或超过全精度网络的性能.

关键词: 深度学习; 网络量化; 知识蒸馏; 模型压缩
中图分类号:TP 391
Low-Bit Quantization of Neural Network Based on Exponential Moving Average Knowledge Distillation
LÜ Junhuan1,2, XU Ke1,2, WANG Dong1,2
1. Institute of Information Science, Beijing Jiaotong University, Beijing 100044
2. Beijing Key Laboratory of Advanced Information Science and Network Technology, Beijing Jiaotong University, Beijing 100044
Corresponding author:
WANG Dong, Ph.D., professor. His research interests include image processing, model compression and chip design.

About Author:
LÜ Junhuan, master student. Her research interests include neural network quantization and model compression.
XU Ke, Ph.D. candidate. His research interests include neural network pruning, quan-tization and model compression.

Fund:National Key Research and Development Program of China(No.2019YFB2204200), Fundamental Research Funds for the Central Universities(No.2020JBM020), Beijing Natural Science Foundation Program(No.4202063)
Abstract

Now the memory and computational cost restrict the popularization of deep neural network application, whereas neural network quantization is an effective compression method. As the number of quantized bits is lower, the classification accuracy of neural networks becomes poorer in low-bit quantization of neural networks. To solve this problem, a low-bit quantization method of neural networks based on knowledge distillation is proposed. Firstly, a few images are exploited for adaptive initialization to train the quantization step of activation and weight to speed up the convergence of the quantization network. Then, the idea of exponential moving average knowledge distillation is introduced to normalize distillation loss and task loss and guide the training of quantization network. Experiments on ImageNet and CIFAR-10 datasets show that the performance of the proposed method is close to or better than that of the full precision network.

Key words: Deep Learning; Network Quantization; Knowledge Distillation; Model Compression

本文责任编委 陈松灿

Recommended by Associate Editor CHEN Songcan

深度卷积神经网络(Deep Convolution Neural Network, DCNN)在图像识别[1]、语音识别[2]、目标检测[3]等领域都取得巨大成功, 但存储和计算成本严重阻碍神经网络在资源受限设备上的应用, 特别是存在实时要求的应用.网络压缩是解决这一问题的有效手段, 目前研究神经网络压缩方法的工作可粗略分为3种:剪枝[4]、量化[5]和知识蒸馏(Knowle-dge Distillation, KD)[6].

神经网络量化(Quantization of Neural Network, QNN)是将神经网络模型中相近的权重参数近似为相同的数值, 性能基本不变的同时减小模型规模、加快运算速度的一种压缩方法.神经网络量化的目标是获得高性能的低比特神经网络模型.将神经网络的32位浮点数权重, 量化为N位定点数.模型规模大约减少为原来的(N/32)%, 因此可减少参数、降低存储.神经网络低比特量化为定点计算, 可加速运算, 降低内存功耗.目前大多数边缘设备通过定点推理提高计算效率和功耗效率.因此, 将神经网络的权重和激活量化为固定位宽成为神经网络与边缘设备兼容的必要条件.与此同时, 硬件加速器的发展也为神经网络量化提供支持.例如, 嵌入式神经网络处理器(Neural-Network Processing Units, NPU), NVIDIA的张量计算核心单元(Tensor Core)及内存计算(Com-pute-in-Memory, CIM)等硬件加速器已针对4位或2位的字节级处理提供支持.

当前学者们已提出许多高效的神经网络低比特量化方法, 低比特量化实现加速是将权重和激活转换为定点表示.其中8比特量化[7]是当前常用的量化方案, 主要优点是可快速量化, 高效生成量化模型, 但是压缩比不高.为了追求更高的压缩比, 达到更好的加速效果, 现有研究倾向于更低比特的量化, 但量化比特数越低, 分类精度也越低.因此, 当前的研究重点在于探索新的量化方案, 在神经网络进行低比特量化的同时, 量化网络接近或高于全精度网络的性能.

深度卷积神经网络的量化包括网络权重的量化和激活值的量化, 其中网络权重的量化是神经网络中每个卷积核权重参数的量化, 激活值的量化是神经网络每层特征图的量化.Choi等[8]提出参数化剪裁激活(Parameterized Clipping Activation, PACT), 使用剪裁激活函数, 引入可训练的参数以限制激活的最大值.Jung等[9]提出量化区间学习(Quantiza-tion-Interval-Learning, QIL), 使用可训练的量化器执行修剪和裁剪, 以端到端的方式, 通过任务损失优化剪辑值和量化间隔.Esser等[10]提出量化步长学习, Jain等[11]提出量化阈值训练(Trained Quantiza-tion Thresholds, TQT), 都引入可训练的量化步长.Zhou等[12]提出增量网络量化(Incremental Network Quantization, INQ), 增量和渐进量化优化训练过程.上述都是均匀量化的方法, 学者们也提出一些非均匀量化解决方案.Zhang等[13]提出学习量化网络(Learned Quantization Networks, LQ-Nets), 训练非均匀量化器, 优化量化过程.

知识蒸馏是神经网络模型压缩方法之一, 广泛应用于计算机视觉任务中.知识蒸馏的思想是将知识从深层教师模型转移到浅层学生模型, 其中关键问题是将教师模型的何种知识传授给学生模型.Gao等[14]提出残差知识蒸馏, 引入辅助结构, 进一步提炼知识.Nowak等[15]提出结构压缩方法, 将多层学到的知识转移到单层.已有一些研究者尝试使用知识蒸馏方法训练量化网络.使用全精度网络作为教师网络, 低比特量化网络作为学生网络.Polino等[16]提出量化蒸馏方法, 将知识转移到权重量化的学生网络.Wei等[17]为确保小型学生网络准确模仿大型教师网络, 首先在特征图上量化全精度教师网络, 然后将知识从量化教师网络转移到量化学生网络.Mishara等[18]提出学徒(Apprentice, AP), 使用相应的全精度网络初始量化网络, 通过蒸馏对量化网络进行微调.由于全精度网络和量化网络存在很大的量化误差, 当量化位宽非常小时, 量化网络的训练往往会陷入局部极小值, 不易收敛.因此, 引入知识蒸馏需要对网络权重和激活的量化步长进行初始化, 避免低精度量化网络不易收敛的问题.

神经网络低比特量化存在的显著困难是量化比特数越低, 网络分类精度也越低.为了解决这一问题, 文中提出基于指数移动平均知识蒸馏的神经网络低比特量化方法.首先利用少量图像进行自适应初始化, 训练激活和权重的量化步长, 加快量化网络收敛.再引入指数移动平均(Exponential Moving Average, EMA)知识蒸馏的思想, 利用EMA对蒸馏损失和任务损失进行归一化, 指导训练量化网络.在ImageNet、CIFAR-10数据集上的分类任务表明, 本文方法接近或超过全精度网络的性能.

1 基于指数移动平均知识蒸馏的神经网络低比特量化方法

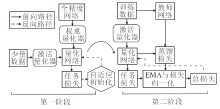
本文提出基于指数移动平均知识蒸馏的神经网络低比特量化方法, 具体框图如图1所示.方法主要分为3部分:1)神经网络量化器.2)网络训练第1阶段.自适应初始化, 通过任务损失更新量化步长.3)网络训练第2阶段.引入教师网络进行EMA知识蒸馏, 利用EMA对蒸馏损失和任务损失进行归一化, 指导网络训练.

图1 本文方法框图Fig.1 Architecture of the proposed method

1.1 网络量化器

对于卷积层或全连接层, 使用x表示网络输入向量, y表示网络输出向量, w表示权重值, b表示偏置, l表示层数, f表示卷积后的操作.给定具有n层的前馈神经网络, 下一层输入可表示为

xl+1=f(yl)=f(wlxl+bl).

本文的网络量化器设计参考TQT, 目标是得到可进行低精度整数运算的深度卷积神经网络模型.在神经网络训练过程中, 需对卷积层权重和每层的激活值进行量化.定义权重量化器:

w^=Q(w)=round[clip( wsw, N, P)]· sw, (1)

其中, w表示量化前的权重值, w^表示量化后权重值, sw表示权重的量化步长, N=- 2mw-1, P= 2mw-1-1, mw表示权重量化比特数, clip(· )函数表示对权重进行剪切, 执行饱和操作, round(· )函数表示将连续值映射到离散值上, 执行舍入操作.

同时激活量化器:

x^=Q(x)=round[clip( xsa, min, max)]· sa, (2)

其中, x表示量化前的激活值, x^表示量化后激活值, sa表示激活值量化步长, min=0, max= 2ma-1, ma表示激活量化比特数.

本文的网络量化器为均匀量化器, 旨在通过神经网络训练优化激活和权重量化步长.关键问题在于网络训练时如何反向更新量化步长, 因此可转化为求解网络损失关于量化步长的梯度问题.式(1)和式(2)中舍入操作的梯度处处为0或未定义, 使基于梯度的训练无法进行.解决这个问题的一种方法是使用直通估计器[19]以近似梯度, 将舍入操作的梯度近似为1:

∂x^∂x= 1, min≤xsa≤max0, xsa< min, xsa> max

以激活为例, 网络损失值L对于量化步长sa的梯度可表示为

∂L∂sa= ∂L∂x^∂x^∂sa.(3)

利用直通估计器, 激活量化后量化步长的梯度为

∂x^∂sa= ⌊xsa⌉-xsa, min< ⌊xsa⌉< maxmin, ⌊xsa⌉< minmax, ⌊xsa⌉> max

本文神经网络卷积层量化流程如图2所示, 包括卷积层输入x经激活量化器的激活量化, 及卷积核权重经权重量化器的权重量化, 后经批归一化层和激活函数得到输出层y.

图2 神经网络卷积层量化流程图Fig.2 Flow chart of neural network convolution quantization

1.2 自适应初始化

优化量化网络的量化步长是本文方法的关键问题.训练量化网络中引入知识蒸馏, 常规方法是使用全精度网络的参数直接通过量化器赋给量化网络, 再使用蒸馏方法对量化网络进行微调.但是, 将全精度网络的参数直接放入量化器作为量化网络的参数, 由于量化网络与全精度网络存在较大差异, 所以会导致很大的量化误差.简单地将量化和蒸馏结合并不能充分利用蒸馏的积极影响, 容易导致网络性能降低.这是由知识蒸馏的正则化特性和量化网络的有限表达能力所致.这可能引起量化网络在训练时陷入不良的局部极小值.为了缓解此问题并为蒸馏提供一个良好的起点, 本文提出自适应初始化方法, 先集中优化量化步长, 为EMA知识蒸馏训练提供起点.

自适应初始化作为量化网络训练的第一阶段, 首先将权重量化步长初始值设置为每层权重的均值减去3倍的标准差再除以2b-1, b为量化位宽, 激活初始值设置为每层激活最大值除以2b-1.自适应初始化阶段全部冻结神经网络参数, 只更新权重和激活量化步长的梯度.不同于以往工作只通过最小化全精度网络和量化网络间的量化误差优化量化网络, 本文通过最小化量化网络的任务损失, 使用随机梯度下降反向传播更新量化步长, 优化量化网络.任务损失在分类任务中使用交叉熵损失函数, 定义如下:

LCE=- 1n∑c∑i=1ncilog2( pcL(zi)), (4)

其中, ci表示目标标签向量, pcL(zi)表示量化网络Softmax输出, c表示类别数, z表示网络输出, n表示输入批大小.

自适应初始化可表示为

L=F(sa, sw),

其中, L表示任务损失, sa表示激活的量化步长, sw表示权重的量化步长, F(· )表示神经网络损失计算公式.

自适应初始化应用任务损失即标准交叉熵损失训练量化网络的起始阶段.具体实现过程如算法1 所示.

算法1 自适应初始化

输入 3 000幅训练集图像data, 学习率η ,

预训练模型权重w,

输出 量化模型权重 w^, 激活量化步长sa,

权重量化步长sw

初始量化模型 w^=Q(w)

For x=1:data do

Forward

计算量化输出等于量化网络

根据式(4)计算损失L

Backward:

冻结网络参数

根据式(3)计算 ∂L∂sw、 ∂L∂sa

根据s=s-η ∂L∂s更新量化步长sa、sw

End

1.3 指数移动平均知识蒸馏

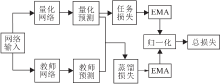
本文量化网络训练的第2阶段使用EMA知识蒸馏方法训练低比特量化网络, 具体框架如图3所示.全精度网络作为教师网络, 量化网络作为学生网络.经过第一阶段自适应初始化训练, 加快量化网络的收敛, 避免蒸馏过程中容易陷入局部最小值的问题.

图3 EMA知识蒸馏框图Fig.3 Flow chart of EMA knowledge distillation

为了提高量化网络的分类准确率, 将量化网络与教师网络具有相同的任务响应作为训练目标.因此本阶段的目标在于缩小全精度教师网络和量化网络之间预测结果的差异.教师网络并不直接参与训练, 只作为量化网络的目标标签.本文使用交叉熵损失强制2个网络预测结果的相似性, 蒸馏损失LKD定义为教师网络预测Softmax输出 pcR(zi)和量化网络预测Softmax输出 pcL(zi)之间的交叉熵损失:

LKD=- 1n∑c∑i=1npcR(zi)log2( pcL(zi)).(5)

改造训练量化网络的损失函数, 利用EMA对蒸馏损失和任务损失进行归一化, 用于指导训练量化网络, 对蒸馏损失和任务损失分别进行EMA, 两者EMA的比例作为蒸馏损失的权重, 可平衡蒸馏损失和任务损失在训练中的作用, 同时保证损失函数的稳定性.本文损失函数定义为

Loss=α LCE+(1-α ) L¯CEL¯KDLKD, (6)

其中, LCE表示任务损失, LKD表示蒸馏损失, L¯CE表示任务损失的EMA, L¯KD表示蒸馏损失的EMA, α 表示可变比例因子.

在第2阶段量化网络时, 目标标签和教师网络预测结果作为软目标标签共同指导训练, 具体实现过程如算法2所示.

算法2 EMA知识蒸馏

输入 数据集图像 all data,

初始化后量化模型权重 w^,

初始化后激活量化步长sa,

初始化后权重量化步长sw

输出 量化模型权重 w^, 激活量化步长sa,

权重量化步长sw

For x=1:all data do

Forward:

计算量化输出等于量化网络

计算教师输出等于教师网络

根据式(5)计算LKD

根据式(6)计算Loss

Backward:

更新网络参数

根据式(3)计算 ∂L∂sw、 ∂L∂sa

根据s=s-η ∂L∂s更新量化步长sa、sw

End

1.4 网络训练

本文方法的训练过程包括自适应初始化阶段和EMA知识蒸馏训练阶段.第1阶段自适应初始化, 使用1.1节的量化器进行量化, 激活和权重量化步长作为可学习的参数, 其余网络参数被冻结.第2阶段恢复网络所有参数的梯度传播, 更改训练网络的损失函数.使用随机梯度下降和反向传播训练量化网络, 直通估计器计算通过round函数的梯度.本文网络与其它量化方案一致, 4比特量化表示将第一层和最后一层量化为8比特, 网络其余层量化为4比特.

2 实验及结果分析

本文实验选用CIFAR-10[20]、ImageNet[21]数据集.网络选择MobileNetV1[22]、MobileNetV2[23]、DarkNet19[24]、ResNet-18[25]、ResNet-20[25]、ResNet-50[25]、ResNet-56[25].

在CIFAR-10数据集上, 设置训练轮数为150轮, 第一阶段使用自适应矩估计(Adaptive Moment Estimation, Adam)优化器[26], 学习率设置为0.001, 学习率衰减策略为指数衰减策略.第二阶段使用随机梯度下降(Stochastic Gradient Descent, SGD)优化器, 学习率设置为0.01, 学习率衰减策略为余弦退火策略.

在ImageNet数据集上, 训练轮数为90轮, 等于或小于当前大多量化方法的训练周期. 第1阶段使用Adam优化器, 学习率设置为0.01, 学习率衰减策略为指数衰减策略.第2阶段使用SGD优化器, 学习率设置为0.01, 学习率衰减策略为余弦退火策略.

2.1 自适应初始化的影响

本节通过开展消融实验验证自适应初始化对量化网络的影响.ResNet-18、ResNet-50、MobileNetV1、MobileNetV2、DarkNet19在ImageNet数据集上4比特量化的分类精度如表1所示, 5种神经网络进行5轮量化训练.两者起始值为相同的预训练权重.由表1可见, 5种网络执行自适应初始化, 分类精度均高于未初始化的结果.使用自适应初始化的网络在五轮训练下就已收敛.未进行初始化的量化网络容易陷入局部极小点, 收敛速度慢或不收敛, Mobile-NetV2在5轮训练后仍不收敛, 分类精度为22.08%.添加自适应初始化后, MobileNetV2在5轮训练后分类精度达到68.34%.

表1 初始化对各网络分类精度的影响 Table 1 Influence of initialization on classification accuracy of different networks %

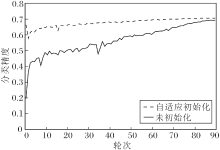
ResNet-18在ImageNet数据集上4比特量化的分类精度对比曲线如图4所示, 图中实线为预训练权重进入量化器作为量化网络的参数后再进行训练的结果, 激活和权重的量化步长未经过初始化, 网络收敛缓慢.虚线为执行自适应初始化训练结果.加入自适应初始化的网络收敛迅速, 在训练的前几轮就已收敛, 最终的分类精度也优于未经过初始化的训练模型.

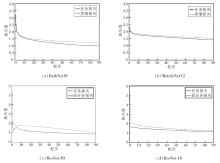
图4 ResNet-18在ImageNet数据集上的分类精度Fig.4 Classification accuracy of ResNet-18 on ImageNet dataset

同时, 对比本文的自适应初始化方法和最小化量化误差方法.最小化量化误差方法使用均方误差作为损失函数.在ImageNet上使用不同初始化方法, ResNet-18、ResNet-50、MobileNetV1、MobileNetV2的4比特量化的分类精度对比如图5所示.

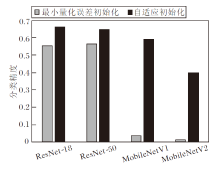图5 各网络使用不同初始化方法后的分类精度Fig.5 Classification accuracy comparison of different networks with different initialization methods

相比最小量化误差初始化方法, 本文的自适应初始化方法具有鲁棒性, 初始化效果更优.实验表明, 神经网络量化训练使用少量图像进行自适应初始化, 可使量化网络快速收敛.由此说明本文的自适应初始化方法的有效性.

2.2 指数移动平均知识蒸馏的影响

本文对教师网络的选用开展如下消融实验, 对于ResNet-18、MobileNetV1、MobileNetV2, 分别用各自对应的全精度网络和ResNet-50作为教师网络进行EMA知识蒸馏训练, 结果如表2所示.由表可见, ResNet-50作为教师网络表现更优.

表2 教师网络对分类精度的影响 Table 2 Influence of teacher network on classification accuracy %

4种网络在引入EMA知识蒸馏和未使用知识蒸馏的4比特量化的分类精度如表3所示.两者采用相同的自适应初始化的方法, ResNet-50作为教师网络, 4种网络在使用EMA知识蒸馏下的分类精度均高于未引入知识蒸馏, 这说明EMA知识蒸馏的有效性.

表3 EMA知识蒸馏对分类精度的影响 Table 3 Influence of EMA knowledge distillation on classification accuracy %
2.3 实验对比

本节选择如下量化方法进行对比实验:PACT[8]、QIL[9]、TQT[11]、LQ-Nets[13]、可微软量化(Differen-tiable Soft Quantization, DSQ)[27]、附带偏移的学习量化步长(Learned Step-Size Quantization with Offset, LSQ+)[28]、硬件感知自动量化(Hardware-Aware Automated Quantization, HAQ)[29].各方法在CIFAR-10数据集上2比特量化的分类精度如表4所示.激活位宽(Activation bit-width, A)与权重位宽(Weight bit-width, W)均量化为2比特(W2A2).由表可知, 3种方法均获得较高的分类精度.

各方法在ImageNet数据集上4比特量化结果的分类精度如表5所示.本文方法ResNet-18的4比特量化结果为71.10%, ResNet-50的4比特量化结果为76.62%, 均为最优值.因为ResNet网络的权重近似于正态分布, EMA知识蒸馏通过调整权重分布, 进一步平衡舍入误差与剪切误差, 量化误差更小, 超过全精度网络性能.

表4 3种方法在CIFAR-10数据集上的分类精度 Table 4 Classification accuracy of 3 methods on CIFAR-10 dataset %
表5 7种方法在ImageNet数据集上的分类精度 Table 5 Classification accuracy of 7 methods on Imagenet dataset %

PACT、HAQ和本文方法在ImageNet数据集上4比特量化的分类精度如表6所示.

表6 3种方法在ImageNet数据集上的分类精度 Table 6 Classification accuracy of 3 methods on ImageNet dataset

由表6可见, 本文方法在MobileNetV1的4比特量化结果为71.05%, 相比PACT、HAQ, 本文方法分类精度分别提升3.6%和8.6%.对比Mobile-NetV2的4比特量化结果, PACT和DSQ的量化结果与全精度网络性能相差很大.MobileNetV2在低比特情况下不容易量化, 这是因为MobileNetV2具有深度可分离卷积, 权重分布较分散, 相比其它模型, 神经网络模型的数据不具有一般性, 因此低比特量化时会产生很大的量化误差.实验表明, 本文方法对于MobileNet这种具有深度可分离卷积的网络是友好的.而由DarkNet19的4比特量化结果可知, TQT的激活量化为8比特, 权重量化为4比特, 相比TQT, 本文方法网络压缩效果更优, 同时分类精度更高.2.4 收敛性分析为了探究EMA知识蒸馏对量化网络的影响, 可视化ResNet-20在CIFAR-10数据集上2比特量化的权重分布, 结果如图6所示.由图可知, (a)中数据分布类似于正态分布, 而(b)中数据分布出现4个峰值, 容易与2比特量化的4个量化值对齐, 从而减少量化误差.引入EMA知识蒸馏后, 改变量化网络的数据分布, 使网络更容易量化.

图6 ResNet-20的2比特量化的权重可视化分布Fig.6 Weight visualization distribution of 2-bit quantization of ResNet-20 (a)Weight of full precision network; (b)Weight of quantization network

本文方法在4个网络下的任务损失、蒸馏损失及是否使用EMA知识蒸馏的任务损失对比如图7所示.由图可知, DarkNet19、MobileNetV2的任务损失与蒸馏损失在几轮内就已收敛, 这表明本文方法的有效性.从ResNet-18、ResNet-50中是否使用EMA知识蒸馏的任务损失对比可看出, 本文方法的任务损失收敛更快, 最终任务损失更小, 分类精度更高.

图7 主流网络损失对比Fig.7 Comparison of mainstream network losses

3 结束语

本文提出基于指数移动平均知识蒸馏的神经网络低比特量化方法, 同时量化激活和权重.首先使用一部分数据进行自适应初始化, 冻结其它参数, 只更新权重和激活的量化步长.在这一阶段, 通过最小化任务损失训练量化步长, 给EMA知识蒸馏训练网络提供良好的起点.下一阶段通过EMA知识蒸馏提高量化网络的性能.对蒸馏损失和目标损失进行损失归一化, 将量化网络引至良好的局部最小值.自适应初始化和EMA知识蒸馏的策略在泛化和找到良好的局部最小值方面具有良好的协同作用.实验表明, 本文方法在CIFAR-10、ImageNet数据集上取得较优结果.ImageNet数据集上4比特量化的分类精度基本上可达到全精度网络.目前对于更低比特量化的探索仍在继续, 在保持高精度的同时降低量化比特数是今后的研究方向.

参考文献
[1] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet Classification with Deep Convolutional Neural Networks // Proc of the 25th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2012: 1097-1105. [本文引用:1]
[2] HINTON G, DENG L, YU D, et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Processing Magazine, 2012, 29(6): 82-97. [本文引用:1]
[3] REDMON J, DIVVALA S, GIRSHICK R, et al. You Only Look Once: Unified, Real-Time Object Detection // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 779-788. [本文引用:1]
[4] HAN S, POOL J, TRAN J, et al. Learning Both Weights and Connections for Efficient Neural Networks // Proc of the 28th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2015, I: 1135-1143. [本文引用:1]
[5] WANG P S, HU Q H, ZHANG Y F, et al. Two-Step Quantization for Low-Bit Neural Networks // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 4376-4384. [本文引用:1]
[6] HINTON G, VINYALS O, DEAN J. Distilling the Knowledge in a Neural Network[C/OL]. [2021-03-25]. https://export.arxiv.org/pdf/1503.02531. [本文引用:1]
[7] JACOB B, KLIGYS S, CHEN B, et al. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2018: 2704-2713. [本文引用:1]
[8] CHOI J, WANG Z, VENKARANI S, et al. PACT: Parameterized Clipping Activation for Quantized Neural Networks[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1805.06085v2.pdf. [本文引用:2]
[9] JUNG S, SON C, LEE S, et al. Learning to Quantize Deep Networks by Optimizing Quantization Intervals with Task Loss // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4345-4354. [本文引用:2]
[10] ESSER S K, MCKINSTRY J L, BLANI D, etal. Learned Step Size Quantization[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1902.08153v1.pdf. [本文引用:1]
[11] JAIN S R, GURAL A, WU M, etal. Trained Quantization Thre-sholds for Accurate and Efficient Fixed-Point Inference of Deep Neural Networks[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1903.08066v2.pdf. [本文引用:2]
[12] ZHOU A J, YAO A B, GUO Y W, etal. Incremental Network Quantization: Towards Lossless CNNs with Low-Precision Weights[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1702.03044v2.pdf. [本文引用:1]
[13] ZHANG D Q, YANG J L, YE D Q Z, et al. LQ-Nets: Learned Quantization for Highly Accurate and Compact Deep Neural Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 373-390. [本文引用:2]
[14] GAO M Y, SHEN Y J, LI Q Q, et al. Residual Knowledge Disti-llation[C/OL]. [2021-03-25]. https://arxiv.org/pdf/2002.09168v1.pdf. [本文引用:1]
[15] NOWAK T S, CORSO J J. Deep Net Triage: Analyzing the Importance of Network Layers via Structural Compression[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1801.04651.pdf. [本文引用:1]
[16] POLINO A, PASCANU R, ALISTARH D. Model Compression via Distillation and Quantization[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1802.05668.pdf. [本文引用:1]
[17] WEI Y, PAN X Y, QIN H W, et al. Quantization Mimic: Towards Very Tiny CNN for Object Detection // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 274-290. [本文引用:1]
[18] MISHRA A, MARR D. Apprentice: Using Knowledge Distillation Techniques to Improve Low-Precision Network Accuracy[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1711.05852.pdf. [本文引用:1]
[19] BENGIO Y, LÉONARD N, COURVILLE A. Estimating or Propagating Gradients through Stochastic Neurons for Conditional Computation[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1308.3432v1.pdf. [本文引用:1]
[20] KRIZHEVSKY A. Learning Multiple Layers of Features from Tiny Images[C/OL]. [2021-03-25]. https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf [本文引用:1]
[21] RUSSAKOVSKY O, DENG J, SU H, et al. ImageNet Large Scale Visual Recognition Challenge. International Journal of Computer Vision, 2015, 115(3): 211-252. [本文引用:1]
[22] HOWARD A G, ZHU M L, CHEN B, et al. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1704.04861.pdf. [本文引用:1]
[23] SANDLER M, HOWARD A, ZHU M L, et al. MobileNetV2: Inverted Residuals and Linear Bottlenecks // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 4510-4520. [本文引用:1]
[24] REDMON J, FARHADI A. YOLO9000: Better, Faster, Stronger // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 6517-6525. [本文引用:1]
[25] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:4]
[26] KINGMA D P, BA J. Adam: A Method for Stochastic Optimization[C/OL]. [2021-03-25]. https://arxiv.org/pdf/1412.6980.pdf. [本文引用:1]
[27] GONG R H, LIU X L, JIANG S H, et al. Differentiable Soft Quan-tization: Bridging Full-Precision and Low-Bit Neural Networks // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 4851-4860. [本文引用:1]
[28] BHALGAT Y, LEE J, NAGEL M, et al. LSQ+: Improving Low-Bit Quantization through Learnable Offsets and Better Initialization // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition Workshops. Washington, USA: IEEE, 2020: 2978-2985. [本文引用:1]
[29] WANG K, LIU Z J, LIN Y J, et al. HAQ: Hardware-Aware Automated Quantization with Mixed Precision // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 8604-8612. [本文引用:1]