融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法

引用本文

董婵娟, 李胜, 何熊熊, 马悦. 融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法. 模式识别与人工智能, ,34(2): 106-116
DONG Chanjuan, LI Sheng, HE Xiongxiong, MA Yue. Point of Interest Recommendation Algorithm Integrating Geo-Category Information and Implicit Social Relationship. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,34(2): 106-116. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202102002
Permissions

《模式识别与人工智能》编辑部所有

融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法

董婵娟¹, 李胜¹, 何熊熊¹, 马悦¹

1.浙江工业大学信息工程学院杭州 310023

通信作者：

李胜,博士,副教授,主要研究方向为图像处理、压缩感知、推荐系统等.E-mail:shengli@zjut.edu.cn.

作者简介:

董婵娟,硕士研究生,主要研究方向为数据挖掘、推荐系统.E-mail:2237462096@qq.com.

何熊熊,博士,教授,主要研究方向为信号处理、医疗图像处理、推荐系统等.E-mail:hxx@zjut.edu.cn.

马悦,硕士研究生,主要研究方向为图像处理、推荐系统.E-mail:1285788475@qq.com.

收稿日期: 2020-07-15 接受日期: 2020-11-11

资助项目: 国家自然科学基金项目(No.61873239,61675183)、浙江省重点研发计划项目(No.2020C03074)资助

摘要

针对现有大多数兴趣点推荐算法都存在签到数据稀疏、社交关系难以获取、用户个性难以考虑等问题,文中提出融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法.首先考虑用户签到种类信息,同时分解用户签到地点矩阵和用户签到种类矩阵,减小签到数据稀疏带来的影响.再在显式社交关系的基础上,使用信息熵的方法度量用户的隐式社交关系,缓解社交网络稀疏的问题,并通过正则化的方法在矩阵分解模型中加入该隐式社交关系.最后,使用自适应核密度估计方法个性化建模地理信息对用户签到行为的影响,提高推荐的准确性.在Foursquare、Yelp数据集上的实验验证文中算法的有效性.

关键词: 兴趣点推荐; 矩阵分解; 自适应核密度估计; Renyi熵

中图分类号:TP 391

Point of Interest Recommendation Algorithm Integrating Geo-Category Information and Implicit Social Relationship

DONG Chanjuan¹, LI Sheng¹, HE Xiongxiong¹, MA Yue¹

1.College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023

Corresponding author:
LI Sheng, Ph.D., associate professor. His research interests include image processing, compressive sensing and recommendation system ).

AboutAuthor:
DONG Chanjuan, master student. Her research interests include data mining and re-commendation system.
HE Xiongxiong, Ph.D., professor. His research interests include signal processing, medical image processing and recommendation system.
MA Yue, master student. Her research interests include image processing and reco-mmendation system.

Fund:Supported by National Natural Science Foundation of China(No.61873239,61675183), Key Research and Development Program of Zhejiang Province(No.2020C03074)

Abstract

Aiming at the problems in the existing point of interest recommendation algorithms, such as check-in data sparsity, difficulties in obtaining social relation and lack of consideration of user individuality, a point of interest recommendation algorithm integrating geo-category information and implicit social relationship is proposed. Firstly, user check-in category information is considered, and user check-in location matrix and category matrix are decomposed simultaneously to reduce the impact of data sparsity. On the basis of explicit social relations, the method of information entropy is employed to measure user implicit social relations to alleviate the sparse problem of social networks, and then the user implicit social relations are added to the matrix factorization model by regularization method. Finally, the adaptive kernel density estimation method is adopted to personalize the impact of geographic information on user check-in behavior to improve the accuracy of recommendation. Experiments on Foursquare and Yelp datasets verify the effectiveness of the proposed algorithm.

Key words: Key Words Point of Interest Recommendation; Matrix Factorization; Adaptive Kernel Density Estimation; Renyi Entropy

文章图片

本文责任编委杨健

Recommended by Associate Editor YANG Jian

现阶段移动和无线通信领域快速进步, 同时也使基于位置的社交网络(Location-Based Social Net-works, LBSNs)得到迅速发展, 如 Facebook、Yelp、Gowalla和Foursquare等.对于全球数百万用户来说, 使用这种媒体已经成为他们日常生活的一部分^{[1, 2, 3, 4]}.LBSNs服务积累了大量的用户数据, 为开发个性化的兴趣点(Point of Interest, POI)推荐系统提供良好的契机.事实上, 准确和个性化的POI推荐是LBSNs业务的关键需求^{[1, 5, 6]}.由于地理位置信息庞大, 用户容易忽略潜在感兴趣的POI, 需要在海量数据中进行搜索, 而个性化的推荐系统可帮助用户轻松找到相关的POI.而且, 由于用户之间的差异性, 商家向不同的用户精准推荐他们想要的POI非常困难, 个性化的推荐系统可帮助商家发现潜在客户, 提高利润.

POI推荐的主要方法之一是协同过滤技术^[2], 它通过用户POI签到矩阵计算用户对未访问的POI的偏好评分.然而, 由于用户只访问LBSNs中较小的一部分POI, 用户签到矩阵高度稀疏, 协同过滤技术难以发挥作用.因此, 上述方法的推荐质量通常较低.

自Netflix大奖竞赛后, 基于矩阵分解(Matrix Factorization, MF)技术的推荐算法^[7]因其良好的可扩展性及处理大规模数据的准确预测能力, 受到学术界和工业界的广泛关注.近年来, 随着对矩阵分解的深入研究, 人们研究得到更复杂的模型.例如, 基于隐式信息的矩阵分解(Singular Value Decompos-ition++, SVD++)^[8], 基于核密度估计的偏好模型^[9], 基于双正则化的矩阵分解模型^[10]等.相比传统的矩阵分解, 更复杂的矩阵分解都加入上下文信息, 如类别信息、社交信息、地理位置信息.类别信息是指每个地点都有所属的类别, 地点类别表示所属服务类型, 如果用户喜欢访问某些类别的地点, 他可能访问更多属于该类别的地点.社交信息是指在LBSNs中, 一个人可能更喜欢他的朋友高度推荐的POI, 即朋友比陌生人更倾向于有更多的共同兴趣.因此一些学者^{[3, 11]}认为可通过研究用户之间的朋友关系提高推荐性能.地理位置信息是指在LBSNs中, POI编码为经纬度, 将POI推荐与传统推荐系统中的书籍、音乐、电影等其它物品推荐区分.POI推荐的研究^{[2, 5]}表明, 人们更倾向于访问他们去过地点附近的POI, 导致基于用户选择的POI空间聚类现象.

在LBSNs中, POI通常有多个层次类别, 这些类别信息表示位置的语义含义, 因此用户在给定位置的签到反映他对相应类别的偏好.为了缓解用户签到数据的稀疏性, 在一些研究^{[12, 13, 14]}中加入种类信息, 取得较好的效果.Liu等^[12]提出类别感知POI推荐模型, 对用户类别转移矩阵使用矩阵分解, 得到用户访问的下一个地点种类, 再结合幂律分布得到用户的推荐列表.He等^[13]通过个性化贝叶斯排序预测用户可能会去的下一个地点种类, 根据空间影响力和类别影响力对类别预测筛选的候选POI进行排序.Chen等^[14]建立用户类别转移的三阶张量, 使用张量分解得到用户可能访问的下个类别, 使用距离加权的超文本敏感主题搜索(Hypertext Induced Topic Search, HITS)计算用户可能访问的地点.

但是上述方法通常需要经过两步向用户推荐感兴趣的地点:1)构造用户种类转移矩阵、用户种类转移三阶张量或用户时间种类张量, 用于预测用户最有可能会去的K₁个地点种类.2)利用一些地理位置信息或其它上下文信息, 在每个种类中选择用户最有可能会去的K₂个地点.最后推荐K₁K₂个地点给用户.但是上述方法都不能直接选出用户感兴趣的地点, 在1)中选择用户感兴趣的种类个数K₁时, K₁的值也会对最后的推荐结果产生明显的影响, 因此在top K(K=K₁K₂)推荐时需要掌握好K₁和K₂的取值.

目前一些学者在试图提高推荐质量时, 将用户的社交关系作为最重要的社会信息类型之一并融入推荐系统中^{[15, 16, 17, 18]}, 取得一定的成果.为了有效整合社交信息与传统的矩阵分解模型, 学者们从不同的角度进行建模.Ma等^[19]提出基于联合矩阵分解的社交推荐(Social Recommendation Using Probabilistic Matrix Factorization, SoRec)模型, 在概率矩阵分解的基础上, 加入社交关系矩阵, 共享用户特征矩阵, 建立用户偏好与好友之间的关系.Ma等^[20]提出基于矩阵分解的社交关系正则化推荐模型(Recommender Systems with Social Regularization, SoReg), 通过物品相似度计算用户和朋友之间喜好的差异.然而, 上述方法只是基于用户特征共享, 并未从社交关系的角度进行深入分析.Yang等^[21]分别从信任者和被信任者的角度提出基于信任的矩阵分解(Trust-Based MF, TrustMF)模型.Yang等^[22]提出基于信任的概率矩阵分解(Trust Based Probability MF, TrustPMF)模型, 为TrustMF提供概率解释.

但是, 上述基于社交关系的推荐系统仍存在局限性.在LBSNs中, 用户只和少数其他用户建立社交关系, 用户之间留下大量模糊稀疏的关系, 即从LBSNs收集的数据并不平衡, 用户之间的显式社交关系形成非线性关系.此外, 现有研究大多只考虑用户的显式社交关系值, 忽视许多有价值的隐式社交关系及其特点.值得注意的是, 已经建立社交关系的朋友不可能有完全相似的兴趣.可见, 显式社交关系可能包含过多的噪声和干扰, 从而影响推荐系统的性能.而拥有相似兴趣的用户之间会存在隐式社交关系, 如用户u₁、u₂访问过相同的地点l, 那么用户u₁、u₂之间可能存在隐式社交关系.

现有POI推荐算法通常根据地理学第一定律(Tobler's First Law of Geography)进行地理信息的建模.Liu等^[23]假设用户对POI的偏爱与这个POI到用户访问过的POI的距离之间成反比关系.Ye等^[24]研究用户签到活动中表现的空间聚类现象, 利用幂律分布对其建模.在现实生活中, 用户访问的POI通常分布在几个中心附近, Cheng等^[25]提出多中心高斯分布模型.上述研究普遍将所有用户的地理位置影响建模为共同的距离分布, 或认为所有用户对地点的偏好和位置的距离之间存在相同的反比例关系.但是, 多种因素(如其他用户过去的签到活动、用户性格等)同样可揭示地理位置对用户签到行为的实际影响.

基于上述分析, 本文提出融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法(Point of Interest Recommendation Algorithm Integrating Geo-Category Information and Implicit Social Relationship, CSGWMF).首先考虑用户签到种类信息, 提出同时分解用户签到地点矩阵和用户签到种类矩阵的思路, 减小签到数据稀疏带来的影响.再在显式社交关系的基础上, 使用信息熵的方法度量用户的隐式社交关系, 缓解社交网络稀疏的问题, 并将该社交关系通过正则化的方法加入矩阵分解模型中.最后, 使用自适应核密度估计的方法个性化建模地理信息对用户签到行为的影响, 提高推荐的准确性.在Foursquare、Yelp数据集上的实验验证本文算法的有效性.

1 融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法

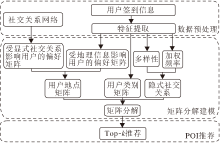
融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法框架如图1所示, 整体框架分为三部分:数据预处理、矩阵分解建模和POI推荐.具体如下.

	Figure Option View Download New Window
	图1 本文算法框图Fig.1 Framework of the proposed algorithm

1)构建用户签到地点矩阵和用户签到种类矩阵.构建好这两个矩阵后在用户签到种类矩阵的协助下分解用户签到地点矩阵.

2)挖掘用户的社交关系.用户的社交关系包括显式社交关系和隐式社交关系.计算显式社交网络中用户的相似度, 根据协同过滤方法计算用户对每个地点的偏好.提取用户隐式社交关系, 首先度量两位用户共同签到过的地点的多样性(两位用户共同签到过的地点越多, 多样性程度越高), 然后根据相应位置受欢迎程度分别度量每个共同访问地点的权重值(又称为加权频率), 最后基于用户共同签到过的地点的多样性和加权频率计算用户之间的隐式社交关系.最终将用户的隐式社交关系作为正则项加入矩阵分解中.

3)通过核密度估计的方法建模用户的地理位置信息, 得到用户对每个地点的偏好.融合用户的自身偏好和地理位置信息、显式社交信息.

1.1 构建用户签到地点矩阵和用户签到种类矩阵

矩阵分解是推荐系统里常用方法, 是为电影推荐典型场景中评分预测而设计的, 在这种情况下, 可直接得到用户评分矩阵.然而, 在POI推荐中, 只能得到用户的签到频率矩阵, 大量的用户和地点使用户签到矩阵更稀疏.为了解决类似问题, Hu等^[7]提出加权矩阵分解(Weighted MF, WMF)模型.根据Lian等^[26]的实验可知, 加权矩阵分解模型会使POI推荐准确率更高.WMF给签到矩阵中的缺失项分配一个较小的权重, 再根据用户地点的签到频率给未缺失项分配一个较大的权重, 签到频率越高, 权重越大.具体数学描述如下:

L= $\min_{U, V} \frac{1}{2} \overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}}$ W_i_,_j(R_i_,_j-U_i ${V^{T}}_{j}$ )²+ $\frac{1}{2}$ (‖ U‖ 2+‖ V‖ ²).

其中:R表示用户签到地点, 是0, 1矩阵, 用户i访问过地点j, R_i_,_j=1, 否则R_i_,_j=0; $\frac{1}{2}$ λ (‖ U‖ ²+‖ V‖ ²)是为了防止过拟合; W表示加权矩阵, 本文采用和WMF类似的加权方式,

W_i_,_j= $\{\begin{array}{l} 1, & r_{i, j} = 0 \\ 1 + lo g_{2} (1 + 10^{ε} r_{i, j}), & r_{i, j} \neq 0 \end{array}$

ε 表示控制加权值随着签到频率增加的速率.

在日常生活中, 用户行为具有一定的目的性, 因此为了解决数据稀疏性问题, 可考虑POI的类别信息.在基于信任关系的矩阵分解(Trust Singular Value Decomposition, TrustSVD)^[27]中, 同时分解用户评分矩阵和显式信任矩阵, 得到用户特征矩阵、物品特征矩阵和显式信任特征矩阵.类似地, 同时分解用户签到地点矩阵R和用户签到种类矩阵C, 得到用户特征矩阵U, 地点特征矩阵V, 种类特征矩阵P, 即

L= $\min_{U, V} \frac{1}{2} \overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}}$ W1_i_,_j(R_i_,_j-U_i ${V^{T}}_{j}$ )²+ $\frac{δ}{2} \overset{m}{\sum_{i = 1}} \overset{y}{\sum_{k = 1}}$ W2_i_,_k(C_i,_k-U_i ${P^{T}}_{k})$ ²+ $\frac{λ_{1}}{2}$ (‖ U‖ ²+‖ V‖ ²+‖ P‖ ²), R≈ UV^T, C≈ UP^T. (1)

其中:δ 用于调节POI与POI类别对建模用户偏好的比例; C表示用户签到种类矩阵, 如果用户i访问过某一类别k, C_i_,_k=1, 否则C_i_,_k=0; U为R、C分解后的共有矩阵, 即R和C通过U相互影响.

1.2 社交关系对推荐的影响

社交关系为推荐系统提供重要的上下文信息.具体地说, 可利用用户之间的社交关系获取用户相似性, 作为协同过滤模型的输入.因此, 一些POI推荐系统利用社交关系作为补充数据, 提高推荐性能.

研究表明, 社交关系对提高POI推荐的准确性影响显著^[6].然而, 显式的社交关系数据通常是部分可用的, 甚至是不可用的.特别是在Foursquare数据集上, 社交关系网络更稀疏, 即使他们在社交网络上有社交关系, 但由于地域不同、距离较远, 他们可能对POI没有相似的选择.因此本文同时研究显式社交关系与隐式社交关系.

如果用户和朋友之间共同签到过的地点越多, 那么用户和朋友之间的兴趣越相似.这里使用Jaccard相似性计算用户和朋友之间的相似度:

$S_{i, f}^{E}$ = $\frac{| L_{i} ⋂ L_{f} |}{| L_{i} ⋃ L_{f} |}$ ,

其中, L_i表示用户i签到过的地点的集合, L_f表示用户i的朋友f签到过的地点的集合.

使用t_i_,_j表示受显式社交关系影响, 用户i对地点j的偏好程度:

t_i_,_j= $\frac{\sum_{f \in F} S_{i, f}^{E} I_{f, j}}{\sum_{f \in F} S_{i, f}^{E}}$ ,

其中, F表示用户i的朋友集合, I_f_,_j表示指示函数, 如果i的朋友f访问过地点j, I_f_,_j=1, 否则I_f_,_j=0.

如何测量用户之间的隐式社交关系是一个挑战.Pham等^[28]通过分析用户的签到信息, 提出EBM(Entropy-Based Model), 通过两种独立的方法, 即多样性(度量用户之间关于共同签到地点个数的差异性)和加权频率(考虑共同签到地点的受欢迎程度, 分别度量每个共同签到地点的影响)测量隐式社交关系, 并通过实验验证此方法可用于推断用户的隐式社交关系, 但是并未把这种隐式社交关系应用到POI推荐中来.本文将EBM计算的隐式社交关系用于矩阵分解中, 作为正则项, 最后对用户推荐感兴趣的地点.

通过两位用户共同访问的地点个数测量用户之间共同签到地点的多样性, 推断用户之间建立社交关系的可能性.假设有3位用户u₁、u₂、u₃, 不同的用户之间共同访问过的地点如下:

c₁₂=[5, 0, 2, 3, 0], c₁₃=[3, 2, 2, 1, 2], c2₃₌[0, 6, 0, 0, 4].

其中:c₁₂表示用户u₁、u₂共同访问的POI组成的向量, 每个元素表示用户u₁、u₂共同访问每个地点的次数, c₁₃、c₂₃类似.观察3个向量可发现用户u₁和u₂, 用户u₁和u₃, 用户u₂和u₃共同访问过地点的总次数都为10, 但是访问过的地点个数却不同.用户u₁、u₂共同访问过3个地点, 用户u₁、u₃共同访问过5个地点, 用户u₂、u₃共同访问过2个地点, 因此, c₁₃比c₁₂更多样化, 而c₁₂比c₂₃更多样化.当用户之间存在社交关系时, 通常会一起游览不同的地方, 反之, 用户之间访问更多相同的地点, 他们之间更可能存在社交关系, 因此, 本文认为共同签到地点的多样性有助于推断用户的隐式社交关系.这里使用Renyi熵^[28]估计用户之间共同签到地点的多样性, 量化随机变量的不确定性.

基于Renyi的用户i、e共同签到地点的多样性估计表示如下:

D_i_,_e=exp( $H_{i, e}^{R}$ )= exp[ $\frac{1}{q - 1}$ (log₂ $\sum_{l}$ ( $\frac{c_{ie, l}}{f_{i, e}}$ )^q)]=[ $\sum_{l, c_{ie, l} \neq 0}$ ( $\frac{c_{ie, l}}{f_{i, e}}$ )^q] $^{\frac{1}{1 - q}}$ .

其中:c_ie_,_l表示用户i和e共同访问地点l的次数, 称为局部频率; f_i_,_e= $\sum_{l}$ c_ie_,_l, 表示用户i、e共同访问地点的总次数, 称为总频率; q表示一个常数, 控制局部频率c_ie_,_l的敏感性.

经过计算用户u₁、u₂、u₃, 得

D₁₂=2.979, D₁₃=4.971 6, D₂₃=1.995 9.

由于用户u₁、u₃共同签到5个地点, 用户u₂、u₃共同签到2个地点, 所以用户u₁、u₃访问地点的多样性程度更高, 更有可能建立社交关系.

使用位置熵描述位置的受欢迎程度.V_u_,_l表示用户u在地点l的签到次数, V_l表示所有用户在地点l的总签到次数.从V_l中随机抽取一次签到, 属于用户u的概率P_u_,_l=V_u_,_l/V_l, 如果把这个事件定义为一个随机变量, 它的不确定性由香农熵给出, 即

H_l=- $\sum_{u, P_{u, l} \neq 0}$ P_u_,_llog₂P_u_,_l.

位置熵的值越大表示这个地方越受欢迎, 反之, 位置熵的值越小意味着一个只有越少访客的私人场所, 如私人住宅.利用位置熵(地点的受欢迎程度)作为加权频率对c_ie_,_l进行加权:

F_i_,_e= $\sum_{l}$ c_ie_,_lexp(-H_l).

加权频率描述在受欢迎的地点发生的事件对隐式社交关系的影响.受欢迎的位置具有较高的位置熵H_l, 导致exp(-H_l)值较低, 从而受欢迎的地点加权值较小.另一方面, 对于不太受欢迎的地点或较隐私的地点, exp(-H_l)的值较高, 加权值较大.如果两位用户共同访问过的地点是私人住宅等不太受欢迎的小地方, 这两位用户之间的社交关系较强.

最后通过综合多样性和加权频率衡量用户之间的隐式社交关系.使用 $S_{i, e}^{I}$ 表示两位用户之间的隐式社交关系:

$S_{i, e}^{I}$ =D_i_,_eF_i_,_e.

本文需要把 $S_{i, e}^{I}$ 归一化在[0, 1]内.

为了在矩阵分解的过程中考虑隐式社交关系对用户行为的影响, 在式(1)的后面加上正则项

$\frac{λ_{2}}{2} \overset{M}{\sum_{i = 1}}$ ‖ U_i- $\sum_{a \in F (i)} S_{i, a}^{I}$ U_a‖ ².

1.3 地理位置信息对推荐的影响

Tobler^[29]认为世间万物都是息息相关的, 距离较近的两个物体之间的相关性强于距离较远的两个物体.幂律分布和高斯混合分布都基于用户的整体签到记录, 对地理信息进行建模, 虽然在一定程度上捕捉用户的签到行为, 但忽略用户签到行为存在个性化偏差的事实.因此为了更好地建模用户的签到行为, 使用核密度估计建模, 为了使核密度估计的参数更少, 采用自适应带宽.主要步骤如下.

1)距离样本收集.用户签到过的任意两个地点p、g之间的距离d_o=dis(p, g), 由于签到信息是经纬度信息, 如(41.485 499, -81.799 178), 需要通过球面半正矢公式计算地点之间的距离.

2)距离分布估计.核密度分布估计^{[2, 6]}如下:

f(d_x_,_o)= $\frac{1}{| D | h}$ $\sum_{d_{o} \in D}$ K( $\frac{d_{x, o} - d_{o}}{h}$ ).

其中:d_x_,_o表示l_x、l_o之间的距离, l_o表示用户u_i签到过的地点, l_x={l₁, l₂, …, l_n}表示用户未签到过的地点; D表示收集到的距离样本信息; K(x)表示核函数, 这里使用最常见的高斯核函数^{[2, 6, 9]},

K(x)= $\frac{1}{\sqrt[]{2 π}}$ exp(- $\frac{x^{2}}{2}$ );

h表示带宽, 使用的是自适应带宽^[2],

$h = (\frac{4 {\overset{︿}{σ}}^{5}}{3 n})^{\frac{1}{5}} \approx 1.06 \overset{︿}{σ} n^{- \frac{1}{5}}$ ,

$\overset{︿}{σ}$ 表示样本的标准差.

3)计算用户u_i对未签到过的地点l_x的访问概率.文献[2]采用平均概率, 但是在现实生活中用户访问每个地点的次数都不一样, 因此本文根据用户访问地点的次数对核密度估计计算相关概率加权:

g_i_,_x= $\frac{\sum_{o \in l_{o}} f (d_{x, o}) r_{i, o}}{\sum_{o \in l_{o}} r_{i, o}}$ ,

其中r_i_,_o表示用户i访问地点o的次数.

1.4 算法步骤

在WMF的基础上融合种类信息、社交关系及地理位置信息后的目标函数如下:

L= $\min_{U, V} \frac{1}{2} \overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}}$ W1_i_,_j[R_i_,_j-(U_i ${V^{T}}_{j}$ +E_i_,_j)]²+ $\frac{δ}{2} \overset{m}{\sum_{i = 1}} \overset{y}{\sum_{k = 1}}$ W2_i_,_k(C_i_,_k-U_i ${P^{T}}_{k}$ )²+ $\frac{λ_{2}}{2} \overset{m}{\sum_{i = 1}}$ ‖ U_i- $\sum_{a \in F (i)} S_{i, a}^{I}$ U_a‖ ²+

$\frac{λ_{1}}{2}$ (‖ U‖ ²+‖ V‖ ²+‖ P‖ ²). (2)

其中: $\frac{δ}{2} \overset{m}{\sum_{i = 1}} \overset{y}{\sum_{k = 1}}$ W2_i_,_k(C_i_,_k-U_i ${P^{T}}_{k}$ )² 表示在分解用户签到地点矩阵R的同时分解用户签到种类矩阵C, C分解为用户特征矩阵U和种类特征矩阵P; $\frac{λ_{2}}{2} \overset{m}{\sum_{i = 1}}$ ‖ U_i- $\sum_{a \in F (i)} S_{i, a}^{I}$ U_a‖ ²表示用户u_i受其隐式社交关系朋友F(i)的影响; E_i_,_j=α G_i_,_j+β T_i_,_j, G_i_,_j表示受地理位置影响用户i对地点j偏好, T_i_,_j表示受显式社交关系影响用户i对地点j的偏好; α 表示G_i_,_j的权重, β 表示T_i_,_j的权重.

本文使用梯度下降法优化式(2)中的目标函数.

首先固定V、P, 对U求导:

$\frac{\partial L}{\partial U_{i}}$ = $\overset{n}{\sum_{j = 1}}$ W1_i_,_j[(U_i ${V^{T}}_{j}$ +E_i_,_j)-R_i_,_j]V_j+δ $\overset{y}{\sum_{k = 1}}$ W2_i_,_k(U_i ${P^{T}}_{k}$ -C_i_,_k)P_k+λ ₂(U_i- $\sum_{a \in F (i)} S_{i, a}^{I}$ U_a)-λ ₂ $\sum_{a \in F (i)}$ S_a_,_i(U_a- $\sum_{b \in F (a)} S_{a, b}^{I}$ U_b)+λ ₁U_i. (3)

固定U、P, 对V求导:

$\frac{\partial L}{\partial V_{j}}$ = $\overset{m}{\sum_{i = 1}}$ W1_i_,_j[(U_i ${V^{T}}_{j}$ +E_i_,_j)-R_i_,_j]U_i+λ ₁V_j.(4)

固定U、V, 对P求导:

$\frac{\partial L}{\partial P_{k}}$ =δ $\overset{m}{\sum_{i = 1}}$ W2_i_,_k(U_i ${P^{T}}_{k}$ -C_i_,_k)U_i+λ ₁P_k.(5)

本文算法的伪代码如下.

算法1 CSGWMF

输入用户签到地点矩阵R, 用户签到种类矩阵C, 加权矩阵W1、W2,

受地理信息影响的偏好矩阵G,

受显式社交关系影响的偏好矩阵T,

基于信息熵的隐式社交关系矩阵S^I

输出 Top-k POI推荐列表

step 1 初始化隐藏特征矩阵U, V, P.

step 2 迭代:

step 2.1 固定V、P, 通过式(3)更新U_i,

U_i← U_i-ξ $\frac{\partial L}{\partial U_{i}}$ .

step 2.2 固定U、P, 通过式(4)更新V_j,

V_j← V_j-ξ $\frac{\partial L}{\partial V_{j}}$ .

step 2.3 固定U、V, 通过式(5)更新P_k,

P_k← P_k-ξ $\frac{\partial L}{\partial P_{k}}$ .

直至

$\frac{| L (U^{(t)}, V^{(t)}, P^{(t)}) - L (U^{(t - 1)}, V^{(t - 1)}, P^{(t - 1)}) |}{L (U^{(t - 1)}, V^{(t - 1)}, P^{(t - 1)})} < τ$ ,

迭代停止.

step 3 计算 $\overset{︿}{R}$ , $\overset{︿}{R}$ =UV^T+α G+β T.

step 4 对偏好预测矩阵 $\overset{︿}{R}$ 中每位用户的偏好排序, 选择用户未去过的、排名位于前k的地点推荐给用户.

1.5 时间复杂度分析

算法整体的时间复杂度由两部分组成.首先计算用户之间的隐式社交关系的时间复杂度, 基于用户显式关系的用户对地点的偏好的时间复杂度, 基于核密度估计的用户对地点的偏好的时间复杂度.再计算矩阵分解的时间复杂度.由于上下文信息的计算不参与矩阵分解的迭代计算, 属于离线执行, 未考虑复杂度和计算开销.因此这里主要考虑矩阵分解的时间复杂度.

矩阵分解的时间复杂度由代价函数的时间复杂度和潜在因子梯度下降时的时间复杂度组成.代价函数的时间复杂度为O(d(|R|+|C|)), 其中, |R|表示用户访问过的地点, |C|表示用户访问过的地点种类, d为隐藏特征的维度.U_i的时间复杂度为

O(d(|R|+|C|)+dk),

V_j的时间复杂度为O(d|R|), P_k 的时间复杂度为O(d|C|), 其中, k为Top-k隐式朋友数.矩阵分解的整体时间复杂度为

O(d(|R|+|C|)+dk).

2 实验及结果分析

2.1 实验环境

实验使用在POI推荐算法中应用较广的2个数据集:Foursquare数据集和Yelp数据集.Foursquare数据集包括11 326位用户在182 968个地点的1 385 223条签到数据, 稀疏度为6.7× 10^-4.Yelp数据集包括30 887位用户在18 995个地点的860 888条签到数据, 稀疏度为1.5× 10^-3 .在这两个数据集中除了用户的签到数据以外还有用户地点种类信息和用户之间的社交关系, 数据集的具体信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

在数据预处理时, Foursquare数据集上删除签到地点少于10个的人和签到人数少于10人的地点, Yelp数据集上删掉签到地点少于30个的人和签到人数少于30人的地点.在处理后的数据集中随机挑选80%的数据为训练集, 剩下的20%的数据为测试集.重复上述实验, 最终结果取5次实验的平均值.

2.2 评价指标

本文采用准确率和召回率评估推荐的效果.

准确率

Precision@k= $\frac{1}{mk} \overset{m}{\sum_{u = 1}} | ψ_{u}^{P}$ ∩ $ψ_{u}^{T}$ |;

召回率

Recall@k= $\frac{1}{m} \overset{m}{\sum_{u = 1}} \frac{| ψ_{u}^{P} ⋂ ψ_{u}^{T} |}{|ψ_{u}^{T}|}$ .

其中:m表示用户的总个数, k表示最后给每位用户推荐的地点个数, $ψ_{u}^{p}$ 表示根据本文算法对用户u推荐的地点集合, $ψ_{u}^{T}$ 表示测试集里u访问过的地点集合.

2.3 参数对实验的影响

参数δ 控制用户签到种类对矩阵分解的影响, 首先分析在矩阵分解模型中只有用户的自身偏好与种类影响时的效果, 即α =β =λ ₂=0, λ ₁=0.001, 绘制当δ =0, 0.2, 0.4, 0.6, 0.8, 1.0, k=5时的准确率和召回率.如图2所示, 在Foursquare、Yelp数据集上, 当δ =0.2时, 准确率和召回率均处于最高值, 说明在矩阵分解中加入种类信息可提高推荐性能.后面的实验均选择δ =0.2.

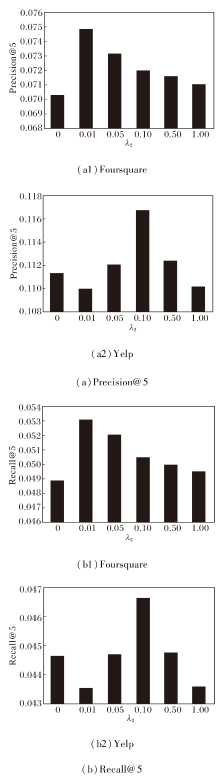
	Figure Option View Download New Window
	图2 δ 对实验结果的影响Fig.2 Influence of parameter δ on experimental results

当隐式社交关系作为正则项加入矩阵分解时, 参数λ ₂控制其对推荐性能的影响, 即α =β =0, δ =0.2, λ ₁=0.001.绘制当λ ₂=0, 0.01, 0.05, 0.10, 0.50, 1.00, k=5时的准确率和召回率曲线, 如图3所示.

	Figure Option View Download New Window
	图3 参数λ ₂对实验结果的影响Fig.3 Influence of parameter λ ₂ on experimental results

由图3可知, 在Foursquare数据集上, 当λ ₂变大时, 准确率和召回率都变高, 当λ ₂超过0.01后, 准确率和召回率开始下降, 即当λ ₂=0.01时准确率和召回率同时达到最大值.在Yelp数据集上, 当λ ₂取不同值时, 准确率和召回率的变化较大, 当 λ ₂=0.1时, 准确率和召回率均处于最高点.由此说明在本文算法中加入隐式社交关系可提高推荐性能.

2.4 实验结果对比

本节选择如下算法进行对比实验, 验证本文算法的有效性.

1)基于核密度估计的个性化地理位置推荐(Personalized Geo-Social Location Recommenda-tion, iGSLR)^[2].采用核密度估计方法对地理位置信息建模, 将个性化地理影响与社会影响整合到统一的地理社会推荐框架中.

2)WMF^[7].用于解决隐式反馈的一种有效方法, 根据用户的签到次数给用户签到矩阵分配不同的权重.

3)基于朋友签到信息的兴趣点推荐(the Aug-mented Square Error Based Matrix Factorization, ASMF)^[4].利用签到信息、社交网络信息、地理位置信息定义3种朋友关系.利用2种不同的损失函数将3种类型的签到信息合并到矩阵分解模型中.

4)基于位置视角的邻居感知矩阵分解(Lo-cation Neighborhood-Aware Weighted Probabilistic Matrix Factorization, LWMF)^[1].从位置角度探讨POI之间的地理关系, 提出位置邻域感知加权概率矩阵分解的方法.

各算法在2个数据集上的准确率和召回率对比如图4所示.在推荐长度k=5, 10, 15, 20时, 本文算法的准确率和召回率都最高.当k=5时, 在Fours-quare数据集上, 相比LWMF, 本文算法的准确率提高8.4%, 召回率提高11.3%.在Yelp数据集上, 相比LWMF, 本文算法的准确率提高5.8%, 召回率提高10.8%.

	Figure Option View Download New Window
	图4 各算法在2个数据集上的实验结果对比Fig.4 Experimental result comparison of different algorithms on 2 datasets

iGSLR利用协同过滤的思想, 通过用户朋友之间居住距离的远近查找具有相似兴趣的用户, 用于预测用户对特定POI的偏好, 再和通过核密度估计计算用户对地点的偏好简单地进行线性融合.iGSLR的基本思想是最基础的基于用户的协同过滤, 性能不及WMF.本文算法和ASMF、LWMF都是在WMF的基础上融入上下文信息, 性能优于WMF, 说明加入上下文信息可有效改善数据的稀疏性问题, 提高推荐性能.本文算法性能优于ASMF、LWMF, 说明本文算法在WMF的基础上能更好融入各种上下文信息.相比WMF, 本文算法在用户的签到数据稀疏时具有以下优势:1)根据用户的签到种类信息更好地约束用户特征矩阵.2)不仅可根据用户在社交网络上拥有的显式社交朋友推断用户对未签到过的地点的偏好, 还可通过用户的签到信息找到用户的隐式社交朋友, 对用户进行推荐.3)通过个性化分析每个用户访问过的地点的分布关系预测用户对未访问过的地点的偏好.

本文还进行如下对比实验, 验证本文算法中的种类信息、社交关系及地理位置信息的有效性.具体对比算法如下.

1)WMF.只考虑用户的自身偏好, 没有加入上下文信息.

2)GWMF.本文算法只考虑用户的自身偏好和地理位置信息.

3)CWMF.本文算法只考虑用户的自身偏好和种类信息.

4)SWMF.本文算法只考虑用户的自身偏好和社交关系.

5)CGWMF.本文算法考虑用户的自身偏好、种类信息和地理位置信息.

6)SGWMF.本文算法考虑用户的自身偏好、社交关系和地理位置信息.

7)CSWMF.本文算法考虑用户的自身偏好、种类信息和社交关系.

8)CSGWMF.本文算法考虑用户自身偏好、种类信息、社交关系和地理位置信息.

在Foursquare、Yelp数据集上验证上下文信息的有效性, 具体结果如表2所示.

表2 上下文信息的有效性验证 Table 2 Validation of contextual information

由表2可知, GWMF、CWMF、SWMF都只在WMF的基础上加入一种上下文信息, SWMF效果最优, 并且这3种算法的准确率和召回率均高于WMF.这说明分别加入这3种上下文信息都是有效的, 在显式社交关系的基础上, 通过信息熵的方法引入用户的隐式社交关系对实验结果的影响大于同时分解用户签到地点矩阵和用户签到类别矩阵、个性化建模用户的地理信息的影响.CGWMF、SGWMF、CSWMF都在WMF的基础上加入2种上下文信息, CSWMF效果最优, 并且这3种算法的准确率和召回率都高于GWMF、CWMF、SWMF, 说明相比融合一种上下文信息, 融合两种上下文信息能更好地解决数据稀疏的问题, 并且结合种类信息和社交关系能更好地发挥作用.CSGWMF在WMF 的基础上加入种类信息、社交关系、地理位置信息, 准确率和召回率最高, 说明本文算法能较好地融入上下文信息, 并且上下文信息考虑得越多, 效果越优.这与人们在实际生活中对地点的选择也是一致的, 用户在选择感兴趣的地点时不仅仅是对某个地点的偏好, 也反映用户对这类地点的偏好, 同时还会受朋友和地点距离的影响.

3 结束语

本文提出融合地理信息、种类信息与隐式社交关系的兴趣点推荐算法.在矩阵分解模型中同时分解用户签到地点矩阵和用户签到种类矩阵, 有效缓解签到数据稀疏性.在考虑显式社交关系的同时融入隐式社交关系, 以正则项的方式加入矩阵分解模型中, 缓解社交网络的稀疏性, 提高推荐性能.还使用自适应核密度估计方法个性化建模地理因素的影响, 提高推荐精度.由于用户的签到行为不仅和本文研究的几种上下文信息有关, 还和时间有关, 因此今后将继续研究时间对用户签到行为的影响, 更好地预测用户未来的访问地点.

参考文献

文献选项

[1]	GUO L, WEN Y F, LIU F G. Location Perspective-Based Neighborhood-Aware POI Recommendation in Location-Based Social Networks. Soft Computing, 2019, 23(22): 11935-11945. [本文引用:3]
[2]	ZHANG J D, CHOW C Y. iGSLR: Personalized Geo-Social Location Recommendation: A Kernel Density Estimation Approach // Proc of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York, USA: ACM, 2013: 334-343. [本文引用:8]
[3]	GAO R, LI J, DU B, et al. Exploiting Geo-Social Correlations to Improve Pairwise Ranking for Point-of-Interest Recommendation. China Communications, 2018, 15(7): 180-201. [本文引用:2]
[4]	LI H Y, GE Y, HONG R C, et al. Point-of-Interest Recommendations: Learning Potential Check-Ins from Friends // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Disco-very and Data Mining. New York, USA: ACM, 2016: 975-984. [本文引用:2]
[5]	REN Y Q, WANG Z, SUN X N, et al. A Multi-element Hybrid Location Recommendation Algorithm for Location Based Social Networks. IEEE Access, 2019, 7: 100416-100427. [本文引用:2]
[6]	PAN Z G, CUI L, WU X Y, et al. Deep Potential Geo-Social Relationship Mining for Point-of-Interest Recommendation. IEEE Access, 2019, 7: 99496-99507. [本文引用:4]
[7]	HU Y F, KOREN Y, VOLINSKY C. Collaborative Filtering for Implicit Feedback Datasets // Proc of the 8th IEEE International Conference on Data Mining. Washington, USA: IEEE, 2008: 263-272. [本文引用:3]
[8]	KUMAR R, VERMA B K, RASTOGI S S, et al. Social Popularity Based SVD++ Recommender System. International Journal of Computer Applications, 2014, 87(14): 33-37. [本文引用:1]
[9]	GAO R, LI J, LI X F, et al. A Personalized Point-of-Interest Re-commendation Model via Fusion of Geo-Social Information. Neurocomputing, 2018, 273: 159-170. [本文引用:2]
[10]	DU R Z, LU J J, CAI H Y. Double Regularization Matrix Factorization Recommendation Algorithm. IEEE Access, 2019, 7: 139668-139677. [本文引用:1]
[11]	SI Y L, ZHANG F Z, LIU W Y. An Adaptive Point-of-Interest Recommendation Method for Location-Based Social Networks Based on User Activity and Spatial Features. Knowledge-Based Systems, 2019, 163: 267-282. [本文引用:1]
[12]	LIU X, LIU Y, ABERER K, et al. Personalized Point-of-Interest Recommendation by Mining Users' Preference Transition // Proc of the 22nd ACM International Conference on Information and Know-ledge Management. New York, USA: ACM, 2013: 733-738. [本文引用:2]
[13]	HE J, LI X, LIAO L J. Category-Aware Next Point-of-Interest Recommendation via Listwise Bayesian Personalized Ranking // Proc of the 26th International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2017: 1837-1843. [本文引用:2]
[14]	CHEN J L, LI X, CHEUNG W K, et al. Effective Successive POI Recommendation Inferred with Individual Behavior and Group Pre-ference. Neurocomputing, 2016, 210: 174-184. [本文引用:2]
[15]	DIVYAA L R, PERVIN N. Towards Generating Scalable Persona-lized Recommendations: Integrating Social Trust, Social Bias, and Geo-Spatial Clustering. Decision Support Systems, 2019, 122. DOI: DOI:10.1016/j.dss.2019.05.006. [本文引用:1]
[16]	SI Y L, ZHANG F Z, LIU W Y. CTF-ARA: An Adaptive Method for POI Recommendation Based on Check-in and Temporal Features. Knowledge Based Systems, 2017, 128: 59-70. [本文引用:1]
[17]	孟祥福, 张霄雁, 唐延欢, 等. 基于地理-社会关系的多样性与个性化兴趣点推荐. 计算机学报, 2019, 42(11): 2574-2590. (MENG X F, ZHANG X Y, TANG Y H, et al. A Diversified and Personalized Recommendation Approach Based on Geo-Social Relationships. Chinese Journal of Computers, 2019, 42(11): 2574-2590. ) [本文引用:1]
[18]	王瑞琴, 潘俊, 冯建军. 基于信任计算和矩阵分解的推荐算法. 模式识别与人工智能, 2018, 31(9): 786-796. (WANG R Q, PAN J, FENG J J. Recommendation Algorithm Based on Trust Computation and Matrix Factorization. Pattern Re-cognition and Artificial Intelligence, 2018, 31(9): 786-796. ) [本文引用:1]
[19]	MA H, YANG H X, LYU M R, et al. SoRec: Social Recommendation Using Probabilistic Matrix Factorization // Proc of the 17th ACM Conference on Information and Knowledge Management. New York, USA: ACM, 2008: 931-940. [本文引用:1]
[20]	MA H, ZHOU D Y, LIU C, et al. Recommender Systems with Social Regularization // Proc of the 4th ACM International Confe-rence on Web Search and Data Mining. New York, USA: ACM, 2011: 287-296. [本文引用:1]
[21]	YANG B, LEI Y, LIU D Y, et al. Social Collaborative Filtering by Trust // Proc of the 23rd International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2013: 2747-2753. [本文引用:1]
[22]	YANG B, LEI Y, LIU J M, et al. Social Collaborative Filtering by Trust. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1633-1647. [本文引用:1]
[23]	LIU B, FU Y J, YAO Z J, et al. Learning Geographical Prefe-rences for Point-of-Interest Recommendation // Proc of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2013: 1043-1051. [本文引用:1]
[24]	YE M, YIN P F, LEE W C, et al. Exploiting Geographical Influence for Collaborative Point-of-Interest Recommendation // Proc of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2011: 325-334. [本文引用:1]
[25]	CHENG C, YANG H Q, KING I, et al. Fused Matrix Factorization with Geographical and Social Influence in Location-Based Social Networks // Proc of the 26th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2012: 17-23. [本文引用:1]
[26]	LIAN D F, ZHAO C, XIE X, et al. GeoMF: Joint Geographical Modeling and Matrix Factorization for Point-of-Interest Recommendation // Proc of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2014: 831-840. [本文引用:1]
[27]	GUO G B, ZHANG J, YORKE-SMITH N. TrustSVD: Collaborative Filtering with Both the Explicit and Implicit Influence of User Trust and of Item Ratings // Proc of the 29th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2015: 123-129. [本文引用:1]
[28]	PHAM H, SHAHABI C, LIU Y. EBM: An Entropy-Based Model to Infer Social Strength from Spatiotemporal Data // Proc of the ACM SIGMOD International Conference on Management of Data. New York, USA: ACM, 2013: 265-276. [本文引用:2]
[29]	TOBLER W R. A Computer Movie Simulating Urban Growth in the Detroit Region. Economic Geography, 1970, 46(2): 234-240. [本文引用:1]

2019

0.0

... 对于全球数百万用户来说,使用这种媒体已经成为他们日常生活的一部分^[1,2,3,4] ...

... 事实上,准确和个性化的POI推荐是LBSNs业务的关键需求^[1,5,6] ...

... 4)基于位置视角的邻居感知矩阵分解(Lo-cation Neighborhood-Aware Weighted Probabilistic Matrix Factorization, LWMF)^[1] ...

2013

0.0

... 对于全球数百万用户来说,使用这种媒体已经成为他们日常生活的一部分^[1,2,3,4] ...

... POI推荐的主要方法之一是协同过滤技术^[2],它通过用户POI签到矩阵计算用户对未访问的POI的偏好评分 ...

... POI推荐的研究^[2,5]表明,人们更倾向于访问他们去过地点附近的POI,导致基于用户选择的POI空间聚类现象 ...

... 核密度分布估计^[2,6]如下: ...

... K(x)表示核函数,这里使用最常见的高斯核函数^[2,6,9], ...

... h表示带宽,使用的是自适应带宽^[2], ...

... 文献[2]采用平均概率,但是在现实生活中用户访问每个地点的次数都不一样,因此本文根据用户访问地点的次数对核密度估计计算相关概率加权: ...

... 1)基于核密度估计的个性化地理位置推荐(Personalized Geo-Social Location Recommenda-tion, iGSLR)^[2] ...

2018

0.0

... 对于全球数百万用户来说,使用这种媒体已经成为他们日常生活的一部分^[1,2,3,4] ...

... 因此一些学者^[3,11]认为可通过研究用户之间的朋友关系提高推荐性能 ...

2016

0.0

... 对于全球数百万用户来说,使用这种媒体已经成为他们日常生活的一部分^[1,2,3,4] ...

... 3)基于朋友签到信息的兴趣点推荐(the Aug-mented Square Error Based Matrix Factorization, ASMF)^[4] ...

2019

0.0

... 事实上,准确和个性化的POI推荐是LBSNs业务的关键需求^[1,5,6] ...

... POI推荐的研究^[2,5]表明,人们更倾向于访问他们去过地点附近的POI,导致基于用户选择的POI空间聚类现象 ...

2019

0.0

... 事实上,准确和个性化的POI推荐是LBSNs业务的关键需求^[1,5,6] ...

... 研究表明,社交关系对提高POI推荐的准确性影响显著^[6] ...

... 核密度分布估计^[2,6]如下: ...

... K(x)表示核函数,这里使用最常见的高斯核函数^[2,6,9], ...

2008

0.0

... 自Netflix大奖竞赛后,基于矩阵分解(Matrix Factorization, MF)技术的推荐算法^[7]因其良好的可扩展性及处理大规模数据的准确预测能力,受到学术界和工业界的广泛关注 ...

... 为了解决类似问题,Hu等^[7]提出加权矩阵分解(Weighted MF, WMF)模型 ...

... 2)WMF^[7] ...

2014

0.0

... 例如,基于隐式信息的矩阵分解(Singular Value Decompos-ition++, SVD++)^[8],基于核密度估计的偏好模型^[9],基于双正则化的矩阵分解模型^[10]等 ...

2018

0.0

... 例如,基于隐式信息的矩阵分解(Singular Value Decompos-ition++, SVD++)^[8],基于核密度估计的偏好模型^[9],基于双正则化的矩阵分解模型^[10]等 ...

... K(x)表示核函数,这里使用最常见的高斯核函数^[2,6,9], ...

2019

0.0

... 例如,基于隐式信息的矩阵分解(Singular Value Decompos-ition++, SVD++)^[8],基于核密度估计的偏好模型^[9],基于双正则化的矩阵分解模型^[10]等 ...

2019

0.0

... 因此一些学者^[3,11]认为可通过研究用户之间的朋友关系提高推荐性能 ...

2013

0.0

... 为了缓解用户签到数据的稀疏性,在一些研究^[12,13,14]中加入种类信息,取得较好的效果 ...

... Liu等^[12]提出类别感知POI推荐模型,对用户类别转移矩阵使用矩阵分解,得到用户访问的下一个地点种类,再结合幂律分布得到用户的推荐列表 ...

2017

0.0

... 为了缓解用户签到数据的稀疏性,在一些研究^[12,13,14]中加入种类信息,取得较好的效果 ...

... He等^[13]通过个性化贝叶斯排序预测用户可能会去的下一个地点种类,根据空间影响力和类别影响力对类别预测筛选的候选POI进行排序 ...

2016

0.0

... 为了缓解用户签到数据的稀疏性,在一些研究^[12,13,14]中加入种类信息,取得较好的效果 ...

... Chen等^[14]建立用户类别转移的三阶张量,使用张量分解得到用户可能访问的下个类别,使用距离加权的超文本敏感主题搜索(Hypertext Induced Topic Search, HITS)计算用户可能访问的地点 ...

2019

0.0

... 目前一些学者在试图提高推荐质量时,将用户的社交关系作为最重要的社会信息类型之一并融入推荐系统中^{[15,16,17,18]},取得一定的成果 ...

2017

0.0

... 目前一些学者在试图提高推荐质量时,将用户的社交关系作为最重要的社会信息类型之一并融入推荐系统中^{[15,16,17,18]},取得一定的成果 ...

2019

0.0

孟祥福, 张霄雁, 唐延欢, 等. 基于地理-社会关系的多样性与个性化兴趣点推荐. 计算机学报, 2019, 42(11): 2574-2590.

(MENG X

, ZHANG X

, TANG Y

, et al. A Diversified and Personalized Recommendation Approach Based on Geo-Social Relationships. Chinese Journal of Computers, 2019, 42(11): 2574-2590. )

... 目前一些学者在试图提高推荐质量时,将用户的社交关系作为最重要的社会信息类型之一并融入推荐系统中^{[15,16,17,18]},取得一定的成果 ...

2018

0.0

王瑞琴, 潘俊, 冯建军. 基于信任计算和矩阵分解的推荐算法. 模式识别与人工智能, 2018, 31(9): 786-796.

(WANG R

, PAN

, FENG J

. Recommendation Algorithm Based on Trust Computation and Matrix Factorization. Pattern Re-cognition and Artificial Intelligence, 2018, 31(9): 786-796. )

... 目前一些学者在试图提高推荐质量时,将用户的社交关系作为最重要的社会信息类型之一并融入推荐系统中^{[15,16,17,18]},取得一定的成果 ...

2008

0.0

... Ma等^[19]提出基于联合矩阵分解的社交推荐(Social Recommendation Using Probabilistic Matrix Factorization, SoRec)模型,在概率矩阵分解的基础上,加入社交关系矩阵,共享用户特征矩阵,建立用户偏好与好友之间的关系 ...

2011

0.0

... Ma等^[20]提出基于矩阵分解的社交关系正则化推荐模型(Recommender Systems with Social Regularization, SoReg),通过物品相似度计算用户和朋友之间喜好的差异 ...

2013

0.0

... Yang等^[21]分别从信任者和被信任者的角度提出基于信任的矩阵分解(Trust-Based MF, TrustMF)模型 ...

2017

0.0

... Yang等^[22]提出基于信任的概率矩阵分解(Trust Based Probability MF, TrustPMF)模型,为TrustMF提供概率解释 ...

2013

0.0

... Liu等^[23]假设用户对POI的偏爱与这个POI到用户访问过的POI的距离之间成反比关系 ...

2011

0.0

... Ye等^[24]研究用户签到活动中表现的空间聚类现象,利用幂律分布对其建模 ...

2012

0.0

... 在现实生活中,用户访问的POI通常分布在几个中心附近,Cheng等^[25]提出多中心高斯分布模型 ...

2014

0.0

... 根据Lian等^[26]的实验可知,加权矩阵分解模型会使POI推荐准确率更高 ...

2015

0.0

... 在基于信任关系的矩阵分解(Trust Singular Value Decomposition, TrustSVD)^[27]中,同时分解用户评分矩阵和显式信任矩阵,得到用户特征矩阵、物品特征矩阵和显式信任特征矩阵 ...

2013

0.0

... Pham等^[28]通过分析用户的签到信息,提出EBM(Entropy-Based Model),通过两种独立的方法,即多样性(度量用户之间关于共同签到地点个数的差异性)和加权频率(考虑共同签到地点的受欢迎程度,分别度量每个共同签到地点的影响)测量隐式社交关系,并通过实验验证此方法可用于推断用户的隐式社交关系,但是并未把这种隐式社交关系应用到POI推荐中来 ...

... 这里使用Renyi熵^[28]估计用户之间共同签到地点的多样性,量化随机变量的不确定性 ...

1970

0.0

... 3 地理位置信息对推荐的影响Tobler^[29]认为世间万物都是息息相关的,距离较近的两个物体之间的相关性强于距离较远的两个物体 ...