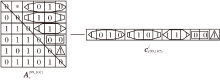本文研究的动态网络节点集为V, 边集为E, 节点间连边为无向边.按一定时间窗口将动态演化的网络划分为N+1个时间快照{G₁, G₂, …, G_N, G_N+1}.每个快照使用无向图G_t=(V, E_t)表示, V={v₁, v₂, …, v_n}为网络节点集合, E_t⊆|V|× |V|为t时刻网络中边的集合.

动态网络链接预测问题描述如下.已知N个历史快照{G₁, G₂, …, G_N}的网络信息, 预测G_N+1时间片中节点对(i, j)之间是否存在链接L^(N+1)(i, j):

f:{G₁, G₂, …, G_N}→ L^(N+1)(i, j),

其中

L^(N+1)(i, j)= 1, (i, j)∈E(N+1)0, (i, j)∉E(N+1)

本文提出基于节点表征和子图结构的动态网络链接预测方法(d_n2v_PWL).方法结构如图1所示, 由4个模块组成:表征节点向量、捕获链接局部子图结构特征、融合链接特征、分类预测.首先基于node2vec拼接每个历史时间片的节点表征向量.再基于PWL捕获预测节点对在各个历史时间片的局部子图结构特征, 拼接这些向量, 记为链接的局部子图结构特征表示.然后将预测节点对的节点表征向量融合为链接表征向量, 并与链接的局部子图结构特征向量拼接.最终将得到的链接表示输入到随机森林分类器中.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 d_n2v_PWL框图Fig.1 Framework of d_n2v_PWL

1.2.1 表征节点向量

给定动态网络{G₁, G₂, …, G_N}, 对每个历史时间片分别应用node2vec, 学习历史快照中节点的嵌入向量.

node2vec可有效学习网络中节点的连续特征表示.相比传统的网络表征方法, node2vec在Deep-walk的基础上引入深度优先搜索和广度优先搜索两种有偏的随机游走方式, 分别通过引入返回参数p和输出参数q控制有偏游走.

如图2所示, p用于控制游走过程中返回上一个顶点的可能性, p设置越大, 节点在游走过程中返回上一个节点的概率越小.参数q用于控制游走的方式:当q> 1时, 游走时倾向于选择围绕起始点的节点序列, 该过程类似于广度优先遍历; 当q< 1时, 游走时倾向于选择远离起始点的节点序列; 当p=q=1时, node2vec与Deepwalk游走方式相同.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 node2vec随机游走过程示意图Fig.2 Illustration of random walk procedure of node2vec

基于文献[16]的设置, 本文删除历史快照中有关测试集的边, 再将各个历史快照分别输入node2-vec中.对于每个历史时间片, 首先基于p、q值计算随机游走转移的概率, 得到随机游走的节点序列后, 将这些节点序列输入skip-gram模型中, 学习节点的表示.最后, 得到节点i在各个历史时间片的表征向量V it, t=1, 2, …, N, 拼接该节点在所有时间快照的向量表示, 得到N+1时刻的i节点表示, 记为

s_i=[ vi1‖ vi2‖ …‖ viN].

其中:‖ 表示2个向量按行拼接, 例如

[[0.1, 0.3]‖ [0.8, -0.2]]⇒ [0.1, 0.3, 0.8, -0.2].

同理, 对于j节点,

s_j=[ vj1‖ vj2‖ …‖ vjN].

1.2.2 捕获链接局部子图结构特征

为了充分利用链接的局部拓扑信息, 首先抽取未来时间片中, 目标节点对在不同时间片中对应的局部子图, 再分别对不同时间片上的局部子图结构进行重新编码, 目的是为了更好地度量历史时间片与未来时间片中局部子图结构的相似性.最后, 利用编码完成的局部子图, 构建未来时刻链接的局部子图结构表示.具体过程如下.

1)抽取局部子图.对于要预测的目标节点对(i, j), 基于每个历史快照G_t, 添加节点i、 j, 再分别添加它们的1跳邻居, 2跳邻居, 以此类推, 直至局部子图中节点个数为k个或没有邻居节点, 得到包含k个节点的局部子图 Gtij.为了便于表达, 记该局部子图的节点集为U.

2)局部子图编码.不同时间片中目标节点对周围的局部子图结构越相似, 目标节点对形成链接的可能性越相似.于是, 为了度量不同时间片中目标节点对周围的局部子图结构的相似性, 对局部子图结构进行重新编码, 如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 局部子图编码过程Fig.3 Process of local subgraph coding

具体编码过程如下所示.

(1)计算子图 Gtij中节点u∈ U的初始编号:

c(u)=f(d(u, i)d(u, j)).(1)

其中:i, j表示目标节点对; d(x, y)为节点x、y之间的最短距离; f:R^k→ C^k为映射函数, 即将k个节点映射为有序整数.

例如, 目标节点对(99, 107)的初始编码为1, 子图中其余节点按照式(1)编码, 得到图3中的子图初始编号.

(2)利用PWL不断迭代更新子图中的节点编号, 直到算法收敛, 为所有的节点编好独立的序号.PWL更新如下:

c'(u)=f(c(u)+ ∑z⊆Γ(u)ln(p(c(z)))「∑z'⊆Γ(u)ln(p(c(z')))⌉), (2)

其中, c'(· )为节点更新后的编号, c(· )为节点初始编号, Γ (u)为节点u的邻居, p(n)表示第n个素数, 如p(0)=2, p(1)=3, 4, …

例如, 对于图3得到的初始编号的子图, 循环使用式(2), 直到为所有节点编好独立的序号, 见图3中子图最终编号.

3)生成局部子图结构特征表示.当得到局部子图的最终编号后, 构建邻接矩阵 Atij.行列按照节点的编号大小排列.取每个子图的上三角矩阵triu( Atij), 按行依次拼接上三角矩阵的各行元素(去除目标节点对元素 Atij[1, 2])作为目标节点对(i, j)的局部子图结构特征表示 cijt.

如图4所示, 对于目标节点对(99, 107), 在某个时间段t得到的局部子图的邻接矩阵表示为 At(99, 107), 该节点对的局部子图结构特征表示为c(99, 107)t.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 链接的局部子图结构表示Fig.4 Local subgraph structure representation of link

4)生成下一时刻链接的局部子图结构表示.分别将各个时间快照上生成的子图结构表示进行拼接, 生成第N+1时刻链接的局部子图结构表示, 记为

l_ij=[ cij1‖ cij2‖ …‖ cijN].

1.2.3 链接表示及分类预测

在基于网络表示学习的链接预测方法中, 链接表示通常构建为两个节点向量的拼接或对应元素相乘.对比拼接或对应元素相乘这两种方法后发现, 计算节点i的表示s_i和节点j的表示s_j的元素对应乘积, 作为两个节点之间的交互表示预测效果更好, 即

h_ij=s_i☉s_j.

其中☉表示两个向量逐个元素乘积.

例如,

s_i=[0.1, -0.2], s_j=[0.5, 0.7],

h_ij=[0.1× 0.5, -0.2× 0.7]=[0.05, -0.14].

本文将基于node2vec的链接表征向量和链接的局部子图结构表示进行拼接, 记为

e_ij=[h_ij‖ l_ij].

G_N+1的边被随机划分为训练集和测试集, 在建立网络表征模型前, 移除历史快照中包含的测试集, 随机选取相同数量的负例样本.对于训练集和测试集中的每条边, 利用本文方法得到链接表示后, 将训练集的链接表示用于训练二分类器, 再预测测试集中链接是否存在.对比逻辑回归(Logistic Regression)、随机森林(Random Forest, RF)、梯度提升回归树(Gra-dient Boosted Regression Tree)和全连接神经网络在各个数据集上的实验效果, 本文选用在大多数数据集上分类性能较优的RF作为二分类器.

本文的实验数据来源于Network Repository Website, 共5个数据集^[23].

1)Enron-Employee(Emp).2002年2月至2004年2月Enron员工之间的电子邮件通信网络, 8个时间片, 相邻两个时间片之间间隔3个月.

2)Radoslaw(Rad).2010年1月2日至2010年9月30日中型制造网络员工之间的电子邮件通信网络, 9个时间片, 相邻两个时间片之间间隔1个月.

3)Facebook-Forum(Fac).用户在2004年5月至2004年10月的论坛活动, 6个时间片, 相邻两个时间片之间间隔一个月.

4)Contacts-Dublin(Dub).2009年5月11日至2009年7月5日人际接触网络, 8个时间片, 相邻两个时间片之间间隔一周.

5)Reality-Call(Rea).2004年9月27日至2005年1月2日麻省理工学院小型移动电话网, 7个时间片, 相邻两个时间片之间间隔两周.

数据集的基本信息如表1所示.

表1

Table 1

表1(Table 1)

表1 实验数据集 Table 1 Experimental datasets 名称 节点数 链接数 边密度 Rad 167 3251 0.2345 Emp 150 1588 0.1421 Fac 899 7046 0.0175 Dub 6454 24097 0.0012 Rea 6416 7250 0.0004

表1 实验数据集 Table 1 Experimental datasets

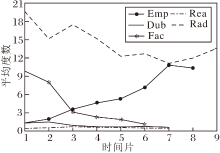
实验分析不同数据集节点的平均度随时间片变化情况, 如图5所示, 即节点的度数变化反映节点的邻居变化情况.由图可看出, 不同数据集中每个时间片的节点分布稀疏情况和节点邻居变化情况不同.除Emp数据集外, 其他4个数据集的节点邻居基本呈现下降趋势, 因此链接的消失比增长更快.Rea数据集上每个时间片数据都很稀疏.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各数据集上节点平均度随时间片变化情况Fig.5 Average node degree changing with time slices on the datasets

实验中共涉及3个主要模块, 每个模块涉及的参数值如下.PWL中子图节点数k=10, RF中决策树个数n=80.在node2vec中, 训练窗口大小为10, 随机游走经过每个节点次数为10, 随机游走的每个路径包含节点数为80, 节点表征维度为128.

实验采用链接预测常用的评估指标:接收者操作特征曲线下面积(Area Under Curve, AUC)值和平均精确度(Average Precision, AP)值.AUC为评价二分类模型优劣的常用指标, AUC值越高, 表明模型表现的效果越优.AP值计算准确率-召回率(Precision-Recall, PR)曲线下的面积.PR曲线用于稀疏数据集的检测.当负样本较大时, ROC曲线无法正确评估模型.因此采用只考虑正样本的PR曲线, 更好地评估模型.

为了说明本文方法的有效性、灵活性、鲁棒性, 采用如下对比方法.

1)静态链接预测方法.不考虑时间信息, 将动态网络的所有时间片合并为一张大的静态网络, 随后划分训练集和测试集, 进行训练, 预测网络中的链接状态, 包括如下多种方法.

(1)共同邻居(Common Neighbors, CN)^[3].认为2个节点之间的相似分数由共同邻居数目决定:

Score(v_i, v_j)=|Γ (v_i)∩ Γ (v_j)|.

(2)杰卡德系数(Jaccard Coefficient, JC)^[4].节点对的相似性定义为共同邻居的数目与邻居总数的比值:

Score(v_i, v_j)= |Γ(vi)⋂Γ(vj)||Γ(vi)⋃Γ(vj)|.

(3)资源分配(Resource Allocation, RA)^[5].认为节点v_i、v_j之间的相似性分数可定义为v_i通过间接链接从v_j获得的资源, 每个间接链接贡献一部分资源:

Score(v_i, v_j)= ∑v∈Γ(vi)⋂Γ(vj)1Γ(v).

(4)局部路径(Local Path, LP)^[6].考虑网络的路径信息, 两节点之间的相似性分数计算为两节点之间长度为2和3的路径数目:

Score(v_i, v_j)= A(vi, vj)2+β A(vi, vj)3,

其中, A表示网络的邻接矩阵, β 为可调参数.

上述4种方法主要基于训练集获得得分矩阵, 根据得分矩阵计算测试集上节点对形成链接的概率.

(5)node2vec^[9].使用node2vec学习由训练集构成的静态网络中节点的表示向量, 预测链接的表示通过对应节点向量的元素对应乘积得到, 最后将正负例样本输入到随机森林分类器中建立链接预测模型.

(6)PWL.基于WLNM^[10], 与原文不同的是采用随机森林作为分类器, 因为经过实验测试发现, 随机森林分类器训练的效果优于原文神经网络训练得到的结果.

2)动态链接预测方法.考虑时序信息, 利用历史快照得到的信息, 获取未来网络链接的表示, 最后建立分类模型(下述模型中分类器都表示随机森林分类器), 包括如下几种方法.

(1)连续时间动态网络表征(Continuous Time Dynamic Network Embeddings, CTDNE).基于文献[16], 将时序信息表示在网络中边的权重上, 使用node2vec以时序递增的方式随机游走网络, 产生节点的表示向量, 最后将节点向量的元素对应乘积输入到分类器中.

(2)基于node2vec的动态网络链接预测(Dyna-mic Network Link Prediction Based on node2vec, d_n2v).通过node2vec捕获每个历史快照上节点的表示向量.将得到的各个历史快照中节点表示的元素对应乘积作为边的表示.将前N个历史快照拼接得到的边表示输入到分类器中.

(3)基于PWL的动态网络链接预测(Dynamic Network Link Prediction Based on Palette Weisfeiler Lehman, d_PWL).基于PWL的设计, 抽取每个历史时间片中目标节点对的局部子图结构表示.为了捕捉子图结构的演化, 拼接这些子图结构特征表示作为下一时刻边的局部子图结构表示.最后将得到的边表示输入到分类器中进行链接预测.

(4)基于GCN的动态网络链接预测(Dynamic Network Link Prediction Based on Graph Convolu-tional Network, d_GCN).类似于d_n2v, 但采用GCN获得节点的向量表示.

(5)基于LSTM的动态网络链接预测(Dynamic Network Link Prediction Based on Long Short-Term Memory, d_LSTM).基于LSTM, 通过捕获每个时间片网络结构演变的情况, 预测未来时刻的网络结构图, 即将每个时间片的邻接矩阵输入LSTM中, 预测最后一个时间片的邻接矩阵, 得到邻接矩阵的行向量作为节点表示, 节点表示元素的对应乘积作为边表示.分别获取训练集和测试集的边表示, 输入到分类器中进行训练.

(6)本文方法(d_n2v_PWL)._n2v意味着历史快照中节点的向量表征通过node2vec实现; _PWL表示链接的局部子图结构信息被融入到最后的链接表示中.

2.4.1 链接预测的有效性

不同方法在每个数据集上的AUC值和AP值如表2和表3所示, 表中— 表示算力限制.

表2

Table 2

表2(Table 2)

表2 各方法在5个数据集上的AUC值 Table 2 AUC values of different methods on 5 datasets 方法 Rad 数据集 Emp 数据集 Fac 数据集 Rea 数据集 Dub 数据集 CN 92.37 86.01 65.51 52.06 89.51 JC 85.99 85.23 63.60 52.03 89.54 RA 93.13 87.82 65.47 52.06 89.53 LP 92.82 86.73 79.68 55.26 95.02 node2vec 88.39 89.04 62.56 64.63 96.19 PWL 90.56 84.13 75.72 99.05 97.83 CTDNE 84.99 90.24 92.42 93.07 98.52 d_n2v 90.68 90.18 93.79 97.31 98.75 d_PWL 88.37 85.19 93.08 99.93 98.71 d_GCN 90.52 89.22 86.87 99.52 82.86 d_LSTM 88.94 84.77 86.02 — — d_n2v_PWL 96.60 91.28 95.50 99.83 100.00

表2 各方法在5个数据集上的AUC值 Table 2 AUC values of different methods on 5 datasets

表3

Table 3

表3(Table 3)

表3 各方法在5个数据集上的AP值 Table 3 AP values of different methods on 5 datasets 方法 Rad 数据集 Emp 数据集 Fac 数据集 Rea 数据集 Dub 数据集 CN 91.29 83.85 63.75 51.93 89.49 JC 82.22 85.21 57.13 50.77 89.55 RA 92.78 87.77 64.46 52.18 89.55 LP 92.21 85.77 77.42 55.60 95.01 node2vec 86.84 86.93 58.40 60.96 97.10 PWL 88.52 82.97 72.94 98.53 98.22 CTDNE 82.11 91.00 92.85 91.01 96.94 d_n2v 88.09 91.66 93.27 96.63 97.42 d_PWL 82.77 84.20 90.81 99.91 97.49 d_GCN 89.42 89.44 86.02 90.58 81.71 d_LSTM 87.04 84.84 84.63 — — d_n2v_PWL 95.97 92.68 95.34 99.82 100.00

表3 各方法在5个数据集上的AP值 Table 3 AP values of different methods on 5 datasets

分析上述实验结果, 得出如下结论.

1)d_n2v_PWL在5个数据集上均获得较优的预测结果.对比之前静态链接预测方法和动态链接预测方法得到的最高分数(见表2和表3中斜体数字):在AUC指标上, d_n2v_PWL分别提高3.47%, 1.04%, 1.71%, -0.1%, 1.25%; 在AP指标上, d_n2v_PWL分别提高3.19%, 1.02%, 2.07%, -0.09%, 1.78%.

2)对比node2vec和d_n2v, PWL和d_PWL, 实验结果表明, 使用静态网络表示方法获取历史快照的链接表征向量, 拼接作为预测网络的链接表示可改进动态网络链接预测的准确度, 然而并非适用于所有静态网络链接预测方法和所有的数据集.在Rad数据集上, 直接使用PWL获得的结果优于d_PWL.另外, 不同的静态网络表示方法扩展为动态链接预测方法在不同数据集上效果有所不同.在Rea数据集上, d_PWL的预测效果优于d_n2v, 而在其它数据集上, d_n2v的预测效果更优.

3)整体研究发现, d_n2v_PWL在稀疏数据集和稠密数据集上都可获得不同程度的改进.在较稠密的数据集Rad上, 相比d_n2v, d_n2v_PWL的AUC值提高5.92%, AP值提高7.88%.在较稀疏的数据集Rea上, 相比d_n2v, d_n2v_PWL的AUC值提高2.52%, AP值提高3.19%.

2.4.2 时间片数量的影响

本节主要研究时间片数量对方法预测结果的影响.d_n2v、d_PWL、d_GCN、d_n2v_PWL在5个数据集上的AUC值随使用时间片数量的变化趋势如图6所示.AP值的变化趋势与其类似, 在此不再赘述.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 时间片数量对预测结果的影响Fig.6 Influence of time slice number on model prediction results

由图6可见, 随着近期时间片数量的增长, 方法预测结果趋于稳定.在Rad数据集上, 当使用近期时间片数量超过5时, d_n2v_PWL预测结果增长不大.在Emp、Fac数据集上, 使用近期时间片数量超过3后, d_n2v_PWL预测性能不再发生较大变化.在Rea数据集上, 预测性能一直保持接近100%.在Dub数据集上, 当使用近期7个时间片时, d_n2v_PWL达到100%的预测结果.此外, d_n2v_PWL综合d_n2v和d_PWL的优点, 即节点相似特征和局部子图结构特征, 几乎在不同时间片数量上的结果均达到最高.

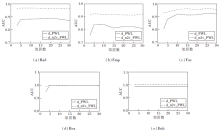
2.4.3 子图节点数目的影响

本节研究方法抽取的局部子图中的节点数目对链接预测结果的影响.图7对比d_PWL和d_n2v_PWL在5个数据集上的AUC值随局部子图节点数目增大的变化情况, AP值趋势相同.由图可见, 当改变局部子图的邻居数目时, d_PWL的AUC值变化幅度较大, d_n2v_PWL可获得更优的预测结果, 受局部子图节点数目影响不大.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 局部子图节点数目对预测结果的影响Fig.7 Influence of local subgraph node numbers on prediction results

在Rad、Emp、Fac数据集上, 当局部子图中考虑的节点数目较少时, d_PWL预测结果较低.随着局部子图节点数目的增长, 预测结果开始变优.当增长到一定程度后预测结果开始下降.在Rad数据集上, 当局部子图考虑的节点个数为3时, d_PWL预测结果极低, 而当其增长到5时, 预测结果明显变好, 节点个数增长到25时, 预测结果开始降低.d_n2v_PWL可一直维持较好的预测结果.在Rea数据集上, 当局部子图考虑的节点个数为3时, d_PWL预测结果较低, 节点数增长到5之后, d_PWL、d_n2v_PWL预测结果基本维持稳定, 前后变化幅度不超过0.002.在Dub数据集上, 随着局部子图邻居节点个数的改变, d_PWL和d_n2v_PWL的性能均保持不变.