基于低秩表示的标记分布学习算法

引用本文

刘睿馨, 刘新媛, 李晨. 基于低秩表示的标记分布学习算法. 模式识别与人工智能, ,34(2): 146-156
LIU Ruixin, LIU Xinyuan, LI Chen. Label Distribution Learning Method Based on Low-Rank Representation. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,34(2): 146-156. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202102006
Permissions

《模式识别与人工智能》编辑部所有

基于低秩表示的标记分布学习算法

刘睿馨¹, 刘新媛¹, 李晨¹

1.西安交通大学软件学院西安 710049

通信作者：

李晨,博士,讲师,主要研究方向为多媒体技术、模式识别.E-mail:lynnlc@126.com.

作者简介

刘睿馨,硕士研究生,主要研究方向为机器学习.E-mail:sweetylrx@stu.xjtu.edu.cn.

刘新媛,博士研究生,主要研究方向为机器学习.E-mail:xinyuan.liu@stu.xjtu.edu.cn.

收稿日期: 2020-08-03 接受日期: 2020-12-09

资助项目: 国家自然科学基金项目(No.61573273)资助

摘要

针对标记分布学习算法忽略标记相关性信息及数据存在异常和噪声值的情况,文中提出基于低秩表示的标记分布学习算法(LDL-LRR).利用特征空间的基线性表示样本信息,实现对原始特征空间数据的降维.将低轶表示(LRR)迁移至标记空间,对模型施加低秩约束,把握数据的全局结构.分别使用增广拉格朗日乘子法和拟牛顿法求解LRR和目标函数,再通过最大熵模型预测标记分布.在10个数据集上的对比实验表明,LDL-LRR性能良好,效果稳定.

关键词: 标记多义性; 单标记学习(SLL); 多标记学习(MLL); 标记分布学习(LDL); 低秩表示(LRR)

中图分类号:TP 181

Label Distribution Learning Method Based on Low-Rank Representation

LIU Ruixin¹, LIU Xinyuan¹, LI Chen¹

1.School of Software Engineering, Xi'an Jiaotong University, Xi'an 710049

Corresponding author:
LI Chen, Ph.D., lec-turer. Her research interests include multi-media technology and pattern recognition.

AboutAuthor:
LIU Ruixin, master student. Her research interests include machine learning.
LIU Xinyuan, Ph.D. candidate. Her research interests include machine learning.

Fund:Supported by National Natural Science Foundation of China(No. 61573273)

Abstract

Label correlations, noises and corruptions are ignored in label distribution learning algorithms. Aiming at this problem, a label distribution learning method based on low-rank representation(LDL-LRR)is proposed. The base of the feature space is leveraged to represent the sample information, and consequently dimensionality reduction of the data in the original feature space is achieved. To capture the global structure of the data, low-rank representation is transferred to the label space to impose low-rank constraint to the model. Augmented Lagrange method and quasi-Newton method are employed to solve the LRR and objective function, respectively. Finally, the label distribution is predicted by the maximum entropy model. Experiments on 10 datasets show that LDL-LRR produces good performance and stable effect.

Key words: Key Words Label Ambiguity; Single-Label Learning; Multi-label Learning(MLL); Label Distribution Learning(LDL); Low-Rank Representation(LRR)

文章图片

本文责任编委于剑

Recommended by Associate Editor YU Jian

单标记学习(Single-Label Learning, SLL)和多标记学习(Multi-label Learning, MLL)是目前常用于数据标注的机器学习模型^[1], 二者都关注标记是否描述实例, 当数据语义信息丰富^[1]时MLL更有效.但是标记描述实例的程度往往不同, 基于均匀标记分布假设的MLL无法区分多个标记的主次关系, 不适用于需要定性考虑标记是否描述实例且定量考虑标记对于实例的相对重要性的问题.

Geng^[2]提出标记分布学习(Label Distribution Learning, LDL), 解决标记描述实例的程度问题.标记分布学习给每个描述实例的标记分配一个描述度, 并假设所有标记的描述度之和为1.这种方式概念简洁, 可准确区分标记对于实例的重要程度差异, 适用于复杂问题, 应用场景广泛.

Geng等^{[3, 4]}提出改进迭代尺度-标记分布学习算法(Improved Iterative Scaling-Learning from Label Distributions, IIS-LLD)、条件概率神经网络(Condi-tional Probability Neural Network, CPNN)、自适应标记分布学习算法(Adaptive Label Distribution Lear-ning, ALDL), 解决面部年龄估计问题.Zhou等^[5]提出情绪分布学习(Emotion Distribution Learning, EDL), 解决面部表情识别问题.Ling等^[6]提出软视频解析算法(Soft Video Parsing, SP), 解决软视频解析问题.但是, 上述算法都忽略标记间的相关性, 阻碍方法性能提升.因此, Xu等^[7]提出批注不完整的标记分布学习算法(LDL with Incomplete Annotation, IncomLDL), 假设均匀随机丢失标记分布矩阵的元素, 并引入迹范数作为正则化项, 利用标记相关性深入学习标记空间的隐藏信息.Jia等^[8]提出利用标记相关性的标记分布学习方法(LDL Method by Exploi-ting the Label Correlation, LDL-LC), 引入距离函数计算标记间的全局相关性信息.Zheng等^[9]提出局部利用样本相关性的标记分布学习算法(LDL Algorithm by Exploiting Sample Correlations Locally, LDL-SCL), 对数据进行聚类, 保证类内的实例共享相同的标记相关性信息.

已有的标记分布学习方法大多为监督信息完整的数据设计, 然而为实例分配真实的标记分布需要花费大量的人力和时间成本^[7], 当数据中存在噪声或异常值时, 无法保证标记信息的完整性, 且标记间相关性的获取难度增加.因此, 本文提出基于低秩表示(Low-Rank Representation, LRR)^{[10, 11]}的标记分布学习算法(LDL Method Based on LRR, LDL-LRR).LRR充分考虑样本间的相关性信息和子空间结构^[12], 保证所有数据在其自表达下构成的系数矩阵的秩最小, 并获取数据集的全局相关性信息.由于系数矩阵遵循最低秩准则, 在对有噪声和异常值的原始数据进行重构时具有鲁棒性.通过增广拉格朗日乘子法(Augmented Lagrange Method, ALM)求解LRR, 并使用拟牛顿法(BFGS)对优化问题进行求解.在10个真实世界数据集上的实验表明, LDL-LRR在常用的评估指标上都取得一定提升, 这验证本文算法的有效性和优越性.

1 相关工作

为了方便介绍, 本节预先给出主要的符号定义.实例的特征空间X=[x₁, x₂, …, x_n]^T∈ Rⁿ^×^q, 维度为q, 第i个实例x_i∈ X.标记集Y={y₁, y₂, …, y_c}, c表示标记集的大小, 即描述实例的标记个数, y_j表示第j个标记. $d_{x_{i}}^{y_{j}}$ 表示标记y_j描述实例x_i的程度, 记作描述度.每个标记的描述度都应满足

$d_{x_{i}}^{y_{j}}$ ∈ [0, 1], $\overset{c}{\sum_{j = 1}} d_{x_{i}}^{y_{j}}$ =1,

x_i的标记分布d_i=[ $d_{x_{i}}^{y_{1}}$ ; $d_{x_{i}}^{y_{2}}$ ; …; $d_{x_{i}}^{y_{c}}$ ]^T, 所有实例的标记分布构成的标记分布矩阵

D^*=[d₁, d₂, …, d_n]^T∈ Rⁿ^×^c.

Geng等^{[3, 4]}在解决面部年龄估计问题时给出标记分布学习的形式化定义, 认为标记分布是一种类似概率分布的数据结构, 与概率分布具有相同的约束条件, 可使用条件概率的形式表示描述度, 即

$d_{x_{i}}^{y_{j}}$ =P(y_j|x_i).

给定训练集

S={(x₁, d₁), (x₂, d₂), …, (x_n, d_n)},

标记分布学习的目标是求解参数向量θ , 使参数模型P(y_j|x_i; θ )生成与给定实例x_i的真实标记分布d_i尽可能相似的标记分布.

目前常见的标记分布学习算法主要基于如下3种设计策略^{[2, 13]}.

策略1是问题转化(Problem Transformation, PT)^[13], 即将每个标记分布学习训练样本(x_i, d_i)转化成c个带有权重的单标记学习训练样本(x_i, y_i), 权重由标记的描述度 $d_{x_{i}}^{^{y_{j}}}$ 给出, 经过重采样的训练样本集可使用单标记学习算法处理.基于此策略设计的算法有PT-Bayes(PT:Bayes)^[13]和PT-SVM(PT:Support Vector Machine)^[13].

策略2是算法改造(Algorithm Adaptation, AA)^[13], 即将传统的单标记学习算法或多标记学习算法改造成可处理标记分布学习问题的算法.基于该策略设计的算法有基于k近邻(k Nearest Neighbor, kNN)改造的AA-kNN^[13]和基于反向传播(Back Propagation, BP)神经网络改造的AA-BP^[13].

策略3是根据标记分布学习的特点设计专用算法(Specialized Algorithm, SA)^[13].专用算法的设计通常涵盖输出模型、目标函数和优化方法三部分.标记分布学习算法的输出模型常选取最大熵模型^[14], 目标函数常采用Kullback-Leibler(KL)散度^[15]度量真实标记分布与预测标记分布之间的相似性, 优化方法各有不同, SA-IIS^[13]、SA-BFGS^[13]分别选取改进迭代尺度算法(Improved Iterative Scaling, IIS)^[16]和BFGS^[17]优化目标函数.实验表明策略3优于前两种策略^[2], 因此基于策略3形成由输出模型、目标函数和优化方法构成的标记分布学习算法设计的泛化框架.

部分现有的专用算法在目标函数中引入标记间的相关性度量, 提高标记分布学习模型的性能.LDL-LC^[8]使用度量不同标记间的欧氏距离获取标记间的全局相关信息.LDL-SCL^[9]使用k-means^[18]对训练数据进行聚类, 位于同类内的实例共享相同的标记相关性信息, 即标记间的局部相关性信息.将最大熵模型拆分为原始特征部分和附加特征部分, 在附加特征部分及惩罚项引入局部相关性信息.基于低秩近似的标记相关性标记分布学习(LDL with Label Correlations via Low-Rank Approximation, LDL-LCLR)^[19]通过核范数近似获取全局相关性, 通过k-means聚类获取局部相关性, 并通过交替方向乘子法(Alternating Direction Method of Multi-pliers, ADMM)求解目标函数.算法为目标函数引入秩函数的凸包核范数, 但未考虑对真实标记分布与预测标记分布之间差异的控制.

2 基于低秩表示的标记分布学习算法

2.1 低秩表示

数据集矩阵X=[x₁, x₂, …, x_n]可以被字典矩阵(基矩阵)A=[a₁, a₂, …, a_m]线性表示为

X=AC, (1)

其中C=[c₁, c₂, …, c_n]为线性组合表达系数矩阵.数据集X中每个数据样本都可由其它数据样本的线性组合表示为

x_i= $\sum_{j \neq i}$ C_ijx_j.

将所有数据样本及其表达系数C_ij按一定方式排成矩阵, 则式(1)等价于:

X=XC, (2)

并且C应满足当x_i和x_j属于不同子空间时, 有C_ij=0.式(2)使用数据集本身表示数据, 称为数据的自表达(Self-representation)^[20].

为了提高算法对噪声或异常值的鲁棒性, 本文以低秩表示作为基本假设, 增强矩阵C各行(列)间的相关性, 通过特征空间的基线性表示所有样本信息及其全局关系, 将原始数据投影至更低维的线性子空间上, 凸显数据的类内相似性和类间差异性^{[10, 11, 21]}.基于自表达子空间的特性, 选取X本身作为字典矩阵, 构造如下低秩优化问题:

$\min_{C}$ rank(C), s.t. X=XC.(3)

考虑数据样本存在噪声和异常值, 并且现实世界的数据点大多位于仿射子空间而非线性子空间中, 故假设

X=XC+E,

则式(3)重写为

$\min_{C, E}$ rank(C)+λ ‖ E‖ _{2, 0}, s.t. X=XC+E.(4)

其中, E为数据样本的噪声和异常值, rank(C)为C的秩函数, ‖ · ‖ _{2, 0}为l_{2, 0}范数, λ 为平衡两部分影响程度的低秩系数.

由于秩函数的离散性, 式(4)得到的低秩优化问题是一个非凸的NP-hard问题^[22].为了易于求出唯一最优解, 需要对式(4)进行凸松弛.Fazel^[23]已经证明矩阵核范数是秩函数在矩阵谱范数意义下单位球上的最佳凸逼近, 因此可利用凸核范数近似替代非凸秩函数^{[24, 25]}, 同时将l_{2, 0}范数松弛为其凸包l_{2, 1}范数^[11], 得到如下凸优化问题:

$\min_{C, E}$ ‖ C‖ _*+λ ‖ E‖ _{2, 1}, s.t. X=XC+E,

其中, ‖ · ‖ _*为矩阵的核范数, ‖ · ‖ _{2, 1}为l_{2, 1}范数, λ > 0为平衡两项权重的噪声系数.由于l_{2, 1}范数迫使E的列趋于0, 因此本文假设异常值是样本特定(Sample-Specific)^[10]的, 即只有部分向量受到异常值干扰.引入J作为辅助变量:

$\min_{C, E}$ ‖ J‖ _*+λ ‖ E‖ _{2, 1}, s.t. X=XC+E, C=J.(5)

解决凸优化问题的方法有牛顿法、最速下降法和增广拉格朗日乘子法^{[26, 27]}等, 本文采用增广拉格朗日乘子法.构造式(5)的增广拉格朗日函数:

$\min_{C, E, J, Y_{1}, Y_{2}, μ}$ ‖ J‖ _*+λ ‖ E‖ _{2, 1}+ < Y₁, X-XC-E> +< Y₂, C-J> +

$\frac{μ}{2}$ ( ${‖ X - XC - E ‖}_{F}^{2} + ‖ C - J ‖$ ) $‖_{F}^{2}$ (6)

其中, < · , · > 为两个矩阵的点积, Y₁、Y₂为拉格朗日乘子, μ > 0为正项的惩罚标量.为了方便求解, 将式(6)表述为矩阵的迹的形式:

$\min_{C, E, J, Y_{1}, Y_{2}, μ}$ ‖ J‖ _*+λ ‖ E‖ _{2, 1}+

tr( ${Y^{T}}_{1}$ (X-XC-E))+tr( ${Y^{T}}_{2}$ (C-J))+ $\frac{μ}{2}$ ( $‖ X - XC - E ‖_{F}^{2}$ + $‖ C - J ‖_{F}^{2}$ ). (7)

由于式(7)无约束条件, 可将该优化问题划分为如下子问题, 通过交替方向乘子法对变量进行优化.

1)更新J.固定变量C和E, 保留式(7)中有关J的项:

‖ J‖ _*+tr[ ${Y^{T}}_{2}$ (C-J)]+ $\frac{μ}{2}$ ‖ C-J $‖_{F}^{2}$ .

求得J的更新公式:

J=arg min( $\frac{1}{μ}$ ‖ J‖ _*+ $\frac{1}{2} ‖ J - (C + \frac{Y_{2}}{μ}) ‖_{F}^{2}$ ).

2)更新C.固定变量J和E, 保留式(7)中有关C的项:

-tr( ${Y^{T}}_{1}$ XC)+tr( ${Y^{T}}_{2}$ C)+ $\frac{μ}{2}$ [tr(-2XT^XC+CT^XT^XC+2ET^XC)+tr(C^TC-J^TC-C^TJ)].

求关于C的偏导, 并令其偏导等于0, 可得C的更新公式:

C=(I+X^TX)^-1· (X^TX-X^TE+J+ $\frac{1}{μ}$ (X^TY₁-Y₂)).

3)更新E.固定变量C和J, 保留式(7)中有关E的项:

‖ E‖ _{2, 1}-tr( ${Y^{T}}_{1}$ E)+ $\frac{μ}{2}$ [tr(-2E^TX+2E^TXC+E^TE)].

求得E的更新公式:

E=arg min( $\frac{λ}{μ}$ ‖ E‖ _{2, 1}+ $\frac{1}{2} ‖ E - (X - XC + \frac{Y_{1}}{μ} {) ‖}_{F}^{2}$ ).

4)更新乘子.对于拉格朗日乘子Y₁、Y₂, 可通过阶跃为μ 的梯度上升进行更新^{[28, 29]}:

Y₁=Y₁+μ (X-XC-E), Y₂=Y₂+μ (C-J).

通过

μ =min(nμ , μ _max)

更新μ .选择合适的初始值, 依照上述求解过程交替迭代, 直至满足收敛条件

‖ X-XC-E $‖_{\infty}$ < ε , ‖ C-J $‖_{\infty}$ < ε

或达到最大迭代次数, 即可获取最优解 $\overset{︿}{J}$ 、 $\overset{︿}{C}$ 和 $\overset{︿}{E}$ .

2.2 标记分布学习算法

基于低秩表示的标记分布学习算法(LDL-LRR)符合专用算法^[13]的设计策略, 由输出模型、目标函数和优化方法构成.

第1节已经提出, 描述度可使用条件概率的形式表示, 假设P(y|x)为参数模型, 记作P(y|x; θ ).本文采用最大熵模型作为输出模型:

P(y_l|x_i; θ )= $\frac{1}{Z_{i}}$ exp( $\sum_{k}$ θ _l_,_k $x_{i}^{k}$ ).(8)

其中:

Z_i= $\sum_{l}$ exp( $\sum_{k}$ θ _l_,_k $x_{i}^{k}$ )

为归一化项, 保证描述实例的所有标记描述度之和为1; θ 为描述原始特征和标记分布之间关系的系数矩阵, θ _l_,_k为θ 中的元素; $x_{i}^{k}$ 为训练集X中的第i个实例x_i的第k个原始特征.为了获取模型的最优参数 $\overset{}{θ}$ , 构造如下目标函数表达式:

M(θ )= $\min_{θ}$ (L(θ )+λ ₁Ω (θ )+λ ₂Ψ (θ )), (9)

其中, L(θ )为定义在训练数据上的损失函数, Ω (θ )为控制模型复杂度的正则化项, Ψ (θ )为表征原始特征空间信息及标记间相关性信息的函数, λ ₁、λ ₂为调节这3项重要性的非负参数.

损失函数L用于度量真实标记分布D_i与预测标记分布P(y|x_i; θ )之间的相似性, 常用的度量函数有欧氏距离、Jeffrey分歧、KL散度等^[30].多个对比实验^[31]表明KL散度的表现最稳定, 即

KL_J(Q_a‖ Q_b)= $\sum_{j} Q_{a}^{j}$ ln( $\frac{Q_{a}^{j}}{Q_{b}^{j}}$ ),

其中, $Q_{a}^{j}$ 、 $Q_{b}^{j}$ 分别为标记分布Q_a、Q_b的第j个元素.本文基于KL散度构造损失函数:

L(θ )= $\overset{n}{\sum_{i = 1}} \overset{c}{\sum_{l = 1}}$ ( $d_{x_{i}}^{y_{l}}$ ln( $\frac{d_{x_{i}}^{y_{l}}}{P (y_{l} | x_{i})}$ )), (10)

其中, $d_{x_{i}}^{y_{l}}$ 为标记y_l对实例x_i的真实描述度, P(y_l|x_i)为标记y_l对实例x_i的预测描述度.

式(9)的第2项为关于θ 的正则化项:

Ω (θ )=‖ θ $‖_{F}^{2}$ , (11)

其中, ‖ · ‖ _F为矩阵的Frobenius范数, 作用是控制模型的复杂度, 防止模型因过拟合导致算法泛化能力的下降.

此外, 根据平滑假设^[32], 可将从特征空间得到的低秩特性迁移到标记空间, 使标记空间获得相似的低秩结构.故式(9)的第3项表示为

${Ψ (θ) = ‖ P (y | x; θ) - P (y | x; θ) \overset{︿}{C} ‖}_{F}^{2}$ = $‖$ (I- ${\overset{︿}{C}}^{T}$ )P(y|; θ )^T $‖_{F}^{2}$ (12)

其中, P(y|x; θ )为预测的标记分布, $\overset{︿}{C}$ 为特征空间的最低秩表示, 通过控制P(y|x; θ )与其自表达P(y|x; θ ) $\overset{︿}{C}$ 之间的距离可有效地对标记分布进行预测.

将式(10)~式(12)代入式(9), 利用2.1节求得最优解 $\overset{︿}{C}$ , 得到待优化的最终目标函数:

M(θ )= $\min_{θ}$ ( $\overset{n}{\sum_{i = 1}} \overset{c}{\sum_{l = 1}}$ ( $d_{x_{i}}^{y_{l}}$ ln( $\frac{d_{x_{i}}^{y_{l}}}{P (y_{l} | x_{i})}$ ))+

λ ₁‖ θ $‖_{F}^{2}$ +λ ₂‖ (I- ${\overset{︿}{C}}^{T}$ )P(y|x; θ )^T $‖_{F}^{2}$ )=

$\min_{θ}$ ( $\overset{n}{\sum_{i = 1}} \overset{c}{\sum_{l = 1}}$ ( $d_{x_{i}}^{y_{l}}$ ln( $\frac{d_{x_{i}}^{y_{l}}}{P (y_{l} | x_{i})}$ ))+λ ₁tr(θ ^Tθ )+

λ ₂tr(P(y|x; θ )(I- $\overset{︿}{C}$ )(I- ${\overset{︿}{C}}^{T}$ )P(y|x; θ )^T)).

本文选取拟牛顿法L-BFGS(Limited-BFGS)^[17] 求解目标函数M(θ ), 主要思想是根据伪Hessian矩阵的递归关系式得到最优的搜索方向, 有效节约内存空间.求取M(θ )关于θ _r的二阶泰勒展开式:

M(θ _r₊₁)≈ M(θ _r)+Ñ M(θ _r)^TΔ + $\frac{1}{2}$ Δ ^TH(θ _r)Δ , (13)

其中, Ñ M(θ _r)为目标函数M(θ )在θ _r处的梯度, H(θ _r)为目标函数M(θ )在θ _r处的Hessian矩阵, Δ =(θ _r₊₁-θ _r)为参数变化量.假设M(θ )为凸函数, 则H(θ _r)为正定的, 对式(13)关于Δ 求导并令其导数等于0, 可得到全局极值点:

Δ _r=-H^-1(θ _r)Ñ M(θ _r).

以解出的Δ _r作为搜索方向向量, 并选择满足Wolfe准则的α _r作为步长, 则θ 的迭代公式为

θ _r₊₁=θ _r+α _rΔ _r.

求解-H^-1(θ _r)需要先计算目标函数M(θ )的梯度Ñ M(θ ):

$\frac{\partial M}{\partial θ_{l, k}}$ =- $\overset{n}{\sum_{i = 1}} d_{x_{i}}^{y_{l}} x_{i}^{k}$ + $\overset{n}{\sum_{i = 1}}$ ( $x_{i}^{k}$ P(y_l|x_i))+2λ ₁θ _l_,_k+

λ ₂{(x^T(I- $\overset{︿}{C}$ )(I- ${\overset{︿}{C}}^{T}$ )X+

(X^T(I- $\overset{︿}{C}$ )(I- ${\overset{︿}{C}}^{T}$ )X)^T)θ }_l_,_K.

由于拟牛顿法仅需满足

Ñ M(θ _r)-Ñ M(θ _r_-1)=H(θ _r)(θ _r-θ _r_-1),

且尽量确保H(θ _r)与H(θ _r_-1)接近, 因此可得出H^-1(θ _r)的迭代公式:

H^-1(θ _r)=(I- $\frac{(θ_{r} - θ_{r - 1}) (\nabla M (θ_{r}) - \nabla M (θ_{r - 1} {))}^{T}}{(\nabla M (θ_{r}) - \nabla M (θ_{r - 1} {))}^{T} (θ_{r} - θ_{r - 1})}$ )·

H^-1(θ _r_-1)· (I- $\frac{(\nabla M (θ_{r}) - \nabla M (θ_{r - 1})) (θ_{r} - θ_{r - 1})^{T}}{(\nabla M (θ_{r}) - \nabla M (θ_{r - 1} {))}^{T} (θ_{r} - θ_{r - 1})}$ )+

$\frac{(θ_{r} - θ_{r - 1}) (θ_{r} - θ_{r - 1})^{T}}{(\nabla M (θ_{r}) - \nabla M (θ_{r - 1} {))}^{T} (θ_{r} - θ_{r - 1})}$ .

L-BFGS通过存储最近的m个(θ _r-θ _r_-1)和(Ñ M(θ _r)-Ñ M(θ _r_-1)), 近似估计H^-1(θ _r), 直到满足收敛条件或是达到最大迭代次数.最优解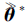代入式(8), 求得标记分布P(y|x; θ ).

由于标记分布定义每个标记的描述度

$d_{x_{i}}^{y_{j}}$ ∈ [0, 1], $\overset{c}{\sum_{j = 1}} d_{x_{j}}^{y_{j}}$ =1,

因此最终输出的标记分布D_output需满足

$\overset{c}{\sum_{n = 1}} d_{x_{i}}^{y_{j}}$ =1.

而归一化指数函数softmax可将模型的预测结果映射至指数函数上, 保证实数输出的映射结果在[0, +¥ )内, 再对映射后的预测结果进行归一化, 既保证每个标记的描述度 $d_{x_{i}}^{y_{j}}$ ∈ [0, 1], 又保证

$\overset{c}{\sum_{j = 1}} d_{x_{j}}^{y_{j}}$ =1,

故采用softmax对标记分布P(y|x; θ )进行归一化处理, 得到最终输出的标记分布D_output.

3 实验及结果分析

3.1 实验数据集

选取10个现实世界数据集, 前8个数据集为Yeast系列数据集, 数据来自基于出芽的酿酒酵母进行的生物学实验^[33], 共计2 465个酵母基因实例.每个酵母基因与一个长度为24的描述程度向量关联, 向量中的元素表示一天24 h内不同时刻的基因表达水平, 归一化后组成相应基因的标记分布.Yeast系列数据集共有10个, 本文仅选用标记数目大于等于4的数据集, 原因是LDL-LRR通过标记间的相关性信息可提高预测的性能表现, 标记不足会导致相关性缺失.最后2个数据集是基于面部表情数据集JAFFE^[34]和BU-3DFE^[35]改造的标记分布数据集SJAFFE和SBU-3DFE, 各包含213幅和2 500幅具有243维特征的灰度图像, 每幅图像分别由60人和23人在6个基本情绪标记(快乐、悲伤、惊讶、恐惧、愤怒和厌恶)上进行5级评分, 情绪强度由每种情绪的平均得分定义, 归一化后得到情绪标记对图像样本的描述度.数据集特征如表1所示.

表1 实验数据集 Table 1 Experimental datasets

本文实验的数据集包括无异常值干扰的数据集和异常值干扰的数据集.无异常值干扰的数据集无需对原始数据集进行任何操作, 异常值干扰的数据集需要对原始数据集随机加入样本的特定异常值(Sample-Specific Corruption)^[11], 具体操作为从原始数据集中随机选取10%的样本, 并为其生成随机的标记分布.

3.2 评估指标

本文采用5种评估指标对LDL进行评估, 分别是切比雪夫距离(Chebyshev Distance)、克拉克距离(Clark Distance)、堪培拉测度(Canberra Metric)、余弦系数(Cosine Coefficient)和相交相似度(Inter-section Similarity).前三者评估两种标记分布之间的距离, 评估指标越小性能越优; 后两者度量两种标记分布之间的相似性, 评估指标越大性能越优.评估指标的详情如下.

1)Chebyshev distance:

Dis₁= $\max_{j}$ |P_j-Q_j|.

2)Clark distance:

Dis₂= $\sqrt[]{{\overset{c}{\sum_{j = 1}} (\frac{| P_{j} - Q_{j} |}{P_{j} + Q_{j}})}^{2}}$ .

3)Canberra metric:

Dis₂= $\overset{c}{\sum_{j = 1}} (\frac{| P_{j} - Q_{j} |}{| P_{j} + Q_{j} |})$ .

4)Cosine coefficient:

Sim₁= $\overset{c}{\sum_{j = 1}}$ min(P_j, Q_j).

5)Intersection similarity:

Sim₂= $\overset{c}{\sum_{j = 1}} \sqrt[]{P_{j} Q_{j}}$ .

3.3 实验设置

为了验证LDL-LRR的有效性, 选用如下对比算法.

1)基于问题转化策略设计的PT-Bayes^[13]和PT-SVM^[13].通过重采样将标记分布数据集转换成单标记数据集, 在单标记数据集上训练单标记Bayes分类器和SVM分类器, 将分类器输出结果转换成标记分布.

2)基于算法改造策略设计的AA-kNN^{[13, 31]}和AA-BP^[13].AA-kNN通过实例x的k近邻的标记分布均值预测x的标记分布, AA-BP通过最小化真实标记分布与神经网络输出的标记分布之间误差的平方和求解标记分布.

3)专用算法SA-IIS^[13]和SA-BFGS^[13].SA-IIS使用改进迭代尺度算法优化目标函数, SA-BFGS基于BFGS通过一阶梯度函数优化目标函数.

4)LDL-LC^[8].引入距离函数计算标记间的全局相关性信息.

5)LDL-SCL^[9].保证类内的实例共享相同的标记相关性信息.

6)LDL-LCLR^[19].通过核范数近似获取全局相关性信息, 通过k-means聚类^[18]获取局部相关性信息.

本文的对比实验参数均与原文一致, LDL-LC的参数

λ ₁=0.1, λ ₂=0.01.

LDL-SCL的参数

λ ₁=0.001, λ ₂=0.001, λ ₃=0.001.

LDL-LCLR的参数

λ ₁=0.000 1, λ ₂=0.001, λ ₃=0.001, λ ₄=0.001, k=4, ρ =1.

LDL-LRR的参数λ =0.001, λ ₁、λ ₂取值范围为{0.000 1, 0.001, …, 0.1}.

3.4 实验结果

对于每个无异常值干扰的数据集, 都采用十折交叉验证(Ten-Fold Cross Validation)的方法, 将数据集随机分成10份, 选取9份作为训练集, 1份作为测试集, 重复该过程10次, 并记录在该数据集上所有评估算法的平均值和标准差, 保证评估结果的可靠性.由于篇幅限制, 仅对Yeast-alpha、SJAFFE数据集的实验结果进行展示, 如表2和表3所示, 10种算法在每个数据集上的各项指标分别进行排名, 使用黑体数字表示性能最佳.对它们在所有数据集上的排名求平均, 保留小数点后两位, 平均排名如表4所示.

表2 各算法在Yeast-alpha数据集上的指标值对比 Table 2 Index value comparison of different algorithms on Yeast-alpha dataset

表3 各算法在SJAFFE数据集上的指标值对比 Table 3 Index value comparison of different algorithms on SJAFFE dataset

表4 各算法在10个数据集上的平均排名及标准差 Table 4 Average rank and standard deviation of different algorithms on 10 datasets

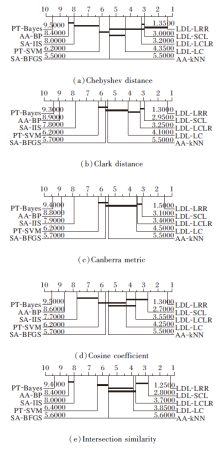
为了更直观合理地对比10种算法效果的差异, 图1绘制在5项评估指标下的临界差分图(Critical Difference Diagram, CD), 对其进行排名, 位置越靠右的算法性能越优.需要注意的是, 如果两种算法在所有数据集上的平均排名至少相差一个临界差值, 性能会有显著不同.若两种算法的性能差异并不显著, 使用粗线进行连接.

	Figure Option View Download New Window
	图1 各算法在5项评估指标上的CD图Fig.1 CD diagrams of different algorithms on 5 evaluation criterions

对10种算法在5项评估指标上的排名表现求均值和标准差, 可看出LDL-LRR的综合排名最佳.相比LDL-LC、LDL-SCL、LDL-LCLR, LDL-LRR排名更稳定.

为了进一步探索在数据存在噪声或异常值的问题场景下LDL-LRR的表现, 需要在异常值干扰的数据集上进行相同实验.使用十折交叉验证方法, 将加入异常值的数据集随机分成10份, 选取9份作为训练集, 剩下的1份对应的无异常值干扰的数据集作为测试集.重复该过程10次, 记录在数据集上所有评估方法的平均值和标准差.综合考虑表4中平均值和标准差结果, 选取LDL-LC和LDL-LCLR进行对比实验, 结果如表5和表6所示.

表5 各算法在有10%异常值的Yeast-alpha数据集上的指标值对比 Table 5 Index value comparison of different algorithms on Yeast-alpha dataset with 10% corruptions

表6 各算法在有10%异常值的SJAFFE数据集上的指标值对比 Table 6 Index value comparison of different algorithms on SJAFFE dataset with 10% corruptions

综合表2~表6及图1的实验结果, 可得到如下结论.

1)10种标记分布学习算法的总体排名为:LDL-LRR> LDL-LCLR> LDL-SCL> LDL-LC>

AA-kNN> SA-BFGS> PT-SVM>

SA-IIS> AA-BP> PT-Bayes.

在10个数据集上, LDL-LRR在绝大多数情况下最优.由图1可得, LDL-LRR始终处于CD图的最右端, 与大部分算法都具有显著性差异, 由此体现LDL-LRR的优越性.

2)LDL-LRR、LDL-LCLR、LDL-SCL、LDL-LC效果优于PT、AA、SA, 原因在于LDL-LRR、LDL-LCLR、LDL-SCL、LDL-LC利用标记间的相关性对标记空间的隐藏信息进行深入挖掘, 为模型的预测提供额外信息, 因此在解决标记分布学习问题时性能得到明显提升.

3)LDL-LRR的效果优于LDL-LCLR、LDL-SCL、LDL-LC, 相比排名第2的LDL-LCLR, LDL-LRR在Yeast系列数据集上的Chebyshev distance、Clark dis-tance、Canberra metric指标上取得1%~3%的效果提升, 在特征维数更多的面部表情识别数据集SJAFFE、SBU3DFE上取得3%~5%的效果提升.当数据集10%的样本加入异常值后, 仍能取得1%~5%的效果提升.其原因在于标记分布学习中的数据满足低秩子空间的假设, 即可被投影到更低维的线性子空间, 使数据的类内相似性和类间差异性更突出, 因此利用LRR可充分考虑样本间的相关性信息和子空间结构, 在数据存在噪声和异常值的情况下仍具有鲁棒的表现, 在各数据集上都能取得良好的效果.

3.5 参数分析

本节研究LDL-LRR对参数设置的敏感性.由于篇幅限制, 仅在Yeast-alpha数据集上对5项评估指标结果进行分析, 结果如图2所示.

	Figure Option View Download New Window
	图2 Yeast-alpha数据集上参数对5个评价指标值的影响Fig.2 Influence of parameters on 5 measures on Yeast-alpha dataset

由于仅变动低秩系数λ 时实验结果的变化幅度非常小, 可忽略不计, 因此取中间值λ =0.001.对于超参数λ ₁, 它的作用是约束正则化项, λ ₁越大意味着相比训练数据, 模型越倾向于拟合正则化项Ω (θ )的特性.为了防止过拟合, λ ₂取值范围固定在{0.000 1, 0.001, …, 0.1}.同理, 约束LRR的超参数λ ₂的取值范围也应固定在{0.000 1, 0.001, …, 0.1}, 令使用KL散度度量预测标记分布和真实标记分布相似度的损失函数占据主导地位.

由图2可看出, 只要在合适的取值范围内选取超参数, 就能使LDL-LRR具有良好、稳定的表现, 这也体现LDL-LRR的鲁棒性.

4 结束语

标记分布学习是单标记学习和多标记学习的推广, 在处理标记模糊性问题时具有优越性.与已有的绝大多数LDL不同, 本文提出基于低秩表示的标记分布学习算法(LDL-LRR), 将原始数据投影至低维的线性子空间, 通过特征空间的基线性表示所有样本信息及其全局关系, 并将从特征空间迁移到标记空间的最低秩表示加入目标函数, 对模型施加低秩约束.在真实数据集上的实验表明, LDL-LRR适用于标记分布学习框架, 性能良好且鲁棒性较强.今后将进一步优化标记分布学习算法的低秩表示结构, 如给LRR模型增加对称约束, 通过保留高维数据的子空间结构确保数据点对的权一致性, 从而约束标记分布模型, 提高准确性和鲁棒性.

参考文献

文献选项

[1]	XU N, LIU Y P, GENG X. Label Enhancement for Label Distribution Learning[J/OL]. [2020-07-26]. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8868206. [本文引用:2]
[2]	GENG X. Label Distribution Learning. IEEE Transactions on Know-ledge and Data Engineering, 2016, 28(7): 1734-1748. [本文引用:3]
[3]	GENG X, SMITHMILES K, ZHOU Z H. Facial Age Estimation by Learning from Label Distributions[C/OL]. [2020-07-26]. https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/aaai10LLD.pdf. [本文引用:2]
[4]	GENG X, YIN C, ZHOU Z H. Facial Age Estimation by Learning from Label Distributions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(10): 2401-2412. [本文引用:2]
[5]	ZHOU Y, XUE H, GENG X. Emotion Distribution Recognition from Facial Expressions // Proc of the 23rd ACM International Conference on Multimedia. New York, USA: ACM, 2015: 1247-1250. [本文引用:1]
[6]	LING M G, GENG X. Soft Video Parsing by Label Distribution Learning. Frontiers of Computer Science, 2019, 13(2): 302-317. [本文引用:1]
[7]	XU M, ZHOU Z H. Incomplete Label Distribution Learning // Proc of the 26th International Conference on Artificial Intelligence. New York, USA: ACM, 2017: 3175-3181. [本文引用:2]
[8]	JIA X Y, LI W W, LIU J Y, et al. Label Distribution Learning by Exploiting Label Correlations // Proc of the 32 AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2018: 3310-3317. [本文引用:3]
[9]	ZHENG X, JIA X Y, LI W W. Label Distribution Learning by Exploiting Sample Correlations Locally // Proc of the 32 AAAI Confe-rence on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2018: 4556-4563. [本文引用:3]
[10]	LIU G C, LIN Z C, YU Y. Robust Subspace Segmentation by Low-Rank Representation // Proc of the 26th International Conference on Machine Learning. New York, USA: ACM, 2010: 663-670. [本文引用:3]
[11]	LIU G C, LIN Z C, YAN S C, et al. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Transactions on Pa-ttern Analysis and Machine Intelligence, 2013, 35(1): 171-184. [本文引用:4]
[12]	李骜, 刘鑫, 陈德运, 等. 基于低秩表示的鲁棒判别特征子空间学习模型. 电子与信息学报, 2020, 42(5): 1223-1230. (LI A, LIU X, CHEN D Y, et al. Robust Discriminative Feature Subspace Learning Based on Low Rank Representation. Journal of Electronics and Information Technology, 2020, 42(5): 1223-1230. ) [本文引用:1]
[13]	耿新, 徐宁. 标记分布学习与标记增强. 中国科学(信息科学), 2018, 48(5): 521-530. (GENG X, XU N. Label Distribution Learning and Label Enhancement. Scientia Sinica(Informationis), 2018, 48(5): 521-530. ) [本文引用:17]
[14]	BERGER A L, DELLA PIETRA V J, DELLA PIETRA S A. A Maximum Entropy Approach to Natural Language Processing. Computational Linguistics, 1996, 22(1): 39-71. [本文引用:1]
[15]	YANG X, GAO B B, XING C, et al. Deep Label Distribution Learning for Apparent Age Estimation // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 102-108. [本文引用:1]
[16]	DELLA PIETRA S, DELLA PIETRA V, LAFFERTY J. Inducing Features of Rand om Fields. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(4): 380-393. [本文引用:1]
[17]	NOCEDAL J, WRIGHT S J. Numerical Optimization. Berlin, Ger-many: Springer, 2006. [本文引用:2]
[18]	KANUNGO T, MOUNT D M, NETANYAHU N S, et al. An Efficient k-means Clustering Algorithm: Analysis and Implementation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 881-892. [本文引用:2]
[19]	REN T T, JIA X Y, LI W W, et al. Label Distribution Learning with Label Correlations via Low-Rank Approximation // Proc of the 28th International Joint Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2019: 3325-3331. [本文引用:2]
[20]	王卫卫, 李小平, 冯象初, 等. 稀疏子空间聚类综述. 自动化学报, 2015, 41(8): 1373-1384. (WANG W W, LI X P, FENG X C, et al. A Survey on Sparse Subspace Clustering. Acta Automatica Sinica, 2015, 41(8): 1373-1384. ) [本文引用:1]
[21]	TANG H Y, ZHU J H, ZHENG Q H, et al. Label Enhancement with Sample Correlations via Low-Rank Representation // Proc of the AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2020: 5932-5939. [本文引用:1]
[22]	胡文玉, 李声豪, 涂志辉, 等. *联合 l_p/l₂, _p范数极小化的序列子空间聚类算法. 模式识别与人工智能, 2020, 33(3): 221-233. (HU W Y, LI S H, TU Z H, et al. Sequential Subspace Clus-tering via Joint l_p/l₂, _p-Norms Minimization. Pattern Recognition and Artificial Intelligence*, 2020, 33(3): 221-233. ) [本文引用:1]
[23]	FAZEL M. Matrix Rank Minimization with Applications[Z/OL]. [2020-07-26]. http://faculty.washington.edu/mfazel/orals3.pdf. [本文引用:1]
[24]	CANDÈS E J, RECHT B. Exact Matrix Completion via Convex Optimization[C/OL]. [2020-07-26]. https://arxiv.org/pdf/0805.4471.pdf. [本文引用:1]
[25]	KESHAVAN R H, MONTANARI A, OH S. Matrix Completion from Noisy Entries // Proc of the 22nd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2009: 952-960. [本文引用:1]
[26]	史加荣, 郑秀云, 魏宗田, 等. 低秩矩阵恢复算法综述. 计算机应用研究, 2013, 30(6): 1601-1605. (SHI J R, ZHENG X Y, WEI Z T, et al. Survey on Algorithms of Low-Rank Matrix Recovery. Application Research of Computers, 2013, 30(6): 1601-1605. ) [本文引用:1]
[27]	BERTSEKAS D P. Constrained Optimization and Lagrange Multiplier Methods. Salt Lake City, USA: Academic Press, 1982. [本文引用:1]
[28]	LIN Z C, CHEN M M, MA Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. Journal of Structural Biology Mathematical Programming, 2010, 181(2): 116-127. [本文引用:1]
[29]	张茁涵, 曹容玮, 李晨, 等. 隐式低秩稀疏表示的多视角子空间聚类. 模式识别与人工智能, 2020, 33(4): 344-352. (ZHANG Z H, CAO R W, LI C, et al. Latent Low-Rank Sparse Multi-view Subspace Clustering. Pattern Recognition and Artificial Intelligence, 2020, 33(4): 344-352. ) [本文引用:1]
[30]	CHA S H. Comprehensive Survey on Distance/Similarity Measures between Probability Density Functions. International Journal of Mathematical Models and Methods in Applied Science, 2017, 1(4): 300-307. [本文引用:1]
[31]	赵权, 耿新. 标记分布学习中目标函数的选择. 计算机科学与探索, 2017, 11(5): 708-719. (ZHAO Q, GENG X. Selection of Target Function in Label Distribution Learning. Journal of Frontiers of Computer Science and Technology, 2017, 11(5): 708-719. ) [本文引用:2]
[32]	ZHU X J. Semi-supervised Lear-ning with Graphs. Ph. D. Dissertation. Pittsburgh, USA: Carnegie Mellon University, 2005. [本文引用:1]
[33]	EISEN M B, SPELLMAN P T, BROWN P O, et al. Cluster Ana-lysis and Display of Genome-Wide Expression Patterns. Proceedings of the National Academy of Sciences of the United States of America, 1998, 95(25): 14863-14868. [本文引用:1]
[34]	LYONS M, AKAMATSU S, KAMACHI M, et al. Coding Facial Expressions with Gabor Wavelets // Proc of the 3rd IEEE International Conference on Automatic Face and Gesture Recognition. Washington, USA: IEEE, 1998: 200-205. [本文引用:1]
[35]	YIN L J, WEI X Z, SUN Y, et al. A 3D Facial Expression Database for Facial Behavior Research // Proc of the 7th International Conference on Automatic Face and Gesture Recognition. Washington, USA: IEEE, 2006: 211-216. [本文引用:1]

0.0

... 单标记学习(Single-Label Learning, SLL)和多标记学习(Multi-label Learning, MLL)是目前常用于数据标注的机器学习模型^[1],二者都关注标记是否描述实例,当数据语义信息丰富^[1]时MLL更有效 ...

2016

0.0

... Geng^[2]提出标记分布学习(Label Distribution Learning, LDL),解决标记描述实例的程度问题 ...

... 目前常见的标记分布学习算法主要基于如下3种设计策略^[2,13] ...

... 实验表明策略3优于前两种策略^[2],因此基于策略3形成由输出模型、目标函数和优化方法构成的标记分布学习算法设计的泛化框架 ...

0.0

... Geng等^[3,4]提出改进迭代尺度-标记分布学习算法(Improved Iterative Scaling-Learning from Label Distributions, IIS-LLD)、条件概率神经网络(Condi-tional Probability Neural Network, CPNN)、自适应标记分布学习算法(Adaptive Label Distribution Lear-ning, ALDL),解决面部年龄估计问题 ...

... Geng等^[3,4]在解决面部年龄估计问题时给出标记分布学习的形式化定义,认为标记分布是一种类似概率分布的数据结构,与概率分布具有相同的约束条件,可使用条件概率的形式表示描述度,即 ...

2013

0.0

2015

0.0

... Zhou等^[5]提出情绪分布学习(Emotion Distribution Learning, EDL),解决面部表情识别问题 ...

2019

0.0

... Ling等^[6]提出软视频解析算法(Soft Video Parsing, SP),解决软视频解析问题 ...

2017

0.0

... 因此,Xu等^[7]提出批注不完整的标记分布学习算法(LDL with Incomplete Annotation, IncomLDL),假设均匀随机丢失标记分布矩阵的元素,并引入迹范数作为正则化项,利用标记相关性深入学习标记空间的隐藏信息 ...

... 已有的标记分布学习方法大多为监督信息完整的数据设计,然而为实例分配真实的标记分布需要花费大量的人力和时间成本^[7],当数据中存在噪声或异常值时,无法保证标记信息的完整性,且标记间相关性的获取难度增加 ...

2018

0.0

... Jia等^[8]提出利用标记相关性的标记分布学习方法(LDL Method by Exploi-ting the Label Correlation, LDL-LC),引入距离函数计算标记间的全局相关性信息 ...

... LDL-LC^[8]使用度量不同标记间的欧氏距离获取标记间的全局相关信息 ...

... 4)LDL-LC^[8] ...

2018

0.0

... Zheng等^[9]提出局部利用样本相关性的标记分布学习算法(LDL Algorithm by Exploiting Sample Correlations Locally, LDL-SCL),对数据进行聚类,保证类内的实例共享相同的标记相关性信息 ...

... LDL-SCL^[9]使用k-means^[18]对训练数据进行聚类,位于同类内的实例共享相同的标记相关性信息,即标记间的局部相关性信息 ...

... 5)LDL-SCL^[9] ...

2010

0.0

... 因此,本文提出基于低秩表示(Low-Rank Representation, LRR)^[10,11]的标记分布学习算法(LDL Method Based on LRR, LDL-LRR) ...

... 为了提高算法对噪声或异常值的鲁棒性,本文以低秩表示作为基本假设,增强矩阵C各行(列)间的相关性,通过特征空间的基线性表示所有样本信息及其全局关系,将原始数据投影至更低维的线性子空间上,凸显数据的类内相似性和类间差异性^[10,11,21] ...

... 由于l_2,1范数迫使E的列趋于0,因此本文假设异常值是样本特定(Sample-Specific)^[10]的,即只有部分向量受到异常值干扰 ...

2013

0.0

... 因此,本文提出基于低秩表示(Low-Rank Representation, LRR)^[10,11]的标记分布学习算法(LDL Method Based on LRR, LDL-LRR) ...

... Fazel^[23]已经证明矩阵核范数是秩函数在矩阵谱范数意义下单位球上的最佳凸逼近,因此可利用凸核范数近似替代非凸秩函数^[24,25],同时将l_2,0范数松弛为其凸包l_2,1范数^[11],得到如下凸优化问题: ...

... 无异常值干扰的数据集无需对原始数据集进行任何操作,异常值干扰的数据集需要对原始数据集随机加入样本的特定异常值(Sample-Specific Corruption)^[11],具体操作为从原始数据集中随机选取10%的样本,并为其生成随机的标记分布 ...

2020

0.0

李骜, 刘鑫, 陈德运, 等. 基于低秩表示的鲁棒判别特征子空间学习模型. 电子与信息学报, 2020, 42(5): 1223-1230.

(LI

, LIU

, CHEN D

, et al. Robust Discriminative Feature Subspace Learning Based on Low Rank Representation. Journal of Electronics and Information Technology, 2020, 42(5): 1223-1230. )

... LRR充分考虑样本间的相关性信息和子空间结构^[12],保证所有数据在其自表达下构成的系数矩阵的秩最小,并获取数据集的全局相关性信息 ...

2018

0.0

... 目前常见的标记分布学习算法主要基于如下3种设计策略^[2,13] ...

... 策略1是问题转化(Problem Transformation, PT)^[13],即将每个标记分布学习训练样本(x_i,d_i)转化成c个带有权重的单标记学习训练样本(x_i,y_i),权重由标记的描述度 dxiyj给出,经过重采样的训练样本集可使用单标记学习算法处理 ...

... 基于此策略设计的算法有PT-Bayes(PT:Bayes)^[13]和PT-SVM(PT:Support Vector Machine)^[13] ...

... 策略2是算法改造(Algorithm Adaptation, AA)^[13],即将传统的单标记学习算法或多标记学习算法改造成可处理标记分布学习问题的算法 ...

... 基于该策略设计的算法有基于k近邻(k Nearest Neighbor, kNN)改造的AA-kNN^[13]和基于反向传播(Back Propagation, BP)神经网络改造的AA-BP^[13] ...

... 策略3是根据标记分布学习的特点设计专用算法(Specialized Algorithm, SA)^[13] ...

... 标记分布学习算法的输出模型常选取最大熵模型^[14],目标函数常采用Kullback-Leibler(KL)散度^[15]度量真实标记分布与预测标记分布之间的相似性,优化方法各有不同,SA-IIS^[13]、SA-BFGS^[13]分别选取改进迭代尺度算法(Improved Iterative Scaling, IIS)^[16]和BFGS^[17]优化目标函数 ...

... 2 标记分布学习算法基于低秩表示的标记分布学习算法(LDL-LRR)符合专用算法^[13]的设计策略,由输出模型、目标函数和优化方法构成 ...

... 1)基于问题转化策略设计的PT-Bayes^[13]和PT-SVM^[13] ...

... 2)基于算法改造策略设计的AA-kNN^[13,31]和AA-BP^[13] ...

... 3)专用算法SA-IIS^[13]和SA-BFGS^[13] ...

1996

0.0

2015

0.0

1997

0.0

2006

0.0

... 本文选取拟牛顿法L-BFGS(Limited-BFGS)^[17] 求解目标函数M(#cod#x003b8 ...

2002

0.0

... LDL-SCL^[9]使用k-means^[18]对训练数据进行聚类,位于同类内的实例共享相同的标记相关性信息,即标记间的局部相关性信息 ...

... 通过核范数近似获取全局相关性信息,通过k-means聚类^[18]获取局部相关性信息 ...

2019

0.0

... 基于低秩近似的标记相关性标记分布学习(LDL with Label Correlations via Low-Rank Approximation, LDL-LCLR)^[19]通过核范数近似获取全局相关性,通过k-means聚类获取局部相关性,并通过交替方向乘子法(Alternating Direction Method of Multi-pliers, ADMM)求解目标函数 ...

... 6)LDL-LCLR^[19] ...

2015

0.0

王卫卫, 李小平, 冯象初, 等. 稀疏子空间聚类综述. 自动化学报, 2015, 41(8): 1373-1384.

(WANG W

, LI X

, FENG X

, et al. A Survey on Sparse Subspace Clustering. Acta Automatica Sinica, 2015, 41(8): 1373-1384. )

Sparse subspace clustering (SSC) is a newly developed spectral clustering-based framework for data clustering. High-dimensional data usually lie in a union of several low-dimensional subspaces, which allows sparse representation of high-dimensional data with an appropriate dictionary. Sparse subspace clustering methods pursue a sparse representation of high-dimensional data and use it to build the affinity matrix. The subspace clustering result of the data is finally obtained by means of spectral clustering. The key to sparse subspace clustering is to design a good representation model which can reveal the real subspace structure of high-dimensional data. More importantly, the obtained representation coefficient and the affinity matrix are more beneficial to accurate subspace clustering. Sparse subspace clustering has been successfully applied to different research fields, including machine learning, computer vision, image processing, system identification and others, but there is still a vast space to develop. In this paper, the fundamental models, algorithms and applications of sparse subspace clustering are reviewed in detail. Limitations existing in available methods are analyzed. Problems for further research on sparse subspace clustering are discussed.

School of Mathematics and Statistics, Xidian University, Xi'an 710126

稀疏子空间聚类(Sparse subspace clustering, SSC)是一种基于谱聚类的数据聚类框架. 高维数据通常分布于若干个低维子空间的并上, 因此高维数据在适当字典下的表示具有稀疏性. 稀疏子空间聚类利用高维数据的稀疏表示系数构造相似度矩阵, 然后利用谱聚类方法得到数据的子空间聚类结果. 其核心是设计能够揭示高维数据真实子空间结构的表示模型, 使得到的表示系数及由此构造的相似度矩阵有助于精确的子空间聚类. 稀疏子空间聚类在机器学习、计算机视觉、图像处理和模式识别等领域已经得到了广泛的研究和应用, 但仍有很大的发展空间. 本文对已有稀疏子空间聚类方法的模型、算法和应用等方面进行详细阐述, 并分析存在的不足, 指出进一步研究的方向.

... 式(2)使用数据集本身表示数据,称为数据的自表达(Self-representation)^[20] ...

2020

0.0

2020

0.0

... 由于秩函数的离散性,式(4)得到的低秩优化问题是一个非凸的NP-hard问题^[22] ...

2020

0.0

2009

0.0

2013

0.0

史加荣, 郑秀云, 魏宗田, 等. 低秩矩阵恢复算法综述. 计算机应用研究, 2013, 30(6): 1601-1605.

(SHI J

, ZHENG X

, WEI Z

, et al. Survey on Algorithms of Low-Rank Matrix Recovery. Application Research of Computers, 2013, 30(6): 1601-1605. )

... 解决凸优化问题的方法有牛顿法、最速下降法和增广拉格朗日乘子法^[26,27]等,本文采用增广拉格朗日乘子法 ...

1982

0.0

... 解决凸优化问题的方法有牛顿法、最速下降法和增广拉格朗日乘子法^[26,27]等,本文采用增广拉格朗日乘子法 ...

2010

0.0

... 的梯度上升进行更新^[28,29]: ...

2020

0.0

张茁涵, 曹容玮, 李晨, 等. 隐式低秩稀疏表示的多视角子空间聚类. 模式识别与人工智能, 2020, 33(4): 344-352.

(ZHANG Z

, CAO R

, LI

, et al. Latent Low-Rank Sparse Multi-view Subspace Clustering. Pattern Recognition and Artificial Intelligence, 2020, 33(4): 344-352. )

... 的梯度上升进行更新^[28,29]: ...

2017

0.0

... )之间的相似性,常用的度量函数有欧氏距离、Jeffrey分歧、KL散度等^[30] ...

2017

0.0

赵权, 耿新. 标记分布学习中目标函数的选择. 计算机科学与探索, 2017, 11(5): 708-719.

(ZHAO

, GENG

. Selection of Target Function in Label Distribution Learning. Journal of Frontiers of Computer Science and Technology, 2017, 11(5): 708-719. )

... 多个对比实验^[31]表明KL散度的表现最稳定,即 ...

... 2)基于算法改造策略设计的AA-kNN^[13,31]和AA-BP^[13] ...

2005

0.0

... 此外,根据平滑假设^[32],可将从特征空间得到的低秩特性迁移到标记空间,使标记空间获得相似的低秩结构 ...

1998

0.0

... 1 实验数据集选取10个现实世界数据集,前8个数据集为Yeast系列数据集,数据来自基于出芽的酿酒酵母进行的生物学实验^[33],共计2 465个酵母基因实例 ...

1998

0.0

... 最后2个数据集是基于面部表情数据集JAFFE^[34]和BU-3DFE^[35]改造的标记分布数据集SJAFFE和SBU-3DFE,各包含213幅和2 500幅具有243维特征的灰度图像,每幅图像分别由60人和23人在6个基本情绪标记(快乐、悲伤、惊讶、恐惧、愤怒和厌恶)上进行5级评分,情绪强度由每种情绪的平均得分定义,归一化后得到情绪标记对图像样本的描述度 ...

2006

0.0