基于对抗图卷积网络的链接预测模型

引用本文

唐晨, 赵杰煜, 叶绪伦, 俞书世. 基于对抗图卷积网络的链接预测模型. 模式识别与人工智能, ,34(2): 95-105
TANG Chen, ZHAO Jieyu, YE Xulun, YU Shushi. Link Prediction Model Based on Adversarial Graph Convolutional Network. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, ,34(2): 95-105. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202102001
Permissions

《模式识别与人工智能》编辑部所有

基于对抗图卷积网络的链接预测模型

唐晨¹, 赵杰煜¹, 叶绪伦¹, 俞书世¹

1.宁波大学信息科学与工程学院宁波 315211

通信作者：

赵杰煜,博士,教授,主要研究方向为计算智能、模式识别、自然人机交互.E-mail:zhao_jieyu@nbu.edu.cn.

作者简介：

唐晨,硕士研究生,主要研究方向为图神经网络、模式识别.E-mail:952304255@qq.com.

叶绪伦,博士,讲师,主要研究方向为贝叶斯学习、凸优化.E-mail:yexulun@nbu.edu.cn.

俞书世,硕士研究生,主要研究方向为生成对抗网络、模式识别.E-mail:406258696@qq.com.

收稿日期: 2020-09-27 接受日期: 2021-02-02

资助项目: 国家自然科学基金项目(No.62071260,62006131)资助

摘要

大部分的链接预测模型在挖掘节点相似性时过于依赖已知的链接信息,但在真实世界中,已知的观测链接数量通常较少.因此,为了提高模型的鲁棒性,需要提高解耦模型对链接信息的依赖并挖掘节点的潜在特征.文中考虑节点特征和链接之间的潜在关系,提出基于对抗图卷积网络的链接预测模型.首先利用节点间的相似性度量填充邻接矩阵中部分未知链接,缓解链接稀疏对图卷积模型的影响.再利用对抗网络深度挖掘节点特征和链接之间的潜在联系,降低模型对链接的依赖.在真实数据集上的实验表明,文中模型在链接预测问题上具有较好的表现力,在链接稀疏的情况下性能依旧较稳定,同时适用于大规模数据集.

关键词: 链接预测; 对抗网络; 图卷积网络; 隐空间

中图分类号:TP 391

Link Prediction Model Based on Adversarial Graph Convolutional Network

TANG Chen¹, ZHAO Jieyu¹, YE Xulun¹, YU Shushi¹

1.Faculty of Electrical Engineering and Computer Science, Ning-bo University, Ningbo 315000

Corresponding author:
ZHAO Jieyu, Ph.D., professor. His research interests include computational intelligence, pattern recognition and natural human-computer interaction.

AboutAuthor:
TANG Chen, master student. His research interests include graph neural network and pattern recognition.
YE Xulun, Ph.D., lecturer. His research interests include Bayesian learning and convex optimization.
YU Shushi, master student. Her research interests include generative adversarial networks and pattern recognition

Fund:Supported by National Natural Science Foundation of China(No.62071260,62006131)

Abstract

Most link prediction models rely too much on the known link information while mining node similarity. However, the number of the known observed links is small in the real world. To improve the robustness of the model, it is crucial to decouple the dependence of the model on the link information and mine the underlying features of nodes. In this paper, a link prediction model based on adversarial graph convolutional network is proposed with the consideration of the potential relationship between node features and links. Firstly, the similarity metric between nodes is utilized to fill in some unknown links in the adjacency matrix to alleviate the influence of link sparsity on the graph convolution model. Then, the adversarial network is employed to deeply mine the underlying connections between node features and links to reduce the dependence of the model on links. Experiments on real datasets show that the proposed model achieves better performance on link prediction problem and the performance remains relatively stable under link sparsity. Moreover, the proposed model is applicable to large-scale datasets.

Key words: Key Words Link Prediction; Adversarial Network; Graph Convolutional Network; Hidden Space

文章图片

本文责任编委吴飞

Recommended by Associate Editor WU Fei

链接预测旨在利用已观测到的链接预测潜在或暂未被观测到的链接.链接预测广泛应用于不同领域.例如:在生物学领域, 链接预测可分析蛋白质之间的相互作用^[1], 研究破坏病毒结构的方法; 在互联网领域, 链接预测为用户推荐可能感兴趣的人^[2]或为用户推荐可能感兴趣的商品等^[3]; 在生活领域, 链接预测可用于网约车的订单预测^[4]、交通的流量预测等^[5], 为人们的出行提供便利.

传统的链接预测模型大都利用图论的相关知识挖掘潜在特征, 这类方法可分为3类:基于相似性的方法、基于矩阵分解的方法、基于机器学习的方法.基于相似性的方法需要先定义相似度, 较经典的有共同邻居(Common Neighbor, CN)相似度^[6]、Jaccard相似度^[7]和SimRank相似度^[8]等.基于矩阵分解的方法将链接预测问题视为矩阵变换问题, 提取并利用潜在特征完成预测任务^{[9, 10]}.基于机器学习的方法将链接预测视为分类问题, 例如:Guimerà 等^[11]将图中的节点进行分组, 以节点分组的归属决定链接是否存在; de Sá 等^[12]利用链接的权重和支持向量机训练分类模型.传统方法虽然运算效率较高, 但无法获取深层次的特征.

近年来, 图神经网络(Graph Neural Network, GNN) 被广泛应用于潜在特征挖掘上, 尤其是图卷积网络(Graph Convolutional Network, GCN)^[13]的提出, 为解决节点分类、链接预测、图生成等热点问题提供思路.Schlichtkrull等^[14]在自编码器、DistMult^[15]的基础上, 利用参数共享和稀疏约束技术, 提出关系图卷积网络(Relational Graph Convolutional Net-works, R-GCN).为了避免平等地对待邻域中的不同节点, Shang等^[16]在R-GCN的基础上引入加权GCN, 定义具有相同关系类型的两个相邻节点之间的相关性, 提出结构感知卷积网络(Structure-Aware Convolutional Network, SACN).Li等^[17]利用节点和对应的邻域构建子图, 设计图到序列的信息融合机制(Graph to Sequence Generator, Graph2Seq), 学习图中的节点表示.Kipf等^[18]假设每个节点在隐空间中符合高斯分布, 提出图变分自编码器模型(Varia-tional Graph Autoencoder, VGAE).Pan等^[19]利用生成对抗网络(Generative Adversarial Networks, GAN)^[20]约束节点在隐空间的分布, 进一步提出基于对抗规范的图变分自编码器(Adversarially Regularized VGAE, ARVGAE).

然而, 目前基于GNN的链接预测模型依旧存在2个局限性.1)大部分模型要求图的链接数量足够多, 即观测的链接数量至少占50%^[21], 但是在现实世界中, 通常无法满足这个先验条件, 传统方法难以奏效, 因此, 如何充分挖掘稀疏图的潜在信息就显得尤为重要.GCN被证明在提取特征方面的有效性, 但却很难处理稀疏图的情况.GCN的一个关键步骤是特征聚合, 如果链接缺失严重, 邻域信息挖掘不够充分, 都会影响GCN提取特征的能力.2)深度学习模型虽然在挖掘深层次特征方面效果优于传统方法, 但是目前大部分基于深度学习的链接预测模型忽略图的整体性.未观测链接通常以空链接(两个节点不存在关联)的形式输入模型中, 影响训练数据和测试数据的分布, 学到的模型也会有所偏差.

图卷积按照卷积方式的不同分为基于谱域的图卷积和基于空间域的图卷积.基于谱域的图卷积主要依靠傅里叶变换^{[22, 23]}.基于空间域的图卷积主要考虑邻域的选择, 故衍生出很多特殊的处理方法.Niepert等^[24]对节点邻居先排序再选取.Hamil-ton等^[25]对邻居节点进行随机采样.Chen等^[26]在全局范围内挑选邻域.Chen等^[27]利用控制变量的方法采样任意大小的邻域.Veli $\overset{ˇ}{c}$ kovic等^[28]将注意力机制应用到图上.两种类型的图卷积都能充分利用结构信息和属性信息, 因此, 将图卷积应用在链接预测问题上是直观做法.

自GoodFellow等^[20]提出GAN后, 产生很多经典的变体和应用, 如可生成指定标签图像的条件生成对抗网络(Conditional GAN, CGAN)^[29]、可生成高分辨率图像的深度卷积生成对抗网络(Deep Convolutional GAN, DCGAN)^[30]、可生成多样性图像的Wassertein生成对抗网络(Wassertein GAN, WGAN)^[31]等.鉴于GAN强大的生成能力, 本文设计对抗网络以生成属性和结构之间的内在联系.

本文提出基于对抗图卷积网络的链接预测模型(Link Prediction Model Based on Adversarial Graph Convolution Network, LPAGC).利用传统度量填充邻接矩阵, 送入GCN中以提取潜在特征.采取自编码器作为模型的主体框架, 通过对抗博弈的思想设计等变网络, 建立链接和原始节点特征之间的联系, 将链接的增益效果蕴含到模型参数中.具体来说, LPAGC先利用观测图的链接信息和原始的节点特征将节点映射至隐空间.再去除观测图的链接信息, 仅利用原始节点特征将节点映射至与前者相同的隐空间, 据此得到同个节点两种状态下的特征表示.然后设计判别器判别潜在特征在生成时是否有链接信息的存在.最后通过无链接信息的预测结果逼近有链接信息的预测结果, 解耦链接信息对节点潜在特征的影响.

1 基于对抗图卷积的链接预测模型

1.1 基本定义

完整的无向图可表示成G={X, V, E}, 其中, V为点集, X∈ R^N^×^F为节点的原始特征矩阵, E为边集.使用|V|表示节点的数量, |E|表示链接的数量.真实世界中的图通常并不是以完整的形式呈现, 而是部分被观测的.本文假设已知观测图的所有节点(即X、V), 但是链接E缺失, 因此, 图形式上表示为G_O={X, V, E_O}, E_O∈ E,

链接预测问题是在已知G_O的情况下, 预测G_P={X, V, E_P}, 其中E_P=E-E_O.为了处理问题方便, 通常使用邻接矩阵A代替E_O, A=[a_ij]∈ R^N^×^N.如果v_i∈ V, v_j∈ V并且(v_i, v_j)∈ E_O, a_ij=1; 否则, a_ij=0.

1.2 模型整体框架

LPAGC的整体结构如图1所示.上半部分为标准的自编码器网络, 先利用原始特征矩阵X和原始邻接矩阵A构造新的邻接矩阵 $\overset{︿}{A}$ , 将 $\overset{︿}{A}$ 和X作为编码器(GCN)的输入.本文设计2个编码器, 分别学习高斯分布的期望μ 和方差σ ².从标准高斯分布N(0, 1)中采样, 利用学习的期望和方差, 得到新的节点表示Z, 再通过解码器重构链接信息.下半部分分为2个模块:负样本构造和对抗网络设计(判别器).负样本构造分两步:首先利用编码器仅将原始特征X作为输入, 学习负样本的高斯分布参数μ '和σ '², 再采用与上述相同的采样方式获取负样本的节点表示Z'.判别器通过区分在获取负样本Z'和正样本Z的过程中链接信息是否参与, 达到间接约束编码器的目的, 降低链接信息对模型的耦合性.

	Figure Option View Download New Window
	图1 本文模型整体框图Fig.1 Framework of the proposed model

1.2.1 改进的图卷积神经网络

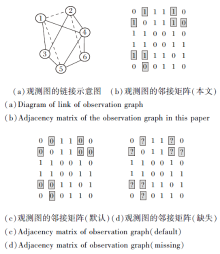
将原始GCN应用在链接预测任务上存在一个明显的问题, 如图2所示, (a)中虚线表示未观测的链接, 实线表示已观测的链接, 观测图邻接矩阵最准确的表现形式应是(d)所示, 但是当前大部分链接预测模型是将邻接矩阵视为(c)中的形式, 这限制GCN的特征提取能力.进一步观察图2可发现, (a)中节点1、2有共同的邻居, 可认为1、2结构相似, 两者之间很可能存在链接.同理, 节点1、5之间也能得出相似的结论.受此启发, 本文先利用节点浅层特征的相似性衡量链接存在的可能性, 然后选取置信度较高的链接去填充原始的邻接矩阵(如图2(b)), 最后将相对稠密的邻接矩阵输入GCN中提取潜在特征.显然, 上述操作可能会产生少量的虚假链接, 本文通过计算多个度量标准(如余弦相似度、共同邻居)的得分, 综合考虑后再进行邻接矩阵的填充, 降低虚假链接出现的概率.

	Figure Option View Download New Window
	图2 邻接矩阵的区别Fig.2 Difference of adjacency matrix

图2(b)中邻居信息显然比(c)中邻居信息更充分, 因此本文以原始特征矩阵X∈ R^N^×^F和原始邻接矩阵A作为启发式信息, 结合显式函数填充部分缺失值, 最终得到用于填充的矩阵:

A'=r(A, X)=σ (X^TX)∩ CN(A)∈ R^N^×^N,

其中, r表示一个函数或一个神经网络, 用于获取链接的可能得分, 本文直接以函数的形式给出.A'_ij为综合考虑节点之间余弦相似度、共同邻居的结果, 得分越高的节点越有可能存在链接.此时, 新邻接矩阵

$\overset{︿}{A}$ =norm(A'+A),

其中norm表示对矩阵进行归一化.从编码器看, $\overset{︿}{A}$ 比A更稠密, 提供的信息更充分, 更易于模型的学习.从解码器上看, 使用原始邻接矩阵A作为构建损失函数的依据能保证模型的鲁棒性.

1.2.2 自编码器网络

本文以自编码器模型作为基本的链接预测框架.对于给定的图G_O, 从概率角度出发, 学习编码模型q_ϕ, 在假设每个节点在隐空间符合标准高斯分布的前提下, 将节点在隐空间的潜在特征Z定义为:

q_ϕ(Z|X, $\overset{︿}{A}$ )= $\overset{| V |}{\prod_{i = 1}}$ q_ϕ(z_i|X, $\overset{︿}{A}$ ), q_ϕ(z_i|, X, $\overset{︿}{A}$ )=N(z_i|μ _i,diag( $σ_{i}^{2}$ )),

其中, Z∈ R^N^×^d, z_i表示节点i在隐空间的潜在特征, μ _i、 $σ_{i}^{2}$ 表示节点i满足的高斯分布的均值和方差.高斯分布的参数可通过GCN学习得到:

μ =GCN_μ( $\overset{︿}{A}$ , X)=RELU( $\overset{︿}{A}$ · RELU( $\overset{︿}{A}$ X $W_{μ}^{(0)}$ ) $W_{μ}^{(1)}$ ),

log₂σ ²=GCN_σ( $\overset{︿}{A}$ , X)=RELU( $\overset{︿}{A}$ · RELU( $\overset{︿}{A}$ X $W_{σ}^{(0)}$ ) $W_{σ}^{(1)}$ ), (1)

其中, $W_{μ}^{(*)}$ 和 $W_{σ}^{(*)}$ 表示神经网络层(* )需要学习的参数,

RELU(· )=max(0, · )

表示激活函数.若隐空间中每个节点潜在特征满足的分布已知, 通过采样可得到对应的样本.根据已知样本, 可构建链接的解码模型:

p_θ(A|Z)= $\overset{N}{\prod_{i = 1}} \overset{N}{\prod_{j = 1}}$ p_θ( ${\tilde{A}}_{ij}$ |z_i, z_j),

其中

p_θ( ${\tilde{A}}_{ij}$ |z_i, z_j)=σ ( ${z^{T}}_{i}$ z_j).

上述自编码器可通过减小其变分下界L_r来优化GCN的参数:

L_r(φ , θ )= $E_{q_{θ} (Z | X, A)}$ [log₂p_θ( $\tilde{A}$ |Z)]-KL[q_θ(Z|X, A)‖ p_θ(Z)]=

$E_{q_{θ} (Z | X, A)}$ [log₂p_θ( $\tilde{A}$ |Z)]-KL(N(μ , log₂σ ₂)‖ N(0, I))=

- $\sum_{(i, j) \in E^{t}}$ [A_ijlog₂p_θ( ${\tilde{A}}_{ij}$ |Z)-(1-A_ij)log₂(1-p_θ( ${\tilde{A}}_{ij}$ |Z))]- $\frac{1}{2} \overset{d}{\sum_{i}} \overset{N}{\sum_{j}}$ ( $μ_{ji}^{2}$ + $σ_{ji}^{2}$ -log₂ $σ_{ji}^{2}$ -1), (2)

其中, φ 表示编码器的网络参数, θ 表示解码器的网络参数, KL[· ‖ · ]表示KL散度, E^t表示用于训练的链接, d表示潜在特征的维度, μ _ji、 $σ_{ji}^{2}$ 表示节点i学习得到的分布均值和分布方差的第j个分量.

1.2.3 等变网络

目前大部分用于链接预测的自编码器模型还存在一个问题, 如图3所示.

已知节点i、 j之间存在被观测到的链接e_ij, 在GCN将i、 j映射到隐空间得到z_i、 z_j的过程中利用e_ij这个链接信息, 然后自编码器的解码部分通过聚合z_i、 z_j重构e_ij, 这确实符合自编码器逻辑.但是在未观测到链接e_jk的情况下, j、k在映射过程中并未利用e_jk这个链接信息, 所以按照上述方法训练, 自编码器很大程度上是无法重构链接.既然所有的节点都参与训练, 那么所有的链接应该满足同个分布, 将未观测的链接统一视为空链接, 这会引导模型向错误的方向学习, 并不合理.

以此为动机, 本文引入迁移学习的思想, 利用对抗学习的策略, 在自编码器的基础上, 设计等变网络, 在保证性能的情况下减小链接信息对模型的影响, 让模型在观测链接稀疏的情况下仍保持稳定性.迁移学习是将从源域上学到的知识迁移到目标域上, 本文把观测图G_O和未观测图G_P中的链接看成是2个分布D_A(源域)、D_I(目标域), 将从G_O上学到的知识迁移到G_P上, 使模型从不同局部(子图)上学到的知识保持一致性.

	Figure Option View Download New Window
	图3 节点在隐空间的分布差异Fig.3 Distribution difference of nodes in hidden space

等变网络的实现依靠负样本的构建和对抗网络的设计.负样本是在观测图的基础上经过适当的变换获得, 本文直接去除链接信息, 利用节点原始特征独自编码, 得到相应的负样本.而正样本是在保留链接信息的情况下, 利用GCN让节点和邻居节点的原始特征共同完成编码.对抗网络的判别器采用全连接网络.

1.3 理论分析

本文希望在编码过程中尽量减少信息的损失, 所以下面从互信息熵的角度分析, 证明新邻接矩阵的设计确实可提高潜在特征和原始特征的互信息熵下界.

互信息熵是一个随机变量中包含另一个随机变量的信息量, 它是一个对称的度量.编码器可看成是一个单映射的过程, 即

f:{X^k|X^k∈ R^N^×^F} $_{k = 1}^{| X |} | \to {Z^{m} | Z^{m} \in R^{N \times d}}_{m = 1}^{| Z |}$ ,

其中, {X^k|X^k∈ R^N^×^F $}_{k = 1}^{| X |}$ 为原始特征的有限集合, {Z^m|Z^m∈ R^N^×^d $}_{m = 1}^{| Z |}$ 为潜在特征的有限集合, |X|、|Z|表示集合的元素个数, |Z|≪|X|.对于每个m=1, 2, …, |Z|, 存在集合

δ ^m={X^k|f(X^k)=Z^m},

所以在给定m的情况下, 有

p(Z^m)p(X^k)=p(Z^m) $\overset{| X |}{\sum_{i = 1}}$ p(Z^m)p(Xⁱ|Z^m)=p(Z^m)p(X^k, Z^m)=p(Z^m)² $\frac{p (X^{k})}{\sum_{X' \in δ^{m}} p (X')}$ .

现假设X符合均匀分布, 对于∀ m=1, 2, …, |Z|, ∀ m'=1, 2, …, |Z|, 满足|δ ^m|=|δ ^m'|, 则X和Z的互信息熵为

MI(X, Z)= $\overset{| Z |}{\sum_{i}} \overset{| X |}{\sum_{j}}$ p(X^j, Zⁱ)log₂( $\frac{p (X^{j}, Z^{i})}{p (X^{j}) p (Z^{i})}$ )=

$\overset{| Z |}{\sum_{i}} \overset{| δ^{i} |}{\sum_{j}}$ p(X^j, Zⁱ)log₂( $\frac{p (X^{j}, Z^{i})}{p (X^{j}) p (Z^{i})}$ )=

$\overset{| Z |}{\sum_{i}} \overset{| δ^{i} |}{\sum_{j}}$ p(X^j)log₂( $\frac{1}{p (Z^{i})}$ )=

- $\frac{| X |}{| Z | | X |}$ log₂( $\overset{| Z |}{\prod_{i}}$ p(Zⁱ))≥ log₂|Z|.

所以只要函数r设计得足够复杂, 就能使|Z'|> |Z|, 这就相当于提高互信息熵的下界, 让潜在特征更好地保留原始特征的重要成分.

下面从误差的角度分析, 证明对抗网络的设计确实有助于缩小分类的误差上界.

节点i、 j的链接在映射之前可表示成

l_ij=aggr'(x_i, x_j),

在隐空间可表示成

e_ij=aggr(z_i, z_j),

其中, aggr'(· , · )、aggr(· , · )表示聚合函数, 可以是简单的拼接、相加、相乘, 也可以是复杂的神经网络.从e_ij到链接的映射函数在形式上可表示为

$\tilde{g}$ (e_ij)= $E_{l_{ij} ~ {\tilde{D}}_{A}}$ [(l_ij)|f(x_i, $\overset{︿}{A}$ )=z_i, f(x_j, $\overset{︿}{A}$ )=z_j]

其中, ${\tilde{D}}_{A}$ 表示链接在原始空间(映射之前)中的分布, g表示真实的标签函数, g(· )=1表示链接存在, 反之不存在, f表示将节点映射到隐空间的函数(编码器).将链接预测视为二分类问题, 需要在隐空间之后再设计一个分类函数h, 判断e_ij是1还是0.形式上可将分类损失(重构损失)定义为

$ξ_{D_{A}}$ = $E_{e_{ij} ~ D_{A}}$ [| $\tilde{g}$ (e_ij)-h(e_ij)|].

图从无链接发展为有链接存在一个演变过程, 此过程和节点的原始特征关联紧密.为了建立有链接和无链接之间的差异, 本文构造节点的另一种状态:去除图的链接信息但是保持节点原始特征信息不变, 再将节点映射到与上述相同的隐空间, 学习每个节点对应的分布的均值μ '和方差σ '²:

μ '=GCN_{μ '}(I, X)=

RELU(RELU(X $W_{μ'}^{(0)}$ ) $W_{μ'}^{(1)}$ , log₂(σ '²)=GCN_σ_'(I, X)=

RELU(RELU( ${X W}_{σ'}^{(0)}$ ) $W_{σ'}^{(1)}$ ). (3)

在已知高斯分布参数(式(1)和式(3)所示)的条件下, 采样得到隐空间正负样本节点的潜在特征表示.潜在节点特征有如下两点作用:1)经过解码器重构邻接矩阵, 2)构造链接的表示(e_ij=aggr(z_i, z_j)和e'_ij=aggr(z'_i, z'_j)).本文构造一个等变的神经网络f, 以e_ij作为基准, 缩小e_ij和e'_ij在模型表现能力上的差距, 让模型在链接缺失的情况下也能有效学习.假设{e_ij}和{e'_ij}在隐空间满足概率分布D_A和D_I, 上述观点从概率论的角度分析, 目的是让D_I向D_A逼近.为了量化两个分布之间的差异, 本文将D_A和D_I之间的HΔ H距离^[32]定义为d_{HΔ H}(D_A, D_I), 形式如下:

d_{HΔ H}(D_A, D_I)=2 $\underset{h_{2} \in F}{\sup_{h_{1} \in F}}$ | $P_{D_{A}}$ (ε ^*)- $P_{D_{I}}$ (ε ^*)|=

2 $\sup_{η \in HΔH}$ | $P_{D_{A}}$ {ε * :η (ε * )=1}- $P_{D_{I}}$ {ε * :η (ε * )=1}|≤

2 $\sup_{η \in H_{d}}$ | $P_{D_{A}}$ {ε * :η (ε * )=1}- $P_{D_{I}}$ {ε * :η (ε * )=1}|=

2 $\sup_{η \in H_{d}}$ | $P_{D_{A}}$ {ε * :η (ε * )=1}+ $P_{D_{I}}$ {ε * :η (ε * )=0}-1|,

ε * ={e_ij:h₁(e_ij)≠ h₂(e_i_j), (x_i, x_j)∈ E_O, h₁∈ F, h₂∈ F}_.(4)

其中, F为二值函数的集合, η 为二值函数,

HΔ H={η :η (ε ^*)=1},

H_d为比HΔ H更复杂的函数集合.可以将

α (η )= $P_{D_{A}}$ {ε ^*:η (ε ^*)=1}+ $P_{D_{I}}$ {ε * :η (ε * )=0}

看成是求解最优判别器的问题, 因此为了得到d_{HΔ H}(D_A, D_I)上界, 需要找到合适的函数η , 使符合D_A分布的链接都被判断为1, 符合D_I分布的链接都被判断为0.此外, 令

Z_h={ε :h(ε )=1}

表示被分类器h判定为1的潜在链接特征, 理想情况下的分类器应该满足

h^*=arg $\min_{h}$ ( $ξ_{D_{A}}$ (h)+ $ξ_{D_{I}}$ (h)), (5)

可预先定义一般分类器h和最优分类器h^*之间的距离:

$P_{D_{I}}$ [Z_h⊕ $Z_{h^{*}}$ ]= $P_{D_{I}}$ [{ε :h(ε )=1}⊕{ε :h* (ε )=1}], (6)

其中Z_h⊕ $Z_{h^{*}}$ 表示h和h^*意见不一致的链接的集合.据此可得到无链接情况下的链接预测误差上界:

$ξ_{D_{I}}$ (h)≤ $λ_{D_{I}}$ + $P_{D_{I}}$ [Z_h⊕ $Z_{h^{*}}$ ], (7)

其中 $λ_{D_{I}}$ 表示最优分类器下的分类误差, 即 $ξ_{D_{I}}$ (h^*).联合式(4), 对式(5)右边部分进行缩放, 可得

$λ_{D_{I}}$ + $P_{D_{I}}$ [Z_h⊕ $Z_{h^{*}}$ ]≤ $λ_{D_{I}}$ + $P_{D_{A}}$ [Z_h⊕ $Z_{h^{*}}$ ]+| $P_{D_{A}}$ [Z_h⊕ $Z_{h^{*}}$ ]- $P_{D_{I}}$ [Z_h⊕ $Z_{h^{*}}$ ]|, (8)

如果h和h^*意见不同, 至少有一个分类器是错误的, 所以有

$P_{D_{A}}$ [Z_h⊕ $Z_{h^{*}}$ ]≤ $ξ_{D_{A}}$ (h)+ $λ_{D_{A}}$ .(9)

利用式(5)~式(9), 得到最终误差上界:

$ξ_{D_{I}}$ (h)≤ $ξ_{D_{A}}$ (h)+ $\frac{1}{2}$ d_{HΔ H}(D_A, D_I)+ $λ_{D_{I}}$ + $λ_{D_{A}}$ .

本文根据编码过程中是否利用链接信息, 使用D_A、D_I表示这两种情况下潜在特征的概率分布, 进而分析对抗网络对缩小误差上界的作用.从推导结果上看, 若要减小链接信息对模型的影响, 需要降低分类函数h在D_A上的错误率及D_A、D_I两个概率分布之间的距离(即让判别器最终无法分辨), 所以不仅需要优化重构损失L_r, 还需要优化对抗损失L_d:

L_d(φ , ϕ )= $\frac{1}{2 | E^{t} |}$ [ $\overset{| E^{t} |}{\sum_{k}}$ y_klog₂( ${\hat{y}}_{k}$ )+(1-y_k)log₂(1- ${\hat{y}}_{k}$ )], (10)

e_ij=concat(z_i, z_j), e'_ij=concat(z'_i, z'_j),

E^t={e_ij|(i, j)∈ E_O}∪ {e'_ij|(i, j)∈ E_O},

y_k= $\{\begin{array}{l} 1, & E_{k}^{t} \in {e_{ij} | (i, j) \in E_{O}} \\ 0, & E_{k}^{t} \in {{e'}_{ij} | (i, j) \in E_{O}} \end{array}$

其中, φ 表示编码器的模型参数, ϕ 表示判别器的模型参数, e_ij、e'_ij表示两种状态下链接的潜在特征表示, y_k表示训练集E^t中第k个元素的标签, $E_{k}^{t}$ 表示E^t中第k个元素.在训练过程中, 存在一个博弈的过程, 即希望学到的潜在特征不仅能使重构损失最小化, 还能混淆判别器, 使判别器损失最大化.这是一个互相对抗、互相促进的过程, 具体表示如下:

L(φ , θ , ϕ )= $\min_{φ, θ} \max_{ϕ}$ L_r(φ , θ )-λ L_d(φ , ϕ ),

其中, L_r如式(2)所示, L_d如式(10)所示, λ 表示一个权衡因子, 平衡在迭代过程中约束损失函数的作用.

1.4 时间复杂度和可扩展性分析

LPAGC的时间开销主要在编码器、解码器、判别器, 将它们占用的时间分别定义为T_e、T_dc和T_d, 总的时间定义为T.

在中等规模的数据集上, 编码器采用2个两层的GCN, 解码器采用内积计算, 判别器利用两层全连接, 因此, 不同的时间复杂度可表示如下:

T_e=O(2[(NFhid₁+‖ A‖ ₀F)+

(N· hid₁· hid₂+‖ A‖ ₀hid₁)]),

T_d_c=O(N²hid₂),

T_d=O(2N· hid₂· hid₃+N· hid₃· hid₄),

其中, ‖ A‖ ₀表示邻接矩阵非零的个数, N表示节点个数, F表示输入的特征维度, hid₁、hid₂表示编码器隐含层神经元个数, hid₃、hid₄表示判别器隐含层神经元个数.

在大规模数据集上, 解码器和判别器相同, 编码器采用2个两层的GraphSAGE^[25], 此时

T_e=O(Nb^L(F· hid₁+hid₁· hid₂)),

其中, b表示采样个数, L=2表示网络层数.因此时间复杂度为

T=T_e+T_dc+T_d.

编码器是LPAGC能否应用于不同规模数据集的关键因素.目前, 在图数据上, 图卷积的表现能力较优越, 但是, GCN受限于图的节点个数和聚合机制, 网络层数不能太深且无法应用于大规模图.GraphSAGE虽然支持批量训练, 但训练较慢, 采样个数随层数指数增长, 效果和效率都弱于GCN.换而言之, LPAGC的性能和GCN是正相关的, 但是本文并未对GCN面临的挑战做出过多的改进, 如异构图、超大规模图、有向图等问题.

2 实验及结果分析

本节通过实验验证LPAGC的鲁棒性和泛化性.实验主要在中等规模数据集和大规模数据集上展开.中等规模的数据集用于验证LPAGC的性能及改进效果, 大规模数据集主要为了说明LPAGC的泛化性.对于这两种规模的数据集, LPAGC的整体框架并无过多的改动, 只是在中等规模的数据集上采用GCN提取特征, 而在大规模数据集上采用GraphSAGE.

实验环境如下:操作系统为Windows10 64bit, GPU为NVIDIAGeForceRTX2080Ti, CPU为Intel(R) Core(TM) i5-9600K, 频率为3.70 GHz, 硬盘为SamsungSSD860EVO 500 GB, 存储器为32 GB DDR4, 编程语言及环境为Python3.6+Pytorch1.0.

2.1 中等规模数据集上的实验

本文采用3个真实的引文数据集^[33]:Cora、Citeseer、Pubmed.Cora数据集是由2 708篇机器学习领域相关的论文组成, 一篇论文至少引用或被引用于另外一篇论文, 每篇论文的特征使用1 433个单词表示, One-hot编码.Citeseer数据集是由3 327篇机器学习领域相关的论文组成, 保留论文间引用和被引用的关系, 每篇论文的特征使用3 703个单词表示.Pumed数据集由19 717篇生物医学领域相关的论文组成, 保留论文之间的引用和被引用关系, 每篇论文使用500个单词表示.论文之间的引用和被引用关系均视为无向连接.实验数据集具体情况如表1所示.

表1 中等规模数据集信息 Table 1 Medium-scale datasets information

本文将编码器设计为两层图卷积网络, 各层的维度分别为72和16.解码器通过计算节点潜在特征向量的内积实现.判别器由三层感知层组成, 维度为{32, 32, 2}.本文利用高斯分布N(0, 0.1)初始化网络权重, 以RELU函数作为激活函数, 使用自适应力矩估计(Adaptive Moment Estimation, Adam)作为优化器, 设置学习率为0.001.

此外, 选择平均精确度(Average Precision, AP)和受试者工作特征曲线(Receiver Operating Characteristic Curve, ROC)下的面积(Area Under Curve, AUC)作为模型性能的评价指标.AP表示正样本中被预测为正的概率, 反映分类器对正例的识别准确程度和对正例的覆盖能力之间的权衡.AUC体现排序的概念, 当随机挑选一个正样本和一个负样本时, AUC表示当前的分类模型将正样本排在负样本前面的概率, AP和AUC值越大表示模型的性能越优.

对比的5个链接预测模型如下.

1)深度游走(Deep Walk, DW)^[34].通过截断DW得到一个节点的序列, 再将序列送入skipgram模型中学习节点的表示.

2)谱聚类(Spectral Clustering, SC)^[35].基于图论的知识, 使用最小的权重损失划分子图, 优化指示向量矩阵, 获取节点的潜在特征.

3)自编码(Graph Autoencoder, GAE)^[18].使用图卷积网络代替感知层编码器, 通过降低邻接矩阵的重构损失优化模型性能.

4)变分图编码(VGAE)^[18].GAE变体, 每个节点都符合高斯分布, 通过GCN网络学习高斯分布, 再通过采样的方法获取相同分布的一个节点, 重构邻接矩阵, 根据损失优化网络性能.

5)基于对抗规则的变分图自编码(ARVGAE)^[19].VGAE的扩展, 每个节点都符合高斯分布的假设, 约束节点学习的分布在隐空间确实符合高斯分布, 并用于增强模型的学习能力.

随机从数据集中移除15%的链接, 其中, 10%的链接作为测试集的样本, 5%的链接作为验证集的样本.85%的链接作为训练集的样本.然后从不存在的链接中随机采样相同数量的虚假链接作为负样本.模型训练结束后, 计算得到对应的AUC值和AP值, 各模型在3个数据集上的性能如表2所示.

在表2中, LPAGC_A表示仅采用填充邻接矩阵的方法, LPAGC_B表示仅采用对抗网络的方法, LPAGC表示两种方法均采用.从AUC和AP的结果上看, 原始节点特征和深度学习的方法能使模型更具鲁棒性, 这是因为节点的原始特征和链接存在复杂的关系, 利用深度学习能捕获该层次的信息.其次, 从LPAGC_B和VGAE的数据对比可看出, 对抗网络的设计拉近测试集分布和训练集分布的距离, 实验表明, 本文模型的预测性能具有较大提升.

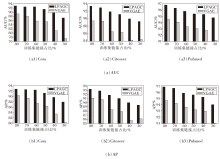
下面设置不同稀疏度的训练样本, 验证本文模型的鲁棒性, 作为对比的模型是同样以自编码器为主的VGAE.分别以80%、70%、60%、50%、40%、30%的链接作为训练集, 其余链接作为测试集, 具体性能对比如图4所示.由图可知, 本文模型在链接数量稀疏的情况下依旧保持较优性能, 模型的表现能力下降趋于平缓, 比VGAE更稳定.

表2 各模型在中等规模数据集上的性能对比 Table 2 Performance comparison of models on medium-scale datasets %

	Figure Option View Download New Window
	图4 各模型在不同稀疏度上的性能对比Fig.4 Performance comparison of models with different sparsity

隐空间的特征维度是影响模型性能的重要超参数, 如图5所示, 在Cora、Citeseer数据集上, 使用0.5(AUC+AP)作为度量, 将隐空间的特征维度分别设为4, 8, 16, 32, 64, 得到对应的度量值.由图可看出, 将隐空间的特征维度设置为16时, 在3个数据集上均取得较优效果.

	Figure Option View Download New Window
	图5 隐空间维度对模型性能的影响Fig.5 Influence of hidden space dimension on model performance

2.2 大规模数据集上的实验

在大规模数据集上进行进一步的实验.数据集采用预处理的Reddit、PPI数据集, 具体信息见表3.对于每个数据集, 移除40%的链接信息并将它们作为测试数据的正样本, 另外采用随机采样的方式选择同等数量的虚假链接作为测试数据的负样本.

表3 大规模数据集信息 Table 3 Large-scale datasets information

编码器采用两层空间图卷积GraphSAGE, 维度分别设为32和16, 解码器通过计算节点潜在特征的内积实现, 对抗网络采用两层全连接网络, 维度分别设为32和2.模型权重初始化采用高斯分布N(0, 0.1), 激活函数采用RELU, 优化器选择SGD(Stochastic Gradient Descent), 迭代次数设为200.

对比模型如下.

1)DW^[34].

2)大规模信息网络嵌入(Large-Scale Informa-tion Network Embedding, LINE)^[37].将节点根据关系的疏密程度映射到向量空间中, 不仅仅只考虑一阶的关系, 即两个点之间直接具有较大权值的边相连就认为它们较相似, 同时考虑二阶关系, 即两个点也许不直接相连, 但是如果它们的一阶公共邻居较多, 那么它们也被认为是较相似的.

3)Weisfeiler-Lehman神经机(Weisfeiler-Lehman Neural Machine, WLNM)^[38].首先对于网络中的每条边, 抽取一个子图(一个边连接的封闭子图), 再将封闭子图进行图编码, 转换为连接矩阵形式, 然后将连接矩阵输入网络, 进行一个边链接预测模型的学习.

各模型在大规模数据集上的性能对比如表4所示.由表可看出, LPAGC在大规模数据集上仍然能媲美其它模型, 但是由于LPAGC在构建子图时未考虑全局信息的损失, 所以提升的幅度不够明显, 甚至在Reddit数据集上略微逊色于WLNM.

表4 各模型在大规模数据集上的性能对比 Table 4 Performance comparison of models on large-scale datasets %

3 结束语

本文提出基于对抗图卷积的链接预测模型(LPAGC), 将节点原始特征融入邻接矩阵中, 提高GCN抓取特征的能力.构造链接的正负样本, 利用对抗网络的训练机制, 减小模型对链接信息的依赖.LPAGC继承GCN和对抗网络的优点, 在链接预测任务上取得较优性能.实验表明, 在链接稀疏的情况下模型也能保持稳定.未来考虑将LPAGC应用到动态图、有向图和多关系图中.

参考文献

文献选项

[1]	STANFIELD Z, COSKUN M, KOYUTÜRK M. Drug Response Prediction as a Link Prediction Problem. Scientific Reports, 2017, 7(1): 1-13. [本文引用:1]
[2]	GUO L, MA J, CHEN Z M, et al. Learning to Recommend with Social Contextual Information from Implicit Feedback. Soft Computing, 2015, 19(5): 1351-1362. [本文引用:1]
[3]	LI X, CHEN H. Recommendation as Link Prediction in Bipartite Graphs: A Graph Kernel-Based Machine Learning Approach. Decision Support Systems, 2013, 54(2): 880-890. [本文引用:1]
[4]	GENG X, LI Y G, WANG L Y, et al. Spatiotemporal Multi-graph Convolution Network for Ride-Hailing Demand Forecasting // Proc of the AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2019: 3656-3663. [本文引用:1]
[5]	GUO S N, LIN Y F, FENG N, et al. Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting // Proc of the AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2019: 922-929. [本文引用:1]
[6]	NEWMAN M E J. Clustering and Preferential Attachment in Growing Networks. Physical Review E, 2001, 64. DOI: DOI:10.1103/PhysRevE.64.025102. [本文引用:1]
[7]	LIBEN-NOWELL D, KLEINBERG J . The link-Prediction Problem for Social Networks. Journal of the American Society for Information Science and Technology, 2007, 58(7): 1019-1031. [本文引用:1]
[8]	JEH G, WIDOM J. SimRank: A Measure of Structural-Context Si-milarity // Proc of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2002: 538-543. [本文引用:1]
[9]	AHMED N M, CHEN L, WANG Y L, et al. DeepEye: Link Prediction in Dynamic Networks Based on Non-negative Matrix Factorization. Big Data Mining and Analytics, 2018, 1(1): 19-33. [本文引用:1]
[10]	MENON A K, ELKAN C. Link Prediction via Matrix Factorization // Proc of the European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer, 2011, II: 437-452. [本文引用:1]
[11]	GUIMERÀ R, SALES-PARDO M. Missing and Spurious Interactions and the Reconstruction of Complex Networks. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(52): 22073-22078. [本文引用:1]
[12]	DE SÁ H R, PRUDÊNCIO R B C. Supervised Link Prediction in Weighted Networks // Proc of the International Joint Conference on Neural Networks. Washington, USA: IEEE, 2011: 2281-2288. [本文引用:1]
[13]	KIPF T N, WELLING M. Semi-supervised Classification with Graph Convolutional Networks[C/OL]. [2020-08-27]. http://arxiv.org/pdf/1609.02907.pdf. [本文引用:1]
[14]	SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling Relational Data with Graph Convolutional Networks // Proc of the European Semantic Web Conference. Berlin, Germany: Springer, 2018: 593-607. [本文引用:1]
[15]	YANG B S, YIH W T, HE X D, , et al. Embedding Entities and Relations for Learning and Inference in Knowledge Bases[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1412.6575.pdf. [本文引用:1]
[16]	SHANG C, TANG Y, HUANG J, et al. End-to-End Structure-Aware Convolutional Networks for Knowledge Base Completion // Proc of the AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2019: 3060-3067. [本文引用:1]
[17]	LI W D, ZHANG X Y, WANG Y Q, et al. Graph2Seq: Fusion Embedding Learning for Knowledge Graph Completion. IEEE Access, 2019, 7: 157960-157971. [本文引用:1]
[18]	KIPF T N, WELLING M. Variational Graph Auto-encoders[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1611.07308.pdf. [本文引用:3]
[19]	PAN S R, HU R Q, FUNG S F, et al. Learning Graph Embedding with Adversarial Training Methods. IEEE Transactions on Cybernetics, 2020, 50(6): 2475-2487. [本文引用:2]
[20]	GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative Adversarial Nets // Proc of the 27th International Confe-rence on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2014, II: 2672-2680. [本文引用:2]
[21]	GROVER A, LESKOVEC J. node2vec: Scalable Feature Learning for Networks // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 855-864. [本文引用:1]
[22]	BRUNA J, ZAREMBA W, SZLAM A, , et al. Spectral Networks and Locally Connected Networks on Graphs[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1312.6203.pdf. [本文引用:1]
[23]	DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering // Proc of the 30th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2016: 3844-3852. [本文引用:1]
[24]	NIEPERT M, AHMED M, KUTZKOV K. Learning Convolutional Neural Networks for Graphs // Proc of the 33rd International Conference on Machine Learning. Berlin, Germany: Springer, 2016: 2014-2023. [本文引用:1]
[25]	HAMILTON W L, YING Z, LESKOVEC J. Inductive Representation Learning on Large Graphs // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 1025-1035. [本文引用:2]
[26]	CHEN J F, MA T F, XIAO C. FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1801.10247.pdf. [本文引用:1]
[27]	CHEN J F, ZHU J, SONG L, et al. Stochastic Training of Graph Convolutional Networks with Variance Reduction // Proc of the 35th International Conference on Machine Learning. Berlin, Germany: Springer, 2018: 942-950. [本文引用:1]
[28]	VELIČKOVIC P, CUCURULL G, CASANOVA A, et al. Graph Attention Networks[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1710.10903.pdf. [本文引用:1]
[29]	MIRZA M, OSINDERO S. Conditional Generative Adversarial Nets[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1411.1784.pdf. [本文引用:1]
[30]	RADFORD A, METZ L, CHINTALA S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks[C/OL]. [2020-08-27]. https://arxiv.org/pdf/1511.06434.pdf. [本文引用:1]
[31]	ARJOVSKY M, CHINTALA S, BOTTOU L. Wasserstein Generative Adversarial Networks // Proc of the 34th International Conference on Machine Learning. Berlin, Germany: Springer, 2017: 214-223. [本文引用:1]
[32]	BEN-DAVID S, BLITZER J, CRAMMER K, et al. A Theory of Learning from Different Domains. Machine Learning, 2010, 79(1/2): 151-175. [本文引用:1]
[33]	SEN P, NAMATA G, BILGIC M, et al. Collective Classification in Network Data. AI Magazine, 2008, 29(3): 93-106. [本文引用:1]
[34]	PEROZZI B, AL-RFOU R, SKIENA S. Deepwalk: Online Lear-ning of Social Representations // Proc of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2014: 701-710. [本文引用:2]
[35]	TANG L, LIU H. Leveraging Social Media Networks for Classification. Data Mining and Knowledge Discovery, 2011, 23(3): 447-478. [本文引用:1]
[36]	STARK C, BREITKREUTZ B J, REGULY T, et al. BioGRID: A General Repository for Interaction Datasets. Nucleic Acids Research, 2006, 34: D535-D539. [本文引用:1]
[37]	TANG J, QU M, WANG M Z, et al. Line: Large-Scale Information Network Embedding // Proc of the 24th International Confe-rence on World Wide Web. Berlin, Germany: Springer, 2015: 1067-1077. [本文引用:1]
[38]	ZHANG M H, CHEN Y X. Weisfeiler-Lehman Neural Machine for Link Prediction // Proc of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2017: 575-583. [本文引用:1]

2017

0.0

... 例如:在生物学领域,链接预测可分析蛋白质之间的相互作用^[1],研究破坏病毒结构的方法 ...

2015

0.0

... 在互联网领域,链接预测为用户推荐可能感兴趣的人^[2]或为用户推荐可能感兴趣的商品等^[3] ...

2013

0.0

... 在互联网领域,链接预测为用户推荐可能感兴趣的人^[2]或为用户推荐可能感兴趣的商品等^[3] ...

2019

0.0

... 在生活领域,链接预测可用于网约车的订单预测^[4]、交通的流量预测等^[5],为人们的出行提供便利 ...

2019

0.0

... 在生活领域,链接预测可用于网约车的订单预测^[4]、交通的流量预测等^[5],为人们的出行提供便利 ...

2001

0.0

... 基于相似性的方法需要先定义相似度,较经典的有共同邻居(Common Neighbor, CN)相似度^[6]、Jaccard相似度^[7]和SimRank相似度^[8]等 ...

2007

0.0

... 基于相似性的方法需要先定义相似度,较经典的有共同邻居(Common Neighbor, CN)相似度^[6]、Jaccard相似度^[7]和SimRank相似度^[8]等 ...

2002

0.0

... 基于相似性的方法需要先定义相似度,较经典的有共同邻居(Common Neighbor, CN)相似度^[6]、Jaccard相似度^[7]和SimRank相似度^[8]等 ...

2018

0.0

... 基于矩阵分解的方法将链接预测问题视为矩阵变换问题,提取并利用潜在特征完成预测任务^[9,10] ...

2011

0.0

... 基于矩阵分解的方法将链接预测问题视为矩阵变换问题,提取并利用潜在特征完成预测任务^[9,10] ...

2009

0.0

... 等^[11]将图中的节点进行分组,以节点分组的归属决定链接是否存在 ...

2011

0.0

... 等^[12]利用链接的权重和支持向量机训练分类模型 ...

2020

0.0

... 近年来,图神经网络(Graph Neural Network,GNN) 被广泛应用于潜在特征挖掘上,尤其是图卷积网络(Graph Convolutional Network,GCN)^[13]的提出,为解决节点分类、链接预测、图生成等热点问题提供思路 ...

2018

0.0

... Schlichtkrull等^[14]在自编码器、DistMult^[15]的基础上,利用参数共享和稀疏约束技术,提出关系图卷积网络(Relational Graph Convolutional Net-works, R-GCN) ...

0.0

... Schlichtkrull等^[14]在自编码器、DistMult^[15]的基础上,利用参数共享和稀疏约束技术,提出关系图卷积网络(Relational Graph Convolutional Net-works, R-GCN) ...

2019

0.0

... 为了避免平等地对待邻域中的不同节点,Shang等^[16]在R-GCN的基础上引入加权GCN,定义具有相同关系类型的两个相邻节点之间的相关性,提出结构感知卷积网络(Structure-Aware Convolutional Network, SACN) ...

2019

0.0

... Li等^[17]利用节点和对应的邻域构建子图,设计图到序列的信息融合机制(Graph to Sequence Generator, Graph2Seq),学习图中的节点表示 ...

0.0

... Kipf等^[18]假设每个节点在隐空间中符合高斯分布,提出图变分自编码器模型(Varia-tional Graph Autoencoder, VGAE) ...

... 3)自编码(Graph Autoencoder, GAE)^[18] ...

... 4)变分图编码(VGAE)^[18] ...

2020

0.0

... Pan等^[19]利用生成对抗网络(Generative Adversarial Networks, GAN)^[20]约束节点在隐空间的分布,进一步提出基于对抗规范的图变分自编码器(Adversarially Regularized VGAE, ARVGAE) ...

... 5)基于对抗规则的变分图自编码(ARVGAE)^[19] ...

0.0

... 自GoodFellow等^[20]提出GAN后,产生很多经典的变体和应用,如可生成指定标签图像的条件生成对抗网络(Conditional GAN, CGAN)^[29]、可生成高分辨率图像的深度卷积生成对抗网络(Deep Convolutional GAN, DCGAN)^[30]、可生成多样性图像的Wassertein生成对抗网络(Wassertein GAN, WGAN)^[31]等 ...

2016

0.0

... 1)大部分模型要求图的链接数量足够多,即观测的链接数量至少占50%^[21],但是在现实世界中,通常无法满足这个先验条件,传统方法难以奏效,因此,如何充分挖掘稀疏图的潜在信息就显得尤为重要 ...

0.0

... 基于谱域的图卷积主要依靠傅里叶变换^[22,23] ...

2016

0.0

... 基于谱域的图卷积主要依靠傅里叶变换^[22,23] ...

2016

0.0

... Niepert等^[24]对节点邻居先排序再选取 ...

2017

0.0

... Hamil-ton等^[25]对邻居节点进行随机采样 ...

... 在大规模数据集上,解码器和判别器相同,编码器采用2个两层的GraphSAGE^[25],此时 ...

0.0

... Chen等^[26]在全局范围内挑选邻域 ...

2018

0.0

... Chen等^[27]利用控制变量的方法采样任意大小的邻域 ...

0.0

... Veli cˇkovic等^[28]将注意力机制应用到图上 ...

0.0

2017

0.0

2010

0.0

... H距离^[32]定义为d_{H#cod#x00394 ...}

2008

0.0

... 1 中等规模数据集上的实验本文采用3个真实的引文数据集^[33]:Cora、Citeseer、Pubmed ...

2014

0.0

... 1)深度游走(Deep Walk, DW)^[34] ...

... 1)DW^[34] ...

2011

0.0

... 2)谱聚类(Spectral Clustering, SC)^[35] ...

2006

0.0

2015

0.0

... 2)大规模信息网络嵌入(Large-Scale Informa-tion Network Embedding, LINE)^[37] ...

2017

0.0

... 3)Weisfeiler-Lehman神经机(Weisfeiler-Lehman Neural Machine, WLNM)^[38] ...