空间众包任务m(mission)定义为如下5元组:

m=< Pl_m, Pt_m, Dl_m, Dt_m, G_m> .

其中:Pl_m表示任务m的出发地; Pt_m表示任务m在出发地的指定出发时间, 即任务最晚出发时间, 超过该时间点任务未被分配或工作者接取任务后仍未到达任务出发地Pl_m, 则该任务会被取消; Dl_m表示任务m的目的地; Dt_m表示工作者完成任务抵达目的地Dl_m时的到达时间; G_m表示工作者完成任务m所获的报酬.

空间众包工作者w(worker)定义为如下3元组:

w=< l_w, w_w, o_w> .

其中:l_w表示工作者当前所处的空间位置; w_w表示工作者在空闲状态下已等待的时间; o_w表示工作者当前状态, 任务工作中o_w=1或空闲待分配时o_w=0.

工作者其余相关要素的设定如下.

1)上下线时间.本文主要目标是优化工作者在整个工作阶段的长期收益, 因此假设在分配过程中所有工作者都处于在线状态.

2)移动速度.本文假设所有工作者接取任务的移动速度相同, 由接取任务的移动时间及搜索可行任务的间隔时间来体现.

3)任务搜索半径.由于平台需要实时考虑工作者与任务的距离, 确保工作者能在任务取消时间之前到达指定出发地, 因此本文工作者的任务搜索半径需要随时间动态变化, 具体过程见2.1节的动作搜索.

累积总收益TR(TotalRevenue)定义为整个分配时期多个阶段所有任务分配取得的收益之和:

$T R=\sum_{t=0}^{T} \sum_{w=1}^{n\left(W_{t}\right)} \sum_{m=1}^{n\left(M_{t}\right)} G_{m} x_{w m}, s. t. \sum_{w=1}^{n\left(W_{t}\right)} x_{w m} \leqslant 1, \sum_{m=1}^{n\left(M_{t}\right)} x_{w m} \leqslant 1, x_{w m} \in\{0, 1\} .$

其中:x_wm表示是否将任务m分配给工作者w(分配为1, 不分配为0); t表示当前分配的时间, T表示分配终止时间; n(W_t)表示在t时刻处于空闲状态的工作者集合W_t的数量; n(M_t)表示在t时刻可分配任务集合M_t的数量; 约束条件表示工作者与任务为一对一分配, 一个任务只能分配给一个工作者, 一个工作者也只能接受一个任务.

本文考虑决策对未来收益的影响, 优化目标并非单个任务分配阶段的总收益或单个工作者的累积收益最大, 而是使整个分配过程从状态开始到结束时所有工作者取得的整体收益最大, 即最大化累积总收益TR.在实际任务分配中, 由于并不能提前已知整个分配时期所有任务的全部信息, 因此不能直接对TR求最大值, 需要将任务分配问题考虑为多阶段序贯决策问题, 并基于MDP对其建模.

将强化学习应用于空间众包任务分配的关键问题是如何在任务分配过程中基于MDP进行建模.为了简化模型的复杂度, 本文从单个空间众包工作者的视角进行MDP建模, 相关定义如下.

智能体Agent定义为单个空间众包工作者, 需要正确判断任务价值, 做出合理决策.

状态s定义为当从单个众包工作者视角进行MDP建模时, 需要包含工作者当前所处的时空状态, s=(l_w, t), 其中, l_w为工作者w的空间位置, t表示当前时间.

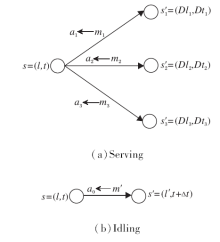
智能体Agent主要通过动作a实现状态s的转变, 而工作者时空状态s的改变主要存在执行任务(serving)与空闲状态寻找任务(idling)2种方式, 如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 两种不同类型的状态转变方式Fig.1 Two different types of state transition mode

1)工作者当前状态s=(l, t), 若周围存在可分配的任务, 如m₁、m₂、m₃, 则动作a₁、a₂、a₃分别对应这3个可行任务, 选择执行动作a_m会从当前状态s转变到对应的下一个状态s'=(Dl_m, Dt_m), 其中, Dl_m表示任务m的目的地, Dt_m表示任务m的完成时间.因此, 考虑利用下一个状态s'的时空特征描述动作a, 同时由于任务完成时间Dt_m在完成任务m前不可知, 因此令动作a_m=(Dl_m).

2)工作者当前状态s=(l, t), 若周围暂时不存在可分配的任务, 如处于较偏远的地区, 则处于空闲状态的工作者会考虑原地停留或前往周围地区寻找任务, 对应下一个状态s'=(l', t+Δ t), 表示工作者在空闲状态下经过Δ t时间移动到位置l'.因此, 构造报酬为0的虚任务

m'=< l, t, l', t+Δ t, 0> ,

对应的动作a仍采用下一个状态s'的空间特征表示, 即a_m'=(l').

工作者当前状态下所有可执行的动作a_m组成的集合由动作集A表示, 获取方法详见2.1节.

回报r(s, a_m)表示在状态s下完成动作a_m获取的收益, 即该任务的报酬G_m.若选择停留原地或空闲状态下移动寻找任务, 回报r=0.

状态动作价值Q(s, a)表示工作者在状态s下采取动作a, 未来能在分配终止时间之前获得的总收益的期望:

$Q(s, a)=E\left[\sum_{t=0}^{T} \gamma^{t} r\left(S_{t}, A_{t}\right) \mid S_{0}=s, A_{0}=a\right]$,

其中γ 为未来奖励的折扣因子.状态动作价值Q用于评估该任务在当前状态相对于未来的预期价值, Q越大, 说明采取该动作越有可能在未来获得越多的回报.同时, 根据定义可知, 随着工作者不断花费时间完成分配的任务, 已获得的总回报将越来越大, 与之相反, Q值将随时间接近终止时间而逐渐减小.当工作者即将到达终止时间时, 将没有时间来完成任务而获取回报, Q值在距离终止状态越近则越接近于0.

策略π (s)表示工作者在状态s下应该采取怎样的动作a, 从而使期望累积回报最大化.基于状态动作价值Q(s, a)的贪婪策略,

a=π (s)=arg maxaQ(s, a).(1)

状态价值V(s)表示工作者从状态s开始遵循策略π 直到状态结束时将能获得的预期累积回报, 假设在分配过程中始终使用基于状态动作价值Q(s, a)的贪婪策略, 则

V(s)=Q(s, π (s))= maxa∈AQ(s, a).

通过上述MDP建模, 将任务分配问题转化为多阶段序贯决策问题进行求解, 利用状态动作价值Q评估任务的未来价值, 将优化目标从最大化整个分配时期的累积总收益TR转化为在每阶段分配时最大化总预期收益:

$T R_{\mathrm{MDP}}=\sum_{w=1}^{n\left(W_{t}\right)} \sum_{m=1}^{n\left(M_{t}\right)} Q\left(s_{w}, a_{m}\right) x_{w m}, s.t. \sum_{w=1}^{n\left(W_{t}\right)} x_{w m} \leqslant 1, \sum_{m=1}^{n\left(M_{t}\right)} x_{w m} \leqslant 1, x_{w m} \in\{0, 1\} .$ (2)

综上所述, 空间众包任务分配问题最终转化为针对状态动作价值Q值的求解及工作者与任务的一对一匹配, 从而实现在每个阶段任务分配时不仅考虑到工作者的时空状态以及该任务的当前价值, 更考虑到任务完成状态的未来价值.

由于空间众包任务的时空属性, 并非当前所有的任务m对工作者来说都是可行的动作a_m, 即并非每对(工作者w, 任务m)都存在相对应的Q(s_w, a_m).可行的任务需要满足如下时空约束条件.

1)任务指定的出发地需要在工作者的附近, 搜索范围过大会产生很多不合理的任务, 导致工作者前往目的地耗费大量时间, 与优化目标在一定时间段内获取最大收益违背, 同时搜索范围过小会无法探索很多可行的动作, 得不到最优解.

2)工作者由当前地点前往任务指定出发地需要花费一定时间, 平台在分配任务时留有充足的时间保证工作者能赶在任务取消前到达出发地.

因此, 文中工作者的搜索半径需要随时间动态变化, 以搜索真实可行的动作集.此外, 当在最大搜索范围内仍然无法搜索到合适的动作时, 通过构造虚任务(G_m=0)使动作集A不为空, 即停留在原地或短距离移动到附近地点.

算法 1 动作搜索Action_Search

输入 当前状态s=(l_w, t), 初始化A={},

当前时刻待分配任务集M_t,

最大搜索层L_max, 每次搜索间隔时间Δ T,

每次搜索半径扩大Δ L, 状态终止时间T

输出 动作集A

for n=1, 2, …, L_max do

A˙← {a_m|m∈ M_t, 且满足时空约束条件}

时空约束条件:

t+(n-1)Δ T< Pt_m≤ t+nΔ T

Plm-lw2≤ nΔ L

A← A+ A˙

end for

if A={} then

构造虚任务

m'=< l_w, t, l_w+random(0, L_max), min(t+nΔ T, T), 0>

A← {a_m'}

end if

return A

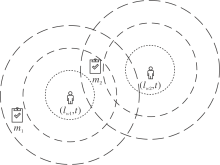
针对一位工作者的动作搜索过程如图2所示, 在t时刻工作者w处于l_w位置, 若对工作者w执行动作搜索, 即搜索出发时间在(t, t+Δ t)时间段内且出发地Pl_m在第L₁层圆内的任务, 再搜索出发时间在(t+Δ t, t+2Δ t)时间段内且出发地Pl_m在第L₂层圆内的任务, ……, 依此类推, 直到搜索至最终层或状态终止时间.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 动作搜索过程Fig.2 Process of action search

基于工作者当前所处的时空状态, 众包平台考虑任务的指定出发时间及出发地点等时空属性, 通过动作搜索策略实现从任务集M到动作集A的映射.如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 搜索可行动作集Fig.3 Searching feasible action set

图3中, 虚线表示工作者w与任务m之间不存在相应的Q(s_w, a_m), 后续在工作者与任务的一对一匹配过程中需要将其匹配边权重设为0.

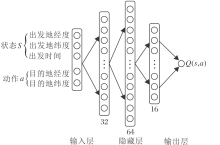
根据状态动作价值Q(s, a)的定义, 由于需要采用连续的时空信息作为输入, 状态动作空间的维度极大, 因此强化学习中传统的查表法(如Q_learning)难以求解, 需要借助深度神经网络处理高维连续数据的优势, 采用深度Q学习网络(Deep Q Network, DQN)预测状态动作价值Q.具体的深度神经网络结构如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 深度神经网络结构Fig.4 Structure of deep neural network

强化学习的目标是在智能体与环境的不断交互中寻找最优策略π ^* , 使工作者从状态s开始遵循该策略, 直到结束时得到的期望累积回报最大.本文策略利用历史数据模拟智能体与环境的交互过程.首先, 从历史任务数据中构造训练所需的样本序列{s, a, r, s'}, 存入回放缓存记忆库, 待积累到一定的数量后进行小批量随机抽取, 作为深度神经网络模型训练的输入.然后, 通过动作搜索算法筛选在状态s'下满足时空约束条件的动作a'的集合A', 采取基于下一个状态Q(s', a')的贪婪策略更新Q(s, a).最后, 在训练完成后, 将工作者及任务的实时时空信息作为输入, 输出为状态动作价值Q的预测值.为了得到更快的收敛速度与更好的稳定控制效果, 结合双网络DQN(Double DQN, DDQN)^[30]的思想进行优化改进, 针对任务分配的实际特点对模型的输入进行一定处理, 具体算法步骤如下.

算法 2 基于改进DQN的求解算法

输入 历史任务数据集H, 初始化回放缓存记忆库R,

初始化状态动作价值深度神经网络Q,

参数θ , 初始化目标网络 Q˙, 参数 θ˙=θ

输出 训练完毕后的网络Q, 参数θ

1.在回放记忆库R中加入一定数量的终止状态序列

{(s, a, r, s')|s'为终止状态}

2.for step=1, 2, …, N do

3. 从H中随机移除一条历史任务记录< Pl_m, Pt_m,

Dl_m, Dt_m, G_m> , 由此产生一条序列并存储到R中:

{s=(Pl_m, Pt_m), a=(Dl_m), r=G_m,

s'=(Dl_m, Dt_m)}

4. 从R中小批量随机采样{(s, a, r, s')}

5. 对每个s'搜索可行动作集A'← Action_Search(s')

6. 计算目标值y.若s'是终止状态, y← r; 若s'不是

终止状态, y← r+γ Q˙(s', arg maxa'∈A'Q(s', a'; θ ); θ˙)

7. 根据损失函数L(θ )=(y-Q(s, a; θ ))², 对网络

参数θ 进行梯度下降更新

8. 每隔C步更新目标网络参数 θ˙=θ

9.end for

在算法第1步中, 由于Q值在终止状态下等于0, 同时终止状态数据占总体数据比例较小, 通过将终止状态的数据提前加入回放记忆库中, 能加快训练过程收敛速度.在算法第5步中, 由于任务完成过程中的接取动作并不产生收益, 只有在接取动作完成后的服务过程才产生收益, 因此在经过动作搜索筛选工作者可行的任务集A'后, 需要结合工作者的时空状态s', 针对任务集A'中每个a'计算接取时间作为神经网络的时间输入, 并以a'的出发地与目的地作为地点输入.最后, 由于在实际任务分配中无法提前得知准确的任务完成时间Dt_m, 因此输入中a仅考虑任务的目的地, 任务的完成时间在训练过程中由状态s'中的出发地点及出发时间体现.

为了简化模型的复杂度, 从单个众包工作者视角进行MDP建模, 但实际任务分配过程中, 每轮分配都可能存在多个空闲待分配的工作者, 因此不能直接根据式(1)采取基于状态动作价值Q(s, a)的贪婪策略, 应从全局的角度根据式(2)进行任务分配.

如图5所示, 分别对w₁、w₂工作者进行动作搜索, 假设得出满足条件的动作集

A_w1={m₁, m₂}, A_w2={m₂},

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 全局任务分配示意图Fig.5 Illustration of global task allocation

从单个工作者w₁的视角出发, 若根据模型输出的预测结果得出接取任务m₂的Q值大于任务m₁, 对于w₁工作者来说, 由式(1)的贪婪策略分配任务m₂获得最大收益, 但此时w₂工作者将没有合适的任务可以分配, 从而并未达到全局最优.因此需要利用加权二分图匹配算法求解式(2), 使所有工作者的整体总收益最大.

本文采用运筹优化中的KM(Kuhn-Munkres)算法, 以状态动作价值Q作为二分图匹配的权重, 实现长期累积收益的全局优化.

综上所述, 通过深度强化学习对历史任务数据离线学习得到关于Q值的预测模型, 将利用动作搜索算法获取可行任务的实时时空信息作为输入, 以模型输出的预测值作为二分图匹配的权重, 在多阶段实时任务分配过程中利用KM算法全局优化长期累积收益, 具体的动态在线分配过程如下.

1)初始化当前时间t=0, 每轮分配间隔时间Δ t, 终止时间T, 所有工作者W={< l_w, w_w, o_w> }.

2)选取当前t时刻所有处于空闲的工作者(W'={w'|w'∈ W, o_w=0})的状态s_w'=(l_w', t)及待分配任务集M_t.

3)从M_t中对工作者w'搜索可行任务集A_w'=Action_search(s_w'), 利用训练好的Q网络计算A_w'中每个任务m的Q(s_w', a_m).

4)利用KM算法进行二分图匹配, 将Q(s_w', a_m)作为空闲工作者w'与任务m的匹配权重, 其余未关联匹配边权重设为0.

5)由二分图匹配结果分配任务, 更新工作者状态.本轮获得任务分配的工作者:w_w=0, o_w=1.本轮未获得任务分配的工作者:w_w=w_w+Δ t.更新待分配任务集, 删除已分配的任务.当前时间t=t+Δ t.

6)判断是否到达终止时间t≥ T:若达到, 结束过程; 若未达到, 过程更新工作者状态.对于已完成任务的工作者:当t≥ Dt_m, 令l_w=Dl_m, o_w=0.一段时间内仍未获得任务分配的工作者会在附近随机移动:当w_w≥ T_wait时, 令l_w=l_w+random(1, L).更新待分配任务集, 删除已错过出发时间的任务{m|t≥ Pt_m}, 添加在Δ t时间内新分布的任务.

为了验证本文策略在解决空间众包大规模任务分配问题上的有效性, 实验部分选取2016年1月份纽约出租车真实出行数据集, 共计10 337 540条原始数据, 详细记录每次出租车上下客的时间和地理位置(经纬度, 精确到小数点后6位)、行程距离、行程费用、乘客数量等信息.输入数据的正确性及处理数据的方式对算法的准确性具有较大影响, 因此在建模训练前需要通过数据清洗, 过滤不符合实际的错误数据, 结合算法需求进行特征处理, 同时通过数据分析为后续模型中参数设定提供参考.

原始数据集包含很多异常出租车出行数据, 如上下客经纬度的离群值, 偏离实际正常出租车出行的行程时间与行程距离(如行程距离过长但行程时间过短等), 因此需要通过数据清洗检测异常行程, 将其从数据集中删除.清洗后的数据共计8 822 438条, 约占原始数据的85%.

结合算法要求, 提取描述时空信息及收益回报所需的特征(上下客的时间、经纬度及行程费用), 并从时间与空间的角度进行相应的特征处理.

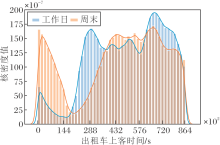
从时间角度上看, 首先, 利用一个月前三周的数据作为训练集, 约占使用数据的75%, 后一周作为测试集, 约占使用数据的25%.其次, 出租车在工作日的出行规律不同于周末, 如图6所示.由图可见, 出行时间分布存在较大差异, 出行高峰期出现的时间也存在较大差距.因此, 将每周工作日与周末的数据分离, 分别进行训练.最后, 对一整天的时间进行分段处理, 减少预测的时间跨度, 提高算法对Q值预测的准确率, 加速算法收敛.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 工作日与周末出行时间分布Fig.6 Distribution of travel time on weekdays and weekends

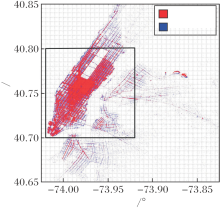
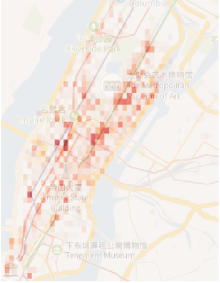
从空间角度上看, 空间位置坐标由经纬度表示, 作为连续变量且精确到6位小数, 原始数据集的上下客位置坐标容易受到纽约城市中高层建筑、密集区域、天气时间等因素的影响, 导致获得错误的坐标, 因此需要对原始经纬度数据进行处理.首先统计上下车位置分布, 截取经度处于[-74.02° , -73.92° ]内、纬度处于[40.70° , 40.80° ]内的正方形区域, 如图7所示.然后将该正方形区域离散为50× 50个二维正方形单元, 每个正方形单元大小约为200 m× 200 m, 单元内的所有坐标均由该正方形单元的左下角数字表示.最后, 筛选上下车位置坐标都位于截取正方形区域内的行程数据, 约占全部区域数据的85%, 统计某日上午9 h 10 min内所有行程数据的上车位置分布, 其热力图如图8所示, 图中颜色越深表明该区域作为出发地的行程越多.由图可见, 纽约曼哈顿城市中存在较明显的出行冷热区.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 选取区域示意图Fig.7 Illustration of selected area

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 上车位置分布热力图Fig.8 Heat map of distribution of pick-up locations

基于python实现本文策略, 利用pytorch构建深度神经网络模型, 使用Windows 10操作系统, PC平台处理器为2.2 GHz Inter(R) Core(TM) i7-8750H, 内存为16 GB.

参数的选择可能影响求解结果, 有一般性原则可遵循及相关文献^{[28, 29, 30]}可参考.折扣因子γ 衡量后续状态动作价值对总回报的权重, 因此一般取值接近 1, 本文设γ = 0.95.学习率α = 0.001, 回放缓存记忆库容量R=10 000, 采样批量为64.网络参数θ 采取随机初始化策略, 目标网络参数 θ˙延迟更新步数C=300, 采用ReLu激活函数, 选用自适应矩估计算法(Adaptive Moment Estimation, Adam)替代随机梯度下降算法(Stochastic Gradient Descent, SGD).

本文将任务分配问题转化为带权二分图的最优匹配问题, 将预测任务未来价值的Q值作为权值, 在每轮分配阶段利用KM算法达到全局最优.因此, 对比策略设计的关键在于如何设计二分图匹配的边权, 以实现整个分配过程所有工作者累积总收益最大化的优化目标, 具体计算如下:

$\max \sum_{w=1}^{n\left(W_{t}\right)} \sum_{m=1}^{n\left(M_{t}\right)} c_{w m} x_{w m}, s.t. \sum_{w=1}^{n\left(W_{t}\right)} x_{w m} \leqslant 1, \sum_{m=1}^{n\left(M_{t}\right)} x_{w m} \leqslant 1, x_{w m} \in\{0, 1\} .$

其中:c_wm表示二分图中工作者w与任务m的权值, 在本文策略中

cwmDQN=Q(s_w, a_m).

具体对比策略如下.

1)基于查表法Q-learning的分配策略(Tabula-Based Q-learning, Q_learning)^[27].对状态价值V(s)按照分钟级粒度建表, 利用时序差分法(Temporal-Difference, TD)不断更新V(s), 得到状态动作价值Q(s, a)作为二分图匹配的边权, 即

cwmQ_learning=Q(s_w, a_m).

对比Q_learning(without deep networks)与本文策略(with deep networks), 验证引入深度神经网络的效果.

2)最大即时任务收益的贪婪策略(Reward Gree-dy, RG).在每轮分配时将任务即时收益作为KM算法边权, 即令 cwmRG=r_m.策略仅能保证当前每轮分配的总收益最大, 未考虑决策对未来的影响, 可作为基线策略.

3)最小接取距离的贪婪策略(Pick_up Distance Greedy, PG).从最小化接取成本的角度考虑最大化累积收益, 改进最短距离优先策略(Close Distance Priority, CDP)^[11]、就近任务分配策略(Assign Nea- rest Taxi to Passenger, ANTP)^[31]等距离优先策略, 在接取距离相同时优先选择即时收益较大的任务, 即令

cwmPG=-D(l_w, Pl_m)+λ r_m,

其中D(l_w, Pl_m)表示从工作者l_w前往任务出发地Pl_m的接取距离.策略通过λ (取较小的固定值)实现在接取距离相同时选择即时收益r_m较大的任务, 期望通过减少接取任务的时间以增大服务时长, 提升工作者的累积收益.

4)最小位置熵优先策略(Least Location Entropy Priority, LLEP)^[11].从最大化任务分配数量的角度考虑最大化累积收益, 利用空闲工作者的分布设计启发式的策略.如果一个任务位于工作者较多的地区, 这个任务将来更有可能被执行, 因此给予位于工作者稀疏区域的任务更高的分配优先级, 使其在位于工作者密集区域的任务之前被分配, 从而分配更多的任务.

根据设计出发点, 引入位置熵Entropy(l)衡量区域工作者分布情况:

Entropy $(l)=-\sum_{w \in W_{l}} P_{l}(w) \log _{2} P_{l}(w), P_{l}(w)=\frac{\left|O_{w l}\right|}{\left|O_{l}\right|}$, 其中, Owl表示工作者w访问位置l的次数, Ol表示位置l被访问的总次数.如果某区域存在许多工作者以相同的比例访问, 则位置熵较高; 否则, 如果到访该区域仅有少数工作者, 则位置熵较低.

因此, 在任务分配的过程中, 每轮优先分配位置熵较低的任务, 保证工作者较少地区的任务优先执行, 等到下一轮分配时, 会存在很多位置熵较高的任务, 该区域必然存在较多的空闲工作者, 这样遗留下来的任务大概率能够得到分配.算法既能保证当前工作者稀疏区域的任务能被分配, 也能使位置熵较高区域的任务在下一时刻被分配, 因此提高整个时间段内的总体分配数量, 提升工作者的累积收益.

由于不同时间段的空闲工作者分布存在较大差异, 因此, 在每轮分配前会根据最近10 min的空闲工作者分布, 重新计算此时的位置熵作为权值, 即令

cwmLLEP=-Entropy(l).

5)最大化系统自定义效用函数的分配策略(An Optimal Algorithm Based on the Idea of Kuhn-Munkres,

KMBA)^[31].从众包平台的角度考虑出租车派单问题, 设计系统效用函数

U=N_wm-λ T_wm

作为KM算法的权值, 其中, N_wm、T_wm分别表示将订单m分配给司机w, 司机取得的净利润及乘客需要等待的时间, 并通过λ (λ ≥ 0)调节司机收益与乘客体验, 则

N_wm=α D(Pl_m, Dl_m)-β (D(l_w, Pl_m)+D(Pl_m, Dl_m)), Tw_m=Tm₊tp_ick=Tm₊ D(lw, Plm)v

其中:D(· , · )是距离函数, 表示两点之间的实际路径距离; α 表示司机每公里的收入; β 表示司机每公里的成本; D(l_w, Pl_m)表示司机接取乘客的距离; D(Pl_m, Dl_m)表示订单的行程距离; T_wm表示乘客需要等待的时间, 包括订单从乘客提交到成功分配的等待时间T_m、成功分配后司机的接取时间t_pick; v表示司机的接取速度.

由于本文考虑的优化目标为最大化整个分配时期所有工作者(司机)的累积收益, 暂未涉及乘客体验的优化, 因此令λ =0, KMBA转变为收入最大化分配策略(Maximize Net Profit of Taxis, MNPT)^[31], 即 cwmKMBA=N_wm=(α -β )D(Pl_m, Dl_m)-β D(l_w, Pl_m).该策略假设司机收益与司机载客行驶距离线性相关, 期望在最大化司机收益的同时尽量减小接单距离.

实验选取训练集工作日期间上下客时间在6时至12时这段时间内的出行数据, 并对输入层数据进行归一化处理, 消除量纲, 按照本文策略迭代直至收敛.利用测试集5个工作日6时至12时的出行数据, 模拟真实环境下的大规模任务分配情况.工作者的初始化需要设定每位工作者的出现时间及位置, 若随机初始化则难以保证工作者的时空分布符合实际, 因此, 实验依据任务的出发时间进行排序, 选取前N个任务对应的出发时间及地点, 作为N位工作者的出现时间及位置.实验记录每位工作者在6 h内的累积收入, 并统计所有工作者的平均累积收入, 分别取前5%收入最低与最高的工作者, 用于计算平均最低收入与平均最高收入.

表1为初始化800位工作者6 h的任务分配对比实验结果.由表可见, 对于平均累积收益, 本文策略在所有工作日期间均达到最优, 相比其它策略, 收益提升2%~10%, 对比次优的Q_learning仍稳定提升1.5%~4%, 说明本文策略的可行性与有效性.对于平均最低收益, 相比其它策略, 本文策略、Q_learning此类强化学习算法提升12%~60%, 说明该类策略充分考虑当前决策对未来的影响, 避免工作者仅注重当下收益而忽视更长远的收益, 使所有工作者在多阶段的任务分配过程中都能取得相对较大的累积收益.对于平均最高收益, 对比Q_learning, 本文策略多日稳定最优, 说明引入深度神经网络对动作状态价值的评估更准确, 本文策略取得最大累积收益的上限更高.

表1

Table 1

表1(Table 1)

表1 各策略在工作日的收益对比 Table 1 Income comparison of different strategies on weekdays 分配策略 周一 周二 周三 周四 周五 平均 累积 收益 本文策略 Q_learning RG PG LLEP KMBA 242.47 238.84 227.64 235.67 230.10 235.18 246.16 242.28 231.17 239.57 231.64 239.10 256.13 247.77 235.27 244.53 235.25 243.86 256.61 250.58 239.12 248.49 238.99 248.05 266.49 256.23 246.39 255.57 243.82 253.68 平均 最低 收益 本文策略 Q_learning RG PG LLEP KMBA 190.23 190.47 134.75 149.14 169.28 134.34 191.70 198.62 131.19 155.22 164.12 124.05 200.18 186.45 130.38 151.61 158.90 126.85 202.50 201.50 130.09 151.12 169.34 138.43 179.37 159.45 124.63 126.34 137.77 112.67 平均 最高 收益 本文策略 Q_learning RG PG LLEP KMBA 273.65 270.32 263.60 270.69 260.03 274.40 277.47 273.81 269.21 272.97 262.20 278.48 289.17 281.28 273.68 279.08 266.15 286.18 287.77 280.23 278.74 282.70 268.66 287.31 301.06 292.51 289.22 293.55 277.95 299.68

表1 各策略在工作日的收益对比 Table 1 Income comparison of different strategies on weekdays

下面主要从时空角度分析工作日期间6时至12时Q值的变化情况, 并对比V值分布差异, 分析本文策略优于Q_learning的原因.

从时间角度上看, 结合MDP建模中对状态动作价值Q的定义, Q值会随时间不断下降, 在终止状态时接近于0, 根据算法迭代收敛后的神经网络对处于多个地区单元不同时间的Q值进行预测, 随时间的变化结果如图9所示.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 Q值变化示意图Fig.9 Illustration of variation of Q value

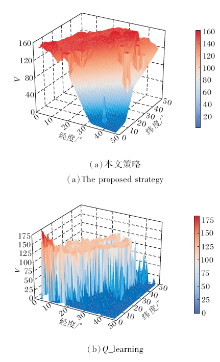
从空间角度上看, 地区间由于本身的地理特征及人群密度不同造成任务出发地的分布存在一定规律性, 导致同一时间不同地区的V值也相应变化.如图10(a)所示, z轴表示某日8时的实时最大Q值, 即实时状态V值.图中右下部分对应纽约曼哈顿之外的城市, 这些城市中出租车出行的数据量较少, 处于该地的工作者难以得到及时的任务分配, 属于任务发生的“ 冷区” .从左下到右上部分区域对应纽约曼哈顿城市中心, V值远高于周围区域, 属于任务发生的“ 热区” .左上部分地区由于没有相应的出行记录, 因此该部分区域在训练过程中没有相关的学习过程, V值预测受到模型整体参数的影响, 本身无实际意义.图中V值的波动体现不同地区间存在较大差异.

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 2种策略在某日8时的V值对比Fig.10 V value comparison of 2 strategies at 8 o'clock on

与本文策略通过深度神经网络直接输出Q值作为对比, Q_learning在实验时间段(6时至12时)内每隔5 min建立一个50× 50(对应离散为50× 50正方形单元格的实验区域)的V值查询表, 通过TD迭代更新V值直至收敛.建表的时间窗口选取5 min, 这是因为:时间间隔设置过小, 实验时间段内需要建表的数量增加, 同时在每个时间窗口内没有足够的订单数据充分迭代更新V值使其逼近真实值.时间间隔设置过大, 在线二分图匹配时得出的Q值对各订单区分不够明显, 预测精度有所下降.对比本文策略, Q_learning的局限性表现如下.

1)V值波动较大.对比图10发现, 相比本文策略, 针对同一时刻相邻地区, 通过Q_learning查表法得出的V值波动较大.不同于本文策略采用连续的时空信息作为输入, Q_learning需要根据时间窗口建表查表, 因此不同于图9中平滑的曲线, 查表法得出的Q值呈现梯形下降, 即同一地区相近时刻的V值曲线并不平滑, 同样存在较大波动.

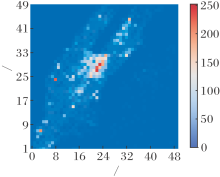
2)迭代收敛较慢.如图11所示.不同地区V值迭代更新次数差异较大, 不同于本文策略中每个订单都会通过梯度回传更新神经网络每层参数, TD更新对每个订单仅更新表中对应状态的V(s), 即表中每个V值的迭代次数对应5 min内从该地出发的订单数, 地区之间、表之间相互独立, 无信息共享, 对于出行数据较少的冷区, V值迭代收敛较慢.

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 V值通过TD更新的迭代次数Fig.11 Iterations of V value updated by TD

本文从单个工作者的视角建模, 对自身的状态及任务价值进行评估, 但是在大规模任务分配问题时较多的工作者之间会相互影响, 如工作者接取一个任务会影响到周围的工作者无法接取此任务, 因此, 需要通过调整工作者初始化的数量, 进一步分析本文策略的性能.初始化司机的出现时间需要依据开始一段时间内订单的出发时间, 如上述多日对比实验中800位司机对应前800个订单的出发时间, 分布在06∶ 00∶ 01~06∶ 10∶ 58这段约11 min的时间窗口内, 通过调整时间窗口的长度可控制订单数量, 确定初始化对应数量的司机, 如表2所示.

表2

Table 2

表2(Table 2)

表2 初始化司机数量 Table 2 Number of drivers initialized 时间窗口/min 3 5 8 10 12 15 18 20 司机数量 230 371 573 722 899 1176 1472 1680

表2 初始化司机数量 Table 2 Number of drivers initialized

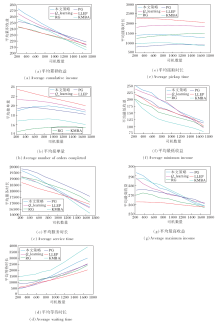
实验记录每位工作者的累积收入、接单量、服务(载客状态)时长、等待(未分单空载状态)时长、接取(已分单接客状态)时长, 统计所有工作者的平均累积收入、平均接单量、平均服务时长、平均等待时长、平均接取时长, 分别取前40位收入最低与最高的工作者计算平均最低收入与平均最高收入, 实验结果如图12所示.下面综合图中实验结果并结合实际任务分配特点进行策略对比分析.

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 6种分配策略的性能对比Fig.12 Performance comparison of 6 different allocation strategies

分配策略的平均接单量曲线较平稳, 由此可见, 环境中的订单数量始终充足(图12(b)), 分配环境始终处于供小于需的状态, 司机有足够的订单可供选择.但是, 司机间存在竞争关系, 随着司机数量的增加, 平均累积收益(图12(a))、平均服务时长(图12(c))等均有不同程度的衰减.

RG作为基线, 每轮分配最大化当前即时收益之和, 由平均累积收益可见当前短期收益的贪婪策略并不能取得良好的长期累积收益(图12(a)), 并且即时收益较大的订单一般行程时间较长, 因此接单量明显小于其它策略(图12(b)).

PG是实际应用中最常用的策略^{[4, 11, 31]}, 实验中也验证其在司机数量增大时衰减程度相对较低, 在司机数量大于1 200时能取得最高的累积收益(图12(a)), 该策略可按照设计预期实现最短接取时长(图12(e)), 在实验供小于需的环境下能始终保持较高的平均服务时长(图12(c)), 从而间接提高平均累积收益.

LLEP利用司机历史分布信息, 追求最大化接单量(图12(b)).策略给予位于司机稀疏区域的订单更高的分配优先级, 高优的订单(处于司机稀疏区域)一般距离司机(大概率处于司机密集区域)较远, 相应地会增加司机的接取距离, 导致接取时长在所有策略中最高(图12(e)), 最终平均累积收益始终处于较低水平(图12(a)).

KMBA通过设计效用函数实现组合优化, 期望在最大化累积收益的同时尽量减小接单距离.策略假设订单价格与载客行驶距离线性相关, 但实际中订单的价格与距离并非简单的线性关系, 还会受到供需、交通、天气等环境因素的影响^[15].例如, 取上午九时前五分钟的所有订单, 根据行程距离与价格绘制散点图, 如图13所示.

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 订单行程收益散点图Fig.13 Scatter plot of order travel distance and revenue

由图13可见, 仅靠行程距离线性拟合订单价格会存在较大偏差, 从而对司机取得的累积收益产生错误预估.因此, 随着司机数量增多, 服务时长及累积收益衰减严重(图12(a)、(c)), 性能大幅降低.

本文策略能在需求大于供应的情况下取得较优的分配效果, 维持与PG类似较高的订单量(图12(b)), 在服务时长低于PG时仍能达到更高的收益, 说明本文策略能结合时空特征对订单进行一定的选择.尤其是平均最低收益稳定优于其它策略(图12(f)), 说明本文策略可避免由于贪婪而选取当前收益较高但未来收益较低的订单, 而是选择有利于长期收益的订单.但是, 随着司机数量的增加, 相比其它策略, 在平均服务时长上下降幅度较大(图12(c)), 导致累积收益有着相对较大的衰减(图12(a)), 最终在司机数量大于1 200时累积收益低于PG.

Q_learning的实验结果与本文策略类似, 在司机数量小于1 200时, 平均累积收益仅次于本文策略, 可见在性能上本文策略仍优于Q_learning.随着司机数量逐渐增多, 此时限制强化学习算法性能的瓶颈不再是Q值预测是否精准, 因此Q_learning的累积收益逐渐逼近本文策略, 并且在平均累积收益上都有较大幅度的衰减(图12(a)).

根据上述分析, 随着司机数量增多, 本文策略由于平均服务时长相对下降较大导致收益衰减较多, 而PG可实现最短接取时长, 从而提高服务时长.在实际应用中可考虑结合两种策略, 设计基于本文策略+PG的组合策略:在接取距离相同时优先选择Q值较大的任务, 即

cwm+=-D(l_w, Pl_m)+λ Q(s_w, a_m),

期望在减少接取时长的同时最大化未来预期收益.

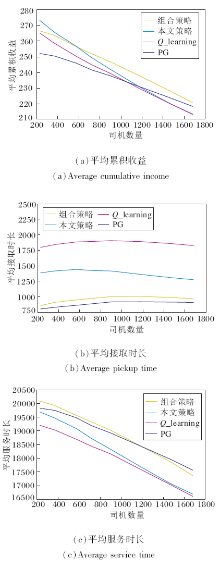
4种策略实验结果如图14所示.随着司机数量增多, 组合策略的平均累积收益稳定提高, 在司机数量大于1 200时, 对比PG, 平均累积收益提升2.0%, 对比本文策略, 平均累积收益提升3.4%(平均接取时长降低24.9%, 平均服务时长提高4.3%).可见组合策略能缩短接取时长, 提高服务时长, 同时借助Q值尽可能选取有利于长期收益的订单, 使本文策略在司机数量处于较大规模时仍能带来平均累积收益的提升.

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 4种分配策略的性能对比Fig.14 Performance comparison of 4 different allocation strategies

本文策略随着司机数量的增加在平均累积收益上具有相对较大的衰减, 主要原因如下:1)工作者之间相互存在关联, 实际的Q值会由于工作者的竞争而产生一定改变, 由于单个工作者视角建模的局限, 对于多位工作者竞争产生的状态变化难以及时捕捉.2)未考虑相关背景信息, 例如供需实时特征、周围空闲工作者数量及任务数量.由于缺少实时的供需背景信息, 容易错误估计自身的状态动作价值Q, 指导工作者前往某个真实状态价值并不高的“ 热区” , 例如可能会因为过多的工作者都被分配前往到该地区, 导致该“ 热区” 供应大于需求, 存在多个工作者相互竞争, 致使工作者不一定能选择到预期的最优任务, 因此会对后续的任务分配存在一定影响.