引用本文
刘会东, 杜方, 余振华, 宋丽娟. 基于强化学习的无标签网络剪枝. 模式识别与人工智能, 2021,34(3): 214-222
LIU Huidong, DU Fang, YU Zhenhua, SONG Lijuan. Label-Free Network Pruning via Reinforcement Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(3): 214-222.  
Doi: 10.16451/j.cnki.issn1003-6059.202103003
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于强化学习的无标签网络剪枝
刘会东1, 杜方1,2, 余振华1,2, 宋丽娟1,2
1.宁夏大学 信息工程学院 银川 750021
2.宁夏大学 宁夏大数据与人工智能省部共建协同创新中心银川 750021
通讯作者:

余振华,博士,讲师,主要研究方向为机器学习、计算机视觉、生物信息学.E-mail:zhyu@nxu.edu.cn.

作者简介:

刘会东,硕士研究生,主要研究方向为网络压缩、强化学习.E-mail:liuhuidong_nxu@163.com.

杜 方,博士,教授,主要研究方向为大数据管理、人工智能.E-mail:dfang@nxu.edu.cn.

宋丽娟,博士,副教授,主要研究方向为图像处理、计算机视觉.E-mail:slj@nxu.edu.cn.

收稿日期: 2020-09-23 接受日期: 2020-10-24
资助项目: 国家自然科学基金项目(No.61901238); 宁夏自然科学基金项目(No.2018AAC03020,2018AAC03025)资助
摘要

为了消除深度神经网络中的冗余结构,找到具备较好性能和复杂度之间平衡性的网络结构,提出基于无标签的全局学习方法(LFGCL).LFGCL学习基于网络体系结构表示的全局剪枝策略,可有效避免以逐层方式修剪网络而导致的次优压缩率.在剪枝过程中不依赖数据标签,输出与基线网络相似的特征,优化网络体系结构.通过强化学习推断所有层的压缩率,采用深度确定性策略梯度算法探索最优网络结构.在多个数据集上的实验表明,LFGCL性能较优.

关键词: 深度神经网络(DNN); 网络剪枝; 网络架构搜索; 强化学习
中图分类号:TP 183
Label-Free Network Pruning via Reinforcement Learning
LIU Huidong1, DU Fang1,2, YU Zhenhua1,2, SONG Lijuan1,2
1. School of Information Engineering, Ningxia University, Yinchuan 750021
2. Collaborative Innovation Center for Ningxia Big Data and Artificial Intelligence Co-founded by Ningxia Municipality and Ministry of Education, Ningxia University, Yinchuan 750021
Corresponding author:
YU Zhenhua, Ph.D., lecturer. His research interests include machine learning, computer vision and bioinformatics.

AboutAuthor:
LIU Huidong, master student. His research interests include network compression and reinforcement learning.
DU Fang, Ph.D., professor. Her research interests include big data management and artificial intelligence.
SONG Lijuan, Ph.D., associate professor. Her research interests include image proce-ssing and computer vision.

Fund:National Natural Science Foundation of China(No.61901238); Natural Science Foundation of Ningxia Province(No.2018AAC03020,2018AAC03025)
Abstract

To remove redundant structures from deep neural networks and find a network structure with a good balance between capability and complexity, a label-free global compression learning method(LFGCL) is proposed. A global pruning strategy is learned based on the network architecture representation to effectively avoid the appearance of the suboptimal compression rate owing to network pruning in a layer-by-layer manner. LFGCL is independent from data labels during pruning, and the network architecture is optimized by outputting similar features with the baseline network. The deep deterministic policy gradient algorithm is applied to explore the optimal network structure by inferring the compression ratio of all layers through reinforcement learning. Experiments on multiple datasets show that LFGCL generates better performance.

Key words: Key Words Deep Neural Network(DNN); Network Pruning; Network Architecture Search; Reinforcement Learning

本文责任编委 胡包钢

Recommended by Associate Editor HU Baogang

近年来, 深度神经网络(Deep Neural Network, DNN)在图像分类[1, 2, 3]、目标检测[4, 5]等许多计算机视觉任务上已取得显著效果.然而, DNN因其庞大的参数和复杂的计算, 导致在资源有限的设备上部署大型的DNN仍然面临着巨大挑战.目前, 解决这一问题的一个可行方法是在不严重影响模型精度的情况下压缩大型DNN[6], 而网络剪枝方法就是提高DNN性能的压缩技术之一.

网络剪枝方法去除非结构化的权重或结构化的卷积核、通道和层, 消除网络中冗余的连接.Han等[7]提出混合压缩框架, 结合权重剪枝[8]、参数量化和Huffman编码技术, 得到较优的压缩效果.然而, 非结构化剪枝会导致不规则的权重张量, 需要再借助特殊的硬件和软件包以提升计算效率.相比之下, 结构化剪枝可更好地压缩网络.Lin等[9]提出动态的神经网络剪枝框架, 为网络的每层动态选择合适的卷积核, 适应不同的识别任务.Lin等[10]提出基于生成对抗性网络的松弛软掩码算法, 移除不重要的块、分支和通道.Lin等[11]提出基于每层特征图秩的大小移除低秩特征图的卷积核.Mussay等[12]基于神经元的核心集理论, 提出与数据无关的网络剪枝算法, 通过上一层神经元的核心集移除下一层中冗余的神经元.

网络架构搜索方法也是长期以来模型压缩的研究热点之一, 最初的工作是基于手工设计和领域知识完成稀疏网络架构搜索[13, 14, 15].研究表明, 结合网络架构搜索和强化学习, 可有效提高找到最佳网络架构的可能性.Baker等[16]基于Q学习设计网络架构搜索算法, 通过经验知识对网络架构进行有条件的采样, 并根据具体任务自动生成高性能的DNN.Bello等[17]使用循环神经网络采样体系结构超参数, 设计性能更优的网络架构.但是, 从零开始设计稀疏且高性能的DNN需要更复杂的计算, 所以从基线网络中寻找性能优良的稀疏网络体系结构成为近年来另一个研究热点.Ashok等[18]提出两阶段压缩方法, 首先去除重要性较低的层, 然后通过策略梯度强化学习方法对各层进行压缩.He等[19]通过深度确定性策略梯度算法(Deep Deterministic Policy Gradient, DDPG)[20]学习网络体系结构各层的压缩率.Chin等[21]学习网络体系结构各层卷积核的全局排名, 寻找性能优良的稀疏网络体系结构.

虽然现有的网络剪枝和架构搜索方法取得较大进展, 但局部剪枝会导致次优的稀疏网络架构, 现有的许多压缩方法都是以逐层方式寻找网络的稀疏结构, 缺乏对网络结构全局信息的有效利用, 这种分层策略往往产生次优压缩结果.其次, 现有方法存在严重的标签依赖性, 大多数现有方法在剪枝过程中需要依赖标签数据, 导致在标签不可用时应用受到限制.

基于上述分析, 本文提出基于无标签的全局学习方法(Label-Free Global Comparison Learning, LFGCL), 在对预训练网络模型进行压缩的过程中不依赖于数据标签, 最小化剪枝网络与基线网络(Baseline Network)输出特征之间的差异性, 优化剪枝网络体系结构.将网络剪枝过程建模为马尔科夫决策过程(Markov Decision Process, MDP), 获得所有层的压缩率, 可从预先训练的基线网络中找到性能良好的稀疏网络架构.在多个数据集上的实验表明本文方法性能较优.

1 相关工作
1.1 强化学习

强化学习(Reinforcement Learning, RL)[22]本质是构建一个马尔可夫决策过程(MDP), 对问题进行建模.MDP由智能体(Agent)、环境(Environment)、状态(State)、动作(Action)、奖励(Reward)、状态转移概率(Possibility)组成.智能体是强化学习的本体, 作为学习者或决策者.环境是智能体外部所有事物, 通常指状态的集合.状态是对环境的描述, 可理解为一连串问题解决的步骤.动作是智能体的动作集合, 表示智能体在某一状态下采取的策略.奖励是智能体与环境交互的一种反馈信号, 用于指导智能体策略的发展.状态转移概率是智能体通过执行动作从当前状态到下一个状态的概率.

MDP也是智能体与环境的交互过程.智能体在当前状态执行一个动作后进入下一个新的状态, 并且环境会根据智能体所做的动作而产生相应的奖励值, 然后智能体在新的状态根据奖励值继续执行新的动作, 如此循环, 智能体与环境会不断地交互, 产生新的策略, 并通过新的策略改善自身的行为.智能体采用策略可分为确定性策略和随机性策略, 确定性策略是从状态空间到动作空间的映射函数, 随机性策略是在给定状态下, 智能体选择某个动作的概率分布.智能体执行一系列累积回报评判策略, 累积得到的奖励值越大, 认为该策略越优.累积回报有两种计算方式:1)在有限时界的情况下, 计算从当前状态到结束状态所有奖励之和; 2)在无时界的情况下, 设置奖励折扣因子γ 计算累积回报, 0≤ γ ≤ 1.当γ =0时, 智能体只考虑下一步的回报; 当γ 值越趋近于1, 会越多地考虑当前步数之后的奖励, 通常情况下需要考虑奖励值以修改γ 值.

1.2 模型压缩

近年来, 出现很多模型压缩方法, 可分为网络剪枝、低秩分解、知识蒸馏、量化.

低秩分解技术将几个小的权重矩阵替换原本较大的权重矩阵, 消除网络中存在的冗余.常用方法有奇异值分解(Singular Value Decomposition, SVD), SVD分解是将较复杂的张量矩阵分解为多个简单张量矩阵相乘的形式.Denton等[23]提出SVD分解技术, 使用SVD分解后矩阵近似神经网络的权重矩阵.Tai等[24]根据SVD分解的思想, 提出从零开始训练低秩约束卷积神经网络的方法, 可在不损失精度的情况下提升速度.虽然低秩分解技术逐渐应用于模型压缩中, 并在全连接层中达到较优的效果, 但在卷积层中压缩的效果欠优, 需要对网络进行逐层微调, 费时费力.

Caruana等[25]提出知识蒸馏技术, 并应用于模型压缩中.首先训练一个复杂网络, 再根据复杂网络的输出作为监督信号, 训练一个简单的网络.Hinton等[26]将知识蒸馏的框架用于神经网络, 将复杂网络和简单网络共同的输出作为目标函数, 并将复杂网络的知识通过蒸馏的方式传递给简单网络.在此基础上, Dong等[27]提出知识迁移结合神经网络架构的搜索方法, 对网络进行稀疏架构搜索, 通过知识蒸馏方法获得网络中适当的深度和宽度.

量化技术减少神经网络参数所占的浮点数位数, 降低网络模型所占的存储空间.可使用32位长度的浮点型数表示神经网络模型参数, 但在实际应用中不需要保留较高的精度, 可通过牺牲精度降低每个权值所需占用的空间.Jacob等[28]提出仅依靠整数近似神经网络中浮点计算的量化方案, 将权重和激活值都量化为8位整数, 仅将几个参数量化为32位整数, 使MobileNet架构的性能在延迟与准确性之间的权衡中得到明显提升.Li等[29]在二值化的基础上, 将32位的浮点数使用1、0、-1表示, 提出神经网络三值化方法.

网络剪枝算法也可分为剪枝算法研究和剪枝策略研究.本文提出的LFGCL是对网络模型逐层剪枝策略的改进.将网络剪枝过程建模为MDP, 剪枝网络作为环境, 网络模型的表征信息作为状态值, 网络每层浮点运算(Floating Point of Operations, FLOPs)压缩率作为动作值, 压缩率和模型性能的度量作为奖励值.通过智能体的迭代学习, 可在给定网络压缩目标下找到网络模型每层最优的压缩率.

2 基于无标签的全局学习方法
2.1 问题定义

在无标签方法的研究中, 基线网络中最后一个全连接层的输出特征使用f(X, W)表示, 其中, X表示网络中的输入图像, W表示权重张量.在结构化剪枝的过程中, 网络剪枝的基本单元是卷积核和神经元, 目的是在不严重影响模型精度的情况下找到一个较少的权重张量W'.记最终修剪的结构为c, 最后一个全连接层的输出特征为g(X, W').为了减少模型性能损失, f(X, W)和g(X, W')之间差异应尽可能小, 为此, 均方误差(Mean Squared Error, MSE)损失定义如下:

Lc= 12n∑i‖ f(Xi, W)-g(Xi, W') ‖22,

其中n表示输入的样本数量.最小化MSE损失可有效减少网络模型的性能损失, 基于MSE损失可定义类似准确率的度量指标:

Rca=exp(-Lc),

用于评估不同的网络结构.为了区分具有相似模型性能的不同稀疏网络模型, 参考之前对奖励值的设置研究[18], 本文进一步定义模型效率的度量方法.该度量方法可对剪枝过程中具有最小损失而较大压缩率的稀疏网络模型提供更高的分数, 即

Rce=C(2-C), C=1- FcFb,

其中, C表示剪枝网络相对基线网络FLOPs压缩比, Fc表示剪枝网络的浮点预算, Fb表示基线网络的浮点预算.

结合模型性能和模型效率度量, 得到反映每个稀疏网络模型优劣的分数:

Rc= Rca· Rce.(1)

寻找最优稀疏网络体系结构等价于搜索获得最高度量分数Rc的体系结构.

2.2 方法框架

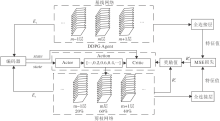
LFGCL框图如图1所示.首先, 使用基线网络对目标网络进行初始化, 基于网络结构的特征化表示, 利用DDPG将所有层的压缩率直接映射为一个动作值.再由剪枝算法根据压缩率对网络结构进行压缩.然后, 将压缩后的网络作为新的目标网络, 进行迭代压缩, 直到满足预先设定的目标压缩率.同时, 对智能体进行训练, 使每次压缩后的目标网络和基线网络的全连接层输出特征之间的差异最小化.网络框架可分为两部分:网络架构搜索和剪枝算法.

LFGCL具体步骤如下.

1)网络模型表征信息的提取.首先提取待剪枝网络模型相应的特征, 包括层类型ty等信息.再使用1个全连接层作为编码器对表征信息进行编码, 输入为网络模型相应的特征, 输出为1× m维向量, 其中m表示网络层数.最后将该向量作为DDPG的state信息.

2)获取每层的压缩率.使用DDPG中的Actor网络, 根据1)中获取的状态信息得到网络模型各层的剪枝率.Actor网络输入为state、输出为m× 1维的向量, 每维表示对应的层压缩率, m表示网络层数.

3)网络剪枝.基于权值绝对值大小对每层的卷积核排序, 根据每层的压缩率对网络进行剪枝.

4)训练DDPG.使用式(1)定义的奖励值函数评估剪枝策略, 对DDPG网络进行训练以改善剪枝策略.

图1 LFGCL框图Fig.1 Framework of LFGCL

2.3 网络架构搜索

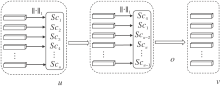
由于网络架构搜索空间巨大, 本文采用迭代的方式寻找目标网络体系结构, 这需要提取网络结构有效的表征信息, 区分不同的稀疏网络架构.根据文献[19]的研究, 可使用一维张量(ty, h, w, flop, stride, k, r)表示网络架构.其中:ty表示层的类型, 1表示全连接层, 0表示卷积层; h、w分别表示每层输出特征图的高和宽; flop表示剪枝后网络相对基线网络的每层FLOPs压缩率; stride表示每层的步长, 1表示全连接层的stride; k表示每层卷积核或神经元的大小, 1表示神经元的大小; r表示剪枝后网络相对基线网络每层输出通道大小的比值.每个体系结构c的特征信息可表示为Sc, 基于上述的张量表示, 可较容易表示网络架构在迭代剪枝中的任何变化.

寻找一个简化的网络体系结构可作为一种顺序决策过程进行处理, 文献[18]工作也表明, MDP在处理这类问题时较有效.通常可使用元组M={S, A, P, R, γ }表示网络架构搜索过程.

S表示状态空间.给定一个网络体系结构c, Sc被视为MDP的状态.随着网络修剪过程不断推进, 网络体系结构逐渐被压缩, 导致MDP在不同状态之间发生转换.

A表示动作空间.动作空间可使用m维的连续空间表示, 其中m为网络层数, 每维表示相应层的压缩率.在每个时间步骤中, 选择一个动作用于通道剪枝, 将当前网络体系结构转换为另一个体系结构.

P表示状态转换函数(State Transition).给定一个状态S, 动作A总是以100%的概率将当前网络体系结构转换为一个新的体系结构S', 因此状态转换是确定性的.

R表示奖励值.网络体系结构的奖励是反映体系结构好坏的度量分数, 对于生成的每个体系结构c, Rc表示奖励值.

γ 表示奖励折扣因子.在剪枝过程中, 智能体需要考虑第t个时间步骤后更多的奖励值, 设置γ =1.

根据上述MDP, 本文利用强化学习进行策略推理.在第t个时间步, 智能体从环境中接收状态St, 并输出动作At作为所有层的压缩率.遵循预定义的网络剪枝策略, 网络模型被简化为一个新的体系结构, 环境的状态从St转移到St+1.同时, 将奖励值Rt反馈给智能体.每个回合的最大迭代次数设为50, 在策略学习探索的过程中, 从基线网络的初始状态开始, 智能体与环境交互根据进行状态序列采样.

由于动作空间是连续空间, 本文采用基于离线策略的DDPG进行有效的探索学习.DDPG由Actor网络和Critic网络组成, Actor网络执行每个状态到某一动作的直接映射, 定义确定性策略, 该动作通常与截断正态分布产生的噪声混合, 用于提高智能体的探索能力, 定义如下:

π˙(s)~TN(π (s|θ π ), σ 2, 0, 1).

在探索过程中, 参数σ 在每个回合(Episode)初始化为0.5, 并在每个迭代(Epoch)之后呈指数衰减.在每次参数更新迭代中, 从缓冲区中进行采样, 最大化平均奖励值以更新Actor网络, 定义如下:

$\nabla_{\theta^{\pi}} J \approx \left.\left.\quad \frac{1}{N} \sum_{i=1}^{N} \nabla_{a} Q(s, a)\right|_{s=s_{i}, a=\pi\left(s_{i}\right)} \nabla_{\theta^{\pi}} \pi\left(s \mid \theta^{\pi}\right)\right|_{s=s_{i}}$,

其中Critic网络Q(s, a)为与状态s和动作a相关的Q值.

为了更新网络, 目标值定义为

yi=ri+γ Q'(si+1, π '(si+1|θ π ')|θ Q'),

其中, π '(s|θ π ')为Actor网络的目标值, Q'(s, a|θ Q')为Critic网络的目标值.Critic网络通过尽量减少估计值和目标网络值的损失进行更新, 即

L= 1N∑i=1N(yi-Q(si, ai|θ Q))2.

2.4 网络剪枝方法

网络剪枝可分为网络层剪枝和层内卷积核的剪枝, 本文方法只对层内的卷积核进行剪枝.在文献[30]中已证明权重绝对值之和的大小可作为重要性分数, 用于表示卷积核或神经元的重要性.因此本文将权重绝对值之和的大小作为卷积核或神经元重要性的判断指标.对每层卷积核的修剪过程如图2所示.

图2 网络剪枝算法框图Fig.2 Framework of network pruning algorithm

具体网络剪枝过程如下.

1)对卷积核的重要性进行排序.在每层中, 计算卷积核或神经元的重要性分数, 并根据重要性分数按从小到大的方式对卷积核或神经元进行排序.

2)计算当前层需要删除卷积核的个数.假设该层给定的压缩率为o, 卷积核的个数为u, 需要删除的卷积核个数v=ou, 如果v为小数, 对其进行向下取整操作, 只保留整数部分.

3)删除当前层不重要的卷积核.如果v< u, 直接删除前v个卷积核.如果v=u, 即当前层要修剪的卷积核个数等于剩余的卷积核个数, 为了保证前后层之间的连通性, 在该层保留重要性分数最高的那个卷积核.

3 实验及结果分析
3.1 实验环境

实验使用的数据集为CIFAR-10和CIFAR-100[31].网络模型使用VGGNet(Visual Geometry Group Network)[32]和残差网络(Residual Network, ResNet)[33].

CIFAR-10数据集包含10个类别的60 000幅32× 32的彩色图像, 每个类别有6 000幅图像.CIFAR-100数据集和CIFAR-10数据集类似, 包含100个类别的60 000幅32× 32的彩色图像, 每个类别有600幅图像.

VGGNet网络模型使用VGG-16网络, VGG-16网络由13个卷积层和3个全连接层组成.为了提高VGG-16网络的收敛性, 参考文献[30], 将VGG-16网络更改为由13个卷积层和2个全连接层组成的结构, 前13个卷积层保持不变, 最后2个全连接层中神经元的个数分别为512和10.

ResNet网络模型使用ResNet-56和ResNet-110网络, 主要由残差块和残差连接组成.其中一个残差块包含多个卷积层, 对于一个残差块, 除非块中有快捷连接, 否则输入和输出特征映射的大小必须相等.所以为了保持每块的输出通道不变, LFGCL只压缩每个块中除最后一层之外的卷积层.

对于CIFAR-10、CIFAR-100数据集, 将原始数据集分割为包含45 000幅图像的训练集和包含5 000幅图像的验证集.网络模型训练过程中的参数设置如下:迭代次数(Epoch)设为300; 批量大小(Batchsize)为256; 学习率初始化为0.1, 在迭代150次和255次时分别递减10倍.优化器采用随机梯度下降算法, 动量大小为0.9, 权重衰减大小为5× 10-4.同时, 为了避免网络模型在训练中出现过拟合现象, 本文采用随机打乱、零填充和随机取样等技术进行数据增强[13].

参考文献[19], 本文方法的参数设置如下:Actor网络包含2个隐藏层, 每层有300个神经元; Critic网络包含1个隐藏层, 每层有300个神经元; 缓冲区大小设为600, 批量大小设为32; Actor网络的学习率设为0.001, Critic网络的学习率设为0.002; 目标网络软更新的超参数τ =0.01; 回合次数设为600.

3.2 VGGNet网络实验结果

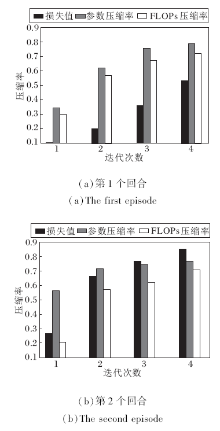
本文方法在网络剪枝过程中不依赖数据标签信息, 计算验证集上的MSE损失, 评估压缩后的网络模型性能.为了验证损失值和压缩率之间的关系, 在CIFAR-10数据集上对VGG-16网络进行压缩实验, 并随机选取2个回合的修剪结果进行分析, 具体如图3所示.随着参数和FLOPs压缩率的上升, 损失值也逐渐上升, 说明在剪枝过程中, 转换损失值可作为评估不同稀疏网络体系结构的度量指标.

图3 在CIFAR-10数据集上VGG-16网络的剪枝结果Fig.3 Pruning result of VGG-16 network on CIFAR-10 dataset

在剪枝过程中, 设定一个FLOPs压缩目标作为DDPG在每个回合上探索的终止条件, 让智能体进行多个回合的探索学习, 在实现FLOPs压缩目标的同时尽可能地减少精度损失.为了探究在不同的FLOPs压缩目标下各层FLOPs和参数的压缩情况, 采用70%、62%和50%的FLOPs压缩目标, 在CIFAR-10数据集上对VGG-16网络进行压缩实验, 结果如图4所示.在不同的FLOPs压缩目标下, 第8、9、10和12层的剪枝力度最大, 表明这些层在整个网络结构中具有最不重要的卷积核和神经元.同时也说明, 学习网络体系结构的表征信息, 可有效找到网络体系结构中每层适当的压缩率.

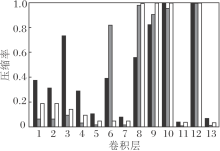图4 在不同FLOPs压缩目标下VGG-16网络各层的剪枝结果Fig.4 Pruning results of each layer of VGG-16 network with different FLOPs compression targets

为了进一步验证本文方法的可行性, 使用如下对比方法:GAL(Generative Adversarial Learning)[10]、HRank(High Rank of Feature Maps)[11]、SSS(Sparse Structure Selection)[34].VGG-16网络的剪枝结果如表1所示.

表1 各方法在CIFAR-10数据集上VGG-16网络的剪枝结果 Table 1 Pruning results of VGG-16 network by different methods on CIFAR-10 dataset %

由表1可见, 在相近的精度损失下, LFGCL可压缩更多的参数和FLOPs.SSS在0.33%的精度损失下, 可压缩66.70%的参数和36.30%的FLOPs, 而LFGCL在0.37%的精度损失下可压缩92.32%的参数和62.70%的FLOPs.此外, GAL在0.54%的精度损失下, 可压缩82.20%的参数和45.20%的FLOPs.HRank在0.53%的精度损失下, 可压缩82.90%的参数和65.30%的FLOPs.LFGCL压缩87.82%的参数和70.40%的FLOPs, 只损失0.43%的精度.上述结果表明在DNN中, LFGCL可进行有效压缩.

3.3 ResNet网络实验结果

为了进一步评估LFGCL在具有残差结构模型中的适用性, 利用CIFAR-10数据集对ResNet-56和ResNet-110网络进行压缩实验, 并与其它的通道剪枝方法进行对比.具体对比方法如下:GAL[10]、HRank[11]、AMC(AutoML for Model Compression)[19]、TAS(Transformable Architecture Search)[27]、LFPC(Learning Filter Pruning Criteria)[35]、SFP(Soft Filter Pruning)[36]、FPGM(Filter Pruning via Geo-metric Median)[37].各方法在CIFAR-10数据集上的剪枝结果如表2和表3所示.

表2 各方法在CIFAR-10数据集上ResNet-56网络的剪枝 结果 Table 2 Pruning results of ResNet-56 network by different methods on CIFAR-10 dataset %
表3 各方法在CIFAR-10数据集上ResNet-110网络的剪枝结果 Table 3 Pruning results of ResNet-110 network by different methods on CIFAR-10 dataset %

在表2中, AMC压缩50%的FLOPs会导致0.9%的精度损失, 而LFGCL压缩61.95%的FLOPs只有0.38%的精度损失, 说明在ResNet网络模型中通过深度确定性策略梯度算法学习的全局剪枝策略优于分层剪枝策略, LFGCL可找到网络各层更优的压缩率.此外, 相比GAL和LFPC, LFGCL的压缩结果更优.在表2中, GAL在提升0.12%精度的情况下, 可压缩11.80%的参数和37.60%的FLOPs, 而LFGCL在0.33%的精度提升下可压缩35.26%的参数和41.64%的FLOPs.LFPC压缩52.90%的FLOPs会导致0.35%的精度损失, 而LFGCL在相近的精度损失下可压缩61.95%的FLOPs, 结果表明无论是在剪枝过程中不使用标签信息还是寻找网络每层最优的压缩率, LFGCL对稀疏网络架构的探索都更高效, 在较少的精度损失下可找到更稀疏的网络体系结构.同时, 相比SFP和TAS, LFGCL在2种ResNet网络上效果都更优, 可在更低精度损失下找到稀疏网络架构的深度和宽度.相比FPGM和HRank, LFGCL在ResNet-56网络上可取得较好的结果.但在更深的网络结构ResNet-110中, FPGM和HRank却优于LFGCL.由于ResNet-110网络层数较大, 网络结构的搜索空间显著增大, LFGCL在此高维连续空间中搜索最优的网络结构需要巨大的计算量, 因此在计算量有限的情况下, LFGCL容易收敛到局部最优解.

为了验证LFGCL在更复杂的分类任务上的性能, 利用CIFAR-100数据集对ResNet-56和ResNet-110网络进行压缩实验, 选择SFP、TAS、FPGM为对比方法, 结果如表4和表5所示.在表4中, LFGCL在压缩51.64% FLOPs和27.61%参数的情况下只造成0.36%的精度损失, 性能明显最优.在表5中, 在压缩约50%FLOPs的情况下, FLGCL导致0.49%的精度损失, 而其它方法的精度损失在1.59%和2.86%之间.

表4 各方法在CIFAR-100数据集上ResNet-56网络的剪枝结果 Table 4 Pruning results of ResNet-56 network of different methods on CIFAR-100 dataset %
表5 各方法在CIFAR-100数据集上ResNet-110网络的剪 枝结果 Table 5 Pruning results of ResNet-110 network of different methods on CIFAR-100 dataset %

上述实验表明, LFGCL适用于剪枝具有残差块的ResNet网络模型, 也表明LFGCL在简单和复杂的数据集上都能找到性能和效率均衡的稀疏网络架构.

4 结束语

为了避免对网络体系结构进行逐层修剪而导致次优的稀疏网络架构及在剪枝过程中对标签数据的依赖性, 提出基于无标签的全局网络剪枝方法(LFGCL).不同于现有的剪枝方法, LFGCL在剪枝过程中不需要使用样本的标签信息, 适用性较强.利用深度确定性策略梯度算法, 根据网络模型的表征信息, LFGCL可有效寻找各层的压缩率.实验表明, 在常规和复杂的网络模型上, LFGCL较有效, 在极少的精度损失下压缩更多的参数和FLOPs.今后将考虑在更大的数据集上进行评估和测试, 更全面地验证LFGCL的有效性.

参考文献
[1] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet Classification with Deep Convolutional Neural Networks // Proc of the 25th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2012: 1097-1105. [本文引用:1]
[2] KORTYLEWSKI A, HE J, LIU Q, et al. Compositional Convolutional Neural Networks: A Deep Architecture with Innate Robustness to Partial Occlusion // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 8940-8949. [本文引用:1]
[3] KIM I, BAEK W, KIM S, et al. Spatially Attentive Output Layer for Image Classification // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 9533-9542. [本文引用:1]
[4] GUO C X, FAN B, ZHANG Q, et al. AugFPN: Improving Multi-scale Feature Learning for Object Detection // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 12595-12604. [本文引用:1]
[5] REN S Q, HE K M, GIRSHICK R, et al. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. [本文引用:1]
[6] 林景栋, 吴欣怡, 柴毅, 等. 卷积神经网络结构优化综述. 自动化学报, 2020, 46(1): 24-37.
(LIN J D, WU X Y, CHAI Y, et al. Structure Optimization of Convolutional Neural Networks: A Survey. Acta Automatica Sinica, 2020, 46(1): 24-37. ) [本文引用:1]
[7] HAN S, MAO H Z, DALLY W J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding // Proc of the International Conference on Learning Representation. Washington, USA: IEEE, 2016: 3-7. [本文引用:1]
[8] HAN S, POOL J, TRAN J, et al. Learning Both Weights and Connections for Efficient Neural Networks // Proc of the 28th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2015: 1135-1143. [本文引用:1]
[9] LIN J, RAO Y M, LU J W, et al. Runtime Neural Pruning // Proc of the 31st International Conference on Neural Information Proce-ssing Systems. Cambridge, USA: The MIT Press, 2017: 2181-2191. [本文引用:1]
[10] LIN S H, JI R R, YAN C Q, et al. Towards Optimal Structured CNN Pruning via Generative Adversarial Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 2790-2799. [本文引用:3]
[11] LIN M B, JI R R, WANG Y, et al. HRank: Filter Pruning Using High-Rank Feature Map // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 1529-1538. [本文引用:3]
[12] MUSSAY B, OSADCHY M, BRAVERMAN V, et al. Data-Independent Neural Pruning via Coresets[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1907.04018.pdf. [本文引用:1]
[13] HOWARD A G, ZHU M L, CHEN B, et al. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications [C/OL]. [2020-07-13]. https://arxiv.org/pdf/1704.04861.pdf. [本文引用:2]
[14] ZHANG T, QI G J, XIAO B, et al. Interleaved Group Convolutions // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 4373-4382. [本文引用:1]
[15] ZHANG X Y, ZHOU X Y, LIN M X, et al. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 6848-6856. [本文引用:1]
[16] BAKER B, GUPTA O, NAIK N, et al. Designing Neural Network Architectures Using Reinforcement Learning[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1611.02167.pdf. [本文引用:1]
[17] BELLO I, ZOPH B, VASUDEVAN V, et al. Neural Optimizer Search with Reinforcement Learning[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1709.07417.pdf. [本文引用:1]
[18] ASHOK A, RHINEHART N, BEAINY F, et al. N2N Learning: Network to Network Compression via Policy Gradient Reinforcement Learning[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1709.06030v1.pdf. [本文引用:3]
[19] HE Y H, LIN J, LIU Z J, et al. AMC: AutoML for Model Compression and Acceleration on Mobile Devices // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 784-800. [本文引用:4]
[20] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous Control with Deep Reinforcement Learning[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1509.02971.pdf. [本文引用:1]
[21] CHIN T W, DING R Z, ZHANG C, et al. Towards Efficient Model Compression via Learned Global Ranking // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 1518-1528. [本文引用:1]
[22] SUTTON R S, BARTO A G. . Reinforcement Learning: An Introduction. Cambridge, USA: The MIT Press, 1998. [本文引用:1]
[23] DENTON E, ZAREMBA W, BRUNA J, et al. Exploiting Linear Structure within Convolutional Networks for Efficient Evaluation // Proc of the 27th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2014: 1269-1277. [本文引用:1]
[24] TAI C, XIAO T, ZHANG Y, et al. Convolutional Neural Networks with Low-Rank Regularization[C/OL]. [2020-07-13]. https://arxiv.org/abs/1511.06067.pdf. [本文引用:1]
[25] CARUANA R, NICULESCU-MIZIL A. Model Compression // Proc of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2006: 535-541. [本文引用:1]
[26] HINTON G, VINYALS O, DEAN J. Distilling the Knowledge in a Neural Network[C/OL]. [2020-07-13]. https://arxiv.org/abs/1503.02531.pdf [本文引用:1]
[27] DONG X Y, YANG Y. Network Pruning via Transformable Architecture Search // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2019: 759-770. [本文引用:2]
[28] JACOB B, KLIGYS S, CHEN B, et al. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2018: 2704-2713. [本文引用:1]
[29] LI F F, ZHANG B, LIU B. Ternary Weight Networks[C/OL]. [2020-07-13]. https://arxiv.org/abs/1605.04711.pdf. [本文引用:1]
[30] LI H, KADAV A, DURDANOVIC I, et al. Pruning Filters for Efficient ConvNets[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1608.08710.pdf. [本文引用:2]
[31] KRIZHEVSKY A, HINTON G. Learning Multiple Layers of Features from Tiny Images. Master Dissertation. Toronto, Canada: University of Toronto, 2009. [本文引用:1]
[32] SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition[C/OL]. [2020-07-13]. https://arxiv.org/pdf/1409.1556.pdf. [本文引用:1]
[33] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:1]
[34] HUANG Z H, WANG N Y. Data-Driven Sparse Structure Selection for Deep Neural Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 304-320. [本文引用:1]
[35] HE Y, DING Y H, LIU P, et al. Learning Filter Pruning Criteria for Deep Convolutional Neural Networks Acceleration // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 2006-2015. [本文引用:1]
[36] HE Y, KANG G L, DONG X Y, et al. Soft Filter Pruning for Accelerating Deep Convolutional Neural Networks // Proc of the 27th International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2019: 2234-2240. [本文引用:1]
[37] HE Y, LIU P, WANG Z W, et al. Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2019: 4340-4349. [本文引用:1]