引用本文
张铭津, 彭晓琪, 郭杰, 李云松, 王楠楠, 高新波. 基于多残差网络的结构保持超分辨重建. 模式识别与人工智能, 2021,34(3): 232-240
ZHANG Mingjin, PENG Xiaoqi, GUO Jie, LI Yunsong, WANG Nannan, GAO Xinbo. Structure-Preserving Super-Resolution Reconstruction Based on Multi-residual Network. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(3): 232-240.  
Doi: 10.16451/j.cnki.issn1003-6059.202103005
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于多残差网络的结构保持超分辨重建
张铭津1,2, 彭晓琪1, 郭杰1, 李云松1, 王楠楠1, 高新波1,3
1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室 西安 710071
2.中国科学院西安光学精密机械研究所 中国科学院光谱成像技术重点实验室 西安 710119
3.重庆邮电大学 图像认知重庆市重点实验室 重庆 400065
通讯作者:

高新波,博士,教授,主要研究方向为模式识别、计算机视觉.E-mail:gaoxb@cqupt.edu.cn.

作者简介:

张铭津,博士,副教授,主要研究方向为模式识别、计算机视觉.E-mail:mjinzhang@xidian.edu.cn.

彭晓琪,硕士研究生,主要研究方向为模式识别、计算机视觉.E-mail:xqpengxidian@163.com.

郭 杰,博士,副教授,主要研究方向为图像传输与处理.E-mail:jguo@mail.xidian.edu.cn.

李云松,博士,教授,主要研究方向为图像传输与处理.E-mail:ysli@mail.xidian.edu.cn.

王楠楠,博士,教授,主要研究方向为模式识别、计算机视觉.E-mail:nnwang@xidian.edu.cn.

收稿日期: 2020-09-25 接受日期: 2021-02-05
资助项目: 国家自然科学基金青年基金项目(No.61902293); 陕西省高校科协人才托举计划项目(No.20200103); 中国科学院光谱成像技术重点实验室开放基金项目(No.LSIT201901W); 中央基本科研业务费新教师创新项目(No.XJS200112)资助
摘要

针对图像超分辨率重建中几何结构扭曲和细节缺失等问题,文中提出基于多残差网络的结构保持超分辨重建算法.在小波变换域和梯度域上进行深度学习.文中算法包含3种残差网络.残差梯度网络用于结构及边缘信息的重建.残差小波变换网络从整体上进行图像高频信息的重建.残差通道注意力网络通过调整网络注意力,着重学习重要的通道特征,从局部恢复图像高频信息,提高重建效率.实验表明,文中算法在定量结果和视觉效果方面均取得较优表现.

关键词: 超分辨率重建; 深度学习; 多残差网络; 结构保持
中图分类号:TP 391.4
Structure-Preserving Super-Resolution Reconstruction Based on Multi-residual Network
ZHANG Mingjin1,2, PENG Xiaoqi1, GUO Jie1, LI Yunsong1, WANG Nannan1, GAO Xinbo1,3
1. State Key Laboratory of Integrated Services Networks, Xidian University, Xi'an 710071
2. Key Laboratory of Spectral Imaging Technology, Xi'an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi'an 710119
3. Chongqing Key Laboratory of Image Cognition, Chongqing University of Posts and Telecommunications, Chongqing 400065
Corresponding author:
GAO Xinbo, Ph.D., professor. His research interests include pa-ttern recognition and computer vision.

AboutAuthor:
ZHANG Mingjin, Ph.D., associate professor. Her research interests include pattern recognition and computer vision.
PENG Xiaoqi, master student. Her research interests include pattern recognition and computer vision.
GUO Jie, Ph.D., associate professor. His research interests include image transmission and processing.
LI Yunsong, Ph.D., professor. His research interests include image transmission and processing.
WANG Nannan, Ph.D., professor. His research interests include pattern recognition and computer vision.

Fund:Youth Fund of National Natural Science Foundation of China(No.61902293); Young Talent Fund of University Association for Science and Technology in Shaanxi(No.20200103); Open Research Fund of CAS Key Laboratory of Spectral Imaging Technology(No.LSIT201901W); Fundamental Research Funds for the Central Universities(No.XJS200112)
Abstract

Aiming at the problems of geometric structure distortion and missing details in image super-resolution reconstruction, a structure-preserving super-resolution reconstruction algorithm based on multi-residual network is proposed. Deep learning is carried out in the wavelet transform domain and the gradient domain. Three kinds of residual networks are introduced. The structure and the edge information are reconstructed by the residual gradient network. The high-frequency information of the image is reconstructed as a whole by the residual wavelet transform network. The network attention is adjusted by the residual channel attention network , the important channel features are emphatically learned, and the high frequency information of the image is recovered locally. Experiments show that the proposed algorithm achieves better performance in both quantitative results and visual effects.

Key words: Key Words Super-resolution Reconstruction; Deep Learning; Multi-residual Networks; Structure Preservation

本文责任编委 徐勇

Recommended by Associate Editor XU Yong

图像超分辨率(Super Resolution, SR)旨在从低分辨率(Low Resolution, LR)图像中恢复高分辨率(High Resolution, HR)图像.SR[1, 2, 3, 4, 5]为计算机视觉领域的基本问题, 应用于多种图像分析任务, 包括安全监控[6]、医学影像[7]、行人再识别[8, 9, 10]等.由于每个LR图像可能对应多个HR图像, 因此是一个不适定的逆问题.

近年来, 深度学习发展迅速, 研究人员将其与图像的超分辨率[11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]重建结合, 取得有效成果.Dong等[11]提出超分辨率卷积神经网络(SR Convolutional Neural Networks, SRCNN), 将深度学习与图像超分辨结合, 在重建效果与速度方面均有重大改进.然而, SRCNN网络过浅导致感受野较小、计算量较大、收敛速度较慢.为了使网络从低分辨率图像中学习更多信息, 增强重建性能, 通常需要增加网络层数.然而, 简单的增加层数会给网络的训练带来难度, 丢失图像细节信息, 降低重建图像的质量.

因此, 研究人员提出基于残差结构[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]的算法, 通过学习图像的高频细节, 恢复高质量的图像, 解决图像退化问题.Kim等[12]将残差结构应用于卷积网络中, 并将深度设计为20层, 得到非常深的卷积网络(Accurate Image Super-Resolution Using Very Deep Convolutional Networks, VDSR)结构.Tai等[13]将全局残差结构及局部残差结构与多权重递归操作结合, 并将网络规模提升至52层, 得到深度递归残差网络(Deep Recursive Residual Network, DRRN).Tai等[17]还受到人类大脑皮层的启发, 设计长期记忆网络模型(Memory Network, MemNet), 深度达80层, 记忆单元利用门控机制自适应地保留和存储信息, 从而建立长期记忆.Choi等[18]提出具有选择单元的深度卷积神经网络(Deep Convolutional Neural Networks with Selection Units, SelNet), 设计非线性单元, 即选择单元(Selection Unit, SU), 这是对修正线性单元(Rectified Linear Unit, ReLU)的优化, 能更灵活地处理非线性功能.Li等[19]设计多尺度残差网络(Multi-scale Residual Network, MSRN), 充分利用多尺度特征及全局特征, 具有较好的可扩展性.级联残差网络(Cascading Residual Network, CARN)[20]为一种轻量级网络, 设计目的是为了适用于实际场景, 因此关注网络的速度, 同时保证较优性能.网络采用局部级联和全局级联的方式, 获取丰富的信息.He等[21]根据常微分方程, 设计用于图像超分辨率重建的网络结构(Ordinary Differential Equa-tion Inspired Schemes for Super-Resolution Network, OISR), 并将改进的前向欧拉公式用于残差块的设计.He等[21]还联系网络与微分动力学系统, 对残差块及超分辨率的映射过程做出数学解释.Zhang等[22]结合注意力机制与图像超分辨问题, 设计残差通道注意力网络(Residual Channel Attention Net-work, RCAN), 可自适应地学习重要的通道特征, 提高表达能力.RCAN采用残差中的残差(Residual in Residual, RIR)结构, 并结合长跳连接和短跳连接, 有效降低训练难度, 提升网络效率.

现有算法虽然可生成高逼真度的超分辨率图像, 但始终存在几何结构失真及缺少锐利边缘和精细纹理等问题.这些方法大多只采用单一功能的残差网络, 没有根据图像的几何结构、纹理等特征选择具有特定功能的网络, 缺乏灵活性和针对性.因此, 本文提出基于多残差网络的结构保持超分辨重建算法, 改变以往只在空间域进行深度特征提取的方式, 转而在梯度域和小波变换域上设计深度网络, 并加入残差通道注意力网络以调整网络关注图像的重要信息, 有利于获得完整清晰的几何结构.本文提出的多残差网络包括残差梯度网络、残差小波变换网络及残差通道注意力网络.残差梯度网络能锐化几何图形的边缘, 保留图像的结构信息.残差小波变换网络通过小波变换产生四个子带, 包含图像的高频信息和低频信息, 有利于纹理细节部分的恢复重建.残差通道注意力网络能调整网络的注意力, 使网络关注到重要的特征, 提高图像的重建效果.

1 基于多残差网络的结构保持超分辨重建算法
1.1 网络结构

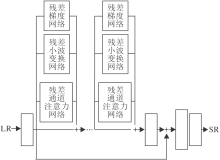
本文的多残差网络结构如图1所示.网络主要由3个模块组成:特征预提取模块(Feature Pre-extraction Module, FPM)、特征映射模块(Feature Mapping Module, FMM)、重建模块(Reconstruction Module, RM).

图1 多残差网络框图Fig.1 Framework of multi-residual network

整个网络的输入记为XLR.在特征预提取模块中, 采用一个卷积层进行初始特征的提取:

F0=fFPM(XLR),

其中, fFPM(· )表示特征提取网络的卷积运算, F0表示从XLR中提取的特征.

在特征映射中, 选择3种具有特定处理功能的残差块, 并嵌入可扩展残差组中, 以进行图像超分辨重建.这种结构突破残差学习的僵化, 更具灵活性.将第N个残差块的输入记为FN-1, 残差运算

RN(FN-1)=RG, N(FN-1)+RDWT, N(FN-1)+RCA, N(FN-1),

其中, RG, N(FN-1)表示残差梯度网络, RDWT, N(FN-1)表示残差小波变换网络, RCA, N(FN-1)表示残差通道注意力网络, 在残差梯度网络中, 提取输入特征图的梯度并通过简单的残差块, 再经过卷积层, 得到残差结果.通过残差梯度网络, 能有效捕获图像的几何信息, 保留图像的边缘细节.在残差小波变换网络中, 对输入特征进行二维离散小波变换, 产生4个子带(即近似、水平、垂直和对角线), 将4个子带输入卷积层, 提取图像的低频特征信息和高频特征信息, 最后进行二维离散小波逆变换.残差小波网络能有效恢复图像的高频细节信息.

将F0通过第1个多残差块, 输出结果:

F1=F0+R1(F0).

同理可得:

F2=F1+R2(F1), ︙FN=FN-1+RN(FN-1),

其中, FN表示第N个残差计算的结果.经过N次残差提取, 可得到完全提取的特征.将FN通过卷积层, 得

FCV=fCV(FN), FFMM=FCV+F0,

其中FFMM表示特征映射模块的输出.将FFMM通过一个上采样块和一个卷积层, 得到重建后的图像:

X︿SR=fRM(FFMM)=fMRN(XLR),

其中fRM(· )表示重建模块(RM)的函数, fMRN(· )表示整个网络 (Multi-residual Network, MRN) 的函数. X︿SR为MRN的输出结果, 应与XHR尽可能地匹配.对于训练集 {XLRk, XHRk}k=1l, L1损失函数[23]的定义如下:

L(Θ )= 1l∑k=1l‖ fMRN( XLRk) -XHRk‖ 1,

其中, XLRk为第 k 个输入图像, XHRk为对应的高分辨率图像, l为训练对的数目.

1.2 残差梯度网络

自然图像中包含丰富的几何结构及边缘信息, 而在重建过程中, 几何结构通常会出现不期望的弯曲、断裂等现象, 边缘也可能存在模糊等问题, 极大地破坏重建图像的视觉效果.为了更好地保留几何结构, 获得清晰的边缘, 引入残差梯度网络.计算相邻像素之间的差异获得图像的梯度图[24], 残差梯度块的目标是实现梯度图从LR模式到HR模式的转换.残差梯度网络包括梯度块和卷积层.在梯度块中, 首先获取输入图像的梯度图, 再将其通过一个简单的残差块进行特征提取.

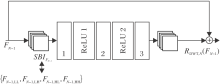
图像是一个二维的离散数组, 通过推广二维连续型求函数偏导的方法, 求得图像的偏导数, 即在(x, y)处的最大变化率, 即梯度.残差梯度网络的具体操作过程如图2所示, 考虑第N个残差块, 输入为FN-1, 有

gy= ∂FN-1(x, y)∂y=FN-1(x, y+1)-FN-1(x, y),

图2 残差梯度网络框图Fig.2 Flow chart of residual gradient network

则(x, y)处的梯度表示为

$\nabla F_{N-1} \equiv \operatorname{grad}\left(F_{N-1}\right) \equiv\left[g_{x}, g_{y}\right]^{\mathrm{T}}=\left[\frac{\partial F_{N-1}}{\partial x}, \frac{\partial F_{N-1}}{\partial y}\right]^{\mathrm{T}}$

大小为

$M(x, y)=\operatorname{mag}\left(\nabla F_{N-1}\right)=\sqrt{g_{x}^{2}+g_{y}^{2}}$.

由于梯度强度足以反映图像中局部区域的锐利程度, 因此不考虑梯度方向信息, 采用梯度强度图作为梯度图.梯度图可看作是另一种图像, 因此可利用图像到图像转换的技术, 学习两种梯度图之间的映射关系.转换过程等效于从LR边缘到HR边缘的空间分布转换.由于梯度图的大多数区域都接近于0, 因此网络可将更多的注意力集中在边缘的空间关系上, 以此捕获结构信息, 并为重建图像生成近似梯度图.将提取的梯度特征通过一个卷积层, 即可得到残差梯度网络的残差结果RG, N(FN-1).

1.3 残差小波变换网络

残差梯度网络从水平、垂直两个方向保留图像的几何结构信息, 增强图像边缘, 但忽略其它方向的信息, 对图像的高频细节恢复不足, 因此, 本文引入残差小波变换网络, 保留图像的低频信息, 以及水平、垂直和对角方向的高频信息, 包括几何结构及纹理细节等.离散小波变换[25]是一种域变换, 通常用于图像处理.图像进行小波变换后为LL、LH、HL、HH四个子带, 其中LL子带与其它3个子带系数相差较大, 小波系数本质上是稀疏的, 学习小波系数的残差进一步增强这种稀疏性.稀疏性有助于加快训练过程, 因为它仅在很少的系数中包含大量信息.离散小波变换可通过低通滤波器和高通滤波器逐层分离图像.在将图像分解并通过离散小波变换剥离后, 获得包含不同频率信息的多个图像.可通过对不同的图像执行特定的操作, 实现更有针对性的处理.

残差小波变换网络的具体操作过程如图3所示, 考虑第N个残差块, 输入为FN-1, 首先对FN-1进行二维离散小波变换, 获得具有丰富频率信息的4个子带图像(Sub-bands Images, SBI):

$S B I_{F_{N-1}}=\left\{F_{N-1, \mathrm{LL}}, F_{N-1, \mathrm{LH}}, F_{N-1, \mathrm{HL}}, F_{N-1, \mathrm{HH}}\right\}$.

图3 残差小波变换网络框图Fig.3 Framework of residual wavelet transform network

其中:FN-1, LL为低频子带图像, 提取图像主要的结构元素; FN-1, LH、FN-1, HL、FN-1, HH为高频信息丰富的图像, 主要提取图像的细节信息.

然后, 将这4种图像输入卷积层中以提取特征, 再对提取的特征信息进行二维离散小波逆变换, 得到RDWT, N(FN-1).

1.4 残差通道注意力网络

自然图像中信息分布不均, 特征携带的信息具有不同的重要性.残差小波变换网络主要从整体上学习图像的高频信息, 没有根据其重要程度进行学习.为了使网络专注于具有更丰富信息的特征, 进一步恢复重要细节, 采用残差通道注意力块.该残差块能根据不同输入自适应地缩放通道特征, 给重要特征分配更大的权重, 从而使网络将注意力调整到重要特征的学习中.

首先使用全局平均池将全局空间信息压缩至统计量y.对于第N个残差块, 输入为FN-1, 对其进行预处理后得到T=T1, T2, …, TC, 具有C个特征图, 大小为H× W.可通过将FN-1缩小空间尺寸H× W获得统计量y∈ R, 则y的第c个元素为

yc=HGP(xc)= 1H×W∑i=1H∑j=1WTc(i, j),

其中, Tc(i, j)表示第c个特征Tc在位置(i, j)的值, HGP(· )表示全局池函数.

为了通过全局平均池化层从聚合信息中充分捕获通道依赖关系, 采用具有S形函数的简单门控机制:

SCA=f(φ 2(δ (φ 1y))),

其中, f(· )表示S型门控函数, δ (· )表示ReLU函数, φ 1表示卷积层的权重, 以缩减比r进行通道缩减.在被ReLU函数激活后, 低维信号随后由权重为φ 2的信道放大层以比率r增加.

然后, 获得最终的通道统计信息s, 用于重新缩放输入T, 得到残差通道注意力网络的残差结果:

RCA, N(FN-1)=[s1T1, …, scTc, …, sCTC],

其中, sc表示第c个通道中的比例因子, Tc表示第c个通道中的特征图.

通过通道注意力, 残差通道注意力块中的残差分量能自适应地调整比例, 从而增强网络的学习能力.

2 实验及结果分析
2.1 实验环境

本文将DIV2K[26]作为训练数据集, 并在Set5数据集[27]、Set14数据集[28]、BSD100数据集[29]、Urban100数据集[30]上进行测试.通过双三次插值对HR图像进行下采样, 得到LR输入.

在特征预提取模块(FPM)中, 卷积核大小为3× 3.在残差梯度网络中, 卷积核大小为3× 3.在残差小波变换网络中:第1层包含128个大小为4× 9× 9的滤波器; 第2层包含64个大小为128× 1× 1的滤波器, 用于非线性特征映射; 第3层包含4个大小为64× 5× 5的滤波器, 用于获得重建图像的4个残差子带; 每层输出都加入ReLU激活函数, 生成除最后一层以外的非线性激活映射.在残差通道注意力网络和特征映射网络(FMN)的其它卷积层都具有C=64个滤波器, 卷积核大小为3× 3.

在残差通道注意力网络中, 通道缩减层的滤波器数分别为C/r=4, 即缩减比r=16.重建模块(RM)中的最后1个卷积层包括b个卷积核大小为3× 3的滤波器.由于网络的深度取决于模块的个数N, 因此N的取值直接影响着网络性能.在网络中, N=22.当N> 22时, 网络性能有一定幅度的下降.

本文采用2个评价标准:峰值信噪比(Peak Signal-to-Noise Ratio, PSNR), 大小为信号最大功率与噪声功率的比值.一般来讲, 比值越大, 重建效果越优.然而, 在一些情况下, PSNR值越大, 效果反而越差.因此, 引入结构相似性(Structural Similarity, SSIM)[31], 对比原始图像与重建图像整体结构相似度, SSIM值越大, 表明两幅图像相似程度越高.两种指标结合可更全面评估重建图像的质量.

为了验证本文算法性能, 采用如下对比算法:SRCNN[11]、VDSR[12]、DRRN[13]、MemNet[17]、Sel-Net[17]、MSRN[19]、CARN[20]、OISR[21].

2.2 小波变换和梯度的影响

为了验证残差小波变换网络的影响, 从网络中删除残差梯度结构.放大倍数为4时小波变换网络和梯度网络对PSNR值的影响如表1所示.由表可知, 当小波变换和梯度结构都被移除时, 在4个数据集上的PSNR值都很低.在加入小波变换后, 在4个数据集上的PSNR值均有很大的提升.这些对比表明残差小波变换网络的有效性, 表明小波变换过程中对图像高频细节的提取大幅提高重建的性能.

表1 小波变换网络和梯度网络对PSNR值的影响 Table 1 Effect of wavelet transform network and gradient network on PSNR

进一步研究残差梯度网络的效果.相比没有残差梯度块的网络, 添加残差梯度块后的网络性能均有明显提升, 由此验证残差梯度块的有效性, 残差梯度块中对图像边缘细节的提取有助于提升图像的重建性能.

2.3 定量分析

评价图像超分辨重建质量分为主观评价和客观评价.主观评价是指通过人眼判定图像质量, 具有片面性, 因此通常作为评价图像质量的辅助指标.客观指标包括PSNR和SSIM.

各算法在4个数据集上进行不同放大倍数重建的PSNR值与SSIM值对比如表2所示.

表2 各算法在4个数据集上的客观指标值对比 Table 2 Comparison of objective index values of algorithms on 4 datasets

由表2可看出, SRCNN的结果最差, 2种客观指标均为最低, 这是由于算法只采用3个卷积层, 学习的图像信息较少.MSRN与OISR的客观指标相对较高, MSRN充分利用图像的层次特征, 而OISR改进残差块, 增强网络的学习能力.本文算法的2种客观指标均为最高.在Urban数据集上进行放大倍数为2的重建, PSNR值为32.68, SSIM值为0.932 8.Urban数据集上多为具有丰富几何结构的建筑物, 上述结果说明本文算法针对几何结构的恢复具有优越性.这是由于3种残差网络的结合使网络从各方向学习图像的整体结构信息和局部结构信息, 能极大程度地对几何结构进行恢复.

2.4 视觉效果分析

各算法的视觉效果如图4所示.由图可见, 本文算法的视觉效果图的几何结构清晰, 无严重变形, 而其它方法出现几何结构扭曲等现象, 视觉效果不佳.SRCNN的视觉效果最差, 右边效果图中窗户木条的形状出现严重扭曲.MSRN及OISR效果较优, 能较准确地恢复一部分几何结构, 但仍然存在部分失真.例如, 在右边效果图中, 部分窗户木条歪斜.本文算法具有最优的视觉效果, 由图(i)可看出, 对于2幅图像中窗户的结构, 本文算法均可准确恢复, 这表明本文算法能捕获图像中几何结构特征.

图4 各算法的视觉效果图对比Fig.4 Comparison of visual effects of different algorithms

另外, 本文算法对纹理细节的恢复也最优.这是由于本文算法采用多残差网络, 残差梯度网络保留图像上水平、垂直方向的几何结构信息, 残差小波变换网络从整体上保留高频信息, 补充除水平、垂直方向以外的边缘信息, 残差通道注意力网络关注重要的高频信息, 从局部上进一步恢复重要的高频细节.3种残差网络学习的信息互补, 较好地保留图像的几何结构, 恢复更多的高频纹理细节.视觉效果表明, 本文算法可学习更多的结构信息, 有助于通过保留几何结构生成更逼真的重建图像.

2.5 高倍率放大的结果分析

为了进一步进行视觉效果分析, 表3列出放大倍数为8时MSRN和本文算法的PSNR值对比, 并在图5中给出相应的视觉效果对比.由于缩放因子很大, LR图像包含SR的信息非常有限, 丢失许多高频细节信息, 因此重建图像变得十分困难, 现有的大多数算法重建结果较差, 会产生模糊、变形等现象.由图5可看出, MSRN的结果会产生扭曲的结构.例如, 在左边效果图中, MSRN重建的条纹发生严重变形, 而本文算法较好地保留图像的几何信息, 正确修复图像中的几何形状和边缘细节, 产生更优结果.另外, 从表3中可看出, 在4个数据集上, 本文算法的PSNR均明显高于MSRN.

表3 8倍超分辨率时两种算法的PSNR值对比 Table 3 PSNR of 2 algorithms for 8 times super resolution

图5 8倍超分辨率时两种算法的视觉效果图对比Fig.5 Performance comparison of 2 algorithms for 8 times super resolution

3 结束语

本文提出基于多残差网络的结构保持超分辨重建算法.首先, 将低分辨率图像通过一个特征预提取模块, 粗略提取图像特征.再将提取的特征通过N个多残差网络进行精细化处理.残差梯度网络主要用于恢复图像水平、垂直方向的结构信息, 增强图像边缘.残差小波变换网络从多个方向保留图像整体的高频信息, 包括结构信息及纹理细节等.残差通道注意力网络专注于恢复重要的图像特征, 从局部上恢复重要的高频信息.最后, 将精细化的特征通过重建模块, 得到高分辨率图像.实验结果表明本文算法的有效性, 极大程度地保留图像几何结构和纹理细节, 网络性能较高, 重建图像质量较佳.

参考文献
[1] 付利华, 孙晓威, 赵宇, 等. 基于运动特征融合的快速视频超分辨率重构方法. 模式识别与人工智能, 2019, 32(11): 1022-1031.
(FU L H, SUN X W, ZHAO Y, et al. Fast Video Super-Resolution Reconstruction Method Based on Motion Feature Fusion. Pattern Recognition and Artificial Intelligence, 2019, 32(11): 1022-1031. [本文引用:1]
[2] LEDIG C, THEIS L, HUSZÁR F, et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 105-114. [本文引用:1]
[3] DONG C, CHEN C L, TANG X O. Accelerating the Super-Resolution Convolutional Neural Network // Proc of the 14th European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 391-407. [本文引用:1]
[4] 付利华, 卢中山, 孙晓威, 等. 融合参考图像的人脸超分辨率重构方法. 模式识别与人工智能, 2020, 33(4): 325-336.
(FU L H, LU Z S, SUN X W, et al. Face Super-Resolution Reconstruction Method Fusing Reference Image. Pattern Recognition and Artificial Intelligence, 2020, 33(4): 325-336. ) [本文引用:1]
[5] SHI W Z, CABALLERO J, HUSZÁR F, et al. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1874-1883. [本文引用:1]
[6] ZOU W W W, YUEN P C. Very Low Resolution Face Recognition Problem // Proc of the 4th IEEE International Conference on Biometrics: Theory, Applications and Systems. Washington, USA: IEEE, 2010. DOI: DOI:10.1109/BTAS.2010.5634490. [本文引用:1]
[7] SHI W Z, CABALLERO J, LEDIG C, et al. Cardiac Image Super-Resolution with Global Correspondence Using Multi-atlas PatchMatch // Proc of the International Conference on Medical Image Computing and Computer Assisted Intervention. Berlin, Germany: Springer, 2013: 9-16. [本文引用:1]
[8] 郑少飞, 汤进, 罗斌, 等. 基于改进损失函数的多阶段行人属性识别方法. 模式识别与人工智能, 2018, 31(12): 1085-1095.
(ZHENG S F, TANG J, LUO B, et al. Multistage Pedestrian Attribute Recognition Method Based on Improved Loss Function. Pattern Recognition and Artificial Intelligence, 2018, 31(12): 1085-1095. ) [本文引用:1]
[9] 蒋桧慧, 张荣, 李小宝, 等. 融合直接度量和间接度量的行人再识别. 模式识别与人工智能, 2018, 31(2): 167-174.
(JIANG H H, ZHANG R, LI X B, et al. Pedestrian Re-identification Fusing Direct Metric and Indirect Metric. Pattern Recognition and Artificial Intelligence, 2018, 31(2): 167-174. ) [本文引用:1]
[10] 刘丽, 郑洋, 付冬梅. 改进YOLOv3网络结构的遮挡行人检测算法. 模式识别与人工智能, 2020, 33(6): 568-574.
(LIU L, ZHENG Y, FU D M, et al. Occluded Pedestrian Detection Algorithm Based on Improved Network Structure of YOLOv3. Pattern Recognition and Artificial Intelligence, 2020, 33(6): 568-574. ) [本文引用:1]
[11] DONG C, LOY C C, HE K M, et al. Learning a Deep Convolutional Network for Image Super-Resolution // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2014: 184-199. [本文引用:3]
[12] KIM J, LEE J K, LEE K M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1646-1654. [本文引用:4]
[13] TAI Z, YANG J, LIU X M. Image Super-Resolution via Deep Recursive Residual Network // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 2790-2798. [本文引用:4]
[14] KIM J, LEE J K, LEE K M. Deeply-Recursive Convolutional Network for Image Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1637-1645. [本文引用:2]
[15] HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:2]
[16] LIM B, SON S, KIM M, et al. Enhanced Deep Residual Networks for Single Image Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 136-144. [本文引用:2]
[17] TAI Y, YANG J, LIU X M, et al. MemNet: A Persistent Memory Network for Image Restoration // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 4549-4557. [本文引用:5]
[18] CHOI J S, KIM M. A Deep Convolutional Neural Network with Selection Units for Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 1150-1156. [本文引用:3]
[19] LI J C, FANG F M, MEI K F, et al. Multi-scale Residual Network for Image Super-Resolution // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 527-542. [本文引用:4]
[20] AHN N, KONG B, SOHN K A. Fast, Accurate, Lightweight Super-Resolution with Cascading Residual Network // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 252-268. [本文引用:4]
[21] HE X Y, MO Z T, WANG P S, et al. Ode-Inspired Network Design for Single Image Super-Resolution // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 1732-1741. [本文引用:5]
[22] ZHANG Y L, LI K P, LI K, et al. Image Super Resolution Using Very Deep Residual Channel Attention Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Sprin-ger, 2018: 294-310. [本文引用:3]
[23] LAI W S, HUANG J B, AHUJA N, et al. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 5835-5843. [本文引用:1]
[24] SUN J, XU Z B, SHUM H Y. Gradient Profile Prior and Its Applications in Image Super-Resolution and Enhancement. IEEE Transactions on Image Processing, 2010, 20(6): 1529-1542. [本文引用:1]
[25] KUMAR N, VERMA R, SETHI A. Convolutional Neural Networks for Wavelet Domain Super Resolution. Pattern Recognition Letters, 2017, 90: 65-71. [本文引用:1]
[26] TIMOFTE R, AGUSTSSON E, VAN GOOL L, et al. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 1110-1121. [本文引用:1]
[27] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-Complexity Single-Image Super-Resolution Based on Nonnegative Neigh-bor Embedding // Proc of the British Machine Vision Conference. Berlin, Germany: Springer, 2012: 1-10. [本文引用:1]
[28] DE SOUZA FARIA G, KIM H Y. Differential Audio Analysis: A New Side-Channel Attack on Pin Pads. International Journal of Information Security, 2019, 18: 73-84. [本文引用:1]
[29] MARTIN D, FOWLKES C C, TAL D, et al. A Database of Human Segmented Natural Images and Its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics // Proc of the International Conference on Computer Vision. Washington, USA: IEEE, 2001: 416-423. [本文引用:1]
[30] HUANG J B, SINGH A, AHUJA N. Single Image Super-Resolution from Transformed Self-exemplars // Proc of the IEEE Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 5197-5206. [本文引用:1]
[31] WANG Z, BOVIK A C, SHEIKH H R, et al. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. [本文引用:1]