引用本文
应时辉, 杨菀, 杜少毅, 施俊. 基于深度学习的医学影像配准综述. 模式识别与人工智能, 2021,34(4): 287-299
YING Shihui, YANG Wan, DU Shaoyi, SHI Jun. Deep Learning Based Medical Image Registration: A Review. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(4): 287-299.  
Doi: 10.16451/j.cnki.issn1003-6059.202104001
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于深度学习的医学影像配准综述
应时辉1, 杨菀1, 杜少毅2, 施俊3
1.上海大学 理学院 数学系 上海 200444
2.西安交通大学 人工智能学院 人工智能与机器人研究所 西安 710049
3.上海大学 通信与信息工程学院 上海 200444
通信作者:

施 俊,博士,教授,主要研究方向为医学影像分析.E-mail:junshi@shu.edu.cn.

作者简介:

应时辉,博士,教授,主要研究方向为医学图像配准.E-mail:shying@shu.edu.cn.

杨 菀,硕士研究生,主要研究方向为医学图像配准的深度学习方法.E-mail:yangw1997@shu.edu.cn.

杜少毅,博士,教授,主要研究方向为医学图像配准.E-mail:dushaoyi@gmail.com.

收稿日期: 2020-06-03 接受日期: 2020-12-03
资助项目: 国家自然科学基金项目(No.11971296,81627804,61671281)、上海市科学技术委员会项目(No.18010500600,17411953400)资助
摘要

图像配准是医学影像处理与智能分析领域中的重要环节和关键技术.传统的图像配准算法由于复杂性较高、计算代价较大等问题,无法实现配准的实时性要求.随着深度学习方法的发展,基于学习的图像配准方法也取得显著效果.文中系统总结基于深度学习的医学图像配准方法.具体地,将方法归为3类:监督学习,无监督学习和对偶监督/弱监督学习.在此基础上,分析和讨论各自优缺点.进一步,着重讨论近年来提出的正则化方法,特别是基于微分同胚表示的正则和基于多尺度的正则.最后,根据当前医学图像配准方法的发展趋势,展望基于深度学习的医学图像配准方法.

关键词: 图像配准; 深度学习; 形变场; 微分同胚; 多尺度正则
中图分类号:TP 391 文章编号:2021,34(4):287-299
Deep Learning Based Medical Image Registration: A Review
YING Shihui1, YANG Wan1, DU Shaoyi2, SHI Jun3
1. Department of Mathematics, College of Sciences, Shanghai Uni-versity, Shanghai 200444
2. Institute of Artificial Intelligence and Robotics, College of Artificial Intelligence, Xi'an Jiaotong University, Xi'an 710049
3. School of Communication and Information Engineering, Shang-hai University, Shanghai 200444
Corresponding author:
SHI Jun, Ph.D., professor. His research interests include me-dical image analysis.

AboutAuthor:
YING Shihui, Ph.D., professor. His research interests include medical image registration.
YANG Wan, master student. Her research interests include deep learning for medical image registration.
DU Shaoyi, Ph.D., professor. His research interests include medical image registration.

Fund:Supported by National Natural Science Foundation of China(No.11971296,81627804,61671281), Project of Shanghai Science and Technology Commission of Shanghai Municipality(No.18010500600,17411953400)
Abstract

Image registration is a key technology in the field of medical image processing and intelligent analysis. The real-time registration cannot be accomplished due to the high complexity and computational cost of traditional registration methods. With the development of deep learning, learning based image registration methods achieve remarkable results. In this paper, the medical image registration methods based on deep learning are systematically summarized and divided into three categories, including supervised learning, unsupervised learning and dual supervised learning. On this basis, the advantages and disadvantages for each category are discussed. Furthermore, the regularization methods proposed in recent years are emphatically discussed, especially based on diffeomorphism and multi-scale regularization. Finally, the medical image registration methods based on deep learning are prospected according to the development trend of the current medical image registration methods.

Key words: Image Registration; Deep Learning; Displacement Vector Field; Diffeomorphism; Multi-scale Regularization

本文责任编委 辛景民

Recommended by Associate Editor XIN Jingmin

图像配准是针对同一对象在不同条件下获取的图像间建立对应关系的过程, 即求解图像之间的空间对应关系或形变场.它是医学影像处理与智能分析领域中的重要环节与关键技术, 具有重要的应用价值.例如, 在临床实践中, 同一解剖结构在不同的医学模态下显示独特的组织特征, 为了更好地诊断疾病或辅助手术, 需对多种模态影像进行融合以达到图像中信息互补的目的.此外, 在手术导航[1]、图像分割[2]、图像重建[3]、图谱构建[4]等问题中都需要进行图像配准.

自图像配准问题提出后, 研究人员构思大量方法.按照方法的构建方式, 可将现有方法分为传统的基于模型的图像配准方法和近年来提出的基于数据的图像配准方法.

基于模型的图像配准方法是指运用确定的物理模型描述配准过程, 优点在于过程的可解释性.从模型求解方法的角度出发, 传统基于模型的医学图像配准算法分为参数化方法和整体变分方法.

参数化方法是对非刚性配准模型中的变量——形变(微分同胚)在某类基下进行逼近, 从而将形变的求解转化为对参数的优化问题, 如基于B样条(B-Spline)的配准算法[5]及推广的向量样条方法[6]、基于径向对称基(Radially Symmetric Basis)的配准算法[7]、基于薄板样条(Thin-Plate Spline, TPS)的配准算法[8, 9, 10, 11]、基于Lie群参数化的配准算法[12]等.采用参数化方法的优点在于根据具体配准问题的要求对形变进行合理的约束变得容易实现, 减少局部极小点的个数, 提高算法的鲁棒性.此外, 由于参数化, 原问题转化为有限维的极小化问题, 因此, 有更多更优的数值方法可应用于问题的求解中, 求解速度较快.不足之处在于, 由于参数的维数不是很高, 参数化后的近似模型与原问题之间差距较大, 这使配准精度降低.

整体变分方法是将能量泛函对形变进行一阶变分, 得到相应的Euler-Lagrange方程, 再通过相应的偏微分方程数值方法对原问题进行求解.该类方法包括大形变微分同胚度量映射方法(Large Defor-mation Diffeomorphic Metric Mappings, LDDMM)[13]、基于LDDMM的Diffeomorphic Demons方法[14]、基于变形理论(Theory of Metamorphosis)的配准方法[15, 16]等.这类方法具有较坚实的数学基础和理论保障, 并具有较好的通用性.不足之处在于变量是无穷维的, 相比参数化方法, 具有更多的局部极小点.此外, 该类方法的数值求解较复杂, 求解速度较慢, 无法达到实际应用中的速度要求.

尽管传统的图像配准算法已取得很大的成功, 但是仍存在复杂性较高和计算代价较大等问题.因此, 学者们提出基于数据的图像配准方法, 即如何通过一个学习模型去逼近图像到形变场之间的映射.Krizhevsky等[17]在ImageNet图像竞赛中凭借卷积神经网络Alex-Net获得冠军后, 引发学术界对深度学习的研究热潮.随后, 基于深度学习的图像配准算法得到迅猛发展.不同于传统方法, 深度学习配准网络通过网络训练, 学习到图像对之间的线性映射关系或非线性映射关系.任意一对图像输入训练好的配准网络中, 只需要一次前向运算就可得到预测的变换参数或形变场.基于深度学习的图像配准算法在一定程度上可弥补传统方法的适应性较差和复杂度较高等问题.

因此, 本文对基于深度学习的医学图像配准算法进行分类讨论.虽然已有一些关于医学图像配准的综述[18, 19, 20, 21], 但不同的是, 本文着重于讨论医学图像配准中使用的正则化方法, 即如何将传统的模型驱动的配准算法与当前数据驱动的配准算法进行有效融合, 获得性能更优的配准方法.

1 数据驱动的医学图像配准方法

根据模型性质, 近年来基于数据驱动的医学图像配准算法可分为监督学习模型、无监督学习模型和对偶监督/弱监督学习模型.

1.1 监督学习模型

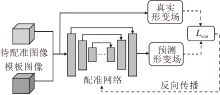
监督学习是指在训练过程中, 使用形变的标签信息, 即已知训练数据的形变向量场.常见的监督学习框架如图1所示.

图1 监督学习的配准模型框图Fig.1 Registration model framework of supervised learning

一般地, 监督学习的损失函数为

L(f, m, ϕ , ϕ gt)=Lsim(ϕ , ϕ gt)+λ Lreg(ϕ ).

其中: f表示模板图像; m表示待配准图像; ϕ 表示预测的形变场或变换参数; ϕ gt 表示真实的形变场信息或变换参数; Lsim(ϕ , ϕ gt)度量预测的形变场或变换参数ϕ 与真实形变场或变换参数ϕ gt之间的相似性; Lreg(ϕ )表示正则项, 对预测的形变做出约束; λ 表示参数, 平衡相似项与正则项之间的比例.

不同于图像分割等分类任务, 图像配准本质上是生成型的任务, 难以通过人工标注获得真实的标签信息.在目前可以获得的数据集中, 大部分的标签信息是医生手工标注的两幅图像上对应的少量地标和感兴趣的解剖结构上的分割掩码, 而深度学习需要大量的形变场标签信息以学习网络参数.因此在基于监督学习的配准方法中, 常用的形变标签有如下3种.

1)随机生成的形变.对于刚性变换或仿射变换, 变换参数的个数是固定的, 可事先给出每个变换参数合理的变化范围.在给出的区间上, 对每个参数进行随机采样, 按照这个参数配置, 对图像进行刚性或仿射变换, 将这个参数配置作为初始的图像和变换后的图像间的真实变换参数, 从而实现基于监督学习的配准网络训练.同理, 对于非线性形变, 也可在每个形变维度上, 提前设定形变的变化范围.随机生成的形变虽然可满足网络训练的需求, 但是这样的形变与真实世界中存在的形变差异较大, 训练的模型无法较好地泛化到临床实践中的数据.

Chee等[22]使用随机生成的变换参数作为标签信息, 利用仿射配准网络(Affine Image Registration Network, AIRNet), 回归三维大脑数据的仿射变换参数.在特征提取部分, 使用2个并行且参数共享的编码器分别提取待配准图像和模板图像的特征.实验中除处理常规的单模态配准外, 还执行T1模态和T2模态图像之间的多模态配准任务.相比SimpleITK中的仿射变换技术, Chee等[22]的方法配准速度由166.537 s提升至0.738 s.Salehi等[23]对初始图像进行任意平移和旋转, 将对应的形变参数作为初始图像与变换后的图像之间的真实形变参数.损失函数中不仅包括预测的刚性变换参数与真实形变参数之间的误差, 还包括测地距离.实验表明, 加入测地距离的模型表现优于仅有变换参数误差的模型.Sloan等[24]设计卷积神经网络(Convolu-tional Neural Network, CNN)和全卷积网络(Fully Convolutional Network, FCN)架构的2种深度学习网络, 用于解决二维图像刚性配准问题, 随机生成真实变换参数.在单模态实验中, CNN和FCN的表现优于simpleITK.在多模态实验中, 基于CNN和FCN的方法可达到与SimpleITK相当的配准效果.Sun等[25]同样使用随机生成的刚性变换参数.不同的是, 在实现计算机断层扫描(Computed Tomo-graphy, CT)与超声(Ultrasound, US)数据之间的配准时, 利用CT与US图像之间的近似转换关系, 将多模态配准转化成单模态配准.这种处理方式在临床真实数据上的表现较差.Eppenhof等[26]对B样条控制点上的形变进行任意采样, 再经过插值方法, 得到真实的形变场数据.此方法在三维肺部CT数据上的配准精度与Elastix相当.

2)由传统配准方法获得的形变.通过Demons、SyN(Symmetric Image Normalization)等传统方法计算图像对之间的形变场, 将获得的形变场作为这对图像间的形变场标签, 用于训练配准网络.获得的标签信息虽然能在一定程度上避免在真实世界中存在的形变差异性很大的问题, 但由这种形变场训练的模型很难规避传统方法中存在的问题, 较难解决图像差异过大的配准问题, 由这种方法获得的形变场训练的网络模型在处理大形变问题时也表现欠佳.

在Yang等[27]的实验中, 真实的形变场是由LDDMM产生的, 训练的网络无论在精度上还是速度上, 都超越Cao等[28]的方法.Rohé 等[29]利用数据集中已有的分割信息, 将配准问题转化成曲面配准问题(Surface Matching), 生成分割区域的形变场, 并插值成整幅图像的形变场.为了使形变场具有微分同胚的性质, 将上述得到的形变场以静止速度场(Stationary Velocity Fields, SVF)的形式进行表征, 得到的SVF作为标签信息.相比基于局部相关性度量的Log-demons方法(Local Correlation Criteria Based Log-demons, LCC Log-demons), 基于SVF表征的网络(SVF Network, SVF-net)在配准速度上有所提升, 在平均Dice分数(Mean Dice's Similarity Coefficient, mean DSC)和Hausdorff距离等指标上的值高于LCC Log-demons.除右心室心肌(Right Ventricle Myocardium, RVM)和左心室血池(Left Ventricle Blood Pool, LVBP)这2个区域, 其它2个区域的形变场的光滑程度和LCC Log-demons接近.Cao等[30]先使用SyN获得三维大脑数据的形变场, 利用脑区的分割数据, 使用Diffeomorphic Demons进一步调整形变场.

3)基于模型生成的形变.例如基于统计外观模型(Statistical Appearance Model, SAM)[31]生成的形变场数据.深度学习中为了得到更好的训练效果, 往往需要大量的训练数据.在计算机视觉任务中通常对可用的数据进行某些特定的变换, 如旋转、裁剪、改变图像的对比度、随机增加噪声等, 增强模型的几何不变性, 提高模型的泛化能力.但当仅有少量医学图像样本可用于训练时, 上述简单的图像增强(Data Augmentation)技术对配准网络的训练并不十分有效.由数据驱动的图像增强技术是学习医学图像样本中具有代表性的形状和外观模型, 合成更符合现实世界中的图像样本, 更有利于模型的泛化.

Uzunova等[31]从少量的医学图像数据中学习SAM, 利用SAM生成大量真实形变场数据.Dosovitskiy等[32]使用仿射变换、随机生成和基于SAM的3种方法生成真实形变场, 实验显示基于SAM生成的形变训练的网络模型的配准精度高于基于随机生成和仿射配准生成的变换参数训练的模型.

1.2 无监督学习模型

在配准中, 由于很难手动获得真实的形变场, 而人工合成的标签信息可能会引入不必要的误差等, 于是学者们提出无监督学习或自监督学习.在无监督学习中, 网络的学习是由配准后的图像与模板图像之间的相似性驱动的.目标函数的一般形式如下:

L(f, m, ϕ )=Lsim(f, m∘ ϕ )+λ Lreg(ϕ ),

其中, m∘ ϕ 表示变形后的待配准图像, Lsim(f, m∘ ϕ )度量模板图像与变形后的待配准图像之间的相似性.

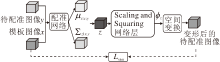
已有的基于无监督学习的工作可分为3类.1)在保真项中, 利用灰度值强度或分布等计算模板图像与变形后的待配准图像之间的相似性, 常用的相似性度量有归一化的交叉相关性(Normalization Cross Correlation, NCC), 归一化的互信息(Norma-lized Mutual Information, NMI), 残差平方和(Sum Squared Residual, SSD)等.2)在更高层面上度量图像的相似性, 如利用深度学习网络提取的特征计算模板图像与变形后的待配准图像之间的相似性.3)使用生成对抗网络(Generative Adversarial Network, GAN)中的判别器衡量模板图像与变形后的待配准图像之间的相似性.常见的无监督学习网络框架如图2所示.

图2 无监督学习的配准模型框图Fig.2 Registration model framework of unsupervised learning

de Vos等[33]提出端到端的无监督网络框架, 实现二维心脏磁共振成像(Magnetic Resonance Image, MRI)图像配准.网络的输出是B样条控制点上的形变, 使用三次B样条插值成整幅图像的形变场.网络使用NCC计算变形后的待配准图像与模板图像的相似性.相比Elastix, 平均Dice分数从0.79提升到0.80, 同时计算速度在0.049 s左右.其它工作[34, 35]同样使用NCC计算变形后的待配准图像与模板图像的相似性.Ghosal等[36]利用FCN构建图像对之间的残差平方和的紧上界(Upper Bound Sum of Squared Difference, UB-SSD).最小化模板图像和变形后的待配准图像间的UB-SSD, 达到进一步提升配准精度的目的.在残差平方和, 峰值信噪比(Peak Signal to Noise Ratio, PSNR)和结构相似性(Structural Similarity, SSIM)等指标上, 结合上述方法的配准算法的实验结果优于Log-demons.Sheikhjafari等[37]使用自编码器学习潜在的特征表达, 实现二维的心脏数据配准.将自编码器中学习的潜在特征输入FCN中, 预测形变场.将模板图像和形变后的待配准图像之间残差的绝对误差之和(Sum of Absolute Error, SAE)作为损失函数.在MICCAI Automated Cardiac Diagnosis Challenge(ACDC)数据集上的实验效果优于Punithakumar等[38]的方法.Stergios等[39]使用均方误差(Mean Squared Error, MSE)衡量待配准图像与参考图像的差异性.Balakrishnan等[40]提出基于无监督学习的通用框架Voxelmorph, 解决配准问题.Voxelmorph采用U-Net[41]的网络结构, 嵌入空间变换网络(Spatial Transformer Networks, STN)[42]模块, 在网络中将预测的形变场应用在待配准图像上, 实验中尝试NMI、NCC等度量.现在Voxelmorph常被用来作为其它深度学习解决医学图像配准问题的方法的基准.Kuang等[43]提出解决T1模态的大脑MRI图像配准的快速图像配准模型(Fast Image Registration, FAIM).网络框架与Voxelmorph相似, 但在正则项中加入形变场的L2范数, 进一步约束预测的形变场.FAIM在LBPA40、Mindboggle 101数据集上的实验效果优于Voxelmorph.Sun等[45]使用无监督方法处理多模态配准任务.网络在特征提取部分, 采用并行的2个编码器, 对不同模态的图像对提取特征.在衡量形变后的待配准图像与模板图像的相似性时, 融合灰度值强度和梯度信息.该方法在三维大脑数据上达到具有竞争力的配准效果.

Yoo等[46]利用STN和自编码器解决电镜图像配准问题.如果两幅图像经过编码后的特征相似, 这两幅图像也应该很相似.基于这种先验知识, 使用特征的相似性替代待配准图像与模板图像之间的相似性度量.利用重建损失, 训练适用于电镜图像的自编码器.同时使用STN实现图像对之间的配准.在CREMI挑战赛的果蝇数据上, 电镜图像配准网络(Serial-Section Electron Microscopy Image Regis-tration Network, ssEMnet), Elastix和bUnwarpJ[47]得到的mean DSC分别为0.83, 0.73和0.60.

Fan等[48]使用生成对抗网络, 利用判别器衡量配准的质量, 将错误配准的信息反馈给生成器.在判别器的训练中, 将形变后的待配准图像视作负例, 模板图像视为正例.在实验中对比传统方法Demons和SyN、基于监督学习的方法和基于SSD或相关系数(Correlation Coefficient, CC)度量的无监督学习的方法, 基于生成对抗网络的方法在LBPA40数据集上达到最高的mean DSC.这表明提出的对抗式相似性度量在处理配准任务时是有效的.Lei等[49]在处理腹部CT图像配准时, 提出和Fan等[48]类似的对抗式相似性度量.Fu等[50]将粗配准网络(Coarse-Net)和细配准网络(Fine-Net)结合在一个大的网络框架中, 实现从粗到精的配准.在每个子网络中, 都包含一个判别器, 在该种尺度下衡量形变后的待配准图像与模板图像之间的差异.Fan等[51]应用GAN处理单模态数据时, 起初将正例设为一对已配准好的图像对, 即理想的图像对应该是完全相等的两幅图像, 因为设定过于严苛, 并且与实际应用不符, 因此适当放松要求, 将模板图像和待配准图像的线性组合与模板图像组成的图像对视为正例.利用GAN结构实现无监督学习, 可解决多模态配准任务中难以定义多模态图像间的相似性的问题.目前没有很好的多模态图像间的相似性度量方式, GAN中的判别器是以学习到的网络的方式衡量图像间的相似性, 省去提前选定度量方式的困扰.

1.3 对偶监督/弱监督学习

对偶监督学习是指在训练过程中不仅使用样本的标签信息, 还度量图像间的相似性.Fan等[52]提出大脑影像配准网络(Brain Image Registration Network, BIRNet), 使用对偶监督的学习方法, 得到三维大脑核磁共振图像的形变场, 目标函数中不仅度量模板图像与变形后的待配准图像之间的相似性, 还度量预测的形变场与真实形变场之间的相似性.与此同时, 引入多尺度的结构, 进一步提升实验效果.

Yan等[53]使用GAN结构, 实现三维核磁共振图像与经直肠超声(Trans-Rectal Ultrasound, TRUS)图像的刚性配准.在生成器的训练过程中, 使用无监督学习的目标函数, 在判别器的训练中使用监督学习的目标函数.相比无监督学习, 对偶监督学习充分利用有标签的样本数据信息, 可在一定程度上弥补无监督学习的不足, 但还是不能避免需要使用标签信息的限制.还有一种较特别的对偶监督学习方法, 是Cao等[54]在实现CT与MRI多模态图像配准时设计的.利用已经对齐的CT与MRI图像对, 将多模态配准问题转化成单模态图像配准问题, 使用模态内的相似性度量代替模态间的相似性度量.在损失函数中, 不仅计算CT-CT图像间的差异性, 还计算MRI-MRI图像之间的相似性.

弱监督学习是指在训练过程中使用的不是完整的形变场信息, 而是分割的标签信息或地标的标签信息.Hu等[55]利用分割的标签信息, 在更高的结构信息上进行度量, 将预测的形变场应用在待配准图像上, 相应的分割区域也进行相应的形变.在设置损失函数时, 不是计算图像间的相似性, 而是计算形变后待配准图像分割感兴趣区域与模板图像上感兴趣区域间的重叠度.结合全局配准网络(Global-Net)和局部配准网络(Local-Net), 实现由粗到精的配准.Hu等[56]不仅使用腺体分割的标签信息, 还使用对抗式损失约束生成的形变场.将判别器的训练正例设为由有限元方法合成的形变场, 负例设为由生成器预测的形变场, 从而使预测的形变场具有有限元方法合成的形变场中的某些性质.实验表明, 此方法可解决分割标签有限的情况下出现的过拟合问题.随着分割任务难度的降低, 在实际应用中容易获得图像中感兴趣区域的分割结果.分割数据仅在训练阶段需要, 在测试阶段并不需要, 在实际应用中不会增加耗时.弱监督学习在一定程度上缓解配准任务中需要大量真实形变场的压力, 相比随机生成的形变场, 弱监督学习更能适应现实世界中的数据.相比无监督学习, 弱监督学习中使用的分割掩码在一定程度上充分利用可获得的数据信息, 进一步指导模型的训练.

2 正则化方法

从第1节的讨论中可看到, 无论是基于模型的配准方法还是基于数据的配准方法, 要么存在计算复杂度较高、实时性不足的问题, 要么存在过程的不可解释和鲁棒性不足等问题.这些问题的本质原因是医学图像配准是一个高度病态的反问题:一方面要保证形变后的图像要足够地相似(数据驱动), 一方面要求形变应该满足某种先验性质(模型驱动).因此, 如何融合两类方法的优势, 形成性能更优的配准算法就成为目前配准算法研究的热点问题.由于基于深度学习的配准网络大多是回归网络框架, 对形变场表征的解空间过大, 因此为了进一步限制搜索空间, 避免求解陷于局部最小值, 需要通过某种先验引入适当的正则化条件, 避免预测不合理的形变场.在基于深度学习的配准网络中, 最常见的正则化方法通过惩罚形变场的梯度的L2范数等, 得到光滑的预测形变场.已有的正则化工作主要分为基于微分同胚的正则和基于多尺度的正则.

2.1 基于微分同胚表示的正则化模型

假设f∶ M→ N是流形之间的同胚, 如果f和 f-1都是光滑映射, 称f是微分同胚映射.由于微分同胚表征的变形可微且可逆, 因此可保证变形后的待配准图像的拓扑结构保持不变.基于微分同胚的正则化方法可归类如下2种.

1)基于静止速度场(SVF)的表征[57], 即形变场是由如下的常微分方程定义的:

∂ϕ(t)∂t=v(ϕ (t)),

其中, ϕ (0)=Id, 表示恒等变形, 对v从时间t=[0, 1]进行积分, 得到最终的形变场ϕ (1).在这种表征下, 形变场ϕ 是微分同胚映射的一个单参数化子群且ϕ (1)=exp(v).对静止的速度场进行积分, 常用的数值解法为收缩乘方法(Scaling and Squaring)[57].由单参数化子群的性质可得, 对于任何标量t和t', 有

exp((t+t')v)=exp(tv)∘ exp(t'v),

其中∘ 为与李群相关的复合运算.假设

ϕ(1/2N)≈ id+2-Nv,

利用上述性质进行N次迭代求出微分同胚的ϕ (1).

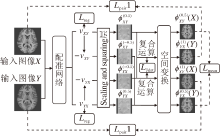
Yang等[27]利用深度学习网络预测初始的动量场, 再结合LDDMM求出形变场, 在一定程度上可保证形变的微分同胚.文献[29]与之类似, 但输出静止速度场.Dalca等[58]提出的概率生成模型如图3所示.将配准问题看作变分推理, 不仅实现端到端的形变场预测, 还提供不确定性估计.网络的前半部分将待配准图像和模板图像作为输入, 输出SVF的均值与方差, 从先验分布中采样用于生成形变场的SVF, 通过可微的Scaling and Squaring层得到微分同胚的形变场.相比SyN和Voxelmorph, Dalca等[58]的概率生成模型在mean DSC上略有提升, 雅可比行列式非正的体素数量也有所降低.

图3 基于微分同胚的概率生成模型框图Fig.3 Probability generation model based on diffeomorphism

Krebs等[59]利用条件变分自编码器(Condi-tional Variational Autoencoder, CVAE)解决三维的心脏MRI图像配准问题.提出的条件变分自编码器在编码阶段将形变信息使用一个低维的随机特征向量z表征, 并希望z的分布与先验分布接近.在解码阶段, 将待配准图像作为条件, 将图像配准问题转化成重建问题, 通过构建基于对称的局部交叉相关系数的损失函数, 惩罚变形后的待配准图像和参考图像之间的差异.得到SVF后, 通过高斯光滑层和Sca-ling and Squaring层得到最终的形变场, 从而保证规则且微分同胚的形变.在ACDC的三维心脏MRI数据上, Krebs等[59]的方法计算均方根误差(Root Mean Squared Error, RMSE)、mean DSC和Hausdorff距离等评价指标, 略优于或基本与LCC Log-demons和Voxelmorph相当.同时实验将病理性形变迁移到健康的图像中, 得到的形变与病理性形变相似, 但变形后的图像与健康图像的解剖结构相适应.此外, 实验使用测试集中的z可视化学习到的z空间的结构, 验证概率编码结构用于其它形变分析, 如形变迁移和聚类任务的可能性.

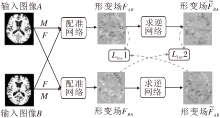
2)通过设计合理的网络结构, 直接对图像对之间的非线性映射进行可逆约束.针对大脑核磁共振图像的配准问题, Zhang[60]在Voxelmorph的通用框架上提出ICNet(Inverse-Consistent Network), 框架如图4所示.在ICNet中, 对图像对执行相互变形, 通过Linv惩罚两个形变场与其对应的逆形变场的差异, 达到对形变的微分同胚约束.此外, 为了减少形变中出现的不合理折叠, 引入反折叠的正则项Lant. ICNet不仅在Dice分数(Dice's Similarity Coeffi-cient, DSC)等评价指标上优于Log-demons、SyN和Voxelmorph, 而且大幅加快配准的速度.配准时间大约在0.25 s, 而Log-demons需要约1 h, SyN需要2 h.

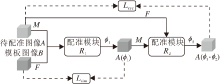
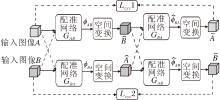
图4 ICNet的网络框图Fig.4 Architecture of ICNet

与之类似的, Lu等[61]提出解决心脏医学影像配准问题的CIRNet(Cycle Image Registration Net-work).CIRNet由两个配准网络模块R1、R2串联而成, 如图5所示.待配准图像经过模块R1得到变形后的图像, 作为新的待配准图像.将初始的待配准图像作为新的模板图像, 一起输入模块R2.如果由CIRNet逼近的形变映射具有一定的微分同胚性质, 那么经过模块R2得到的变形后的图像应与初始的待配准图像保持一致, 即施加Lcyc(Cycle-Identity Loss)的约束形变是微分同胚的.在实验中, 由CIRNet得到的DSC超过Elastix.相比同样是深度学习框架的Voxelmorph, 二者的计算速度相当.Voxelmorph在左心室内膜(Left Ventricular Endo-cardium, LVE), 左心室心包(Left Ventricular Peri-cardium, LVP)和右心室心内膜(Right Ventricular Endocardium, RVE)区域上的DSC分别为80.86%、77.74%、71.29%. CIRNet将精确度分别提升到83.56%、80.81%、72.58%.对比参考图像与待配准图像间的残差, 由CIRNet得到的残差图的均值与方差为0.022±0.0007, 由Elastix和Voxelmorph得到的实验结果分别为0.035±0.0020和0.035±0.0015.在消融实验中, 未加入Lcyc的网络框架在LVE、LVP和RVE区域的DSC分别为81.24%、79.46%、71.79%, 表明加入的正则项可进一步提升配准精度.

图5 CIRNet的网络框图Fig.5 Architecture of CIRNet

Kim等[62]结合ICNet和CIRNet的特点(如图6所示), 不仅通过级联的网络模块实现新的待配准图像与初始待配准图像间的配准, 以及引入循环一致性损失Lcyc, 还对参考图像和待配准图像执行相互配准, 进一步提高网络的配准性能.此外, 利用2幅相同的图像输入配准网络中得到的配准后的图像应该与原图像一致的先验知识, 引入Lide.评价标准是基于由专家标注的20个地标, 计算相应的配准误差(Target Registration Error, TRE).由实验结果可看出, Kim等[62]的方法在三维肝脏CT数据上的配准表现与Voxelmorph相当, 但略逊于Elastix.为了验证正则项的效果, 实验还计算配准后的图像中雅可比行列式非正的体素的比例.相比Voxelmorph, Kim等[62]的方法将雅可比行列式非正体素的比例由0.032 7%降至0.017 5%.结果表明循环一致性损失确实能在一定程度上保证形变的拓扑不变性.

图6 文献[62]方法的网络框图Fig.6 Architecture of method in reference[62]

Mok等[63]提出对称的微分同胚网络模型(Sy-mmetric Diffeomorphic Neural Network, SYMNet), 如图7所示.该模型不仅采用SVF的表征, 还对模板图像和待配准图像执行相互配准, 直接输出一对微分同胚的形变场.将图像对X、Y输入FCN后, 输出将图像X配准到Y的静止速度场vXY, 将图像Y配准到X的静止速度场vYX.再通过Scaling and Squaring层, 计算 ϕXY(0.5), ϕXY(-0.5), ϕYX(0.5)和 ϕYX(-0.5).在定义图像相似性损失时, 不仅度量变形后的图像X、Y之间及变形后的图像Y、X之间的相似性, 还度量当t=0.5时, 变形后的图像X与变形后的图像Y之间的相似性, 从而保证形变的可逆性.同时为了引入局部保持方向不变的约束, 在正则项中加入对形变中雅可比矩阵的行列式非正的局部区域的惩罚, 进一步保证形变的拓扑不变性.在基于地图集的三维大脑MRI图像的配准任务中, 由SYMNet得到的26个解剖结构上的mean DSC为0.738, 超过SyN、Voxelmorph和同样是基于SVF表征的深度学习网络框图[58].在雅可比行列式非正的体素数目的统计中, SYMNet框图得到的结果近乎为零.这些表明由SYMNet计算的形变场是微分同胚的.

图7 SYMNet的网络框图Fig.7 Architecture of SYMNet

在早期阶段, 研究者将微分同胚与深度学习结合的方法大多使用基于SVF的表征.最初基于SVF的表征工作利用深度学习预测SVF, 但积分部分仍是传统的计算方法, 无法达到端到端的要求, 后续将积分部分也以深度学习的框架嵌入网络中, 在测试阶段只需将图像对输入到网络中就可得到预测形变场.如今针对微分同胚正则的深度学习工作逐渐增多, 大都尝试设计不同的网络结构, 使预测的形变场具有微分同胚的性质.这种方法在训练过程中常需要串联多个网络, 在网络中实现图像对之间的逆向变换, 对计算资源的要求较高.Mok等[63]结合SVF表征和网络中图像对间逆向变换实现, 为后续的研究提供新的参考思路.同时通过实验可看出, 这种结合无论是在配准精度上还是在保持拓扑结构不变性上, 都超越基于SVF表征的方法[58].

2.2 基于多尺度的正则

在计算机视觉领域中, 多尺度是有效的正则化手段, 广泛应用于图像分类[64]、图像分割[65]、目标检测[66]等任务.多尺度技术可分为空间域上的多尺度、时间域上的多尺度和频率域上的多尺度.计算机视觉中常用的多尺度技术是空间域上的多尺度, 也叫做多分辨率正则.这种多尺度技术是指在不同的尺度下对图像进行表征, 实现信息的互补.大的尺度的图像表征包含全局的语义信息, 具有一定的鲁棒性, 但缺乏各异性的局部信息.小尺度下的图像表征具有丰富的局部细节信息, 对于提高分类准确性、分割精度等具有重要意义, 但过分注意局部信息, 忽视全局信息, 增加模型训练的难度, 容易使模型求解陷于局部极小值, 产生过拟合的问题.结合多个尺度的图像表征就是将多个层次的信息进行融合, 从多个角度分析和筛选信息.此外, 将多尺度正则引入医学图像配准算法中, 可在一定程度上帮助解决大形变配准问题, 但不可避免地会增加计算资源的损耗.

Sokooti等[67]使用深度学习网络实现端到端的三维胸部CT图像的非刚性配准.网络的输入是在中心体素附近提取的多个分辨率的图像块(Patch), 以便于在后续特征提取中融合多尺度的语义信息.Sokooti等[67]的方法在实验效果上优于单一分辨率的B样条方法, 与多分辨率的B样条方法表现相近, 但配准速度得到提升.Li等[35]使用FCN预测三维大脑MRI数据的非刚性形变.在解码器部分输出不同分辨率的形变场, 将低分辨率的形变场产生的损失也加入损失函数中.最后得到的形变场比ANTs(Advanced Normalization Tools)在视觉上更锐利, 在LPBA40数据集上得到的54个感兴趣脑区的mean DSC达到0.72.Fan等[52]提出解决三维大脑MRI配准问题的BIRNet, 不仅将待配准图像与模板图像之间的残差图和梯度图信息与图像对一起作为网络输入, 还在多个特征尺度上输出多个分辨率的形变场.通过惩罚预测的多个尺度的形变场与真实形变场之间的差异, 进一步提高配准精度.

de Vos等[34]延续传统配准方法里多阶段配准的思路, 将多个CNN堆叠成一个大的网络框架, 实现从粗到细的图像配准.每个小的CNN输出的是不同间距下的B样条控制点上的形变.相比单阶段的网络框架, 多阶段的网络框架可有效提高配准的精度, 得到的形变场显示更少的折叠.在和Elastix效果相当的情况下, 速度提升近350倍.Stergios等[39]使用大的CNN同时预测图像对之间的仿射变换和非刚性形变.不同于文献[34], 文献[39]算法在训练过程中是将仿射形变和非刚性形变联合训练, 而文献[34]是先训练可预测仿射参数的网络, 固定网络参数, 再训练下一个小的处理局部非线性形变的CNN.相比只输出局部非线性形变场的网络方法, 同时输出仿射变换参数的方法在三维肺部CT数据上的mean DSC从81.75±7.88提升至82.34±7.68, 在基于地标的评价指标上约提升0.5%.Zhao等[68]将预测仿射变换参数的网络与处理非线性形变的网络级联成大的网络VTN(Volume Tweening Network).在三维肝脏数据中, VTN的配准精度超过ANTs、Elastix和Voxelmorph.在大脑数据集中, VTN的配准精度高于Elastix, 但略逊于ANTs.Zhao等[69]尝试级联多个VTN, 提高配准精度.级联后的网络在损失一定计算效率时, 在多个数据集上的配准都超过ANTs和Elastix.Fu等[50]利用GAN解决三维肺部CT配准问题, 并使用多尺度的网络结构.文中首先将下采样后的图像输入Coarse-Net中, 得到基于整幅图像的全局配准, 再利用Fine-Net进行基于Patch的局部配准.在训练时, 每个网络中都包含生成器和判别器.判别器用于惩罚不合理的变形后的待配准图像, 而不是惩罚预测的形变场, 因此不需要真实的形变场数据.此外, 由于肺部图像配准的特性, Fu等[50]发现在配准前, 应用肺部血管增强技术, 突出重要的血管结构, 可进一步提升肺部配准的准确性.在DIRLAB数据集上的配准精度超过一些传统的配准方法.

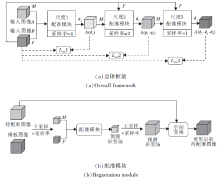
Jiang等[70]提出多尺度联合训练的网络模型(Multi-scale DIR Framework with Unsupervised Joint Training of Convolutional Neural Network, MJ-CNN), 框图如图8所示, 结合3个配准模块, 在不同尺度上对图像进行配准, 从而避免模型求解陷于极小值.与文献[34]模型的训练思路类似, 分别依次训练这3个模块, 但在最后对这3个模块进行联合训练, 以达到最优的端到端的参数配置.在测试阶段, 先将图像对下采样到原来的四分之一, 将其作为输入, 输入到第1个配准模型中, 输出的形变场经过上采样恢复到与原来图像对相同的尺寸, 将上采样后的形变场作为初始形变场, 得到粗配准的移动图像.再将形变后的待配准图像与模板图像下采样到原来的二分之一, 输入到第2个配准模型中, 希望第2个模型能预测形变场的残差.同样地, 将得到的形变后的待配准图像与模板图像输入第3个配准模块中.最终得到的图像对之间的形变场是3个模块中得到的形变场的复合.

MJ-CNN在DIRLAB数据集上的配准误差为1.66±1.44 mm, 而没有加入肺部分割数据的Elastix得到的配准误差为2.17±3.22 mm.在处理10 mm以上的大形变时, MJ-CNN的配准精度明显高于基于Patch的多尺度正则化算法[34].同时实验显示在SPARE数据集上训练的网络模型可较好地泛化到DIRLAB数据集上, 表明MJ-CNN具有较好的鲁棒性.

图8 MJ-CNN的网络框图Fig.8 Architecture of MJ-CNN

上述提到的多尺度技术都是空间域上的多尺度正则, 在损失计算效率的前提下, 一定程度上提高算法的鲁棒性和配准精度.这些工作中有基于Patch的多尺度正则方法和基于整幅图像的方法.基于Patch的多尺度方法可减轻计算资源的压力, 但预设的Patch的尺寸大小对配准结果会产生一些影响, 太小的尺寸会导致配准的上下文信息太少, 太大的尺寸可能使预测的中心点的局部变形不准确.而且将Patch拼接成整幅图像时, 有可能在Patch的边缘部分会出现不符合实际的伪影.此外, 基于Patch的多尺度正则方法受到Patch的大小限制, 在处理大形变问题时的配准精度不高, 而基于整幅图像的多尺度方法会消耗大量的计算资源, 相比基于Patch的多尺度方法, 基于整幅图像的方法可用的训练数据数量明显减少, 这也会对模型的训练及效果产生影响.

3 深度学习配准算法的研究展望

近年来, 虽然基于深度学习的医学图像配准算法在速度和精度上都具有一定的提升, 但仍存在一些问题.为了更好地将图像配准算法运用到实际中, 本节讨论未来可能的研究方向.

1)将深度学习与传统的图像配准算法结合.从第1节的讨论中可看出, 基于深度学习的图像配准算法计算效率较高, 可满足实际应用中的速度要求, 但模型的泛化能力差强人意, 需要大量的数据用于网络的训练, 这种要求在某些应用场景下是非常苛刻的.传统的图像配准算法的通用性较好, 算法表现较稳定.在处理解剖结构差异性较大的图像时, 如腹部图像等, 传统的图像配准算法的表现往往优于基于深度学习的配准算法.但是, 传统的配准算法大多需要进行多次迭代, 无法满足某些任务的实时性要求, 如手术导航等.将确定性的传统算法与基于大量数据训练的深度学习结合, 可较好地规避二者的缺点, 进一步提升图像配准算法的实用性, 具有较强的研究价值.目前已有的将深度学习与图像配准算法结合的研究可分为如下两方面:(1)将卷积神经网络作为图像的特征提取器, 再利用传统算法进行配准, 利用深度学习可较好地提取图像特征的特点, 避免传统方法中手动设置滤波器的困扰.如Wu等[71]使用堆叠的CAE(Convolutional Auto-Encoder)学习图像特征, 再结合其它基于特征的图像配准算法计算图像对之间的映射关系.但这种方法不是端到端的, 特征提取和配准分开, 学习的特征不是针对配准任务, 在一定程度上会造成配准精度的损失.(2)在监督学习和对偶监督学习中, 利用传统方法得到的形变场“ 隐性” 地指导网络的训练, 使预测的形变场具有传统方法中设定的一些形变场的性质.但这种“ 隐性” 的指导不能强硬地规定形变场的性质, 预测的形变场与期待结果仍存在一定差距.另外, 还有部分工作是将传统方法中已得到理论证明的正则约束嵌入到深度学习网络中, Heinrich等[72]将平均场推理嵌入深度学习网络中, 以达到对形变场的进一步约束.如何使传统方法中表现优异的其它正则约束以深度网络的形式得到有效表达, 需要进一步的研究.

2)利用深度学习实现数据自适应的形变正则.为了进一步缩小搜索空间, 解决反问题的算法往往会提出各种正则项.这种正则项的提出往往是针对某个特定问题, 并且是根据已有的先验知识预先设定的.从对正则项的讨论可看出, 在医学图像配准任务上基于深度学习的正则项研究相对较少, 主要围绕微分同胚的约束和多尺度的正则化处理手段.基于深度学习的图像配准算法大多希望形变是微分同胚的、得到的形变场是光滑的等, 但有可能在某些区域强调形变场的光滑, 反而会与实际的形变产生冲突.Jiang等[70]在实验中发现, 肺部边界的滑动运动(Sliding Motion)使该区域的形变场产生折叠, 这与损失函数中对不光滑不规则的形变场进行惩罚是相互矛盾的.通过设计数据自适应的正则, 规避上述错误, 可进一步提升配准精度.目前已有的多尺度方法是在图像上进行均匀的采样操作, 如果能将数据自适应正则与多尺度正则结合, 让数据自适应地选择在哪些区域进行多种尺度的信息融合, 可避免有些区域上不必要的采样和计算.因此, 未来应该更多关注于如何借助深度学习实现区域自适应的正则.

4 结束语

本文从监督学习、无监督学习和对偶监督/弱监督学习三个角度对图像配准的深度学习模型进行回顾与分析.结合模型驱动方法, 从正则项设计的角度出发, 对基于深度学习的医学图像配准算法进行进一步讨论.建议基于模型的配准学习算法与基于数据的配准学习算法进行融合, 认为这样更有助于提高算法性能.虽然基于深度学习的医学图像配准算法可大幅提升配准速度, 并且在一定程度上可获得较优的配准效果, 这仍值得进一步研究和改进.

参考文献
[1] GOU S P, CHEN L L, GU Y, et al. Large-Deformation Image Re-gistration of CT-TEE for Surgical Navigation of Congenital Heart Di-sease. Computational and Mathematical Methods in Medicine, 2018. DOI: 10.1155/2018/4687376. [本文引用:1]
[2] HAN X, HOOGEMAN M S, LEVENDAG P C, et al. Atlas-Based Auto-Segmentation of Head and Neck CT Images // Proc of the International Conference on Medical Image Computing and Compu-ter-Assisted Intervention. Berlin, Germany: Springer, 2008: 434-441. [本文引用:1]
[3] LI R J, JIA X, LEWIS J H, et al. Real-Time Volumetric Image Reconstruction and 3D Tumor Localization Based on a Single X-Ray Projection Image for Lung Cancer Radiotherapy. Medical Physics, 2010, 37(6): 2822-2826. [本文引用:1]
[4] DALCA A V, RAKIC M, GUTTAG J, et al. Learning Conditional Deformable Templates with Convolutional Networks[C/OL]. [2021-01-29]. https://arxiv.org/pdf/1908.02738.pdf. [本文引用:1]
[5] XIA M H, LIU B D. Image Registration by "Super-Curves". IEEE Transactions on Imaging Processing, 2004, 13(5): 720-732. [本文引用:1]
[6] SORZANO C O S, THEVENAZ P, UNSER M. Elastic Registration of Biological Images Using Vector-Spline Regularization. IEEE Tran-sactions on Biomedical Engineering, 2005, 52(4): 652-663. [本文引用:1]
[7] ROHDE G K, ALDROUBI A, DAWANT B W. The Adaptive Bases Algorithm for Intensity-Based Nonrigid Image Registration. IEEE Transactions on Medical Imaging, 2003, 22(11): 1470-1479. [本文引用:1]
[8] BOOKSTEIN F L. Principal Warps: Thin-Plate Splines and the Decomposition of Deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(6): 567-585. [本文引用:1]
[9] CHUI H L, RANGARAJAN A. A New Point Matching Algorithm for Non-rigid Registration. Computer Vision and Image Understand ing, 2003, 89(2/3): 114-141. [本文引用:1]
[10] JOHNSON H J, CHRISTENSEN G E. Consistent Land mark and Intensity-Based Image Registration. IEEE Transactions on Medical Imaging, 2002, 21(5): 450-461. [本文引用:1]
[11] SHEN D G, DAVATZIKOS C. HAMMER: Hierarchical Attribute Matching Mechanism for Elastic Registration. IEEE Transactions on Medical Imaging, 2002, 21(11): 1421-1439. [本文引用:1]
[12] YING S H, PENG J G, DU S Y, et al. Lie Group Framework of Iterative Closest Point Algorithm for n-D Data Registration. International Journal of Pattern Recognition and Artificial Intelligence, 2009, 23(6): 1201-1220. [本文引用:1]
[13] BEG M F, MILLER M I, TROUVÉ A, et al. Computing Large Deformation Metric Mappings via Geodesic Flows of Diffeomorphisms. International Journal of Computer Vision, 2005, 61(2): 139-157. [本文引用:1]
[14] VERCAUTEREN T, PENNEC X, PERCHANT A, et al. Diffeomorphic Demons: Efficient Non-parametric Image Registration. NeuroImage, 2009, 45(S1): S61-S72. [本文引用:1]
[15] TROUVÉ A, YOUNES L. Metamorphoses through Lie Group Action. Foundations of Computational Mathematics, 2005, 5(2): 173-198. [本文引用:1]
[16] HOLM D D, TROUVE A, YOUNES L. The Euler-Poincare Theory of Metamorphosis. Quarterly of Applied Mathematics, 2009, 67(4): 661-685. [本文引用:1]
[17] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet Cla-ssification with Deep Convolutional Neural Networks // Proc of the 25th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2012: 1097-1105. [本文引用:1]
[18] HASKINS G, KRUGER U, YAN P K. Deep Learning in Medical Image Registration: A Survey. Machine Vision and Applications, 2020, 31(11): 489-497. [本文引用:1]
[19] FU Y B, LEI Y, WANG T H, et al. Deep Learning in Medical Image Registration: A Review[C/OL]. [2020-06-04]. https://arxiv.org/pdf/1912.12318v1.pdf. [本文引用:1]
[20] ZITOVÁ B, FLUSSER J. Image Registration Methods: A Survey. Image and Vision Computing, 2003, 21(11): 977-1000. [本文引用:1]
[21] HILL D L G, BATCHELOR P G, HOLDEN M, et al. Medical Image Registration. Physics in Medicine and Biology, 2001, 46(3): R1-R45. [本文引用:1]
[22] CHEE E, WU Z Z. AIRNet: Self-supervised Affine Registration for 3D Medical Images Using Neural Networks[C/OL]. [2021-01-29]. https://arxiv.org/pdf/1810.02583.pdf. [本文引用:2]
[23] SALEHI S S M, KHAN S, ERDOGMUS D, et al. Real-Time Deep Registration with Geodesic Loss [C/OL]. [2021-01-29]. http://export.arxiv.org/pdf/1803.05982v1. [本文引用:1]
[24] SLOAN J M, GOATMAN K A, SIEBERT J P. Learning Rigid Image Registration-Utilizing Convolutional Neural Networks for Medical Image Registration // Proc of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies. Berlin, Germany: Springer, 2018, II: 89-99. [本文引用:1]
[25] SUN Y Y, MOELKER A, NIESSEN W J, et al. Towards Robust CT-Ultrasound Registration Using Deep Learning Methods // Proc of the International Workshop on Understand ing and Interpreting Machine Learning in Medical Image Computing Applications. Berlin, Germany: Springer, 2018: 43-51. [本文引用:1]
[26] EPPENHOF K A I, PLUIM J P W. Pulmonary CT Registration through Supervised Learning with Convolutional Neural Networks. IEEE Transactions on Medical Imaging, 2019, 38(5): 1097-1105. [本文引用:1]
[27] YANG X, KWITT R, NIETHAMMER M. Fast Predictive Image Registration[C/OL]. [2021-01-29]. http://wwwx.cs.unc.edu/~mn/sites/default/files/yang_arxiv_2016.pdf. [本文引用:2]
[28] CAO T, SINGH N, JOJIC V, et al. Semi-coupled Dictionary Learning for Deformation Prediction // Proc of the 12th IEEE International Symposium on Biomedical Imaging(ISBI). Washington, USA: IEEE, 2015: 691-694. [本文引用:1]
[29] ROHÉ M M, DATAR M, HEIMANN T, et al. SVF-Net: Learning Deformable Image Registration Using Shape Matching // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2017: 266-274. [本文引用:2]
[30] CAO X H, YANG J H, ZHANG J, et al. Deformable Image Registration Based on Similarity-Steered CNN Regression // Proc of the International Conference on Medical Image Computing and Compu-ter-Assisted Intervention. Berlin, Germany: Springer, 2017: 300-308. [本文引用:1]
[31] UZUNOVA H, WILMS M, HANDELS H, et al. Training CNNs for Image Registration from Few Samples with Model-Based Data Augmentation // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2017: 223-231. [本文引用:2]
[32] DOSOVITSKIY A, FISCHER P, ILG E, et al. FlowNet: Learning Optical Flow with Convolutional Networks // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 2758-2766. [本文引用:1]
[33] DE VOS B, BERENDSEN F F, VIERGEVER M A, et al. End-to-End Unsupervised Deformable Image Registration with a Convolutional Neural Network // Proc of the International Workshop on Deep Learning in Medical Image Analysis. Berlin, Germany: Springer, 2017: 204-212. [本文引用:1]
[34] DE VOS B, BERENDSEN F F, VIERGEVER M A, et al. A Deep Learning Framework for Unsupervised Affine and Deformable Image Registration. Medical Image Analysis, 2019, 52: 128-143. [本文引用:6]
[35] LI H M, FAN Y. Non-rigid Image Registration Using Fully Convolutional Networks with Deep Self-supervision[C/OL]. [2021-01-29]. https://arxiv.org/ftp/arxiv/papers/1709/1709.00799.pdf. [本文引用:2]
[36] GHOSAL S, RAY N. Deep Deformable Registration: Enhancing Accuracy by Fully Convolutional Neural Net. Pattern Recognition Letters, 2017, 94: 81-86. [本文引用:1]
[37] SHEIKHJAFARI A, NOGA M, PUNITHAKUMAR K, et al. Unsupervised Deformable Image Registration with Fully Connected Generative Neural Network[C/OL]. [2021-01-29]. https://openreview.net/pdf?id=HkmkmW2jM. [本文引用:1]
[38] PUNITHAKUMAR K, BOULANGER P, NOGA M. A GPU-Acce-lerated Deformable Image Registration Algorithm with Applications to Right Ventricular Segmentation. IEEE Access, 2017, 5: 20374-20382. [本文引用:1]
[39] STERGIOS C, MIHIR S, MARIA V, et al. Linear and Deformable Image Registration with 3D Convolutional Neural Networks // Proc of the International Workshop on Reconstruction and Analysis for Moving Organ, Breast, and Thoracic Images. Berlin, Germany: Springer, 2018: 13-22. [本文引用:3]
[40] BALAKRISHNAN G, ZHAO A, SABUNCU M R, et al. An Unsupervised Learning Model for Deformable Medical Image Registration // Proc of the IEEE/CVF Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2018: 9252-9260. [本文引用:1]
[41] RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutio-nal Networks for Biomedical Image Segmentation // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2015: 234-241. [本文引用:1]
[42] JADERBERG M, SIMONYAN K, ZISSERMAN A, et al. Spatial Transformer Networks // Proc of the 28th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2015, II: 2017-2025. [本文引用:1]
[43] KUANG D Y, SCHMAH T. FAIM-A ConvNet Method for Unsupervised 3D Medical Image Registration // Proc of the International Workshop on Machine Learning in Medical Imaging. Berlin, Germany: Springer, 2019: 646-654. [本文引用:1]
[44] VIALARD F X, RISSER L, RUECKERT D, et al. Diffeomorphic 3D Image Registration via Geodesic Shooting Using an Efficient Adjoint Calculation. International Journal of Computer Vision, 2012, 97(2): 229-241. [本文引用:1]
[45] SUN L, ZHANG S T. Deformable MRI-Ultrasound Registration Using 3D Convolutional Neural Network // Proc of the Internatio-nal Workshop on Simulation, Image Processing, and Ultrasound Systems for Assisted Diagnosis and Navigation. Berlin, Germany: Springer, 2018: 152-158. [本文引用:1]
[46] YOO I, HILDEBRAND D G C, TOBIN W F, et al. ssEMnet: Se-rial-Section Electron Microscopy Image Registration Using a Spatial Transformer Network with Learned Features // Proc of the International Workshop on Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Berlin, Germany: Springer, 2017: 249-257. [本文引用:1]
[47] ARGANDA-CARRERAS I, SORZANO C O S, MARABINI R, et al. Consistent and Elastic Registration of Histological Sections Using Vector-Spline Regularization // Proc of the International Workshop on Computer Vision Approaches to Medical Image Analysis. Berlin, Germany: Springer, 2006: 85-95. [本文引用:1]
[48] FAN J F, CAO X H, XUE Z, et al. Adversarial Similarity Network for Evaluating Image Alignment in Deep Learning Based Re-gistration // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2018: 739-746. [本文引用:2]
[49] LEI Y, FU Y B, HARMS J, et al. 4D-CT Deformable Image Re-gistration Using an Unsupervised Deep Convolutional Neural Network // Proc of the International Workshop on Artificial Intelligence in Radiation Therapy. Berlin, Germany: Springer, 2019: 26-33. [本文引用:1]
[50] FU Y B, LEI Y, WANG T H, et al. LungRegNet: An Unsupervised Deformable Image Registration Method for 4D-CT Lung. Medical Physics, 2020, 47(4): 1763-1774. [本文引用:3]
[51] FAN J F, CAO X H, WANG Q, et al. Adversarial Learning for Mono- or Multi-modal Registration. Medical Image Analysis, 2019. DOI: 10.1016/j.media.2019.101545. [本文引用:1]
[52] FAN J F, CAO X H, YAP P T, et al. BIRNet: Brain Image Re-gistration Using Dual-Supervised Fully Convolutional Networks. Medical Image Analysis, 2019, 54: 193-206. [本文引用:2]
[53] YAN P K, XU S, RASTINEHAD A R, et al. Adversarial Image Registration with Application for MR and TRUS Image Fusion // Proc of the International Workshop on Machine Learning in Medical Imaging. Berlin, Germany: Springer, 2018: 197-204. [本文引用:1]
[54] CAO X H, YANG J H, WANG L, et al. Deep Learning Based Inter-modality Image Registration Supervised by Intra-modality Similarity // Proc of the International Workshop on Machine Learning in Medical Imaging. Berlin, Germany: Springer, 2018: 55-63. [本文引用:1]
[55] HU Y P, MODAT M, GIBSON E, et al. Label Driven Weakly-Supervised Learning for Multimodal Deformable Image Registration // Proc of the 15th IEEE International Symposium on Biomedical Imaging. Washington, USA: IEEE, 2018: 1070-1074. [本文引用:1]
[56] HU Y P, MODAT M, GIBSON E, et al. Weakly-Supervised Con-volutional Neural Networks for Multimodal Image Registration. Medical Image Analysis, 2018, 49: 1-13. [本文引用:1]
[57] ARSIGNY V, COMMOWICK O, PENNEC X, et al. A Log-Euclidean Framework for Statistics on Diffeomorphisms // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2006: 924-931. [本文引用:2]
[58] DALCA A V, BALAKRISHNAN G, GUTTAG J, et al. Unsupervised Learning for Fast Probabilistic Diffeomorphic Registration // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2018: 729-738. [本文引用:4]
[59] KREBS J, MANSI T, MAILHE B, et al. Unsupervised Probabilistic Deformation Modeling for Robust Diffeomorphic Registration // Proc of the International Workshop on Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Su-pport. Berlin, Germany: Springer, 2018: 101-109. [本文引用:2]
[60] ZHANG J. Inverse-Consistent Deep Networks for Unsupervised Deformable Image Registration[C/OL]. [2021-01-29]. https://arxiv.org/pdf/1809.03443.pdf. [本文引用:1]
[61] LU Z W, YANG G Y, HUA T C, et al. Unsupervised Three-Dimensional Image Registration Using a Cycle Convolutional Neural Network // Proc of the IEEE International Conference on Image Processing. Washington, USA: IEEE, 2019: 2174-2178. [本文引用:1]
[62] KIM B, KIM J, LEE J, et al. Unsupervised Deformable Image Registration Using Cycle-Consistent CNN // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2019: 166-174. [本文引用:3]
[63] MOK T C W, CHUNG A C S. Fast Symmetric Diffeomorphic Image Registration with Convolutional Neural Networks // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 4643-4652. [本文引用:2]
[64] HUANG G, CHEN D L, LI T H, et al. Multi-scale Dense Convolutional Networks for Efficient Prediction[C/OL]. [2021-01-29]. https://arxiv.org/pdf/1703.09844v1.pdf. [本文引用:1]
[65] ZHAO H S, SHI J P, QI X J, et al. Pyramid Scene Parsing Network // Proc of the IEEE Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2017: 6230-6239. [本文引用:1]
[66] DENG L Y, YANG M, LI T Y, et al. RFBNet: Deep Multimodal Networks with Residual Fusion Blocks for RGB-D Semantic Segmentation[C/OL]. [2021-01-29]. https://arxiv.org/pdf/1907.00135v2.pdf. [本文引用:1]
[67] SOKOOTI H, DE VOS B, BERENDSEN F, et al. Nonrigid Image Registration Using Multi-scale 3D Convolutional Neural Networks // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Sprin-ger, 2017: 232-239. [本文引用:2]
[68] ZHAO S Y, LAU T F, LUO J, et al. Unsupervised 3D End-to-End Medical Image Registration with Volume Tweening Network. IEEE Journal of Biomedical and Health Informatics, 2020, 24(5): 1394-1404. [本文引用:1]
[69] ZHAO S Y, DONG Y, CHANG E, et al. Recursive Cascaded Networks for Unsupervised Medical Image Registration // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 10599-10609. [本文引用:1]
[70] JIANG Z R, YIN F F, GE Y, et al. A Multi-scale Framework with Unsupervised Joint Training of Convolutional Neural Networks for Pulmonary Deformable Image Registration. Physics in Medicine and Biology, 2020, 65(1). DOI: 10.1088/1361-6560/ab5da0. [本文引用:2]
[71] WU G R, KIM M, WANG Q, et al. Scalable High-Performance Image Registration Framework by Unsupervised Deep Feature Re-presentations Learning. IEEE Transactions on Biomedical Engineering, 2016, 63(7): 1505-1516. [本文引用:1]
[72] HEINRICH P M. Closing the Gap between Deep and Conventional Image Registration Using Probabilistic Dense Displacement Networks // Proc of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Germany: Springer, 2019: 50-58. [本文引用:1]