基于自适应稀疏结构学习的神经精神疾病特征选择方法

引用本文

郝世杰, 郭艳蓉, 陈涛, 汪萌, 洪日昌. 基于自适应稀疏结构学习的神经精神疾病特征选择方法. 模式识别与人工智能, 2021,34(4): 311-321
HAO Shijie, GUO Yanrong, CHEN Tao, WANG Meng, HONG Richang. Feature Selection Method for Neuropsychiatric Disorder Based on Adaptive Sparse Structure Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(4): 311-321. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202104003
Permissions

《模式识别与人工智能》编辑部

基于自适应稀疏结构学习的神经精神疾病特征选择方法

郝世杰^1,², 郭艳蓉^1,², 陈涛^1,², 汪萌^1,², 洪日昌^1,²

1.合肥工业大学大数据知识工程教育部重点实验室合肥 230601

2.合肥工业大学计算机与信息学院合肥 230601

通信作者:

郭艳蓉,博士,副研究员,主要研究方向为计算机视觉、医学图像分析.E-mail:yrguo@hfut.edu.cn.

作者简介:

郝世杰,博士,副教授,主要研究方向为模式识别、图像处理与分析.E-mail:hfut.hsj@gmail.com.

陈涛,博士研究生,主要研究方向为卷积神经网络、多模态融合.E-mail:Chentao.hfut@mail.hfut.edu.cn.

汪萌,博士,教授,主要研究方向为模式识别、数据挖掘、多媒体信息处理.E-mail:eric.mengwang@gmail.com.

洪日昌,博士,教授,主要研究方向为模式识别、多媒体问答.E-mail:hongrc.hfut@gmail.com.

收稿日期: 2020-07-26 接受日期: 2020-12-10

资助项目: 国家重点研发计划项目(No.2019YFA0706200)、国家自然科学基金项目(No.62072152,61702156,61772171,61876056)、安徽省自然科学基金项目(No.1808085QF188)、中央高校基本科研业务费专项资金(No.PA2020GDKC0023,PA2019GDZC0095)资助

摘要

在计算机辅助诊断神经精神疾病研究中,需要专业人士为样本进行诊断级的语义标注,耗费大量时间和精力,因此,以无监督的方式开展神经精神疾病辅助诊断研究具有重要意义.文中提出基于自适应稀疏结构学习的无监督特征选择方法,用于精神分裂症和阿兹海默症辅助诊断.在统一框架下同时学习稀疏表示和数据流形结构,并在该框架中采用一般化范数对稀疏学习的重构误差进行建模,不断迭代更新数据集的流形结构,解决传统特征选择方法存在的鲁棒性不足问题.在精神分裂症和阿兹海默症两个公共数据集上的实验表明文中方法在神经精神疾病分类中的有效性.

关键词: 无监督特征选择; 自适应稀疏结构学习; 流形学习; 神经精神疾病研究

中图分类号:TP 30 文章编号:2021,34(4):311-321

Feature Selection Method for Neuropsychiatric Disorder Based on Adaptive Sparse Structure Learning

HAO Shijie^1,², GUO Yanrong^1,², CHEN Tao^1,², WANG Meng^1,², HONG Richang^1,²

1. Key Laboratory of Knowledge Engineering with Big Data, Hefei University of Technology, Hefei 230601

2. School of Computer Science and Information Engineering, Hefei University of Technology, Hefei 230601

Corresponding author:
GUO Yanrong, Ph.D., associate professor. Her research interests include computer vision and medical image analysis.

AboutAuthor:
HAO Shijie, Ph.D., associate professor. His research interests include pattern recognition, image processing and analysis.
CHEN Tao, Ph.D. candidate. Her research interests include convolution neural network and multimodal fusion.
WANG Meng, Ph.D., professor. His research interests include pattern recognition, data mining and multimedia information processing.
HONG Richang, Ph.D., professor. His research interests include pattern recognition and multimedia Q&A.

Fund:Supported by National Key R&D Program of China(No.2019YFA0706200), National Natural Science Foundation of China(No.62072152,61702156,61772171,61876056), Natural Science Foundation of Anhui Province(No.1808085QF188), Fundamental Research Funds for the Central Universities(No.PA2020GDKC0023,PA2019GDZC0095).

Abstract

In the research of computer-aided diagnosis techniques for neuropsychiatric diseases, professionals are required to perform diagnostic-level semantic annotations on samples, and it is time-consuming and labor-intensive. Therefore, it is of great importance to develop unsupervised techniques for the computer-aided diagnosis on neuropsychiatric diseases. In this paper, an unsupervised feature selection method based on adaptive sparse structure learning is proposed and applied to the task of diagnosis on Schizophrenia and Alzheimer's disease. The sparse representation and the data manifold structure are simultaneously learned in a unified framework. In this framework, the generalized norm is adopted to model the reconstruction error of sparse learning. The manifold structure of the whole dataset is iteratively updated. The lacking of robustness in the traditional feature selection methods is relieved. Experiments on two public datasets of Schizophrenia and Alzheimer's disease demonstrate the effectiveness of the proposed method in classification of neuropsychiatric diseases.

Key words: Unsupervised Feature Selection; Adaptive Sparse Structure Learning; Manifold Learning; Neuropsychiatric Disorder Study

文章图片

本文责任编委杜少毅

Recommended by Associate Editor DU Shaoyi

神经精神疾病的临床表现为大脑认知功能紊乱, 如精神分裂症(Schizophrenia, SZ)和阿兹海默症(Alzheimer's Disease, AD)等.这些疾病为社会带来巨大困扰和负担.在神经精神疾病研究中, 神经影像学生物标记物是此类疾病诊疗研究的重要依据.例如, 在精神分裂症的诊断中, 可使用功能性核磁共振图像和结构性核磁共振图像提取神经生物学信息^[1]作为诊疗依据.对于阿兹海默症, 神经影像学数据和认知测试数据都被视为区分AD与前驱期轻度认知障碍(Mild Cognitive Impairment, MCI)或正常对照(Normal Control, NC)的重要特征^[2].一般来说, 这类研究中获得的多模态数据特征往往可从不同角度反映患者脑部的异常^{[3, 4]}.

然而, 这些高维特征往往会受到大量噪声、冗余和无关因素的影响, 对模式分类模型性能产生不利影响.因此, 如何从这些特征中进一步挖掘与疾病诊断高度相关的信息以提高诊断能力, 是一个具有挑战性的问题^{[5, 6, 7]}.针对这一问题, 研究人员提出基于特征选择算法的解决思路.这类算法可依据样本标签分为3类^[8]:1)有监督特征选择算法.依赖数据集及其语义标签训练模型, 进而选择有区分度的特征.2)半监督特征选择算法.假定数据集上含有少量标记样本和大量未标记样本, 进而协同有标记样本和无标记样本进行特征选择模型的训练.3)无监督算法.只需要原始数据集, 无需这些样本具有语义标注.具体来说特征选择尝试确定原始特征子集, 去除不相关的特征, 保留相关特征^{[9, 10, 11]}.

根据特征选择设计方法, 特征选择算法大致可分为3类:1)过滤型特征选择; 2)包裹型特征选择; 3)嵌入型特征选择.过滤型特征选择利用某个评价指标衡量特征的重要性, 每个特征具有一个重要性权重, 根据权重重要性对所有特征进行排序, 通过指定的阈值选择相应的特征, 过滤型特征选择不涉及后续的模型学习.拉普拉斯评分方法(Laplacian Score)^[12]通过评估每个特征的性能对特征进行排序.基于改进互信息的特征选择(Modified Mutual Information Based Feature Selection, MMIFS)^[13]通过解析选择最佳特征进行分类.这种基于互信息的特征选择算法可处理线性相关和非线性相关的数据特征.包裹型特征选择直接将最终的学习器性能作为特征子集的评价准则.从性能角度上说, 包裹型特征选择更优, 但它需要多次训练学习器, 计算成本较高, 容易过拟合.Rodrigues等^[14]提出基于最优路径的包裹型特征选择算法, 将特征选择问题建模为基于二进制的优化技术.嵌入型特征选择是在建模过程中进行特征选择.特征选择也可作为训练过程的一部分, 优化训练过程中的目标函数, 获得有用的特征.嵌入型特征选择与包裹型特征选择相似, 但计算成本较低, 不易过度拟合.因此近年来嵌入型特征选择以其良好的性能受到越来越多的关注.例如, 嵌入式无监督特征选择(Embedded Unsupervised Feature Selection, EUFS)^[15]通过稀疏学习直接将特征选择嵌入聚类算法中.

考虑到生物医学应用中获取大量的标记信息是一项耗时、昂贵的任务, 如邀请高水平专业人员为病例样本逐一标记诊断级的标注.相反, 未标记的数据相对容易获取.基于这一特殊背景, 以无监督的方式设计有效的特征选择算法具有重要研究意义和应用价值.谱学习试图在低维空间中保持高维数据的相似性, 这是一类重要的无监督特征选择算法, 如谱特征选择(Spectral Feature Selection, SPEC)^[16], 多簇特征选择(Multi-cluster Feature Selection, MCFS)^[17]和最小冗余谱特征选择(Minimum Redundancy Fea-ture Selection, MRFS)^[18].这些方法存在的问题是分别进行结构学习和特征选择.为了解决这一问题, 学者们提出同时进行流形学习和稀疏回归的方法, 如联合嵌入学习和稀疏回归(Joint Embedding Lear-ning and Sparse Regression, JELSR)^[19].这些方法在特征表示中嵌入数据流形结构, 提高性能.

尽管这些方法在挖掘判别性特征方面具有一定优势, 但仍存在一些亟待解决的问题.1)传统的损失项(如l_F范数或最小二乘损失)和稀疏正则化项(即l₁范数)难以在噪声鲁棒性、数据拟合性、模型稀疏性之间取得最佳平衡.2)相关算法选择采用固定的拉普拉斯矩阵描述数据的流形结构, 指导特征选择过程.然而, 由于原始数据集中存在噪声和冗余特征, 直接根据该数据集获得拉普拉斯矩阵且不对其加以持续更新优化, 会降低模型的性能^[20].

为了解决上述问题, 本文提出基于自适应稀疏结构学习的神经精神疾病特征选择方法, 在统一的框架中进行稀疏表示和流形结构学习.基于字典学习策略从原始数据中提取数据基, 将所有数据投影到基于字典的低维空间中, 完成特征表示和拉普拉斯矩阵的联合自适应学习.本文分别采用2种一般化范数, 即l_2,_r范数(0< r< 2)和l_2,_p(0< p< 1)范数, 用于构建损失项和正则项, 提高模型的灵活性.为了提高模型的鲁棒性, 利用自适应流形结构学习方法(Adaptive Sparse Structure Learning, ASSL), 减小噪声和冗余对内蕴流形结构的影响.基于上述思路, 构建包含多个任务的联合目标函数, 采用迭代优化的方法进行求解, 即每个子任务可以基于另一

个子任务的输出进行迭代更新.最后从理论上证明上述求解过程可收敛.

1 基于自适应稀疏结构学习的神经精神疾病特征选择方法

基于自适应稀疏结构学习的神经精神疾病特征选择方法框图如图1所示.首先, 根据神经精神疾病诊疗过程中采集的多模态信息(如基于脑影像提取的生物标记、被试者信息等), 利用字典学习获得基空间.在此基础上, 进行自适应稀疏结构学习, 获得稀疏表示和流形结构.进行特征选择后, 利用k-means进行聚类, 完成无监督分类的任务.

	Figure Option View Download New Window
	图1 本文方法流程图Fig.1 Flowchart of the proposed method

1.1 字典学习

字典学习任务表示如下:

$\min_{B, Z}$ ‖ X-BZ $‖_{F}^{^{2}}$ +η $\overset{n}{\sum_{j = 1}}$ ‖ z^j‖ ₁, s.t. $\overset{m}{\sum_{i = 1}} \overset{k}{\sum_{j = 1}} b_{i, j}^{2}$ 1.

其中:B∈R^m^×^k为基矩阵, 每列表示一个基向量; Z∈R^k^×ⁿ为待学习的数据表示; η 为用于平衡损失项和正则化项的权重参数.

$\overset{m}{\sum_{i = 1}} \overset{k}{\sum_{j = 1}} b_{i, j}^{2}$ ≤ 1

这一约束条件旨在避免B值过大, 否则会导致Z中值过小.本文使用稀疏建模软件(Sparse Modeling Software, SPAMS)^[21]求解基矩阵B.

1.2 自适应稀疏结构学习

基于基矩阵B, 本文方法目标是学习数据X的稀疏特征表示S, 而特征选择可通过选择S中的非零行实现.

为了获得S, 本文构建目标函数J(S, W):

arg $\min_{S, W}$ J(S, W)=‖ X-BS $‖_{_{2, r}}^{^{r}}$ +α‖ S $‖_{_{2, p}}^{^{p}}$ + β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖sⁱ-s^j $‖_{_{2}}^{^{2}}$ w_ij₊λ $\overset{n}{\sum_{i = 1}}$ ‖w_i $‖_{_{2}}^{^{2}}$

s.t.∀ w_i1=1, w_ii=₀,

w_ij≥ 0, j∈N(i),

w_ij=0, j∉N(i).(1)

其中:X∈R^m^×ⁿ为训练数据集, n列表示n个数据样本, 每个样本表示为一个m维的列向量; N(i)为样本i的邻域; ‖ X‖ _r_,_p为X的广义范数,

‖ X‖ _r_,_p=( $\overset{m}{\sum_{i = 1}}$ ( $\overset{n}{\sum_{j = 1}}$ |x_ij|^r) ^{$^{\frac{p}{r}}$}) ^{$^{\frac{1}{p}}$}.

J(S, W)中的各项含义详细描述如下.

目标函数J的第1项为损失项, 在基空间B的基础上, 最小化原始数据矩阵X与BS之间的重构误差‖ X-BS $‖_{_{2, r}}^{^{r}}$ , 可将学习的S视为原始数据X在基空间B的投影.本文选择一般化范数l_2,_r衡量该误差损失项, 而不是通常的l_F范数.因为l_2,_r范数阶r直接影响损失项性能.当r相对较小时, 损失项对异常点的鲁棒性更强, 而当r相对较大时, 损失项的数据拟合性更优.

目标函数J的第2项为正则化项, 避免学习S过程出现过拟合.通常情况下, 将S中的相应元素设置为零以体现S的稀疏性, 这实际上等同于保留重要特征并去除不重要的特征.考虑到l_2,_p(0< p< 1)范数可生成比l₁范数和l_{2, 1}范数更稀疏的解, 因此采用一般化范数达到稀疏性, 即‖ S $‖_{_{2, p}}^{^{p}}$ .

目标函数J的第3项和第4项意在特征学习过程中仍保持原始数据的流形结构, 为此引入基于图的拉普拉斯矩阵(Graph Laplacian):

$\sum_{i \neq j}$ ‖ sⁱ-s^j $‖_{_{2}}^{^{2}}$ w_ij=tr(SLS^T).

其中:

w_ij= $\{\begin{array}{l} \exp (- \frac{‖ x^{i} - x^{j} ‖^{2}}{σ}), & j \in N (i) \\ 0, & j \notin N (i) \end{array}$

用于衡量第i个样本和第j个样本之间的相似度; σ 为缩放参数; L为拉普拉斯矩阵, 可由L=D-W得到, W为相似度矩阵, D为对角矩阵, 对角线元素为W的列元素之和.由于W矩阵度量数据集X中所有邻近样本间的相似性, 也可视为数据集X的图结构表示, 拉普拉斯矩阵L进一步反映X的流形结构.

值得注意的是, 由于原始特征往往受到噪声和冗余元素的影响, 难以保证拉普拉斯矩阵L的可靠性.换言之, 在优化目标函数J的过程中, 若L无法充分表示数据集X的内蕴流形结构, 会阻碍模型性能的进一步提升.因此, 本文在优化目标函数J过程中, 不但优化S, 还一并迭代更新W, 实现挖掘更符合数据内蕴流形结构的目标.基于此种情况, 构建目标函数J中的流形结构优化项:

β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖ sⁱ-s^j $‖_{_{2}}^{^{2}}$ w_ij+λ $\overset{n}{\sum_{i = 1}}$ ‖ w_i $‖_{_{2}}^{^{2}}$ ,

s.t. ∀ w_i1=1, w_ii=0,

w_ij≥ 0, j∈N(i),

w_ij=0, j∉N(i).(2)

其中:β 、λ 为权重参数; 1为元素均为1的列向量.对w_i的约束是为避免无意义解.

2 目标函数求解与收敛性分析

2.1 目标函数求解

在求解目标函数J(S, W)时, 由于S和W具有耦合关系, 难以同时优化求解, 因此, 本节通过交替优化该目标函数, 即固定一个变量更新另一个变量, 直到满足预定义收敛准则为止.

更新S.当固定W时, 式(1)转化为最小化目标函数:

J(S)=‖ X-BS $‖_{_{2, r}}^{^{r}}$ +‖ S $‖_{_{2, p}}^{^{p}}$ +β tr(SLS^T).

对上述函数求S的偏导数, 可得

$\frac{\partial J (S)}{\partial S}$ =-2B^TD₁(X-BS)+2αD₂S+2β SL, (3)

其中, D₁、D₂均为对角矩阵, D₁对角线元素为 $\frac{r}{2 ‖ x_{i} - B s_{i} ‖_{_{2}}^{^{2 - r}}}$ , D₂对角线元素为 $\frac{p}{2 ‖ s_{i} ‖_{_{2}}^{^{2 - p}}}$ .令式(3)为0, 整理可得

(B^TD₁B+2αD₂)S+Sβ L=B^TD₁X,

其中, B^TD₁B+2αD₂和β L都是半正定矩阵, 对其进行奇异值分解, 得

B^TD₁B+2αD₂=UC₁U^T, β L=VC2_VT^,

其中, U、V为酉矩阵, 上式进一步表示为

UC₁U^TS+SVC₂V^T=B^TD₁X.

将上述方程左右两侧的U^T和V分别相乘, 可得

C₁U^TSV+U^TSVC₂=U^TB^TD₁XV,

其中,

C₁_/₂=diag( $σ_{1 / 2}^{(1)}$ , $σ_{1 / 2}^{(2)}$ , …, $σ_{1 / 2}^{(m)}$ ), σ ₁_/₂=sign( $(C_{1 / 2})_{i}^{i}$ )(max( |(C₁_/₂ $)_{i}^{i}$ |)).

为了简化表示, 上式可用

ψ=U^TSV, Ω=U^TB^TD₁XV

表示, 因此得

C₁ψ+ψC₂=Ω.

在此采用梯度迭代法求解上述矩阵方程组, 得到稀疏矩阵:

S=UψV^T.(4)

更新W.再固定S时, 式(1)中的第1项和第2项可视作常数.更新W时, 目标函数J可简化为

β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖ sⁱ-s^j $‖_{_{2}}^{^{2}}$ w_ij+λ $\overset{n}{\sum_{i = 1}}$ ‖ w_i $‖_{_{2}}^{^{2}}$ ,

s.t. ∀ w_i1=1, w_ii=0,

w_ij≥ 0, j∈N(i),

w_ij=0, j∉N(i).(5)

令h_ij=‖ sⁱ-s^j $‖_{_{2}}^{^{2}}$ , 式(5)可进一步转化为

$\min_{w_{i}}$ ||w_i+ $\frac{β}{2 λ}$ h_i ${||}_{_{2}}^{^{2}}$ ,

s.t. ∀ w_i1=1, w_ii=0,

w_ij≥ 0, j∈N(i),

w_ij=0, j∉N(i).(6)

对式(6)构造拉格朗日函数:

$\min_{w_{i}}$ ||w_i+ $\frac{β}{2 λ}$ h_i ${||}_{_{2}}^{^{2}}$ -τ (w_i1-1)-η ^T ${w^{T}}_{i}$ ,

其中, τ 、η 为拉格朗日乘子.最终得到闭式解:

w_ij= ( $- \frac{β}{2 λ} h_{ij} {+ τ)}_{+}$ .(7)

综上所述, 本文自适应稀疏结构学习方法整体优化过程如下.

算法1 自适应稀疏结构学习

输入原始数据集X∈R^m^×ⁿ, 基B∈R^m^×^k

输出表示矩阵S∈R^k^×ⁿ

初始化随机初始化表示矩阵S,

基于X初始化拉普拉斯矩阵L∈Rⁿ^×ⁿ

重复

构建(B^TD₁B+αD₂), β L,

根据式(4)更新矩阵S,

根据式(7)更新矩阵W,

更新拉普拉斯矩阵L=D-W,

直至收敛

2.2 收敛性分析

本节证明2.1节中求解过程的收敛性, 即证明第t+1次迭代时目标函数取值小于第t次迭代.遵循文献[22]、文献[23], 可得

‖ X-BS⁽^t⁾ $‖_{_{2, r}}^{^{r}}$ +α‖ S⁽^t⁾ $‖_{_{2, p}}^{^{p}}$ +β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖ (sⁱ)⁽^t⁾-(s^j)⁽^t⁾ $‖_{_{2}}^{^{2}} w_{ij}^{(t + 1)}$ +λ $\overset{n}{\sum_{i = 1}}$ ‖ $w_{i}^{(t + 1)} ‖_{_{2}}^{^{2}}$ ≤ ‖ X-BS^(t) $‖_{_{2, r}}^{^{r}}$ α‖ S^(t) $‖_{_{2, p}}^{^{p}}$ β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖ $(s^{i})^{(t)}$ $(s^{j})^{(t)} ‖_{_{2}}^{^{2}} w_{ij}^{(t)}$ λ $\overset{n}{\sum_{i = 1}}$ ‖ $w_{i}^{(t)} ‖_{_{2}}^{^{2}}$ (8)

固定W⁽^t⁾更新S⁽^t⁾, 可得

‖ X-BS⁽^t⁺¹⁾ $‖_{_{2, r}}^{^{r}}$ +α‖ S⁽^t⁺¹⁾ $‖_{_{2, p}}^{^{p}}$ +β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖ (sⁱ)⁽^t⁺¹⁾-(s^j)⁽^t⁺¹⁾ $‖_{_{2}}^{^{2}} w_{ij}^{(t + 1)}$ +λ $\overset{n}{\sum_{i = 1}}$ ‖ $w_{i}^{(t + 1)} ‖_{_{2}}^{^{2}}$ ≤ ‖ X-BS^(t) $‖_{_{2, r}}^{^{r}}$ α‖ S^(t) $‖_{_{2, p}}^{^{p}}$ β $\overset{n}{\sum_{i = 1 j = 1}}$ ‖(sⁱ)^(t)-(s^j)^(t) $‖_{_{2}}^{^{2}} w_{ij}^{(t + 1)}$ λ $\overset{n}{\sum_{i = 1}}$ ‖ $w_{i}^{(t + 1)} ‖_{_{2}}^{^{2}}$ (9)

最终, 基于式(8)和式(9)进一步可得

‖ X-BS⁽^t⁺¹⁾ $‖_{_{2, r}}^{^{r}}$ +α‖ S⁽^t⁺¹⁾ $‖_{_{2, p}}^{^{p}}$ +β tr(S⁽^t⁺¹⁾L⁽^t⁺¹⁾ $(S^{(t + 1)})^{T}$ )+λ $\overset{n}{\sum_{i = 1}}$ ‖ $w_{i}^{(t + 1)} ‖_{_{2}}^{^{2}}$ ≤ ‖ X-BS^(t) $‖_{_{2, r}}^{^{r}}$ α‖ S^(t) $‖_{_{2, p}}^{^{p}}$ +β tr(S^(t)L^(t) $(S^{(t)})^{T}$ )+λ $\overset{n}{\sum_{i = 1}}$ ‖ $w_{i}^{(t)} ‖_{_{2}}^{^{2}}$

基于上述分析, 可看出2.1节优化方法可使目标函数J(S, W)在迭代过程中单调减少, 从而确保收敛性.

3 实验及结果分析

3.1 实验数据集

本文选取如下2个公开的神经精神疾病数据集进行评估:精神分裂症数据集和阿兹海默症数据集.

精神分裂症数据集是由美国国立卫生研究院的COBRE(Centers of Biomedical Research Excellence)中心创建的疾病数据集(https://www.kaggle.com/c/mlsp-2014-mri/overview), 包括精神分裂症患者(SE)40人, 正常对照组(NC)46人.数据集上包含2种模态的图像特征:1)从功能磁共振成像获得的脑功能网络连通性特征(379维), 2)从结构磁共振成像中获得的源基形态计量特征(33维).本文使用这2种模态特征完成无监督的特征选择, 用于精神分裂症患者与正常人的无监督聚类(NC vs.SZ)任务.

阿兹海默症数据集来自阿兹海默症神经影像计划(Alzheimer's Disease Neuroimaging Initiative, ADNI)数据库(http://adni.loni.usc.edu).本文采用遗传信息、人口统计学信息、认知测试数据及核磁共振成像中不同脑区的测量值等662维的多模态生物标记物, 实验中共有 628名受试者, 主要包括正常对照组(NC)190人、轻度认知障碍患者(MCI)304人、阿兹海默症患者(AD)134人.本文方法应用在该数据集上, 进行一系列的聚类任务, 用于区分不同疾病阶段的受试者, 具体包含以下任务:NC vs.AD, NC vs.MCI, MCI vs.AD, NC vs.MCI& AD.

阿兹海默症和精神分裂症同属于神经精神类疾病, 两者发病机制差异较大, 因此对特定脑疾病的发生发展机制进行研究是十分有意义的.针对不同疾病, 本文方法可有效处理大批量、高维度的医疗数据, 实现辅助医生进行疾病诊断的目的.本文方法同样可扩展到其它脑部疾病的辅助诊断发生发展机制研究中.

3.2 参数设置

考虑到有标签数据获取的难度和较大的人力成本开销, 在实验设置中, 采用无监督的聚类分析验证本文方法.通过学习无监督的聚类模型, 在验证本文方法有效性时, 可着眼于特征表示本身产生的贡献.相比受监督学习下的分类模型, 虽然无监督的聚类分析在精确度上可能有所降低, 但可更直观地验证本文方法的有效性.

遵从文献[24]的实验设置, 在求解目标函数时, 需要根据交叉验证预先设置α, β , λ , r, p.对于所有需考虑邻居节点的方法, 设置邻居节点的数目为5.不同任务在不同的参数设置下将获得不同的聚类结果.因此, 在完成目标函数优化后, 根据获得矩阵S的l_2,_p范数值, 将非零元素行视为具有判别性特征, 将全零元素行视为无判别性的特征.在此基础上, 将各判别性特征对应的l_2,_p范数进行降序排序, 选取前100个判别性较高的特征.最后, 根据特征选择结果完成实验.

3.3 评价指标

本文选取基于无监督特征选择的常用评价指标进行量化评估, 包括聚类准确度(ACC)、F1值(F1_measure)、精确率(Precision)和召回率(Re-call).假设h_i为真实类标签, g_i为预测类标签, C为类数量, ACC可定义为

ACC= $\frac{1}{C} \overset{C}{\sum_{i = 1}}$ δ(h_i, map(g_i)),

其中:δ(·, ·)为指示函数, 如果x=y, δ(x, y)=1, 否则δ(x, y)=0; 引入的map(·)函数用于预测聚类标签, 以最大限度地匹配真实标签.在此基础上分别用TP表示真阳性, TN表示真阴性, FP表示假阳性, FN表示假阴性, 则

Precision= $\frac{TP}{TP + FP}$ , Recall= $\frac{TP}{TP + FN}$ , F1_measure= $\frac{2 \times Precision \times Recall}{(Precision + Recall)}$

上述评价指标分数越高, 说明方法性能越优.

3.4 对比算法

1)基线方法(Baseline).为了验证特征选择的有效性, 所有特征都直接输入分类器执行聚类任务.

2)非负判别特征选择(Non-negative Discrimi-native Feature Selection, NDFS)^[25].通过谱聚类理解输入样本的聚类标签, 同时进行选择特征.

3)联合图稀疏编码(Joint Graph Sparse Coding, JGSC)^[26].在统一的框架内同时考虑流形学习和谱聚类, 并采用l_F范数进行特征选择.

4)鲁棒联合图稀疏编码(Robust JGSC, RJGSC)^[27].采用l_{2, 1}范数提高模型的鲁棒性.

5)基于自适应图不相关正则化特征选择(Unco-rrelated Regulation with Adaptive Graph for Feature Selection, URAFS)^[28].将数据结构保留在流形结构中, 引入基于最大熵原理的图正则化项, 将数据的局部几何结构嵌入流形学习中.

6)图正则化无监督特征选择(Graph Regula-rized Unsupervised Feature Selection, GRUFS)^[29].使用l_{2, 1}范数表示残差矩阵, 使用基于l₁范数的拉普拉斯正则化项保持数据的局部几何结构, 减少噪声数据对特征选择的影响.

7)泛化稀疏结构学习(General Sparse Structure Learning, GSSL).为了验证自适应图学习的有效性, 构建本文方法的一个中间版本, 目标函数是式(1)的前3项, 仅优化S.

8)自适应稀疏结构学习(ASSL).在统一的框架下同时优化S和W, 即本文方法.

3.5 参数敏感性分析

本节主要讨论损失范数阶r和正则化范数阶p对方法性能的影响.选取

r=0.25, 0.50, 0.75, 1.00, 1.25, 1.50, 1.75, 2.00; p=0.25, 0.50, 0.75, 1.00.

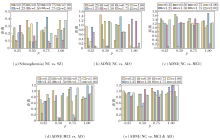
针对不同任务, 遍历r、p, 样本与聚类中心的距离如图2和图3所示.由图可看到, 相比GSSL, ASSL类间所有的点与该类质心距离之和更小、更稳定.上述结果证实更新W的有效性.此外, 图2和图3是相同任务和不同参数设置下GSSL和ASSL的类间样本与质心距离和, 由图2和图3可看出, ASSL的聚类距离结果对r、p更鲁棒.

	Figure Option View Download New Window
	图2 r、p不同时GSSL在不同任务上类间所有的样本与该类质心距离之和Fig.2 Sum of distances between all samples and centroid of GSSL on different tasks with different r and p

	Figure Option View Download New Window
	图3 r、p不同时ASSL在不同任务上类间所有样本与该类质心距离之和Fig.3 Sum of distances between all samples and centroid of ASSL on different tasks with different r and p

3.6 实验结果对比

各方法在不同任务上的指标值对比如表1~表4所示.

表1 各方法在不同任务上的聚类准确度对比 Table 1 Clustering accuracy comparison of different methods on different tasks %

表2 各方法在不同任务上的F1值对比 Table 2 F1_measure comparison of different methods on different tasks %

表3 各方法在不同任务上的精确率对比 Table 3 Precision comparison of different methods on different tasks %

表4 各方法在不同任务上的召回率对比 Table 4 Recall comparison of different methods on different tasks %

由表1可看出, Baseline在所有任务中都表现不佳, 其余方法的聚类精度都明显优于Baseline.这说明特征选择对各项任务的性能提升作用显著, 另一方面, 也说明Baseline将所有特征直接输入模型中, 受到各类噪声、冗余和无关特征的负面影响.

由表1可看到, ASSL取得较优的无监督分类结果.在四项任务中, ASSL分别比次优方法提高5.67%(NC vs.SZ)、9.50%(NC vs.AD)、5.20%(MCI vs.AD)、2.39%(NC vs.MCI& AD).而在NC vs.MCI任务中, ASSL也取得次优的聚类精度.从表2~表4可看到, 在精确率和召回率两个指标方面, ASSL在各任务上大多取得最优或次优结果, 在F1值方面, ASSL全部取得最优结果.

ASSL求解过程具有良好的收敛性.由图4给出的ASSL在不同聚类任务上目标函数收敛曲线可看到, ASSL在不同任务求解过程中目标函数取值均能快速下降且达到稳定, 这与收敛性理论分析一致.

	Figure Option View Download New Window
	图4 ASSL在不同任务上目标函数的收敛曲线Fig.4 Convergence curves of objective function for different clustering tasks by ASSL

4 结束语

本文提出基于自适应稀疏结构学习的无监督特征选择方法, 应用于辅助诊断神经精神疾病中, 取得较优的无监督聚类结果.本文方法有助于解决临床中样本缺乏诊断级语义标注、数据含有噪声和冗余等问题.

对本文研究的深入和拓展主要分为如下方面:在方法层面上, 考虑到本文学习到的字典是固定的, 今后可进一步将字典学习也纳入优化过程.在应用层面上, 可将本文方法应用于其它神经精神疾病的计算机辅助诊断中, 如癫痫病、抑郁症等.此外, 对于具有多个时间点的病例数据, 可通过特征学习技术对神经精神疾病发展过程的生物标记进行挖掘与追踪.

参考文献

文献选项

[1]	BODAPATI A S, JENKINS L M, SHARMA R P, et al. Visual Memory Uniquely Predicts Anhedonia in Schizophrenia but not Bipolar Disorder. Journal of Neuropsychology, 2019, 13(1): 136-146. [本文引用:1]
[2]	LEE G, NHO K, KANG B, et al. Predicting Alzheimer's Disease Progression Using Multi-modal Deep Learning Approach. Scientific Reports, 2019, 9. DOI: 10.1038/s41598-018-37769-z. [本文引用:1]
[3]	FRANZMEIER N, RUBINSKI A, NEITZEL J, et al. Functional Connectivity Associated with TAU Levels in Ageing, Alzheimer's, and Small Vessel Disease. Brain, 2019, 142(4): 1093-1107. [本文引用:1]
[4]	CHOI J Y, LEE B. Combining of Multiple Deep Networks via Ensemble Generalization Loss, Based on MRI Images, for Alzheimer's Disease Classification. IEEE Signal Processing Letters, 2020, 27: 206-210. [本文引用:1]
[5]	LIU H, YU L. Toward Integrating Feature Selection Algorithm for Classification and Clustering. IEEE Transaction on Knowledge and Data Engineering, 2005, 17(4): 491-502. [本文引用:1]
[6]	LI X P, WANG Y D, RUIZ R. A Survey on Sparse Learning Models for Feature Selection. IEEE Transactions on Cybernetics, 2020. DOI: 10.1109/TCYB.2020.2982445. [本文引用:1]
[7]	郑建炜, 路程, 秦梦洁, 等. 联合特征选择和光滑表示的子空间聚类算法. 模式识别与人工智能, 2018, 31(5): 409-418. (ZHENG J W, LU C, QIN M J, et al. Subspace Clustering via Joint Feature Selection and Smooth Representation. Pattern Recognition and Artificial Intelligence, 2018, 31(5): 409-418. ) [本文引用:1]
[8]	LI J D, CHENG K W, WANG S H, et al. Feature Selection: A Data Perspective. ACM Computing Surveys, 2017, 50(6). DOI: 10.1145/3136625. [本文引用:1]
[9]	ALZUBI J A. Diversity-Based Boosting Algorithm. International Jour-nal of Advanced Computer and Applications, 2016, 7(5): 524-529. [本文引用:1]
[10]	ALZUBI J, NAYYAR A, KUMAR A. Machine Learning from Theory to Algorithms: An Overview // Proc of the 2nd International Conference on Computational Intelligence. Berlin, Germany: Sprin-ger, 2018. DOI: 10.1088/1742-6596/1142/1/012012. [本文引用:1]
[11]	YANG Y, SHEN H T, MA Z G, et al. l_{2, 1}-norm Regularized Discriminative Feature Selection for Unsupervised Learning // Proc of the 22nd International Joint Conference on Artificial Intelligence. New York, USA: ACM, 2011: 1589-1594. [本文引用:1]
[12]	HE X F, CAI D, NIYOGI P. Laplacian Score for Feature Selection // Proc of the 18th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2005: 507-514. [本文引用:1]
[13]	AMBUSAIDI M A, HE X J, NANDA P, et al. Building an Intrusion Detection System Using a Filter-Based Feature Selection Algorithm. IEEE Transactions on Computers, 2016, 65(10): 2986-2998. [本文引用:1]
[14]	RODRIGUES D, PEREIRA L A M, NAKAMURA R Y M, et al. A Wrapper Approach for Feature Selection Based on Bat Algorithm and Optimum-Path Forest. Expert Systems with Applications, 2014, 41(5): 2250-2258. [本文引用:1]
[15]	WANG S H, TANG J L, LIU H, et al. Embedded Unsupervised Feature Selection // Proc of the 29th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2015: 470-476. [本文引用:1]
[16]	ZHAO Z, LIU H. Spectral Feature Selection for Supervised and Unsupervised Learning // Proc of the 24th International Confe-rence on Machine Learning. New York, USA: ACM, 2007: 1151-1157. [本文引用:1]
[17]	CAI D, ZHANG C Y, HE X F. Unsupervised Feature Selection for Multi-cluster Data // Proc of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2010: 333-342. [本文引用:1]
[18]	ZHAO Z, WANG L, LIU H. Efficient Spectral Feature Selection with Minimum Redundancy // Proc of the 24th AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2010: 673-678. [本文引用:1]
[19]	HOU C P, NIE F P, LI X L, et al. Joint Embedding Learning and Sparse Regression: A Framework for Unsupervised Feature Selection. IEEE Transactions on Cybernetics, 2014, 44(6): 793-804. [本文引用:1]
[20]	NG A Y, JORDAN M I, WEISS Y. On Spectral Clustering: Ana-lysis and an Algorithm // Proc of the 14th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2001: 849-856. [本文引用:1]
[21]	MAIRAL J, BACH F, PONCE J, et al. Online Learning for Matrix Factorization and Sparse Coding. Journal of Machine Learning Research, 2010, 11: 19-60. [本文引用:1]
[22]	LEI C, ZHU X F. Unsupervised Feature Selection via Local Structure Learning and Sparse Learning. Multimedia Tools and Applications, 2018, 77(22): 29605-29622. [本文引用:1]
[23]	PENG H Y, FAN Y. A General Framework for Sparsity Regula-rized Feature Selection via Iteratively Reweighted Least Square Minimization // Proc of the 31st AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2017: 2471-2477. [本文引用:1]
[24]	LI J D, WU L, DANI H, et al. Unsupervised Personalized Feature Selection // Proc of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2018: 3514-3521. [本文引用:1]
[25]	LI Z C, YANG Y, LIU J. Unsupervised Feature Selection Using Nonnegative Spectral Analysis // Proc of the 26th AAAI Confe-rence on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2012: 1026-1032. [本文引用:1]
[26]	ZHU X F, WU X D, DING W, et al. Feature Selection by Joint Graph Sparse Coding // Proc of the SIAM International Conference on Data Mining. Berlin, Germany: Springer, 2013: 803-811. [本文引用:1]
[27]	ZHU X F, LI X L, ZHANG S C, et al. Robust Joint Graph Sparse Coding for Unsupervised Spectral Feature Selection. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(6): 1263-1275. [本文引用:1]
[28]	LI X L, ZHANG H, ZHANG R, et al. Generalized Uncorrelated Regression with Adaptive Graph for Unsupervised Feature Selection. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(5): 1587-1595. [本文引用:1]
[29]	TANG C, ZHU X Z, CHEN J J, et al. Robust Graph Regularized Unsupervised Feature Selection. Expert Systems with Applications, 2018, 96: 64-76. [本文引用:1]

2019

0.0

... 例如,在精神分裂症的诊断中,可使用功能性核磁共振图像和结构性核磁共振图像提取神经生物学信息^[1]作为诊疗依据 ...

2019

0.0

... 对于阿兹海默症,神经影像学数据和认知测试数据都被视为区分AD与前驱期轻度认知障碍(Mild Cognitive Impairment, MCI)或正常对照(Normal Control, NC)的重要特征^[2] ...

2019

0.0

... 一般来说,这类研究中获得的多模态数据特征往往可从不同角度反映患者脑部的异常^[3,4] ...

2020

0.0

... 一般来说,这类研究中获得的多模态数据特征往往可从不同角度反映患者脑部的异常^[3,4] ...

2005

0.0

... 因此,如何从这些特征中进一步挖掘与疾病诊断高度相关的信息以提高诊断能力,是一个具有挑战性的问题^[5,6,7] ...

2020

0.0

... 因此,如何从这些特征中进一步挖掘与疾病诊断高度相关的信息以提高诊断能力,是一个具有挑战性的问题^[5,6,7] ...

2018

0.0

... 因此,如何从这些特征中进一步挖掘与疾病诊断高度相关的信息以提高诊断能力,是一个具有挑战性的问题^[5,6,7] ...

2017

0.0

... 这类算法可依据样本标签分为3类^[8]:1)有监督特征选择算法 ...

2016

0.0

... 具体来说特征选择尝试确定原始特征子集,去除不相关的特征,保留相关特征^[9,10,11] ...

2018

0.0

... 具体来说特征选择尝试确定原始特征子集,去除不相关的特征,保留相关特征^[9,10,11] ...

2011

0.0

... 具体来说特征选择尝试确定原始特征子集,去除不相关的特征,保留相关特征^[9,10,11] ...

2005

0.0

... 拉普拉斯评分方法(Laplacian Score)^[12]通过评估每个特征的性能对特征进行排序 ...

2016

0.0

... 基于改进互信息的特征选择(Modified Mutual Information Based Feature Selection, MMIFS)^[13]通过解析选择最佳特征进行分类 ...

2014

0.0

... Rodrigues等^[14]提出基于最优路径的包裹型特征选择算法,将特征选择问题建模为基于二进制的优化技术 ...

2015

0.0

... 例如,嵌入式无监督特征选择(Embedded Unsupervised Feature Selection, EUFS)^[15]通过稀疏学习直接将特征选择嵌入聚类算法中 ...

2007

0.0

... 谱学习试图在低维空间中保持高维数据的相似性,这是一类重要的无监督特征选择算法,如谱特征选择(Spectral Feature Selection, SPEC)^[16],多簇特征选择(Multi-cluster Feature Selection, MCFS)^[17]和最小冗余谱特征选择(Minimum Redundancy Fea-ture Selection, MRFS)^[18] ...

2010

0.0

2010

0.0

2014

0.0

... 为了解决这一问题,学者们提出同时进行流形学习和稀疏回归的方法,如联合嵌入学习和稀疏回归(Joint Embedding Lear-ning and Sparse Regression, JELSR)^[19] ...

2001

0.0

... 然而,由于原始数据集中存在噪声和冗余特征,直接根据该数据集获得拉普拉斯矩阵且不对其加以持续更新优化,会降低模型的性能^[20] ...

2010

0.0

... 本文使用稀疏建模软件(Sparse Modeling Software, SPAMS)^[21]求解基矩阵B ...

2018

0.0

... 遵循文献[22]、文献[23],可得 ...

2017

0.0

... 遵循文献[22]、文献[23],可得 ...

2018

0.0

... 遵从文献[24]的实验设置,在求解目标函数时,需要根据交叉验证预先设置#cod#x003b1 ...

2012

0.0

... 2)非负判别特征选择(Non-negative Discrimi-native Feature Selection, NDFS)^[25] ...

2013

0.0

... 3)联合图稀疏编码(Joint Graph Sparse Coding, JGSC)^[26] ...

2017

0.0

... 4)鲁棒联合图稀疏编码(Robust JGSC, RJGSC)^[27] ...

2019

0.0

... 5)基于自适应图不相关正则化特征选择(Unco-rrelated Regulation with Adaptive Graph for Feature Selection, URAFS)^[28] ...

2018

0.0

... 6)图正则化无监督特征选择(Graph Regula-rized Unsupervised Feature Selection, GRUFS)^[29] ...