引用本文
石雪, 徐海平, 李纯明. 本征图像分解的可变尺度局部分析与集成方法. 模式识别与人工智能, 2021,34(4): 322-332
SHI Xue, XU Haiping, LI Chunming. A Scalable Local Analysis and Integration Approach to Intrinsic Image Decomposition. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(4): 322-332.  
Doi: 10.16451/j.cnki.issn1003-6059.202104004
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
本征图像分解的可变尺度局部分析与集成方法
石雪1, 徐海平1, 李纯明1
1.电子科技大学 信息与通信工程学院 成都 611731
通信作者:

李纯明,博士,教授,主要研究方向为计算机视觉、医学图像分析.E-mail:cmli@ieee.org.

作者简介:

石 雪,博士研究生,主要研究方向为图像处理、医学图像分析.E-mail:xueshi@ieee.org.

徐海平,博士,讲师,主要研究方向为图像处理、机器学习.E-mail:haiping@mju.edu.cn.

收稿日期: 2020-07-09 接受日期: 2021-02-26
资助项目: 国家自然科学基金项目(No.G0561671135)资助
摘要

针对自然图像与磁共振图像,提出本征图像分解的统一的数学模型与算法,解决这两类图像中的重要问题:1)自然图像的光照和反射图像的估计,2)磁共振图像中的偏移场估计与分割.文中数学模型只需要一个基本的假设,即观察到的图像可近似为两个具有不同特性的本征图像的乘积:一个光滑的图像,简称为S-图像;一个近似为分片常量的图像,简称为L-图像.为了充分利用本征图像的特性,提出可变尺度局部分析与集成的方法.由于S-图像的光滑性,使用低阶泰勒展开式或更一般的光滑基函数的线性组合以局部逼近.得到的局部光滑逼近可通过整个感兴趣区域(ROI)的局部区域覆盖及其对应的单位分解扩展成整个ROI上的光滑图像,同时得到图像分割结果和L-图像.实验表明,文中方法对图像的两个本征因子的假设较弱,适用于更广泛的图像.目前方法已在磁共振图像及自然图像中进行测试,得到较优结果.

关键词: 本征图像; 图像分割; 光照与反射图像; 磁共振成像
中图分类号:TP 391.41 文章编号:2021,34(4):322-332
A Scalable Local Analysis and Integration Approach to Intrinsic Image Decomposition
SHI Xue1, XU Haiping1, LI Chunming1
1. School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu 611731
Corresponding author:
LI Chunming, Ph.D., professor. His research interests include computer vision and medical image analysis.

AboutAuthor:
SHI Xue, Ph.D. candidate. Her research interests include image processing and medical image analysis.
XU Haiping, Ph.D., lecturer. Her research interests include image processing and machine learning.

Fund:Supported by National Natural Science of Foundation of China(No.G0561671135)
Abstract

A unified mathematical model and an algorithm are proposed to solve the problems of the estimation of illumination and reflectance images of a natural image and the segmentation and bias field estimation of a magnetic resonance image(MRI). The proposed model only requires a basic assumption that the observed image can be approximated by the product of two intrinsic images with different properties. One of the two intrinsic images is a smooth image, S-image, and the other is a piece-wise approximately constant image, L-image. To fully exploit the properties of the intrinsic images, a scalable local analysis and integration(SLAI) approach is proposed for the problem of intrinsic image estimation. Due to the smoothness of the S-image, a low order Taylor expansion or a linear combination of general smooth basis functions is utilized to locally approximate the S-image. The obtained local smooth approximation of the S-image can be extended to a smooth image on the entire region of interest(ROI) using partition of unity subordinate to a cover of ROI. Meanwhile, the segmentation result and the estimation of the L-image are obtained. The proposed method is based on a weaker assumption than the methods in the literature, and therefore it is applicable to more images. The proposed method produces satisfactory results on MR images and natural images.

Key words: Intrinsic Image; Image Segmentation; Illumination and Reflectance Image; Magnetic Resonance Imaging

本文责任编委 杜少毅

Recommended by Associate Editor DU Shaoyi

在文献[1]中, 本征图像表示场景图像的两个乘性因子——光照图像和反射图像.光照图像反映场景的光照变化情况, 可用于恢复场景中物体表面的三维几何模型.反射图像刻画场景中物体表面的反射率, 是幅近似分片常量的图像, 可用于图像分割.从一张场景图像估计它的两张乘性本征图像是计算机视觉中的一个重要问题.在磁共振成像(Magnetic Resonance Imaging, MRI)中, 有类似的图像分解模型, 即一幅磁共振图像有两个乘性因子:刻画磁场不均匀性的偏移场, 刻画组织(如脑白质、脑灰质等)物理性质的真实图像[2, 3, 4].这两个领域有一个共同的特点, 即从一幅图像估计它的两个乘性本征因子, 通常称为本征图像分解或本征图像估计[5, 6].

在计算机视觉领域中, 单一图像的本征图像分解是一个不适定问题.需要利用反射率和光照的先验知识, 才能成为一个适定问题.一个基本的假设是反射率是分片近似常量的, 光照是光滑的[7, 8, 9].由此, 学者们引入一些额外的假设.Shen等[10]和Zhao等[11]将非局部纹理信息用于本征图像分解.Bousseau等[12]提出利用局部反射率的低秩结构和一些人工辅助指导优化最小二乘系统.Barron等[3, 13]提出两种基于形状、反射率和光照的方法.Chen等[14]在本征图像分解中使用深度线索.Shen等[15]在本征图像分解中使用反射的局部稀疏表示方法和全局稀疏表示方法.Li等[16]假设光照图像是光滑的, 反射图像是近似分片常量, 并基于此假设提出本征图像分解的一个变法模型.Yang等[17]在文献[16]的基础上, 引入水平集表示和分裂Bregman算法, 加速本征图像分解和分割.Baslamisli等[18]提出有监督、端到端的深度学习框架, 把语义分割和本征图像分解看作一个联合的过程, 探索它们之间的相互关系.Fan等[19]将边缘信息作为先验条件, 提出端到端、可训练、统一的网络架构, 用于本征图像分解.Kimmel等[6]假设光照图像和反射图像都是光滑的, 基于这个假设提出本征图像分解的变分方法.针对本征图像的不同假设, 学者们也提出多种方法分解本征图像[20, 21, 22, 23].Tappen等[20]提出基于多线索和置信度传播算法的本征图像分解算法.

在MRI领域中解决灰度不均匀图像分割时, 大多数情况是和偏移场估计同步交替进行.Li等[24]提出能量极小化方法, 可同时对MRI进行偏移场估计和图像分割, 处理光照不均匀图像, 对初始条件具有较强的鲁棒性.Li等[25]把能量最小化方法扩展到基于区域的水平集图像分割中, 交替进行水平集演化和偏移场估计.Wang等[26]在水平集方法的基础上, 使用混合区域拟合函数同时进行区域分割和偏移场估计.Cai等[27]基于信息熵和Bayesian分类器, 设计自适应尺度变化活动轮廓模型, 进行交替分割和偏移场估计.Li等[28]提出乘性本征成分优化算法(Multiplicative Intrinsic Component Optimization, MICO), 优化估计MRI的两个乘性因子, 同时实现偏移场估计和组织分割.Yang等[29]在MICO的基础上, 使用水平集函数重新描述MICO的能量函数, 使用光滑函数近似分片表示.Wan等[30]交替使用3D U-Net预测膝盖结构的分割图, 使用局部卷积滤波估计偏移场.

尽管上述这两个不同领域的问题有相似之处, 但目前还不清楚这两个领域中的任何一种方法是否可以互用.磁共振图像的偏移场方法[31]通常依赖于偏移场的强光滑(缓慢变化)假设, 较好地使用低阶多项式和其它信息进行近似, 如基于图谱信息等.但是自然图像中的光照变化的程度比磁共振图像中的偏移场更复杂.因此, 现有的磁共振图像的偏移场估计方法不适用于对自然光照图像进行估计.

本文将两个不同领域的问题统一在同个数学模型中.假设磁共振图像中的偏移场(或自然图像中的光照图像)的光滑性及真实图像(或自然图像中的反射图像)的分片近似于常数的性质.将本征图像分解问题表述为一个寻找最优光滑图像(简称为S-图像)和分片常量图像(简称为L-图像)的最优化问题, 使它们的乘积最优拟合观测到的图像.L-图像的估计同时给出一个分割结果.本文提出基于可变尺度局部分析与集成方法(Scalable Local Analysis and Integration, SLAI), 仅对本征图像进行最基本的假设, 即S-图像的光滑性和L-图像的近似分片常量性, 可应用于满足这两个基本假设的更广泛的图像.

1 相关知识

在计算机视觉领域, 观察到的图像是一幅彩色图像, 可使用RGB通道r、g、b表示成向量值函数:

I(x)=[r(x), g(x), b(x)]T,

其中T为转置算子.本文只考虑入射光是白光的情形.在这种情形下, 自然图像成像模型表示为

I(x)=s(x)R(x), (1)

其中, I为自然图像, s为光照图像, R为反射图像.

在医学图像领域, 也有类似的模型:

I(x)=b(x)J(x).(2)

其中:I为观测到的磁共振图像; b为刻画成像设备中的B0场和B1场不均匀性的一个因子, 通常称为偏移场; J为刻画扫描对象内部组织的物理性质(如水分子密度和质子密度等)的因子, 称为真实图像.图像I和两个乘性因子b和J都是灰度图像.

在上述两个领域的成像模型(1)、(2)中, 左边的图像是已知的观测图像, 右边的两个乘性因子(统称为本征图像)都是未知的.从已知的观测图像估计这两个未知的乘性因子, 在这两个领域中都是重要的问题, 然而现有文献对这两个领域中的类似问题却采取不同的解决方法[20, 21, 22, 23].

Li等[28]针对核磁共振图像, 把偏移场b(x) 表示成一组光滑基函数线性组合:

b(x)=wTG(x).

其中:

G(x)=[g1(x), g2(x), …, gM(x)]T,

为由基函数g1(x), g2(x), …, gM(x)构成的列向量;

w=[w1, w2, …, wM]T

为由基函数的系数w1, w2, …, wM构成的列向量.

真实图像J可近似为一个分片常量图像:

J(x)= c1, x∈Ω1c2, x∈Ω2︙cN, x∈ΩN

其中:Ωi为未知、待分割的区域; ci为Ji在每个区域Ω上的取值, 满足

⋃i=1NΩi=Ω,

当i≠ j时, Ωi∩ Ωj=Ø , ui(x)为Ωi的隶属度函数.这样, 对b和J的估计问题转化为寻找最佳b 和J, 使

F(b, J)=∫ Ω|I(x)-b(x)J(x)|2dx= ∫ Ω|(x)-wTG(x) ∑i=1Nciui(x)|2dx

极小化.

通过上式对b和J的优化问题又转化为对向量w和隶属度函数ui与常数ci的优化问题.

针对自然图像的光照图像与反射图像估计问题, Li等[16]提出局部化的模糊C均值方法.对图像域Ω中的每个点x定义局部能量函数:

Jxloc(U, c, S(x))= ∑i=1N∫ uiq(y)K(x-y)|I(y)-S(x)ci|2dy.

其中,

U=[u1, u2, …, uN], c=[c1, c2, …, cN],

K为局部化的窗口函数.本文采用截断的高斯函数,

K(u)= 1aexp(-|u|22σ2), |u|≤ρ0, |u|> ρ

其中, a为归一化的常数, 使∫ K(u)=1, σ 为高斯函数的标准差, ρ为邻域Ox的半径.

对于整个图像域, 定义全局能量函数:

J(U, c, S)=∫ ∑i=1Nuiq(y)di(I(y))dy, (3)

其中

di(I(y))≜∫ K(x-y)|I(y)-S(x)ri|2dx.

这样, 对反射图像R的估计就转化为对常数向量ri 和隶属度函数ui的优化问题.

对于光照图像S的优化, Li等[16]基于能量函数(3)导出一个简洁的闭式解.

2 问题定义与数学工具
2.1 问题定义

本征图像的概念最初是在计算机视觉中用于表示一个场景图像的两个有物理意义的乘性因子——光照图像和反射图像, 这是基于光学成像的物理得到的一个成像模型.在MRI中也有类似成像模型, 即一个观测到的磁共振图像也有两个有物理意义的乘性因子——反映磁场不均匀性的偏移场和刻画扫描对象内部组织的物理性质(如水分子密度和质子密度等)的因子, 通常称为真实图像.本文把这两个领域的成像模型中的乘性因子统称为本征图像.基于它们共同的数学形式和性质, 提出解决这两个领域中的本征图像分解问题的统一的数学模型.

对于自然图像, 其中一个本征图像是反射图像, 描述图像场景中物体表面的一种独特的物理属性——物体表面的反射率[7, 8, 9], 因此它是近似于分片常量的图像.对于广泛的一类自然图像, 其中物体表面是光滑的, 那么光照图像也是光滑的[29, 31, 32, 33].

对于磁共振图像, 其中一个本征图像描述具有被扫描组织的某种物理性质(如质子密度等), 因此它也是近似分片常量的图像, 称为真实图像[29, 31, 32, 33].另一个本征图像反映MRI设备中的磁场不均匀性, 也是一个光滑变化的图像.

式(1)中的自然图像和式(2)中的磁共振图像成像模型具有相同的乘性本征图像分解形式, 本征图像具有相同的空间特性.为了统一论述这两类图像的本征图像分解问题, 将式(1)和式(2)统一写成

I(x)=S(x)L(x).(4)

其中:S为光滑的本征图像, 简称为S-图像; L为近似分片常量的图像, 简称为L-图像.

基于自然图像和磁共振图像共同形式的成像模型(4), 本文提出统一的本征图像分解方法.把本征图像分解问题转化成寻求最佳的S-图像和最佳的L-图像, 使能量函数

F(S, L)=∫ Ω|I(x)-S(x)L(x)|2dx(5)

最小.

直接对S和L能量极小化显然是一个不适定问题.本文充分利用S-图像的光滑性和L-图像近似分片常量的性质, 把这两个变量S和L设定在两个特定的函数子空间内, 即S 在光滑函数空间内, L在分片常量函数空间内, 把式(5)中的能量函数F转化成不同的形式, 使能量极小化是一个适定问题, 从而实现有效的本征图像分解.

2.2 数学分析工具

本文所需的数学工具是常用的数学分析工具——单位分解.它常用于把局部函数扩并为整体函数, 反之也能把整体函数分解为局部函数进行处理.在欧氏空间和流形理论中, 单位分解是有用的技术[34, 35, 36], 常用于将局部区域上的光滑函数延拓为整个区域(或感兴趣区域(Region of Interest, ROI))上的光滑函数, 同时保持局部函数原有的一些属性.本文将图像视为连续图像域D⊂Rd上的函数.将维度d=2, 3分别对应二维图像和三维图像.只对图像域D中ROI进行本征图像分解, 这个区域可以是整个图像域D, 即Ω=D, 也可以是D的一个感兴趣的子区域, 即Ω⊂D.给定Ω的一个开覆盖{Ωα}及对应的一族非负光滑函数φα, 使得

Ω⊂ ∪αΩα,

且

sup p(φα)={x∶ φ(x)≠ 0}⊂Ωα,

对所有x∈Ω,

∑αφα=1,

满足如上性质的函数族{φα}称为从属于区域Ω的开覆盖{Ωα}的单位分解.给定一个从属于Ω 覆盖的{Ωα}的单位分解子区域{φα}, 及每个局部区域Ωα上的光滑函数fα, 定义整个区域Ω的函数f:

f~(x)= ∑αφα(x)fα(x), (6)

f~(x)把局部区域Ωα上的光滑函数fα光滑地延拓到整个区域Ω.延拓后的函数仍具有局部函数的性质, 如函数的光滑性和接近于某个函数的逼近性质.

基于上述的单位分解的概念, 本文设f为Ω上的一个函数, 给定从属于Ω的一个开覆盖{Ωα}的单位分解{φα}, 如果对所有的x∈Ωα∩ Ω, 都有

|fα(x)-f(x)|< ε ,

那么式(6)中定义的 f~就是fα(x)在Ω上的光滑延拓.可证明延拓函数 f~是光滑的并对所有x在Ω上都满足

| f~(x)-f(x)|< ε .

上述结果证明如下.由φα和fα的光滑性可得 f~也是光滑的.从单位分解式(6)得, 对所有x∈Ω,

| f~(x)-f(x)|=| ∑αφα(x)(fα(x)-f(x))|≤ ∑αφα(x)ε =ε .

另一方面, 也利用单位分解把一个积分∫ Ωh(x)dx分解为子区域上的积分之和:

∫ Ωh(x)dx=∫ Ωh(x)( ∑αφα(x))dx= ∑α∫Ωα⋂Ωh(x)φα(x)dx.

3 本征图像分解的可变尺度局部分析与集成方法

本节对自然图像和磁共振图像的分割本征图像分解提出一个统一数学模型.仍使用S和L表示一个图像I的两个本征图像成分, 即S为光滑图像, L为分片常量图像.目前先考虑一个更一般的向量值图像I和L, 但下文的论述都适用于灰度图像, 因此, 本文方法可直接应用于彩色自然图像和灰度值的磁共振图像.

把本征图像分解问题定义为一个寻求最佳的光滑图像和最佳的分片常量图像的问题, 使它们的乘积SL为观测到的图像的最佳逼近, 其中L的分片常量性质和S的光滑性质将被充分融入到本征图像分解的数学模型中.S-图像的光滑性意味着它在局部区域内可使用泰勒展开的低阶项充分逼近.对于二维图像的情形, 在点y=(y1, y2) 的一个邻域Ωy内, 对任意x=(x1, x2)∈Ωy, 函数值S(x)可使用一阶泰勒展开逼近:

S(x)≈ S(y)+ ∑i=12( ∂S(y)∂xi(xi-yi)).(7)

上式还可更简洁地表达为3个基函数g1(x)、g2(x)、g3(x) 的线性组合:

Sy(x)= ∑j=13wjgj(x; y),

其中, wj为组合系数, 基函数gj(x; y)都是在邻域Ωy上的函数,

g1(x; y)=1, g2(x; y)=x1-y1, g3(x; y)=x2-y2.

对三维图像(如MRI三维图像)的情形, 基函数可定义为

g1(x)=1, g2(x)=x1-y1, g3(x)=x2-y2, g4(x)=x3-y3.

容易验证, 对二维和三维的情形, 上述基函数都构成一组正交基.这一基函数的表达方式有利于把S-图像估计问题转化为一个矩阵和向量计算问题.

3.1 S-图像估计

光滑函数可局部近似为低阶多项式的泰勒展开式, 是多项式的线性组合.更一般的情况是, 在局部区域内一些光滑的偏移场函数可使用一组线性组合逼近得到S-图像.先给定区域

Ω0={(x1, x2)∶ |x1|< ρ, |x2|< ρ}

上的一组线性无关的光滑基函数g1(x), g2(x), …, gm(x).区域Ω0是以零点为中心的正方形区域.把区域Ω0平移成以xα=( x1α, x2α) 为中心的区域Ωα:

Ωα={x+xα∶ x∈Ω0}.

显然, 平移函数g1(x-xα), g2(x-xα), …, gm(x-xα)构成定义在Ωα上的一组光滑基函数.因此S-图像可使用线性组合逼近, 即

S(x)≈ ∑j=1mwjαgj(x-xα),

其中 wjα为第j个基函数的系数.上式右侧的线性组合记为Sα(x), 还可写成如下向量乘积的形式:

Sα(x)= wTαG(x-xα), (8)

其中,

wα=[ w1α, w2α, …, wmα]T, G(x-xα)= [g1(x-xα), g1(x-xα), …, gm(x-xα)]T.

在局部区域 Ωα内使用形如式(8) 的光滑函数Sα(x)逼近光滑图像S(x).为了把对S图像的局部光滑逼近延拓到整个区域Ω, 需要Ω的一个覆盖{Ωα}和对应的单位分解{φα}, 利用单位分解的基本性质(7), 把式(5)中的能量写成如下等价形式:

F(S, R)= ∑α∫Ωα⋂Ω|I(x)-S(x)L(x)|2φα(x)dx.

F(s, R)可分解成局部能量之和:

F(S, R)= ∑αEα,

其中

Eα= ∫Ωα⋂Ω|I- wTαG(x-xα)L(x)|2φα(x)dx.

因为

sup p(φα)⊆Ωα,

局部能量Eα还可写为

Eα=∫ Ω|I- wTαG(x-xα)L(x)|2φα(x)dx.

给定L图像, 局部能量Eα是关于变量wα的全局凸函数, 有唯一的全局最优解, 记为 w~α, 且有如下闭式解:

w^α= Aα-1vα.(9)

其中:Aα为m×m的对称矩阵,

Aα=∫ ΩG(x-xα)GT(x-xα)|L(x)|2φα(x)dx;

vα为一个m维的列向量,

vα=∫ ΩG(x-xα)(LT(x)I(x))φα(x)dx.

可证明矩阵Aα是非奇异的, 这就保证式(9)中的矩阵求逆运算是有意义的.在每个子区域Ωα∩ Ω, 通过

Sα(x)= w^TαG(x-xα)

估计S-图像, 将这一函数拓展到对整个区域的光滑函数s(x)的估计 S︿(x), 定义如下:

S︿(x)= ∑αφα(x) w^TαG(x-xα).(10)

只要在局部区域Ωα中每个函数Sα(x)均逼近S(x), 那么在整体区域 Ω 中, 拓展的函数 S︿(x)就是光滑且逼近本征图像S(x).

本文数学模型的建立过程可概括为从局部分析到全局整合的过程.首先S-图像的光滑性使得局部的光滑逼近可使用泰勒展开, 得到一个局部的光滑函数Sα(x), 再通过单位分解拓展到整个ROI.单位分解{φα}是一个从属于Ωα的覆盖, Ωα的尺度可根据图像的灰度变化快慢性质而改变, 本文的本征图像分解方法可称为可变尺度局部分析与集成方法(SLAI).具体而言, 局部区域Ωα的尺度(如一个圆形邻域的半径)可根据图像中光照不均匀或灰度不均匀性的程度设定.对于光照变化很慢或灰度不均匀性很弱的图像, 可把局部区域Ωα取成半径较大的圆形区域, 在此区域上使用低阶多项式对一个光滑函数f进行逼近.对于光照变化较快或灰度不均匀性很强的图像, 在局部区域Ωα取半径较小的圆形区域, 使用同样阶数的多项式对其逼近.对应地, 有更多数目的局部区域Ωα才能实现对整个区域Ω的覆盖.

3.2 L-图像估计

假设L-图像L为近似常数的分片常量, 因此, 可用如下分片常量函数

L︿(x)= l1, x∈R1l2, x∈R2︙ln, x∈Rn

逼近, 其中子区域Ri⊂Ω, i=1, 2, …, m构成Ω的一个分割, 即

Ω= ⋃i=1nRi, Ri∩ Rj=Ø , i≠ j.

还可用l1, l2, …, ln隶属度函数, 则

L= ∑i=1nliui(x),

其中, ui为区域Ri的隶属度函数,

ui(x)= 1, x∈Ri0, x≠Ri

根据式(5), 将能量函数F 改写为

F(S, L)=∫ Ω|I(x)-S(x)L(x)|2dx= ∑i=1n∫Ri|I(x)-S(x)L(x)|2dx= ∑i=1n∫Ri|I(x)-S(x)li|2dx= ∑i=1n∫ Ω|I(x)-S(x)l(i)|2ui(x)dx.

因此, F(S, L)可转化为S、l、u的能量:

F(S, l, u)=F(S, L).

在3.1节已给出估计S的算法.对给定的S, 还需要对变量l、u极小化能量F(S, L, u).

给定变量L和S, 容易证明, 使F(S, u, l)最小的

u= u^=[ u^1, u^2, …, u^n],

其中

u^i(x)= 1, i=imin(x)0, i≠imin(x)

imin(x)=arg mini{|I(x)-S(x)li|}.(11)

给定

u=[u1, u2, …, un]

和S, 使F(S, u, l)最小化的

l=[ l^1, l^2, …, l^n],

其中

l^i= ∫ΩS(x)ui(x)I(x)dx∫ΩS2(x)ui(x)dx.(12)

3.3 算法实现

基于SLAI的数学模型和算法, 建立本征图像分解算法, 可用于自然图像和MRI图像, 算法归结为对变量wα、l、u的优化, 详细过程可总结为如下步骤.

算法 SLAI

step 1 初始化常数向量L=[l1, l2, …, ln]和图像S.

step 2 按照式(11)更新隶属度函数u=[u1, u2, …, un]为 u^=[ u^1, u^2, …, u^n].

step 3 按照式(12)更新常数向量L=[l1, l2, …, ln]为 L︿=[ l^1, l^2, …, l^n].

step 4 按照式(10)将图像S更新为 S︿, 用式(9)对向量wα进行优化.

step 5 检查图像S是否收敛, 如果收敛, 停止迭代, 否则转入step 2.

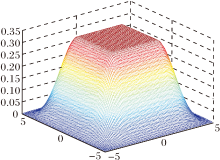
本文对函数φα的构造如下.首先定义单变量函数

ϕ (t)= c0, t> -ρ12ε[1+cos(π(t+ρ)ε)], -ρ< t< -ρ+ε1ε, -ρ+ε≤t≤ρ-ε12ε[1+cos(π(t-ρ)ε)], ρ-ε< t< ρ0, t> ρ

其中, ϕ 为光滑的, sup p(ϕ )⊂[-ρ, ρ].

因此对于sup p(ψ)⊂[-ρ, ρ]2, 变量x1, x2的函数为

ψ(x)=ϕ (x1)ϕ (x2).

图1为ρ=5时的函数ψ.

图1 ρ=5时函数ψFig.1 Function ψ with ρ equal to 5

对于xα, 本文定义以xα为中心的方形区域

Ωα=[-ρ, ρ]2+xα,

使

ψα(x)=ψ(x-xα), sup p(ψα)⊂Ωα.

对感兴趣区域Ω, 选择一系列点{xα}, 使{Ωα}为区域Ω的一个覆盖.定义

φα(x)= ψα(x)∑αψα(x),

可见

∑αφα(x)=1.

因此, {φα}是从属于覆盖{Ωα}的单位分解.需要注意的是, 局部区域Ωα的尺度、位置及基函数gj应根据不同应用中的光照(或磁共振图像的偏移场)的空间性质构建.

对于磁共振图像, 本征图像S为偏移场, 它的变化非常缓慢, 可在一个较大的局部区域内使用低阶多项式逼近, 再使用一个较少的局部区域Ωα覆盖Ω.对于这种情形, Ωα定义为以xα为中心的51×51的局部区域, 邻域中心xα的间距为30个像素.

对于自然图像, 光照变化通常较复杂, 在较大区域Ωα内使用低阶泰勒展开逼近不可行.对于这种情形, 可采用较小的区域Ωα和一阶泰勒展开, 用于近似光照图像S.具体而言, Ωα是以xα为中心的5×5的局部区域.此外, 以xα为中心的区域Ωα应该密集分布.在本文对自然图像的实验中, 局部区域Ωα的中心xα取遍图像中所有的像素.

4 实验及结果分析

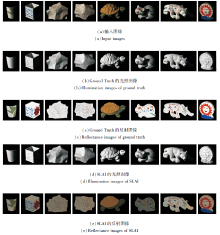
本节在由团队成员使用普通相机拍摄的自然图像组成的图像数据集及MIT数据集[37]上测试SLAI.SLAI在MIT 数据集上的分割结果如图2所示.在团队采集的自然图像数据集上的分割结果如图3所示.

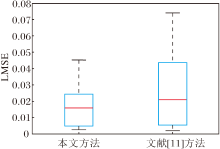
图2 本文方法在MIT数据集上的分割结果Fig.2 Segmentation results of the proposed method on MIT dataset

图3 本文方法在自然图像数据集上的分割结果Fig.3 Segmentation results of the proposed method on natural images

为了定量评估SLAI, 将局部均方误差(Local Mean-Square Error, LMSE)[11, 37]作为度量标准, 评估光照图像的误差.在MIT数据集上进行测试, 使用同组图像数据对比SLAI与文献[11]方法.图4为2种方法的LMSE箱型图.由图可见, SLAI的LMSE低于文献[11]方法, 表明本文方法的误差较小.此外, SLAI除了光照和反射的基本空间特性外, 不需要其它信息或先验知识, 而文献[11]方法和其它现有方法需要额外的信息或先验知识.

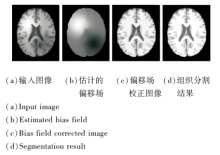
图4 2种方法在MIT数据集上的LMSE箱型图Fig.4 Diagram of LMSE box of 2 methods on MIT dataset

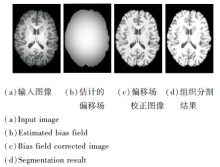
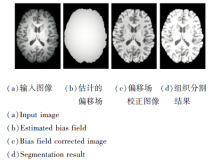
SLAI在磁共振图像中有较好的应用.可使用式(10)中的 S︿估计磁共振图像的偏移场, 用I/ S︿计算偏移场校正图像.通过式(11)计算隶属度函数u1, u2, …, un , 还可得到组织分割结果.

图5(a)为带有严重灰度不均匀性的人工合成磁共振图像, 偏移场估计值 S︿如(b)所示, 组织分割结果如(d)所示.由图可知, 即使有严重的灰度不均匀性, SLAI仍可得到较理想的分割结果.

图5 本文方法对人工合成磁共振图像的分割结果Fig.5 Segmentation result of the proposed method on synthetic MR image

图6和图7为SLAI和SPM对3T磁共振图像的分割结果.

图6 本文方法对3T磁共振图像的分割结果Fig.6 Segmentation result of the proposed method on 3T MR image

图7 SPM对3T磁共振图像的分割结果Fig.7 Segmentation result of SPM on 3T MR image

输入的3T磁共振图像具有明显的灰度不均匀性.SPM可在http://www.fil.ion.ucl.ac.uk/spm/software/下载.由图6和图7可明显看出, SPM在大脑白质上有明显的过分割, 而SLAI与真实的解剖结构较一致.

5 结束语

本文提出可变尺度局部分析与集成方法(SLAI), 既可用于对自然图像的光照图像估计和反射图像估计, 也可用于磁共振图像分割、偏移场估计与校正.该方法仅利用这两类图像中两个乘性本征因子的本征图像共同的基本性质, 即其中一个本征图像(称为S-图像)的光滑性和另一个本征图像(称为L-图像)的近似分片常量的性质.利用S-图像的光滑性得到它的一个局部光滑逼近, 通过单位分解延拓为对S-图像的全局光滑逼近, 同时得到图像分割结果和L-图像估计.本文方法在对自然图像和MRI图像的测试中取得较优结果, 尤其在磁共振图像分割应用中, 本文方法处理严重灰度不均匀性图像的能力很强.与磁共振图像分析的主流软件SPM的对比结果显示, 本文方法在分割精度上的优势明显.在后续工作中, 将使用更大量的自然图像、MRI图像及其它类型图像(如CT等)测试该方法, 使其与更多方法进行定量对比.

参考文献
[1] BARROW H, TENENBAUM J M. Recovering Intrinsic Scene Cha-racteristics from Images // HANSON A, RISEMAN E, eds. Computer Vision Systems. New York, USA: Academic Press, 1978: 3-26. [本文引用:1]
[2] TAPPEN M F, ADELSON E H, FREEMAN W T. Estimating Intrinsic Component Images Using Non-linear Regression // Proc of the IEEE Computer Society Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2006, II: 1992-1999. [本文引用:1]
[3] BARRON J T, MALIK J. Shape, Illumination, Reflectance from Shading. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(8): 1670-1687. [本文引用:2]
[4] BELL S, BALA K, SNAVELY N. Intrinsic Images in the Wild. ACM Transactions on Graphic, 2014, 33(4). DOI: 10.1145/2601097.2601206. [本文引用:1]
[5] WEISS Y. Deriving Intrinsic Images from Image Sequences // Proc of the 8th IEEE International Conference on Computer Vision. Washing-ton, USA: IEEE, 2001, II: 68-75. [本文引用:1]
[6] KIMMEL R, ELAD M, SHAKED D, et al. A Variational Framework for Retinex. International Journal of Computer Vision, 2003, 52(1): 7-23. [本文引用:2]
[7] HORN B K P. Determining Lightness from an Image. Computer Gra-phics and Image Processing, 1974, 3: 277-299. [本文引用:2]
[8] LAND E H, MCCANN J J. Lightness and Retinex Theory. Journal of the Optical Society of America, 1971, 61(1): 1-11. [本文引用:2]
[9] BLAKE A. Boundary Conditions for Lightness Computation in Mondrian World. Computer Vision, Graphics and Image Processing, 1985, 32(3): 314-327. [本文引用:2]
[10] SHEN L, TAN P, LIN S. Intrinsic Image Decomposition with Non-local Texture Cues // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2008. DOI: 10.1109/CVPR.2008.4587660. [本文引用:1]
[11] ZHAO Q, TAN P, DAI Q, et al. A Closed-Form Solution to Re-tinex with Nonlocal Texture Constraints. IEEE Transactions on Pa-ttern Analysis and Machine Intelligence, 2012, 34(7): 1437-1444. [本文引用:5]
[12] BOUSSEAU A, PARIS S, DURAND F. User-Assisted Intrinsic Images. ACM Transactions on Graphics, 2009, 28(5). DOI: 10.1145/1618452.1618476. [本文引用:1]
[13] BARRON J T, MALIK J. Shape, Albedo, Illumination from a Single Image of an Unknown Object // Proc of the IEEE Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2012: 334-341. [本文引用:1]
[14] CHEN Q F, KOLTUN V. A Simple Model for Intrinsic Image Decomposition with Depth Cues // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2013: 241-248. [本文引用:1]
[15] SHEN L, YEO C H. Intrinsic Images Decomposition Using a Local and Global Sparse Representation of Reflectance // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2011: 697-704. [本文引用:1]
[16] LI C M, LI F, KAO C Y, et al. Image Segmentation with Simultaneous Illumination and Reflectance Estimation: An Energy Minimization Approach // Proc of the 12th IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2009: 702-708. [本文引用:4]
[17] YANG Y Y, JIA W J, WU B Y. Simultaneous Segmentation and Correction Model for Color Medical and Natural Images with Intensity Inhomogeneity. The Visual Computer, 2020, 36(4): 717-731. [本文引用:1]
[18] BASLAMISLI A S, GROENESTEGE T T, DAS P, et al. Joint Learning of Intrinsic Images and Semantic Segmentation // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 289-305. [本文引用:1]
[19] FAN Q N, YANG J L, HUA G, et al. Revisiting Deep Intrinsic Image Decompositions // Proc of the IEEE/CVF Conference on Com-puter Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8944-8952. [本文引用:1]
[20] TAPPEN M F, FREEMAN W T, ADELSON E H. Recovering Intrinsic Images from a Single Image // Proc of the 15th International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2002: 1367-1374. [本文引用:3]
[21] JANNER M, WU J J, DULJARNI T D, et al. Self-supervised Intrinsic Image Decomposition // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: The MIT Press, 2017: 5936-5946. [本文引用:2]
[22] CHANG J, CABEZAS R, FISHER III J W. Bayesian Nonparame-tric Intrinsic Image Decomposition // Proc of the European Confe-rence on Computer Vision. Berlin, Germany: Springer, 2014: 704-719. [本文引用:2]
[23] MA W C, CHU H, ZHOU B L, et al. Single Image Intrinsic Decomposition without a Single Intrinsic Image // Proc of the Euro-pean Conference on Computer Vision. Berlin, Germany: Springer, 2018: 211-229. [本文引用:2]
[24] LI C M, XU C Y, ANDERSON A W, et al. MRI Tissue Classification and Bias Field Estimation Based on Coherent Local Intensity Clustering: A Unified Energy Minimization Framework // Proc of the International Conference on Information Processing in Medical Imaging. Berlin, Germany: Springer, 2009: 288-299. [本文引用:1]
[25] LI C M, HUANG R, DING Z H, et al. A Level Set Method for Image Segmentation in the Presence of Intensity Inhomogeneities with Application to MRI. IEEE Transactions on Image Processing, 2011, 20(7): 2007-2016. [本文引用:1]
[26] WANG L, ZHU J B, SHENG M, et al. Simultaneous Segmentation and Bias Field Estimation Using Local Fitted Images. Pattern Re-cognition, 2018, 74: 145-155. [本文引用:1]
[27] CAI Q, LIU H Y, ZHOU S P, et al. An Adaptive-Scale Active Contour Model for Inhomogeneous Image Segmentation and Bias Field Estimation. Pattern Recognition, 2018, 82: 79-93. [本文引用:1]
[28] LI C M, GORE J C, DAVATZIKOS C. Multiplicative Intrinsic Component Optimization(MICO) for MRI Bias Field Estimation and Tissue Segmentation. Magnetic Resonance Imaging, 2014, 32(7): 913-923. [本文引用:2]
[29] YANG Y Y, WANG R F, FENG C. A New Method for Simulta-neous Moderate Bias Correction and Image Segmentation. IET Image Processing, 2019, 13(6): 939-945. [本文引用:3]
[30] WAN F K, SMEDBY Ö, WANG C L. Simultaneous MR Knee Image Segmentation and Bias Field Correction Using Deep Learning and Partial Convolution[C/OL]. [2020-06-12]. https://doi.org/10.1117/12.2512950. [本文引用:1]
[31] ZHANG Y, BRADY M, SMITH S. Segmentation of Brain MR Images through a Hidden Markov Rand om Field Model and the Expectation-Maximization Algorithm. IEEE Transactions on Medical Imaging, 2001, 20(1): 45-57. [本文引用:3]
[32] WELLS III W M, GRIMSON W E L, KIKINIS R, et al. Adaptive Segmentation of MRI Data. IEEE Transactions on Medical Imaging, 1996, 15(4): 429-442. [本文引用:2]
[33] PHAM D L, PRINCE J L. Adaptive Fuzzy Segmentation of Magnetic Resonance Images. IEEE Transactions on Medical Imaging, 1999, 18(9): 737-752. [本文引用:2]
[34] WARNER F W. Foundations of Differentiable Manifolds and Lie Group. Berlin, Germany: Springer-Verlag, 1983. [本文引用:1]
[35] WENDLAND H. Fast Evaluation of Radial Basis Functions: Me-thods Based on Partition of Unity // CHUI C K, SCHUMAKER L L, STÖCKLER J, eds. Approximation Theory X: Wavelets, Splines, and Applications. Nashville, USA: Vand erbilt University Press, 2002: 473-483. [本文引用:1]
[36] POWELL M J D. Approximation Theory and Methods. Cambridge, UK: Cambridge University Press, 1981. [本文引用:1]
[37] GROSSE R, JOHNSON M K, ADELSON E H, et al. Ground Truth Dataset and Baseline Evaluations for Intrinsic Image Algorithms // Proc of the 12th IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2009: 2335-2342. [本文引用:2]