引用本文
宣锴, 王乾. 面向磁共振图像重建的 k空间降采样优化 . 模式识别与人工智能, 2021,34(4): 367-374
XUAN Kai, WANG Qian. Optimizing k-Space Subsampling Pattern toward MRI Reconstruction . PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(4): 367-374.  
Doi: 10.16451/j.cnki.issn1003-6059.202104009
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
面向磁共振图像重建的 k空间降采样优化
宣锴1, 王乾1
1.上海交通大学 生物医学工程学院 上海 200240
通信作者:

王 乾,博士,研究员,主要研究方向为医学图像处理.E-mail:wang.qian@sjtu.edu.cn.

作者简介:

宣 锴,博士研究生,主要研究方向为医学图像处理.E-mail:kaixuan@sjtu.edu.cn.

收稿日期: 2020-08-04 接受日期: 2020-12-30
资助项目: 上海市科学技术委员会科技计划项目(No.19QC1400600)资助
摘要

成像速度是关系磁共振临床应用效能的重要因素,在 k空间中降采样,再配合图像重建,可有效加快成像速度.因此,文中考虑降采样方式对磁共振图像重建质量的影响,在训练深度学习网络进行磁共振图像重建的情况下,提出联合优化 k空间降采样方式与重建模型的方法.从 k空间全采样入手,逐步删除次要的相位编码,直到针对相位编码的采样满足稀疏性要求为止.同时,采样方式的优化是和深度学习图像重建模型参数优化交替进行,即赋予每个相位编码一个权重,通过权重大小确定相位编码的重要性,在优化重建网络参数的同时,完成对 k空间降采样方式的优化.实验表明文中方法可提升磁共振图像重建质量.

关键词: 磁共振图像; 深度学习; 图像重建; 网络剪枝
中图分类号:TP 391 文章编号:2021,34(4):367-374
Optimizing k-Space Subsampling Pattern toward MRI Reconstruction
XUAN Kai1, WANG Qian1
1. School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai 200240
Corresponding author:
WANG Qian, Ph.D., professor. His research interests include medical image processing.

AboutAuthor:
XUAN Kai, Ph.D. candidate. His research interests include medical image processing.

Fund:Supported by the Science and Technology Project of Science and Technology Commission of Shanghai Municipality(No.19QC1400600)
Abstract

Imaging velocity is a major factor affecting clinical applications of magnetic resonance(MR) imaging. And an effective solution of reducing scanning time is to under-sample in k-space and reconstruct the image from under-sampled MR signals. In this paper, the impact of under-sampling pattern on reconstruction quality is analyzed and a joint optimization strategy is proposed to update the under-sampling pattern with image reconstruction model in the context of deep-learning. To optimize the non-continuous under-sampling pattern, it is firstly initialized with full-sampling pattern. Then, relatively less important phase-encodings are gradually pruned until the sparsity requirement in k-space is satisfied. And the optimization of k-space under-sampling pattern is conducted alternatively with that of the reconstruction model. Moreover, the relative importance is estimated with the weight by assigning weight to each phase-coding. Experiments demonstrate that the proposed method improves the quality of the reconstructed MR image compared with the proposed method.

Key words: Magnetic Resonance Image(MRI); Deep Learning; Image Reconstruction; Network Pruning

本文责任编委 左炜亮

Recommended by Associate Editor ZUO Weiliang

磁共振(Magnetic Resonance, MR)成像由于无辐射、非侵入、成像模态丰富等特点, 在临床中得到广泛应用, 然而较长的采集时间是其主要瓶颈之一.考虑到磁共振图像(MR Image, MRI)原始信号的采集是在k空间中进行的, 常用的加速策略之一是在k空间采集信号时降采样, 然后通过一系列重建算法估计与全采样相媲美的磁共振图像.

目前, 在二维k空间采集具有笛卡尔坐标系采样轨迹的磁共振图像在临床实践中得到广泛使用.对应的k空间可使用一个二维复数矩阵表示, 用于储存在k空间编码后采集到的磁共振信号.矩阵的一个坐标轴为相位编码方向, 对应空间编码中的相移; 另一个坐标轴为读出方向, 又称频率编码方向, 对应空间编码后采集到的磁共振信号中不同频率分量.对k空间采集到的全部数据施加二维傅里叶变换, 可重建得到磁共振图像, 因此k空间实际上为频域空间, 较小的相移对应较低的频率, 反之亦然.对于二维k空间采集的磁共振图像来说, 只有在相位编码方向降采样才能实际节省成像扫描时间, 而对于频率编码方向降采样的收益十分有限.

有如下2个基本因素会影响最终的重建图像质量:图像重建方法和降采样方式的设计.许多图像重建方法已成功应用于MR成像.早期, 一些简单的技术, 包括线性滤波、半扫描或零填充, 被用于恢复MRI[1, 2].后来, 更复杂的重建算法, 如基于贝叶斯的图像重建[3, 4]等, 也被应用于该领域.该类重建方案的一个重要方法是Lustig等[5]引入压缩感知(Com-pressed Sensing, CS)[6], 提出CS-MRI.近年来, 借助稀疏编码和深度学习等更强大的机器学习算法, 图像重建质量得到快速提高[7, 8].

在重建技术快速发展的同时, k空间降采样方式的设计却较少被人研究.k空间降采样方式可使用一维二进制(布尔)向量表示, 每个比特表示k空间中对应的相位编码是否需要采集.相比手动设计的降采样方式, 如具有均匀分布[9]或可变密度的随机采样[10], 进行针对性优化后的降采样方式可取得更优的图像重建效果[11].为了能以数据驱动的方式优化离散的采样模式, Zijlstra等[11]采用蒙特卡洛(Monte Carlo)优化, 而Liu等[12]采用贪心算法.对于这些方法, 直接计算一个采样样式的好坏非常费时, 因为如果要进行直接的量化评估, 一般需要将所有的图像都进行重建并统计.当然, 也有一些人采用间接的方法估计一个采样方式的优劣, 如使用基于动量的谱分析方法[13]或基于C-R下界(Cramer-Rao Lower Bound, CRLB)的方法[14].然而这些估计方法适用的重建算法范围往往有限.

如果重建模型具有海量可学习的参数需要优化时(如深度神经网络), 评价一个降采样模式的优劣需要的计算量将变得无法接受.降采样方式是使用一维的布尔向量表示, 因此难以使用基于梯度下降的算法优化.而基于梯度的算法, 如反向传播算法(Back Propagation, BP)等, 被广泛应用于深度神经网络的优化.为了解决这一问题, 学者们在提出一些方法的同时优化降采样方式和深度神经网络, 如使用Sigmoid函数近似采样操作[15], 使用生成对抗网络(Generative Adversarial Network, GAN)中的判别器估计不同相位编码的重要性[16], 甚至使用强化学习策略解决此问题[17].

与此同时, 学者们发现深度神经网络的剪枝任务与降采样方式的优化非常类似.首先, 它们都通过去除网络或相位编码中对总体性能影响较小的部分以得到增益.具体来说, 深度神经网络通过剪除不重要的神经元加速推理过程, 而磁共振成像跳过对图像质量影响较小的相位编码以提高采集速度.然后, 剪枝的过程和降采样的操作都不可微分.除此之外, 在这两个任务中, 精确计算某一部分的重要性均会带来非常大的计算量, 所以这种重要性的计算一般都会被近似处理.在剪枝任务中, 一般神经元的重要性会被权重大小[18]、激活函数输出的稀疏程度[19]或目标方程的泰勒展开[20]等近似.

由此, 本文提出联合优化k空间降采样方式与重建模型的方法, 所需的计算量与仅训练重建模型参数的计算量相当.总体来说, 交替进行k空间降采样方式的优化和神经网络参数的优化, 直到k空间的采样足够稀疏为止.在具体实现上, 在神经网络剪枝的启发下, 将每个相位编码对应的数据都赋以相应的权重, 通过这个权重估计每个相位编码的重要性, 并优化相位编码的采样方式.实验证实本文方法的鲁棒性和有效性.

1 联合优化k空间降采样方式与重建模型的方法

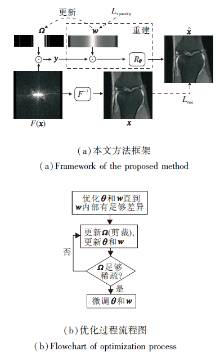
本节首先定义磁共振重建问题, 再提出联合优化k空间降采样方式与重建模型的方法, 方法框架与整个优化过程的流程图如图1所示.

图1 本文方法整体框图Fig.1 Architecture of the proposed method

1.1 磁共振图像重建

一个常见的磁共振图像重建流程如图1(a)所示.对于一个在k空间全采样、空间分辨率为N×N的二维磁共振图像x∈CN×N来说, 记二维离散傅里叶变换操作为F(·), 若并有长度为N的二值降采样方式Ω(Sampling Pattern, 或Sampling Mask), 该降采样方式的稀疏度 Ω0=M, 则k空间中的降采样过程可表示为

y=diag(Ω)F(x),

其中, y∈CN×N为使用零值填充后的k空间数据, 并且y至多有M个非零的列(不同的列表示不同相位编码), diag(·)为一维向量转换为对应二维对角矩阵的操作.不失一般性, 可将MRI重建过程记为Rθ(·), 其中, R为一系列重建操作的综合, θ为相应的可学习参数的集合.例如, 若使用深度神经网络在图像域中重建MRI, 重建过程可表示为逆傅立叶变换和带有参数θ的深层神经网络G:

Rθ(·)=Gθ(F-1(·)),

即先将待恢复的k空间信号通过二维傅里叶变换转换到复数图像空间, 然而k空间的欠采样会导致图像域混叠效果(Aliasing)的产生, 所以再使用神经网络尽可能去除(又称去混叠(Dealiasing))这些伪影, 估计尽可能像全采样磁共振图像x的结果.同时也应注意到, 目前主流的磁共振机器大多使用多线圈采样, 为了简单起见, 本文仅讨论单线圈的情况, 但也可简单拓展到多线圈的情况.

1.2 降采样方式的优化

与Liu等[18]的工作类似, 本文为每个相位编码分配一个权重w, 作为该相位编码重要性的近似估计.具体来说, 如图1(a)所示, 将降采样后的磁共振信号y与实数向量w∈RN沿相位编码方向相乘, 再将得到的结果送入Rθ(·)重建, 得到对全采样磁共振图像x的估计 x^:

x^=Rθ(diag(w)y).

在重建模型的训练过程中, 希望w变得稀疏, 这样可采集较少的相位编码以加速磁共振成像时间, 因此将L1损失函数用于w, 得到对w稀疏性的约束项:

Lsparsity= w1.

当然, 也需要使估计的 x^尽可能接近x.L1范数和L2范数均被广泛运用于磁共振重建中, 为了保持和Bahadir等[15]一致, 也使用图像域的L1范数, 这样得到重建误差损失项:

Lrec= x-x^1.

整个重建过程的损失函数与优化目标可表示为

(1)

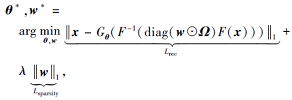
其中, λ 为调节两项权重的超参, ☉为逐元素相乘操作(又称Hadamard乘法), 具体优化可使用随机梯度下降法(Stochastic Gradient Descent, SGD)等进行.另外, 由于降采样方式Ω为一个二值向量, 很难融入SGD中与θ、w一起优化, 所以需要单独处理.

为了解决这一问题, 在整个优化过程中, 采用将降采样方式的优化和重建模型的训练交替进行的策略.具体来说, 在第i次迭代中, θ、w根据式(1)更新, 降采样的方式根据

(2)

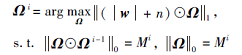
逐渐更新.其中, n为加性噪声, |·|为取绝对值操作.通过实验发现, 加上一些噪声可帮助在优化过程中添加随机性, 从而避免贪心裁剪(式(2))集中发生在局部区域, 而剪裁集中在局部区域通常会导致次优的结果.Mi为在第i次迭代中的希望达到的稀疏程度,

M0=N, Mi=Mi-1-K,

并且Ω0=1, 即扫描所有的相位编码.

式(2)可简单地理解为, 在每次迭代中, 将对应Ω不为0的且具有最小|w|+n的K个相位编码对应的Ω置为0, 即每次迭代中新选择K个影响较小的相位编码跳过扫描.当噪声水平为0时, 式(2)退化为贪心算法.有关使用加性噪声项的更多分析与具体效果, 参见实验部分.

图1(b)使用流程图简要描述训练过程.为了区分重要与次要的相位编码, 首先根据式(1), 使用Ω0训练θ和w, 直到w足够有区分度.然后进入循环迭代交替优化重建网络与降采样方式, 在每次迭代中, 根据式(2)修剪Ω, 然后根据式(1)优化θ和w.这2个优化过程交替进行, 直到Ω满足对采样的稀疏性要求为止.最后, 在Ω已满足所期望稀疏性的前提下, 将Lsparsity的权重置为0, 然后微调θ和w, 使重建的效果达到最优.

2 实验及结果分析

在本节中, 首先在磁共振重建任务上, 对比本文方法与不同的降采样方法.然后, 可视化w, 并对比不同权重λ 下w的变化, 进一步证实本文方法的有效性.

在fastMRI[21]发布的膝关节数据集上进行实验.fastMRI为一个大型的公开数据集, 含有原始的k空间数据, 膝关节数据部分包括质子密度(Proton Density, PD)模态和带脂肪抑制的PD(PD with Fat-Suppression, PDFS)模态.

为了挑选成对的PD和PDFS模态图像, 根据空间分辨率筛选可能的配对图像, 手动检查消除噪声较大或视觉上明显不匹配的图像对.最后从整个fastMRI膝关节训练和验证集中分别筛选227对PD和45对PDFS三维磁共振图像.将三维磁共振体数据沿扫描方向打散为二维切片, 总共使用8 332对二维切片进行训练, 并使用1 665对进行验证.

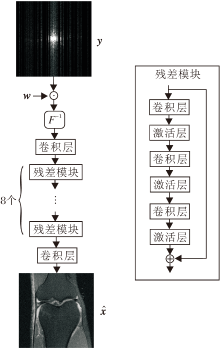
图2为本文使用的神经网络的结构.除输入/输出层外, 共有8个残差模块串联, 每个残差模块包括3层卷积层和3层激活层, 每层卷积网络的通道数均为64, 使用修正线性单元(Rectified Linear Unit, ReLU)激活函数.由于未使用任何归一化层, 通过残差网络达到训练深层卷积神经网络的目的.θ的学习率为0.001, w的学习率设为0.000 1, 都使用带默认超参的自适应动量估计(Adaptive Moment Es-timation, Adam)优化器对其进行优化.在图1(b)中的逐步修剪之前, 首先对θ和w进行8个周期的训练, 并且在每次迭代中, 通过修剪2个相位编码(即K=2)更新Ω, 使用50个批次的训练数据优化θ和w.采取和fastMRI比赛相似的设定, 将所有MRI集中裁剪为320×320(N=320)进行训练, 并且在所有设置中将批次大小设置为10.在预处理方面, 简单图像通过最大值、最小值分别归一化到0和1之间.

图2 重建过程的流程图Fig.2 Flow chart of MRI reconstruction

实验主要是基于PyTorch[22]和SciPy[23]工具包完成.

在图像重建评价指标上, 使用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)对比不同的k空间降采样方式.由于已将图像归一化到0至1之间, 所以

PSNR=-10lg(MSE),

均方误差(Mean Squared Error, MSE)计算公式如下:

MSE= 1N×N∑i=1N×N(xi- x^i)2.

其中:xi为将全采样图像x展开成一维向量后的第i个像素值; x^i为对全采样图像的估计 x^展开后的第i个像素值.

PSNR为定量评价MRI重建任务中重建效果的一个常见指标, 并且和重建损失函数(L1)密切相关.

2.1 磁共振图像重建结果

实验选择对比方法如下:2种广泛使用的降采样方法(随机(Random)和等距(Equispaced)采样)、优化降采样方式的方法[15].在PD和PDFS模态上, 加速比分别为4倍(4×)和8倍(8×)时的PSNR值对比如表1所示.由表可看出, 在所有设定中, 相比通过随机和等距方法给出的降采样方式, 优化过的降采样方式的PSNR值更高.在已优化降采样方式的方法中, 本文提出的无噪声(w/o Noise)方法优于文献[15]方法.在表1中还可看到, 添加一定的噪声(w/Noise)可进一步提高性能.在有噪声的设定中, 使用独立且分布在[-1e-2, 1e-2)内的均匀分布的噪声.

表1 不同降采样方式对应的PSNR值 Table 1 PSNR of different sampling patterns

使用不同算法, 加速倍数为4倍和8倍的PDFS和PD磁共振图像与不同采样方式下的重建结果及与全采样图像(Ground Truth, GT)的重建误差如图3所示.为了更好地看出对应的相位编码, 在降采样方式下使用黄色箭头将其八等份, 中间为小相位差(对应低频), 两侧为大相位差(对应高频).由图可见, 使用学习到的降采样方式得到的重建图像包含更多的细节和更少的伪影, 误差图在视觉上看起来也更优.而且相位编码的采样集中在低频处, 较少涉及或未涉及高频处, 说明在L1重建准则下, 低频部分的重要性大于其它部分.这也可在图1中全采样的k空间示例中看出, 图像的能量大多集中在低频处.

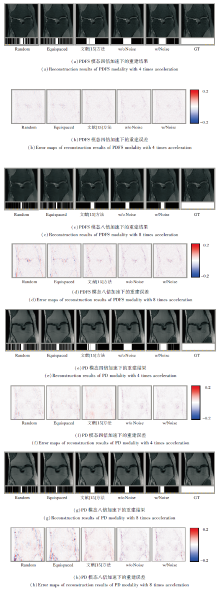图3 不同的采样方式和不同数据下重建图像的可视化对比Fig.3 Visualization comparison of reconstructed images of methods with different subsampling patterns and data

另外值得注意的是, 当式(2)中的噪声n=0时, 本文方法会产生类似低通滤波器的采样方式(但不完全是低通采样, 采样方式并不完全针对零相位差对称), 该结果也表明利用完全贪婪的修剪方法的缺点.事实表明, 完全贪婪的算法不能充分利用不同相位之间的相干性.与完全贪婪的算法相反, 在式(2)中添加噪声使本文方法有机会探索更多区域, 从而缓解这一问题.

2.2 稀疏性约束的效果

式(1)中的稀疏性约束Lsparsity在本文方法中至关重要, 它鼓励w多样化, 而超参λ 调控权重大小, 太大或太小都会影响实验结果.为了对比λ 对实验结果的影响, 使用PDFS序列的数据, 与表1相同的流程, 除了在优化降采样方式时将Mi一直置为N(既只更新w不更新Ω), 并将得到的w可视化.

图4为λ 不同时训练3 000、6 000、9 000、12 000批次后的w值对比.根据经验, 在实验中λ =0.01, 此时重要的相位编码与次要的相位编码的权重差异足够大.

图4 λ 不同时训练不同批次后w值对比Fig.4 Comparison of w after training for different batches with different λ

由图4可知, 如果权重λ 太小(如0.001), λ 几乎不会造成w变化, 只有较大的λ 才能分开低频区和中高频区.然而, 当λ 太大(如0.1)时, 高频和中频的权重之间没有太大差异, 会导致优化的降采样方式的性能下降.这同时也说明低频部分对应的相位编码的重要性远大于中高频部分, 而中高频部分的重要性的区别没有那么显著.这也和图3中的实验结果吻合, 在采样率较低(8×)的情况下, 几乎只采集低频部分, 而在采样率提高到4倍时, 也会采集到一些较高频部分的信息.由图4还可发现, 在λ =0.1, 0.01, 0.001时, 相移接近∓π 处(最高频)的权重w下降都尤其迅速, 通过查阅原始数据发现, 出于某些原因, 即使是全采样的数据, 在∓π 周围也会跳过部分相位不扫描, 直接用0代替, 因此导致这一现象出现.

3 结束语

本文提出联合优化k空间降采样方式与重建模型的方法.针对特定区域、特定模态的磁共振图像, 同时优化直接由训练数据驱动的降采样样式和基于深度学习的图像重建模型.相比单独训练重建模型, 本文联合训练的方法并未引入过多的计算开销.此外, 在优化过程中引入随机探索策略, 避免在优化时执行贪婪的权重修剪, 可以更好地探索不同相位编码之间的相关性.实验证明本文方法的鲁棒性和优越性.最后, 本文探究不同权重下稀疏性约束对降采样方式的影响.

另外, 不同的相位编码对整个图像域都有贡献, 其本身并没有重要或不重要的区别, 而在文中所说的重要性, 指的是在某一具体的图像质量量化指标下, 缺少某一相位编码对重建后该图像质量的影响.因此, 损失函数的设计对重建和降采样方式的学习是指导性的, 不同损失函数对学习的采样方式的影响需要进一步探究, 例如, 使用一些更关注高频信息的损失函数或许可指导采样方式的学习关注更多对应高频的相位编码区域.其它后续研究方向包括:本文方法的广泛应用, 如何更好地估计不同相位编码的重要性等.

参考文献
[1] JACKSON J I, MEYER C H, NISHIMURA D G, et al. Selection of a Convolution Function for Fourier Inversion Using Gridding(Computerised Tomography Application). IEEE Transactions on Medical Imaging, 1991, 10(3): 473-478. [本文引用:1]
[2] FEINBERG D A, HALE J D, WATTS J C, et al. Halving MR Imaging Time by Conjugation: Demonstration at 3. 5 kG. Radiology, 1986, 161(2): 527-531. [本文引用:1]
[3] MARSEILLE G J, DE BEER R, FUDERER M, et al. Nonuniform Phase-Encode Distributions for MRI Scan Time Reduction. Journal of Magnetic Resonance(Series B), 1996, 111(1): 70-75. [本文引用:1]
[4] MCGIBNEY G, SMITH M R, NICHOLS S T, et al. Quantitative Evaluation of Several Partial Fourier Reconstruction Algorithms Used in MRI. Magnetic Resonance in Medicine, 1993, 30(1): 51-59. [本文引用:1]
[5] LUSTIG M, DONOHO D L, SANTOS J M, et al. Compressed Sen-sing MRI. IEEE Signal Processing Magazine, 2008, 25(2): 72-82. [本文引用:1]
[6] DONOHO D L. Compressed Sensing. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [本文引用:1]
[7] RAVISHANKAR S, BRESLER Y. MR Image Reconstruction from Highly Undersampled k-Space Data by Dictionary Learning. IEEE Transactions on Medical Imaging, 2011, 30(5): 1028-1041. [本文引用:1]
[8] WANG S S, SU Z H, YING L, et al. Accelerating Magnetic Resonance Imaging via Deep Learning // Proc of the 13th IEEE International Symposium on Biomedical Imaging. Washington, USA: IEEE, 2016: 514-517. [本文引用:1]
[9] LUSTIG M, DONOHO D, PAULY J M. Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195. [本文引用:1]
[10] TSAI C M, NISHIMURA D G. Reduced Aliasing Artifacts Using Variable-Density k-Space Sampling Trajectories. Magnetic Resonance in Medicine, 2000, 43(3): 452-458. [本文引用:1]
[11] ZIJLSTRA F, VIERGEVER M A, SEEVINCK P R. Evaluation of Variable Density and Data-Driven k-Space Under-Sampling for Compressed Sensing Magnetic Resonance Imaging. Investigative Radiology, 2016, 51(6): 410-419. [本文引用:2]
[12] LIU D D, LIANG D, LIU X, et al. Under-Sampling Trajectory Design for Compressed Sensing MRI // Proc of the 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Washington, USA: IEEE, 2012: 73-76. [本文引用:1]
[13] LEVINE E, HARGREAVES B. On-the-Fly Adaptive k-Space Sam-pling for Linear MRI Reconstruction Using Moment-Based Spectral Analysis. IEEE Transactions on Medical Imaging, 2018, 37(2): 557-567. [本文引用:1]
[14] HALDAR J P, KIM D. OEDIPUS: An Experiment Design Framework for Sparsity-Constrained MRI. IEEE Transactions on Medical Imaging, 2019, 38(7): 1545-1558. [本文引用:1]
[15] BAHADIR C D, DALCA A V, SABUNCU M R. Learning-Based Optimization of the Under-Sampling Pattern in MRI // Proc of the Conference on Information Processing in Medical Imaging. Berlin, Germany: Springer, 2019: 780-792. [本文引用:4]
[16] ZHANG Z Z, ROMERO A, MUCKLEY M J, et al. Reducing Uncertainty in Undersampled MRI Reconstruction with Active Acquisition // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 2049-2058. [本文引用:1]
[17] JIN K H, UNSER M, YI K M. Self-supervised Deep Active Acce-lerated MRI[J/OL]. [2020-07-25]. https://arxiv.org/pdf/1901.04547.pdf. [本文引用:1]
[18] LIU Z, LI J G, SHEN Z Q, et al. Learning Efficient Convolutional Networks through Network Slimming // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 2755-2763. [本文引用:2]
[19] HU H Y, PENG R, TAI Y W, et al. Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures[J/OL]. [2020-07-25]. https://arxiv.org/pdf/1607.03250.pdf. [本文引用:1]
[20] MOLCHANOV P, MALLYA A, TYREE S, et al. Importance Estimation for Neural Network Pruning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 11264-11272. [本文引用:1]
[21] ZBONTAR J, KNOLL F, SRIRAM A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI[J/OL]. [2020-07-25]. https://arxiv.org/pdf/1811.08839.pdf. [本文引用:1]
[22] PASZKE A, GROSS S, MASSA F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library // WALLACH H, LAROCHELLE H, BEYGELZIMER A, et al. , eds. Advances in Neural Information Processing Systems 32. Cambridge, USA: The MIT Press, 2019: 8024-8035. [本文引用:1]
[23] VIRTANEN P, GOMMERS R, OLIPHANT T E, et al. SciPy 1. 0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 2020, 17(3): 261-272. [本文引用:1]