为了选取合适的特征, 首先分析影响组稀疏表示分类方法精度的主要因素.Zhang等^[20]指出, 在由单个特征构建字典的稀疏表示模型中, 若编码系数的非零项越集中在某一类, 判为这一类的可能性越高, 识别效果越优.扩展到多特征字典, 还需满足不同特征能提供互补信息, 即在同个测试样本下, 不同特征的编码系数应具有相同的类级稀疏模式、不同的类内稀疏模式, 也就是说不同特征的编码系数在正确类应尽可能交叉互补.因此选择特征的编码系数需具备如下条件.

1)相同的类级稀疏模式.编码系数的非零项是否集中在正确类(测试样本的类别)c中, 以及集中程度, 可通过稀疏集中指数(Sparsity Concentration Index, SCI)判断, 系数wⁱ的稀疏集中指数定义如下:

$SCI({{w}^{i}})=\left\{ \begin{array}{* {35}{l}} \frac{C}{C-1}\left[ \underset{j=1, 2, \ldots , C}{\mathop{\text{max}}}\, \left( \frac{{{\left\| \left. w_{j}^{i} \right\| \right.}_{1}}}{{{\left\| \left. {{w}^{i}} \right\| \right.}_{1}}} \right)-1 \right], & j=c \\ 0, & j\ne c \\ \end{array} \right.$

2)不同的类内稀疏模式.在正确类中, 编码系数的非零项分布在不同的位置上, 说明由这2个特征构建的字典交叉互补.衡量2个向量之间的分布关系最简单的操作就是对2个向量进行逻辑运算, 其中逻辑或具有从左向右的关联性, 最符合需求, 因此本文通过对正确类的编码系数进行或运算, 获得2个编码系数的分布差异度, 以此探究特征的互补性.为了消除幅值的影响, 统一将系数中非零值替换成1.具体步骤如下.

算法 1 特征优选算法

输入 备选目标集合F={f¹, f², …, f^K},

测试样本的特征向量Y=[y¹, y², …, y^K].

输出 最优特征组合f_final

for i=1 to K do

基于特征fⁱ, 构建独立字典Dⁱ;

通过式(1)求取测试样本yⁱ在字典Dⁱ上的编码系数wⁱ;

计算wⁱ稀疏集中指数value1=SCI(wⁱ);

F_value1(i)=value1;

end for

F_value1降序排列, 选择前一半构成候选特征集f_candidate;

for i₁=1 to K2, i₂=1 to K2do

计算系数的分布差异度value2=or( wci1, wci2);

F_value2(i₁, i₂)=value2;

end for

F_value2降序排列, 选择最大值作为f_final;

return f_final

如何从选定的特征中构建最适合表情分类的字典, 需从字典的不失真重构力和分类判别力这2个方面进行约束.

若要保证分类正确性, 首先应保证字典能不失真重构特征.特征A在字典D上的稀疏表示为

$[{{A}_{1}}, {{A}_{2}}, \ldots , {{A}_{C}}]=[{{D}_{1}}, {{D}_{2}}, \ldots , {{D}_{C}}]\left[ \begin{matrix} X_{1}^{1} & \begin{matrix} X_{2}^{1} & \cdots \\ \end{matrix} & X_{C}^{1} \\ X_{1}^{2} & \begin{matrix} X_{2}^{2} & \cdots \\ \end{matrix} & X_{C}^{2} \\ \begin{matrix} \vdots \\ X_{1}^{C} \\ \end{matrix} & \begin{matrix} \begin{matrix} \vdots \\ X_{2}^{C} \\ \end{matrix} & \begin{matrix} {} \\ \cdots \\ \end{matrix} \\ \end{matrix} & \begin{matrix} \vdots \\ X_{C}^{C} \\ \end{matrix} \\ \end{matrix} \right]+{{N}_{\varepsilon }}, $

其中, Xab为第a类特征A_a在b类子字典D_b的表示系数, a=1, 2, …, C, b=1, 2, …, C, N_ε 为干扰噪声.

本文利用标签对每类特征单独进行学习.例如, 从第a类特征A_a中学习字典D_a包括如下3个部分:由所有类重构特征A_a的总误差

$\left\| \left. {{A}_{a}}-\overset{C}{\mathop{\underset{b=1}{\mathop{\sum }}\, }}\, {{D}_{b}}X_{a}^{b} \right\| \right._{2}^{2}, $

由相同类系数 Xaa重构A_a的误差 Aa-DaXaa22, 由其它类系数 Xab重构的分量

$\overset{C}{\mathop{\underset{\underset{b\ne a}{\mathop{b=1}}\, }{\mathop{\sum }}\, }}\, \left\| \left. {{D}_{b}}X_{a}^{b} \right\| \right._{2}^{2}.$

因此在不失真重构特征集的目的下, 字典优化的目标函数表示如下:

$r({{D}_{a}})=\left\| \left. {{A}_{a}}-\overset{C}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, {{D}_{b}}X_{a}^{b} \right\| \right._{2}^{2}+\left\| \left. {{A}_{a}}-{{D}_{a}}X_{a}^{a} \right\| \right._{2}^{2}+\overset{C}{\mathop{\underset{\underset{b\ne a}{\mathop{b=1}}\, }{\mathop{\sum }}\, }}\, \left\| \left. {{D}_{b}}X_{a}^{b} \right\| \right._{2}^{2}.$(6)

为了使字典更具鉴别力, Yang等^[23]提出将Fisher判别准则tr(S_w(X))-tr(S_B(X))用于编码系数的判别性约束, 但由于类内散布矩阵的奇异性, tr(S_W(X))-tr(S_B(X))存在非凸且不稳定等问题, 因此本文对系数添加采用最大散度差^[24]

p(X)=tr(S_W(X)-∂ S_B(X))

约束, 使同类字典样本更紧密、异类字典之间区别更大, 其中, ∂ 为非负常数, 用于平衡类内散度矩阵S_W(X)和类间散度矩阵S_B(X), 上述散度矩阵数学定义如下:

${{S}_{W}}(X)=\overset{C}{\mathop{\underset{j=1}{\mathop{\sum }}\, }}\, \underset{x\in {{X}_{j}}}{\mathop{\sum }}\, (x-mj){{(x-{{m}_{j}})}^{T}}, $

${{S}_{B}}(X)=\overset{C}{\mathop{\underset{j=1}{\mathop{\sum }}\, }}\, u{{m}_{j}}({{m}_{j}}-m){{({{m}_{j}}-m)}^{T}}, $

其中, m_j为X_j中样本的均值, x为X_j中的样本点, m为所有样本的均值, num_j为j类中的样本数目.

为了保证系数的稀疏性, 对其添加l₁范数:

$f(X)=p(X)+{{\lambda }_{1}}{{\left\| \left. X \right\| \right.}_{1}}.$ (7)

结合式(6)和式(7), 字典优化的目标函数为

$J(D, X)=min\left\{ \overset{C}{\mathop{\underset{a=1}{\mathop{\sum }}\, }}\, ({{D}_{a}})+{{\lambda }_{2}}f(X) \right\}.$ (8)

求解式(8)可获得优化后的字典.具体算法步骤如下.

算法 2 MSDOL

输入 特征A, 迭代次数n, 最小误差ε

输出 字典D^final

从特征A中随机选M列, 构成初始字典D⁰;

iter=1;

while (iter< n||J(D, X)< ε ) do

固定字典D⁰, 迭代拟合式(7), 求得初始系数X⁰;

固定字典X⁰, 迭代拟合式(6), 求得字典D^iter;

将D^iter、X^iter代入式(8), 计算J(D, X);

for m=1 to M do

如果D^iter(∶ , m)的幅值小于1e-6, 删除该列;

end for

iter=iter+1;

end while

return D^final

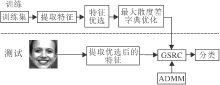
本文方法具体流程如图1所示.各部分介绍如下.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 本文方法流程图Fig.1 Flow chart of the proposed method

1)提取表情特征.表情特征包括纹理特征和几何特征.纹理特征使用图像的强度信息, 根据提取的部位不同可细分为全局纹理特征和局部纹理特征.几何特征通过测量距离、形变等几何分量得到, 可分为全局几何特征和局部几何特征.

为了验证方法的全面性, 本文提取人脸表情的全局纹理特征(灰度共生矩阵(Gray-Level Co-occur-rence Matrix, GLCM)), 局部纹理特征(局部相位量化(Local Phase Quantization, LPQ)和LBP), 全局几何特征(主动形状模型(Active Shape Model, ASM)), 局部几何特征(方向梯度直方图(Histo- gram of Oriented Gradient, HOG)).

2)特征优选.若直接将特征集内所有特征进行组稀疏表示分类, 会增大计算负担, 因此需要先对特征进行优选, 选择最适合且能提供互补信息的特征组合.本文通过十折交叉验证, 选取各数据库最合适的特征组合, 具体为从1)中提取训练样本和测试样本特征, 组成特征集

f={f^LBP, f^LPQ, f^GLCM, f^ASM, f^HOG}

和测试样本向量

y=[y^LBP, y^LPQ, y^GLCM, y^ASM, y^HOG],

根据算法1选择最优特征组合f_final.

3)基于最大散度差准则优化字典.为了提高编码效率和分类性能, 利用算法2对从2)中优选得到的特征进行优化增强, 获得字典D^final, 构建组字典.

4)组稀疏表示分类.提取待测样本的相关特征, 基于3)构建的组字典, 使用ADMM求解式(4), 获得联合系数, 最后根据式(5)求得待测样本的类别.

实验采用JAFFE、CK+数据库.JAFFE数据库包含213个面部表情图像, 包括愤怒、厌恶、恐惧、幸福、悲伤、惊奇、中性表情, 分别包含30、29、32、31、31、30、30幅图像.CK+数据库包含来自123位年龄在18~30岁的受试者的593个图像序列, 包括7类基本表情.选择每个序列的第一帧作为中性图像, 使用每个序列的最后一帧作为面部表情图像.

除分析不同训练样本数对方法的影响以外, 使用十折交叉验证, 重复实验10次, 取平均值作为最终结果.在验证之前, 对人脸图像进行预处理, 基于2只眼睛的位置, 将数据库上面部图像裁剪为64× 64纯人脸图像.采用Sun等^[13]提出的人脸比例图进行裁剪, 具体做法为:假设两眼之间的距离为d, 从眼睛到嘴巴的垂直距离为d, 以眼睛为中心, 向上切0.5d, 向下切1.5d.再分别以左眼、右眼为中心向左向右各切0.5d.基于这些位置关系, 确定图2的人脸比例切割图.由此切割的人脸区域包括眼睛、眉毛、嘴巴这些持久表达表情信息部位和额头脸颊这些瞬时表达表情信息的部位.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 人脸比例切割图Fig.2 Face scale cutting map

对比方法包括SVM、KNN和SRC.SVM采用线性核.KNN中K=10.SRC中关于编码系数的约束参数λ =0.01.本文方法参数λ ₁=λ ₂=0.01.

所有实验都是在PC(Intel Core i7-8700 CPU, 3.20 GHz)和Matlab2018b上进行的.

根据特征优选算法, 从表情识别的5个常见特征(HOG、LBP、LPQ、GLCM、ASM)中选择JAFFE数据库上最优特征组合.

首先考虑特征稀疏集中指数.在JAFFE数据库上, 各特征稀疏集中指数如下:HOG为0.773 0, LBP为0.693 5, LPQ为0.849 5, GLCM为0.475 9, ASM为0.152 5.HOG、LBP、LPQ的编码系数的稀疏集中指数远超过其它特征, 因此再考虑这3个特征间的互补指数, 具体如表1所示.

表1

Table 1

表1(Table 1)

表1 特征间的互补指数 Table 1 Complementary index between features HOG LBP LPQ HOG - 0.3478 0.3265 LBP - - 0.3577 LPQ - - -

表1 特征间的互补指数 Table 1 Complementary index between features

由表1可知, LBP和LPQ间的互补指数最高, 可提供最大互补信息.因此本文选择LBP和LPQ作为JAFFE数据库上的最优特征组合, 基于这2个特征构建字典, 进行组稀疏表示.

此外, 为了验证特征优选算法的有效性, 将特征集上任意2个特征经过字典优化后按照式(2)中的组字典构建的方式组合, 通过组字典稀疏表示进行表情分类, 在JAFFE数据库上的识别精度如表2所示.由表可知, 在JAFFE数据库上, 识别精度最高的特征组合与使用特征优选算法挑选的特征组合一致, 这表明本文特征优选算法在JAFFE数据库上的有效性.另外, HOG、LBP、LPQ任意两者组合的识别精度都高于其它组合, 这是因为这3个特征自身的识别性能较高, 这一点从特征稀疏集中指数也可看出.

表2

Table 2

表2(Table 2)

表2 JAFFE数据库上不同特征组合的识别率对比 Table 2 Comparison of recognition rate of different feature combinations on JAFFE % HOG LBP LPQ GLCM ASM HOG - 96.76 96.28 94.57 92.02 LBP - - 98.71 95.12 94.58 LPQ - - - 96.11 95.58 GLCM - - - - 90.26 ASM - - - - -

表2 JAFFE数据库上不同特征组合的识别率对比 Table 2 Comparison of recognition rate of different feature combinations on JAFFE %

LBP和LPQ组合中一次表情识别精度的混淆矩阵如表3所示.

表3

Table 3

表3(Table 3)

表3 JAFFE数据库上表情识别精度的混淆矩阵 Table 3 Confusion matrix of expression recognition accuracy on JAFFE % 愤怒 厌恶 恐惧 幸福 悲伤 惊奇 中性 愤怒 98.98 1.02 0 0 0 0 0 厌恶 0 100 0 0 0 0 0 恐惧 0 0 97.14 2.86 0 0 0 幸福 0 0 0 100 0 0 0 悲伤 0 0 0 0 99.08 0.92 0 惊奇 0 0 0 0 0 100 0 中性 0 0 0 0 0.51 0.51 98.98

表3 JAFFE数据库上表情识别精度的混淆矩阵 Table 3 Confusion matrix of expression recognition accuracy on JAFFE %

采取同样的方式, 选择最适合CK+数据库的特征组合、特征的稀疏集中指数和特征间的互补指数.

与JAFFE数据库类似, 在CK+数据库上, 特征稀疏集中指数如下:HOG为0.806 9, LBP为0.722 4, LPQ为0.801 7, GLCM为0.298 3, ASM为0.077 0.HOG、LBP、LPQ编码系数的稀疏集中指数较高, 再考虑这3个算子任意两者间的互补指数, 如表4所示.

表4

Table 4

表4(Table 4)

表4 特征间的互补指数 Table 4 Complementary index between features HOG LBP LPQ HOG - 0.2147 0.2348 LBP - - 0.1863 LPQ - - -

表4 特征间的互补指数 Table 4 Complementary index between features

同样地, 将特征集中任意两个特征组合识别精度进行对比, 如表5所示.由表可知, 在CK+数据库上, 识别精度最高的特征组合与使用特征优选算法挑选的特征组合一致.

表5

Table 5

表5(Table 5)

表5 CK+数据库上不同特征组合的识别率对比 Table 5 Comparison of recognition rate of different feature combinations on CK+ dataset % HOG LBP LPQ GLCM ASM HOG - 96.99 97.27 96.40 93.29 LBP - - 95.79 90.55 86.36 LPQ - - - 90.79 82.38 GLCM - - - - 79.01 ASM - - - - -

表5 CK+数据库上不同特征组合的识别率对比 Table 5 Comparison of recognition rate of different feature combinations on CK+ dataset %

HOG和LPQ组合中一次表情识别精度的混淆矩阵如表6所示.

表6

Table 6

表6(Table 6)

表6 CK+数据库上表情识别精度的混淆矩阵 Table 6 Confusion matrix of expression recognition accuracy on CK+ dataset % 愤怒 厌恶 恐惧 幸福 悲伤 惊奇 中性 愤怒 94.63 5.37 0 0 0 0 0 厌恶 0 92.82 5.65 0 0 0 1.53 恐惧 0 0 99.52 0.23 0 0 0.26 幸福 0 0 0 99.25 0 0 0.75 悲伤 0 0 0 0 94.90 4.42 0.68 惊奇 0 0 0 0 0 100 0 中性 0 0 0 0 1.09 0 98.91

表6 CK+数据库上表情识别精度的混淆矩阵 Table 6 Confusion matrix of expression recognition accuracy on CK+ dataset %

对比表2和表5可知:1)在JAFFE数据库上的识别精度高于CK+数据库, 这是因为在JAFFE数据库上, 备选特征间的互补指数更高(见表1和表4).因此, 讨论如何选择最优特征组合时, 要综合考虑特征自身的性能和特征间的互补性能.2)数据库不同, 最优特征组合也不同, 在JAFFE数据库上, 最优的特征组合是LBP和LPQ, 在CK+数据库上, 最优特征组合是LPQ和HOG, 这表明影响特征组合识别精度的因素不仅是特征本身, 与所选的数据库也有很大的关联.

CK+数据库上的样本是在不同光照环境下采集的, 光照不均匀.为了验证本文方法对光照的鲁棒性, 采用直方图均衡手段均匀光照, 将HOG特征与本文方法应用在均匀前后的数据库上进行实验, 具体识别精度如表7所示.

表7

Table 7

表7(Table 7)

表7 CK+数据库上光照均匀前后不同方法识别精度对比 Table 7 Accuracy comparison of different methods before and after illumination uniformity on CK + dataset % 均匀前 均匀后 HOG 89.88 92.82 本文方法 97.27 98.52

表7 CK+数据库上光照均匀前后不同方法识别精度对比 Table 7 Accuracy comparison of different methods before and after illumination uniformity on CK + dataset %

由表7可知, HOG特征在光照均匀化后的CK+数据库上, 识别精度提升约3%, 而本文方法识别精度前后差别不到1%.这表明本文方法在光照均匀和不均匀的条件下识别精度相差很小, 小于 HOG特征, 光照鲁棒性更强.

为了探究方法的泛化能力, 使用不同数量的样本训练方法, 探究其对识别精度的影响.SVM、KNN、SRC均属于单个特征的分类器.为了使实验对比更准确, 采用特征融合中常用的融合方法串联, 在JAFFE数据库上融合LBP与LPQ, 在CK+数据库上融合HOG与LPQ.各方法识别精度结果如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同训练样本对各方法识别精度的影响Fig.3 Influence of different training samples on recognition accuracy of different methods

由图3可知, 随着训练样本数目的减少, 本文方法和组稀疏表示模型识别精度稳定, 而KNN、SVM、SRC性能急剧下降.由此验证组稀疏表示在小样本问题上避免过拟合的有效性.另外, 从本文方法与组稀疏表示模型的结果对比可看出MSDOL的有效性, 它从特征中学习到本质的表情信息用于分类, 大幅提升识别精度.

从分类精度和耗时两方面进行对比.在JAFFE数据库上各方法的识别精度如下:文献[13]方法为65.61%, 文献[15]方法为94.01%, 文献[17]方法为97.30%, 文献[25]方法为94.37%, 文献[26]方法为95.20%, 文献[27]方法为97.18%, 本文方法为98.71%.在CK+数据库上各方法的识别精度如下:文献[14]方法为94.51%, 文献[16]方法为96.10%, 文献[18]方法为91.90%, 文献[26]方法为95.40%, 文献[28]方法为96.92%, 本文方法为97.27%.由此可知, 本文方法在2个数据集上的识别精度都最优.特别地, 在JAFFE数据库上, 相比次优方法(文献[27]方法), 本文方法的识别精度提高超过1%.

各方法的耗时对比如表8所示.

表8

Table 8

表8(Table 8)

表8 各方法的耗时对比 Table 8 Time consumption comparison of different methods 方法 训练时间/min 识别时间/s 文献[13]方法 7.7 2.406 文献[17]方法 5.4 0.755 文献[15]方法 15.0 0.062 文献[27]方法 26.0 5.51e-3 本文方法 7.8 0.268

表8 各方法的耗时对比 Table 8 Time consumption comparison of different methods

在表8中, 文献[13]方法、文献[17]方法与本文方法属于同类方法, 都是利用多个字典进行表情识别.文献[15]方法和文献[27]方法是基于深度学习的方法, 分别利用自动编码的稀疏网络和CNN构建表情识别系统.由表8可知, 本文方法与同类方法的训练时间相当, 识别时间略短.相比基于深度学习的方法, 本文方法虽识别时间较长, 但训练时间远小于两者.