2.1.1 目标函数模型

本文针对SRDCF的问题, 提出目标函数:

$\varepsilon (HW)=\frac{1}{2}\left\| \left. y-\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, {{x}_{k}}* {{h}_{k}} \right\| \right._{2}^{2}+\frac{{{\lambda }_{1}}}{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. \omega \cdot {{h}_{k}} \right\| \right._{2}^{2}+\frac{{{\lambda }_{2}}}{2}\left\| \left. \omega \text{-}{{\omega }_{r}} \right\| \right._{2}^{2}, $

其中, K表示通道数, X=[x₁, x₂, …, x_K]表示初始帧样本循环采集到的样本集, y∈ R^{T× 1}表示理想的相关响应, h_k∈ R^{T× 1}表示当前帧训练的第k个通道滤波器, * 表示卷积运算, λ ₁、λ ₂表示正则项系数.

引入自适应空间正则项$\frac{{{\lambda }_{1}}}{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. \omega \cdot {{h}_{k}} \right\| \right._{2}^{2}$, ω ∈ R^{T× T}, 融入样本信息, 使权重随着目标的变化而变化, 实现空间适应性.$\frac{{{\lambda }_{2}}}{2}\left\| \left. \omega \text{-}{{\omega }_{r}} \right\| \right._{2}^{2}$为权重的约束项, 自适应空间权重ω 结合参考权重ω _r, 避免对空间权重求取最优解时出现过拟合现象.

根据帕塞瓦尔定理, 引入辅助变量:

$\hat{G}=\left[ {{{\hat{g}}}_{1}}, {{{\hat{g}}}_{2}}, \cdots , {{{\hat{g}}}_{k}} \right], {{\hat{g}}_{k}}\in {{C}^{TK\times 1}}.$

将目标函数从时域转化到频域:

$\varepsilon (HW, \hat{G})=\frac{1}{2}\left\| \left. y-\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, {{{\hat{x}}}_{k}}\cdot {{{\hat{g}}}_{k}} \right\| \right._{2}^{2}+\frac{{{\lambda }_{1}}}{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. \omega \cdot {{h}_{k}} \right\| \right._{2}^{2}+\frac{{{\lambda }_{2}}}{2}\left\| \left. \omega \text{-}{{\omega }_{r}} \right\| \right._{2}^{2}, $ (1)

其中, ^表示信号的傅里叶变换, 即

$\hat{y}=\sqrt{T}Fy, {{\hat{x}}_{k}}=\sqrt{T}F{{x}_{k}}, {{\hat{g}}_{k}}=\sqrt{T}F{{g}_{k, }}$

F∈ C^{T× T}为正交矩阵.

2.1.2 目标函数优化

由于目标函数为可微凸函数, 可利用ADMM求取最优解, 减少计算的复杂程度, 加快算法的跟踪速度.式(1)的增广拉格朗日形式^[18]为

$\begin{align} & L(H, W, \hat{G}, \hat{M})=\varepsilon (HW, \hat{G})+ \\ & \frac{\gamma }{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. {{{\hat{g}}}_{k}}-\sqrt{T}F{{h}_{k}} \right\|_{2}^{2}+ \right.\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, {{({{{\hat{g}}}_{k}}-\sqrt{T}F{{h}_{k}})}^{H}}{{{\hat{m}}}_{k}}, \\ \end{align}$

其中, $\hat{M}=\left[ {{{\hat{m}}}_{1}}, {{{\hat{m}}}_{2}}, \cdots {{{\hat{m}}}_{k}} \right]\in {{R}^{T}}^{\times K}$为拉格朗日乘子的傅里叶变换, γ 为正则项步长参数, 上标H表示矩阵的共轭转制.

引入

$V=[{{v}_{1}}, {{v}_{2}}, \ldots , {{v}_{k}}], {{v}_{k}}=\frac{1}{\gamma }{{m}_{k}}, $

式(2)可转化为

$L(H, W, \hat{G}, \hat{M})=\varepsilon (HW, \hat{G})+\frac{\gamma }{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. {{{\hat{g}}}_{k}}-\sqrt{T}F{{h}_{k}}+{{{\hat{v}}}_{k}} \right\|_{2}^{2} \right.$

上式可被分为$\hat{G}$, H, W三个子问题, 可通过对这三个子问题进行迭代得到最优解.

1)求解$\hat{G}$.假设给定H, W, $\hat{V}$ ,

$\hat{G}=\left[ {{{\hat{g}}}_{1}}, {{{\hat{g}}}_{2}}, \cdots , {{{\hat{g}}}_{k}} \right], $

目标函数

${{L}_{{\hat{G}}}}=\frac{1}{2}\left\| \left. \hat{y}-\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, {{{\hat{x}}}_{k}}\cdot {{{\hat{g}}}_{k}}}}\, \right\| \right._{2}^{2}+\frac{\gamma }{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. {{{\hat{g}}}_{k}}-\sqrt{T}F{{h}_{k}}+{{{\hat{V}}}_{k}} \right\|_{2}^{2} \right..$ (3)

求式(3)最小时${{\hat{g}}_{k}}$的值, 需要对${{\hat{g}}_{k}}$进行求导.但是由于式(3)中存在求和运算且$\hat{x}$为带状稀疏变量, 本文不直接对${{\hat{g}}_{k}}$进行求导, 而是考虑单独计算$\hat{y}$中的元素${{\hat{y}}_{k}}$, k=1, 2, …, K.记$\zeta (\hat{G})\in {{R}^{K\times 1}}$, 表示在像素j上$\hat{x}$的值, 那么式(3)可转化为

$\begin{align} & {{L}_{\zeta (\hat{G})}}=\frac{1}{2}\overset{T}{\mathop{\underset{j=1}{\mathop{\sum }}\, }}\, \left\| \left. {{{\hat{y}}}_{j}}-{{\zeta }_{j}}{{(\hat{X})}^{T}}{{\zeta }_{j}}(\hat{G}) \right\| \right._{2}^{2}+ \\ & \frac{\gamma }{2}\overset{T}{\mathop{\underset{j=1}{\mathop{\sum }}\, }}\, \left\| \left. {{\zeta }_{j}}(\hat{G})-{{\zeta }_{j}}(\sqrt{T}FH)+{{\zeta }_{j}}(\hat{V}) \right\| \right._{2}^{2}, \\ \end{align}$

其中,

${{\zeta }_{j}}(\hat{X})\in {{R}^{K\times 1}}, {{\zeta }_{j}}(\hat{V})\in {{R}^{K\times 1}}, {{\zeta }_{j}}(\sqrt{T}FH)\in {{R}^{K\times 1}}.$

根据离散帕塞瓦尔定理, 时域和频域能量相等, 可得

$\begin{align} & {{L}_{{{\zeta }_{j}}(\hat{G})}}=\frac{1}{2T}\left\| \left. {{{\hat{y}}}_{j}}-{{\zeta }_{j}}{{(\hat{X})}^{T}}{{\zeta }_{j}}(\hat{G}) \right\| \right._{2}^{2}+ \\ & \frac{\gamma }{2}\left\| \left. {{\zeta }_{j}}(\hat{G})-{{\zeta }_{j}}(\sqrt{T}FH)+{{\zeta }_{j}}(\hat{V}) \right\| \right._{2}^{2}. \\ \end{align}$

对${{\zeta }_{j}}(\hat{G})$求偏导, 并令其等于0,

$\begin{align} & 0=\frac{1}{T}{{\zeta }_{j}}(\hat{X})\left[ {{{\hat{y}}}_{j}}-{{\zeta }_{j}}{{(\hat{X})}^{T}}{{\zeta }_{j}}(\hat{G}) \right]+ \\ & \gamma \left[ {{\zeta }_{j}}(\hat{G})-{{\zeta }_{j}}(\sqrt{T}FH)+{{\zeta }_{j}}(\hat{V}) \right] \\ \end{align}$

解得

${{\zeta }_{j}}(\hat{G})=\frac{{{\zeta }_{j}}\left( {\hat{X}} \right){{{\hat{y}}}_{j}}+\gamma T\left[ {{\zeta }_{j}}\left( {\hat{V}} \right)-{{\zeta }_{j}}\left( \sqrt{T}FH \right) \right]}{{{\zeta }_{j}}{{\left( {\hat{X}} \right)}^{\text{T}}}{{\zeta }_{j}}\left( {\hat{X}} \right)+\gamma T}.$ (4)

式(4)的时间复杂度为O(TK³), 根据Sherman Morrison公式, 化简得

$\zeta _{j}^{\text{* }}(\hat{G})\text{=}\frac{1}{\gamma T}\left( I-\frac{{{\zeta }_{j}}\left( {\hat{X}} \right){{\zeta }_{j}}{{\left( {\hat{X}} \right)}^{\text{T}}}}{\gamma T+{{\zeta }_{j}}{{\left( {\hat{X}} \right)}^{\text{T}}}{{\zeta }_{j}}\left( {\hat{X}} \right)} \right)\rho $ (5)

其中

$\rho \text{=}{{\hat{y}}_{j}}{{\zeta }_{j}}\left( {\hat{X}} \right)+\gamma {{\zeta }_{j}}\left( \sqrt{T}FH \right)+\gamma {{\zeta }_{j}}\left( {\hat{V}} \right).$

式(5)的时间复杂度为O(TK), 相比式(4), 降低算法复杂度, 缩短运行时间.

2)求解H.假设给定$\hat{G}$, W, $\hat{V}$ , H∈ R^{T× 1}, 目标函数为

${{\varepsilon }_{{{h}_{k}}}}\text{=}\frac{{{\lambda }_{1}}}{2}\left\| \left. \omega \cdot {{h}_{k}} \right\| \right._{2}^{2}+\frac{\gamma }{2}\left\| \left. {{{\hat{g}}}_{k}}-\sqrt{T}F{{h}_{k}}+{{{\hat{V}}}_{k}} \right\| \right._{2}^{2}.$

记

W=diag(ω )∈ R^{T× T}

为ω 的对角矩阵, 则有

ω · h=Wh,

并且令

∂εhk∂hk=0,

可解得

$\begin{align} & h_{k}^{\text{* }}={{\lambda }_{1}}{{W}^{T}}(W{{h}_{k}})-\gamma {{(\sqrt{T}F)}^{T}}\left( {{{\hat{g}}}_{k}}-\sqrt{T}F{{h}_{k}}+{{{\hat{V}}}_{k}} \right)= \\ & \frac{\gamma \sqrt{T}{{F}^{\text{T}}}\left[ \sqrt{T}F\left( {{g}_{k}}+{{v}_{k}} \right) \right]}{{{\lambda }_{1}}{{W}^{\text{T}}}W+\gamma T}=\frac{\gamma T\left( {{g}_{k}}+{{v}_{k}} \right)}{{{\lambda }_{1}}\left( W\cdot W \right)+\gamma T}. \\ \end{align}$ (6)

由式(6)可看出, 对h_k的求解仅需要快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT), 即

${{v}_{k}}=\frac{1}{\sqrt{T}}{{F}^{T}}{{\hat{v}}_{k}}$、 ${{g}_{k}}=\frac{1}{\sqrt{T}}{{F}^{T}}{{\hat{g}}_{k}}$

逐元相乘得到.所以, 式(6)的时间复杂度为

O(KT lg T).

3)求解ω .假设给定H, W, $\hat{V}$ , 对ω 求最优解采用ADMM, 迭代过程如下.目标函数

${{\varepsilon }_{w}}=\frac{{{\lambda }_{1}}}{2}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, \left\| \left. {{D}_{k}}\cdot \omega \right\| \right._{2}^{2}+\frac{{{\lambda }_{2}}}{2}\left\| \left. \omega -{{\omega }_{r}} \right\| \right._{2}^{2}, $ (7)

其中,

D_k=diag(h_k)∈ R^{T× T}.

通过引入辅助变量q, 式(7)可转为增广拉格朗日形式:

$L(\omega , q, m)=\frac{{{\lambda }_{1}}}{2}\left\| \left. {{D}_{k}}\cdot \omega \right\| \right._{2}^{2}+\frac{{{\lambda }_{2}}}{2}\left\| \left. q-{{\omega }_{r}} \right\| \right._{2}^{2}+\frac{\mu }{2}\left\| \left. q-\omega -m \right\| \right._{2}^{2}.$

其中, m表示拉格朗日因子, μ 表示步长参数.由于此模型同样是可微凸函数, 可再次采用ADMM将求解过程分解为如下3个子问题:

ωk=qk-1-mk-1I+λ1μDk,

qk=λ2ωr+μ(ωk+mk-1)λ2+μ,

mk=mk-1+ωk-qk,

其中, 根据μ =min(β μ , μ _max)对μ 进行更新, β =10.

本文算法在训练第1帧图像时, 采用显著性检测的方法, 构造1个带有样本信息的空间权重ω _r.根据温洪发等^[19]对显著性检测的相关算法描述, 并且考虑到本文算法对实时性的要求, 最终决定采用快速调频(Frequency-Tuned, FT)算法^[20]进行显著性检测.FT是将图像的所有频带经过多个高斯带通滤波器的滤波操作后合并, 成为最终的显著图.

高斯滤波器表达式如下:

$\begin{align} & DoG(x, y)=\frac{1}{2\pi }\left[ \frac{1}{\sigma _{1}^{2}}\text{exp}\left( -\left( \frac{{{x}^{2}}+{{y}^{2}}}{2\sigma _{1}^{2}} \right) \right)-\frac{1}{\sigma _{2}^{2}}\text{exp}\left( -\left( \frac{{{x}^{2}}+{{y}^{2}}}{2\sigma _{2}^{2}} \right) \right) \right] \\ & =G(x, y, {{\sigma }_{1}})-G(x, y, {{\sigma }_{2}}), \\ \end{align}$

其中, σ ₁、σ ₂分别是高斯函数的标准差, σ ₁> σ ₂.

显著值表示为

$S(x, y)={{\left\| \left. {{I}_{\mu }}-{{I}_{{{\omega }_{hc}}}}\left( x, y \right) \right\| \right.}_{2}}, $

其中, I_μ 表示图像的平均特征向量, Iωhc表示经过高斯模糊处理后的图像特征向量.由此能保留较完整的边界, 均匀突出显著区域, 得到整体轮廓.本文算法应用显著值在第1帧时对自适应空间权重进行初始化操作, 降低距离目标中心较近区域的权值, 提高距离目标较远的边缘区域的权值, 更精准地抑制非目标区域的响应.

自适应空间正则项的参考权重的初始化为

W_r=W₀· δ S, (8)

其中, W₀表示引用SRDCF中的负高斯形状的空间权重, δ 为固定参数.在后续帧中, 使用式(7)对空间权重进行更新,

4)更新拉格朗日因子:

${{\hat{V}}^{i+1}}={{\hat{V}}^{i}}+\iota \left( {{{\hat{G}}}^{i+1}}-{{{\hat{H}}}^{i+1}} \right), $

其中, ι 表示更新参数, i、i+1表示迭代次数, ${{\hat{G}}^{i+1}}$和${{\hat{H}}^{i+1}}$表示在第i+1次迭代中子问题$\hat{G}$、子问题$\hat{H}$的解.

ι ⁱ⁺¹=min(ι _max, β ι ⁱ),

其中, β =10, ι _max=10 000.

2.1.3 目标定位

当前帧响应图:

${{R}_{t}}={{F}^{-1}}\overset{K}{\mathop{\underset{k=1}{\mathop{\sum }}\, }}\, (\hat{Z}_{t}^{k}\cdot \hat{g}_{t-1}^{k}), $

其中, $Z_{t}^{k}$表示当前帧提取的特征映射, $\hat{g}_{t-1}^{k}$表示上一帧训练好的滤波器的傅里叶形式.计算得到响应图中最大值所在的位置即为跟踪目标的中心区域.

2.2.1 异常分析

在目标跟踪的过程中, 当目标发生平面内/外旋转、超出视野和其它因素引起的外观变化时, 提取特征会出现困难, 相关滤波器对样本的训练容易发生错误.于是本文算法融入异常分析策略, 根据目标在运动过程中与之前帧存在的差异, 判断是否出现异常情况.

由于响应图揭示算法和目标对象之间的相似性, 因此本文算法使用响应图估计目标和之前帧的相似值, 从而判定是否发生异常情况.当物体外观突然变化时, 不会影响模型的学习, 却提升算法的鲁棒性.

通过设置置信分数score作为标准进行验证, 置信分数值定义为

$score=exp(-{{\left\| \left. R_{t-1}^{\text{model}}-{{R}_{t}} \right\| \right.}_{2}}), $ (9)

其中, R^model表示之前得到的响应图模型, R_t表示当前帧计算的响应图.正常情况下, 响应图模型与当前帧的响应图相似, 此时置信分数较高; 当目标开始发生旋转、超出视野或其它异常情况时, 响应图会突然发生巨大变化, 置信分数相应减少.

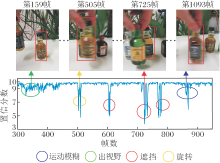
视频序列异常分析如图1所示.由图可知, 在此视频序列中, 当目标正常平稳移动时, 外观几乎未发生变化, 生成的置信分数会维持在较高的数值.当目标发生平面外旋转或模糊运动时, 外观特征变化程度较小, 置信分数值降低.当目标超出视野或被遮挡时, 外观特征变化程度较大, 置信分数大幅减小.因此, 本文的置信分数可用于检验结果的可信度, 并进行异常分析.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 视频序列异常分析示意图Fig.1 Illustration of video sequence anomaly analysis

由于视频序列每帧验证分数的值按正态形式分布, 且score的阈值区间为[0, 10], 所以本文设定当score< 9.5时, 出现异常情况.

2.2.2 策略更新

大多数现有的目标跟踪算法采用逐帧的方式更新外观模型和相关滤波器, 忽略当前帧的跟踪结果可能是不准确的, 盲目地更新外观模型和相关滤波器会导致跟踪器学习到错误的检测对象.

因此, 本文提出更新策略.首先, 在视频的初始帧时, 生成一个新的模型, 并在该帧中学习初始相关滤波器.然后, 直接使用学习到的相关滤波器进行相关运算, 生成响应图模型.最后, 在后续帧中, 验证分数值控制对象外观模型和响应图模型的学习.

从第2帧开始, 利用sigmoid激活函数, 根据上一帧的置信分数值score, 定义动态学习率:

η=α1+ea(b-score), σ=β1+ea(b-score),(10)

其中, α 、 β 为学习参数.由于本文设定score的阈值区间为[0, 10], 在[6.5, 9.5]区间中波动较大, 而sigmoid激活函数的自变量在[-5, 5]区间时变化较大, 所以通过计算, a设为3.3, b设为7.57.

目标的外观模型$\hat{x}_{t}^{\bmod el}$及响应图模型 Rmodelt分别以自适应学习率η 和 σ 进行更新:

$\begin{align} & \hat{x}_{t}^{\bmod el}=\eta \hat{x}_{t-1}^{\bmod el}+(1-\eta ){{{\hat{x}}}_{t}}, \\ & R_{t}^{\text{model}}=\sigma R_{t-1}^{\text{model}}+\left( 1-\sigma \right){{R}_{t}}, \\ \end{align}$

其中t表示当前帧.$\hat{x}_{t}^{\bmod el}$仅用于判断模型是否更新, ${{\hat{x}}_{t}}$用于目标函数的计算.

在同类基于相关滤波的目标跟踪算法中, 本文算法不仅更新对象的外观模型, 而且还学习和更新响应图模型.

并且本文更新策略能实现根据目标外观发生变化的程度, 验证结果的可信度, 并以此自适应选择模型的更新率.这一策略既解决SRDCF依靠记录所有历史帧样本信息造成的跟踪速度过低的问题, 也能提高跟踪精度和稳定性.

空间异常适应性的目标跟踪算法过程如下.

1)初始帧建模.裁剪目标区域, 得到此区域的显著图, 与SRDCF中碗形权重结合, 采用式(8)初始

化空间正则项权重.提取特征, 训练滤波器, 建立响应图模型和目标外观模型.

2)目标定位.将上一帧得到的滤波器与当前帧的搜索区域进行相关运算, 生成响应图, 响应图中最大值所处的位置定为目标中心.

3)采用式(7)更新空间权重, 并训练相关滤波器.

4)模型更新.根据每一帧, 采用式(9)得到的置信分数, 判断目标状态, 选择相应的模型更新速率后, 采用式(10)更新响应图模型和目标外观模型.

5)输出跟踪结果.转至2), 训练下一帧图像的相关滤波器并更新模型.

本文算法选用SRDCF作为基础框架, 并对其进行改进.总体算法框架如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 本文算法总体框图Fig.2 Flow chart of the proposed algorithm

本文选取OTB2013、OTB2015、DTB70、LASOT数据集进行实验.

实验使用的编程软件为GNU Octave, 操作系统为mac OS Mojave 10.14.6, 处理器为Intel Core i7, 2.9 GHz双核CPU, 8 GB内存.

实验中正则项系数λ ₁=1.5, λ ₂=0.006.在对自适应空间正则项权重初始化时δ = 10.在2次使用ADMM时, 迭代次数为2, 正则项参数γ = 1, μ = 1.在更新模型时, 目标外观模型的学习参数α = 0.02, 响应图模型的学习参数σ = 0.9.其余参数与SRDCF一致.

为了客观、有针对性地验证本文算法的有效性, 选取如下6种同类型算法进行对比实验:SRDCF、KCF、BACF、STRCF、ARCF、AutoTrack.

SRDCF使用碗形的空间权重.KCF引入循环矩阵及高斯核.BACF扩大循环器的采样区域, 缩小搜索区域.STRCF引入时间正则项.ARCF抑制检测过程中发生的异常情况.AutoTrack引入局部响应变量, 自适应学习正则项权重.

此外设定各算法的特征提取方式同SRDCF一致, 统一为方向梯度直方图(Histogram of Oriented Gradient, HOG)与颜色名(Color Names, CN)融合进行特征提取, 并采用一次性通过评估(One-Pass Evaluation, OPE)作为评价指标.

7种算法在OTB2013数据集上的成功率与精确率曲线如图3和图4所示.由图可知, 本文算法的成功率和精确率最高, 可见在统一特征提取方式后, 本文算法可实现较优的跟踪效果.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 各算法在3个数据集上的成功率对比Fig.3 Comparison of success rates of different algorithms on 3 datasets

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各算法在3个数据集上的精确率对比Fig.4 Comparison of precision rates of different algorithms on 3 datasets

7种跟踪算法在3个数据集上的平均跟踪速度对比如表1所示.计算方法为总帧数除以总时间.由表可看出, 本文算法构造一个有封闭解的目标函数, 并采用ADMM进行迭代求解, 跟踪速度得到大幅提升.再结合图3和图4, 在OTB2013、OTB2015、DT-B70数据集上进行实验的过程中, 相比其它6种算法, 本文算法成功率和精确率都较高, 满足实时性要求, 跟踪性能较优.

表1

Table 1

表1(Table 1)

表1 各算法在3个数据集上的平均跟踪速度对比 Table 1 Comparison of average tracking speed of different algorithms on 3 datasets 帧/秒 算法 OTB2013 OTB2015 DTB70 本文算法 15.49 15.81 17.95 AutoTrack 16.19 16.23 18.54 BACF 17.36 16.99 16.25 SRDCF 3.01 3.92 8.30 KCF 125.61 131.49 151.23 ARCF 11.21 12.61 16.09 STRCF 19.21 19.65 18.92

表1 各算法在3个数据集上的平均跟踪速度对比 Table 1 Comparison of average tracking speed of different algorithms on 3 datasets 帧/秒

为了进一步验证本文算法的有效性, 对比如下主流跟踪算法:SRDCF、KCF、BACF、AutoTrack、ARCF、ASRCF, Staple(Sum of Template and Pixel-Wise Learners)^[21], ECO(Efficient Convolution Operators)^[22].Staple结合梯度特征和颜色直方图特征, 采用尺度金字塔的方法进行尺度处理.ECO将特征图从离散的空间域转入连续的空间域.ASRCF引入自适应空间正则项.在同一平台上进行实验对比.

各算法的特征提取方法如下:本文算法、SRDCF、AutoTrack、ECO、Staple采用HOG+CN, KCF、BACF采用HOG, ARCF采用HOG+CNN特征, ASR-CF采用HOG+VGG特征.

3.3.1 定量分析

各算法在OTB2013、OTB2015、DTB70、LASOT 数据集上的成功率和精确率对比如表2和表3所示.在表中, 黑体数字表示最优结果, 斜体数字表示次优结果.

表2

Table 2

表2(Table 2)

表2 各算法在3个数据集上的成功率对比 Table 2 Comparison of success rates of different algorithms on 3 datasets 数据集 本文算法 AutoTrack ECO BACF SRDCF ASRCF KCF ARCF Staple OTB2013 0.840 0.797 0.813 0.838 0.757 0.837 0.623 0.863 0.737 OTB2015 0.788 0.780 0.762 0.774 0.711 0.692 0.555 0.845 0.696 DTB70 0.438 0.479 0.453 0.400 0.339 0.469 0.280 0.470 0.265

表2 各算法在3个数据集上的成功率对比 Table 2 Comparison of success rates of different algorithms on 3 datasets

表3

Table 3

表3(Table 3)

表3 各算法在4个数据集上的精确率对比 Table 3 Comparison of precision rates of different algorithms on 4 datasets 数据集 本文算法 AutoTrack ECO BACF SRDCF ASRCF KCF ARCF Staple OTB2013 0.861 0.826 0.837 0.860 0.822 0.893 0.740 0.886 0.781 OTB2015 0.840 0.837 0.810 0.823 0.779 0.901 0.701 0.841 0.782 DTB70 0.642 0.717 0.643 0.593 0.495 0.696 0.468 0.705 0.365 LASOT 0.298 0.289 0.272 0.239 0.227 0.337 0.184 0.299 0.231

表3 各算法在4个数据集上的精确率对比 Table 3 Comparison of precision rates of different algorithms on 4 datasets

由表2和表3可发现, 在OTB2013、OTB2015数据集上, 本文算法的成功率较高, 但精确率低于AS- RCF和ARCF.由于DTB70数据集多为无人机拍摄, 所以本文算法在此数据集上的跟踪效果略低于ASRCF及适用于无人机领域的AutoTrack、ARCF.在LASOT数据集上, 本文算法的精确率略低于ASRCF.

为了更清晰、综合地对比各算法的跟踪性能, 选取OTB2015数据集上视频出现的11种属性:光照变化(Illumination Variation, IV)、尺度变换(Scale Variation, SV)、遮挡(Occlusion, OCC)、非刚性变化(Deformation, DEF)、运动模糊(Motion Blur, MB)、快速运动(Fast Motion, FM)、平面内旋转(In-Plane Rotation, IPR)、平面外旋转(Out-of-Plane Rotation, OPR)、超出视野(Out of View, OV)、复杂背景(Back-ground Clutter, BC)、低分辨率(Low Resolution, LR).

9种算法在OTB2015数据集上各种属性的精确率和成功率得分如表4和表5所示, 在表中, 黑体数字为最优结果, 斜体数字为次优结果.

表4

Table 4

表4(Table 4)

表4 各算法在OTB2015数据集上各种属性的精确率得分 Table 4 Precision rate scores of various attributes of different algorithms on OTB2015 dataset 属性 本文算法 AutoTrack ECO BACF SRDCF ASRCF KCF ARCF Staple IV 0.794 0.735 0.800 0.824 0.754 0.848 0.739 0.835 0.775 SV 0.802 0.838 0.757 0.769 0.736 0.867 0.642 0.820 0.721 OCC 0.861 0.792 0.720 0.740 0.726 0.812 0.632 0.785 0.724 DEF 0.839 0.801 0.765 0.773 0.712 0.785 0.619 0.848 0.747 MB 0.815 0.784 0.736 0.761 0.741 0.857 0.616 0.822 0.692 FM 0.807 0.794 0.789 0.807 0.710 0.843 0.621 0.803 0.710 IPR 0.781 0.813 0.781 0.796 0.703 0.848 0.701 0.804 0.767 OPR 0.881 0.809 0.767 0.785 0.725 0.848 0.685 0.809 0.736 OV 0.771 0.778 0.748 0.765 0.621 0.833 0.501 0.798 0.668 BC 0.875 0.778 0.800 0.830 0.738 0.850 0.713 0.787 0.748 LR 0.746 0.743 0.741 0.739 0.663 0.811 0.560 0.783 0.610

表4 各算法在OTB2015数据集上各种属性的精确率得分 Table 4 Precision rate scores of various attributes of different algorithms on OTB2015 dataset

表5

Table 5

表5(Table 5)

表5 各算法在OTB2015数据集上各种属性的成功率得分 Table 5 Success rate scores of various attributes of different algorithms on OTB2015 dataset 属性 本文算法 AutoTrack ECO BACF SRDCF ASRCF KCF ARCF Staple IV 0.774 0.759 0.776 0.797 0.697 0.825 0.560 0.797 0.708 SV 0.750 0.729 0.689 0.695 0.650 0.815 0.418 0.758 0.596 OCC 0.832 0.745 0.689 0.707 0.670 0.763 0.512 0.755 0.653 DEF 0.781 0.728 0.693 0.705 0.640 0.744 0.503 0.794 0.656 MB 0.758 0.759 0.727 0.734 0.708 0.841 0.563 0.803 0.639 FM 0.803 0.767 0.760 0.766 0.710 0.820 0.526 0.803 0.645 IPR 0.706 0.730 0.704 0.714 0.630 0.792 0.553 0.730 0.668 OPR 0.841 0.740 0.697 0.718 0.635 0.774 0.532 0.753 0.643 OV 0.695 0.722 0.689 0.694 0.561 0.774 0.457 0.722 0.548 BC 0.826 0.796 0.766 0.796 0.660 0.807 0.609 0.751 0.687 LR 0.659 0.654 0.663 0.664 0.562 0.763 0.295 0.683 0.472

表5 各算法在OTB2015数据集上各种属性的成功率得分 Table 5 Success rate scores of various attributes of different algorithms on OTB2015 dataset

由表4和表5可知, 本文算法由于具有空间适应性, 能精准控制背景区域的空间权重, 所以在处理遮挡、平面外旋转、背景杂乱问题时的精确率和成功率均最高.异常适应性能控制更新速率, 在处理形变和快速运动的问题上达到较优效果.

但是, 由于本文算法选取HOG与CN融合的特征提取方式, 使算法在处理光照变化、低分辨率、平面内旋转和运动模糊时的效果差于ASRCF、ARCF.在处理超视野和运动模糊属性时, 会出现将目标区域视为背景区域的情况, 所以本文算法的效果较差.

结合表2和表3发现, 本文算法能在大多数情况下保证实时跟踪的同时, 维持稳定鲁棒的跟踪, 整体跟踪效果较优.

另外, 本文算法每种属性的精确率和成功率得分均高于SRDCF.在OTB2013、OTB2015数据集上, 相比SRDCF的平均精确率(0.800)和平均成功率(0.734), 本文算法的平均精确率(0.866)和平均成功率(0.837)分别提高6.6%和10.3%.

3.3.2 定性分析

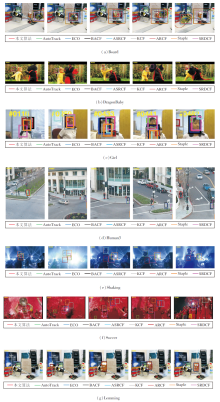
各算法在OTB100数据集上11种属性的视频序列的跟踪结果如图5所示.由图可见, 本文算法跟踪结果较优.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各算法在视频序列上的跟踪结果对比Fig.5 Comparison of tracking results of different algorithms on video sequences

1)非刚性形变(DEF)指目标在运动过程中的外观不断发生变化, 此时空间正则项成为解决此类问题的关键.在Board、DragonBaby、Girl序列上均由于目标发生旋转造成非刚性形变, Soccer、Lemming序列发生由遮挡造成的非刚性形变.在Girl序列中, 从第74帧到292帧, 目标发生2次平面外旋转(OPR), 299帧到342帧, 目标发生2次平面内旋转(IPR).在这期间, ASRCF、SRDCF、ARCF、AutoTrack不能较好地更新目标的外观模型, 只能跟踪到一部分, 由于KCF、ECO、BACF、ARCF、Staple没有自适应的空间正则项, 所以在第411帧时, 目标遇到相似区域遮挡时, 不能降低该区域的权重, 出现漂移现象, 跟踪性能差于本文算法.所以, 本文算法在非刚性形变和旋转变化时的跟踪性能较稳定.

2)在Board序列的第571帧到581帧, 目标发生运动模糊(BM), 此时ECO、BACF、SRDCF、ASRCF由于无法提取到准确特征, 相继发生漂移.跟踪到第665帧时, KCF、SRDCF、Staple、AutoTrack、ARCF跟踪失败.DragonBaby序列从第10帧开始, KCF就出现漂移现象, 导致跟踪失败.在第38帧和第62帧时, ARCF、ECO跟踪失败.在第82帧, BACF、ASR-CF、ARCF、Staple由于目标的快速运动(FM)和尺度变化, 没有及时跟踪到目标, 出现漂移.从初始帧至最后, 目标发生多次旋转和快速运动, 只有本文算法在此期间没有出现漂移.由于本文的异常分析机制可检测出异常情况, 自适应降低目标模型的更新率, 使算法在快速运动的场景下具备较优的鲁棒性.

3)在处理低分辨率(LR)属性时, 最主要的问题是特征提取.目前通用的解决尺度变换(SV)问题方法是改造尺度金字塔.9种算法中, 只有KCF没有处理尺度问题.在Board序列第189帧, ARCF、Auto-Track、Staple由于无法适应目标不断发生的尺度变化, 跟踪框过大, 继续跟踪会导致跟踪精度降低.从Human3序列初始帧至第856帧, 目标分辨率较低, 在第63帧中, 由于相似物体的遮挡, ARCF、BACF、Auto-Track、SRDCF、KCF、Staple跟踪到错误背景, 在第1 680帧时, ASRCF跟踪失败.第1 345帧时目标尺度发生变化, 在这期间只有本文算法可以始终跟踪到目标.但是由于较低的分辨率, 滤波器学习到的特征不够充分, 跟踪到的对象不够精确, 因此本文算法对低分辨率情况的处理需要改进.

4)复杂背景(BC)指目标运动过程中, 会受到背景相似内容的干扰, 对跟踪过程造成一定影响.在Shaking序列的第251帧及Soccer序列第115帧, 由于背景杂乱, KCF、AutoTrack、SRDCF、ARCF均受到错误背景信息的影响, 出现跟踪错误.只有本文算法和BACF可准确跟踪到目标, 其它算法均发生漂移.实验结果表明, 在处理复杂背景时, 本文算法的跟踪效果较优.

5)在Board序列第122帧, 当目标移出视野(OV)后重新回到画面时, Staple、ARCF、KCF、AutoTrack不能适应目标长时间的外观变化, 跟踪错误.在Girl序列的第441帧和Human3序列的第63帧, 出现相似目标遮挡(OCC), 此时, 由于KCF、Staple、ARCF、BACF目标函数中未设置空间正则项, 无法对非目标区域的权重加以控制, 所以在检测区域中出现相似目标时, 滤波器的学习被干扰, 跟踪错误.从Lemming序列第288帧时开始出现遮挡问题, 到第35帧时, 只能利用仅剩的部分目标区域进行有效跟踪, 此时由于本文算法具有自适应的空间正则项, 能降低背景区域的空间权重, 在第375帧目标全部重新回到图像中时, 仍可继续跟踪.本文算法可较好地处理移出视野和遮挡的情况.

6)光照变化(IV)指当前帧由于光线问题, 图像的颜色组成大幅变化.在Shaking序列第60帧和第251帧中, 光照发生变化, 此时由于Staple对颜色特征较敏感, 当光照变化强烈时, 无法提取有效特征, 跟踪失败.ARCF、SRDCF、KCF、AutoTrack均跟踪失败.由于本文的异常检测机制, 能暂停对目标外观模型的学习, 表现出较优的跟踪性能.