假设可观测网络G_O=(V_O, E_O)为潜在完整网络G_T=(V_O∪ V_M, E_O∪ E_M)的一个子集.V_O={v₁, v₂, …, v_n}为可观测网络中的节点集, n为可观测网络的节点数量, E_O⊆V_O× V_O为已知节点间边的集合, V_M为缺失节点的集合, E_M为缺失边的集合.网络G_O中已知节点间不存在缺失边, 缺失边仅为已知节点与缺失节点之间的链接, G_O和G_T是无自循环和重复边的无向网络.

网络补全通过可观测网络G_O, 补全缺失的节点V_M和相关的边E_M, 使推断的网络 G︿与真实网络G_T具有相同结构.具体问题示例如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 网络节点补全问题示例Fig.1 Example of network node completion

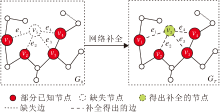
由图1可观测到网络G_O中存在一个缺失节点v₅, v₅与已知节点v₁、v₂、v₃、v₄间有缺失的边e₁、e₂、e₃、e₄.为了补全网络中缺失的部分, 首先通过G_O中可观测节点的信息推断节点对(v₁, v₂)、(v₂, v₃)、(v₃, v₄)、(v₁, v₄)间均存在一个缺失节点.然后进一步推断(v₁, v₂)、(v₂, v₃)、(v₃, v₄)、(v₁, v₄)间缺失的节点是同一节点v₅, 补全网络中缺失的边e₁、e₂、e₃、e₄, 得到完整的网络G_T.

本文提出基于图卷积神经网络的网络节点补全算法(NCGCN), 补全网络中缺失的节点和边.NCGCN包含如下4个步骤:

1)采样.构建封闭子图和特征矩阵.2)特征提取.

获取各封闭子图的图表征.3)学习.实现目标节点对内缺失节点的分类.4)节点合并.推断各目标节点对间缺失节点的关系.

NCGCN框图如图2所示.在生成的随机样本中, 黄色节点表示正例目标节点对, 蓝色节点表示正例节点对的一阶邻接节点, 绿色节点表示反例目标节点对, 灰色节点表示反例节点对的一阶邻接节点, 黑色节点表示经过NCGCN补全的缺失节点.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 NCGCN框图Fig.2 Flowchart of NCGCN

给定一个网络, 本文目标是解决缺失节点数量未知情况下的网络补全问题.基于网络补全的相关研究, NCGCN以目标节点对的封闭子图和特征矩阵为输入, 经过GCN的训练, 输出缺失节点存在的概率.节点对的h-hop封闭子图为网络中由节点

{i|d(i, x)≤ h or d(i, y)≤ h}

组成的子图, 其中, (x, y)为目标节点对, d(i, x)、d(i, y)表示节点i到目标节点x, y的最短距离^[19].

NCGCN的伪代码如算法1所示.因此, 网络补全的第1步是生成包含目标节点对的封闭子图和特征矩阵的训练集.

算法1 NCGCN

输入 可观测网络G_O中随机采样得到的m对节点对的h-hop封闭子图G^h的邻接矩阵A^h, 图G^h的节点特征矩阵X, 卷积层的层数k

输出 各节点对内缺失节点的概率H',

节点对间关系矩阵P

初始化 t=0, k=4, Z⁰=X

Begin

while t< k do

Z^t+1=f( D︿-1A︿Z^tW_t) //计算卷积层的输出

t=t+1

Z^1:t:=「X, Z¹, …, Z^t⌉ //将X与各卷积层得出的结果横向拼接, 得到新的图表征

end while

Z^AP=gnn.AvgPooling(G^h, Z^1:t) //池化

H=f(Z^APW₅+b₁)

H'=f(HW₆+b₂) //利用2个全连接层进行分类运算

Z^AP'=f(Z^APW₇+b₃)

P=f((Z^AP')· (Z^AP')^T) //计算关系矩阵

输出H', P

end

1.2.1 各封闭子图的图表征获取

GCN以封闭子图的邻接矩阵A^h和特征矩阵X作为输入, 通过多层图卷积抽取各封闭子图的结构特征:

Z^t+1=f( D︿-1A︿Z^tW_t).

其中: D︿为度矩阵; A︿=A^h+I, A^h为G_O中随机采样得到m对节点对构造的h-hop封闭子图G^h的邻接矩阵, I为单位矩阵; X∈ R^{n× c}为图G^h的节点特征矩阵, n表示节点数量, c表示每个节点特征向量的维度; Z⁰=X, Z^t∈ Rn×ct为第t层的输出矩阵, c_t为第t层输出矩阵的特征向量维度; W_t∈ Rct×ct+1为将c_t维特征向量映射到c_t+1的第t层权值矩阵; f为非线性激活函数.NCGCN中采用4个连续图卷积层提取各封闭子图结构特征, 即t的最大值为4.

再将G^h的特征矩阵X及各卷积层的输出结果横向拼接, 得

Z^1:t:=「X, Z¹, …, Z^t⌉, Z^1:t∈ Rn×(c+c1+c2+…+ct).

将Z^1:t和G^h作为最大池化层的输入, 得出图表征张量Z^AP∈ Rm×(c+c1+c2+…+ct).

1.2.2 目标节点对内缺失节点的分类

为了对目标节点对内的缺失节点进行分类, 推断节点对内是否存在缺失节点, 本文对经过卷积层、池化层得出的图表征张量Z^AP进行两层连续的全连接运算, 计算各节点对内缺失节点的概率:

H'=f(HW₆+b₂), H=f(Z^APW₅+b₁).

其中:W₅∈ R(c+c1+c2+…+ct)×k'表示可训练全连接层的参数矩阵, k'为自定义的超参数; b₁∈ R^{m× k'}为线性运算过程中产生的偏差; f为非线性激活函数; W₆∈ R^{k'× 1}表示分类运算的权值矩阵, b₂∈ R^{m× 1}为分类过程中产生的偏差.在H'∈ [0, 1]^{m× 1}中, H'_i值越大, 第i个节点对内存在一个缺失节点的可能性越大, 当H'_i=0时, 第i个节点对内不存在缺失节点.深度学习中常用sigmoid、softmax作为分类问题最后一层的激活函数, sigmoid激活函数常用于二分类问题, 而softmax激活函数常用于多分类问题, 且经softmax激活函数输出的向量的概率总和为1.推测节点对内是否存在缺失节点实际上是一个二分类问题, 没有最终求得的概率总和为1的条件限制.因此, 本文在最后一层全连接层采用sigmoid激活函数对节点对内是否存在缺失节点进行分类.

1.2.3 不同目标节点对间缺失节点的关系推断

推断不同目标节点对之间的缺失关系, 实际上是判断不同节点对之间的缺失节点是否同一节点.首先构造目标节点对间的关系矩阵, 矩阵中的数值表示其所在行、列的节点对之间存在的缺失节点是同一节点的概率.在已知图表征Z^AP的前提下, 关系矩阵

P=f(Z^AP· (Z^AP)^T),

但上式中存在一个问题, Z^AP的维度会随抽取节点对个数和节点的特征维数的增加而倍数增长, 这使模型的计算效率和准确性随之迅速下降.为此, 本文进一步对图表征Z^AP的特征维度进行线性变换:

Z^AP'=f(Z^APW₇+b₃),

其中, W₇∈ R(c+c1+c2+…+ct)×k″表示进行特征维度压缩时的权值矩阵, b₃∈ R^{m× k″}为线性运算过程中产生的偏差, f为非线性激活函数, k″为自定义的超参数, 用于改变图表征的维度.改进后的节点间关系矩阵表示为

P=f((Z^AP')· (Z^AP')^T), (1)

其中, P∈ [0, 1]^{m× m}, f为非线性激活函数.在表示节点对关系的矩阵中, P_{i, j}越大, 表示i表示的节点对和j表示的节点对间的缺失节点为同一节点的概率越大, P_{i, j}=0表示i表示的节点对和j表示的节点对间的缺失节点非同一节点.推测不同节点对间的缺失节点是否是同一节点实际上是一个二分类问题, 没有最终求得的概率总和为1的条件限制.因此, 这里采用sigmoid激活函数对不同节点对间的缺失节点是否是同一节点进行分类.

关系矩阵P的结果示例如图3所示, 将正负例样本按左图中的顺序送入连续四层GCN中训练, 得出图表征Z^AP∈ R4×(c+c1+c2+c3+c4).

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 关系矩阵P结果示例Fig.3 Example of relationship matrix P

然后根据式(1)计算得出关系矩阵P∈ [0, 1]^{4× 4}, 关系矩阵P各项数值如右图所示, 矩阵对角线上(1, 1)、(4, 4)颜色较深, (2, 2)、(3, 3)颜色较浅, 表明1表示的节点对和4表示的节点对内存在一个缺失的节点, 而2表示的节点对和3表示的节点对内不存在缺失的节点.(1, 4)、(4, 1)中的颜色深于其它非对角线, 表明1表示的节点对和4表示的节点对中缺失的节点是同一个节点, 即(a)中排序为1和4的封闭子图中的目标节点对间缺失同一节点.

本文通过随机采样的方法构造正例数据集和反例数据集.正例数据集由要去除的节点、去除节点的邻接节点对、封闭子图的节点特征矩阵组成.负例数据集由负例目标节点对、封闭子图的节点特征矩阵组成.

正例数据集的构造分为5步:1)从可观测网络G_O中随机选择互不相连且邻接节点数大于1的n(满足条件的节点数量可能会小于n)个节点.2)记录选择的n个节点的邻接节点的集合后, 在可观测网络G_O中去除这n个节点.3)从每个节点的邻接节点集合中最多选择k对节点, 以每对节点为目标分别构造h-hop封闭子图.在封闭子图中, 确保目标节点对中2个节点的序号分别为0号和1号.4)构造封闭子图的节点特征矩阵.5)生成N个正例样本的数据集.

节点的特征矩阵由每个节点的标签和属性向量组成.节点标签表示节点在封闭子图中的相对位置与重要性, 使不同子图中的节点在结构上尽可能对齐.本文采用双半径节点标记(Double-Radius Node Labeling, DRNL)^[19]的节点标签方法.首先将目标节点对(x, y)的标签均标记为1, 重复更新节点的标签直至收敛, 即

f=1+min(d_x, d_y)+ d/2[(d/2)+(d%2)-1], (2)

其中,

d_x:=d(i, x), d_y:=d(i, y), d:=d_x+d_y,

d(i, x)表示节点i到目标节点x的最短距离, d(i, y)表示节点i到目标节点y的最短距离, f(i)表示序号为i的节点标签, (d/2)、(d%2)分别为d除以2的整数商和余数.

对于封闭子图中与目标节点对不连通的节点标签的计算, 本文提出改进方法.先假设其连通, 此时的不连通子图变成连通子图.再根据式(2)计算节点标签, 将计算得出所有节点到目标节点对的最大值加1表示子图不连通时的节点标签.

负例数据集的构造分为4步:1)随机选择2N个节点对集合, 同时需确保每对节点均不在正例数据集的目标节点对中.选择2N个节点对的目的是得到充足反例数据样本.2)以每对节点为目标构造h-hop封闭子图, 目标节点的序号分别为0号和1号.3)构造封闭子图的节点特征矩阵, 构建方法与正例样本一致.4)生成2N个负例样本的数据集.

最后, 整合得到的正例数据集与反例数据集, 划分为训练集、验证集和测试集.在数据量不大(万级别及以下)的情况下进行深度学习模型训练时, 训练集和测试集的划分比例通常为7:3, 若存在验证集, 则训练集、测试集、验证集的划分比例为6:2:2.本文采用的数据集节点数目在万级以下, 因此, 将正例数据集与反例数据集分别按各自总比例的60%、20%、20%划分为训练集、验证集与测试集.

本文采用交叉熵损失和focal loss^[23]结合的损失函数计算NCGCN的损失.交叉熵损失函数用于计算各目标节点对内缺失节点的向量H'的损失.Focal loss损失函数用于计算不同目标节点对间的缺失节点关系矩阵P的损失.关系矩阵P的损失计算如下:

L2_{i, j}= -α(1-P'i, j)γlnP'i, j, P″i, j=1-(1-α)(P'i, j)γln(1-P'i, j), P″i, j=0

L2'= 1mm∑i, jL2_{i, j},

其中, P'∈ {0, 1}^{m× m}为P进行四舍五入处理后的矩阵, P″为原缺失节点对间的真实关系矩阵, α 为平衡正负样本的超参数, γ =2, 用于调节简单样本权重降低的速率.

NCGCN输出向量H'对关系矩阵P的影响较深, 当向量H'中某行为0时, P中与之相对应的行列均为0, 即当某节点对内不存在缺失节点时, 该节点对必然不会与其它节点对间缺失同一节点.因此, 在计算关系矩阵P的损失时, 为了使运算结果偏向于计算那些向量H'中数值较高的值, 即重点关注向量H'中较高概率存在缺失节点的目标节点对的相互关系, 本文为其赋予权重W₈=H'· H'^T∈ R^{m× m}, W₈数值大小是由向量H'决定.于是, 关系矩阵P的损失进一步变化为

L2″=L2· W₈.(3)

由于向量H'的取值均在0~1之间, 在经过矩阵内积之后得出的权值矩阵W₈的数值普遍偏小, 使其失去应有的作用.为此, 本文将权值矩阵W₈进行数值放大处理.结合式(3), 关系矩阵P的损失最终为

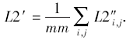
综上所述, NCGCN的损失函数表示如下:

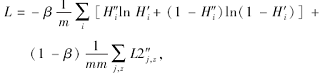
其中 β 为交叉熵损失函数占总损失函数的比重.

实验采用4个网络数据集, 包括随机生成的小世界网络(Small World Network, SWN)、路由器网络(Router Network, RN)和经过数据处理后的真实网络.随机生成的完整网络中分别包含1 000个节点及由节点生成的随机边.真实网络数据集分别为Facebook数据集、NS数据集^[24].Facebook数据集包含4 039个节点和88 234条边.NS数据集是发表网络科学论文的研究人员组成的协作网络数据集, 包含1 589个节点和2 742条边.在所有的实验中将网络视为无向连通网络.

为了评估NCGCN性能, 采用精度(Precision)、召回率(Recall)和F1值作为评价指标, 计算公式如下:

Precision= n1n1+n2, Recall= n1n1+n3,

F1= 2n12n1+n2+n3

其中, n₁为缺失节点被正确预测个数, n₂为不存在缺失节点却被错误预测个数, n₃为缺失节点被错误预测个数.

为了验证本文算法的有效性, 构造如下基线算法.

1)CN_NN.共同邻居节点数量是链路预测中常用的一种指标.基于两节点间的共同邻居数越多, 它们之间存在链接的可能性越大的假设^{[25, 26]}, 本文将该思路用于网络节点补全, 构造基线算法CN_NN.在CN_NN中, 若节点对的共同邻居数越多, 存在缺失节点的可能性越大, 且不同节点对间的共同邻居数越多, 存在同一缺失节点的可能性越大.

2)JACCARD_NN.Jaccard方法^[27]是共同邻居节点方法的改进, 本文将基于Jaccard方法的基线算法称为JACCARD_NN.在JACCARD_NN中, 两节点间的共同邻居数占两节点总邻居数的比重越大, 两节点间存在缺失节点的可能性越大, 不同节点对间的共同邻居数占邻接节点总数的比重越大, 存在同一缺失节点的可能性越大.

3)PA_NN.将基于节点相似性的Preferential Attachment(PA) 链接预测方法^{[28, 29]}用于节点补全, 得到基线算法PA_NN.在PA_NN中, 网络中节点更可能与距离较近且度矩阵较大的节点间存在缺失节点, 并假设节点间至多有一个缺失节点.

4)NCGCN_VAL.相比NCGCN, 基线算法NCGCN_VAL不进行节点对内缺失节点的推断, 直接判断不同节点对间的缺失节点是否是同一节点, 进而补全网络.

5)NCGCN_DRNL.将NCGCN中节点特征矩阵的计算方法改换成DRNL^[19], 得到基线算法NCGCN_DRNL.

所有实验均运行5次, 结果取平均值.各算法在4个数据集上的精度和F1值对比如表1和表2所示.本文根据采用的Ranking方法, 计算各算法在每个数据集上的精度和F1值排名.由表1和表2可看出, NCGCN在4组数据集上精度和F1值均为最高分, 平均排名最佳.NCGCN对NS数据集上缺失数据的补全效果最优, 精度达到71.1%, F1值达到72.5%.由此可见, NCGCN能较好地恢复网络中的缺失数据.此外, 由表1和表2的平均排名可看出, 相比传统算法, 采用深度学习模型的算法可更好地恢复网络中的缺失数据.这表明深度学习在网络补全方面具有较高的应用潜力.

表1

Table 1

表1(Table 1)

表1 各算法在4个数据集上的精度对比 Table 1 Precision comparison of different algorithms on 4 datasets 算法 SWN RN Facebook NS 平均排名 CN_NN 0.018± 0.027 0.014± 0.005 0.034± 0.008 0.052± 0.020 4.50 PA_NN 0.005± 0.001 0.216± 0.056 0.011± 0.005 0.012± 0.012 5.50 JACCARD_NN 0.015± 0.024 0.002± 0.001 0.487± 0.077 0.072± 0.061 4.25 NCGCN_VAL 0.130± 0.012 0.305± 0.013 0.256± 0.007 0.248± 0.008 3.25 NCGCN_DRNL 0.368± 0.009 0.558± 0.032 0.424± 0.040 0.676± 0.030 2.25 NCGCN 0.496± 00.15 0.618± 0.040 0.626± 0.027 0.711± 0.012 1.00

表1 各算法在4个数据集上的精度对比 Table 1 Precision comparison of different algorithms on 4 datasets

表2

Table 2

表2(Table 2)

表2 各算法在4个数据集上的F1值对比 Table 2 F1 comparison of different algorithms on 4 datasets 算法 SWN RN Facebook NS 平均排名 CN_NN 0.011± 0.024 0.023± 0.018 0.065± 0.018 0.096± 0.034 4.75 PA_NN 0.010± 0.001 0.104± 0.039 0.022± 0.010 0.014± 0.011 5.25 JACCARD_NN 0.005± 0.002 0.002± 0.001 0.233± 0.026 0.104± 0.078 5.00 NCGCN_VAL 0.218± 0.019 0.449± 0.065 0.378± 0.009 0.370± 0.015 3.00 NCGCN_DRNL 0.370± 0.014 0.479± 0.041 0.526± 0.011 0.577± 0.017 2.00 NCGCN 0.483± 0.028 0.542± 0.013 0.553± 0.018 0.725± 0.018 1.00

表2 各算法在4个数据集上的F1值对比 Table 2 F1 comparison of different algorithms on 4 datasets

值得注意的是, NCGCN_VAL在RN数据集上的效果远优于2个真实数据集, 而在SWN数据集上, NCGCN_VAL的补全效果不及Facebook、NS数据集.原因在于, 本文认为随机生成的网络数据集不含任何有效信息, 当数据集提取的图结构特征越符合原网络拓扑结构时, 补全效果越优, 而大多数随机生成的网络数据集的补全效果不及真实数据集.相比NCGCN_VAL, NCGCN在各数据集上的表现较优, 真实数据集的补全效果均优于随机生成数据集.这从侧面表明NCGCN的合理性.对比NCGCN与NCGCN_DRNL可发现, NCGCN在精度和F1值上均有不同程度的提高.在NS数据集上, NCGCN精度提高3%, F1值提高14%.这表明对封闭子图中节点标签的算法改进是有效的.

网络中缺失节点比例是影响NCGCN可靠性的重要因素.本文通过改变网络中节点数目, 改变网络中缺失节点的比例.因此, 本节通过改变数据集上节点数量, 测量NCGCN补全网络的精度和F1值, 验证NCGCN的可靠性.

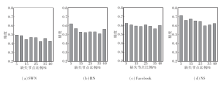
不同缺失比例下NCGCN的实验结果如图4、图5所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 缺失节点比例对精度的影响Fig.4 Effect of missing node ratio on precision

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 缺失节点比例对F1值的影响Fig.5 Effect of missing node ratio on F1

由图可知, 网络中缺失节点的比例对NCGCN的影响不大, 当网络中缺失40%的节点时, NCGCN仍能可靠地恢复网络缺失的部分.需要注意的是, SWN、RN数据集上的精度和F1值低于2个真实数据集, 这是由于SWN、RN数据集上的数据是随机生成的, 数据中没有任何有效信息.NS数据集上的精度和F1值均在0.6以上, 这是因为NS数据集是由发表网络科学论文的研究人员组成的引文网络数据集, 研究人员的研究方向大致相关, 这使网络中的节点相似程度较高.