软覆盖熵及其在多属性群决策中的应用

引用本文

吴家明, 黄哲煌, 李进金, 刘丹玥, 吴哲. 软覆盖熵及其在多属性群决策中的应用. 模式识别与人工智能, 2021,34(6): 541-551
WU Jiaming, HUANG Zhehuang, LI Jinjin, LIU Danyue, WU Zhe. Soft Covering Entropy and Its Applications in Multi-attribute Group Decision-Making. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(6): 541-551. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202106006
Permissions

《模式识别与人工智能》编辑部

软覆盖熵及其在多属性群决策中的应用

吴家明¹, 黄哲煌¹, 李进金^1,², 刘丹玥¹, 吴哲¹

1.华侨大学数学科学学院泉州 362021

2.闽南师范大学数学与统计学院漳州 363000

通讯作者:

黄哲煌,博士,副教授,主要研究方向为粗糙集、粒计算.E-mail:hqufuzzy@163.com.

作者简介:

吴家明,硕士研究生,主要研究方向为粗糙集、不确定性分析及其应用.E-mail:wjmfuzzy@163.com.

李进金,博士,教授,主要研究方向为一般拓扑学、粗糙集、概念格.E-mail:jinjinlimnu@126.com.

刘丹玥,硕士研究生,主要研究方向为粗糙集、不确定性分析及其应用.E-mail:dannylous@163.com.

吴哲,硕士,讲师,主要研究方向为图像处理、机器视觉、模式识别.E-mail:WUzhe33@hqu.edu.cn.

收稿日期: 2021-02-03 接受日期: 2021-04-20

资助项目: 国家自然科学基金项目(No.11871259)、福建省自然科学基金项目(No.2020J02043,2017J01114)资助

摘要

结合软覆盖与信息熵,提出软覆盖信息熵.定义软覆盖信息熵、软覆盖联合熵、软覆盖条件熵,并研究这些熵之间的关系及它们的重要性质.最后给出两种基于软覆盖条件熵的多属性群决策的算法,举例说明这两种算法的结果具有一致性.

关键词: 软覆盖; 信息熵; 条件熵; 多属性群决策

中图分类号:TP301

Soft Covering Entropy and Its Applications in Multi-attribute Group Decision-Making

WU Jiaming¹, HUANG Zhehuang¹, LI Jinjin^1,², LIU Danyue¹, WU Zhe¹

1. School of Mathematical Sciences, Huaqiao University, Quan-zhou 362021

2. School of Mathematics and Statistics, Minnan Normal University, Zhangzhou 363000

Corresponding author:
HUANG Zhehuang,Ph.D., associate professor. His research interests include rough set and granular computing.

About Author:
WU Jiaming, master student. His research interests include rough set, uncertainty analysis and its application.
LI Jinjin, Ph.D., professor.His research interests include topology, rough set and concept lattice.
LIU Danyue, master student. Her research interests include rough set, uncertainty analysis and its application.
WU Zhe, master, lecturer. Her research interests include image processing, machine vision and pattern recognition.

Fund:National Natural Science Foundation of China(No.11871259), Natural Science Foundation of Fujian Province(No.2020J02043,2017J01114)

Abstract

Information entropy and soft coverings are combined to propose soft covering information entropy. Soft covering information entropy, soft covering joint entropy and soft covering conditional entropy are defined. The relationships between these entropies and their important properties are studied. Two kinds of algorithms for multi-attribute group decision making based on soft covering conditional entropy are presented, and the consistency between the results of these two algorithms is illustrated by examples.

Key words: Key Words Soft Covering; Information Entropy; Conditional Entropy; Multi-attribute Group Decision-Making

本文责任编委苗夺谦

Recommended by Associate Editor MIAO Duoqian

粗糙集理论^{[1, 2]}是使用集合论处理某些不确定知识的数学方法.作为解决不确定性的一种工具, 粗糙集只使用内部知识, 而不依赖于先前的模型假设, 因此引起研究人员的广泛关注^{[3, 4, 5, 6, 7]}.但粗糙集需要在给定论域的元素之间产生等价关系, 在现实中这种等价关系很难得到.因此, 研究者们对粗糙集进行扩展, 包括邻域粗糙集^[8]和基于覆盖的粗糙集^{[9, 10, 11]}.随后学者们发现基于覆盖的粗糙集理论的重要性并强调它的很多特征, 此理论越来越受到重视.陈应生等^[12]在多尺度决策信息系统中, 把划分推广为覆盖, 并建立多尺度覆盖决策信息系统模型.

Molodtsov^[13]提出软集理论, 这是另一种处理不确定性的数学工具.相比传统的数学工具, 软集理论最大的优势就是参数工具.软集理论可给出丰富的信息描述和计算操作, 因此, 在信息理论、决策分析、模式识别、数据挖掘中具有重要作用.Li等^[14]结合软集和覆盖的概念, 提出软覆盖的概念和相关的参数约简.根据软粗糙集的思想, 研究人员将这些混合软集模型应用于决策, Feng等^[5] 研究粗糙集和软集, 得出一些重要结论, 并建立基于软粗糙集的多准则群体决策.Zhan等^[15]和Zhang等^[16]提出基于粗糙集的软覆盖的邻域和补邻域, 并应用于多属性群决策.

信息熵是表征不确定性信息的有效工具, 熵及其变体的扩展已应用于粗糙集领域^{[17, 18, 19, 20, 21, 22]}.Liang等^{[23, 24]}提出评价信息系统知识不确定性和模糊性的方法.陈东晓等^[25]从信息粒角度提出基于信息熵研究形式背景的属性约简的方法.Lei等^[26]定义平方粗糙熵, 用于度量图像的粗糙度, 并提出相应的图像阈值分割算法.还有一些研究者基于邻域系统, 建立信息熵及其变体, 并进行特征选择.Wang等^[27]引入邻域可分辨矩阵的概念, 表征特征子集的分类能力, 并构造基于可辨性矩阵的特征评价函数.Sun等^[28]基于模糊邻域多粒度粗糙集, 提出基于模糊神经网络的特征选择方法.Zhang等^[29]使用基于模糊粗糙集的信息熵, 研究增量特征选择.但是, 目前尚未见到软覆盖与信息熵的融合研究.

本文以信息熵理论为基础, 结合软覆盖与信息熵, 提出软覆盖信息熵及其变体以及在多属性群决策中的应用.首先利用软覆盖定义5种类型的软覆盖信息熵并研究其性质, 再定义软覆盖联合熵、软覆盖条件熵.最后利用软覆盖条件熵进行多属性群决策, 并通过2种算法的对比发现结果具有一致性, 说明本文算法合理有效.

1 基础知识

1.1 软集

定义1^[30]K=(G, B)为论域U上的软集, 其中, B⊆E, E为参数; G:B→ P(U), P(U)为U的幂集.序对P=(U, K)称为软近似空间.

定义2^[30] 若(G, B)为论域U上的软集, 若

$\cup_{b}^{\in}$ G(b)=U,

且∀ b∈ B, G(b)≠ Ø , 称(G, B)为软覆盖.

定义3^[15] 令P=(U, C_K)为U上的软覆盖近似空间, 对于∀ x∈ U, x的软邻域定义为

N $_{P}^{1}$ (x)={G(b):b∈ B∧ x∈ G(b)}.

定义4^[15] 令P=(U, C_K)为U上的软覆盖近似空间, 对于∀ x∈ U, x的软补邻域定义为

N $_{P}^{2}$ (x)={t∈ U:x∈ N $_{P}^{1}$ (t)}.

结合软邻域和软补邻域, 可定义另外两种混合软邻域算子:

N $_{P}^{3}$ (x)=N $_{P}^{1}$ (x)∩ N $_{P}^{2}$ (x),

N $_{P}^{4}$ (x)=N $_{P}^{1}$ (x)∪ N $_{P}^{2}$ (x).

定义5^[15] 令P=(U, C_K)为U上的软覆盖近似空间, 对于∀ x∈ U, x的软粘连定义为

N $_{P}^{5}$ (x)= {t∈ U:∀ b∈ B(x∈ G(b)↔ t∈ G(b))}.

1.2 信息熵

定义6^[27] 信息熵的定义为

H(B)= $\overset{m}{\sum_{i = 1}}$ -p(X_i)ln p(X_i),

其中

U/B={X₁, X₂, …, X_m},

X_i的概率

p(X_i)= $\frac{|X_{i}|}{| U |}$ ,

|X_i|为X_i的基数.

定义7^[27] 联合熵的定义为

H(B∪ C)=- $\overset{m}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}}$ p(X_i∩ Y_j)ln p(X_i∩ Y_j),

其中

U/C={Y₁, Y₂, …, Y_n}.

定义8^[27] 条件熵的定义为

H(B|C)描述在已知C的条件下B的不确定性, 显然H(B|C)≥ 0.若∃X_i∈ B, 使对于∀ Y_j∈ C, 有p(X_i|Y_j)=1, 则H(B|C)=0.这意味属性子集B的区分能力完全包含在C中.

2 软覆盖熵及其变体

定义9 令N $_{P}^{r}$ (x), r=1, 2, …, 5, 为x∈ U上的软邻域, 软覆盖熵定义为

其中, |· |表示集合的基数,

N $_{P}^{r}$ ={N $_{P}^{r}$ (x₁), N $_{P}^{r}$ (x₂), …, N $_{P}^{r}$ (x_n)}, r=1, 2, …, 5.

性质1 令N $_{P}^{r}$ (x), r=1, 2, …, 5, 为x∈ U上的软邻域, 则

0≤ H(N $_{P}^{r}$ )≤ ln n.

证明因为N $_{P}^{r}$ (x)为x∈ U上的软邻域, 故

1≤ |N $_{P}^{r}$ (x_i)|≤ |U|,

所以

0≤ H(N $_{P}^{r}$ )≤ ln n.

特别地, 对

∀ x_i∈ U, |N $_{P}^{r}$ (x_i)|=1

时,

H(N $_{P}^{r}$ )=ln n.

对

∀ x_i∈ U, |N $_{P}^{r}$ (x_i)|=|U|

时,

H(N $_{P}^{r}$ )=0.

性质2 令N $_{P}^{r}$ (x), r=1, 2, …, 5, 为x∈ U上的软邻域, 则

1)H(N $_{P}^{5}$ )=H(N $_{P}^{3}$ )≥ H(N $_{P}^{1}$ )≥ H(N $_{P}^{4}$ ),

2)H(N $_{P}^{5}$ )=H(N $_{P}^{3}$ )≥ H(N $_{P}^{2}$ )≥ H(N $_{P}^{4}$ ).

证明先证1).由软邻域定义易知

N $_{P}^{5}$ (x_i)=N $_{P}^{3}$ (x_i)⊆N $_{P}^{2}$ (x_i)⊆N $_{P}^{4}$ (x_i),

故

|N $_{P}^{5}$ (x_i)|=|N $_{P}^{3}$ (x_i)|≤ |N $_{P}^{2}$ (x_i)|≤ |N $_{P}^{4}$ (x_i)|,

所以

H(N $_{P}^{5}$ )=H(N $_{P}^{3}$ )≥ H(N $_{P}^{1}$ )≥ H(N $_{P}^{4}$ ).

再证2).同1)类似证明可得.

例1 学校足球队有5位学生报名, 记为U={x₁, x₂, …, x₅}.社团的成员从5方面对这5位学生进行考核, 记为B={b₁, b₂, …, b₅}, 这5方面分别是耐力、速度、力量、反应能力、团队精神, 这5人在5方面的特征可被记为一个软覆盖K=(G, B), 具体如表1所示.

表1 例1中学生的特征描述K=(G, B) Table 1 Students feature description K=(G, B) in example 1

显然P=(U, C_K)为U上的软覆盖近似空间, 则有

1)若r=1,

N $_{P}^{1}$ (x₁)={x₁, x₂, x₃, x₅}, N $_{P}^{1}$ (x₂)={x₂}, N $_{P}^{1}$ (x₃)={x₃}, N $_{P}^{1}$ (x₄)={x₄}, N $_{P}^{1}$ (x₅)={x₁, x₂, x₃, x₅}.

计算第一类软覆盖熵:

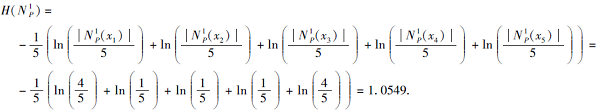
2)若r=2,

N $_{P}^{2}$ (x₁)={x₁, x₅}, N $_{P}^{2}$ (x₂)={x₁, x₂, x₅}, N $_{P}^{2}$ (x₃)={x₁, x₃, x₅}, N $_{P}^{2}$ (x₄)={x₄}, N $_{P}^{2}$ (x₅)={x₁, x₅}.

计算第二类软覆盖熵:

3)若r=3,

N $_{P}^{3}$ (x₁)={x₁, x₅}, N $_{P}^{3}$ (x₂)={x₂}, N $_{P}^{2}$ (x₃)={x₃}, N $_{P}^{2}$ (x₄)={x₄}, N $_{P}^{2}$ (x₅)={x₁, x₅}.

计算第三类软覆盖熵:

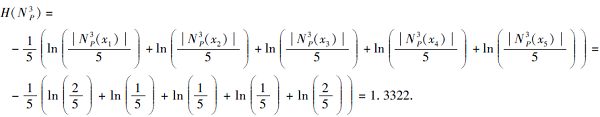
4)若r=4,

计算第四类软覆盖熵:

5)若r=5,

N $_{P}^{5}$ (x₁)={x₁, x₅}, N $_{P}^{5}$ (x₂)={x₂}, N $_{P}^{5}$ (x₃)={x₃}, N $_{P}^{5}$ (x₄)={x₄}, N $_{P}^{5}$ (x₅)={x₁, x₅}.

计算第五类软覆盖熵:

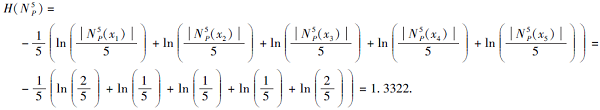
可看出例1符合性质2, 熵值越小说明其不确定性越小, 故对于软邻域N $_{P}^{r}$ , r=1, 2, 3, 4, 5, 软邻域N $_{P}^{4}$ 的不确定性最小.

性质3 令N $_{P}^{^{r_{1}}}$ (x)、N $_{P}^{^{r_{2}}}$ (x)为x∈ U上的软邻域, 其中r₁=1, 2, …, 5, r₂=1, 2, …, 5, 若N $_{P}^{^{r_{1}}}$ ⊆N $_{P}^{^{r_{2}}}$ , 则

H(N $_{P}^{^{r_{1}}}$ )≥ H(N $_{P}^{^{r_{2}}}$ ).

证明

由于N $_{P}^{^{r_{1}}}$ ⊆N $_{P}^{^{r_{2}}}$ , 所以对

∀ x_i∈ U, N $_{P}^{^{r_{1}}}$ (x_i)⊆N $_{P}^{^{r_{2}}}$ (x_i),

有

|N $_{P}^{^{r_{1}}}$ (x_i)|≤ |N $_{P}^{^{r_{2}}}$ (x_i)|,

则

因此可得

H(N $_{P}^{^{r_{1}}}$ )≥ H(N $_{P}^{^{r_{2}}}$ ).

性质3表明软覆盖熵具有单调性.

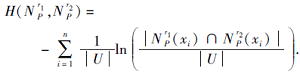
定义10 令N $_{P}^{^{r_{1}}}$ (x)、N $_{P}^{^{r_{2}}}$ (x)为x∈ U上的软邻域, r₁=1, 2, …, 5, r₂=1, 2, …, 5, N $_{P}^{^{r_{1}}}$ 和N $_{P}^{^{r_{2}}}$ 的软覆盖联合熵定义为

性质4 令N $_{P}^{^{r_{1}}}$ (x)、N $_{P}^{^{r_{2}}}$ (x)为x∈ U上的软邻域, r₁=1, 2, …, 5, r₂=1, 2, …, 5, 则

H(N $_{P}^{^{r_{1}}}$ , N $_{P}^{^{r_{2}}}$ )≥ H(N $_{P}^{^{r_{1}}}$ ), H(N $_{P}^{^{r_{1}}}$ , N $_{P}^{^{r_{2}}}$ )≥ H(N $_{P}^{^{r_{2}}}$ ).

证明对于∀ x_i∈ U, 有

N $_{P}^{^{r_{1}}}$ (x_i)∩ N $_{P}^{^{r_{2}}}$ (x_i)⊆N $_{P}^{^{r_{1}}}$ (x_i),

则

|N $_{P}^{^{r_{1}}}$ (x_i)∩ N $_{P}^{^{r_{2}}}$ (x_i)|≤ |N $_{P}^{^{r_{1}}}$ (x_i)|,

所以

因此

H(N $_{P}^{^{r_{1}}}$ , N $_{P}^{^{r_{2}}}$ )≥ H(N $_{P}^{^{r_{1}}}$ ).

同理可得

H(N $_{P}^{^{r_{1}}}$ , N $_{P}^{^{r_{2}}}$ )≥ H(N $_{P}^{^{r_{2}}}$ ).

定义11 令N $_{P}^{^{r_{1}}}$ (x)、N $_{P}^{^{r_{2}}}$ (x)为x∈ U上的软邻域, r₁=1, 2, …, 5, r₂=1, 2, …, 5, N $_{P}^{^{r_{2}}}$ 关于N $_{P}^{^{r_{1}}}$ 的软覆盖条件熵定义为

软覆盖条件熵描述基于已知条件N $_{P}^{^{r_{1}}}$ 和N $_{P}^{^{r_{2}}}$ 的不确定性信息.

性质5 令N $_{P}^{^{r_{1}}}$ (x)、N $_{P}^{^{r_{2}}}$ (x)、N $_{P}^{^{r_{3}}}$ (x)为x∈ U上的软邻域, r₁=1, 2, …, 5, r₂=1, 2, …, 5, r₃=1, 2, …, 5, 满足

1)若N $_{P}^{^{r_{1}}}$ ⊆N $_{P}^{^{r_{2}}}$ , 则H(N $_{P}^{^{r_{2}}}$ |N $_{P}^{^{r_{1}}}$ )=0.

2)若N $_{P}^{^{r_{2}}}$ ⊆N $_{P}^{^{r_{3}}}$ , 则

H(N $_{P}^{^{r_{2}}}$ |N $_{P}^{^{r_{1}}}$ )≥ H(N $_{P}^{3}$ | $N_{P}^{^{r_{1}}}$ ).

证明先证1).显然得证.

再证2).由于

N $_{P}^{^{r_{2}}}$ ⊆N $_{P}^{^{r_{3}}}$ ,

故

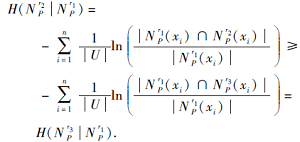
情况1)表示若N $_{P}^{^{r_{1}}}$ 包含在N $_{P}^{^{r_{2}}}$ 中, 则N $_{P}^{^{r_{2}}}$ 不会引入任何关于N $_{P}^{^{r_{1}}}$ 的不确定性信息.情况2)表明软覆盖条件熵H(N $_{P}^{^{r_{2}}}$ |N $_{P}^{^{r_{1}}}$ )是关于N $_{P}^{^{r_{2}}}$ 单调的.需要注意的是, 软覆盖条件熵H(N $_{P}^{^{r_{2}}}$ |N $_{P}^{^{r_{1}}}$ )相对于N $_{P}^{^{r_{1}}}$ 不是单调的.

性质6 令N $_{P}^{^{r}}$ (x), r=1, 2, …, 5, 为x∈ U上的软邻域, 则

1)H(N $_{P}^{5}$ |N $_{P}^{4}$ )=H(N $_{P}^{3}$ |N $_{P}^{4}$ )≥ H(N $_{P}^{1}$ |N $_{P}^{4}$ ),

2)H(N $_{P}^{5}$ |N $_{P}^{4}$ )=H(N $_{P}^{3}$ |N $_{P}^{4}$ )≥ H(N $_{P}^{2}$ |N $_{P}^{4}$ ).

证明先证1).因为N $_{P}^{^{r}}$ (x), r=1, 2, …, 5, 为x∈ U上的软邻域, 故

N $_{P}^{5}$ (x_i)=N $_{P}^{3}$ (x_i)⊆N $_{P}^{1}$ (x_i)⊆N $_{P}^{4}$ (x_i),

所以

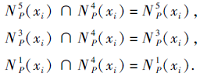
从而

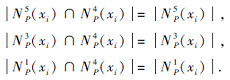
所以

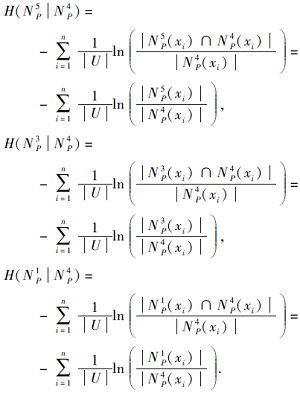
因为

|N $_{P}^{5}$ (x_i)|=|N $_{P}^{3}$ (x_i)|≤ |N $_{P}^{1}$ (x_i)|,

所以

H(N $_{P}^{5}$ |N $_{P}^{4}$ )=H(N $_{P}^{3}$ |N $_{P}^{4}$ )≥ H(N $_{P}^{1}$ |N $_{P}^{4}$ ).

再证2).类似1)的证明可得.

例2 学校排球队有6位学生报名, 记为U={x₁, x₂, …, x₆}.社团的成员从5方面对这6位学生进行考核, 记为B={b₁, b₂, …, b₅}, 这5方面分别是耐力、速度、弹跳、反应能力、团队精神.6人在5方面的特征可被记为一个软覆盖K=(G, B), 具体如表2所示.

表2 例2中学生的特征描述K=(G, B) Table 2 Students feature description K=(G, B) in example 2

则有

3 基于软覆盖熵的多属性群决策应用

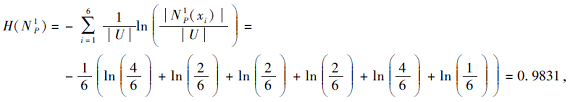
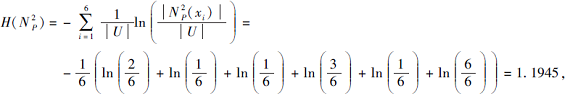
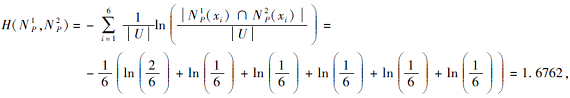
软集模型在决策、综合评价、测度理论等领域都具有较广泛的应用.多属性的群决策是处理决策问题的有效方式, 它可让不同的专家在众多的候选者中做出不同的选择.在此基础上, 根据候选者的特点, 参照所有专家的意见寻找最佳的候选者方案, 如校队选人、学校招聘新教师等.在本文中, 利用软覆盖条件熵进行多属性的群决策.

令 $N_{P}^{r}$ 为U上的软邻域, I_i为U上的一般二元关系,

I_i={I_i(x₁), I_i(x₂), …, I_i(x_n)},

类似软覆盖条件熵, H(I_i|$N_{P}^{r}$)可用于表征$N_{P}^{r}$区分不同决策样本的能力.对于相同的 $N_{P}^{r}$ , H(I_i|$N_{P}^{r}$)值越小, 说明I_i的决策越优.当所有样本被正确分类到它们各自的类别中时, H(I_i|$N_{P}^{r}$)=0.

3.1 问题叙述

首先给出对U最初始的一个描述, 即软集K=(G, B), 如表3所示, 其中

B={b₁, b₂, …, b_m}⊆E.

表3 候选人的特征描述K=(G, B) Table 3 Candidates feature description K=(G, B)

例如在一个学校学生会招新成员的活动中, U表示应聘的所有人, B表示学生会应聘条件, b₁表示性格, b₂表示应变能力等.对于每个对象x_i, i=1, 2, …, n, 属性b_j, j=1, 2, …, m的值使用a_ij表示, a_ij∈ {0, 1}.显然应聘者和应聘条件构成一个软覆盖.假设I={I₁, I₂, …, I_l}表示l位面试官, 对于每个对象x_i, i=1, 2, …, n, I_k, k=1, 2, …, l, x_i的值使用b_ik表示, b_ik∈ {0, 1}.

令K₁=(M, I)为U上的软集, M(I_k)表示面试官I_k对于所有应聘者的选择.例如面试官I_k认为应聘者x₁、x₂可以胜任这个工作, 表示为M(I_k)={x₁, x₂}.I_k(x_i)表示与x_i分类相同的集合.例如, 面试官I_k认为应聘者x₁、x₂可以胜任这个工作, 反之x₃、x₄、x₅、x₆不胜任这个工作, 可记为

I_k(x₁)={x₁, x₂}, I_k(x₃)={x₃, x₄, x₅, x₆}.

记

I_k={I_k(x₁), I_k(x₂), …, I_k(x_n)},

则面试官的选择K₁=(M, I)如表4所示.

表4 面试官的选择K₁=(M, I) Table 4 Interviewers choice K₁=(M, I)

3.2 决策算法

首先给出U上的软覆盖K=(G, B), 软集K₁=(M, I), 这里软覆盖是对U的描述, 软集是专家对于U的选择.根据软覆盖K=(G, B), 可计算每个x_i∈ U的软邻域N $_{P}^{r}$ (x_i), r=1, 2, …, 5.再利用软覆盖熵计算在软覆盖K=(G, B)下, K₁=(M, I)的软覆盖条件熵:

熵值越小表示专家的选择越优.

算法1 基于第一类软邻域多属性群决策算法

step 1 输入集合U, 软覆盖K=(G, B), 软覆盖近似空间(U, C_K).

step 2 输入软集K₁=(M, I), 表示专家组的评估结果.

step 3 由软覆盖K=(G, B)得出软邻域N $_{P}^{1}$ .

step 4 计算基于软覆盖近似空间(U, C_K)的软覆盖条件熵H(I_i|N $_{P}^{1}$ ).

step 5 找出最小值H(I_j|N $_{P}^{1}$ ).

step 6 决策目标为I_j.

例3 一所学校要招募4名教师, 由3位面试官进行面试, 记为I={I₁, I₂, I₃}.有7位应聘者参加面试, 记为U={x₁, x₂, …, x₇}.B表示对7位应聘者的特征描述, 记为B={b₁, b₂, …, b₅}, b₁, b₂, …, b₅分别表示耐心、热情、学历、经验、应变能力.K=(G, B)是对于7位应聘者的特征描述, 如表5所示.表6为3位面试官I₁、I₂、I₃的选择, 则

M(I₁)={x₁, x₂, x₄, x₆}, M(I₂)={x₁, x₂, x₃, x₇},

M(I₃₎={x₂_,x₅_,x₆_,x₇}.

表5 例3中应聘者的特征描述K=(G, B) Table 5 Candidates feature description K=(G, B) in example 3

表6 例3中面试官的选择K₁=(M, I) Table 6 Interviewers choice K₁=(M, I) in example 3

由此可得

N $_{P}^{1}$ (x₁)={x₁, x₂, x₅, x₆}, N $_{P}^{1}$ (x₂)={x₂, x₅, x₆}, N $_{P}^{1}$ (x₃)={x₃, x₆}, N $_{P}^{1}$ (x₄)={x₄, x₆},

N $_{P}^{1}$ (x₅)={x₂, x₅, x₆}, N $_{P}^{1}$ (x₆)={x₆}, N $_{P}^{1}$ (x₇)={x₆, x₇}.

I₁(x₁)=I₁(x₂)=I₁(x₄)=I₁(x₆)={x₁, x₂, x₄, x₆}, I₁(x₃)=I₁(x₅)=I₁(x₇)={x₃, x₅, x₇}.

I₂(x₁)=I₂(x₂)=I₂(x₃)=I₂(x₇)={x₁, x₂, x₃, x₇}, I₂(x₄)=I₂(x₅)=I₂(x₆)={x₄, x₅, x₆}.

I₃(x₂)=I₃(x₅)=I₃(x₆)=I₃(x₇)={x₂, x₅, x₆, x₇}, I₃(x₁)=I₃(x₃)=I₃(x₄)={x₁, x₃, x₄}.

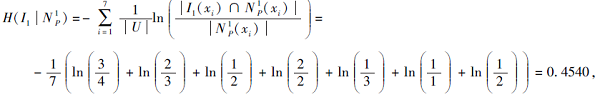
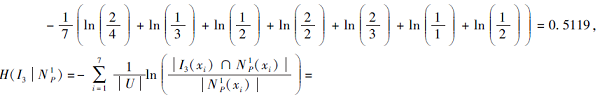
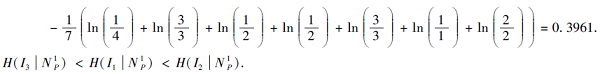
因此选择I₃, 即x₂、x₅、x₆、x₇更能胜任这个工作.同时可认为面试官I₃更公正合理, 更有能力担任面试这个工作.

算法2 基于第二类软邻域多属性群决策算法

step 1 输入集合U, 软覆盖K=(G, B), 软覆盖近似空间(U, C_K).

step 2 输入软集K₁=(M, I), 表示专家组的评估结果.

step 3 由软覆盖K=(G, B)得出软邻域N $_{P}^{2}$ .

step 4 计算基于软覆盖近似空间(U, C_K)的软覆盖条件熵H(I_i|N $_{P}^{2}$ ).

step 5 找出最小值H(I_j|N $_{P}^{2}$ ).

step 6 决策目标为I_j.

例4 由例3可得

N $_{P}^{2}$ (x₁)={x₁}, N $_{P}^{2}$ (x₂)={x₁, x₂, x₅}, N $_{P}^{2}$ (x₃)={x₃}, N $_{P}^{2}$ (x₄)={x₄}, N $_{P}^{2}$ (x₅)={x₁, x₂, x₅},

N $_{P}^{2}$ (x₆)={x₁, x₂, x₃, x₄, x₅, x₆, x₇}, N $_{P}^{2}$ (x₇)={x₇}.

I₁(x₁)=I₁(x₂)=I₁(x₄)=I₁(x₆)={x₁, x₂, x₄, x₆}, I₁(x₃)=I₁(x₅)=I₁(x₇)={x₃, x₅, x₇}.

I₂(x₁)=I₂(x₂)=I₂(x₃)=I₂(x₇)={x₁, x₂, x₃, x₇}, I₂(x₄)=I₂(x₅)=I₂(x₆)={x₄, x₅, x₆}.

I₃(x₂)=I₃(x₅)=I₃(x₆)=I₃(x₇)={x₂, x₅, x₆, x₇}, I₃(x₁)=I₃(x₃)=I₃(x₄)={x₁, x₃, x₄}.

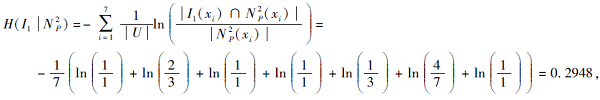
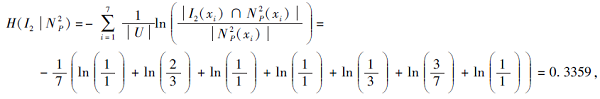
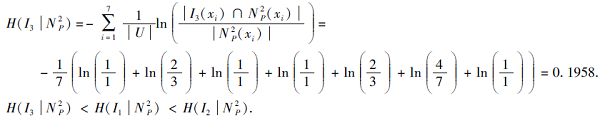
因此选择I₃, 即x₂、x₅、x₆、x₇更能胜任这个工作.同时可认为面试官I₃更公正合理, 更有能力担任面试这个工作.

由结论可发现, 上述两类软邻域的多属性群决策方式具有高度一致性, 均可得出面试官I₃的决策优于面试官I₁、I₂的决策, 这说明上述决策合理可行.

对例3、例4使用不同类型的软覆盖条件熵的决策, 结果如表7所示.由表可看出, 无论r为多少, 得到的最优专家均为I₃.同时还发现, 使用r=1, 2软覆盖条件熵的区别性更明显, 由此可见本文算法具有较高的一致性, 合理可行.

表7 例3和例4中使用不同软邻域的排序结果 Table 7 Sorting results using different soft neighborhoods in example 3 and example 4

r	排序结果
1	H(I₃\|N $_{P}^{1}$ )< H(I₁\|N $_{P}^{1}$ )< H(I₂\|N $_{P}^{1}$ )
2	H(I₃\|N $_{P}^{2}$ )< H(I₁\|N $_{P}^{2}$ )< H(I₂\|N $_{P}^{2}$ )
3	H(I₃\|N $_{P}^{3}$ )< H(I₁\|N $_{P}^{3}$ )=H(I₂\|N $_{P}^{3}$ )
4	H(I₃\|N $_{P}^{4}$ )=H(I₁\|N $_{P}^{4}$ )< H(I₂\|N $_{P}^{4}$ )
5	H(I₃\|N $_{P}^{5}$ )< H(I₁\|N $_{P}^{5}$ )=H(I₂\|N $_{P}^{5}$ )

表7 例3和例4中使用不同软邻域的排序结果 Table 7 Sorting results using different soft neighborhoods in example 3 and example 4

下面进一步用实例对算法进行说明.

例5 一家公司要选择4名员工进行提拔, 现有8位候选人(以x₁, x₂, …, x₈表示).B表示对8位候选人的特征描述, 记为

B={b₁, b₂, …, b₅},

b₁, b₂, …, b₅分别表示业绩、应变能力、热情、领导能力、工作经验.K=(G, B)是对于8位候选人的特征描述, 如表8所示.

表8 例5中应聘者的特征描述K=(G, B) Table 8 Candidates feature description K=(G, B) in example 5

3位主管对8位候选人进行选择, 如表9所示.3位主管I₁, I₂, I₃的选择分别为

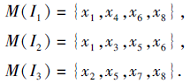
表9 例5中主管的选择K₁=(M, I) Table 9 Superintend choice K₁=(M, I) in example 5

使用不同软覆盖条件熵对例5进行决策, 决策结果如表10所示.由表可看出, 主管I₁的选择更优, 即x₁、x₄、x₆、x₈更适合得到提拔的机会.同时可认为主管I₁更公正合理, 有更好的判断力对员工进行提拔.

表10 例5中使用不同软邻域的排序结果 Table 10 Sorting results using different soft neighborhoods in example 5

r	排序结果
1	H(I₁\|N $_{P}^{1}$ )< H(I₃\|N $_{P}^{1}$ )< H(I₂\|N $_{P}^{1}$ )
2	H(I₁\|N $_{P}^{2}$ )< H(I₃\|N $_{P}^{2}$ )< H(I₂\|N $_{P}^{2}$ )
3	H(I₁\|N $_{P}^{3}$ )< H(I₃\|N $_{P}^{3}$ )=H(I₂\|N $_{P}^{3}$ )
4	H(I₁\|N $_{P}^{4}$ )< H(I₃\|N $_{P}^{4}$ )< H(I₂\|N $_{P}^{4}$ )
5	H(I₁\|N $_{P}^{5}$ )< H(I₃\|N $_{P}^{5}$ )=H(I₂\|N $_{P}^{5}$ )

表10 例5中使用不同软邻域的排序结果 Table 10 Sorting results using different soft neighborhoods in example 5

对5种类型的软覆盖条件熵的决策结果可看出, r=1, 2软覆盖条件熵区别性更明显.由于r=3, 5软邻域实际上是一种等价关系, 要求过于严格, 故得出的结果会较相近.而r=4软邻域的要求过于宽松, 故得出的结果也可能会较相近.因此使用r=1, 2软覆盖条件熵进行多属性群决策效果更优.

4 结束语

本文提出软覆盖信息熵、软覆盖联合熵、软覆盖条件熵的概念, 并研究它们的重要性质及关系.进一步结合软覆盖邻域算子与信息熵, 并推广到多属性群决策的环境下, 在此基础上, 认为r=1, 2软覆盖条件熵值得关注.提出2种基于软覆盖条件熵的算法, 并对2个示例进行充分研究, 经过对比发现, r=1, 2的决策结果区别性更明显, 所有类型的软覆盖条件熵模型的最优结果具有一致性, 由此说明本文决策方法合理可行.今后考虑将信息熵引入模糊信息系统中, 进一步探究在模糊信息系统下的群决策算法.

参考文献

文献选项

[1]	PAWLAK Z. Rough Sets. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356. [本文引用:1]
[2]	PAWLAK Z. Rough Sets and Intelligent Data Analysis. Information Sciences, 2002, 147(1/2/3/4): 1-12. [本文引用:1]
[3]	ALI M I. A Note on Soft Sets, Rough Soft Sets and Fuzzy Soft Sets. Applied Soft Computing, 2011, 11(4): 3329-3332. [本文引用:1]
[4]	纪霞, 赵鹏, 姚晟. 加权多粒度直觉模糊信息系统的粗糙集模型及其决策. 模式识别与人工智能, 2017, 30(11): 971-982. (JI X, ZHAO P, YAO S. Rough Set Model and Decision Research in Intuitionistic Fuzzy Information System Based on Weighted Multi-granulation. Pattern Recognition and Artificial Intelligence, 2017, 30(11): 971-982. ) [本文引用:1]
[5]	FENG F, LIU X Y, LEOREANU-FOTEA V, et al. Soft Sets and Soft Rough Sets. Information Sciences, 2011, 181(6): 1125-1137. [本文引用:2]
[6]	薛占熬, 赵丽平, 张敏, 等. 多粒度支持直觉模糊粗糙集的多属性决策方法. 模式识别与人工智能, 2019, 32(8): 677-690. (XUE Z A, ZHAO L P, ZHANG M, et al. Multi-attribute Decision-Making Method Based on Multi-granulation Support Intuitionistic Fuzzy Rough Sets. Pattern Recognition and Artificial Intelligence, 2019, 32(8): 677-690. ) [本文引用:1]
[7]	ZHANG Q H, XIE Q, WANG G Y. A Survey on Rough Set Theory and Its Applications. CAAI Transactions on Intelligence Technology, 2016, 1(4): 323-333. [本文引用:1]
[8]	LUO S, MIAO D Q, ZHANG Z F, et al. A Neighborhood Rough Set Model with Nominal Metric Embedding. Information Sciences, 2020, 520: 373-388. [本文引用:1]
[9]	ZHANG L, ZHAN J M, XU Z S, et al. Covering-Based General Multigranulation Intuitionistic Fuzzy Rough Sets and Corresponding Applications to Multi-attribute Group Decision-Making. Information Sciences, 2019, 494: 114-140. [本文引用:1]
[10]	WANG Z H, ZHANG X P, DENG J P. The Uncertainty Measures for Covering Rough Set Models. Soft Computing, 2020, 24: 11909-11929. [本文引用:1]
[11]	ZHANG L, ZHAN J M, XU Z S. Covering-Based Generalized IF Rough Sets with Applications to Multi-attribute Decision-Making. Information Sciences, 2019, 478: 275-302. [本文引用:1]
[12]	陈应生, 李进金, 林荣德, 等. 多尺度覆盖决策信息系统的布尔矩阵方法. 模式识别与人工智能, 2020, 33(9): 776-785. (CHEN Y S, LI J J, LIN R D, et al. Boolean Matrix Approach for Multi-scale Covering Decision Information System. Pattern Recognition and Artificial Intelligence, 2020, 33(9): 776-785. ) [本文引用:1]
[13]	MOLODTSOV D. Soft Set Theory-First Results. Computers and Mathematics with Applications, 1999, 37(4/5): 19-31. [本文引用:1]
[14]	LI Z W, XIE N X, WEN G Q. Soft Coverings and Their Parameter Reductions. Applied Soft Computing, 2015, 31: 48-60. [本文引用:1]
[15]	ZHAN J M, WANG Q M. Certain Types of Soft Coverings Based Rough Sets with Applications. International Journal of Machine Learning and Cybernetics, 2019, 10(5): 1065-1076. [本文引用:4]
[16]	ZHANG L, ZHAN J M. Fuzzy Soft β-Covering Based Fuzzy Rough Sets and Corresponding Decision-Making Applications. Internatio-nal Journal of Machine Learning and Cybernetics, 2019, 10(6): 1487-1502. [本文引用:1]
[17]	DENG Z X, ZHENG Z L, DENG D Y, et al. Feature Selection for Multi-label Learning Based on F-Neighborhood Rough Sets. IEEE Access, 2020, 8: 39678-39688. [本文引用:1]
[18]	WANG C Z, HUANG Y, SHAO M W, et al. Feature Selection Based on Neighborhood Self-Information. IEEE Transactions on Cybernetics, 2020, 50(9): 4031-4042. [本文引用:1]
[19]	WANG C Z, HE Q, SHAO M W, et al. A Unified Information Measure for General Binary Relations. Knowledge-Based Systems, 2017, 135: 18-28. [本文引用:1]
[20]	LEI D F, LIANG P, HU J H, et al. New Online Streaming Feature Selection Based on Neighborhood Rough Set for Medical Data. Symmetry, 2020, 12(10). DOI: DOI:10.3390/sym12101635. [本文引用:1]
[21]	WANG C Z, HE Q, SHAO M W, et al. Feature Selection Based on Maximal Neighborhood Discernibility. International Journal of Machine Learning and Cybernetics, 2018, 9: 1929-1940. [本文引用:1]
[22]	REHMAN N, SHAH N, ALI M I, et al. Uncertainty Measurement for Neighborhood Based Soft Covering Rough Graphs with Applications. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 2019, 113: 2515-2535. [本文引用:1]
[23]	LIANG J Y, CHIN K S, DANG C Y, et al. A New Method for Measuring Uncertainty and Fuzziness in Rough Set Theory. International Journal of General Systems, 2002, 31(4): 331-342. [本文引用:1]
[24]	LIANG J Y, WANG F, DANG C Y, et al. A Group Incremental Approach to Feature Selection Applying Rough Set Technique. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(2): 294-308. [本文引用:1]
[25]	陈东晓, 李进金, 林荣德, 等. 基于信息熵的形式背景属性约简. 模式识别与人工智能, 2020, 33(9): 786-798. (CHEN D X, LI J J, LIN R D, et al. Attribute Reductions of Formal Context Based on Information Entropy. Pattern Recognition and Artificial Intelligence, 2020, 33(9): 786-798. ) [本文引用:1]
[26]	LEI B, FAN J L. Image Thresholding Segmentation Method Based on Minimum Square Rough Entropy. Applied Soft Computing, 2019, 84. DOI: DOI:10.1016/j.asoc.2019.105687. [本文引用:1]
[27]	WANG C Z, HU Q H, WANG X Z, et al. Feature Selection Based on Neighborhood Discrimination Index. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(7): 2986-2999. [本文引用:4]
[28]	SUN L, WANG L Y, DING W P, et al. Feature Selection Using Fuzzy Neighborhood Entropy-Based Uncertainty Measures for Fuzzy Neighborhood Multigranulation Rough Sets. IEEE Transactions on Fuzzy Systems, 2021, 29(1): 19-33. [本文引用:1]
[29]	ZHANG X, MEI C L, CHEN D G, et al. Active Incremental Feature Selection Using a Fuzzy-Rough-Set-Based Information Entropy. IEEE Transactions on Fuzzy Systems, 2020, 28(5): 901-915. [本文引用:1]
[30]	YÜKSEL S, TOZLU N, DIZMAN T H. An Application of Multicriteria Group Decision Making by Soft Covering Based Rough Sets. Filomat, 2015, 29(1): 209-219. [本文引用:2]