张志鹏,博士,讲师,主要研究方向为数据挖掘、推荐系统.E-mail:zhipengzhang@lnnu.edu.cn.
作者简介:

任永功,博士,教授,主要研究方向为人工智能、数据挖掘.E-mail:jsj_paper@163.com.

王瑞霞,硕士研究生,主要研究方向为人工智能、数据挖掘.E-mail:1420942208@qq.com.
针对数据稀疏导致推荐系统精确度较低的问题,结合社交网络中丰富的社会化信息及能量扩散在数据稀疏问题上的优良表现,文中提出基于社交网络能量扩散的协同过滤推荐算法.首先利用用户-物品评分矩阵和信任关系具有的传递性计算用户之间信任强度值.再利用社交网络结合用户-物品二分网络,得到物品资源值.最后利用协同过滤方法进行预测评分.在真实数据集上的实验表明,文中算法缓解数据稀疏性,可解决推荐精确度较低的问题.
ZHANG Zhipeng,Ph.D., lecturer. His research interests include data mining and recommender system.
About Author:
REN Yonggong, Ph.D., professor. His research interests include artificial intelligence and data mining.
WANG Ruixia, master student. Her research interests include artificial intelligence and data mining.
To improve the low accuracy caused by sparse data in the recommender system, a collaborative filtering recommendation algorithm based on energy diffusion in social networks is proposed. The abundant social information in social network and the excellent performance of energy diffusion in data sparsity are combined. Firstly, the transitivity of user-item scoring matrix and trust relationship is exploited to calculate the trust intensity value between users. Then, the resource value of items is obtained by combining the social network with the user-item binary network. Finally, the collaborative filtering method is utilized to predict the score. Experiments on real datasets show that the proposed method alleviates data sparsity and solves the problem of low recommendation accuracy.
本文责任编委 梁吉业
Recommended by Associate Editor LIANG Jiye
随着人工智能与大数据的飞速发展, 推荐系统(Recommender System, RS)[1]受到学者们的广泛关注.RS分析用户的行为, 找到用户的个性化需求, 从而将商品推荐给相应用户, 帮助用户找到自己想要但难以发现的商品.现阶段RS广泛用于电子商务和社交网络.
目前在RS中常见的推荐方法为协同过滤(Collaborative Filtering, CF)[2]、基于内容过滤推荐算法和混合过滤推荐算法.CF是应用最普遍的算法之一, 分为基于记忆的协同过滤和基于模型的协同过滤.CF根据目标用户的邻近用户的反馈、评价等信息预测目标用户对未评分物品的评分, 给目标用户推荐Top-n物品.随着社交网络的快速发展, 基于社交网络的推荐已变成一种重要且有成效的方式.
但是, 在CF中存在精确度较低的问题, 其原因在于缺少用户对物品的评分历史数据, 即数据稀疏性, 在某一极端情况下可看作是冷启动的问题.如果在数据量较大且又稀疏的情况下, 相似性计算的耗费会很大, 也难以给用户精准推荐, 影响推荐质量[3].
基于内容的过滤算法是抽取用户和物品的特征信息, 不需要用户对物品评级, 可有效缓解数据稀疏性的问题.Son等[4]采用基于内容的协同过滤方法, 构建多属性的网络, 反映属性之间的关联, 可缓解推荐系统的稀疏性问题, 但挖掘属性有限, 难以构造属性更丰富的网络.
混合过滤算法中常见方法是混合基于内容过滤算法和CF, 在一定程度上可提高推荐质量[5].Tian等[6]结合高校图书和读者的特点, 进行读者的分类和构建评分向量的空间模型, 利用聚类方法结合两者, 在一定程度上缓解数据稀疏问题, 但未利用读者的社会信息, 在分类问题上不具有全面性.
基于社交网络推荐算法和基于图的推荐算法是目前较通用的推荐方式, 通过引入社交网络信息、朋友信息, 有效提高推荐质量, 实现个性化推荐[7].Xu[8]将矩阵分解技术(Matrix Factorization Techni-que)运用到社交网络中, 并考虑各种复杂的因素及社会关系, 提升推荐性能, 但未深入挖掘用户在社交网络中的额外社会化信息, 导致推荐结果不一定准确.Lai等[9]在社交网络的基础上提出基于用户信任关系和物品的流行度推荐算法.根据用户评论推断用户之间的潜在交互, 在一定程度上缓解信息过载的问题, 但在分析用户之间的信任关系时使用0或1描述信任或不信任, 没有具体的数值, 未显著提高推荐精确度.Kart等[10]提出基于监督机器学习的加权二部图链接预测模型, 将用户的项目评论映射为二部图结构, 并优化结构, 提高预测质量, 但未能有效缓解数据稀疏问题.Zhao等[11]提出改进二部图的方法, 提取用户偏好的类型权重特征, 结合用户的相似度构建推荐模型.该方法的性能在一定程度上较优, 但是没有有效缓解数据稀疏的问题, 且存在推荐精确度较低的问题.Jiang等[12]融合信任数据与用户相似度并加入改进的推荐模型, 未缓解数据稀疏问题, 未显著提高推荐精确度.Zhang等[13]利用评分信息构建隐式社交网络, 通过图表示学习方法预测评分, 但没有利用显式社会化信息, 未能有效提高推荐精确度.Guo等[14]提出社会化推荐算法, 将评分信息和社交网络信息分解为低维特征矩阵进行预测评分, 但降维时会导致信息缺失, 未显著提高推荐精度.
针对上述方法存在的问题, 本文提出基于社交网络能量扩散的协同过滤推荐算法(Social Network Energy Diffusion Based CF, SNED).首先运用预测误差方法建立用户信任值计算模型, 计算两位用户之间的信任强度值, 并根据信任传递性挖掘用户之间的隐式信息, 丰富用户之间的社交信息.然后通过参数结合社交网络与用户-物品二分网络, 有效提高推荐系统中推荐物品的精确度.最后利用资源扩散理论, 通过社交网络能量扩散计算物品与物品之间的资源值, 即相似度值.进而通过CF对用户未评分的物品进行预测评分, 向用户提供高精准和高质量的推荐.实验表明, 本文算法可在一定程度上有效缓解数据稀疏性问题, 提高物品推荐的精确度.
根据人类社会学理论, 用户在社交中经常会对和本身具有相同“ 口味” (对同一物品评级)的人产生亲密性, 可以通过这样的亲密性计算信任强度并为用户推荐物品.本文根据用户之间的亲密性建立用户之间直接信任强度计算的模型, 首先将用户对物品的评级值进行标准化, 再计算用户对物品的预测误差评分, 最后根据信任强度计算模型计算两位用户之间的信任强度值.
首先进行数据预处理.为了让信任值结果更精准, 将用户之间的评级值采用大小标准化方法[15], 将评级值标准化到[0, 1]内.根据标准化方法, 将数据集中一个原始的评级值R转化为新的评级值
r=
其中, max、min分别表示用户评分集中最大评级值、最小评级值.根据新的评级值计算直接信任强度.
定义1 为了衡量用户之间直接信任强度, 引入用户Ux对物品Ii的预测误差评分值Prediction error[16].令U为推荐系统中所有用户集合, 用户Ux∈ U, Uy∈ U, I为推荐系统中所有物品集合, 物品Ii∈ I, 则
P
其中,
定义2 用户Ux对用户Uy的直接信任强度值:
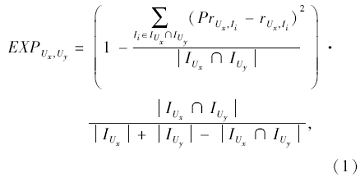
其中,
由于信任关系具有传递性, 当用户之间没有直接信任值时, 可利用信任传递关系挖掘用户之间的间接信任关系, 建立新的关系.用户间接信任关系如图1所示.
定义3 假设用户Ux∈ U(源用户), 用户Ux的信任用户Uy∈ U(中间用户), 同时用户Uy的信任用户Uz∈ U(目标用户), 通过信任传播方法可推断用户Ux在某种程度上可以信任用户Uz, 它们之间的间接信任强度值如下:
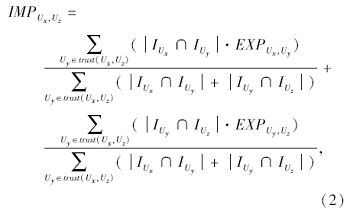
其中, Uy∈ trust(Ux, Uz)表示共同信任用户Ux、Uz的用户集合.
结合式(1)和式(2), 计算用户与用户之间的信任值, 并构成信任矩阵:
Intimacy=EXP+IMP, (3)
其中, EXP表示直接信任矩阵, IMP表示间接信任矩阵.本文利用余弦相似度计算用户之间的相似度:
similarl
其中,
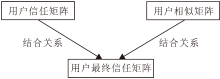
在用户之间的相似度值和信任强度值不为0的情况下, 通过加权思想结合信任强度模型与余弦相似度模型, 得到用户Ux、Uy的最终信任强度模型, 如图2所示.
图2中结合用户的信任矩阵和用户之间的相似矩阵, 得到用户的最终信任矩阵T,
最终信任强度取值范围在[0, 1]内.
经典的基于物品协同过滤算法通过用户间的共同评分计算相似度, 本文算法结合社交网络和用户-物品二分网络[17], 计算物品间的相似度.
构造与用户Ux的度相关的对角矩阵:
Λ U=diag(
其中
与用户Ux信任关系的度相关的对角矩阵如下:
Λ T=diag(
其中
与物品的度相关的对角矩阵如下:
Λ I=diag(
其中
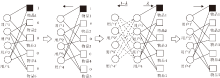
为了提高本文算法的推荐准确度, 混合网络模型扩散步骤如图3所示.图中用户与物品之间的连线表示用户选择其物品, 用户与用户之间的连线表示用户信任该用户, 涂黑的物品表示目标物品.
混合网络扩散步骤具体如下.
1)首先将物品1(图3中涂黑为目标物品)的初始资源值设置为1, 其余物品的初始资源值为0, 得到物品的初始向量:
f0=(f1, …,
2)物品的资源被平均分配给用户, 用户得到资源向量:
h=AUIΛ I f0.
其中, AUI=
3)用户将拥有的λ 资源通过用户- 物品二部图平均分配给选择过的物品, 物品得到资源向量:
f1=λ
4)用户将拥有的1-λ 部分资源通过信任网络给自身的信任用户, 用户得到资源向量:
f2=(1-λ )TΛ Th=(1-λ )TΛ TAUIΛ I f0.
5)信任的用户将获得的资源通过用户- 物品二部图平均分配选择的物品, 物品得到资源向量:
f3=
物品得到最终的资源向量:
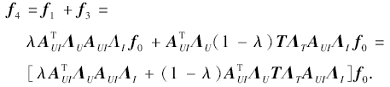
算法的转移矩阵
P=λ
其中
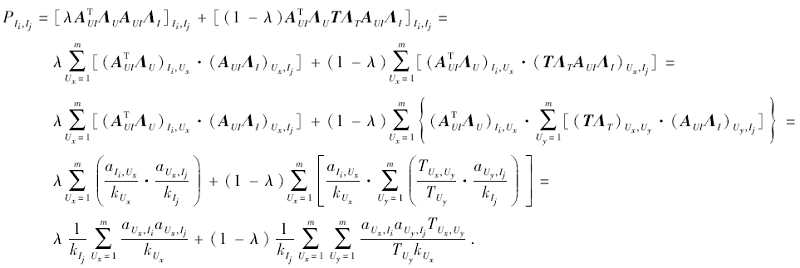
λ ∈ [0, 1],
similarly'
通过参数进行调节:当参数为1时, 所有资源只在用户-物品的二部图中进行扩散; 当参数为0时, 所有资源只在用户-用户社交网络中扩散.
计算用户Ux对未评分物品Ii的预测评分:
rating'
其中, Ii∈
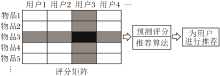
评分预测模型如图4所示.
算法 基于社交网络能量扩散的协同过滤推荐
算法
输入 用户-物品评分矩阵R,
评分标准化矩阵NR,
用户-物品二部图矩阵AUI, λ
输出 为目标用户Ux推荐n个物品
根据用户之间的亲密性计算直接信任强度值;
for x= 1 to card(m) do
for y=1 to card(m) do
根据式(1)计算用户之间直接信任强度值
EX
end for
end for
利用信任传递性计算用户之间的间接信任强度值;
for x=1 to card(m) do
for z=1 to card(m) do
根据式(2)计算用户之间的间接信任强度值
IM
end for
end for
根据式(3)计算信任矩阵Intimacy;
for x=1 to card(m) do
for y=1 to card(m) do
根据式(4)计算用户之间的相似度值
end for
end for
根据式(5)得到用户之间的最终信任矩阵T;
构造关于用户的度对角矩阵Λ U、物品的度对角矩阵Λ I、用户间信任关系的度对角矩阵Λ T;
for i=1 to card(n) do
for j=1 to card(n) do
根据式(6)计算物品间相似矩阵
end for
end for
for ∀ Ii∈
得到Ii的相似物品集合N(Ii)
for ∀ Ij∈ N(Ii) do
根据式(7)计算预测评分
end for
end for
向用户Ux推荐前n个具有最高评分的物品
假设推荐系统中有n个物品, p为用户-物品二分网络中总边数, q为社交网络中的总边数, 协同过滤中相似度算法的时间复杂度为O(n2).本文算法的时间复杂度主要取决于用户-物品二分网络及社交网络.用户-物品二分网络的时间复杂度为O(pn), 社交网络中的时间复杂度为O(qn), 计算复杂网络相似度的时间复杂度为O(pn)+O(qn).在数据稀疏的情况下p、q远小于系统内物品总数量n, 在现实中p、q也不大, 因此本文算法的时间复杂度为O(n)+O(n), 在CF上未产生过高消耗.
本节给出具体实例说明算法步骤.首先给出用户-物品评分矩阵和用户-物品标准化评分矩阵, 如表1和表2所示.
| 表1 用户-物品评分矩阵 Table 1 User-item scoring matrix |
| 表2 用户-物品标准化评分矩阵 Table 2 User-item standardized scoring matrix |
根据式(6)和式(7), 设参数λ =1/2, 计算物品之间的相似度和用户对物品的预测评分, 如表3和表4所示.
| 表3 物品之间的相似度 Table 3 Similarity between items |
| 表4 用户对物品的预测评分 Table 4 User rating scale for item prediction |
例如对用户1进行物品推荐, 由表4可知, 用户1对物品5的预测评分为1.3, 对物品2和物品4的评分值为0.9, 因此将物品5推荐给用户1.
本文选取推荐系统中常见的基于社交网络的FilmTrust、CiaoDVD数据集评估算法性能.具体数据集信息如表5所示.
| 表5 实验数据集 Table 5 Experimental datasets |
数据集上随机选取80%的数据作为训练集, 20%的数据作为测试集, 采用五折交叉验证方法.根据文献[18], 邻近物品集取值为10、20、30、40、50.推荐物品长度n=2, 4, 6, 8, 10, 12.当评分阈值θ ≥ 2时, 该物品为用户喜欢的物品.
采用精确率(Precision)和召回率(Recall)衡量算法分类精度:

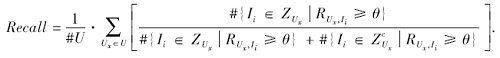
其中:
F1为precision与recall的结合:
F1=
采用平均精度(P)衡量整个推荐系统的平均精确度[19]:
其中,
采用平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE)衡量算法的预测精度:
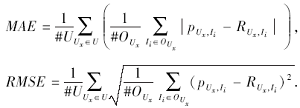
其中:
· 表示缺乏评分值,
为了验证本文算法性能, 选取如下对比算法, 其中前两种算法为本文基础算法.
1)基于物品的协同过滤算法(Item-Based Colla-borative Filtering, IBCF)[20].
2)基于二分网络能量资源扩散推荐算法(Proba-
bilistic Spreading, Probs)[17].
3)基于信任协同过滤推荐算法(Trust-Based Collaborative Filtering, BIPS)[12].运用评级偏差并结合用户之间的相似度, 提高推荐系统的精确度.
4)社交网络中利用图表示方法学习网络嵌入推荐算法(Collaborative User Network Embedding, CUNE)[13].利用评分信息构建隐式社交网络, 通过图表示学习方法进行网络嵌入, 得到嵌入矩阵, 进行预测评分.
5)基于信任的奇异值分解算法(Trust Based Sin-gular Value Decomposition, TrustSVD)[14].将评分信息和社交网络结合, 反馈到矩阵分解模型中, 预测目标用户对未评分物品的评分, 为用户推荐.
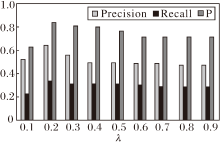
在本文算法(SNED)中引入调节参数λ , 当推荐长度为2, 邻近物品为10, λ 不同时指标值的变化趋势如图5所示.由图可看出, 随着λ 的增大, 指标值都随之增大, 当λ =0.2时指标值达到峰值, 之后小幅下降, 最后趋向平稳.
在2个数据集上进行对比实验, 各算法的邻近物品集为10~50, 推荐物品数为2~12, λ =0.2.各算法在2个数据集上的Precision值对比如表6所示, 表中黑体数字表示最优结果.由表可见, 在大部分情况下, 本文算法的Precision值最高.
| 表6 各算法在2个数据集上的Precision值对比 Table 6 Comparison of precision values of different algorithms on 2 datasets |
各算法在2个数据集上的Recall、F1值、P值分别如图6~图8所示.由图可知, 本文算法的指标值最高, 随着邻近物品数的增加, 逐渐趋于稳定.
各算法在2个数据集上的MAE值和RMSE值对比如图9和图10所示.由图可知, 本文算法的预测精度值最低, 说明本文算法的预测精度最优, 随着邻近物品数的增加, 逐渐趋于稳定.
综合上述实验结果分析如下.对于新物品(新用户), 如果没有用户对该物品评级或评级分布稀疏, 很难找到与目标物品相邻的物品集, 导致推荐系统的精确度较低, 同时影响推荐质量和推荐系统的整体性能.本文算法利用复杂网络计算相似度, 在丰富用户之间社交化信息的同时有效解决上述问题.在社交网络中通过挖掘用户之间更深层的关系及通过混合网络有效计算物品之间的相似值.实验表明, 本文算法能有效提取目标物品的邻近物品集, 提高推荐系统的精确度和推荐质量, 解决目前推荐系统推荐精确度较低的问题.
在大数据与人工智能飞速发展的背景下, 本文提出基于社交网络能量扩散的协同过滤推荐算法, 结合信任朋友信息, 更好地挖掘用户之间的潜在社交信息, 同时结合协同过滤, 实现用户对未评分的物品进行预测评分, 向用户提供更精准的推荐.在Film-Trust、CiaoDVD数据集上的实验表明, 本文算法可大幅提高推荐系统的精确度, 从而提高推荐系统的推荐质量, 并且利用社交网络丰富用户之间的社交化信息、信任信息, 给用户更精准的推荐.今后将继续深入探索复杂网络对计算相似度及推荐结果的影响.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|