引用本文
刘航, 张晓明, 汪长剑. 基于柯西分布和父种轮换机制的种子优化算法. 模式识别与人工智能, 2021,34(7): 581-591
LIU Hang, ZHANG Xiaoming, WANG Changjian. Bean Optimization Algorithm Based on Cauchy Distribution and Parent Rotation Mechanism. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(7): 581-591.  
Doi: 10.16451/j.cnki.issn1003-6059.202107001
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于柯西分布和父种轮换机制的种子优化算法
刘航1, 张晓明1, 汪长剑1
1.安徽大学 物质科学与信息技术研究院 合肥 230039
通讯作者:

张晓明,博士,副教授,主要研究方向为群体智能、智能决策.E-mail:xmzhang@ustc.edu.

作者简介:

刘航,硕士研究生,主要研究方向为群体智能.E-mail:q20301205@stu.ahu.edu.cn.

汪长剑,硕士研究生,主要研究方向为群体智能算法及其应用.E-mail:q20301204@stu.ahu.edu.cn.

收稿日期: 2021-05-13 修回日期: 2021-07-08 接受日期: 2021-07-08
资助项目: 国家重点研发计划项目(No.2017YFD0301303)、安徽省重点研发计划项目(No.201904e01020015)、青海省基础研究计划项目(No.2020-0302-ZJC-0022)、青海省重点研发与转化计划项目(No.2020-0206-0007)资助
摘要

针对目前种子优化算法存在的空间探索能力不足、后代个体分布多样性较弱的问题,文中提出基于柯西分布和父种轮换机制的种子优化算法.首先,构建基于柯西分布的种群分布模型,用于前期探索阶段,提升算法的全局搜索能力.然后,建立基于赌轮法的父种轮换机制,提高后代种群的多样性.最后,构建个体距离阈值、分布方差和后代比例的自适应调整机制,提高算法对复杂优化问题的动态寻优能力.实验表明,文中算法的平均适应度值和弗里德曼检测指标排名均较优.

关键词: 群体智能; 种子优化算法; 柯西分布; 父种轮换; 粒子群优化
中图分类号:TP 18
Bean Optimization Algorithm Based on Cauchy Distribution and Parent Rotation Mechanism
LIU Hang1, ZHANG Xiaoming1, WANG Changjian1
1. Institutes of Physical Science and Information Technology, Anhui University, Hefei 230039
Corresponding author:
ZHANG Xiaoming, Ph.D., associate professor. His research interests include swarm intelligence and intelligent decision making.

About Author:
LIU Hang, master student. His research interests include swarm intelligence.
WANG Changjian, master student. His research interests include swarm intelligence algorithms and their applications.

Fund:National Key Research and Development Program of China(No.2017yfd0301303), Anhui Key Research and Development Program(No.201904e010015), Qinghai Basic Research Program(No.2020-0302-zjc-0022), Qinghai Key Research and Development Program(No.2020-0206-0007)
Abstract

To improve the weak spatial exploration ability and the poor diversity of individual distribution of offspring in current bean optimization algorithm, a bean optimization algorithm based on Cauchy distribution and parent rotation mechanism(BOA-CPR) is presented. Firstly, a population distribution model based on Cauchy distribution is constructed and used in the exploration phase to improve the global search ability of the algorithm. Then, a parent rotation mechanism based on the roulette wheel selection is established to enhance the diversity of offspring. Finally, an adaptive adjustment mechanism for three important parameters, including individual distance threshold, distribution variance and descendant ratio, is designed to improve the dynamic optimization ability of the algorithm for complex optimization problems. Experiments show that BOA-CPR ranks better in average fitness value and Friedman detection index.

Key words: Swarm Intelligence; Bean Optimization Algorithm; Cauchy Distribution; Parent Rotation; Particle Swarm Optimization

本文责任编委 何 清

Recommended by Associate Editor HE Qing

受自然界生物群体习性的启发, Beni等[1]提出群体智能, 蕴含自组织和自协调性.受群体智能的启发, 学者们提出许多群体智能优化算法.此类算法通过个体的互相协作和对外界环境变化的反应可快速找到目标, 现已成为仿生智能优化算法的主流分支.

仿生智能优化算法经过数十年的研究和发展, 现已成功开展对多种复杂优化问题的求解, 应用于多种实际生活生产的优化问题求解中.典型的智能优化算法包括:粒子群优化算法(Particle Swarm Optimization, PSO)、遗传算法(Genetic Algorithm, GA)、差分进化(Differential Evolution, DE)、协方差自适应进化策略(Covariance Matrix Adaptation Evolution Strategy, CMA-ES).

PSO模拟鸟群觅食的行为, 寻找解空间中的最优解, 每个个体分享位置信息, 从当前位置开始搜索, 向最优位置靠近, 不断重复这个过程, 直至到达一个理想的目的地.在问题求解过程中, 所有的粒子通过自身历史最优和种群最优确定下一步的搜索位置, 并更新自身的速度和位置[2].PSO收敛速度较快, 寻优能力较强[3].但是, 由于收敛速度过快这个特点, PSO的全局寻优能力较弱, 容易陷入局部最优, 影响算法的寻优效果.

GA是典型的进化算法, 通过模拟基因的重组与进化完成寻优过程.GA包含3个算子:选择、交叉、变异, 经过多代的基因遗传, 进化出种群中较优个体.但是GA的局部搜索能力较差, 算法求解时间较长, 在进化后期搜索效率较低, 容易产生早熟收敛.

与GA类似, DE也具有选择、交叉、变异算子, 但DE的具体实现方式与GA不同, DE的变异向量是由父代差分向量生成, 与父代个体向量交叉生成新的个体向量[4].然而, DE也与GA一样容易陷入局部最优, 种群规模会随着迭代次数的增加而不断缩小, 算法容易出现停滞现象.

CMA-ES对已找到的优秀的搜索点增加一个随机向量, 改变搜索的步长和方向, 利用这些信息更新协方差矩阵并进行寻优[5].算法利用自身的演化学习机制进行寻优, 并且学习机制具有较强的数学理论基础.CMA-ES的优化效果较优, 但容易出现早熟收敛, 全局的寻优能力较差, 计算复杂度较高, 搜索效率较低.

种子优化算法(Bean Optimization Algorithm, BOA)是受植物种子散射传播方式和种群分布演化规律启发而提出的一种群体智能优化算法[6].算法通过父种选择机制筛选父种, 再通过父种引领机制和种群分布演化模型引导整个种群的进化.算法仿生原理清晰, 结构较简单, 具有较好的寻优性能.

为了使BOA在全局搜索和局部搜索中具有较优的寻优能力, Zhang等[7]提出基于正态分布的BOA, 并且开展灾后恢复重建项目排序的应用研究.Zhang等[8]分析BOA的收敛性能, 证明算法可以以概率1收敛于全局最优解.Feng等[9]提出基于负二项分布模型的混合BOA, 并利用基准测试函数验证算法性能.Zhang等[10]提出混沌BOA, 改善后代种群分布, 提高BOA的全局寻优能力和寻优精度.Zhang等[11]提出基于BOA的群体机器人协同搜索算法.

虽然BOA已表现出较优的优化计算性能, 但在全局搜索和局部寻优能力上依然具有提升空间, 主要表现在BOA使用的分布模型单一, 算法在空间的探索能力不足, 用于搜索的后代分布多样性较弱, 导致算法全局寻优能力较低.并且BOA按照父种适应度值的好坏固定分配各父种产生子代的数量, 会使整个种群过于依赖适应度值较好的父种, 减弱甚至忽略其它父种的作用, 使算法容易陷入局部最优.

针对上述问题, 本文构建基于柯西分布和父种轮换机制的种子优化算法(BOA Based on Cauchy Distribution and Parent Rotation Mechanism, BOA-CPR).首先, 在BOA中改进种群分布机制, 通过柯西分布提高算法的全局寻优性能, 在搜索后期使用单父种的小方差正态分布模型, 提高算法的局部寻优性能, 找到更优质的解.然后, 在算法的全局寻优中加入父种轮换机制, 在前期全局搜索中, 使每个父种生成相同数量的后代个体, 增加算法前期的探索范围, 在算法搜索中后期使用赌轮法选择父种进行后代分布, 每个父种根据当前适应度值占比计算其成为一号父种的概率, 适应度值越优的父种成为一号父种的概率越大, 这样增强种群多样性和算法的全局寻优能力.此外, 构建分布方差、父种距离阈值和后代比例的自适应调整机制, 进一步提升算法的寻优性能, 使算法高效收敛到最优值所在区域.

1 种子优化算法

学者们越来越多的借鉴与研究自然界中的集群行为, BOA是受植物种群分布演化规律启发而构建的一种群体智能优化算法.在自然界中, 植物会不断适应环境进行生存, 只有优秀的植物种群才能应对自然界中的各种环境变化而存活下来[12].植物群体虽然个体相对简单, 但植物的这种集群生存方式可有效利用环境中的资源而生存.植物种群在空间中的分布演化恰似对环境资源的一种搜索[13], 种群内个体也会因为各种环境因素和资源的竞争呈现聚集现象.经过植物种群多代进化繁衍达到对生存环境的最佳适应, 也形成植物生态学中典型的植物种群分布格局[14].

以植物种群分布演化中的种子传播机制建模为例, BOA可看作如下过程:种子先随机播撒在求解空间中, 再根据每个个体的适应度值从中选择一定数量的父种.父种的选择过程为:适应度值最优的为一号父种, 再从剩余个体中选择距离一号父种大于距离阈值的个体, 并且该个体的适应度值优于其它满足条件个体的适应度值.若无合适的个体作为父种, 则将随机生成且满足距离阈值约束的位置作为父种.重复上述操作, 保证每个父种之间的距离都大于阈值, 直至选够指定数量的父种.

BOA在搜索空间中的后代种群分布如图1所示, 每个父种由分布模型在周围位置分别产生一定数量的后代, 适应度值越优的父种可产生越多的后代.再计算后代的适应度值, 适应度值较优的后代又会有机会作为下一代父种去引导整个种群寻优, 这样不断迭代, 整个种群也会逐渐向最优值靠近.

图1 BOA的种群分布Fig.1 Population distribution of BOA

种群分布格局在BOA中起到重要作用, 生态学中常用的种群分布模型有正态分布、负二项分布、柯西分布、泊松分布、奈曼分布等, BOA目前已构建3种种群分布模型, 包括分段函数模型、正态分布模型、负二项分布模型.正态分布是连续的分布模型, 包含期望μ 和方差σ 2这2个参数, 概率密度函数为

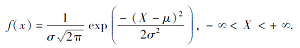
正态分布是自然界较常见的分布, 也是典型的植物种群聚集分布类型[15].

负二项分布又称为帕斯卡分布, 是一种离散的分布模型, 概率密度函数为

其中, p表示一个事件在伯努利实验中每次出现的概率, 计算结果表示在一连串实验中, 这件事件恰好在r+k次实验中在第r次出现的概率值.负二项也是典型的植物种群聚集分布类型, 具有更优的局部搜索能力[9].

上述植物种群分布演化模型的构建有效提升BOA的寻优性能, 但受分布模型特点和进化机制的限制, 存在全局寻优效率不高和种群多样性较差的问题, 还有较大的性能提升空间.自然界植物种群分布格局研究结果中还有大量的分布模型可供仿生借鉴, 通过引入新的分布模型, 可以进一步完善BOA, 提升算法性能.

2 基于柯西分布和父种轮换机制的种子优化算法
2.1 基于柯西分布的种群分布模型

智能算法研究往往关注如何提升算法在全局寻优和局部寻优的综合效果, 避免算法由于提前收敛而陷入局部最优[16].所以, 针对正态分布模型全局寻优性能较弱的问题, 在BOA中引入分布模型— — 柯西分布[17], 使算法能在全局搜索中获得更优效果.柯西分布也称为柯西-洛伦兹分布, 是一种典型的聚集分布, 概率密度函数为

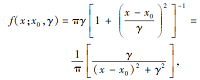
其中, x0表示定义分布峰值位置的位置参数, γ 表示最大值一半处的一半宽度的尺度参数.累积分布函数和逆累积分布函数分别为

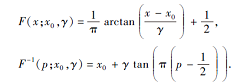
算法通过逆累积分布函数, 可产生基于柯西分布的种子后代.在BOA中由柯西分布代替算法原先的正态分布.由于柯西分布属于自由度为1的T分布, 而正态分布是自由度为+杜拉拉的T分布[18].所以在两者的概率分布图上柯西分布的尾部比正态分布更厚长, 分布范围更广.设随机变量X的期望μ =E[X], 方差

σ 2=Var[X]=E[X-E[x]]2,

k为X的峰度,

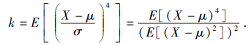
当k=3时, 分布为正态分布; 当k> 3时, 具有比正态分布更重的尾部[19], 如柯西分布; 当k< 3时, 具有比正态分布更轻的尾部.

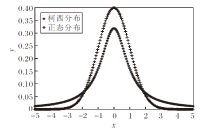
标准正态分布和柯西分布的概率密度图如图2所示.柯西分布的概率密度函数参数设置为x0=0, γ =1, 概率密度函数为

f(x; 0, 1)= 1π(1+x2).

图2 2种分布的概率密度图Fig.2 Probability density for Cauchy distribution and Normal distribution

由图2可看出, 相比正态分布, 柯西分布的尾部更厚长, 在算法中产生的后代会更分散, 后代种群的多样性更优, 更适用于全局寻优, 而小方差的正态分布更适合在搜索后期开展局部寻优.

在BOA-CPR中, 先采用柯西分布进行全局探索, 在搜索后期加入小方差正态分布进行局部寻优, 达到更优的综合寻优效果.

2.2 父种轮换机制

父种轮换机制包含父种平均机制和基于赌轮法的父种选择机制.在算法流程前期, 采用父种平均机制让每个父种的后代分布比例相同, 此部分占整个算法迭代长度的5%, 让每个父种在该阶段都能在自己附近区域进行大范围的寻优, 增加种群的多样性.另外, 在以往的BOA中, 每个父种分布的后代数量比例由其父种的适应度值排序决定, 这种机制导致适应度值优的种子一直保持大比例的后代, 而其它父种的后代个体比例会很小, 容易陷入局部最优.为了在不影响算法收敛速度的前提下增强种群个体的多样性, 在算法迭代计算的中后期引入基于赌轮法的父种选择机制[20], 计算概率公式为

b1= FthFitness(2)+FthFitness(3)2∑i=13FthFitness(i), b2= 12FthFitness(3)2∑i=13FthFitness(i)

其中, FthFitness(n)表示n号父种的适应度值, b1、b2表示由适应度值计算的概率界限, [0, b1]区间表示1号父种产生大比例后代的概率, (b1, b2]区间表示2号父种产生大比例后代的概率, (b2, 1]区间表示3号父种产生大比例后代的概率.在每代都会计算3个父种成为产生大比例后代所占的比例.

表1为示例数据.由表可看出, 3个父种都有产生较多后代的概率, 这样避免一号父种的绝对主导性, 保证种群的多样性, 同时又可以让一号父种被选择的概率最大, 兼顾算法的收敛速度.

表1 基于赌轮法的父种选择示例数据 Table 1 Example data of parent species selection by roulette wheel method
2.3 算法步骤

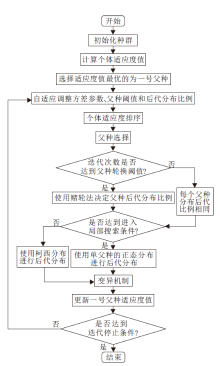
BOA-CPR加入柯西分布, 产生全局性更优的后代个体, 并且在父种的后代分布中加入父种轮换机制, 进一步增强算法的全局寻优性和种群多样性.算法流程如图3所示.

图3 BOA-CPR流程图Fig.3 Flow chart of BOA-CPR

BOA-CPR具体步骤如下.

算法 BOA-CPR

输入 最大迭代次数

输出 最后一代中最优种子的适应度值

step 1 初始化每个个体.

step 2 计算每个个体的适应度值.

step 3 选择适应度值最优的个体作为一号父种.

step 4 计算方差参数、父种的间距阈值参数和后代分布比例参数.

step 5 将个体适应度值排序.

step 6 进行父种选择.

step 7 判断是否达到切换父种轮换分布方式的阈值:若满足, 转入step 8; 否则, 转入step 9.

step 8 使用赌轮法决定父种后代分布比例.

step 9 每个父种产生相同数量的后代.

step 10 判断是否迭代数量达到阈值:若满足进入局部搜索, 转入step 12; 否则, 转入step 11.

step 11 使用柯西分布进行搜索, 产生后代.

step 12 使用单父种的正态分布进行搜索, 产生后代.

step 13 执行变异机制.

step 14 更新一号父种的适应度值.

step 15 判断是否满足结束条件:若不满足, 转入step 4; 否则, 算法结束.

3 实验及结果分析
3.1 实验设置

为了验证BOA-CPR的有效性, 本文使用CEC2013测试集[21]上的28个基准函数对算法进行性能测试, f1f5为单峰函数, f6f20为多峰函数, f21f28为复合函数.这些函数在每个维度上的搜索范围均为[-100, 100].根据CEC2013会议上的统一要求, 最大演化次数设置为100 00D, D为解空间的维度, 本次实验设置为30维, BOA-CPR的种群规模设置为50.

为了使实验结果更准确, 减少随机因素的影响, 在实验中, 每种算法在每个测试函数上独立运行30次, 实验结果取平均值, 并且对实验结果进行弗里德曼检测, 充分利用相关样本的全部信息, 更好地对比不同算法的结果数据优劣.

实验中的BOA-CPR采用自适应方差、自适应阈值和自适应后代比例调整, 并对算法中的柯西分布和正态分布的方差值变化范围进行实验选择.在BOA-CPR中, 方差决定子代的分布趋势, 具有重要的引导作用, 影响整个算法的寻优能力, 所以对算法中的方差进行测试实验, 用于估计BOA-CPR在不同问题中的最佳方差取值.

BOA-CPR同时使用自适应方差以控制算法中柯西分布生成后代的聚集程度, 对方差参数进行实验测试.根据不同函数坐标范围进行调整, 方差基数

BOAstd=Pstd(popmax-popmin),

其中, Pstd表示控制方差和父种之间阈值的参数, 本文设为0.1.柯西分布方差动态调整是随着迭代次数的增加而逐渐减小的, 动态调整系数

所以, 柯西分布的方差自适应调整方式为BOAstd· m.

算法中的距离阈值和后代分布比例的自适应调整公式分别为

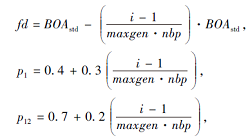
其中, maxgen表示最大迭代次数, nbp表示全局搜索至局部搜索的界限参数, fd表示父种之间的距离阈值, p1、p12表示3个父种后代分布比例界限参数.

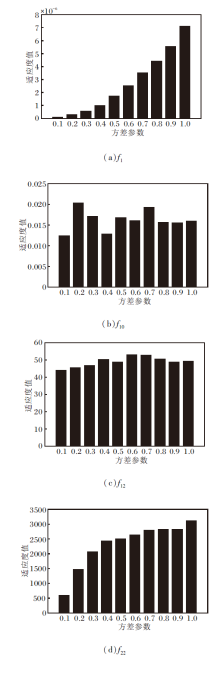
在不同方差参数下, 部分函数适应度值的变化如图4所示.测试函数包括单峰函数、多峰函数和复合函数, 从方差参数实验的显示结果上看, 方差参数在0.1处可得到较好的适应度值, 与通过实验经验获得的较优的方差参数是一致的, 所以在本文的实验中, 将方差参数的初始值固定设置为0.1, 获得更优的寻优效果.并且为了使算法在前期可大范围地探索整个搜索空间, 使算法尽快找到最优区域, 在算法的前期采用较大的方差进行探索, 所以方差参数在前5%的迭代中从1开始, 每经过1%的迭代次数, 方差缩小一半.

图4 不同方差参数对算法适应度值的影响Fig.4 Effect of different variance parameters on adaptation value of the algorithm

3.2 不同策略的有效性分析

为了提高BOA的寻优能力, 增强收敛性和多样性, 本文提出2种改进策略:柯西分布和父种轮换机制.为了验证BOA-CPR中新增策略的有效性, 分别对两种策略进行实验分析.

首先, 对基于柯西分布的BOA和基于正态分布的BOA进行实验对比, 在相同参数下, 观察其在CEC2013测试集上的优化性能, 具体如表2所示, 表中黑体数字表示最优结果.

表2 2种分布的BOA优化性能对比 Table 2 Comparison of BOA optimization performance of 2 kinds of distribution

由表2可看出, 基于柯西分布的BOA有21个函数的平均适应度值优于基于正态分布的BOA, 有1个函数的平均适应度值与基于正态分布的BOA相同, 6个函数的平均适应度值不如基于正态分布的BOA.上述情况表明基于柯西分布的BOA具有更好的寻优效果, 尤其在多峰函数的寻优效果上, 优于基于正态分布的BOA, 但基于正态分布的BOA在单峰函数的寻优效果上优于基于柯西分布的BOA.所以BOA-CPR在最后局部寻优的过程中使用单父种的正态分布以提升搜索效率, 发挥不同分布模型的优势, 增强其在不同函数上的寻优效果.

针对父种轮换的有效性分析, 进行BOA-CPR与去除父种轮换机制的BOA的对比实验, 验证有效性, 实验结果如表3所示, 表中黑体数字表示最优结果.由表可知, 父种轮换机制是有效的, 去除父种轮换机制的BOA, 虽然可略微提升算法在单峰函数上的寻优性能, 但对于多峰函数, 只有在f10、 f11、 f19、 f22上的平均适应度值优于BOA-CPR, 在f26、 f28上的平均适应度值和BOA-CPR相同, 在其它函数上的平均适应度值都差于BOA-CPR.所以加入父种轮换机制的BOA可提升算法的全局寻优性能.

表3 父种轮换机制的有效性 Table 3 Effectiveness of parent rotation mechanism
3.3 与改进PSO的对比实验

本节选择如下11种改进PSO作为对比算法:弗兰肯斯坦的粒子群优化算法(Frankenstein's PSO, FPSO)[22], 正交学习粒子群优化算法(Orthogonal Learning PSO, OLPSO)[23], 结合差分进化的粒子群优化算法(Differential Evolution and PSO, DEP-SO)[24], 使用维度选择方法的粒子群优化算法(PSO Using Dimension Selection Methods, PSODDS)[25], 具有信息共享机制的竞争与合作粒子群优化算法(Competitive and Cooperative PSO with Information Sharing Mechanism, CCPSO-ISM)[26], 自我调节的粒子群优化算法(Self-regulating PSO, SRPSO)[27], 异质综合学习粒子群优化算法(Heterogeneous Com-prehensive Learning PSO, HCLPSO)[28], 遗传学习的粒子群优化算法(Genetic Learning PSO, GLP-SO)[29], 集合式粒子群优化算法(Ensemble PSO, EPSO)[30], 扩展的粒子群优化算法(eXpanded PSO, XPSO)[31], 融入社会影响力的粒子群优化算法(PSO with Social Influence, PSOSI)[32].

这些改进PSO的实验数据和算法设置都与原文献[32]一致, 保证实验的准确性与公平性.每种算法都按照CEC2013会议要求, 运行30次, 取实验结果的平均值.这12种算法的适应度值均值如表4所示, 表中黑体数字表示最优结果.这12种算法在不同类型函数上进行弗里德曼检测的排名数据如表5所示, BOA-CPR的排名情况用黑体数字标记.

表4 各算法在CEC2013测试集上的平均适应度值 Table 4 Mean fitness of different algorithms on CEC2013 dataset
表5 各算法在CEC2013测试集上的弗里德曼检测结果 Table 5 Friedman test results of 12 algorithms on CEC13 dataset

由表4可看出, BOA-CPR在f2和f4上获得最优的平均适应度值, OLPSO、XPSO和GLPSO分别在f1、 f3和f5上获得最优的平均适应度值.结合表5的弗里德曼检测发现, 虽然BOA-CPR获得第二的成绩, 但与最优的PSOSI仅相差0.2.相比其它算法, BOA-CPR的最优平均适应度值提升更大.BOA-CPR在f6、 f8、 f10、 f15、 f16、 f18、 f20上获得最优的平均适应度值, 在表5的弗里德曼检测以3.07的结果取得12种算法中的第一名, 比第二名具有1.06的差距.这充分展现BOA-CPR较优的全局寻优能力, 相比PSO更不易陷入局部最优.BOA-CPR在f23、 f24、 f25和f26上也取得最优的平均适应度值.

由表5可看出, BOA-CPR的弗里德曼检测结果为3.25, 排名第一, 表现出BOA-CPR在不同函数优化中都能表现出良好的搜索性能.综合对比12种算法发现, BOA-CPR获得最优平均适应度值的函数的数量最多, 共计13个函数, 并且在弗里德曼检测排名上以3.36获得第一.无论是最优平均适应度值的函数个数, 还是弗里德曼检测排名, 都展现出BOA-CPR在不同函数优化上的卓越性能.但是对比PSO的变体, BOA-CPR在运行时间上的开销较大, 主要原因是实验中使用的分布函数具有较大的时间开销, 不过BOA-CPR的运行时间开销相比其较好的寻优性能也是可接受的.

3.4 与其它算法的对比实验

为了进一步验证BOA-CPR的有效性, 本节选用如下智能优化算法进行对比:复合差分进化算法(Composite Differential Evolution, CoDE)[33]、具有三父体交叉的遗传算法(GA with Three-Parent Cross-over, TPC-GA)[34]、 带邻域搜索修改的人工蜂群算法(Modified Artificial Bee Colony with Neighborhood Search, MABC-NS)[35]、协方差自适应进化策略(Co-variance Matrix Adaptation Evolution Strategy, CMA-ES)[36].前三种算法数据来自文献[32].

4 种算法的平均适应度值和弗里德曼检测排名如表6所示, 表中黑体数字表示最优结果.由表可知, BOA-CPR在f2、 f4、 f8、 f9、 f15、 f20、 f23、 f24、 f25、 f26、 f27共11个函数上获得最优的平均适应度值, 并且弗里德曼检测排名为2.36, 获得第一.CMA-ES最优的平均适应度值位列第二, 与BOA-CPR只有一个函数之差, 但由于在复合函数上的寻优表现较差, 导致整体弗里德曼检测排名较低.

表6 各算法的对比实验结果 Table 6 Experimental results comparison of different algorithms
4 结束语

本文提出基于柯西分布和父种轮换机制的种子优化算法(BOA-CPR), 在BOA中加入以柯西分布为主的全局寻优和小方差正态分布为辅的局部寻优, 充分利用这两种分布各自的优点, 提升算法的寻优性能.构建父种轮换策略, 并且加入方差、距离阈值、父种后代分布比例的自适应调整机制, 保证算法在不同复杂优化问题和不同迭代次数下, 依然具有良好的寻优能力.上述改进策略的加入, 使BOA-CPR在解决各种复杂问题时, 表现出更优的寻优性能.在CEC2013测试集上对不同类型基准测试函数进行优化实验, 验证BOA-CPR的有效性.

今后将继续进行BOA的研究, 包括进一步提升BOA的局部寻优性能, 改进和完善算法参数的自适应更新机制.另外, 由于BOA前期的收敛速度较快, 虽然算法具有较好的全局性, 但也有较小概率会陷入局部最优的情况, 所以今后可尝试将BOA的搜索过程进行分段处理, 使全局寻优和局部寻优交叉进行, 也是对自然界植物种群生存繁衍的进一步模拟:自然界的植物种群分布演化经过多代之后可能会产生聚集现象, 之后植物种群又会根据环境资源的约束而调整种群的聚集程度, 以便更好地适应生存环境.最后, 在算法性能改进的同时, 进行实际应用问题的测试, 在现实问题的解决中验证算法的应用价值.

参考文献
[1] BENI G, WANG J. Swarm Intelligence in Cellular Robotic Systems // DARIO P, SANDINI G, AEBISCHER P, eds. Robots and Biological Systems: Towards a New Bionics? Berlin, Germany: Sprin-ger, 1989: 703-712. [本文引用:1]
[2] 朱经纬, 方虎生, 邵发明, 等. 具有自适应弹射机制的粒子群算法. 模式识别与人工智能, 2019, 32(2): 108-116.
(ZHU J W, FANG H S, SHAO F M, et al. Self-adaptive Ejector Particle Swarm Optimization Algorithm. Pattern Recognition and Artificial Intelligence, 2019, 32(2): 108-116. ) [本文引用:1]
[3] ELBELTAGI E, HEGAZY T, GRIERSON D. Comparison among Five Evolutionary-Based Optimization Algorithms. Advanced Engineering Informatics, 2005, 19(1): 43-53. [本文引用:1]
[4] 杨启文, 蔡亮, 薛云灿. 差分进化算法综述. 模式识别与人工智能, 2008, 21(4): 506-513.
(YANG Q W, CAI L, XUE Y C. A Survey of Differential Evolution Algorithms. Pattern Recognition and Artificial Intelligence, 2008, 21(4): 506-513. ) [本文引用:1]
[5] LI Z H, ZHANG Q F, LIN X, et al. Fast Covariance Matrix Adaptation for Large-Scale Black-Box Optimization. IEEE Transactions on Cybernetics, 2020, 50(5): 2073-2083. [本文引用:1]
[6] 张晓明, 王儒敬, 宋良图. 一种新的进化算法——种子优化算法. 模式识别与人工智能, 2008, 21(5): 677-681.
(ZHANG X M, WANG R J, SONG L T. A Novel Evolutionary Algorithm-Seed Optimization Algorithm. Pattern Recognition and Artificial Intelligence, 2008, 21(5): 677-681. ) [本文引用:1]
[7] ZHANG X M, SUN B Y, MEI T, et al. Post-Disaster Restoration Based on Fuzzy Preference Relation and Bean Optimization Algorithm // Proc of the IEEE Youth Conference on Information, Computing and Telecommunications. Washington, USA: IEEE, 2010: 271-274. [本文引用:1]
[8] ZHANG X M, WANG H L, SUN B Y, et al. The Markov Model of Bean Optimization Algorithm and Its Convergence Analysis. International Journal of Computational Intelligence Systems, 2013, 6(4): 609-615. [本文引用:1]
[9] FENG T H, XIE Q L, HU H Y, et al. Bean Optimization Algorithm Based on Negative Binomial Distribution // Proc of the International Conference in Swarm Intelligence. Berlin, Germany: Springer, 2015: 82-88. [本文引用:2]
[10] ZHANG X M, FENG T H. Chaotic Bean Optimization Algorithm. Soft Computing, 2018, 22(1): 67-77. [本文引用:1]
[11] ZHANG X M, HU Y Q, LI T J. A Novel Target Searching Algorithm for Swarm UAVs Inspired from Spatial Distribution Patterns of Plant Population. International Journal of Computational Intelligence Systems, 2020, 14(1): 159-167. [本文引用:1]
[12] BURI A, CIANFRANI C, PINTO-FIGUEROA E, et al. Soil Factors Improve Predictions of Plant Species Distribution in a Mountain Environment. Progress in Physical Geography, 2017, 41(6): 703-722. [本文引用:1]
[13] IVERSON L R, MCKENZIE D. Tree-Species Range Shifts in a Changing Climate: Detecting, Modeling, Assisting. Land scape Ecology, 2013, 28(5): 879-889. [本文引用:1]
[14] WIEGAND T, MOLONEY K A. Rings, Circles, Null-Models for Point Pattern Analysis in Ecology. Oikos, 2004, 104(2): 209-229. [本文引用:1]
[15] ZHANG X M, SUN B Y, MEI T, et al. A Novel Evolutionary Algorithm Inspired by Beans Dispersal. International Journal of Computational Intelligence Systems, 2013, 6(1): 79-86. [本文引用:1]
[16] 逯少华, 张晓伟, 鲍承强, 等. 柯西种群分布的自适应范围粒子群优化算法. 计算机应用, 2014, 34(4): 1070-1073.
(LU S H, ZHANG X W, BAO C Q, et al. Adaptive Range Particle Swarm Optimization with the Cauchy Distributed Population. Computer Applications, 2014, 34(4): 1070-1073, 1079. ) [本文引用:1]
[17] DAI W, AU O C, LI S J, et al. Adaptive Search Range Algorithm Based on Cauchy Distribution // Proc of the Visual Communications and Image Processing. Washington, USA: IEEE, 2012. DOI: DOI:10.1109/VCIP.2012.6410741. [本文引用:1]
[18] JONES M C, FADDY M J. A Skew Extension of the t-Distribution, with Applications. Journal of the Royal Statistical Society Series B, 2003, 65(1): 159-174. [本文引用:1]
[19] HODGE B M, MILLIGAN M. Wind Power Forecasting Error Distributions over Multiple Timescales // Proc of the IEEE Power and Energy Society General Meeting. Washington, USA: IEEE, 2011. DOI: DOI:10.1109/PES.2011.6039388. [本文引用:1]
[20] 胡新平, 贺玉芝, 倪巍伟, 等. 基于赌轮选择遗传算法的数据隐藏发布方法. 计算机研究与发展, 2012, 49(11): 2432-2439.
(HU X P, HE Y Z, NI W W, et al. A Privacy-Preserving Data Publishing Method Based on Genetic Algorithm with Roulette Wheel. Computer Research and Development, 2012, 49(11): 2432-2439. ) [本文引用:1]
[21] LIANG J, QU B Y, SUGANTHAN P N, et al. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization. Technical Report, 201212. Zhengzhou, China: Zhengzhou University, 2013. [本文引用:1]
[22] LAZZUS J A. Modeling of Gas-Solid Equilibrium of Binary Systems Aided by Frankenstein PSO. Comptes Rendus Chimie, 2016, 19(5): 630-638. [本文引用:1]
[23] DARWISH A, EZZAT D, HASSANIEN A E. An Optimized Model Based on Convolutional Neural Networks and Orthogonal Learning Particle Swarm Optimization Algorithm for Plant Diseases Diagnosis. Swarm and Evolutionary Computation, 2020, 52. DOI: DOI:10.1016/j.swevo.2019.100616. [本文引用:1]
[24] WANG S H, LI Y Z, YANG H Y. Self-adaptive Mutation Diffe-rential Evolution Algorithm Based on Particle Swarm Optimization. Applied Soft Computing, 2019, 81. DOI: DOI:10.1016/j.asoc.2019.105496. [本文引用:1]
[25] JIN X, LIANG Y Q, TIAN D P, et al. Particle Swarm Optimization Using Dimension Selection Methods. Applied Mathematics and Computation, 2013, 219(10): 5185-5197. [本文引用:1]
[26] LI Y H, ZHAN Z H, LIN S J, et al. Competitive and Cooperative Particle Swarm Optimization with Information Sharing Mechanism for Global Optimization Problems. Information Sciences, 2015, 293(3): 370-382. [本文引用:1]
[27] TANWEER M R, SURESH S, SUNDARARAJAN N. Improved SRPSO Algorithm for Solving CEC 2015 Computationally Expensive Numerical Optimization Problems // Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2015: 1943-1949. [本文引用:1]
[28] CAO Y L, ZHANG H, LI W F, et al. Comprehensive Learning Particle Swarm Optimization Algorithm with Local Search for Multimodal Functions. IEEE Transactions on Evolutionary Computation, 2019, 23(4): 718-731. [本文引用:1]
[29] LIN A P, SUN W, YU H S, et al. Global Genetic Learning Particle Swarm Optimization with Diversity Enhancement by Ring Topo-logy. Swarm and Evolutionary Computation, 2019, 44: 571-583. [本文引用:1]
[30] USMAN M, AMIN A, MUHAMMAD M A, et al. Optimal under Voltage Load Shedding Scheme for a Distribution Network Using EPSO Algorithm // Proc of the 1st International Conference on Power, Energy and Smart Grid. Washington, USA: IEEE, 2018. DOI: DOI:10.1109/ICPESG.2018.8384525. [本文引用:1]
[31] XIA X W, GUI L, HE G L, et al. An Expand ed Particle Swarm Optimization Based on Multi-exemplar and Forgetting Ability. Information Sciences, 2020, 508: 105-120. [本文引用:1]
[32] 宋威, 华子彧. 融入社会影响力的粒子群优化算法. 计算机科学与探索, 2020, 14(11): 1908-1919.
(SONG W, HUA Z Y. Particle Swarm Optimization with Social Influence. Journal of Frontiers of Computer Science and Technology, 2020, 14(11): 1908-1919. ) [本文引用:3]
[33] TRIVEDI A, SANYAL K, VERMA P, et al. A Unified Different-ial Evolution Algorithm for Constrained Optimization Problems // Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2017: 1231-1238. [本文引用:1]
[34] ELSAYED S M, SARKER R A, ESSAM D L. A Genetic Algorithm for Solving the CEC'2013 Competition Problems on Real-Parameter Optimization // Proc of the IEEE Congress on Evolutio-nary Computation. Washington, USA: IEEE, 2013: 356-360. [本文引用:1]
[35] LI G H, CUI L Z, FU X H, et al. Artificial Bee Colony Algorithm with Gene Recombination for Numerical Function Optimization. Applied Soft Computing, 2017, 52: 146-159. [本文引用:1]
[36] SUTTORP T, HANSEN N, IGEL C. Efficient Covariance Matrix Update for Variable Metric Evolution Strategies. Machine Lear-ning, 2009, 75: 167-197. [本文引用:]