引用本文
顾清华, 王楚豪, 江松, 陈露. 基于动态自适应的双档案大规模稀疏优化算法. 模式识别与人工智能, 2021,34(7): 592-604
GU Qinghua, WANG Chuhao, JIANG Song, CHEN Lu. Dual-Archive Large-Scale Sparse Optimization Algorithm Based on Dynamic Adaption. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(7): 592-604.  
Doi: 10.16451/j.cnki.issn1003-6059.202107002
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于动态自适应的双档案大规模稀疏优化算法
顾清华1,2,3, 王楚豪1,2, 江松2,3, 陈露1,2,3
1.西安建筑科技大学 管理学院 西安 710055
2.西安建筑科技大学 矿山系统工程研究所 西安 710055
3.西安建筑科技大学 资源工程学院 西安 710055
通讯作者:

顾清华,博士,教授,主要研究方向为矿业系统工程.E-mail:qinghuagu@126.com.

作者简介:

王楚豪,硕士研究生,主要研究方向为多目标系统优化.E-mail:15503645140@163.com.

江 松,博士,副教授,主要研究方向为智慧矿山的优化建模.E-mail:jiangsong925@163.com.

陈 露,博士研究生,研究方向为多目标系统优化.E-mail:chenlu@xauat.edu.cn.

收稿日期: 2021-03-16 修回日期: 2021-05-25 接受日期: 2021-05-25
资助项目: 国家自然科学基金面上项目(No.51974223)、陕西省自然科学基金杰出青年项目(No.2020JC-44)、陕西省自然科学基础研究计划联合基金项目(No.2019JLP-16)资助
摘要

针对传统大规模优化算法维数过高、过度稀疏、难以平衡等问题,文中提出基于动态自适应的双档案大规模稀疏优化算法,平衡维数和稀疏性对算法的影响,提高算法在解决大规模优化问题上的多样性和收敛性.首先,改变种群分数生成策略,加入自适应参数和惯性权重,增加分数的动态性,改善种群的多样性,使搜索不易陷入局部最优.然后,改变算法的环境选择策略,引入角度截断的思想,有效生成子代.同时引入双档案,分开真实决策变量和二进制决策变量,减少算法的运行时间.在大规模优化问题、稀疏优化问题及实际应用上的测试表明,文中算法保持原有的稀疏性质,同时稳定提升多样性和收敛性,具有较强的竞争性.

关键词: 大规模; 稀疏优化算法; 动态自适应; 惯性权重; 双档案
中图分类号:TP 301.6
Dual-Archive Large-Scale Sparse Optimization Algorithm Based on Dynamic Adaption
GU Qinghua1,2,3, WANG Chuhao1,2, JIANG Song2,3, CHEN Lu1,2,3
1. School of Management, Xi'an University of Architecture and Technology, Xi'an 710055
2. Institute of Mine Systems Engineering, Xi'an University of Architecture and Technology , Xi'an 710055
3. School of Resources Engineering, Xi'an University of Architecture and Technology, Xi'an 710055
Corresponding author:
GU Qinghua, Ph.D., professor. His research interests include mining system engineering.

About Author:
WANG Chuhao, master student. His research interests include multi-objective system optimization.
JIANG Song, Ph. D., associate professor. His research interests include optimization mo-deling of intelligent mine.
CHEN Lu, Ph.D. candidate. His research interests include multi-objective system optimization.

Fund:National Natural Science Foundation of China(No.51974223), Outstanding Youth Project of Shaanxi Natural Science Foundation(No.2020JC-44), Joint Fund Project of Shaanxi Natural Science Basic Research Foundation(No.2019JLP-16)
Abstract

The traditional large-scale optimization algorithms generate high dimensionality and sparseness problems. A dual-archive large-scale sparse optimization algorithm based on dynamic adaptation is proposed to keep the balance of dimensionality and sparseness in the algorithm and improve the diversity and convergence performance of the algorithm in solving large-scale optimization problems. Firstly, the scores strategy for generating population is changed. By adding adaptive parameter and inertia weight, the dynamics of scores is increased, the diversity of the population is improved, and it is not easy to fall into the local optimum. Secondly, the environment selection strategy of the algorithm is changed by introducing the concept of angle truncation, and the offspring is generated effectively. Meanwhile, a double-archive strategy is introduced to separate the real decision variables from the binary decision variables and thus the running time of the algorithm is reduced. The experimental results on problems of large-scale optimization, sparse optimization and practical application show that the proposed algorithm maintains the original sparsity with steadily improved diversity and convergence and strong competitiveness.

Key words: Large-Scale; Sparse Optimization Algorithm; Dynamic Adaptation; Inertial Weight; Dual-Archive

本文责任编委 付 俊

Recommended by Associate Editor FU Jun

在多目标优化问题中, 决策变量的数量呈指数增长, 搜索空间呈大面积扩张趋势, 维数也从单一维度变为多维, 从而形成大规模多目标优化问题(Large-Scale Multi-objective Optimization Problem, LMOP).相比单目标优化问题, LMOP问题更难解决, 这主要是由于高维性质和巨大稀疏区域的性质造成的.现阶段大规模优化的研究方向也是基于这两种性质的优化和完善.但是目前研究表明在解决LMOP问题时很难较好地集成或调整它们的性质特点, 即很难整体消除和中和两个属性之间的冲突点, 只能在单一的属性上进行局部调整约束.

针对高维性质问题, 学者们提出可有效解决大规模问题的多目标进化算法(Multi-objective Evo-lutionary Algorithms, MOEAs).MOEAs多是应用特定的方式改进算法的初始选择策略, 主要分为如下3类.1)改善算法性质, 增强选择压力.改变算法的原始进化策略以进行优化.强化支配关系的非支配排序遗传算法(Non-dominated Sorting Genetic Algori-thm-II of Strengthened Dominance Relation, NSGA-II-SDR)[1]、r-支配关系的非支配排序遗传算法(The r-Dominance Non-dominated Sorting Genetic Algorithm-II, r-NSGA-II)[2]改变非支配排序的支配关系, 将后代的选择压力增加到真实的Pareto最优前沿.Wang等[3]提出双归档多目标优化算法(Improved Two-Archive Algorithm, Two_Arch2), 利用双档案策略, 分别对子代生成进行优化, 同时提出截断策略, 在环境选择中进行种群生成.2)对决策变量进行分类聚合.Zhang等[4]提出大规模多目标优化进化算法(Evolutionary Algorithm for Large-Scale Many-Ob-jective Optimization, LMEA), 从决策变量角度聚类技术对实际决策变量进行多样性和收敛性的分类优化策略.3)改变算法局部参数进行整体效果的优化.顾清华等[5, 6]提出基于改进的非支配精英排序遗传算法(Non-dominated Sorting Genetic Algorithm-II, NSGA-II)的分解约束算法和遗传-混合灰狼算法, 分别改进约束条件和引入3种遗传算子, 提高高维算法的全局收敛性.Zille等[7]提出加权优化框架的进化算法(Weighted Optimization Framework, WO-F), 加入权重向量参数, 确定算子移动方向.Tian等[8]提出群竞争优化的大规模多目标算法(Large-Scale Multi-objective of Competitive Swarm Optimizer Algorithm, LMOCSO), 改变方程式参数, 更新粒子移动方向.

目前稀疏性质在稀疏回归[9]、模式挖掘[10]等方向都具有广泛的研究和应用.在特征选择问题中由于稀疏区域的存在, 最优解的特征值仅占所有候选特征值的一小部分, 选择小部分的特征解即可达到最大化的分类性能.如果采用二进制编码(即每个二进制决策变量指示是否选择一个特征), Pareto最优解的大多数决策变量将为0, 即Pareto最优解是稀疏的, 这导致决策范围为大面积稀疏.因此决策变量与稀疏性之间也存在一定的因果关系.大量的决策变量导致高维, 高维又导致稀疏.如何减少稀疏性就成为一个难题.

关于大规模问题的稀疏性研究目前还处于初级阶段.Tian等[11]提出学习Pareto最优子空间的多目标优化进化算法(Multiobjective Evolutionary Algorithms of the Pareto-Optimal Subspace Learning, MOEA\PSL), 使用有限的Boltzmann和去噪自动编码器, 用于学习决策变量的稀疏分布和Pareto最优子空间的紧凑近似表示.针对单纯研究的稀疏性, Tian等[12]提出基于大规模多目标优化问题的稀疏演化算法(Evo-lutionary Algorithm for Large Scale Sparse MOPs, Sparse-EA), 将实际决策变量和二进制决策变量进行编码整合, 突破算法局限于实际决策变量的单一性.同时在保证算法性能的前提下针对稀疏性提出子代生成策略, 即在编码整合后对每个变量进行分数的制定, 其中二进制决策变量记录应设置为0的决策变量, 从而控制解决方案的稀疏性.但是该算法忽略维数性质, 导致在收敛性和多样性的平衡上效果不佳, 容易陷入局部最优, 不能有效提高解决LMOP问题的效率.

针对上述维数和稀疏性问题, 本文就如何平衡两者的性质优点, 如何通过在大规模稀疏优化算法中运用一些决策变量优化方法和降维技术方面进行思考.大规模稀疏优化算法在初始生成阶段选用的策略较经典, 缺少一些在决策变量优化方面的支撑, 难以快速平衡收敛性和多样性, 容易陷入局部最优.同时因为前期需要处理两种不同类型的决策变量, 运算效率较低, 运行时间相对较长.

针对大规模稀疏优化算法仍存在的一些改进空间, 本文提出基于动态自适应的双档案大规模稀疏优化算法(Dual-Archive Large-Scale Sparse Optimization Algorithm Based on Dynamic Adaption, DLSADA).改变分数制定计算策略, 加入自适应参数和惯性权重.使分数更具有动态性, 同时增加种群的多样性, 使搜索不易陷入局部最优.改变算法的环境选择策略, 引入角度截断的思想, 选择子代中的极限值, 并设置阈值K进行补充和删除, 有效生成子代种群.引入双档案, 分开真实决策变量和二进制决策变量, 提高算法的前期效率, 设置算子翻转参数, 提高算法计算性能.在大规模问题和稀疏问题上进行测试, 结果表明本文算法能在保持稀疏性质的前提下提高自身在大规模问题上的性能, 提升多样性和收敛性.

1 大规模稀疏优化算法

大规模稀疏优化算法是针对和保持稀疏性质提出的进化算法, 主要组成部分如下.

1)实际决策变量和二进制决策变量进行编码的新生成子代种群组成初始化种群, 即算法中的解x由2个分量组成, 分别表示决策变量的真实向量和表示掩码的二进制决策变量.最终决策变量定义为

(x1, x2, …, xn)= (real1· mask1, real2· mask2, …, realn· maskn).

2)种群生成方面采用NSGA-II相似的环境选择策略.随机初始化种群并计算各解的非支配前沿面数目和拥挤距离.在这个过程中确定生成算子的分数, 对子代种群进行非支配排序, 并将解的非支配前沿面数作为决策变量的得分.

3)为了表示稀疏性质, 通过翻转表现将一部分变量表现为0.将Pareto前沿面的层数作为分数进行大小的对比, 并进行翻转表现, 两者中较大值设置为0, 较小值设置为1.

2 基于动态自适应的双档案大规模稀疏优化算法

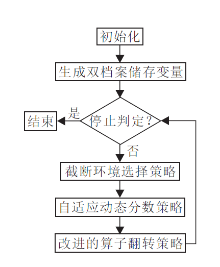
本文提出基于动态自适应的双档案大规模稀疏优化算法(DLSADA), 流程如图1所示.DLSADA伪代码如下.

图1 DLSADA框图Fig.1 Framework of DLSADA

算法 1 DLSADA

输入 种群规模数N, 动态自适应参数个数p,

交互截断分析中决策变量选择解的个数nCit

输出 最终生成种群P

[P, Score]← 初始化种群N

将初始化后的种群分别放入实际变量档案A1和二进制变量档案A2

Pss← 通过二元锦标赛策略和自适应动态分数策略进行种群编码(P, Pss) //见算法 2

[Ps]← 编码后的子代种群进行环境选择操作, 角度截断策略进行交叉变异操作(P, nCit)

while终止迭代条件未满足时do // 见算法 3

Pss'← P∪ 算子翻转策略, 更新子代种群(Pss',

Score, p) //见算法 4

从F父代中根据角度从小到大删除|F1∪ F2∪

…∪ Fk|-N 算子

P← F1∪ F2∪ …∪ Fk

end while

返回 P

算法1为DLSADA的主流程.首先, 初始化种群后, 分别将2种形式的决策变量进行分类, 归档A1和A2, 分别在A1和A2上进行矩阵生成后随机组成混合编码矩阵.然后, 在计算决策算子分数时, 采用自适应动态分数策略取代原有的前沿面计数, 在一定迭代次数后进行角度截断策略和环境选择操作, 最后, 使用算子的迭代翻转策略, 根据分数大小相互对比决定算子的表现与否, 在保证算法具有良好性能的同时弱化算法固有的稀疏性, 提高算法的多样性.

2.1 动态自适应调整策略

在大规模稀疏优化算法的环境选择中, 当算子进行非支配排序时, 会将非支配解集前沿面数设定为一个分数.设定这个分数的原因是基于稀疏算法本身的稀疏性不同, 会通过解决算子之间进行分数大小对比的方式决定该算子表现与否.如果大部分算子不表现自己的性质, 会形成大面积的稀疏性.随着最终决策变量数量的增加, 因为位于同层Pareto前沿面的算子数量较多, 导致分数相同的解决算子越来越多, 使算子无法进一步有效对比, 从而造成局部最优的局面.

基于此种情况, 本文修改分数制定策略, 提出动态自适应调整策略, 核心思想是通过数学函数的变化改变初始化种群的个体状态, 使其前期保持一定的多样性, 在全局搜索的同时推进种群的多样化[13].后期的种群个体趋于局部探索和开发, 最终收敛到全局最优位置.加入自适应参数和惯性权重值[14], 使分数随迭代次数的改变而改变, 增强算法的全局搜索能力, 提高算法的收敛精度, 避免陷入局部最优.改进后的分数更新公式为

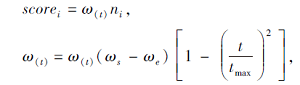
其中, Scorei表示改进后第i个算子的得分数, ni表示第i个算子所在的Pareto前沿面层数, ω s表示初始惯性权重, ω e表示迭代至最大迭代次数时的惯性权重, t表示当前迭代次数, tmax表示最大迭代次数, [1- ttmax2]表示自适应参数.

敏感性测试实验表明, 惯性权重ω s = 0.3, ω e = 0.9时算法性能最优.为了扩大参数的取值变化范围, 随着迭代的进行, 惯性权重从0.3递增至0.9, 原因是迭代开始时算子所在的层数较大, 自适应参数较大[13], 设置较小的惯性权重可使分数趋于平衡.而迭代后期的层数较小, 设置较大的惯性权重可使整体的算法结果呈现平衡状态, 同时使分数更具有可比性和动态性[15].自适应动态分数策略伪代码如下所示.

算法 2 二元锦标赛策略和自适应动态分数策略

(N, p, t)

输入 种群规模数N, 自适应参数p, 迭代次数t,

惯性权重ω , 初始化种群P

输出 编码后的种群Pss, 决策变量的分数Score,

第i行生成第i个解的父代种群Qi

D ← 决策变量的数量;

if 决策变量为实际决策变量then

Dec1 ← 生成D × D 维随机矩阵

A1 ← Dec1放入实际变量档案A1

else if 决策变量为二进制决策变量 then

Dec2 ← 生成D × D维1-0矩阵

A2 ← Dec2放入二进制变量档案A1

end if

Mask ← A1 × A2

Qi← 由Dec和Mask的第i行生成第i个解的父代

种群

[F1, F2, …] ← 对Qi 进行非支配排序

p← 1- ttmax2

ω t← ω s(ω s-ω e)p

// ω s为初始惯性权重, ω e为迭代至最大迭代次数时

的惯性权重,

for i遍历D种群时do

scorei← ω tni // ni表示种群Qi的第i个解集

end for

返回Pss和Scorei

2.2 改进的环境选择截断策略

在环境选择策略中, 大规模稀疏优化算法采用与NSGA-II[16]相似的精英选择策略.这种机制常用于低维决策变量较少且不存在稀疏的优化算法中.在大规模稀疏算法中, 大量变量是分层的, 很大一部分空间是稀疏的.因此不能简单考虑拥挤距离, 容易陷入局部最优.

基于上述讨论, 本文改进环境策略的选择, 仍然使用非支配排序, 但是最后一个解决方案的选择是基于角度而不是距离.从文献[3]和文献[17]可看出, 相比拥挤距离, 角度是一种更全面的测量分集质量的方法, 在其它大规模算法中也得到更广泛的应用.DLSADA在初始化种群时采用计算角度而不是使用距离策略, 这种基于操作角度选择的解决方案称为截断策略.具体步骤如下.

首先, 计算非主导解集的Pareto前沿面层数, 在最后的Pareto前沿面层中选择解的标准化角度, 并在二元锦标赛选择之后生成后代.然后, 采用截断策略选择部分解, 第一步计算并归一化任意两个解的角度, 从中选择极限解.通常, 极端情况是取最小值解决方案角度集中的相对较大值.本文通过敏感性实验设置一个合理的阈值K.当选定的极值集数量超过K值时, 将根据相互作用关系效用大小进行角度的相似性判断, 相互关系越明显, 相似性越大.相互关系

fk(x)|xu=a2, xv=b1< fk(x)|xu=b1, xv=b1,

fk(x)|xu=a2, xv=b1> fk(x)|xu=b1, xv=a2.

计算后的角度会根据相似度大小从选择的解决方案中随机删除一些解, 直到解集数量为K.如果选择的极值集数量不超过K, 将从未选择的集合中选择一定数量的极值解, 使极值集数量达到K, 通常选择极大值解集里的最小值, 再继续下一步操作.环境选择角度截断策略伪代码如下所示.

算法 3 环境选择角度截断策略(P, nCit)

输入 编码后的种群集P, 角度阈值K,

被选择的解决算子集nCit,

输出 P中有相互影响效果的决策变量集Ps

for 所有的 v∈ P do

CitSet ← Ø

随机从P中选择2个算子u、v

if δ (u)δ (v)< 0

u、v视为有相互影响作用的算子

CitSet ← CitSet ∪ {Group(u, v)}

Group ← CitSet所有变量

Ps ← Ps∪ {Group}

end if

end for

从P中删除重复的解决方案

根据截断角度选择最后一层Pareto前沿面中的解

计算每2个解决算子之间的归一化角度

根据归一化角度选择极端最大的解决算子

max(extreme(angle))

通过截断操作选择其余部分解决算子

if sum(choose) > K

根据相互影响效果随机删除几个影响度较大的

解决算子

else

从未选择的解决算子集中选择极限角度解集中

的最小解集min(extreme(angle))以超过设置的

角度阈值K

end if

返回Ps

2.3 双档案存放及翻转参数调整策略

大规模稀疏优化算法采用编码形式, 同时处理实际决策变量和二进制决策变量, 但是在前期初始化随机生成2种不同类型变量的子代需要大量的时间空间进行计算.故本文在大规模稀疏优化算法的基础上增加双档案存放策略, 分别为实际决策变量和二进制决策变量, 进行存档.同时在实际决策变量档案中优先提取自编码适应分数较大的变量进行下一代的优化.加入双档案存放后可缩短算法的运行时间, 节省一定计算空间, 减少算法的时间复杂度, 提高运算效率.

此外, 翻转策略的使用是为了保证算法存在一定的稀疏性:如果算子翻转结果为1, 表现出来; 结果为0, 不表现.但是, 因为本文需要尽可能提高算法的分布收敛等综合性能, 所以选择在算法固有的稀疏性上做出一些让步, 增加解决算子变量表达的可能性, 减少算法的稀疏性, 提高算法的多样性, 从而提高算法的综合性.故本文加入一个较大的阈值(当通过实验敏感度分析设置阈值为0.8时, 算法的实验结果最优)与01之间产生的随机数进行对比结果策略.当随机数小于阈值0.8时, 对比这一部分解决算子的变量分数大小, 然后将分数较小值设置为1(即越小越好, 最小为1), 当随机数大于阈值0.8时, 对比一部分变量将分数较大值设置为0(越大越好, 最大为0).这样做的意义是在保证稀疏性的基础上增加变量表达为1的变量概率, 使算法在整体性能上有所提升.算子翻转策略的伪代码如下所示.

算法 4 算子翻转策略(Pss', Score, p)

输入 种群亲本子代Pss', 决策变量分数Score

输出 一组子代集O

[p, q] ← 随机选择两个亲本 Pss'

p1mask← 二进制亲本(1:N\2)

p2mask← 二进制亲本(N\2+1:N)

设置阈值为0.8

if 随机数(0, 1)< 阈值

[m, n] ← 从非零元素中随机选择2个决策变量

p1mask ∩ q2mask¯// 交叉和变异

if分数m > 分数n

将Omask中的第n个元素设置为1

else

将Omask中的第m个元素设置为1

end if

else

[m, n] ← 从非零元素中随机选择2个决策变量

p1mask¯ ∩ q2mask

if 分数m< 分数n

将Omask中的第n个元素设置为0

else

将Omask中的第m个元素设置为0

end if

end if

生成子代集O

返回 O

3 实验及结果分析
3.1 实验环境

本文选择目前在大规模和稀疏领域最新研究的7种算法进行对比.1)大规模多目标算法:LMOCS-O[8], 线性组合搜索算法(Linear Combination-Based Search Algorithm, LCSA)[19], 方向引导进化算法(Direction Guided Evolutionary Algorithm, DGEA)[20].

2)基于双档案的大规模多模态算法:双归档重组多模态多目标进化算法(A Multi-modal Multiobjective Evolutionary Algorithm Using Two-Archive and Re-combination Strategies, TriMOEATAR)[21].3)最新稀疏性研究算法:MOEA\PSL[11], SparseEA[12], 模式挖掘大规模稀疏优化进化算法(A Pattern Mining Based Evolutionary Large-Scale Sparse Algorithm, PMMOEA)[22].

基准测试问题选择基于大规模算法的常见测试问题LSMOP1LSMOP9[23]与WFG1WFG9[24], 各测试问题的特征性质如表1和表2所示.

表1 LSMOP测试问题的特征分布 Table 1 Feature distribution of LSMOP test problems
表2 WFG测试问题的特征分布 Table 2 Feature distribution of WFG test problems

为了定量评价不同多目标优化算法的性能, 本文选择如下指标.

1)IGD指标:

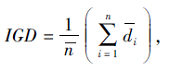
其中, d¯i为目标空间上每个个体与Pareto前沿面中最近个体之间的欧氏距离, n¯为目标空间中个体数.IGD指标可综合反映算法的收敛性和多样性.IGD越小, 找到的解集收敛性和分布性整体效果越优.

2)GD指标:

GD= 1n(∑i=1ndi2)12,

其中, n为Pareto前沿面中的个体数, di为目标空间上个体的每个函数值与Pareto前沿面中最近个体之间的欧氏距离.GD指标用于表示真实Pareto前沿面与算法搜索得到的Pareto最优前沿面之间的距离, GD值越小, 说明解集收敛效果越优.

3)HV指标:

其中, λ 为勒贝格测度, vi为参考点和非支配个体构成的超体积, S为非支配集.HV指标表示由解集中的个体与参考点在目标空间中围成的超立方体的体积.它是衡量算法综合性能的常用指标, 并严格遵守Pareto支配原则.HV值越大, 说明算法的综合性能越优.

实验建立在Matlab平台[25]上, 统计检验方法采用Wilcoxon秩检验[16]中显著性水平为0.05的Wilcoxon秩和检验, 其中, +、-、=分别表示与DLSADA的结果有显著性好、显著性差、在统计学上相似.如果2种算法的最佳中值相同, 则四分位范围(Interquartile Range, IQR)越小, 算法性能越优.

3.2 运行时间及分布性对比

为了对比算法的运行时间, 对比SparseEA和DLSADA进行3目标LSMOP问题的运行时间, 决策变量设置为300, 具体结果如表3所示.由表可见, 在运行LSMOP问题上, DLSADA的运行时间少于SparseEA, 表明通过改进子代初始化环境选择策略可有效提高算法在解决大规模问题上的机动性, 使算法具有更高的竞争性和效率.

表3 2种算法在3目标LSMOP测试问题上的运行时间 Table 3 Running time of 2 algorithms for 3 target LSMOP test problems s

同时, 对于分布性的分析采用基于MaF问题[26]的Pareto前沿面, 因为MaF系列的测试问题是基于DTLZ系列问题[27]改进和提出的最先进的测试问题之一, 能更全面反映复杂峰值问题上的算法分布性解决能力.

选择的分布性指标是Pareto前沿面的覆盖范围(Coverage over Pareto Front, CPF)[27], 这是目前提出的可直观评估分布性性能的通用指标体系.CPF将解决方案集投影到低维超立方体, 并计算投影解决方案集的“ 体积” , 用于评估分布性和扩展性.

CPF公式如下:

CPF= Vol(P')Vol(R), Vol(P')= ∑P∈P'lpM-1, Vol(R)= ∑RlRM-1

其中, P为解集, P'为归一化解集, R为参考点集.

基于MaF问题的特性, 本文选择MaF7问题进行进一步分析.MaF7是混合多峰非连接问题, 可更直观表现算法的前沿面收敛分布情况.

各算法在MaF7问题上的Pareto前沿面图如图2所示.由图可见, LMOCSO、DGEA、TRiMOEATAR位于前沿面的非支配解较少, 多样性和规律性较差.MOEA\PSL可较明显地收敛到Pareto前沿面, 但形成的前沿面较分散, 欠缺一定完整度.相比之下, DLSADA和PMMOEA具有更好的收敛性和多样性, 尤其是PMMOEA有更多的解收敛到Pareto前沿面上, 算法解决能力更具优势.DLSADA和PMMOEA在MaF7问题上的处理结果无特别明显的性能差别.

图2 各算法在MaF7问题上的Pareto前沿面收敛情况Fig.2 CPF of different algorithms for MaF7 problem

图3给出7种算法在3种不同的WFG低维测试问题上的HV变化图.WFG一共9个问题, 从中选择WFG3、WFG5、WFG8.由图3可看出, DLSADA在 WFG5问题上HV 值上升趋势最快, 变化程度较平滑, 说明算法更具优势.但DLSADA优势并不是特别明显, 与Two_Arch2的性能较相近, 甚至在WFG3、WFG8问题上, Two_Arch2的变化趋势具有更明显的增长速度.可能的原因是Two_Arch2在WFG这种线性退化凹型问题上具有一定的性能优势, 而DLSADA更倾向于解决不可分凹型问题, 在整体分布上, 还是DLSADA最全面均衡.不过这仅是低维环境下的情况分布, 不能说明DLSADA在高维环境下的运算性能.

图3 各算法在3种WFG低维问题上的HV变化图Fig.3 HV metric values variation of different algorithms for 3 WFG low-dimensional problems

基于上述分析, 本文在WFG3问题上进行深入研究, 从常规的3目标进化问题变成高维20目标进化问题, 对比算法性能.WFG3 是一个退化问题, 最终结果是一条线性的退化曲线.当目标取到20维时, 算法无法形成一个完整的Pareto前沿面, 只能产生维数和结果的可视化线性图.

各算法在WFG3高维问题上的可视化结果如图4所示.

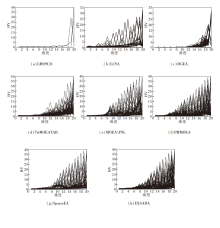图4 各算法在WFG3高维问题上的最佳解集Fig.4 Optimal solution set of different algorithms for WFG3 high-dimensional problems

由图4可见, 无论是从收敛性还是从多样性角度, LMOCSO、LCSA、DGEA、TRiMOEATAR都无法取得良好的解集, 只在1520维处有分散的解集.可能的原因是基于大规模的算法在高维问题上的解集在某一方面限制低维解集分布, 而基于稀疏性质研究的算法MOEA\PSL、PMMOEA、SparseEA在高维问题上都能取得收敛性较好的解集.相比SparseEA, DLSADA无论是在多样性还是收敛性上都有一定提升, 并且不存在高维低维不共存的情况发生, 说明DLSADA在保留一定稀疏性的前提下可有效解决大规模高维多目标问题.

3.3 稀疏性对比分析

除了研究大规模算法的分布收敛性能, 稀疏算法本身固有的稀疏性也是不可忽略的一部分.关于稀疏性问题的研究目前还处于起步阶段, 尽管在现有的多目标测试问题中存在一些稀疏多目标优化问题(Sparse Multi-objective Optimization Problems, SMOP)[12], 但大多无法全面表现MOEAs中SMOP的性能.测试问题和相关算法都不完整, 故本文基于SMOP进行性质检验, 主要是利用大规模算法的稀疏性和决策变量的关联性进行求解.

SMOP问题一共有8个问题, 从中选择3个典型问题进行前沿面的分析.分别是前沿面直线型的SMOP1、凸线型的SMOP4、凹线型的SMOP8.各算法在SMOP问题下的Pareto前沿面收敛情况如图5所示.

图5 各算法在3种SMOP问题上的Pareto前沿面收敛情况Fig.5 CPF of different algorithms for 3 SMOP problems

由图5可看到, LCSA、DGEA、Two_Arch2、LMO-CSO在稀疏性问题上具有明显劣势.原因是算法本身并不具有一定的稀疏性, 而带有稀疏性的MOEA\PSL、SparseEA、DLSADA具有明显优势, 都位于稀疏区间[0, 1]内, 性能方面都是保持自身具有的稀疏性.仔细观察3种算法之间的差别可看出, 3种算法在前沿面的收敛上几乎持平, DLSADA在SMOP8问题上比SparseEA和MOEA\PSL更靠近前沿面, 精度更高.DLSADA的目的是在保持算法固有稀疏性的基础上加强算法大规模问题的解决能力, 所以在稀疏性上的优化和进一步缩小算法的前沿面范围也是今后需要研究的方向.

3.4 综合性能及收敛性对比分析

各算法在3目标LSMOP测试问题上反世代距离(Inverted Generational Distance, IGD)值结果如表4所示.由表可看出, DLSADA在LSMOP问题上的整体性能具有明显提升, 在分布性和收敛性上做到较好的平衡, 但是也存在在某些问题上性能较差的情况.具体来说, 在LSMOP1、LSMOP4、LSMOP5问题上, 相比LCSA、MOEA\PSL, DLSADA性能与其没有显著差距, 说明DLSADA在解决这两种问题时未体现明显的改进机制, 在LSMOP2、LSMOP7问题上, DLSADA差于LMOCSO、DGEA、LCSA, 原因可能是DLSADA还是进行固定的编码子代生成和翻转策略, 在面对混合多峰问题上不能有效进行前沿面判断调整.LCSA是基于线性组合的大规模搜索算法, 在解决LSMOP问题上存在一定的全局最优结果搜索优势, 所以在一些大规模测试问题(如LSMOP3、LSMOP6、LSMOP8)上结果优于DLSADA.此外, 在LSMOP8、LSMOP9问题上, DLSADA明显优于其它7种算法, 表明其在解决这些问题上维持多样性和收敛性的能力较强, 也说明DLSADA在解决可分非线性问题上的性能优势更明显.上述情况说明DLSA-DA综合能力较优.

表4 各算法在LSMOP测试问题上的IGD值对比 Table 4 IGD values of different algorithms for LSMOP test problems

DLSADA与SparseEA在3目标LSMOP测试问题上的GD值对比结果如表5所示.由表可看出, 在LSMOP5LSMOP9问题上, DLSADA的GD值更优, 仅在LSMOP5、LSMOP8问题上未表现出明显性能优势.这说明DLSADA在保持收敛性方面具有较大提升, 通过环境选择的改进保持算法的收敛性, 提升算法整体性能.

表5 各算法在LSMOP测试问题上的GD值对比 Table 5 GD values of different algorithms for LSMOP5 test problems

除了上述综合性能和收敛性的分析, 下面通过一些特殊的测试问题展示算法的分布性和稀疏性.DLSADA和SparseEA在3目标MaF问题100个决策变量下的CPF值对比如表6所示.

表6 各算法在MaF测试问题上的CPF值对比 Table 6 CPF values of different algorithms for MaF test problems

由表6可看出, 除在MaF8、MaF9、MaF12、MaF13上未表现出优势外, DLSADA在其它MaF问题上都有一定进步, 表明在分布性能上有一定提升.MaF14、MaF15问题是决策变量与目标函数之间非均匀相关性的大规模问题, 表明DLSADA更适合解决大规模问题.

4 算法应用仿真

为了研究本文算法的应用意义, 采用汽车耐撞性优化问题进行算法的应用仿真.汽车耐撞性问题的设计要求是在吸能、加速度集成和脚趾板入侵3个目标之间寻找最佳结果[28].这也是算法在权衡不同条件下寻找一个全局最优值的一种测试环境[29].本文采用LMOCSO[8]、MOEA\PSL[11]、SparseEA[12]、LCSA[19]、DGEA[20]、TRiMOEATAR[21]、PMMOEA[22]、DLSADA解决这一问题.实际问题中参数设置如下:最大函数评价次数为100, 决策变量数量为100.在实际问题上运行得到的 IGD 和 HV 平均值作为评价结果.最终得到的结果如表7所示.由表可看出, DLSADA的IGD 平均值仅次于DGEA, 相差不大, 相比其它算法, 分布性质量较优.同时DLSADA的HV平均值仅次于LCSA和DGEA, 表现不如IGD.所以, DLSADA虽然在实际应用上不如DGEA, 但也取得较优的结果, 由此可验证DLSADA具有一定的实际应用价值.

表7 各算法在汽车碰撞优化设计问题上的IGD和HV值 Table 7 IGD and HV values of different algorithms for optimization design of vehicle collision
5 结束语

为了在保持大规模稀疏优化算法固有的稀疏性前提下提高算法的大规模问题解决能力, 更好平衡大规模稀疏优化算法的多样性和收敛性, 本文提出基于动态自适应的双档案大规模稀疏优化算法(DLSADA).首先改变环境选择策略, 加强子代生成的效率和质量, 加强算法的收敛性和多样性的平衡.同时改变算法的分数计算策略, 使分数具有动态自适应性, 加强与算法迭代次数的联系, 更适用于大规模问题中存在的多峰问题.此外, 将实际决策变量和二进制决策变量分别进行存储优化, 加快算法速度, 提高效率.在LSMOP测试问题上的结果显示, DLS-ADA的综合性能在大部分测试问题上具有明显提升, 在小部分测试问题上性能差于LMOCSO.收敛性和多样性实验表明, DLSADA在平衡性能上具有较好提升.稀疏性实验表明, DLSADA在维持原有性能上保持一定的稳定性, 甚至有小幅性能提升.最后在汽车的耐撞性优化问题上表明算法具有的一定应用价值.今后的研究方向应着眼于进一步优化算法稀疏性, 进一步缩小大规模稀疏优化算法的前沿面区间, 同时加强算法的鲁棒性和适配性, 使其适用于更多不同环境下的测试问题.

参考文献
[1] TIAN Y, CHENG R, ZHANG X Y, et al. A Strengthened Dominance Relation Considering Convergence and Diversity for Evolutio-nary Many-Objective Optimization. IEEE Transactions on Evolutionary Computation, 2019, 23(2): 331-345. [本文引用:1]
[2] SAID L B, BECHIKH S, GHEDIRA K. The r-Dominance: A New Dominance Relation for Interactive Evolutionary Multicriteria Decision Making. IEEE Transactions on Evolutionary Computation, 2010, 14(5): 801-818. [本文引用:1]
[3] WANG H D, JIAO L C, YAO X. Two_Arch2: An Improved Two-Archive Algorithm for Many-Objective Optimization. IEEE Transactions on Evolutionary Computation, 2015, 19(4): 524-541. [本文引用:2]
[4] ZHANG X Y, TIAN Y, CHENG R, et al. A Decision Variable Clustering-Based Evolutionary Algorithm for Large-Scale Many-Objective Optimization. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 97-112. [本文引用:1]
[5] 顾清华, 莫明慧, 卢才武, 等. 求解约束高维多目标问题的分解约束支配NSGA-II优化算法. 控制与决策, 2020, 35(10): 2466-2474.
(GU Q H, MO M H, LU C W, et al. Decomposition-Based Constrained Dominance Principle NSGA-II for Constrained Many-Objective Optimization Problems. Control and Decision, 2020, 35(10): 2466-2474. [本文引用:1]
[6] 顾清华, 李学现, 卢才武, 等. 求解高维复杂函数的遗传-灰狼混合算法. 控制与决策, 2020, 35(5): 1191-1198.
(GU Q H, LI X X, LU C W, et al. Hybrid Genetic Grey Wolf Algorithm for High Dimensional Complex Function Optimization. Control and Decision, 2020, 35(5): 1191-1198. ) [本文引用:1]
[7] ZILLE H, ISHIBUCHI H, MOSTAGHIM S, et al. A Framework for Large-Scale Multiobjective Optimization Based on Problem Transfor-mation. IEEE Transactions on Evolutionary Computation, 2018, 22(2): 260-275. [本文引用:1]
[8] TIAN Y, ZHENG X T, ZHANG X Y, et al. Efficient Large-Scale Multi-objective Optimization Based on a Competitive Swarm Optimizer. IEEE Transactions on Cybernetics, 2020, 50(8): 3696-3708. [本文引用:3]
[9] WANG L D, LIU Z P, FENG Y T, et al. A Parameter Estimation Method for Time-Frequency-Overlapped Frequency Hopping Signals Based on Sparse Linear Regression and Quadratic Envelope Optimi-zation. International Journal of Communication Systems, 2020, 33(12): 575-584. [本文引用:1]
[10] 肖文, 胡娟. 稀疏数据频繁项集挖掘算法研究综述. 计算机工程与科学, 2019, 41(5): 780-787.
(XIAO W, HU J. A Survey of Frequent Itemset Mining Algorithms for Sparse Datase. Computer Engineering and Science, 2019, 41(5): 780-787. ) [本文引用:1]
[11] TIAN Y, LU C, ZHANG X Y, et al. Solving Large-Scale Multi-objective Optimization Problems with Sparse Optimal Solutions via Unsupervised Neural Networks. IEEE Transactions on Cybernetics, 2021, 51(6): 3115-3128. [本文引用:3]
[12] TIAN Y, ZHANG X Y, WANG C, et al. An Evolutionary Algorithm for Large-Scale Sparse Multiobjective Optimization Problems. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 380-393. [本文引用:4]
[13] 王依柔, 张达敏. 融合正弦余弦和无限折叠迭代混沌映射的蝴蝶优化算法. 模式识别与人工智能, 2020, 33(7): 660-669.
(WANG Y R, ZHANG D M. Butterfly Optimization Algorithm Combining Sine Cosine and Iterative Chaotic Map with Infinite Co-llapses. Pattern Recognition and Artificial Intelligence, 2020, 33(7): 660-669. ) [本文引用:2]
[14] HEGAZY A E, MAKHLOUF M A, EL-TAWEL G S. Improved Salp Swarm Algorithm for Feature Selection. Journal of King Saud University(Computer and Information Sciences), 2020, 32(3): 335-344. [本文引用:1]
[15] 刘景森, 霍宇, 李煜. 优选策略的自适应蚁狮优化算法. 模式识别与人工智能, 2020, 33(2): 121-132.
(LIU J S, HUO Y, LI Y. Preferred Strategy Based Self-adaptive Ant Lion Optimization Algorithm. Pattern Recognition and Artificial Intelligence, 2020, 33(2): 121-132. ) [本文引用:1]
[16] DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Mu-ltiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. [本文引用:2]
[17] CHUGH T, JIN Y C, MIETTINEN K, et al. A Surrogate-Assisted Reference Vector Guided Evolutionary Algorithm for Computationally Expensive Many-Objective Optimization. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 129-142. [本文引用:1]
[18] SHANG R H, DAI K Y, JIAO L C, et al. Improved Memetic Algorithm Based on Route Distance Grouping for Multiobjective Large Scale Capacitated Arc Routing Problems. IEEE Transactions on Cybernetics, 2017, 46(4): 1000-1013. [本文引用:1]
[19] ZILLE H. Large-Scale Multi-objective Optimisation: New Approaches and a Classification of the State-of-the-Art[C/OL]. [2021-02-28]. https://opendata.uni-halle.de/bitstream/1981185920/32220/1/Zille_Heiner_Dissertation_2019.pdf. [本文引用:2]
[20] HE C, CHENG R, YAZDANI D. Adaptive Offspring Generation for Evolutionary Large-Scale Multiobjective Optimization. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2020. DOI: DOI:10.1109/TSMC.2020.3003926. [本文引用:2]
[21] LIU Y P, YEN G G, GONG D W. A Multi-modal Multi-objective Evolutionary Algorithm Using Two-Archive and Recombination Strategies. IEEE Transactions on Evolutionary Computation, 2019, 23(4): 660-674. [本文引用:2]
[22] TIAN Y, LU C, ZHANG X Y, et al. A Pattern Mining Based Evolutionary Algorithm for Large-Scale Sparse Multi-objective Optimization Problems. IEEE Transactions on Cybernetics, 2020. DOI: DOI:10.1109/TCYB.2020.3041325. [本文引用:2]
[23] CHENG R, JIN Y C, OLHOFER M, et al. Test Problems for Large-Scale Multiobjective and Many-Objective Optimization. IEEE Tran-sactions on Cybernetics, 2017, 47(12): 4108-4121. [本文引用:1]
[24] HUBAND S, HINGSTON P, BARONE L, et al. A Review of Multiobjective Test Problems and a Scalable Test Problem Toolkit. IEEE Transactions on Evolutionary Computation, 2006, 10(5): 477-506. [本文引用:1]
[25] TIAN Y, CHENG R, ZHANG X Y, et al. PlatEMO: A MATLAB Platform for Evolutionary Multi-objective Optimization. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87. [本文引用:1]
[26] VILLALOBOS C A K, COELLO COELLO C A. A New Multi-objective Evolutionary Algorithm Based on a Performance Assessment Indicator // Proc of the 14th Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 2012: 505-512. [本文引用:1]
[27] TIAN Y, CHENG R, ZHANG X Y, et al. Diversity Assessment of Multi-objective Evolutionary Algorithms: Performance Metric and Benchmark Problems. IEEE Computational Intelligence Magazine, 2019, 14(3): 61-74. [本文引用:2]
[28] LIAO X T, LI Q, YANG X J, et al. Multiobjective Optimization for Crash Safety Design of Vehicles Using Stepwise Regression Mo-del. Structural and Multidisciplinary Optimization, 2008, 35(6): 561-569. [本文引用:]
[29] 顾清华, 周煜丰, 李学现, 等. 基于径向空间划分的昂贵多目标进化算法[J/OL]. [2021-02-28]. https: //doi. org/1016383/j. aas. c200791.
(GU Q H, ZHOU Y F, LI X X, et al. Expensive Many-Objective Evolutionary Algorithm Based on Radial Space Division[J/OL]. [2021-02-28]. https://doi.org/10.16383/j.aas.c200791. ) [本文引用:]