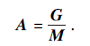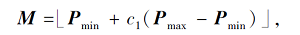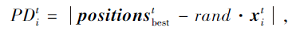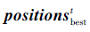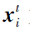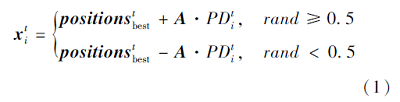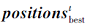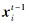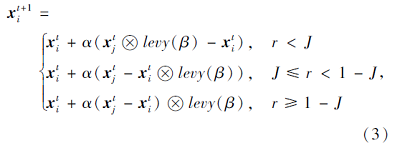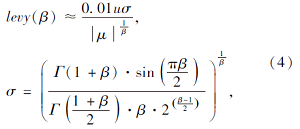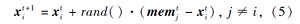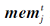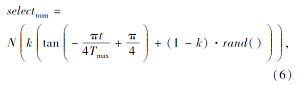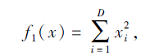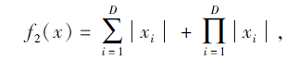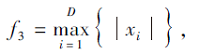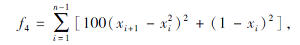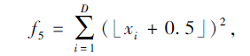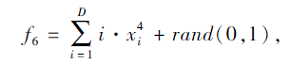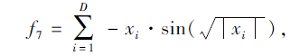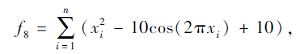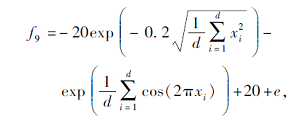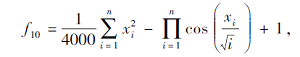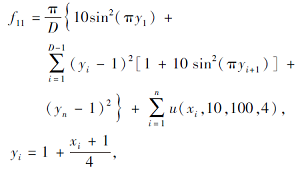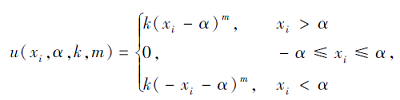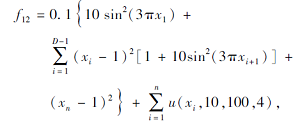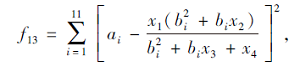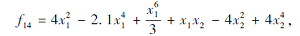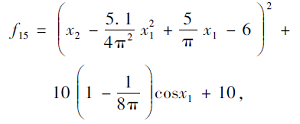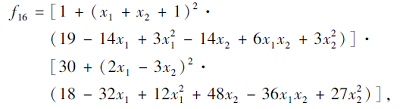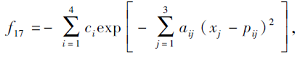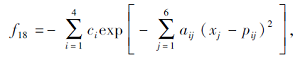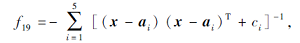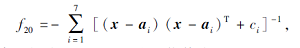优化问题一直是科学研究与工程实践、人工智能、管理决策等领域的研究热点.随着生产规模和科学技术的发展, 优化问题变得越来越复杂.传统精确求解法能求得问题域的精确解, 但算法的复杂度过大, 只适用于求解问题规模较小的领域.同时, 在解决优化问题时需要问题本身连续、可导, 对于多峰、强非线性和动态变化问题不具备全局优化的能力[1].
近年来, 基于生物系统的元启发式算法得到工业界和学术界的广泛关注.学者们从群体智能出发, 提出许多算法, 如粒子群算法(Particle Swarm Opti-mization, PSO)[2]、差分进化算法(Differential Evolu-tional, DE)[3]、布谷鸟算法(Cuckoo Search, CS)[4]、水波算法[5]等.之后, 学者们提出群体智能优化算法.例如, 根据乌鸦的智能行为提出的乌鸦搜索算法(Crow Search Algorithm, CSA)[6]、模拟灰狼群体捕猎行为的灰狼优化算法(Grey Wolf Optimization, GWO)[7]、教与学算法(Teaching-Learning-Based Optimization, TLBO)[8]、共生生物搜索算法[9]、鲸鱼优化算法[10]、原子搜索算法[11]、鹰栖优化算法[12]、樽海鞘群算法(Salp Swarm Algorithm, SSA)[13]等.
基于群体的智能算法具有深入探索搜索空间和返回全局最优解的能力, 在解决实际优化问题方面具有一定的优势.然而, 上述大多数算法的搜索机制相对较单一, 难以解决高维搜索问题.同时, 单一搜索模式具有很强的耦合性, 很难实现全局搜索和局部搜索间的有效协调.另外, 个体空间分布结构对系统整体计算具有调节作用, 这种单一模式的隐式结构关系不利于算法对计算过程的主动控制.因此, 此类架构的群体智能优化算法在求解复杂优化问题时容易出现过早收敛.
TSA与其它智能优化算法一样, 单一模式的搜索方式使被囊动物的觅食活动缺乏机动性和灵活性, 难以跳出局部最优, 算法搜索精度不高.实际上, 自然界中的被囊动物通过自身周围的神经末梢感知水流的变化和同伴的发光, 实现极强的集群行为.TSA采用直接向全局最优值聚集的方式搜索食物, 导致算法的整体搜索不充分, 没有充分利用被囊动物在群体搜索食物时的共享信息, 降低算法的搜索精度和收敛速度.因此, 本文提出信息共享的记忆被囊群算法(Memory TSA with Information Sharing, IS-MTSA).被囊动物在搜索食物过程中通过相互学习, 实现被囊动物个体之间信息的充分交流与共享, 提高算法的全局开拓能力.同时, 通过引入个体的历史最优位置引导搜索, 增强算法搜索的有效性.采用动态自适应调整策略, 动态调节执行信息共享搜索和喷气推进搜索两种策略的个体数量比例, 使算法在迭代初期有较多的个体进行全局搜索, 加速算法收敛到全局最优位置区域.在迭代后期, 进入局部搜索的个体数量增多, 增强最优值附近的局部开发能力.多搜索策略使算法在求解高维复杂问题时具有更多的选择方案, 提高算法性能.
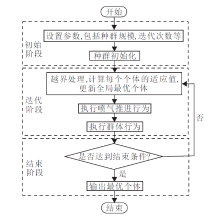
1 被囊群算法被囊群算法[14]是一种元启发式算法, 模拟被囊动物的喷气推进行为和群体行为.喷气推进行为主要利用自身的重力、深海中的水流平流、个体之间的相互作用力, 实现个体之间搜索冲突避免, 同时, 也具有向最优个体移动的能力.喷气推进行为主要由3部分组成:搜索个体冲突避免, 保持接近最佳搜索个体, 向最佳个体的位置移动.群体行为主要为更新搜索个体最优解的位置, 通过被囊动物周围的神经感知水流的变化和同伴的发光确定同伴位置, 共同向目标食物源位置聚集, 达到群体觅食的目的.TSA采用喷气推进行为和群体行为这两种策略, 更真实地模拟海洋中被囊动物群体觅食行为, 达到算法实现简单、跳出局部最优能力强、寻优精度高的目的.TSA具体流程如图1所示.
1.1 喷气推进行为皮囊动物在进行喷气推进前, 需要避免搜索个体之间的冲突.为了避免个体冲突, 计算新的位置向量:
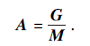
其中:G表示重力, 计算方式由文献[15]给出; M表示搜索个体之间的社会力量,
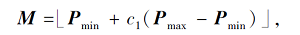
Pmin、Pmax为社交活动的最小值和最大值, c1为[0, 1]内的随机数.
在避免邻居之间的冲突后, 搜索个体朝着最佳邻居的方向发展, 此时需要计算搜索个体与食物源之间的距离.第t次迭代时第i个个体与食物来源之间的距离为
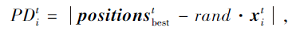
其中, rand为满足[0, 1]均匀分布的随机数, 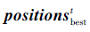 为第t次迭代时种群食物来源位置, 即当前种群最优个体位置,
为第t次迭代时种群食物来源位置, 即当前种群最优个体位置, 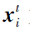 为第t次迭代时种群第i个皮囊个体位置.
为第t次迭代时种群第i个皮囊个体位置.
搜索个体向最佳食物源位置移动, 即
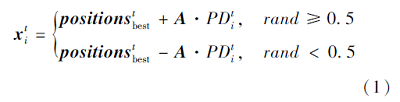
其中, 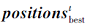 为第t次迭代时种群食物来源位置, A为个体避免冲突计算的位置向量,
为第t次迭代时种群食物来源位置, A为个体避免冲突计算的位置向量,  为当前第i个个体与食物来源之间的距离.
为当前第i个个体与食物来源之间的距离.
1.2 群体行为在避免冲突、计算个体与食物源位置距离后, 皮囊个体采用群体行为向食物源聚集.为了从数学上模拟被囊动物的群体行为, 定义被囊动物的群体行为:

其中, 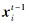 表示上一代被囊个体相对于食物源更新后的位置, c1表示[0, 1]内的随机数.
表示上一代被囊个体相对于食物源更新后的位置, c1表示[0, 1]内的随机数.
2 信息共享的记忆被囊群算法2.1 信息共享搜索策略TSA是仅依照被囊动物喷气推进与群体聚齐的生活习性而建立的群体智能搜索算法.在搜索食物过程中, 被囊动物个体以当前位置为中心, 在当前最优位置(食物源位置)与当前位置的差值构建的扇形区域内进行随机搜索, 未考虑被囊动物行为中的其它智能行为.此种单一模式的搜索方式使被囊动物的觅食活动缺乏机动性和灵活性, 难以跳出局部最优, 导致算法的搜索精度不高.实际上, 自然界中的被囊动物属于无脊椎动物, 相关研究表明, 该类动物除了表现为很强的集群行为以外, 还具有一定的免疫记忆能力与相互学习能力[16, 17].
TSA采用式(1)和式(2)的方式直接向全局最优值聚集, 导致算法的整体搜索不充分, 未充分利用被囊群体在合作搜索食物时的共享信息, 降低算法的搜索精度和收敛速度.本文采用信息共享搜索策略, 实现对领域信息的充分搜索.搜索方式为
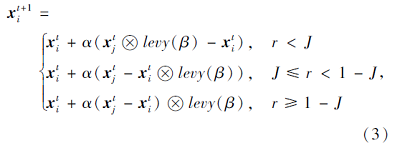
其中:r是满足(0, 1)内均匀分布的随机数; J∈ [0, 1]表示基于概率的变量, 确定种群中的个体采用何种信息共享方式, 为了使种群中的个体能以同等概率选择每种领域搜索方式, J取值为1/3; α 表示领域学习系数;  表示点乘; levy(· )表示满足levy分布的随机数.由于levy分布积分较困难, 文献[16]证明可采用Mantegana算法实现等价计算, 即
表示点乘; levy(· )表示满足levy分布的随机数.由于levy分布积分较困难, 文献[16]证明可采用Mantegana算法实现等价计算, 即
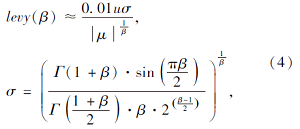
其中, u、 μ 表示[0, 1]内的随机数, β 表示常数.
在式(3)的第1部分, 被囊动物的同伴自由搜索周边领域, 并引导个体向同伴方向搜索; 第2部分搜索个体充分探索自身周围的领域空间; 第3部分引导个体向共享区域进行搜索, 获得新解.该策略的核心思想是采用不同交流算子的个体之间进行信息交换以增加种群的多样性, 充分利用各自的领域信息.此外, 该共享策略使算法在整个优化搜索过程中展现更丰富的随机行为, 避免算法陷入局部最优.
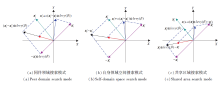
图2为二维搜索空间中信息共享搜索模式的示意图.
2.2 记忆搜索策略被囊动物在群体觅食过程中具有一定的记忆能力, 因此它们除了向领域中的个体学习以外, 还可以以一定的概率向其它个体历史最优位置领域进行搜索, 以加强对个体历史位置的充分搜索.搜索方式
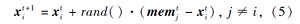
其中, rand()表示[0, 1]内均匀分布的随机数, 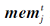 表示个体j在第t次迭代时的记忆值.
表示个体j在第t次迭代时的记忆值.
2.3 子群数量的动态调节在改进的被囊群优化算法中, 部分被囊个体执行喷气推进模式, 部分个体采用信息共享搜索模式, 如何做到合理分配、使种群中的个体执行相应的搜索模式是本文算法的一个关键问题.在迭代初期, 被囊群体中的大多数个体执行信息共享搜索方式, 提高算法的全局开拓能力, 避免陷入局部最优; 在迭代后期, 大多数个体执行喷气推进模式, 增强算法的局部搜索能力, 平衡算法局部开发与全局开拓能力.为了有效执行该方案, 本文引入动态自适应调节策略, 使种群中执行信息共享搜索模式的数量随迭代次数的增加自适应地减少, 而执行喷气推进模式的个体数量自适应地增加.设每次迭代中执行信息共享机制的数量
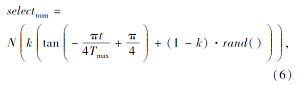
其中, t表示当前迭代次数, Tmax表示最大迭代次数, N表示种群数量, k∈ (0, 1)表示控制系数, 避免算法在迭代初期执行信息共享策略和迭代后期执行喷气推进模式的数量偏高、实现算法的局部开发和全局开拓能力的均衡.
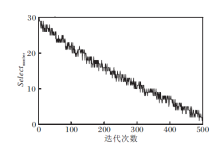
selectnumber的取值在迭代过程中的动态变化如图3所示.由图可看出:在进化初期, selectnumber取值较大, 执行信息共享机制个体较多; 随着迭代次数的增大, selectnumber取值逐渐减小, 执行喷气推进模式的个体逐渐增多.因此, selectnumber取值确保本文算法在迭代前期能保持较好的全局开拓能力, 在迭代后期, 加强局部开拓能力, 在整体上提高算法的搜索精度和收敛速度.
2.4 算法步骤算法 ISMTSA
初始化 种群x
参数设置 种群规模N, 最大迭代次数Tmax,
选择信息共享方式的控制参数J,
数量控制系数k等
计算种群中每个个体的适应度值fit(xi), 记录种群中最优个体位置positionsbest及其适应度值scorebest
记录每个个体的记忆位置memi=xi, fit(memi)=
fit(xi)
t=0
while t< Tmax
for i=1:N
对个体xi进行越界处理
计算个体更新后的适应度值fit(xi)
if fit(xi)< scorebest
scorebest=fit(xi)
positionsbest=xi
end if
if fit(xi)< fit(memi)
fit(memi)=fit(xi)
memi=xi
end if
end for
根据式(6)计算信息共享与记忆搜索的个体的数
量selectnum
for i=1:selectnum%执行信息共享与记忆搜索
p=rand(0, 1)
if rand()< 0.2 %执行记忆搜索策略
= +rand()· (me - ), j≠ i
else%执行信息共享搜索策略
if p< J
= +0.01( ⊗ levy(β )- )
else if p< (1-J)
= +α ( - ⊗ levy(β ))
else
= +α ( - )⊗ levy(β )
end if
end if
end for
for i=selectnum+1:N %执行TSA
执行喷气推进行为
执行群体行为
end for
t=t+1
end while
输出最优被囊个体positionsbest, 适应度值scorebest
3 实验及结果分析3.1 测试基准函数和测试平台仿真实验在操作系统为windows 7, CPU为Intel(R) Core(TM)i5-7400(4核), 内存为8 GB, 主频为3.0 GHz的计算机上实现, 程序采用Matlab 2016b编写.
为了验证算法性能, 本文从文献[17]、文献[18]中选择20个基准测试函数作为实验对象.测试函数具体如下.
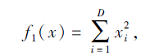
搜索区间为[-100, 100], 理论最优值为0.
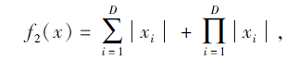
搜索区间为[-10, 10], 理论最优值为0.
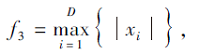
搜索区间为[-100, 100], 理论最优值为0.
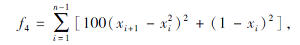
搜索区间为[-30, 30], 理论最优值为0.
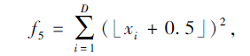
搜索区间为[-100, 100], 理论最优值为0.
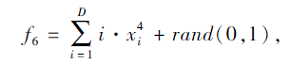
搜索区间为[-1.28, 1.28], 理论最优值为0.
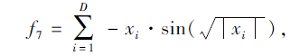
搜索区间为[-500, 500], 理论最优值为-418.9829n.
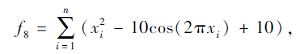
搜索区间为[-5.12, 5.12], 理论最优值为0.
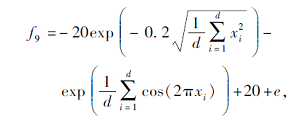
搜索区间为[-32, 32], 理论最优值为0.
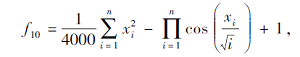
搜索区间为[-600, 600], 理论最优值为0.
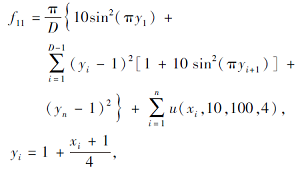
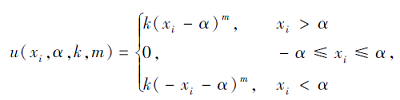
搜索区间为[-50, 50], 理论最优值为0.
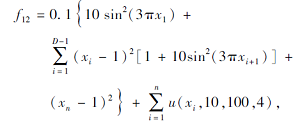
搜索区间为[-50, 50], 理论最优值为0.
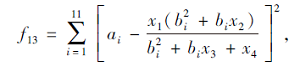
搜索区间为[-5, 5], 理论最优值为0.000 307 5.
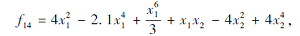
搜索区间为[-5, 5], 理论最优值为-1.031 629.
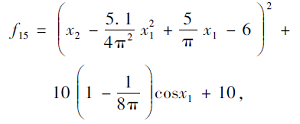
搜索区间为[-5, 10; 0, 15], 理论最优值为0.398.
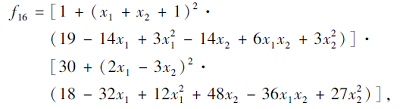
搜索区间为[-2, 2], 理论最优值为3.
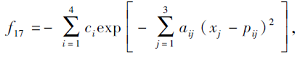
搜索区间为[0, 1], 理论最优值为-3.862 8.
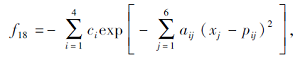
搜索区间为[0, 1], 理论最优值为-3.32.
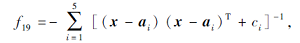
搜索区间为[0, 10], 理论最优值为-10.153 2.
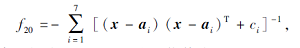
搜索区间为[0, 10], 理论最优值为-10.402 9.
在这20个基准测试函数中: f1~f6为单峰高维函数, 用于测试算法的寻优精度; f7~f12为多峰高维函数, 具有多个局部极值点, 用于测试算法的全局搜索性能; f13~f20为多峰低维函数, 绝大多数函数具有强烈的震荡特征, 局部最优值的数量随函数维数的不同而不同.f1~f12的测试维度为30, 100, 200; f13、 f19、 f20的测试维度为4; f14~f16的测试维度为2; f17的测试维度为3; f18的测试维度为6.由于测试函数集具有代表性和多样性, 因此可客观、公平、全面地评价算法的寻优性能.
3.2 实验结果对比为了对比算法性能, 选取如下对比算法:PSO[2]、DE[3]、CS[4]、CSA[6]、GWO[7]、TLBO[8]、SSA[13]、TSA.
为了对比的合理性和公平性, 各算法的种群规模N=30.对比算法的参数值来自于相应的参考文献.PSO的学习率c1=1.494 45, 学习率c2=1.494 45, 惯性权重  =0.729.DE的交叉概率pCR=0.2, 最小比例因子β min=0.2, 最大比例因子β max=0.8.CS中鸟窝被发现概率pa=0.25.CSA中记忆搜索AP=0.2, 飞行步长fl=2.TLBO中TF 值随机选择为1或2.TSA中社交活动的最小值Pmin=1, 最大值Pmax=4.在ISMTSA中, 确定种群中的个体采用何种信息共享方式的控制概率J=1/3, 执行信息共享策略子群数量的控制系数k =0.9, 社交活动的最小值Pmin=1, 最大值Pmax=4.
=0.729.DE的交叉概率pCR=0.2, 最小比例因子β min=0.2, 最大比例因子β max=0.8.CS中鸟窝被发现概率pa=0.25.CSA中记忆搜索AP=0.2, 飞行步长fl=2.TLBO中TF 值随机选择为1或2.TSA中社交活动的最小值Pmin=1, 最大值Pmax=4.在ISMTSA中, 确定种群中的个体采用何种信息共享方式的控制概率J=1/3, 执行信息共享策略子群数量的控制系数k =0.9, 社交活动的最小值Pmin=1, 最大值Pmax=4.
同时, 对于每个测试函数, 迭代次数为500次, 每种算法均独立运行30次.
单峰高维函数在30维时的测试结果如表1所示, 表中黑体数字为最优结果.由表可看出, ISMTSA的最优值、平均值和最差值都最优.此外, ISMTSA对6个函数获得的标准差最小, 说明算法的鲁棒性最强.
表1
Table 1
表1(Table 1)
 表1 各算法在f1f6函数上的测试结果 Table 1 Test results of different algorithms on f1f6| 函数 | | PSO | DE | CS | CSA | GWO | TLBO | SSA | TSA | ISMTSA |
|---|
| f1 | 最优值 | 4.99e+02 | 1.99e-04 | 1.92e+02 | 5.00e+00 | 5.40e-30 | 1.14e-43 | 2.48e-08 | 2.35e-24 | 4.08e-105 | | 平均值 | 1.34e+03 | 4.54e-04 | 4.22e+02 | 1.67e+01 | 1.55e-27 | 1.06e-42 | 2.67e-07 | 6.99e-22 | 2.56e-87 | | 最差值 | 3.10e+03 | 1.03e-03 | 7.93e+02 | 3.88e+01 | 1.46e-26 | 3.31e-42 | 1.41e-06 | 8.42e-21 | 7.67e-86 | | 方差 | 5.61e+02 | 2.15e-04 | 1.42e+02 | 6.55e+00 | 2.95e-27 | 8.98e-43 | 3.31e-07 | 1.56e-21 | 1.40e-86 | | f2 | 最优值 | 1.50e+01 | 1.53e-03 | 1.90e+01 | 2.09e+00 | 1.22e-17 | 1.91e-22 | 4.64e-06 | 7.76e-15 | 3.07e-53 | | 平均值 | 2.76e+01 | 2.20e-03 | 2.78e+01 | 3.99e+00 | 9.89e-17 | 7.05e-22 | 8.22e-02 | 1.17e-13 | 4.33e-40 | | 最差值 | 4.91e+01 | 3.02e-03 | 4.04e+01 | 5.90e+00 | 3.95e-16 | 1.97e-21 | 1.10e+00 | 5.31e-13 | 1.29e-38 | | 方差 | 8.54e+00 | 3.91e-04 | 5.21e+00 | 1.06e+00 | 9.41e-17 | 4.45e-22 | 2.63e-01 | 1.58e-13 | 2.36e-39 | | f3 | 最优值 | 1.09e+01 | 9.80e+00 | 1.56e+01 | 3.70e+00 | 6.94e-08 | 3.60e-18 | 1.20e-05 | 8.02e-03 | 2.36e-51 | | 平均值 | 1.86e+01 | 1.30e+01 | 2.10e+01 | 6.62e+00 | 7.54e-07 | 1.11e-17 | 2.56e-05 | 3.56e-01 | 4.10e-38 | | 最差值 | 2.94e+01 | 1.75e+01 | 2.65e+01 | 9.64e+00 | 6.17e-06 | 2.90e-17 | 1.03e-04 | 1.72e+00 | 1.22e-36 | | 方差 | 3.92e+00 | 1.98e+00 | 2.81e+00 | 1.58e+00 | 1.16e-06 | 6.19e-18 | 1.72e-05 | 4.48e-01 | 2.22e-37 | | f4 | 最优值 | 2.12e+04 | 4.44e+01 | 8.94e+03 | 1.41e+02 | 2.61e+01 | 2.56e+01 | 3.81e+00 | 2.62e+01 | 4.90e-14 | | 平均值 | 1.52e+05 | 1.59e+02 | 3.90e+04 | 5.19e+02 | 2.73e+01 | 2.64e+01 | 1.57e+02 | 2.84e+01 | 1.20e-10 | | 最差值 | 3.51e+05 | 2.50e+02 | 1.28e+05 | 2.34e+03 | 2.88e+01 | 2.70e+01 | 1.78e+03 | 3.15e+01 | 1.04e-09 | | 方差 | 8.19e+04 | 4.97e+01 | 2.60e+04 | 3.98e+02 | 7.53e-01 | 4.07e-01 | 3.59e+02 | 9.54e-01 | 2.14e-10 | | f5 | 最优值 | 4.37e+02 | 9.49e-05 | 2.66e+02 | 5.08e+00 | 9.95e-05 | 6.99e-04 | 3.54e-10 | 2.55e+00 | 4.93e-17 | | 平均值 | 1.43e+03 | 4.45e-04 | 4.07e+02 | 1.65e+01 | 7.37e-01 | 1.65e-02 | 9.41e-10 | 3.84e+00 | 6.34e-13 | | 最差值 | 3.20e+03 | 8.79e-04 | 6.43e+02 | 5.29e+01 | 1.51e+00 | 9.24e-02 | 1.99e-09 | 5.55e+00 | 7.83e-12 | | 方差 | 5.84e+02 | 1.90e-04 | 8.76e+01 | 9.12e+00 | 3.06e-01 | 2.55e-02 | 3.40e-10 | 7.65e-01 | 1.51e-12 | | f6 | 最优值 | 6.00e-01 | 3.23e-02 | 1.26e-01 | 2.27e-02 | 6.35e-04 | 6.48e-04 | 3.33e-03 | 2.34e-03 | 3.18e-05 | | 平均值 | 1.90e+00 | 5.86e-02 | 2.16e-01 | 5.18e-02 | 2.39e-03 | 1.96e-03 | 1.84e-02 | 1.04e-02 | 2.30e-04 | | 最差值 | 8.19e+00 | 8.10e-02 | 3.56e-01 | 1.17e-01 | 6.15e-03 | 3.39e-03 | 5.38e-02 | 2.59e-02 | 9.46e-04 | | 方差 | 1.53e+00 | 1.32e-02 | 6.20e-02 | 2.48e-02 | 1.38e-03 | 8.14e-04 | 1.45e-02 | 4.90e-03 | 2.00e-04 |
| 表1 各算法在f1f6函数上的测试结果 Table 1 Test results of different algorithms on f1f6 |
多峰高维函数在30维时的测试结果如表2所示, 表中黑体数字为最优结果.由表可看出, 对于f7f9、 f11f12 , ISMTSA在最优值、平均值、最差值和标准差上都达到最优值.对于f10, ISMTSA和TLBO都获得全局最优理想值.
表2
Table 2
表2(Table 2)
 表2 各算法在f7f12函数上的测试结果 Table 2 Test results of different algorithms on f7f12| 函数 | 统计值 | PSO | DE | CS | CSA | GWO | TLBO | SSA | TSA | ISMTSA |
|---|
| f7 | 最优值 | -7474.2 | -11491.3 | -7998.6 | -9643.5 | -7359.4 | -8918.2 | -3439.7 | -6805.4 | -12569.5 | | 平均值 | -6197.3 | -9886.3 | -7443.1 | -7138.2 | -5995.7 | -6729.5 | -2750.4 | -5936.4 | -12569.5 | | 最差值 | -4903.6 | -9108.7 | -7068.4 | -4446.9 | -4698.2 | -4478.7 | -2163.4 | -4630.3 | -12569.5 | | 方差 | 732.6 | 560.8 | 243.3 | 1064.4 | 618.2 | 1277.9 | 310.4 | 507.3 | 6.2e-07 | | f8 | 最优值 | 1.15e+02 | 6.24e+01 | 1.07e+02 | 1.06e+01 | 5.68e-14 | 8.38e+00 | 4.97e+00 | 1.23e+02 | 0 | | 平均值 | 1.64e+02 | 8.81e+01 | 1.41e+02 | 3.37e+01 | 2.00e+00 | 2.59e+01 | 1.54e+01 | 1.89e+02 | 0 | | 最差值 | 2.16e+02 | 9.68e+01 | 1.84e+02 | 5.91e+01 | 1.93e+01 | 8.08e+01 | 2.98e+01 | 2.81e+02 | 0 | | 方差 | 2.49e+01 | 7.69e+00 | 1.80e+01 | 1.07e+01 | 4.07e+00 | 1.82e+01 | 7.05e+00 | 4.26e+01 | 0 | | f9 | 最优值 | 7.59e+00 | 3.32e-03 | 8.09e+00 | 2.70e+00 | 7.19e-14 | 4.44e-15 | 1.01e-05 | 1.30e-12 | 8.88e-16 | | 平均值 | 9.75e+00 | 5.42e-03 | 1.22e+01 | 3.55e+00 | 9.70e-14 | 7.40e-15 | 8.67e-01 | 1.40e+00 | 8.88e-16 | | 最差值 | 1.25e+01 | 1.05e-02 | 1.56e+01 | 5.22e+00 | 1.36e-13 | 7.99e-15 | 2.32e+00 | 3.94e+00 | 8.88e-16 | | 方差 | 1.15e+00 | 1.64e-03 | 1.70e+00 | 6.03e-01 | 1.56e-14 | 1.35e-15 | 9.44e-01 | 1.66e+00 | 0 | | f10 | 最优值 | 5.33e+00 | 5.12e-04 | 2.42e+00 | 1.05e+00 | 0.00e+00 | 0 | 5.42e-02 | 0.00e+00 | 0 | | 平均值 | 1.43e+01 | 1.04e-02 | 4.84e+00 | 1.13e+00 | 4.70e-03 | 0 | 2.26e-01 | 1.22e-02 | 0 | | 最差值 | 3.32e+01 | 5.02e-02 | 7.63e+00 | 1.25e+00 | 2.93e-02 | 0 | 9.25e-01 | 2.59e-02 | 0 | | 方差 | 6.75e+00 | 1.31e-02 | 1.27e+00 | 4.35e-02 | 8.48e-03 | 0 | 1.81e-01 | 8.34e-03 | 0 | | f11 | 最优值 | 5.37e+00 | 1.94e-05 | 6.89e+00 | 8.90e-01 | 1.26e-02 | 7.62e-06 | 1.00e-11 | 9.48e-01 | 2.36e-18 | | 平均值 | 1.89e+01 | 4.98e-05 | 1.17e+01 | 3.50e+00 | 5.22e-02 | 3.97e-03 | 1.08e+00 | 9.59e+00 | 2.39e-15 | | 最差值 | 3.58e+01 | 1.19e-04 | 2.21e+01 | 1.05e+01 | 1.15e-01 | 1.08e-01 | 4.95e+00 | 1.61e+01 | 2.42e-14 | | 方差 | 7.29e+00 | 2.82e-05 | 3.26e+00 | 2.34e+00 | 2.56e-02 | 1.97e-02 | 1.55e+00 | 3.77e+00 | 4.85e-15 | | f12 | 最优值 | 3.42e+01 | 1.04e-04 | 3.15e+01 | 7.88e-01 | 6.35e-02 | 8.83e-04 | 2.75e-11 | 1.88e+00 | 1.18e-16 | | 平均值 | 8.51e+03 | 2.25e-04 | 7.79e+02 | 2.85e+00 | 6.14e-01 | 1.33e-01 | 2.56e-03 | 3.29e+00 | 3.56e-14 | | 最差值 | 6.10e+04 | 4.68e-04 | 9.23e+03 | 1.28e+01 | 1.08e+00 | 4.94e-01 | 1.10e-02 | 4.99e+00 | 2.56e-13 | | 方差 | 1.44e+04 | 1.09e-04 | 1.87e+03 | 2.31e+00 | 2.63e-01 | 1.29e-01 | 4.73e-03 | 7.05e-01 | 6.45e-14 |
| 表2 各算法在f7f12函数上的测试结果 Table 2 Test results of different algorithms on f7f12 |
多峰低维函数(D< 30)的测试结果如表3所示, 表中黑体数字为最优结果.由表可看出, 在最优值上, ISMTSA都搜索到理论最优值, 性能全面优于TSA.对于f13、 f19、 f20, ISMTSA在平均搜索精度、最差值、标准差上都达到最优值.对于f14~f17, ISMTSA的最优值、平均值和最差值都达到全局最优理想值.对于f18, ISMTSA的平均搜索精度仅次于DE, 说明DE适合于求解此类问题.
表3
Table 3
表3(Table 3)
 表3 各算法在f13f20函数上的测试结果 Table 3 Test results of different algorithms on f13f20| 函数 | 统计值 | PSO | DE | CS | CSA | GWO | TLBO | SSA | TSA | ISMTSA |
|---|
| f13 | 最优值 | 0.00032 | 0.00048 | 0.000477 | 0.000307 | 0.000309 | 0.000307 | 0.000621 | 0.000308 | 0.000307 | | 平均值 | 0.00510 | 0.000884 | 0.000686 | 0.000577 | 0.007078 | 0.001051 | 0.004237 | 0.007692 | 0.000308 | | 最差值 | 0.02036 | 0.00572 | 0.000885 | 0.001225 | 0.020363 | 0.020363 | 0.020373 | 0.073972 | 0.000309 | | 方差 | 0.00697 | 0.000925 | 1.00e-04 | 3.56e-04 | 9.56e-03 | 3.65e-03 | 7.34e-03 | 1.51e-02 | 2.99e-07 | | f14 | 最优值 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | | 平均值 | -1.03162 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.02741 | -1.03163 | | 最差值 | -1.03161 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1 | -1.03163 | | 方差 | 0.00000 | 6.71e-16 | 3.30e-12 | 1.92e-12 | 1.50e-08 | 6.12e-16 | 2.42e-14 | 1.09e-02 | 4.12e-12 | | f15 | 最优值 | 0.39789 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397889 | 0.397887 | | 平均值 | 0.39796 | 0.397887 | 0.397887 | 0.397887 | 0.397891 | 0.397887 | 0.397887 | 0.397935 | 0.397887 | | 最差值 | 0.39835 | 0.397887 | 0.397887 | 0.397887 | 0.39797 | 0.397887 | 0.397887 | 0.398149 | 0.397887 | | 方差 | 0.00010 | 0 | 7.33e-10 | 6.00e-13 | 1.49e-05 | 0 | 2.50e-14 | 5.83e-05 | 1.13e-11 | | f16 | 最优值 | 3.00002 | 3 | 3 | 3 | 3 | 3 | 3 | 3.00001 | 3 | | 平均值 | 3.00039 | 3 | 3 | 3 | 3.000037 | 3 | 3 | 21.26796 | 3 | | 最差值 | 3.00202 | 3 | 3 | 3 | 3.000188 | 3 | 3 | 92.03524 | 3 | | 方差 | 0.00048 | 1.31e-15 | 6.46e-11 | 1.44e-11 | 4.49e-05 | 1.20e-15 | 2.75e-13 | 3.33e+01 | 1.30e-09 | | f17 | 最优值 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | | 平均值 | -3.86277 | -3.86278 | -3.86278 | -3.86278 | -3.86114 | -3.86278 | -3.86278 | -3.86264 | -3.86278 | | 最差值 | -3.86270 | -3.86278 | -3.86278 | -3.86278 | -3.8549 | -3.86278 | -3.86278 | -3.86205 | -3.86278 | | 方差 | 0.00002 | 2.71e-15 | 4.17e-11 | 3.15e-11 | 3.02e-03 | 2.70e-15 | 2.29e-12 | 1.47e-04 | 1.19e-07 | | f18 | 最优值 | -3.32186 | -3.322 | -3.32199 | -3.322 | -3.32199 | -3.322 | -3.322 | -3.32126 | -3.322 | | 平均值 | -3.21955 | -3.31683 | -3.3217 | -3.27414 | -3.25876 | -3.3024 | -3.2298 | -3.22685 | -3.28446 | | 最差值 | -2.89553 | -3.2031 | -3.32057 | -3.19805 | -3.08678 | -3.2031 | -3.16687 | -1.84195 | -3.1941 | | 方差 | 0.12742 | 0.022459 | 3.56e-04 | 5.96e-02 | 8.35e-02 | 4.43e-02 | 6.22e-02 | 2.71e-01 | 5.69e-02 | | f19 | 最优值 | -10.11087 | -10.1532 | -10.1532 | -10.1532 | -10.1529 | -10.1532 | -10.1532 | -10.0856 | -10.1532 | | 平均值 | -5.63937 | -9.53641 | -10.1517 | -9.4783 | -9.64331 | -10.0974 | -7.30901 | -5.96186 | -10.1532 | | 最差值 | -2.57757 | -2.68286 | -10.1465 | -5.0552 | -5.05511 | -8.69399 | -2.63047 | -2.56962 | -10.1532 | | 方差 | 3.12219 | 1.921266 | 1.78e-03 | 1.74e+00 | 1.55e+00 | 2.66e-01 | 3.40e+00 | 3.15e+00 | 4.82e-08 | | f20 | 最优值 | -10.35962 | -10.4029 | -10.4028 | -10.4029 | -10.4028 | -10.4029 | -10.4029 | -10.309 | -10.4029 | | 平均值 | -8.35202 | -10.3672 | -10.3845 | -9.87416 | -10.0485 | -9.24066 | -8.02432 | -6.43099 | -10.4029 | | 最差值 | -2.71614 | -9.96865 | -10.2534 | -5.08767 | -5.08766 | -3.7243 | -2.75193 | -1.83263 | -10.4029 | | 方差 | 2.82087 | 0.094987 | 4.00e-02 | 1.61e+00 | 1.34e+00 | 2.38e+00 | 3.25e+00 | 3.41e+00 | 3.30e-09 |
| 表3 各算法在f13f20函数上的测试结果 Table 3 Test results of different algorithms on f13f20 |
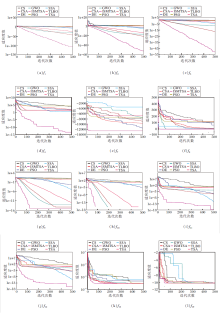
各算法求解部分函数的收敛曲线如图4所示.由图可看出, 相比其它方法, ISMTSA的收敛速度和精度都达到最优, 这进一步说明改进策略的有效性和可行性.
3.3 高维函数上的搜索性能为了验证ISMTSA在高维情况下的搜索性能, 对f1~f12分别进行100维、200维的独立测试.对于每个测试函数, 各算法的参数与3.2节一致.每种算法均独立执行30次, 实验结果如表4和表5所示, 表中黑体数字表示最优结果.
表4
Table 4
表4(Table 4)
 表4 各算法在100维函数上的测试结果 Table 4 Text results of different algorithms on 100-dimensional functions| 函数 | | CS | CSA | DE | GWO | PSO | SSA | TLBO | TSA | ISMTSA |
|---|
| f1 | 平均值
方差 | 1.08e+04
1.30e+03 | 9.10e+02
1.28e+02 | 1.76e+03
2.40e+02 | 1.44e-12
1.17e-12 | 1.20e+04
2.09e+03 | 1.41e+03
4.04e+02 | 2.57e-38
2.33e-38 | 2.59e-10
3.12e-10 | 1.24e-82
5.08e-82 | | f2 | 平均值
方差 | 1.29e+02
1.98e+01 | 2.69e+01
2.22e+00 | 2.96e+01
2.39e+00 | 3.28e-08
1.12e-08 | 1.13e+02
2.28e+01 | 4.67e+01
6.71e+00 | 1.08e-19
6.16e-20 | 2.68e-07
2.39e-07 | 2.74e-41
8.58e-41 | | f3 | 平均值
方差 | 3.60e+01
2.79e+00 | 1.28e+01
1.12e+00 | 9.02e+01
1.77e+00 | 6.96e-01
5.97e-01 | 2.75e+01
3.43e+00 | 2.86e+01
4.12e+00 | 9.04e-16
3.94e-16 | 5.35e+01
1.20e+01 | 4.00e-34
2.17e-33 | | f4 | 平均值
方差 | 3.82e+06
1.04e+06 | 3.16e+04
7.84e+03 | 2.33e+06
6.03e+05 | 9.78e+01
7.12e-01 | 3.49e+06
1.61e+06 | 1.70e+05
1.01e+05 | 9.76e+01
5.50e-01 | 9.83e+01
4.33e-01 | 3.58e-09
1.39e-08 | | f5 | 平均值
方差 | 1.05e+04
1.44e+03 | 9.19e+02
1.42e+02 | 1.89e+03
3.09e+02 | 9.78e+00
8.32e-01 | 1.14e+04
2.22e+03 | 1.33e+03
3.09e+02 | 5.70e+00
7.02e-01 | 1.44e+01
1.04e+00 | 9.99e-13
2.33e-12 | | f6 | 平均值
方差 | 5.88e+00
1.59e+00 | 3.84e-01
7.00e-02 | 3.18e+00
6.04e-01 | 6.91e-03
3.44e-03 | 5.89e+01
4.00e+01 | 2.67e+00
8.09e-01 | 2.92e-03
1.09e-03 | 4.94e-02
2.15e-02 | 2.09e-04
2.08e-04 | | f7 | 平均值
方差 | -1.65e+04
4.43e+02 | -1.53e+04
2.79e+03 | -1.63e+04
4.56e+02 | -1.60e+04
2.62e+03 | -1.20e+04
2.20e+03 | -2.22e+04
1.62e+03 | -1.31e+04
3.03e+03 | -1.33e+04
1.22e+03 | -4.19e+04
5.12e-07 | | f8 | 平均值
方差 | 7.64e+02
3.73e+01 | 3.61e+02
3.73e+01 | 8.02e+02
2.02e+01 | 9.37e+00
6.84e+00 | 8.13e+02
4.75e+01 | 2.40e+02
4.35e+01 | 0
0 | 9.94e+02
1.17e+02 | 0
0 | | f9 | 平均值
方差 | 1.53e+01
1.58e+00 | 5.97e+00
4.02e-01 | 7.55e+00
3.44e-01 | 1.17e-07
4.30e-08 | 1.25e+01
8.66e-01 | 9.97e+00
9.17e-01 | 8.23e-15
1.30e-15 | 9.06e-02
4.96e-01 | 8.88e-16
0 | | f10 | 平均值
方差 | 1.01e+02
1.51e+01 | 9.32e+00
9.90e-01 | 1.71e+01
1.79e+00 | 6.96e-03
1.21e-02 | 1.16e+02
2.86e+01 | 1.24e+01
3.36e+00 | 0
0 | 9.98e-03
1.45e-02 | 0
0 | | f11 | 平均值
方差 | 6.93e+04
7.69e+04 | 8.72e+00
1.93e+00 | 1.38e+06
7.14e+05 | 2.93e-01
6.25e-02 | 1.65e+04
3.56e+04 | 3.43e+01
1.21e+01 | 7.48e-02
1.77e-02 | 1.19e+01
3.55e+00 | 1.66e-15
3.25e-15 | | f12 | 平均值
方差 | 2.29e+06
1.08e+06 | 1.33e+02
3.56e+01 | 5.25e+06
2.12e+06 | 6.77e+00
4.67e-01 | 2.03e+06
1.96e+06 | 3.42e+03
7.01e+03 | 6.63e+00
6.93e-01 | 1.35e+01
2.08e+00 | 1.77e-13
3.35e-13 |
| 表4 各算法在100维函数上的测试结果 Table 4 Text results of different algorithms on 100-dimensional functions |
表5
Table 5
表5(Table 5)
 表5 各算法在200维函数上的测试结果 Table 5 Text results of different algorithms on 200-dimensional functions| 函数 | 统计值 | CS | CSA | DE | GWO | PSO | SSA | TLBO | TSA | ISMTSA |
|---|
| f1 | 平均值
方差 | 3.26e+04
4.61e+03 | 3.18e+03
3.05e+02 | 8.14e+04
6.28e+03 | 1.06e-07
5.71e-08 | 2.77e+04
5.16e+03 | 1.77e+04
2.26e+03 | 5.71e-37
6.05e-37 | 3.83e-06
4.35e-06 | 5.80e-69
3.18e-68 | | f2 | 平均值
方差 | 2.59e+02
1.99e+01 | 6.72e+01
2.57e+00 | 2.69e+03
1.22e+04 | 3.37e-05
7.93e-06 | 2.30e+02
3.02e+01 | 1.58e+02
9.63e+00 | 5.43e-19
2.75e-19 | 4.34e-05
3.11e-05 | 1.55e-38
8.01e-38 | | f3 | 平均值
方差 | 4.33e+01
2.90e+00 | 1.51e+01
1.25e+00 | 9.79e+01
6.49e-01 | 2.84e+01
9.50e+00 | 3.22e+01
3.04e+00 | 3.49e+01
3.24e+00 | 3.23e-15
1.32e-15 | 9.44e+01
3.48e+00 | 4.65e-36
1.58e-35 | | f4 | 平均值
方差 | 1.45e+07
3.54e+06 | 1.65e+05
2.47e+04 | 3.00e+08
2.36e+07 | 1.98e+02
5.42e-01 | 9.10e+06
3.15e+06 | 4.08e+06
8.44e+05 | 1.98e+02
2.81e-01 | 2.16e+02
9.37e+01 | 1.77e-09
5.16e-09 | | f5 | 平均值
方差 | 3.24e+04
3.63e+03 | 3.30e+03
2.41e+02 | 8.26e+04
5.79e+03 | 2.90e+01
1.42e+00 | 2.68e+04
3.82e+03 | 1.73e+04
2.77e+03 | 2.31e+01
1.28e+00 | 3.42e+01
1.49e+00 | 6.07e-11
3.07e-10 | | f6 | 平均值
方差 | 4.18e+01
9.48e+00 | 1.18e+00
2.15e-01 | 6.70e+02
7.38e+01 | 1.53e-02
4.34e-03 | 3.98e+02
1.54e+02 | 1.95e+01
3.33e+00 | 3.21e-03
6.99e-04 | 1.92e-01
6.43e-02 | 0.000174
0.000174 | | f7 | 平均值
方差 | -2.45e+04
6.86e+02 | -2.40e+04
2.83e+03 | -2.31e+04
8.11e+02 | -2.77e+04
5.51e+03 | -1.73e+04
2.89e+03 | -3.49e+04
2.80e+03 | -1.87e+04
5.90e+03 | -1.95e+04
1.41e+03 | -83796.6
1.04e-06 | | f8 | 平均值
方差 | 1.75e+03
4.55e+01 | 1.06e+03
5.73e+01 | 2.21e+03
4.03e+01 | 2.65e+01
1.36e+01 | 1.84e+03
1.15e+02 | 8.28e+02
9.11e+01 | 0
0 | 2.17e+03
2.27e+02 | 0
0 | | f9 | 平均值
方差 | 1.65e+01
1.37e+00 | 6.77e+00
3.55e-01 | 1.76e+01
3.05e-01 | 2.18e-05
5.01e-06 | 1.30e+01
1.46e+00 | 1.31e+01
5.87e-01 | 8.23e-15
1.30e-15 | 2.83e-04
2.38e-04 | 8.88e-16
0 | | f10 | 平均值
方差 | 2.92e+02
3.20e+01 | 2.94e+01
2.58e+00 | 7.46e+02
5.70e+01 | 2.61e-03
9.95e-03 | 2.49e+02
4.61e+01 | 1.47e+02
1.99e+01 | 0
0 | 2.37e-02
3.07e-02 | 0
0 | | f11 | 平均值
方差 | 1.42e+06
1.03e+06 | 1.08e+01
2.12e+00 | 6.78e+08
6.86e+07 | 5.16e-01
5.59e-02 | 3.32e+05
6.24e+05 | 3.72e+03
6.72e+03 | 2.48e-01
2.88e-02 | 5.30e+02
1.13e+03 | 8.42e-15
3.46e-14 | | f12 | 平均值
方差 | 1.40e+07
6.56e+06 | 3.58e+02
9.82e+01 | 1.28e+09
1.89e+08 | 1.67e+01
4.82e-01 | 8.38e+06
6.32e+06 | 1.39e+06
6.58e+05 | 1.86e+01
8.53e-01 | 2.91e+02
1.58e+02 | 2.08e-13
3.41e-13 |
| 表5 各算法在200维函数上的测试结果 Table 5 Text results of different algorithms on 200-dimensional functions |
由表4和表5可看出, 除f8和f10之外, 无论是求解100维还是200维问题, ISMTSA获得的最优值、平均值、最差值、方差都最优.对于f8和f10, ISMTSA和TLBO的搜索结果一致, 都获得全局最优理想值.同时, ISMTSA无论对低维函数(D≤ 100)的搜索, 还是对高维函数的搜索, 搜索结果都非常接近.这些都说明ISMTSA对于高维函数的寻优具有良好性能.
3.4 非参数统计分析为了更好地评价算法, 确定ISMTSA与其它算法的寻优效果是否具有显著性, 在 0.05显著性水平下进行Wilcoxon非参数检验.低维(30维及以下)Wilcoxon检验结果如表6所示.
表6
Table 6
表6(Table 6)
 表6 各算法的Wilcoxon秩和检验的统计结果 Table 6 Statistical results of Wilcoxon rank sum test of different algorithms| 函数 | ISMTSA vs.
CS | ISMTSA vs.
CSA | ISMTSA vs.
DE | ISMTSA vs.
GWO | ISMTSA vs.
PSO | ISMTSA vs.
SSA | ISMTSA vs.
TLBO | ISMTSA vs.
TSA |
|---|
| f1 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f2 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f3 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f4 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f5 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f6 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 4.08e-11★ | 3.02e-11★ | 3.02e-11★ | 4.08e-11★ | 3.02e-11★ | | f7 | 2.99e-11★ | 2.99e-11★ | 2.99e-11★ | 2.99e-11★ | 2.99e-11★ | 2.99e-11★ | 2.99e-11★ | 2.99e-11★ | | f8 | 1.21e-12★ | 1.21e-12★ | 1.21e-12★ | 1.15e-12★ | 1.21e-12★ | 1.21e-12★ | 1.21e-12★ | 1.21e-12★ | | f9 | 1.21e-12★ | 1.21e-12★ | 1.21e-12★ | 1.12e-12★ | 1.21e-12★ | 1.21e-12★ | 1.18e-13★ | 1.21e-12★ | | f10 | 1.21e-12★ | 1.21e-12★ | 1.21e-12★ | 0.002788★ | 1.21e-12★ | 1.21e-12★ | NA◇ | 1.7e-08★ | | f11 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f12 | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | | f13 | 3.02e-11★ | 8.15e-05★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 3.02e-11★ | 0.006669★ | 1.33e-10★ | | f14 | 0.329117◇ | 0.149307◇ | 4.55e-12★ | 3.01e-11★ | 3.01e-11★ | 1.22e-08★ | 4.55e-12★ | 3.01e-11★ | | f15 | 1.96e-10★ | 0.501126★ | 1.21e-12★ | 3.02e-11★ | 3.02e-11★ | 7.32e-07★ | 1.21e-12★ | 3.02e-11★ | | f16 | 1.39e-06★ | 3.21e-08★ | 1.21e-12★ | 3.02e-11★ | 3.02e-11★ | 4.04e-11★ | 1.72e-12★ | 3.02e-11★ | | f17 | 1.56e-08★ | 4.2e-10★ | 1.21e-12★ | 3.02e-11★ | 4.5e-11★ | 4.07e-11★ | 1.21e-12★ | 3.02e-11★ | | f18 | 2.38e-07★ | 0.005084★ | 1.92e-09★ | 0.042067★ | 0.031466★ | 0.09049◇ | 7.24e-06★ | 0.003848★ | | f19 | 3.02e-11★ | 7.38e-10★ | 0.00062★ | 3.02e-11★ | 3.02e-11★ | 0.176128◇ | 0.077439◇ | 3.02e-11★ | | f20 | 3.02e-11★ | 6.12e-10★ | 0.004589★ | 3.02e-11★ | 3.02e-11★ | 0.761828◇ | 0.001546★ | 3.02e-11★ | 最优结果
数量 | 19 | 19 | 20 | 20 | 20 | 17 | 18 | 20 |
| 表6 各算法的Wilcoxon秩和检验的统计结果 Table 6 Statistical results of Wilcoxon rank sum test of different algorithms |
在表6中, ★表示ISMTSA相对对比算法具有显著性, ◇表示ISMTSA相对对比算法无明显差异.
其中显著性水平p< 0.05被认为是针对零假设的充分证据.
由表6可看出, 对比DE、GWO、PSO、TSA, 所有函数的p< 0.05, 说明ISMTSA与这四种算法性能对比是显著的.对比CS、CSA、SSA、TLBO, 分别有19、19、17、18个函数的p< 0.05.从统计学的角度分析出ISMTSA的寻优性能显著优于对比算法的性能.
3.5 参数敏感性分析在ISMTSA中, 执行信息共享搜索模式的数量随迭代次数的增加自适应减少, 而执行喷气推进模式的个体数量却自适应增加, 在算法的迭代前期能保持较好的全局开拓能力, 在迭代后期, 局部开拓能力加强, 从整体上提高算法的搜索精度和收敛速度.因此, 执行信息共享策略的子群数量的控制系数k对算法的搜索结果具有较大影响.
本文选取k=0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 分析k对算法性能的影响.其余参数与3.2节的ISMTSA参数保持一致.每个测试函数在k不同时独立运行30次.
k不同时ISMTSA求解各函数值的结果如表7所示, 表中黑体数字表示最优结果.
表7
Table 7
表7(Table 7)
 表7 k不同时ISMTSA解得的函数值 Table 7 Values of functions by ISMTSA with different k| 函数 | k=0.2 | k=0.3 | k=0.4 | k=0.5 | k=0.6 | k=0.7 | k=0.8 | k=0.9 |
|---|
| f1 | 4.1e-120 | 1.9e-121 | 1.9e-116 | 6.1e-115 | 1.2e-104 | 2.04e-91 | 6.23e-88 | 2.56e-87 | | f2 | 5.95e-58 | 7.33e-61 | 4.12e-55 | 1.22e-57 | 9.7e-53 | 7.26e-46 | 6.03e-47 | 4.33e-40 | | f3 | 8.58e-53 | 3.14e-55 | 1.04e-54 | 8.07e-55 | 7.17e-51 | 3.98e-48 | 2.31e-43 | 4.1e-38 | | f4 | 1.91e-06 | 1.45e-06 | 0.000132 | 4.37e-07 | 5.23e-05 | 1.56e-05 | 0.001292 | 1.2e-10 | | f5 | 1.7e-09 | 1.44e-10 | 9.94e-11 | 1.21e-10 | 2.27e-11 | 1.64e-11 | 4.55e-12 | 6.34e-13 | | f6 | 4.36e-04 | 3.17e-04 | 1.74e-04 | 2.25e-04 | 1.90e-04 | 1.46e-04 | 1.75e-04 | 2.30e-04 | | f7 | -11174.3 | -11608.3 | -11832 | -11862 | -11503.5 | -12095.7 | -12214.2 | -12569.5 | | f8 | 7.927247 | 4.974795 | 3.979836 | 1.989918 | 0 | 0.994959 | 0 | 0 | | f9 | 8.88e-16 | 8.88e-16 | 8.88e-16 | 8.88e-16 | 8.88e-16 | 8.88e-16 | 8.88e-16 | 8.88e-16 | | f10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | f11 | 4.69e-12 | 3.65e-12 | 8.45e-13 | 7.87e-13 | 1.63e-13 | 5.1e-14 | 1.74e-14 | 2.39e-15 | | f12 | 1.88e-10 | 1.04e-10 | 3.97e-11 | 1.58e-11 | 1.75e-12 | 4.88e-13 | 3.14e-13 | 3.56e-14 | | f13 | 0.000976 | 0.000976 | 0.000308 | 0.000308 | 0.000308 | 0.000308 | 0.000308 | 0.000308 | | f14 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | | f15 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | | f16 | 8.4 | 4.8 | 3 | 4.8 | 3.9 | 4.8 | 3.9 | 3 | | f17 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | -3.86278 | | f18 | -3.27731 | -3.27357 | -3.27794 | -3.26578 | -3.27391 | -3.28555 | -3.2821 | -3.28446 | | f19 | -9.64492 | -9.81333 | -9.81485 | -9.98478 | -9.98327 | -10.1532 | -10.1532 | -10.1532 | | f20 | -9.69561 | -10.0486 | -10.2258 | -10.4025 | -10.4029 | -10.4029 | -10.4029 | -10.4029 | 最优结果
数量 | 6 | 7 | 7 | 5 | 8 | 10 | 8 | 15 |
| 表7 k不同时ISMTSA解得的函数值 Table 7 Values of functions by ISMTSA with different k |
由表7可看出, 当k=0.9时, 获得平均最优值的数量分别为15个, 多于取其它值的个数.因此, 本文取k=0.9较合理.
为了研究领域学习系数α 对算法的影响, 选取f4、 f6、 f7、 f8、 f11、 f13、 f14作为测试函数.这7个函数中单峰高维函数3个, 多峰高维函数2个, 多峰低维函数2个.实验中α =0.005, 0.01, 0.05, 0.1, 0.5.其余参数保持相同, 独立运行30次.α 不同时, ISMTSA求解函数值的结果如表8所示.
表8
Table 8
表8(Table 8)
 表8 α 不同时ISMTSA解得的函数值 Table 8 Values of functions by ISMTSA with different α | 函数 | α =0.5 | α =0.1 | α =0.05 | α =0.01 | α =0.005 |
|---|
| f4 | 1.14e-07 | 2.13e-08 | 1.33e-10 | 1.20e-10 | 5.58e-10 | | f6 | 1.65e-04 | 3.94e-04 | 5.11e-04 | 2.30e-04 | 3.43e-04 | | f7 | -10674.3 | -10483.9 | -11049.5 | -12569.5 | -12569.5 | | f8 | 0 | 0 | 0 | 0 | 0 | | f11 | 1.01e-14 | 2.35e-15 | 5.48e-15 | 2.39e-15 | 3.34e-15 | | f13 | 0.000308 | 0.000976 | 0.002313 | 0.000308 | 0.000976 | | f14 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | -1.03163 | 最优结果
数量 | 3 | 3 | 2 | 5 | 3 |
| 表8 α 不同时ISMTSA解得的函数值 Table 8 Values of functions by ISMTSA with different α |
由表8可看出, 当α =0.01时, 获得平均最优值的数量分别为5个, 多于取其它值的个数.因此, 本文取α =0.01作为领域学习系数值.
3.6 时间复杂度分析时间复杂度是反映算法性能的关键指标之一, 直接体现算法执行效果的优劣.在TSA中:设种群规模为N, 问题的维度为d, 产生一个随机数的时间为ω 1, 求解该测试函数的适应度值为f(d), 则TSA在初始化种群阶段的时间复杂度为
T1=O(N(dω 1+f(d)))=O(d+f(d)).
进入迭代阶段后, 总的迭代次数为Tmax, 在喷气推进阶段, 计算每维M、G、A和PD的时间分别设为ω 2、ω 3、ω 4、ω 5, 执行式(1)所需时间为ω 6, 则喷气推进的时间复杂度为
T2=O(Nd(ω 2+ω 3+ω 4+ω 5+ω 6))=O(d).
在群体行为阶段, 设执行式(2)所需要时间为ω 7, 则群体行为阶段的时间复杂度为
T3=O(Nd(ω 7))=O(d).
在边界处理和更新种群个体位置阶段, 设每维边界处理的时间为ω 8, 计算个体适应度值的时间为f(d), 替换最优个体的时间为ω 9, 则执行该阶段的时间复杂度为
T4=O(N(dω 8+dω 9+f(d))=O(d+f(d)).
综上所述, TSA总的时间复杂度为
T(d)=T1+Tmax(T2+T3+T4)=O(d+f(d)).
对于ISMTSA, 种群规模、求解问题的维度、适应度值的求解方式都与TSA一致, 因此, ISMTSA初始阶段的时间复杂度为
T1'=O(d+f(d)).
进入迭代阶段后, 设由式(6)计算信息共享与记忆搜索的个体数量selectnum的时间为σ 1.在执行信息共享与记忆搜索策略时, 按照式(4)计算每维满足levy分布的随机数时间为σ 2, 执行式(5)记忆搜索策略时间为σ 3, 执行式(3)记忆搜索策略时间为σ 4, 此阶段的时间复杂度为
T2'=O(σ 1+0.2selectnumσ 3d+ (1-0.2)selectnumd(σ 2+σ 4))=O(d).
剩余的N-selectnum个体执行TSA的喷气推进行为和群体行为操作相同, 时间复杂度为
T3'=O(d).
在边界处理和更新种群个体位置阶段时间复杂度与TSA一致, 因此, 执行该阶段的时间复杂度为
T4'=T4=O(d+f(d)).
综上所述, ISMTSA总的时间复杂度为
T'(d)=T1'+Tmax(T2'+T3'+T4')=O(d+f(d)).
ISMTSA与TSA的时间复杂度相同.为了更直观对比ISMTSA和TSA的时间复杂度, 采用ISMTSA和TSA, 在相同的测试环境下, 测试5个基准函数, 每个基准函数独立运行30次, 计算平均耗时, 结果如表9所示.
表9
Table 9
表9(Table 9)
 表9 各算法在不同维度时的平均耗时对比 Table 9 Comparison of average consumption time of different algorithms with different dimensions s| 函数 | d=30 | d=100 | d=200 |
|---|
| TSA | ISMTSA | 耗时比例 | | TSA | ISMTSA | 耗时比例 | | TSA | ISMTSA | 耗时比例 | |
|---|
| f6 | 6.26e-03 | 7.68e-03 | 1.23 | 1.55e-02 | 1.76e-02 | 1.13 | 2.91e-02 | 3.22e-02 | 1.11 | | f8 | 4.19e-03 | 5.53e-03 | 1.32 | 9.72e-03 | 1.11e-02 | 1.14 | 1.80e-02 | 1.92e-02 | 1.07 | | f10 | 4.77e-03 | 6.32e-03 | 1.32 | 1.01e-02 | 1.19e-02 | 1.18 | 1.87e-02 | 2.04e-02 | 1.09 | | f11 | 1.11e-02 | 1.26e-02 | 1.13 | 2.64e-02 | 2.79e-02 | 1.06 | 5.08e-02 | 5.09e-02 | 1.00 | | f12 | 1.12e-02 | 1.26e-02 | 1.13 | 2.63e-02 | 2.81e-02 | 1.07 | 4.87e-02 | 5.09e-02 | 1.04 | | 平均值 | 7.51e-03 | 8.96e-03 | 1.23 | 1.76e-02 | 1.93e-02 | 1.12 | 3.30e-02 | 3.47e-02 | 1.06 |
| 表9 各算法在不同维度时的平均耗时对比 Table 9 Comparison of average consumption time of different algorithms with different dimensions s |
由表9可看出, 在测试规模较小的函数时, ISMTSA平均耗时长于TSA, 但随着测试维度的增加, 平均耗时与TSA逐渐保持一致.由于增加执行信息共享与记忆搜索策略时的个体数量的计算时间及产生levy分布的随机数的时间, 当求解问题规模较小时, 此部分耗时所占比例相对较高, 但随着测试维度的增加, 该部分耗时所占比例逐渐减少.由此进一步验证ISMTSA在求解大规模问题上的优势.