多种群伪正态分布估计算法

引用本文

杨启文, 余诗琦, 张美琳, 薛云灿, 陈俊风. 多种群伪正态分布估计算法. 模式识别与人工智能, 2021,34(7): 619-630
YANG Qiwen, YU Shiqi, ZHANG Meilin, XUE Yuncan, CHEN Junfeng. Multiple Populations Based Estimation of Pseudo-Normal Distribution Algorithm. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(7): 619-630. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202107004
Permissions

《模式识别与人工智能》编辑部

多种群伪正态分布估计算法

杨启文¹, 余诗琦¹, 张美琳¹, 薛云灿¹, 陈俊风¹

1.河海大学物联网工程学院常州 213022

通讯作者:

杨启文,博士,副教授,主要研究方向为计算智能、系统优化与控制.E-mail:yangqw@hhu.edu.cn.

作者简介:

余诗琦,硕士研究生,主要研究方向为检测技术、智能系统.E-mail:445603497@qq.com.

张美琳,硕士研究生,主要研究方向为系统调度与优化.E-mail:Zhang_Merlin@163.com.

薛云灿,博士,教授,主要研究方向为智能优化、过程建模与控制.E-mail:ycxue@hhuc.edu.cn.

陈俊风,博士,副教授,主要研究方向为计算智能、大数据分析.E-mail:chen-1997@163.com.

收稿日期: 2020-11-15 修回日期: 2021-03-31 接受日期: 2021-03-31

摘要

为了提高基于正态分布模型的分布估计算法子代候选解的质量,防止早熟收敛,文中提出多种群伪正态分布估计算法.首先,采用佳点集方法进行种群初始化,将种群分为3个子群.然后,采用样本重心取代样本均值的方式,获得伪正态分布模型.最后,融合种群与子群伪正态分布模型,得到子群进化的概率模型.23个基准函数的对比测试表明,文中算法在求解质量和收敛速度上较优.针对多约束条件下的并行装配优化问题,提出工序池、员工池、罚函数等措施,将具有工序约束和人员约束的离散组合优化问题转化为无约束的多种群伪正态分布估计优化问题.工程应用结果表明,只需要将候选解的无限集合修正为有限集合,文中算法可方便地用于离散组合优化问题的快速求解.

关键词: 分布估计算法; 正态分布; 并行装配问题; 多种群

中图分类号:TP 18

Multiple Populations Based Estimation of Pseudo-Normal Distribution Algorithm

YANG Qiwen¹, YU Shiqi¹, ZHANG Meilin¹, XUE Yuncan¹, CHEN Junfeng¹

1. College of Internet of Things Engineering, Hohai University, Changzhou 213022

Corresponding author:
YANG Qiwen, Ph.D., associate professor. His research interests include computational intelligence, sys-tem optimization and control.

About Author:
YU Shiqi, master student. Her research interests include detection technology and inte-lligent system.
ZHANG Meilin, master student. Her research interests include system scheduling and optimization.
XUE Yuncan, Ph.D., professor. His research interests include intelligent optimization, process modeling and control.
CHEN Junfeng, Ph.D., associate profe-ssor. Her research interests include computational intelligence and big data analysis.

Abstract

To improve the quality of the candidate solutions and prevent the premature convergence simultaneously, a multiple populations based estimation of pseudo-normal distribution algorithm(MEPDA) is presented. The population is initialized by the good point set method and it is divided into three subgroups. By replacing sample mean with the gravity center of the samples, a pseudo-normal distribution model is obtained consequently. The probabilistic model for the subgroup evolution is built up by a linear combination of the pseudo-normal distribution models of the population and the subgroup. The comparative optimization tests on 23 benchmark functions show that MEPDA produces higher convergence speed and accuracy of the solutions. To solve the parallel assembly optimization problem with multiple constraints, the process pool, employee pool, penalty function and other measures are proposed to transform the discrete combinational optimization problem with constrained procedures and operators to an unconstrained multi-population based estimation of pseudo-normal distribution optimization problem. An engineering application demonstrates that MEPDA can be applied to the discrete combination optimization problem by just replacing the infinite set of the candidate solutions with a finite one.

Key words: Estimation of Distribution Algorithm; Normal Distribution; Parallel Assembly Problem; Multiple Populations

文章图片

本文责任编委何清

Recommended by Associate Editor HE Qing

分布估计算法(Estimation of Distribution Algo-rithm, EDA)^[1]是基于概率模型的群体优化算法.不同于其它生物启发式群体优化算法, 如遗传算法(Genetic Algorithm, GA)^[2]、粒子群算法(Particle Swarm Optimization, PSO)^[3]、鱼群算法(Fish Swarm Algorithm, FSA)^[4]、蚁群算法(Ant Colony Optimiza-tion, ACO)^[5], EDA通过统计学习, 构建解空间的概率模型, 依据概率模型产生子代候选解^[6].这种策略削弱超强个体在群体进化中的主导作用, 在一定程度上延缓早熟收敛的发生.

EDA依据变量间的相关性, 分为变量无关、双变量相关和多变量相关三类.在变量无关EDA中, 变量之间相互独立、互不影响, 方便计算各自的分布模型, 如单变量边缘分布算法(Univariate Marginal Dis-tribution Algorithm, UMDA)^[7]、紧致遗传算法(Com-pact GA, cGA)^[8].双变量相关EDA采用链式关系或树状结构构建分布模型, 如交互信息最大化的输入聚类法(Mutual Information Maximization for Input Clustering, MIMIC)^[9]、COMIT(Combining Optimizers with Mutual Information Trees)^[10].多变量相关EDA不仅分布模型更复杂, 合适的模型还需通过迭代学习产生, 如因子化分布算法(Factorized Distribution Algorithm, FDA)^[11]、贝叶斯优化算法(Bayesian Optimization Algorithm, BOA)^[12]等.

EDA按照候选解的编码方式, 可分为离散EDA和连续EDA.在离散问题优化时, 候选解通常采用二进制编码或整数编码.连续问题优化通常采用实数编码方式求解.

近年来, EDA的研究逐渐由二进制编码向实数编码发展, 主要侧重于概率模型的改进^[13]及与其它优化算法的融合.张建华等^[14]采用经验分布函数替代正态分布函数, 提出任意分布的连续多变量耦合分布估计算法.王丽芳等^[15]估计各变量的边缘分布函数, 构造Copula函数, 作为产生子代候选解的概率分布模型.

在算法融合方面, 常将EDA与生物启发式优化算法融合.例如, 融合GA与EDA^[16].利用细菌的趋向性运动, 将细菌觅食行为(Bacterial Foraging, BF)引入EDA^[17].另外, 也有学者将传统的优化算法应用于EDA中, 提高EDA的局部搜索能力^[18].

由于EDA的概率模型直接关系到子代候选解的质量, 对概率模型的改进一直备受学者关注^{[19, 20]}.当采用正态分布模型N(μ , σ ²)作为概率模型时, 子代候选解有99.7%分布于μ ± 3σ 范围内.由正态函数性质可知, x=μ 为正态分布模型的最大值位置, 此处附近产生的子代候选解最多.因此, x=μ 附近解空间的适应度决定子代候选解的群体质量.另外, 影响子代候选解分布范围的参数σ , 会直接影响种群的多样性和收敛速度.当σ 过小时, 种群多样性减少, 收敛速度加快, 容易发生早熟收敛.

基于正态分布参数对算法性能的影响, 本文改进传统正态分布参数的计算方法, 提出多种群伪正态分布估计算法(Multiple Populations Based Estima-tion of Pseudo-Normal Distribution Algorithm, MEP-DA).首先, 采用佳点集方法进行种群初始化, 将种群分为3个子群.然后, 采用样本重心取代样本均值, 获得伪正态分布模型.最后, 融合种群与子群伪正态分布模型, 得到子群进化的概率模型.23个基准函数的对比测试表明, 本文算法在求解质量和收敛速度上较优.

另外, 尽管EDA已成功解决调度优化、多维背包、机器学习等领域的技术问题^{[21, 22, 23, 24, 25]}, 但相比GA、PSO等优化算法, EDA的应用广度明显不足.本文针对一类多约束条件下的并行装配作业问题, 将正态分布模型的无限解集修正为有限解集, 使MEPDA能应用于快速求解离散组合优化问题.

1 伪正态分布模型

正态分布是物理、数学及工程学中重要的分布函数, 记为N(μ , σ ²), 概率密度函数

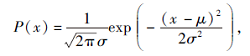
其中, μ 为随机变量的数学期望或均值, σ 为随机变量的标准差,

$\begin{matrix} μ = \bar{x} = \frac{1}{n} \overset{n}{\sum_{i = 1}} x_{i}, σ^{2} = \frac{1}{n} \overset{n}{\sum_{i = 1}} (x_{i} - \bar{x})^{2}, \end{matrix}$ (1)

x_i为第i个随机变量, $\bar{x}$ 为n个随机变量的均值.在x=μ 处, 正态分布函数具有极大值.

由于x=μ 处为极大值的特点, 在EDA中, 将正态分布模型作为产生子代候选解的概率模型时, 将有更多的子代候选解聚集在x=μ 周围.因此, 对于改善子代候选解的质量, μ 的选择非常重要.

由力学知识可知, 重心是一个力矩平衡位置, 以重心为支点的合力距M为0, 即

M= $\overset{N}{\sum_{i = 1}} {\vec{F}}_{i}$ · ${\vec{L}}_{i}$ =0, (2)

其中, ${\vec{F}}_{i}$ 为第i个力向量, ${\vec{L}}_{i}$ 为相应的力臂, 即力的作用点到重心的距离.

将式(2)中N个作用力分为前K个作用力和后N-K个作用力, 得到力矩平衡方程

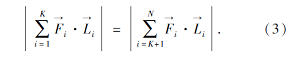
令

$\begin{matrix} F_{L} = \overset{K}{\sum_{i = 1}} {\vec{F}}_{i} (x), F_{R} = \overset{N}{\sum_{i = K + 1}} {\vec{F}}_{i} (x), \end{matrix}$

于是有

F_L· L_L=F_R· L_R,

其中, L_L和L_R分别为左右两侧合力F_L和F_R到重心的力臂.

显然, 在通过重心的作用力中, 合力与其力矩成反比:合力越大, 力臂越短.由于合力是一个区域作用力的集中反映, 这就意味着, 重力系统中重心总是靠近重量较大(或密度较大)的区域.

如果将重力系统泛化为一个解空间, 不同受力点的F(x)看作适应度函数, 那么, 在解空间寻优时, 通过寻找样本重心, 就能快速定位到适应度较高的区域^[26], 尤其是通过重心迭代搜索, 可实现目标精准定位^[27].

本文将传统正态分布模型参数(式(1))修正为

$\begin{matrix} μ = \frac{\overset{n}{\sum_{i = 1}} x_{i} F (x_{i})}{\overset{n}{\sum_{i = 1}} F (x_{i})}, σ^{2} = \frac{1}{n} \overset{n}{\sum_{i = 1}} (x_{i} - \bar{x})^{2}, \end{matrix}$ (4)

其中, F(x_i)> 0为候选解x_i的适应度, μ 为n个样本的重心.将传统正态分布模型平移得到式(4)的正态分布模型.模型的中心位置由样本几何中心迁移到样本的重心位置, 标准差维持不变.

由于正态分布模型(式(4))不再是父代样本的统计模型, 故称为伪正态分布模型.

利用此伪正态分布模型, 有利于快速定位极大值区域.以函数

y=F(x)= $|\frac{\sin x}{x}|$ (5)

为例, 随机选取5个样本

{x|x=-3.5, -2.8, -4.5, 0.5, 1.2},

分别按照式(1)和式(4)计算参数, 得到N(-2.12, 3.11)和N(-0.32, 3.11)2种分布模型.由模型参数可看出, 在相同样本前提下, 根据式(4)所得模型的中心μ =-0.32更靠近式(5)函数的全局极大值位置(x=0).

2 多种群伪正态分布估计算法

由地理知识可知, 山峰附近海拔通常较高.在解空间中也存在类似现象:极值附近的适应度相对较高.因此, 快速定位高适应度区域, 有利于尽早发现全局极值.由于重心具有偏向高适应度区域的属性, 因此, 采用伪正态分布模型(式(4))作为生成子代候选解的概率模型, 会有更多的子代候选解出现在高适应度区域, 有利于提高高适应度区域的搜索效率.

另外, 为了防止算法早熟收敛, 本文采用通行的多种群优化方案, 一方面保持候选解的多样性, 另一方面通过群体间的协作, 提高算法的优化能力.

本文提出的多种群伪正态分布估计算法(MEPDA)主要特征体现为如下4个方面.

1)种群初始化.种群初始化通常有随机初始化和均匀初始化2种方式.

随机初始化简单, 但会导致候选解在解空间的某些区域分布密集, 某些区域分布稀疏.一旦最优解区域无法得到有效采样, 会在一定程度上延长最优解的发现时间.

均匀初始化有3种:正交实验法^[28]、随机均匀设计法^[29]、佳点集法^[30].这3种方法都能对解空间进行均匀采样, 但正交实验法在高维空间内需要较多的采样点^[31], 因此, 正交实验法更适用于低维问题的优化方案.随机均匀设计法与佳点集法的效果相差不大.故本文采用佳点集法进行种群初始化.

2)子群分工.为了兼顾算法的全局探测能力和局部搜索能力, 本文将种群P划分为3个子群, 记为P₁, P₂, P₃.

子群P₁由适应度较高的候选解组成.通常情况下, 适应度较高的候选解会分布在有限的区域内, 因此子群P₁的标准差σ ₁通常较小.子群P₃由适应度较差的一些候选解个体组成.适应度居中的候选解集中于子群P₂中.在大多数情况下, 适应度较差的候选解在解空间中分布很广, 标准差最大.3个子群的标准差σ ₁≤ σ ₂≤ σ ₃.

标准差既反映父代候选解的分布范围, 又是候选解收敛速度的一个重要标志.标准差越小, 意味着子代候选解的聚集度越高.对于由高聚集度候选解建立的分布模型, 下一代标准差小于上一代, 从而实现算法收敛.

在3个子群中, 标准差最小的子群P₁搜索区域最小, 收敛速度最快, 有利于提高全局极值的搜索效率.标准差最大的子群P₃覆盖的搜索区域最大, 担负全局探测功能, 收敛速度最慢.标准差居中的子群P₂介于P₁和P₃之间, 处于漫游搜索状态.

另外, 为了抑制早熟收敛现象的发生, 本文为每个子群的标准差增加缩放因子η _i(η ₁< η ₂< η ₃), 以此调节子代候选解的实际分布区域.

3)信息融合.MEPDA中的3个子群依据各自父代样本建立相应的伪正态分布模型, 但这个模型并不是用于各子群产生子代候选解的概率模型.

为了防止子群P_i封闭进化而导致个体多样性减少, 将各子群P_i的伪正态分布模型N_i(μ _i, $σ_{i}^{2}$ )(i=1, 2, 3)分别与种群P的伪正态分布模型N(μ , σ ²)进行线性组合, 将所得的分布模型 ${\overset{︿}{N}}_{i}$ ( ${\dot{μ}}_{i}$ , ${\dot{σ}}_{i}^{2}$ )(i=1, 2, 3)作为子群P_i生成子代候选解的概率模型, 则

$\begin{array}{l} {\dot{μ}}_{i} = λ_{i} μ_{i} + (1 - λ_{i}) μ, \\ {\dot{σ}}_{i} = η_{i} [λ_{i} σ_{i} + (1 - λ_{i}) σ], \end{array}$ (6)

其中, η _i为标准差缩放因子, λ _i为自适应权系数,

λ _i= $\frac{F (μ)}{F (μ) + F (μ_{i})}$ . (7)

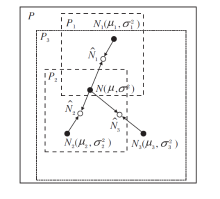
图1为3个子群与种群的信息融合示意图.在图中, 实心圆点表示种群和, μ _i表示3个子群的重心位置, 空心圆点表示修正后的概率模型中心位置 ${\dot{μ}}_{i}$ .

	Figure Option View Download New Window
	图1 3个子群与种群的信息融合示意图Fig.1 Illustration of information fusion of 3 subgroups and population

多数多种群优化算法通过直接交换不同群体之间的特定个体实现信息融合.但在MEPDA中, 子群与种群的信息融合并不是交换各自的部分候选解个体, 而是通过双方分布模型的自适应线性组合, 将种群和子群的分布信息融合到产生子代的概率模型中.

信息融合后的概率模型中心不再是子群重心μ _i, 而是在一定程度上偏向种群重心μ .标准差也受种群标准差σ 的影响, 得到一定程度上的扩张.当某个子群标准差σ _i=0时, 只要种群标准差不为0, 那么修正后的子群标准差就不为0.因此, 子群通过与种群的信息融合, 可在一定程度上延缓子群的收敛速度, 阻止早熟收敛的发生.

4)动态适应度.在重心的计算过程中, 需要确保样本适应度之和大于0.常规的做法是将候选解个体的函数值加上一个固定阈值, 使所有的样本适应度均大于0.但在工程应用中, 阈值如何取值, 依赖于先验知识, 给应用带来不便.

为了避免上述问题, 在计算候选解适应度时, 本文将当前种群的最小函数值f_min作为阈值, 代替传统的固定阈值方案.

例如, 设个体的函数值为y=f(x), 则当前n个候选解的最小函数值为

f_min=min{f(x₁), f(x₂), …, f(x_n)}.

如果是极大值优化问题, 则第i个候选解个体的适应度

F(x_i)=f(x_i)-f_min+0.001. (8)

如果是极小值优化问题, 可将极小值优化问题转化为极大值优化问题, 适应度

F(x_i)= $(f (x_{i}) - f_{\min} {+ 0.001)}^{- 1}$ . (9)

由于每代种群的候选解个体不尽相同, 导致f_min发生改变, 形成动态阈值.因此, 即使相同的个体x_i, 在不同的迭代周期内, 也可能存在不同的适应度, 呈现一种动态变化现象.

由上述4个特点构成的MEPDA伪代码如下.

算法 MEPDA

Begin

设置最大迭代次数genMax、候选解范围Bound、

标准差缩放因子η _i(i=1, 2, 3);

设置子群规模S_i(i=1, 2, 3), 计算种群规模

S=S₁+S₂+S₃;

佳点集方法产生初始种群P⁰;

统计初始种群的最小值 $f_{\min}^{0}$ ;

根据式(8)或式(9)计算初始种群适应度F⁰(x);

记录P⁰中的最优个体x及f(x);

For t = 0:genMax

根据式(4)计算P^t的伪正态分布模型N(μ , σ ²);

将种群P^t按适应度从大到小分成 $P_{1}^{t}$ 、 $P_{2}^{t}$ 、 $P_{3}^{t}$

子群;

For i = 1:3

根据式(4)计算子群 $P_{i}^{t}$ 伪正态分布模型

N_i(μ _i, $σ_{i}^{2}$ );

根据式(6)、式(7)计算子群 $P_{i}^{t}$ 的概率模型

${\overset{︿}{N}}_{i}$ ( ${\dot{μ}}_{i}$ , ${\dot{σ}}_{i}^{2}$ );

根据群体规模S_i和概率模型 ${\overset{︿}{N}}_{i}$ ( ${\dot{μ}}_{i}$ , ${\dot{σ}}_{i}^{2}$ )产生

子代 ${\overset{︿}{P}}_{i}^{t}$ ;

根据参数范围Bound对子代进行校验;

End For

剔除P^t+ ${\overset{︿}{P}}_{1}^{t}$ + ${\overset{︿}{P}}_{2}^{t}$ + ${\overset{︿}{P}}_{3}^{t}$ 中的重复个体, 统计最小

值 $f_{\min}^{t + 1}$ , 计算群体适应度;

选择适应度较高的S个个体, 组成下一代种群

P^t⁺¹;

记录P^t⁺¹中的最优个体x及f(x).

End For

End Begin

3 实验及结果分析

为了测试MEPDA的寻优性能, 选择23个基准函数^[32]进行极小值寻优实验.这23个基准函数分为3类: f₁f₇为高维单峰值函数, f₈f₁₃为高维多峰值函数, f₁₄f₂₃为低维多峰值函数.

对比的优化算法如下:快速进化规划算法(Fast Evolutionary Programming, FEP)^[32]、分布估计算法(Estimation of Distribution Algorithm, EDA)^[33]、粒子群算法(PSO)^[34]、遗传算法(GA)^[34].

对比实验中, 所有算法的种群规模S=90.MEPDA中3个子群大小均为30, 标准差缩放因子η ₁=1, η ₂=3, η ₃=5.

首先分析初始化方式对收敛速度的影响.从3类测试函数中各选取2个函数作为实验函数.为了说明种群的不同初始化方式对收敛速度的影响, MEPDA的初始种群分别采用随机初始化和佳点集初始化2种方式.

表1列出t=0, 5, 10, 15, 20时的最优解, 表中黑体数字为最优结果.由表可知, 当初始化(t=0)时, 只有函数f₁₂的随机初始化最优值优于佳点集初始化最优值.但算法迭代至第10代后, 佳点集初始化得到的最优值便超过随机初始化的最优值.

表1 初始化方式对收敛速度的影响 Table 1 Effect of initialization methods on convergence speed

在迭代搜索过程中, 虽然函数f₆在第5代和第10代时, 随机初始化的最优值优于佳点集初始化的最优值, 但在随后的优化过程中, 佳点集种群搜索得到的最优值又优于随机种群的搜索结果.对于函数f₁₈, 佳点集初始化方法在第10代就找到函数最小值, 而随机初始化的MEPDA在第15代才找到函数最小值.

由表1不难看出, 种群采用佳点集方法初始化后, 候选解在空间均匀分布, 最优解附近被采样的概率增大, 收敛速度也得到提高.

为了测试不同优化策略对算法收敛速度的影响, 将5种优化算法均采用佳点集方式进行种群初始化, 从相同的初始种群开始优化.最大迭代次数genMax=50, 测试函数仍为上述选出的6个代表性函数.

图2给出5种算法在6个测试函数上的收敛曲线.

	Figure Option View Download New Window
	图2 各算法在6个函数上的收敛曲线对比Fig.2 Comparison of convergence curves of different algorithms on 6 functions

由图2中收敛曲线可看出, MEPDA的收敛速度最快.

EDA在高维单峰值函数f₃(x)、 f₆(x)及高维多峰值函数f₁₂(x)上的优化速度排名第二, 但在高维多峰值函数f₉(x)及低维多峰值函数上的收敛速度较慢.而MEPDA在6个函数上的优化速度均快于EDA.对比实验说明, 在相同条件下, 改进后的概率模型不仅优化速度较快, 还克服EDA在多峰值函数优化方面的不足, 提升算法的综合性能.

设置5种算法的最大迭代次数genMax=500, 其它参数维持不变.每个测试函数独立优化10次, 取10次优化结果的平均值作为求解质量.测试结果如表2所示, 表中黑体数字为最优结果.

表2 各算法在23个函数上的求解质量对比 Table 2 Comparison of solution qualities of different algorithms on 23 functions

为了能给5种优化算法在23个基准函数上的求解质量进行排名, 按照每个函数的寻优结果, 从小到大进行排序, 根据排序进行赋分:最优解适应度最大的算法得1分, 最优解适应度最小的算法得5分; 如果排序相同, 算法得分相同.然后, 分别计算5种算法在23个基准函数上的平均得分, 得分最少, 说明算法综合性能最佳.

表3给出5种算法的统计结果.从23个基准函数的单项测试排名可看出, MEPDA在16个基准函数上排名第一, 优势明显.

表3 各算法求解质量排名 Table 3 Solutions quality rank of different algorithms

从上述对比实验可看出, MEPDA在收敛速度和求解质量方面都得到极大改善, 综合性能表现最佳.

4 本文算法在车间并行装配调度问题上的应用

4.1 车间并行装配调度问题

车间作业调度问题(Job-Shop Scheduling Prob-lem, JSP)^[35]是一类组合优化问题, 涉及航班调度^[36]、生产规划^[37]、物流运输^[38]等多种工程应用领域, 是典型的NP-hard问题.工程应用中的约束条件较多, 满足系统要求的解也不唯一, 这些既影响待求解问题的建模, 也对优化算法的应用提出更高要求.

本文研究一类多重约束条件下的车间并行装配作业调度问题.具体描述为:设有M个待装配设备, 每个设备的装配工序必须按照指定的顺序完成, 每道工序均有指定的完成时间和所需人数限制, 不同设备之间的部分工序也存在先后顺序要求.由于参加装配任务的员工总数有限, 需要这些参与装配的员工在不同装配线上进行分工合作, 因此, 本文所述车间装配作业的优化问题是一类既有工序约束, 又有员工约束的调度问题^[39].

上述工程问题可转化为如下约束条件下的优化问题.

定义 1 M个设备的装配工序矩阵

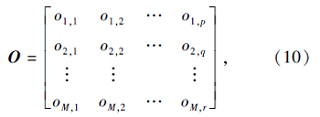
其中o_i_,_j为第i个设备的第j个装配工序.

定义 2 完成装配工序的时间矩阵

T= $[\begin{array}{l} t_{1, 1} & t_{1, 2} & \dots & t_{1, p} \\ t_{2, 1} & t_{2, 2} & \dots & t_{2, q} \\ ︙ & ︙ & ︙ \\ t_{M, 1} & t_{M, 2} & \dots & t_{M, r} \end{array}]$ ,

其中t_i_,_j为完成第i个设备的第j个装配工序所需时间.

定义 3 参与装配作业的员工矩阵

W= $[\begin{array}{l} w_{1, 1} & w_{1, 2} & \dots & w_{1, p} \\ w_{2, 1} & w_{2, 2} & \dots & w_{2, q} \\ ︙ & ︙ & ︙ \\ w_{M, 1} & w_{M, 2} & \dots & w_{M, r} \end{array}]$ ,

其中w_i_,_j为第i个设备的第j个装配工序所需人数.

若每个装配工序的开始时间和结束时间分别表示为b_i_,_j和f_i_,_j(i为设备号, j为装配工序序号), 给定参与装配任务的员工总数N, 则待优化的约束问题可描述为:求装配工序矩阵O中每道工序的作业序列{o_i_,_j}及其起始时间{b_i_,_j}, 使装配任务的总完工时间最短, 即

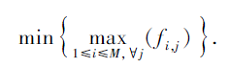
工序约束条件分别如下.设备i内部的工序时间约束为

(b_i_,_j≥ f_i_,_j_-1)∩ (f_i_,_j-b_i_,_j=t_i_,_j), (11)

即同一设备中, 后一工序的开始时间应该晚于前一工序的结束时间.不同设备间的工序时间约束为

b_i_,_j≥ f_m_,_n, (12)

即设备i的第j个工序开始时间应该晚于设备m的第n个工序的结束时间.

员工人数约束条件如下:

$\max_{\forall i, \forall j}$ (w_i_,_j)≤ N, (13)

表示每个工序参与的人数不得超过总人数N;

∀ t, $\overset{M}{\sum_{i = 1}}$ w_i_,_j≤ N, (14)

表示任意t时刻参与装配工作的在线人数不得超过总人数N.

4.2 求解车间并行装配调度问题

由于JSP的复杂性, 应用传统最优化技术存在较大困难, 而群体优化技术不苛求问题解析或可微等条件, 在解决JSP问题上具有优势^{[40, 41, 42, 43, 44]}.

本文利用MEPDA求解这类工序和员工受限的装配调度问题.

4.2.1 候选解编码

JSP问题与连续函数优化问题不同, 解空间大多是离散的, 候选解有多种表达方式.

在本文所述JSP问题中, 工序矩阵(式(10))的不同工序编号连接成串, 以编码串的方式构成候选解.工序编号在编码串中的先后排位关系表示为工序间的先后装配顺序.

工序矩阵(式(10))中工序编号既可采取唯一编码方式, 也可采取非唯一编码方式.

唯一编码方式是指工序矩阵中的每个元素编号没有重复, 如

O= $[\begin{array}{l} 1 & 2 & 3 & 4 \\ 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 & 13 \end{array}]$ ,

这种编码方式十分直观, 每台设备中的编号大小表示作业顺序, 解码方便.

由于唯一编码方式事先按照编号大小约定工序间的先后关系, 因此, 可行解的编码串必须同时满足4个子串

{1, 2, 3, 4}、{5, 6}、{7, 8, 9}、{10, 11, 12, 13}

定义的先后关系, 如

C={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}

或

C={1, 5, 7, 2, 10, 3, 6, 8, 11, 4, 9, 12, 13}

等.但候选解在随机产生过程中, 难以兼顾4个子串定义的位序要求, 容易形成较多的不可行解.

针对唯一编码的不足, 本文采用非唯一编码方式, 即设备n的工序号全部使用n表示.例如:4台设备的装配工序矩阵

O= $[\begin{array}{l} 1 & 1 & 1 & 1 \\ 2 & 2 \\ 3 & 3 & 3 \\ 4 & 4 & 4 & 4 \end{array}]$ , (15)

所得的候选解编码串

C={1, 1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 4, 4}

或

C={1, 2, 3, 1, 4, 1, 2, 3, 4, 1, 3, 4, 4}

等.由于同一设备的装配工序均采用相同编码, 在候选解编码串中无位序关系约束, 因此, 候选解编码串不存在不可行解问题, 但设备编号对应的工序关系需要由解码协议进行定义和解释.

为了便于候选解编码串的随机生成, 本文提出工序池解决方案, 即将工序编码矩阵中的所有元素放入一个集合中, 这个集合即为工序池.

以式(15)的工序矩阵为例, 初始的工序池集合

X={x|x=1, 1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 4, 4}. (16)

候选解生成时, 只需从工序池中随机抽取设备号, 再顺位放入候选解编码串中, 同时删除工序池X中的相应设备号.由此可见, 利用工序池, 产生候选解编码串的过程较简单.

4.2.2 约束条件处理

MEPDA是一种无约束连续优化算法, 而本文所述JSP问题存在约束条件(式(11)-式(14)).为了能将有约束优化问题转化为无约束优化问题, 提出如下解决方案.

1)解码协议.本文约定解码协议为:相同设备号在编码串中出现的位序表示该设备的对应工序号.例如, 对于第n台设备, 第1个编码n对应于工序o_n_{, 1}, 第2个编码n对应于工序o_n_{, 2}……以此类推.

表4给出一个编码串的工序解码示例.解码协议利用设备号在编码串中出现的先后关系, 映射同一设备内的工序先后关系, 既解决编码串中设备号的工序定义, 又同时避免式(11)所示的同一设备内的工序先后冲突的问题.

表4 候选解解码示例 Table 4 Decoding illustration of a candidate solution

2)罚函数.编码串的解码协议虽然解决同一设备内的工序约束问题, 但却无法解决不同设备间的工序约束问题.

为了解决式(12)所示不同设备间的工序约束问题, 定义适应度函数

F=T^*+f,

其中, f=λ T^*为罚函数,

λ = $\{\begin{array}{l} 0, & s_{i, j} \geq f_{m, n} \\ 1, & s_{i, j} < f_{m, n} \end{array}$

T^*为不考虑式(12)条件下的最短完工时间, λ 为惩罚系数.当式(12)约束条件满足时, λ =0; 当式(12)约束条件不满足时, λ =1.通过改变λ 取值, 将约束条件不满足时的完工时间扩大1倍.这样, 不满足式(12)的候选解, 因适应度差而降低其在分布模型建模时的影响程度.

3)员工池.为了解决作业员工的人数约束问题, 引入员工池概念, 将待岗员工编号存放在员工池中.以4人参与的装配任务为例, 初始的员工池

Y={y|y=1, 2, 3, 4},

其中1、2、3、4分别为员工编号.

在候选解解码过程中, 随装配工序进入排班过程, 也从待岗的员工池中抽调相应人数的员工, 即从员工池Y中去掉相应的员工编号.每当装配作业结束时, 相应的作业员工编号重新进入员工池.当员工池中的人数无法满足当前工序的作业人数时, 一直等待, 直至员工池中的人数满足当前工序的作业人数为止.

通过设立待岗的员工池, 既可确保在岗员工总数不超过参加装配任务的全部员工数(即满足约束条件式(13)), 又确保每个员工在同一时间只能参加一个装配工序的作业(即满足约束条件式(14)).

4.2.3 离散候选解的产生

依据非唯一编码原则, 候选解的每个编码位取值只能是工序池X中限定的设备编号, 它们在解空间中是不连续的.因此, 将MEPDA应用于离散组合优化问题时, 需要针对概率模型, 给出有限候选解的生成算法.

设备编号x_i在概率模型中对应的概率为 $\overset{︿}{P}$ (x_i), 则根据该模型产生子代的伪代码如下.

while X≠ Ø

从工序池X中随机挑选一个设备编号x_i;

产生01之间的随机数作为概率P(x_i);

当 $\overset{︿}{P}$ (x_i)≥ P(x_i)时, C← C+x_i, X← X-x_i;

End while

4.3 工程案例

某特殊行业的设备维护、组装只能通过人工协作完成.为了提高设备的装配效率, 缩短装配时间, 需要根据作业的员工人数制定相应的作业工序, 达到完工时间最短的目标要求.

根据既往的训练数据, 每个装配工序的平均作业时间矩阵T(单位min)和所需的参与人数矩阵W分别为

T= $[\begin{array}{l} 15 & 5 & 10 & 5 \\ 15 & 25 \\ 5 & 5 & 30 \\ 5 & 5 & 10 & 5 \end{array}]$ , W= $[\begin{array}{l} 5 & 2 & 2 & 2 \\ 4 & 2 \\ 2 & 2 & 2 \\ 2 & 2 & 2 & 2 \end{array}]$ .

参与装配作业的员工总数N=5, 同时, 待装配的4台设备间存在如下工序约束.

1)设备1的第2号装配工序o_{1, 2}必须在设备3的第2号工序o_{3, 2}之前完成.

2)设备1的第3号装配工序o_{1, 3}必须在设备4的第3号工序o_{4, 3}之前完成.

为了验证MEPDA在求解装配作业优化问题上的可行性和有效性, 按照第3节设置实验参数.

采用非唯一编码方式, 即4台设备分别编号为1、2、3、4, 得到工序矩阵(式(15))和工序池(式(16)).

表5为利用MEPDA优化得到的6个最优编码串.这6种方案的最短完工时间均为85 min.

表5 MEPDA优化后的6个最优候选解 Table 5 Six optimal candidate solutions optimized by MEPDA min

根据2个工序约束条件可知:在候选解编码串中, 第2个1应该排在第2个3前面, 第3个1应该排在第3个4前面.依此位序规律, 对6个候选解编码串进行逐一核对, 均满足约束条件要求.

以表5中的候选解1、2为例, 解码后得到的工序排班表如表6所示.由表可看出, 编码串中的设备编号尽管存在先后排位顺序, 但依据解码协议生成的工序排班表中, 有些工序可同时开始, 这是因为待岗人数满足下一个相邻工序的作业人数要求, 如工序O_{1, 2}和工序O_{2, 2}、工序O_{3, 3}和工序O_{4, 1}均可同时开始装配作业.

表6 2个候选解的工序排班表 Table 6 Process scheduling of 2 candidate solutions

5 结束语

基于正态模型参数在候选解进化过程中的不同作用, 结合极值区域高适应度的特点, 本文提出多种群伪正态分布估计算法(MEPDA), 改进正态分布模型的参数计算方法, 以样本重心代替样本均值, 提高高适应度区域的采样概率, 改善候选解质量.同时, 采取标准差缩放因子、佳点集初始化等措施, 既防止搜索区域的快速收敛, 又提高种群的多样性.MEPDA在23个基准函数的对比测试中, 收敛速度较快, 寻优精度较高.

针对具有多重约束条件的离散优化问题, 本文通过解码协议、员工池及罚函数, 解决设备装配问题中的工序约束及人数约束问题.通过对工序编号的概率测试方式, 解决离散候选解的生成问题, 使应用于连续优化问题的MEPDA也能方便应用于离散组合优化问题.今后, 将进一步研究全局重心与子群局部重心之间的有机联系, 探索更高效的算法框架, 并将其应用于更复杂的组合优化问题.

参考文献

文献选项

[1]	王圣尧, 王凌, 方晨, 等. 分布估计算法研究进展. 控制与决策, 2012, 27(7): 961-966, 974. (WANG S Y, WANG L, FANG C, et al. Advances in Estimation of Distribution Algorithms. Control and Decision, 2012, 27(7): 961-966, 974. ) [本文引用:1]
[2]	王赞, 樊向宇, 邹雨果, 等. 一种基于遗传算法的多缺陷定位方法. 软件学报, 2016, 27(4): 879-900. (WANG Z, FAN X Y, ZOU Y G, et al. Genetic Algorithm Based Multiple Faults Localization Technique. Journal of Software, 2016, 27(4): 879-900. ) [本文引用:1]
[3]	韩红桂, 卢薇, 乔俊飞. 一种基于多样性信息和收敛度的多目标粒子群优化算法. 电子学报, 2018, 46(2): 315-324. (HAN H G, LU W, QIAO J F. A Multiobjective Particle Swarm Optimization Algorithm Based on the Diversity Information and Convergence Degree. Acta Electronica Sinica, 2018, 46(2): 315-324. ) [本文引用:1]
[4]	段其昌, 唐若笠, 徐宏英, 等. 粒子群优化鱼群算法仿真分析. 控制与决策, 2013, 28(9): 1436-1440. (DUAN Q C, TANG R L, XU H Y, et al. Simulation Analysis of the Fish Swarm Algorithm Optimized by PSO. Control and Decision, 2013, 28(9): 1436-1440. ) [本文引用:1]
[5]	许凯波, 鲁海燕, 黄洋, 等. 基于双层蚁群算法和动态环境的机器人路径规划方法. 电子学报, 2019, 47(10): 2166-2176. (XU K B, LU H Y, HUANG Y, et al. Robot Path Planning Based on Double-Layer Ant Colony Optimization Algorithm and Dynamic Environment. Acta Electronica Sinica, 2019, 47(10): 2166-2176. ) [本文引用:1]
[6]	PELIKAN M, GOLDBERG D E, LOBO F G. A Survey of Optimization by Building and Using Probabilistic Models. Computational Optimization and Applications, 2002, 21(1): 5-20. [本文引用:1]
[7]	MÜHLENBEIN H. The Equation for Response to Selection and Its Use for Prediction. Evolutionary Computation, 1997, 5(3): 303-346. [本文引用:1]
[8]	HARIK G R, LOBO F G, GOLDBERG D E. The Compact Genetic Algorithm. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 287-297. [本文引用:1]
[9]	周树德, 孙增圻. 分布估计算法综述. 自动化学报, 2007, 33(2): 113-124. (ZHOU S D, SUN Z Q. A Survey on Estimation of Distribution Algorithms. Acta Automatica Sinica, 2007, 33(2): 113-124. ) [本文引用:1]
[10]	BALUJA S, DAVIES S. Using Optimal Dependency-Trees for Com-binatorial Optimization // Proc of the 14th International Conference on Machine Learning. New York, USA: ACM, 1997: 30-38. [本文引用:1]
[11]	MÜHLENBEIN H, MAHNIG T. Convergence Theory and Applications of the Factorized Distribution Algorithm. Journal of Computing and Information Technology, 1999, 7(1): 19-32. [本文引用:1]
[12]	PELIKAN M, GOLDBERG D E, CANTU P E. BOA: The Baye-sian Optimization Algorithm // Proc of the 1st Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 1999, I: 525-532. [本文引用:1]
[13]	左先亮, 郭莉莉, 高尚. 改进分布估计算法解决多约束集装箱装载问题. 科学技术与工程, 2014, 14(11): 216-220. (ZUO X L, GUO L L, GAO S. Solution to Multi-constraints Container Loading Problem Based on Improved Estimation of Distribution Algorithm. Science Technology and Engineering, 2014, 14(11): 216-220. ) [本文引用:1]
[14]	张建华, 曾建潮. 经验分布函数概率模型的分布估计算法. 计算机工程与应用, 2011, 47(8): 33-35. (ZHANG J H, ZENG J C. Estimation of Distribution Algorithms Using Empirical Distribution Function as Probability Model. Computer Engineering and Applications, 2011, 47(8): 33-35. ) [本文引用:1]
[15]	王丽芳, 曾建潮, 洪毅. 利用Copula函数估计概率模型并采样的分布估计算法. 控制与决策, 2011, 26(9): 1333-1337, 1342. (WANG L F, ZENG J C, HONG Y. Estimation of Distribution Algorithm Modeling and Sampling by Means of Copula. Control and Decision, 2011, 26(9): 1333-1337, 1342. ) [本文引用:1]
[16]	PEÑA J M, ROBLES V, LARRANAGA P, et al. GA-EDA: Hybrid Evolutionary Algorithm Using Genetic and Estimation of Distribution Algorithms // Proc of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems. Berlin, Germany: Springer, 2004: 361-371. [本文引用:1]
[17]	王雪松, 程玉虎, 郝名林. 基于细菌觅食行为的分布估计算法在预测控制中的应用. 电子学报, 2010, 38(2): 333-339. (WANG X S, CHENG Y H, HAO M L. Estimation of Distribution Algorithm Based on Bacterial Foraging and Its Application in Predictive Control. Acta Electronica Sinica, 2010, 38(2): 333-339. ) [本文引用:1]
[18]	李静. 一种基于单纯形法的分布式估计算法. 科学技术与工程, 2014, 14(32): 262-265. (LI J. Estimation of Distribution Algorithms Based on Simplex Method. Science Technology and Engineering, 2014, 14(32): 262-265. ) [本文引用:1]
[19]	LIANG Y S, REN Z G, HE M, et al. An Efficient Estimation of Distribution Algorithm with Rank-One Modification and Population Reduction. Biosystems, 2019, 181: 58-70. [本文引用:1]
[20]	POURMOHAMMADBAGHER L, EBADZADEH M M, SAFABAKHSH R. Graphical Model Based Continuous Estimation of Distribution Algorithm. Applied Soft Computing, 2017, 58(1): 388-400. [本文引用:1]
[21]	陈静, 林雅婷, 周清旭, 等. 基于峰值匹配分布式估计算法的光纤布拉格光栅传感网络重叠光谱的波长解调. 光子学报, 2019, 48(4): 79-86. (CHEN J, LIN Y T, ZHOU Q X, et al. Wavelength Demodulation of a Spectrally Overlapped Fiber Bragg Grating Sensor Network Based on Peak Match Estimation of Distribution Algorithm. Acta Photonica Sinica, 2019, 48(4): 79-86. ) [本文引用:1]
[22]	杨晓林, 胡蓉, 钱斌, 等. 增强分布估计算法求解低碳分布式流水线调度. 控制理论与应用, 2019, 36(5): 803-815. (YANG X L, HU R, QIAN B, et al. Enhanced Estimation of Distribution Algorithm for Low Carbon Scheduling of Distributed Flow Shop Problem. Control Theory and Applications, 2019, 36(5): 803-815. ) [本文引用:1]
[23]	杨志家, 王子, 汪扬, 等. 车辆合乘问题的两阶段分布式估计算法. 交通运输系统工程与信息, 2016, 16(2): 164-169. (YANG Z J, WANG Z, WANG Y, et al. Two-Stage Estimation of Distribution Algorithm to Solve Multi-vehicle Carpooling Problem. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(2): 164-169. ) [本文引用:1]
[24]	张建. 分布式估计算法在考虑差异工件的并行批处理机调度中的应用. 计算机系统应用, 2019, 28(6): 213-220. (ZHANG J. Application of Estimation of Distribution Algorithm to Parallel Batch Processing Machines with Non-identical Job Sizes. Computer Systems and Applications, 2019, 28(6): 213-220. ) [本文引用:1]
[25]	HAO X, GEN M, LIN L, et al. Effective Multi-objective EDA for Bi-criteria Stochastic Job-Shop Scheduling Problem. Journal of Intelligent Manufacturing, 2017, 28(3): 833-845. [本文引用:1]
[26]	杨启文, 杨远慧, 薛云灿, 等. 全局最优的邻域估计. 控制与决策, 2012, 27(8): 1269-1272. (YANG Q W, YANG Y H, XUE Y C, et al. Prospecting Neighborhood of Global Optimum. Control and Decision, 2012, 27(8): 1269-1272. ) [本文引用:1]
[27]	杨启文, 王术彬, 薛云灿, 等. 蛇形缠绕机理及其在视觉定位中的应用. 计算机科学与应用, 2013, 3(1): 30-35. (YANG Q W, WANG S B, XUE Y C, et al. The Mechanism of Snake-Enlacing and Its Application to Visual Positioning. Compu-ter Science and Application, 2013, 3(1): 30-35. ) [本文引用:1]
[28]	蔡自兴, 江中央, 王勇, 等. 一种新的基于正交实验设计的约束优化进化算法. 计算机学报, 2010, 33(5): 855-864. (CAI Z X, JIANG Z Y, WANG Y, et al. A Novel Constrained Optimization Evolutionary Algorithm Based on Orthogonal Experimental Design. Chinese Journal of Computers, 2010, 33(5): 855-864. ) [本文引用:1]
[29]	陈明华, 周本达, 任哲. 随机化均匀设计遗传算法. 高校应用数学学报A辑, 2010, 25(3): 279-284. (CHEN M H, ZHOU B D, REN Z. Genetic Algorithm Based on Rand om Uniform Design. Applied Mathematics: A Journal of Chinese Universities(Series A), 2010, 25(3): 279-284. ) [本文引用:1]
[30]	龙文, 梁昔明, 徐松金, 等. 聚类佳点集交叉的约束优化混合进化算法. 计算机研究与发展, 2012, 49(8): 1753-1761. (LONG W, LIANG X M, XU S J, et al. A Hybrid Evolutionary Algorithm Based on Clustering Good-Point Set Crossover for Constrained Optimization. Journal of Computer Research and Development, 2012, 49(8): 1753-1761. ) [本文引用:1]
[31]	张铃, 张钹. 佳点集遗传算法. 计算机学报, 2001, 24(9): 917-922. (ZHANG L, ZHANG B. Good Point Set Based Genetic Algorithm. Chinese Journal of Computers, 2001, 24(9): 917-922. ) [本文引用:1]
[32]	YAO X, LIU Y, LIN G M. Evolutionary Programming Made Faster. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. [本文引用:2]
[33]	SEBAG M, DUCOULOMBIER A. Extending Population-Based Incremental Learning to Continuous Search Spaces // Proc of the International Conference on Parallel Problem Solving from Nature. Berlin, Germany: Springer, 1998: 418-427. [本文引用:1]
[34]	余胜威. MATLAB优化算法案例分析与应用. 北京: 清华大学出版社, 2014. (YU S W. Case Analysis and Application of MATLAB Optimization Algorithm. Beijing, China: Tsinghua University Press, 2014. ) [本文引用:2]
[35]	LIAN Z G. A Local and Global Search Combine Particle Swarm Optimization Algorithm for Job-Shop Scheduling to Minimize Ma-kespan. Discrete Dynamics in Nature and Society, 2010(4). DOI: DOI:10.1155/2010/838596. [本文引用:1]
[36]	CHEN C H, YAN S Y, CHEN M. Applying Lagrangian Relaxation-Based Algorithms for Airline Coordinated Flight Scheduling Problems. Computers and Industrial Engineering, 2010, 59(3): 398-410. [本文引用:1]
[37]	TOLEDO C F M, DE SILVA ARANTES M, DE OLIVEIRA R R R, et al. Glass Container Production Scheduling through Hybrid Multi-population Based Evolutionary Algorithm. Applied Soft Computing Journal, 2013, 13(3): 1352-1364. [本文引用:1]
[38]	DAO S D, ABHARY K, MARIAN R. Optimization of Partner Selection and Collaborative Transportation Scheduling in Virtual Enterprises Using GA. Expert Systems with Applications, 2014, 41(15): 6701-6717. [本文引用:1]
[39]	KRESS D, MÜLLER D, NOSSACK J. A Worker Constrained Flexible Job Shop Scheduling Problem with Sequence-Dependent Setup Times. OR Spectrum, 2018, 41(2): 179-217. [本文引用:1]
[40]	WANG Z, ZHANG J H, YANG S X. An Improved Particle Swarm Optimization Algorithm for Dynamic Job Shop Scheduling Problems with Rand om Job Arrivals. Swarm and Evolutionary Computation, 2019, 51. DOI: DOI:10.1016/j.swevo.2019.100594. [本文引用:1]
[41]	ZHU Z W, ZHOU X H. An Efficient Evolutionary Grey Wolf Optimizer for Multi-objective Flexible Job Shop Scheduling Problem with Hierarchical Job Precedence Constraints. Computers and Industrial Engineering, 2020, 140. DOI: DOI:10.1016/j.cie.2020.106280. [本文引用:1]
[42]	ZHANG G H, HU Y F, SUN J H, et al. An Improved Genetic Algorithm for the Flexible Job Shop Scheduling Problem with Multiple Time Constraints. Swarm and Evolutionary Computation, 2020, 54. DOI: DOI:10.1016/j.swevo.2020.100664. [本文引用:1]
[43]	李强, 刘晓峰. 基于模拟植物生长算法的云作业调度模型. 系统仿真学报, 2018, 30(12): 4649-4658. (LI Q, LIU X F. Cloud Job Scheduling Model Based on Improved Plant Growth Algorithm. Journal of System Simulation, 2018, 30(12): 4649-4658. ) [本文引用:1]
[44]	LIU M, YAO X F, LI Y X. Hybrid Whale Optimization Algorithm Enhanced with Lévy Flight and Differential Evolution for Job Shop Scheduling Problems. Applied Soft Computing, 2020, 87. DOI: DOI:10.1016/j.asoc.2019.105954. [本文引用:1]

2012

0.0

... 分布估计算法(Estimation of Distribution Algo-rithm, EDA)^[1]是基于概率模型的群体优化算法 ...

2016

0.0

... 不同于其它生物启发式群体优化算法,如遗传算法(Genetic Algorithm, GA)^[2]、粒子群算法(Particle Swarm Optimization, PSO)^[3]、鱼群算法(Fish Swarm Algorithm, FSA)^[4]、蚁群算法(Ant Colony Optimiza-tion, ACO)^[5],EDA通过统计学习,构建解空间的概率模型,依据概率模型产生子代候选解^[6] ...

2018

0.0

2013

0.0

2019

0.0

2002

0.0

1997

0.0

... 在变量无关EDA中,变量之间相互独立、互不影响,方便计算各自的分布模型,如单变量边缘分布算法(Univariate Marginal Dis-tribution Algorithm, UMDA)^[7]、紧致遗传算法(Com-pact GA, cGA)^[8] ...

1999

0.0

2007

0.0

... 双变量相关EDA采用链式关系或树状结构构建分布模型,如交互信息最大化的输入聚类法(Mutual Information Maximization for Input Clustering, MIMIC)^[9]、COMIT(Combining Optimizers with Mutual Information Trees)^[10] ...

1997

0.0

1999

0.0

... 多变量相关EDA不仅分布模型更复杂,合适的模型还需通过迭代学习产生,如因子化分布算法(Factorized Distribution Algorithm, FDA)^[11]、贝叶斯优化算法(Bayesian Optimization Algorithm, BOA)^[12]等 ...

1999

0.0

2014

0.0

... 近年来,EDA的研究逐渐由二进制编码向实数编码发展,主要侧重于概率模型的改进^[13]及与其它优化算法的融合 ...

2011

0.0

... 张建华等^[14]采用经验分布函数替代正态分布函数,提出任意分布的连续多变量耦合分布估计算法 ...

2011

0.0

... 王丽芳等^[15]估计各变量的边缘分布函数,构造Copula函数,作为产生子代候选解的概率分布模型 ...

2004

0.0

... 例如,融合GA与EDA^[16] ...

2010

0.0

... 利用细菌的趋向性运动,将细菌觅食行为(Bacterial Foraging, BF)引入EDA^[17] ...

2014

0.0

... 另外,也有学者将传统的优化算法应用于EDA中,提高EDA的局部搜索能力^[18] ...

2019

0.0

... 由于EDA的概率模型直接关系到子代候选解的质量,对概率模型的改进一直备受学者关注^[19,20] ...

2017

0.0

... 由于EDA的概率模型直接关系到子代候选解的质量,对概率模型的改进一直备受学者关注^[19,20] ...

2019

0.0