本节回顾有关形式概念分析的基本概念和性质.

定义1^[2] 称(U, A, I)为一个形式背景, 其中:

U={x₁, x₂, …, x_n}

为对象集, 每个x_i(i≤ n)称为一个对象;

A={a₁, a₂, …, a_m}

为属性集, 每个a_j(j≤ m)称为一个属性; I为U和A之间的二元关系, I⊆U× A.若(x, a)∈ I, 称x具有属性a.

形式背景可表示为一个二维表, 其中每行表示一个对象, 每列表示一个属性, 行列交叉处的1表示(x, a)∈ I, 0表示(x, a)∉I.

对于形式背景(U, A, I), 在对象子集X⊆U和属性子集B⊆A上分别定义算子:

X^* ={a|a∈ A, ∀ x∈ X, (x, a)∈ I},

B^* ={x|x∈ U, ∀ a∈ B, (x, a)∈ I}.

特别地, 对于∀ x∈ U, a∈ A, 记{x}^* 为x^* , {a}^* 为a^* .

设(U, A, I)为形式背景, 若二元对(X, B)满足X^* =B且X=B^* , 称(X, B)是一个形式概念, 简称概念.X称为概念的外延, B称为概念的内涵.

对于形式背景(U, A, I), ∀ X₁⊆U, X₂⊆U, X⊆U, B₁⊆A, B₂⊆A, B⊆A, 可得如下基本性质:

1)X₁⊆X₂⇒ X2*⊆ X1*, B₁⊆B₂⇒ B2*⊆ B1*;

2)X⊆X^{* *} , B⊆B^{* *} ;

3)X^* =X^{* * *} , B^* =B^{* * *} ;

4)X⊆B^* ⇔ B⊆X^* ;

5)(X₁∪ X₂)^* = X1*∩ X2*, (B₁∪ B₂)^* = B1*∩ B2*;

6)(X₁∩ X₂)^* ⊇ X1*∪ X2*, (B₁∩ B₂)^* ⊇ B1*∪ B2*;

7)(X^{* *} , X^* )和(B^* , B^{* *} )都是概念.

使用L(U, A, I)表示形式背景(U, A, I)中所有概念的集合, 对于

∀ (X₁, B₁)∈ L(U, A, I), (X₂, B₂)∈ L(U, A, I),

在偏序关系

(X₁, B₁)≤ (X₂, B₂)⇔ X₁⊆X₂(⇔ B₁⊇B₂)

下, 可证明

(X₁, B₁)∧ (X₂, B₂)=(X₁∩ X₂, (B₁∪ B₂)^{* *} ), (X1_, B1₎∨ (X2_, B2₎=((X1_∪ X2₎* ^{* ,} B1_∩ B2₎

也是概念, 从而L(U, A, I)是格, 并且是完备格, 称为(U, A, I)的概念格.

定义2^[2] 若L(U, A₁, I₁)和L(U, A₂, I₂)是2个概念格, 且对于∀ (X', B')∈ L(U, A₂, I₂), 总存在(X, B)∈ L(U, A₁, I₁), 使得X'=X, 则称L(U, A₁, I₁)细于L(U, A₂, I₂), 记作

L(U, A₁, I₁)≤ L(U, A₂, I₂).

对于对象集与属性集均相同的2个概念格中的不同概念, 还可定义概念之间的包含关系, 称概念(X, B)包含于(X', B'), 即

(X, B)⊆(X', B')

当且仅当X⊆X'且B⊆B'.基于概念之间的包含关系, 定义概念包含映射如下.

定义3^[26] 设

L₁=L(U, A, I₁), L₂=L(U, A, I₂),

定义L₁到L₂上的概念包含映射ζ ∶ L₁→ L₂, 使得对于任意2个概念(X, B)∈ L₁, (Y, C)∈ L₂,

ζ ((X, B))=(Y, C)

当且仅当

(X, B)⊆(Y, C)

且不存在(Y', C')∈ L(U, A, J), 使得

(Y', C')≤ (Y, C), (X, B)⊆(Y', C').

在对2个不同形式背景对应的概念格进行研究时, 针对概念格间定义的映射, 给出相关定义及定理如下.

定义4^[2] 设(U, A, I)和(V, C, J)为2个形式背景,

α ∶ P(U)→ P(V)

为从U到V上的一个映射,

β ∶ P(A)→ P(C)

为从A到C上的一个映射.若对于(V, C, J)中的任意外延Y, 原像α ^-1(Y)为(U, A, I)中的一个概念外延, 则称映射α 是外延连续的; 若对于(V, C, J)中任意内涵B, 原像β ^-1(B)为(U, A, I)的一个内涵, 则称映射β 是内涵连续的.若α 是外延连续的且β 是内涵连续的, 则称映射对(α , β )是连续的.若对于∀ (X, B)∈ L(U, A, I), (β (B)^* , α (X)^* )为(V, C, J)中的概念, 则称映射对(α , β )是保概念的.若映射对(α , β )同时满足保概念且连续, 则称为概念可靠的.

对于定义3中给出的概念包含映射ζ , 可将其分解为外延之间的映射α :P(U)→ P(U)和内涵之间的映射β :P(A)→ P(A), 文献[26]证明该映射对是连续且保概念的, 即是概念可靠的.

定理1^[2] 若(α , β )∶ (U, A, I)→ (V, C, J)为一个概念可靠映射, 则

(X, B)|→ (β (B)^* , α (X)^* )

是从(U, A, I)到(V, C, J)的完全同态.

在形式背景(U, A, I)中给定属性集A的一个划分A_π ={A_i }i=1k, A₁, A₂, …, A_k为该属性集的k个属性类.在实际应用中, 属性集A根据语义或先验知识进行预分类, 从而满足数据分析的不同需求, 更具普遍性.

在该属性分类的基础上, 将集合A_π 视为一个新的属性集, 其中的每个属性类A_i视为一个属性, 在某一对象拥有某一属性类当且仅当其具有该分类下所有属性这一语义要求时, 能够给出悲观分类形式背景的定义.

定义5 悲观分类形式背景 设(U, A, I)为形式背景, 给定属性集A的一个划分A_π ={A_i }i=1k, 称(U, A_π , I πp)为形式背景(U, A, I)在A_π 下的悲观分类形式背景, 其中

I πp={(x, A_i)∈ U× A_π |∀ a∈ A_i, (x, a)∈ I}.

若不加说明, 本文中(U, A_π , I πp)均表示形式背景(U, A, I)在属性集A的划分A_π ={A_i }i=1k下的悲观分类形式背景.在(U, A_π , I πp)下, 定义对象子集X⊆U和属性子集族C⊆A_π 上的算子:

X^{* p}={A_i|A_i∈ A_π , ∀ x∈ X, (x, A_i)∈ I πp},

C* ^p={x|x∈ U, ∀ Ai_∈ C, (x, Ai)∈ I πp}.

若二元对(X, C)满足X^{* p}=C且X=C^{* p}, 称(X, C)为一个悲观分类概念.

对于形式背景(U, A_π , I πp), 对于∀ X₁⊆U, X₂⊆U, X⊆U, C₁⊆A_π , C₂⊆A_π , C⊆A_π , 可得如下基本性质:

1)X₁⊆X₂⇒ X2* p⊆ X1* p, C₁⊆C₂⇒ C2* p⊆ C1* p;

2)X⊆X^{* p* p}, C⊆C^{* p* p};

3)X^{* p}=X^{* p* p* p}, C^{* p}=C^{* p* p* p};

4)X⊆C^{* p}⇔ C⊆X^{* p};

5)(X₁∪ X₂)^{* p}= X1* p∩ X2* p, (C₁∪ C₂)^{* p}= C1* p∩ C2* p;

6)(X₁∩ X₂)^{* p}⊇ X1* p∪ X2* p, (C₁∩ C₂)^{* p}⊇ C1* p∪ C2* p.

使用L(U, A_π , I πp)表示悲观分类形式背景中所有概念的集合, 记

(X₁, C₁)≤ (X₂, C₂)⇔ X₁⊆X₂(⇔ C₁⊇C₂),

称L(U, A_π , I πp)为(U, A, I)的悲观分类概念格, 定理2给出上确界、下确界, 并证明是一个完备格.

定理2L(U, A_π , I πp)为一个完备格, 上确界、下确界分别为

(X₁, C₁)∨ (X₂, C₂)=((X₁∪ X₂)^{* p* p}, C₁∩ C₂), (X1_, C1₎∧ (X2_, C2₎=(X1_∩ X2_, (C1_∪ C2₎* ^{p* p)}.

证明 对于

∀ (X₁, C₁)∈ L(U, A_π , I πp),

(X₂, C₂)∈ L(U, A_π , I πp),

(X₁∪ X₂)^{* p* p* p}=(X₁∪ X₂)^{* p}= X1* p∩ X2* p=C₁∩ C₂,

(C₁∩ C₂)^{* p}=( X1* p∩ X2* p)^{* p}=(X₁∪ X₂)^{* p* p},

即((X₁∪ X₂)^{* p* p}, C₁∩ C₂)是L(U, A_π , I πp)中的一个概念.

再证((X₁∪ X₂)^{* p* p}, C₁∩ C₂)为上确界.由

C₁∩ C₂⊆C₁, C₁∩ C₂⊆C₂,

有

(X₁, C₁)≤ ((X₁∪ X₂)^{* p* p}, C₁∩ C₂)

且

(X₂, C₂)≤ ((X₁∪ X₂)^{* p* p}, C₁∩ C₂),

则其为上界.

下证((X₁∪ X₂)^{* p* p}, C₁∩ C₂)是最小上界.设(X', C')为L(U, A_π , I πp)的一个上界, 满足

(X₁, C₁)≤ (X', C'), (X₂, C₂)≤ (X', C'),

则有

C'⊆C₁, C'⊆C₂,

即

C'⊆C₁∩ C₂,

则有

((X₁∪ X₂)^{* p* p}, C₁∩ C₂)≤ (X', C').

由(X', C')的任意性可知, ((X₁∪ X₂)^{* p* p}, C₁∩ C₂)是最小上界, 即上确界.

同理可证(X₁∩ X₂, (C₁∪ C₂)^{* p* p})为一个概念, 且为下确界.

在给出悲观分类形式背景及其概念格的基础上, 引理1描述原形式背景中的概念导出算子与悲观分类形式背景中的概念导出算子之间的关系.

需要注意的是, 在本文描述中, C表示由属性类构成的属性集族, A_i表示单个属性类, ∪ A_i表示单个或多个属性类包含的属性构成的集合.

引理1 设(U, A_π , I πp)为悲观分类形式背景, X⊆U, C⊆A_π , 则有如下性质:

1)X^{* p}={A_i∈ A_π |A_i⊆X^* },

2) ∪Ai∈X* pA_i⊆X^* ,

3)C^{* p}=( ∪Ai∈CA_i)^* .

证明 先证1).设A_i∈ X^{* p}, 则对于∀ x∈ X, 有(x, A_i)∈ I πp, 从而对于∀ a∈ A_i, 都有(x, a)∈ I, 即a∈ X^* , 则A_i⊆X^* , 即

A_i∈ {A_i∈ A_π |A_i⊆X^* },

进而

X^{* p}⊆{A_i∈ A_π |A_i⊆X^* }.

另一方面, 设

A_i∈ {A_i∈ A_π |A_i⊆X^* },

则对于∀ a∈ A_i, 均有(x, a)∈ I, 从而有A_i∈ X^{* p}, 即有

{A_i∈ A_π |A_i⊆X^* }⊆X^{* p}.

综上所述, 1)成立.

再证2).由1)的证明过程易得, 对于∀ A_i∈ X^{* p}, 都有A_i⊆X^* , 则2)显然成立.

最后证3).设x∈ C^{* p}, 则对于∀ A_i∈ C, (x, A_i)∈ I πp, 从而对于∀ a∈ A_i, 有(x, a)∈ I, 即有

x∈ ( ∪Ai∈CA_i)^* ,

则

C^{* p}⊆( ∪Ai∈CA_i)^* .

另一方面, 设

x∈ ( ∪Ai∈CA_i)^* ,

则对于

∀ a∈ ∪Ai∈CA_i, (x, a)∈ I,

从而对于∀ A_i∈ C, a∈ A_i, 有(x, A_i)∈ I πp, 即x∈ C^{* p}, 则

( ∪Ai∈CA_i)^* ⊆C^{* p},

即3)成立.

结合引理1给出的算子之间的关系, 可获得原概念格与悲观分类概念格之间的关系, 以及此种关系下定义的2个概念格之间的映射的性质.

定理3 设L(U, A_π , I πp)为悲观分类概念格, 若(X, C)∈ L(U, A_π , I πp), 则(X, X^* )∈ L(U, A, I), 进一步可有

L(U, A, I)≤ L(U, A_π , I πp),

该偏序关系即为一般概念格之间的偏序关系.

证明 由(X, C)∈ L(U, A_π , I πp), 有

X^{* p}=C, C^{* p}=X,

由引理1中3), 有

X=C^{* p}=( ∪Ai∈CA_i)^* ,

则

(X, X^* )=(( ∪Ai∈CA_i)^* , ( ∪Ai∈CA_i)^{* *} )∈ L(U, A, I),

则进一步得L(U, A, I)≤ L(U, A_π , I πp).

定理4 设L(U, A_π , I πp)为悲观分类概念格:

1)定义φ 为L(U, A_π , I πp)到L(U, A, I)上的一个映射,

∀ (X, C)∈ L(U, A_π , I πp), φ ((X, C))=(X, X^* ),

则φ 是一个保交映射;

2)定义ψ 为L(U, A, I)到L(U, A_π , I πp)上的一个映射,

∀ (X, B)∈ L(U, A, I), ψ ((X, B))=(X^{* p* p}, X^{* p}),

则ψ 是一个保序映射;

3)ψ 􀳱φ ∶ L(U, A_π , I πp)→ L(U, A_π , I πp)是一个恒等映射.

证明 先证1).对于

∀ (X₁, C₁)∈ L(U, A_π , I πp),

(X2_, C2)∈ L(U, Aπ _, I πp),

由引理1中3), 有

X₁= C1* p=( ∪Ai∈C1A_i)^* , X₂= C2* p=( ∪Ai∈C2A_i)^* ,

则有

X1* *=( ∪Ai∈C1A_i)^{* * *} =( ∪Ai∈C1A_i)^* =X₁,

X2* *( ∪Ai∈C2Ai)^{* *} =( ∪Ai∈C2A_i)=X2_,

从而有

( X1*∪ X2*)^{* *} =( X1* *∩ X2* *)^* =(X₁∩ X₂)^* .

因此有

$\begin{aligned}\varphi(& \left.\left(X_{1}, C_{1}\right) \wedge\left(X_{2}, C_{2}\right)\right)=\\& \varphi\left(X_{1} \cap X_{2}, \left(C_{1} \cup C_{2}\right)^{* p * p}\right)=\\& \left(X_{1} \cap X_{2}, \left(X_{1} \cap X_{2}\right)^{* }\right)=\\& \left(X_{1} \cap X_{2}, \left(X_{1}^{* } \cup X_{2}^{* }\right)^{* * }\right)=\\& \left(X_{1}, X_{1}^{* }\right) \wedge\left(X_{2}, X_{2}^{* }\right)=\\& \varphi\left(X_{1}, C_{1}\right) \wedge \varphi\left(X_{2}, C_{2}\right) .\end{aligned}$

再证2).对于

∀ (X₁, B₁)∈ L(U, A, I), (X₂, B₂)∈ L(U, A, I),

若(X₁, B₁)≤ (X₂, B₂), 即X₁⊆X₂, 则 X1* p⊇ X2* p, 则对于

ψ ((X₁, B₁))=( X1* p* p, X1* p),

ψ ((X2_, B2))=( X2* p* p, X2* p),

有

ψ ((X₁, B₁))≤ ψ ((X₂, B₂)).

最后证3).对于(X, C)∈ L(U, A_π , I πp), 由

X^{* p}=C, X^{* p* p}=X,

易得

ψ 􀳱φ (X, C)=(X, C).

在此基础上, 通过一般的概念格构造算法得到悲观分类概念格.

定理5 设(U, A, I)为形式背景, 给定属性分类A_π ={A_i }i=1k, 则有

L(U, A_π , I πp)={( Xπp, Bπp)| (X, B)∈ L(U, A, I)},

其中

Xπp=[ ∪Ai∈AπAi⊆BA_i]^* , Bπp={A_i|A_i∈ A_π , A_i⊆B}.

证明 设(X, C)∈ L(U, A_π , I πp), 由定理3可知∃(X, B)∈ L(U, A, I), 其中B=X^* .由引理1中1), 有

C=X^{* p}={A_i|A_i⊆X^* }={A_i|A_i⊆B},

又由引理1中3), 有

X=C^{* p}=( ∪Ai∈CA_i)^* =( ∪Ai⊆BA_i)^* ,

则有

$\begin{array}{l}L\left(U, \mathcal{A}_{\pi}, I_{\pi}^{p}\right) \subseteq \\\qquad\left\{\left(\left(\cup_{A_{i} \in \mathcal{A}_{\pi} \atop A_{i} \in B} A_{i}\right)^{* }, \left\{A_{i} \mid A_{i} \subseteq B\right\}\right)\right. \\\mid \forall(X, B) \in L(U, A, I)\} .\end{array}$

另一方面, 对于(X, B)∈ L(U, A, I), A_i⊆B, 由引理1中3),

$\begin{aligned}\left\{A_{i} \mid A_{i} \subseteq B\right\}^{* p}=& \left(\bigcup_{A_{i} \subseteq B} A_{i}\right)^{* } \\\left(\left(\bigcup_{A_{i} \subseteq B} A_{i}\right)^{* }\right)^{* _{p}}=& \left\{A_{i} \mid A_{i} \subseteq B\right\}^{* p * p}=\\& \left\{A_{i} \mid A_{i} \subseteq B\right\}, \end{aligned}$

则

(( ∪Ai⊆BA_i)^* , {A_i|A_i⊆B})∈ L(U, A_π , I πp).

由此二者相等.

从构建悲观分类概念格的角度出发, 本文给出直接由原概念格生成其悲观分类概念格的方法, 对应的概念生成算法如算法1所示.

算法1 形式背景的悲观分类概念生成算法

输入 形式背景(U, A, I),

属性集上的划分A_π ={A_i }i=1k

输出 悲观分类概念集L(U, A_π , I πp)

step 1 构建原概念格内涵集

L_A(U, A, I)={B⊆A|X, B)∈ L(U, A, I)}={Bj}_j=1^m

step 2 对于每个B_j∈ L_A(U, A, I), 遍历A_π ={A_i }i=1k, 若A_i⊆B_j, 使其属于关于内涵B_j的悲观分类概念内涵 Bjπp.

step 3 构建所有悲观分类概念内涵的集合{ Bjπp}j=1m, 去重, 得到悲观分类概念内涵集

L_A(U, A, I πp)={ Blπp}l=1n.

step 4 针对每个悲观分类概念内涵 Blπp, 计算其悲观分类概念外延 Xlπp=(∪ Blπp)^* .

step 5 以二元组的形式返回所有的 Xlπp和 Blπp, 算法结束.

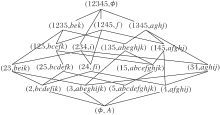
例1 考察5名中学生的学科成绩情况.设U={1, 2, …, 5}表示对象集, 表示5名学生; A={a, b, …, k}表示属性集, 表示11门学科.根据各学科思维方式的不同, 将其划分为4个学科领域, 以

A_π ={A₁, A₂, A₃, A₄}

表示, 其中:A₁={a, b}为语言类学科, 分别表示语文和英语; A₂={c, d, e, f}为理工类学科, 分别表示数学、物理、化学、生物; A₃={g, h, i}为文史类学科, 分别表示政治、历史、地理; A₄={j, k}为艺术类学科, 分别表示音乐和美术.为了针对性地根据不同学生在不同学科领域的总体表现对其进行生涯规划, 进一步处理学生学科成绩表.将学科成绩位于班级前50%的学生认定为在该学科中表现良好, 并以1表示, 否则表示为0, 形成如表1所示的形式背景(U, A, I), 概念格如图1所示.

表1

Table 1

表1(Table 1)

表1 例1的形式背景(U, A, I) Table 1 Formal context(U, A, I) of example 1 U a b c d e f g h i j k 1 1 1 1 0 1 1 1 1 0 1 1 2 0 1 1 1 1 1 0 0 1 0 1 3 1 1 0 0 1 0 1 1 1 1 1 4 1 0 0 0 0 1 1 1 1 1 0 5 1 1 1 1 1 1 1 1 0 1 1

表1 例1的形式背景(U, A, I) Table 1 Formal context(U, A, I) of example 1

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 例1的概念格L(U, A, I)Fig.1 Concept lattice L(U, A, I) of example 1

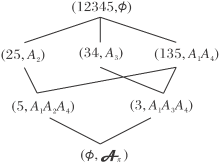
在“ 某学生在某学科领域中所有学科均表现良好, 则其适合进一步研究或从事该学科领域相关的方向或工作” 这一语义下, 研究(U, A, I)的悲观分类形式背景, 形成如表2所示的形式背景(U, A_π , I πp), 根据定理5得到对应的悲观分类概念格如图2所示.

表2

Table 2

表2(Table 2)

表2 例1的悲观分类形式背景(U, Aπ , I πp) Table 2 Pessimistic classified formal context(U, Aπ , I πp) of example 1 U A1 A2 A3 A4 1 1 0 0 1 2 0 1 0 0 3 1 0 1 1 4 0 0 1 0 5 1 1 0 1

表2 例1的悲观分类形式背景(U, Aπ , I πp) Table 2 Pessimistic classified formal context(U, Aπ , I πp) of example 1

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 例1的悲观分类概念格L(U, Aπ , I πp)Fig.2 Pessimistic classified concept lattice L(U, Aπ , I πp) of example 1

悲观分类概念格L(U, A_π , I πp)从同时具有的角度, 研究不同学生对于各学科领域的掌握程度, 根据该层级结构可清晰地对学生进行分类, 从而实现生涯规划或学科互助的目的.以悲观分类概念(5, A₁A₂A₄)为例, 学生5在语言类、理工类、艺术类学科表现均为良好, 而在文史类学科中存在弱势, 因此在进行专业选择时更适合于选择理工类学科.

不同于悲观分类形式背景, 本节在某一对象拥有某一属性类当且仅当其具有该分类下至少一个属性这一语义下, 定义形式背景在给定属性分类下的乐观分类形式背景.

定义6 乐观分类形式背景 设(U, A, I)为形式背景, 给定属性集A的一个划分A_π ={A_i }i=1k, 则称(U, A_π , I πo)为形式背景(U, A, I)在划分A_π 下的乐观分类形式背景, 其中

I πo={(x, A_i)∈ U× A_π |∃a∈ A_i, (x, a)∈ I}.

若不加说明, 文中(U, A_π , I πo)均表示形式背景(U, A, I)在属性集A的划分A_π ={A_i }i=1k下的乐观分类形式背景.在(U, A_π , I πo)下, 定义对象子集X⊆U和属性子集族C⊆A_π 上的算子如下:

X^{* o}={A_i|A_i∈ A_π , ∀ x∈ X, (x, A_i)∈ I πo},

C^{* o}={x|x∈ U, ∀ Ai_∈ C, (x, Ai)∈ I πo}.

其性质与悲观分类形式背景下的算子性质类似.若二元对(X, C)满足X^{* o}=C且X=C^{* o}, 则称(X, C)是一个乐观分类概念.使用L(U, A_π , I πo)表示乐观分类形式背景中所有概念的集合, 可证明L(U, A_π , I πo)是一个完备格, 称为(U, A, I)的乐观分类概念格, 上确界、下确界分别为

(X₁, C₁)∨ (X₂, C₂)=((X₁∪ X₂)^{* o* o}, C₁∩ C₂), (X1_, C1₎∧ (X2_, C2₎=(X1_∩ X2_, (C1_∪ C2₎* ^{o* o)}.

引理2 设(U, A_π , I πo)为乐观分类形式背景, X⊆U, C⊆A_π , 则有如下性质:

1)X^{* o}={A_i∈ A_π |a∈ X^* , a∈ A_i},

2)X^* ⊆ ∪Ai∈X* oA_i,

3)C^{* o}⊇( ∪Ai∈CA_i)^* .

证明 先证1).设A_i∈ X^{* o}, 则对于∀ x∈ X, 有(x, A_i)∈ I πo, 即∃a∈ A_i, 使得(x, a)∈ I, 则a∈ X^* 且

A_i∈ {A_i∈ A_π |a∈ X^* , a∈ A_i},

则

X^{* o}⊆{A_i∈ A_π |a∈ X^* , a∈ A_i}.

另一方面, 设

A_i∈ {A_i∈ A_π |a∈ X^* , a∈ A_i},

则∃a∈ A_i且a∈ X^* , 则对于∀ x∈ X, 有(x, a)∈ I, 则(x, A_i)∈ I πo, 即A_i∈ X^{* o}, 则

{A_i∈ A_π |a∈ X^* , a∈ A_i}⊆X^{* o},

即1)成立.

再证2).由1)有

X^{* o}={A_i∈ A_π |a∈ X^* , a∈ A_i},

即对于∀ x∈ X, 若∃x∈ A_i, 有(x, a)∈ I, 则(x, A_i)∈ I πo, 显然有

X^* ⊆ ∪Ai∈X* oA_i.

最后证3).设x∈ ( ∪Ai∈CA_i)^* , 则对于∀ a∈ ∪Ai∈CA_i, 有(x, a)∈ I, 即对于∀ A_i∈ C, (x, A_i)∈ I πo, 则x∈ C^{* o}, 有

C^{* o}⊇( ∪Ai∈CA_i)^* .

引理2给出在乐观分类形式背景下的概念导出算子与原形式背景中的概念导出算子之间的关系.由于乐观分类形式背景在定义上较宽泛, 乐观分类概念格与原概念格之间不再满足严格的细于关系, 仅满足概念之间的包含关系.

定理6 设L(U, A_π , I πo)为乐观分类概念格, 则对于∀ (Y, C)∈ L(U, A_π , I πo), ∃(X, B)∈ L(U, A, I), 有

X⊆Y, B⊆ ∪Ai∈CA_i.

证明 设(Y, C)∈ L(U, A_π , I πo), 则Y=C^{* o}, 即对于∀ x∈ Y, A_i∈ C, 有(x, A_i)∈ I πo.由乐观分类形式背景的二元关系

I πo={(x, A_i)∈ U× A_π |∃a∈ A_i, (x, a)∈ I},

对于∀ A_i∈ A_π , Ai* o= ∪a∈Aia^* , 则对于∀ a∈ A_i, 有a^* ⊆ Ai* o.进一步, 对于∀ a∈ ∪Ai∈CA_i, 至少存在一个Y的子集, 使得对于该子集中任意对象x, 有(x, a)∈ I, 则从概念的角度出发, 至少存在一个对象子集X⊆Y, 为L(U, A, I)的一个概念外延.

另一方面, 对于对象子集Y, 由Y=C^{* o}, 则对于∀ x∈ Y, A_j∈ A_π /C, 有(x, A_j)∉I πo, 从而对于∀ a∈ A_j, (x, a)∉I, 则对于对象子集X⊆Y, ∀ x∈ X, a∈ ∪Aj∈Aπ/CA_j, 有(x, a)∉I, 进而

B=X^* ⊆ ∪Ai∈CA_i.

进一步, 定义L(U, A, I)到L(U, A_π , I πo)上的映射τ ∶ L(U, A, I)→ L(U, A_π , I πo), 即对于任意2个概念

(X, B)∈ L(U, A, I), (Y, C)∈ L(U, A_π , I πo), τ ((X, B))=(Y, C),

当且仅当X⊆Y, B⊆ ∪Ai∈CA_i且不存在

(Y', C')∈ L(U, A_π , I πo),

使得(Y', C')≤ (Y, C)且

X⊆Y, B⊆ ∪Ai∈CA_i.

可看到, 在将分类形式背景中的属性类视作属性集合时, B⊆ ∪Ai∈CA_i与概念包含关系中要求的属性之间的包含关系是一致的, 因此这样定义的映射τ 与概念包含映射ζ 在本质上是相同的, 其具有的性质也相同, 因此映射

τ ∶ L(U, A, I)→ L(U, A_π , I πo)

将L(U, A, I)中的外延和内涵分别映射到L(U, A_π , I πo)中的外延和内涵上, 并且为连续的.另外, 映射τ 将L(U, A, I)中每个概念均映射到L(U, A_π , I πo)中的概念上, 因此该映射是保概念的.由于映射τ 是连续且保概念的, 则其为概念可靠的.在将映射τ 分解为映射对的情况下, 根据定理1可直接得到如下定理7.

定理7 设(U, A, I)为形式背景, 给定属性分类A_π ={A_i }i=1k, L(U, A_π , I πo)为其在属性分类A_π 下的乐观分类概念格, 则映射

τ ∶ L(U, A, I)→ L(U, A_π , I πo)

是一个完全格同态.

在此基础上, 通过一般的概念格构造算法得到乐观分类概念格.

定理8 设(U, A, I)为形式背景, 给定属性分类A_π ={A_i }i=1k, 则有

L(U, A_π , I πo)= {( Xπo, Bπo)| (X, B)∈ L(U, A, I)},

其中

Xπo= ∩Ai∈AπAi⋂B≠Ø( ∪a∈Aia^* ),

Bπo{A_i|A_i∈ Aπ _, Ai_∩ B≠ Ø }.

证明 对于(Y, C)∈ L(U, A_π , I πo), 由定理6, ∃(X, B)∈ L(U, A, I), 有X⊆Y且B⊆ ∪Ai∈CA_i, 对于(X, B), (Y^{* *} , Y^* )∈ L(U, A, I), 有X⊆Y⊆Y^{* *} , 即X⊆Y^{* *} , 则有(X, B)≤ (Y^{* *} , Y^* ), 则B⊇Y^* , 由引理2中2), 有

Y^* ⊆∪ Y^{* o}= ∪Ai∈CA_i,

则有

Y^* ⊆B⊆ ∪Ai∈CA_i,

对于∀ a∈ Y^* , 有a∈ B, 进而有A_i∩ B≠ Ø , 则

C=Y^{* o}={A_i},

其中

A_i∈ A_π , A_i∩ B≠ Ø .

另外, 对于A_i∈ C,

$\begin{aligned} A_{i}^{* o}=& \left\{x \mid x \in U, \exists a \in A_{i}, x I a\right\}=\\ & \cup_{a \in A_{i}}\{x \mid x \in U, x I a\}=\cup_{a \in A_{i}} a^{* }, \end{aligned}$

则

$\begin{gathered} C^{* o}=\left\{x \mid x \in U, \forall A_{i} \in C, \exists a \in A_{i}, x I a\right\}= \\ \bigcap_{A_{i} \in C}\left\{x \mid x \in U, \exists a \in A_{i}, x I a\right\}= \\ \bigcap_{A_{i} \in C} A_{i}^{* o}=\bigcap_{A_{i} \in C}\left(\cup_{a \in A_{i}} a^{* }\right), \end{gathered}$

即

Y=C^{* o}= ∩Ai∈C( ∪a∈Aia^* ).

另一方面, 对于(X, B)∈ L(U, A, I), 令

C={A_i|A_i∈ A_π , A_i∩ B≠ Ø },

则

C^{* o}= ∩Ai∈CAi* o= ∩Ai∈C( ∪a∈Aia^* )

且由

Ai* o= ∪a∈Aia^* , ∩Ai∈CAi* o=C^{* o},

有

( ∩Ai∈C( ∪a∈Aia^* ))^{* o}=C={A_i},

故

( ∩Ai∈C( ∪a∈Aia^* ), {A_i})∈ L(U, A_π , I πo).

最后给出由原概念格直接生成乐观分类概念格的方法, 对应的概念生成算法如算法2所示.

算法2 形式背景的乐观分类概念生成方法

输入 形式背景(U, A, I),

属性集上的划分A_π ={A_i }i=1k

输出 乐观分类概念集L(U, A_π , I πo)

step 1 构建原概念格内涵集

L_A(U, A, I)= {B⊆A|(X, B)∈ L(U, A, I)}={Bj}_j=1^m

step 2 对于每个B_j∈ L_A(U, A, I), 遍历A_π ={A_i }i=1k, 若A_i∩ B_j≠ Ø , 则使其属于关于内涵B_j的乐观分类概念内涵 Bjπo.

step 3 构建所有乐观分类概念内涵的集合{ Bjπo}j=1m, 去重, 得到乐观分类概念内涵集

L_A(U, A, I πo)={ Blπo}l=1n.

step 4 针对每个乐观分类概念内涵 Blπo, 计算乐观分类概念外延

Xlπo= ∩Ai∈Blπo( ∪a∈Aia^* ).

step 5 以二元组的形式返回所有的 Xlπo和 Blπo, 算法结束.

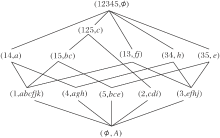
例2(续例1) 结合同一学科领域各学科思维方式类似这一特点, 为了帮助学生进一步挖掘学科潜力, 如表3所示, 形式背景(U, A, J)将学科成绩位于班级前20%的学生认定为在该学科中表现优秀, 表示为1, 否则表示为0, 概念格如图3所示.

表3

Table 3

表3(Table 3)

表3 例2的形式背景(U, A, J) Table 3 Formal context (U, A, J) of example 2 U a b c d e f g h i j k 1 1 1 1 0 0 1 0 0 0 1 1 2 0 0 1 1 0 0 0 0 1 0 0 3 0 0 0 0 1 1 0 1 0 1 0 4 1 0 0 0 0 0 1 1 0 0 0 5 0 1 1 0 1 0 0 0 0 0 0

表3 例2的形式背景(U, A, J) Table 3 Formal context (U, A, J) of example 2

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 例2的概念格L(U, A, J)Fig.3 Concept lattice L(U, A, J) of example 2

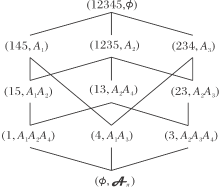
在“ 某学生在某学科领域中至少有一门学科表现优秀, 则其具有在这一学科领域继续发展的潜力” 这一语义下, 研究(U, A, J)的乐观分类形式背景, 形成形式背景如表4所示, 根据定理8得到对应的乐观分类概念格如图4所示.

表4

Table 4

表4(Table 4)

表4 例2的乐观分类形式背景(U, Aπ , J πo) Table 4 Optimistic classified formal context (U, Aπ , J πo) of example 2 U A1 A2 A3 A4 1 1 1 0 1 2 0 1 1 0 3 0 1 1 1 4 1 0 1 0 5 1 1 0 0

表4 例2的乐观分类形式背景(U, Aπ , J πo) Table 4 Optimistic classified formal context (U, Aπ , J πo) of example 2

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 例2的乐观分类概念格L(U, Aπ , J πo)Fig.4 Optimistic classified concept lattice L(U, Aπ , J πo) of example 2

乐观分类概念格L(U, A_π , J πo)从至少具有一个的角度, 研究学生在各学科领域是否具有优秀科目, 根据这一结果可从学生个体出发, 结合其可能具有的学科潜力因材施教.以乐观分类概念(1235, A₂)为例, 学生1、学生2、学生3、学生5在理工科学科中均有优秀科目, 可通过建立理工科学习小组, 进一步挖掘理工学科潜力.

从例1和例2可看到, 悲观分类概念格和乐观分类概念格因其不同的分类逻辑分别适用于实际应用中的不同情境, 满足数据分析过程中的不同需求.

鉴于概念格理论良好的数学性质及其对于实际数据的可解释性, 针对不同形式的数据集和多种数据分析目标都具有较强的适用性.结合现实语义中不同情境下属性的分类逻辑, 本文直观定义悲观分类形式背景和乐观分类形式背景, 分别研究分类形式背景与原形式背景之间算子、概念的关系.再从概念格的角度分别阐述2种分类概念格与原概念格间的关系, 并通过定义映射进一步研究原概念和分类概念间的对应.最后给出2种分类概念格的构造定理.可以看到, 本文未从如何对属性进行聚类这一问题出发, 而是更多地从实际角度聚焦于在给定属性分类的情况下对象与属性类之间关系的定义方式, 研究不同定义方式下构成的新的形式背景和概念格.

出于简化模型的考虑, 本文现有的研究仅涉及2种较极端的情况, 即悲观分类和乐观分类, 而在现实生活中往往会出现更丰富的分类逻辑.另外, 在实际中会出现更复杂的情境, 单个形式背景中的不同属性类可能会具有不同的分类逻辑, 因此针对该类混合分类问题的研究也具有一定的实际意义.