面向限价指令簿趋势分析的网络集成模型

引用本文

吕雪瑞, 张莉. 面向限价指令簿趋势分析的网络集成模型. 模式识别与人工智能, 2021,34(8): 751-759
L#cod#x000dc; Xuerui, ZHANG Li. Network Ensemble Model for Trend Analysis of Limit Order Books. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(8): 751-759. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202108008
Permissions

《模式识别与人工智能》编辑部

面向限价指令簿趋势分析的网络集成模型

吕雪瑞¹, 张莉^1,²

1.苏州大学计算机科学与技术学院苏州 215006

2.苏州大学机器学习与类脑计算国际合作联合实验室苏州 215006

通讯作者:

张莉,博士,教授,主要研究方向为机器学习、模式识别、图像处理.E-mail:zhangliml@suda.edu.cn.

作者简介:

吕雪瑞,硕士研究生,主要研究方向为机器学习、深度学习、金融时间序列分析.E-mail:20194227038@stu.suda.edu.cn.

About Author:
LÜ Xuerui, master student. Her research interests include machine learning, deep learning and financial time series analysis.

收稿日期: 2021-04-28 接受日期: 2021-06-16

资助项目: 江苏省高校自然科学研究项目(No.19KJA550002)、江苏省六大人才高峰项目(No.XYDXX-054)、江苏高校优势学科建设工程项目资助

摘要

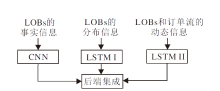
为了更好地分析限价指令簿(LOBs)的趋势,文中提出面向LOBs趋势分析的网络集成模型(NEM-LOB).模型融合2个长短期记忆(LSTM)子模型和1个卷积神经网络(CNN)子模型.一个LSTM子模型可通过LOBs的分布信息捕捉全局时间依赖性,另一个LSTM子模型可通过LOBs和订单流的动态信息捕捉全局动态性.CNN子模型通过LOBs的事实信息提取局部特征.最后,结合3个子模型,提取特征以获得预测结果.在FI-2010数据集上的实验表明NEM-LOB通过引入订单流信息,能对LOBs进行更好的趋势分析.

关键词: 订单流; 限价指令簿(LOBs); 集成模型; 卷积神经网络(CNN); 长短期记忆(LSTM)

中图分类号:TP183

Network Ensemble Model for Trend Analysis of Limit Order Books

LÜ Xuerui¹, ZHANG Li^1,²

1. School of Computer Science and Technology, Soochow University, Suzhou 215006

2. Joint International Research Laboratory of Machine Learning and Neuromorphic Computing, Soochow University, Suzhou 215006

Corresponding author:
ZHANG Li, Ph.D., professor. Her research interests include machine learning, pattern recognition and image processing.

Fund:Natural Science Foundation of Jiangsu Higher Education Institutions(No.19KJA550002), Six Talent Peak Project of Jiangsu Province(No.XYDXX-054), Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions

Abstract

To analyze the trend of limit order books(LOBs) better, a network ensemble model for trend analysis of LOBs(NEM-LOB) is proposed. Two long short-term memory(LSTM) sub-models and one convolutional neural network sub-model are integrated in NEM-LOB. One LSTM sub-model captures the global temporal dependence through the distribution information of LOBs. The other LSTM sub-model captures the global dynamics through the dynamic information of LOBs and order streams. The local features are extracted through the factual information of LOBs. Finally, three sub-models are combined to extract features to obtain prediction results. Experiments on FI-2010 dataset show that NEM-LOB makes a better trend analysis for LOBs by combining order streams.

Key words: Key Words Order Streams; Limit Order Books(LOBs); Ensemble Model; Convolutional Neural Network(CNN); Long Short-Term Memory(LSTM)

文章图片

本文责任编委高阳

Recommended by Associate Editor GAO Yang

近年来, 随着金融市场的完善, 资本市场吸引越来越多的投资个体和投资机构.在金融市场高频交易的过程中产生海量的金融时间序列数据, 如市场数据、K线数据、限价指令簿(Limit Order Books, LOBs)、订单流数据等^{[1, 2]}.本文关注LOBs和订单流的趋势分析.作为一种金融时间序列, LOBs可反映投资者预期价格水平, 增强投资者与相应的交易市场的交互信息, 有助于理解金融指标的相互依赖性^[3].然而, LOBs具有低信噪比、非平稳和非线性的特点, 因此, 对LOBs的分析是一项具有挑战性的任务.研究者们针对市场指令的流动性、非对称效应等特点进行研究^{[4, 5]}, 发现LOBs具有价格发现功能.

学者们利用经典统计学、传统机器学习和深度学习预测股票的价格趋势.首先, 在有关经典统计学模型的研究中, 张传海等^[5]提取刻画LOBs的信息变量, 建立向量自回归模型, 研究价格动态的非对称效应, 判断未来价格走势.Tran等^[6]利用多线性判别分析和加权多通道时间序列回归方法, 预测LOBs的中间价格.但上述方法对假设条件具有很强的依赖性.

Ntakaris等^[7]认为机器学习和经典统计学具有较大区别, 机器学习不需要一系列的假设条件, 因此具有更好的通用性.经典机器学习方法^{[7, 8, 9, 10]}被应用于LOBs的分析.Kercheval等^[8]使用多类支持向量机捕捉高频LOBs的动态性, 并自动对中间价格、价差等指标进行实时预测.Ntabaris等^[9]从技术和定量分析中提取手工特征, 提出自适应逻辑线性回归结合特征选择方法, 预测股票价格走势.

另一些研究者们着重探讨深度学习的研究^{[10, 11, 12, 13, 14, 15, 16, 17]}.Tsantekidis等^[10]提出一种卷积神经网络方法, 用于预测未来的中间价格走势.Niñ o等^[11]将LOBs数据进行类图像表示, 并使用卷积神经网络(Convolutional Neural Network, CNN)识别隐藏特征.Passalis等^[12]提出数据驱动自适应归一化层, 利用平稳特征进行价格趋势分析.Mä kinen等^[13]结合注意力机制与CNN, 预测股票价格走势.可是, 上述模型使用卷积层处理时间序列时, 忽略LOBs的层级结构.为了解决这一问题, Zhang等^[14]提出针对LOBs的深度卷积神经网络(Deep CNN for Limit Order Books, DeepLOB), 在设计卷积层时考虑LOBs的层级结构.DeepLOB使用2个卷积层学习局部层级关系, 再使用1个卷积层融合所有LOBs的相关特征.除此之外, Tran等^[15]提出时间注意增强双线性网络(Temporal Attention-Augmented Bilinear Net-work, TABN), 融合双线性映射和注意力机制.TABN设置时间维度和注意力机制的权重, 用于提高模型对时间信息的注意力.但是, DeepLOB和TABN仅使用不完整的交易信息, 即LOBs的事实信息.

一般来说, 订单流包含所有的限价指令、市价指令和撤销指令, 而LOBs是由未成交的限价指令构成^[18].因此, 订单流包含所有的交易订单, 而LOBs只包含部分未成交的订单^[19].为了充分利用源自LOBs和相应订单流的信息, 本文提出面向LOBs趋势分析的网络集成模型(Network Ensemble Model for Trend Analysis of LOBs, NEM-LOB), 结合1个CNN子模型和2个长短期记忆网络(Long Short-Term Memory, LSTM)子模型.修改DeepLOB的一个模块, 作为NEM-LOB的一个子模型, 可学习相邻五级限价指令之间的相互关系和多个周期的短期相关性, 从而形成LOBs的局部特征.采用2个LSTM子模型, 其中:1个子模型学习LOBs的分布信息, 捕捉全局时间依赖性; 另一个子模型从LOBs和订单流中捕捉全局动态性.连接2个LSTM子模型的输出, 形成全局特征.以此通过LOBs和订单流分析LOBs的中间价格趋势.在公开数据集FI-2010上的实验验证本文模型的有效性.

1 面向限价指令簿趋势分析的网络集成模型

面向限价指令簿趋势分析的网络集成模型(NEM-LOB)框架如图1所示.在NEM-LOB中:设计1个CNN子模型, 用于处理LOBs的事实信息; 设计2个LSTM子模型, 用于处理LOBs和订单流的相关信息.分别通过CNN和LSTMs获取局部模式和全局时间依赖性.后端集成策略提供一种混合方式, 用于融合3组特征信息.

	Figure Option View Download New Window
	图1 NEM-LOB框图Fig.1 Framework of NEM-LOB

1.1 卷积神经网络子模型

金融市场的高频交易指令有2种:限价指令和市价指令.投资者以指定的价格和数量向交易所发出委托指令.如果指定价格是最佳的可成交价格, 形成市价指令; 否则, 生成限价指令.市价指令和限价指令均可能在将来的某个时间点成交, 若指令未成交, 则该指令可被撤销, 生成撤销指令.在t时刻, 对未完成的限价指令进行价格排序后, 相同价格的挂单量相加, 即可得到该价格对应的挂单总量.

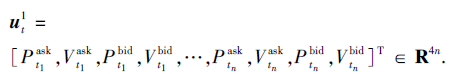
通常来说, t时刻的限价指令簿数据包含n级限价指令, 其中第i级的限价指令包括预买入价格 $P_{t_{i}}^{bid}$ 、预买入挂单量 $V_{t_{i}}^{bid}$ 、预卖出价格 $P_{t_{i}}^{ask}$ 、预卖出挂单量 $V_{t_{i}}^{ask}$ .例如, 买入指令的第1级价格是买方提供的最高价格, 而卖出指令的第1级价格是卖方提供的最低价格.在t时刻, 令LOBs的特征向量表示为

再令CNN子模型的输入特征矩阵为

$U_{t}^{1}$ =[ $u_{t - m + 1}^{1}$ , $u_{t - m + 2}^{1}$ , …, $u_{t}^{1}$ ]^T∈ R^m^{× 4}ⁿ,

其中m为过去时刻特征向量的个数.

NEM-LOB借鉴DeepLOB的第一个模块, 对其增加上采样层并修改卷积核的大小.这个改进模型作为NEM-LOB的CNN子模型, 一共包含9层, 如图2所示.Con₂、Con₃、Con₄、Con₆、Con₈均是二维卷积层, 下标表示层数.MP₅、MP₇均是最大池化层, 下标表示层数.

	Figure Option View Download New Window
	图2 CNN子模型结构图Fig.2 Architecture of CNN sub-model

LOBs拥有多个级别.在t时刻, LOBs的第i个级别包含4个特征:P $_{t_{i}}^{ask}$ 、V $_{t_{i}}^{ask}$ 、P $_{t_{i}}^{bid}$ 、V $_{t_{i}}^{bid}$ .S₁是上采样层, 用于放大输入类图像 $U_{t}^{1}$ , 其中采样核大小为2× 2.为了覆盖相邻5级限价指令, 设计卷积层Con₂.根据移动平均的思想, 设计卷积层Con₃、Con₄, 用于覆盖相同特征多个时间跨度的信息.MP₅用于去除时间维度的冗余信息.Con₆用于覆盖多个时间跨度的信息.MP₇用于减少网络参数数量.Con₈用于集成时间维度和特征维度的信息.另外, Con₃、Con₄、Con₆的填充值设置均为“ same” .在NEM-LOB中, 最后一层F₉是全连接层, 包含16个神经元.

1.2 长短期记忆网络子模型

为了更好地分析LOBs的趋势, 利用更多的信息, 这些信息源自同一只股票的LOBs和相应的订单流^[2].为此, 引入额外信息, 包括LOBs的分布信息、LOBs和订单流的动态信息.为了处理这些信息, NEM-LOB采用2个LSTM子模型:LSTM I和LSTM II, 分别处理分布信息和动态信息.2个LSTM子模型均包含1个变形层和1个LSTM层, LSTM单元数为16.首先依据文献[8]介绍这些信息, 然后描述LSTM单元.

LOBs的分布信息可表示为a₁~a₄.

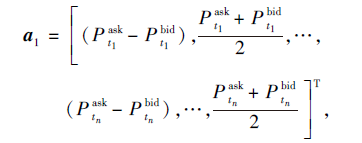
表示同级别的异向价差和多个级别的中间价格, 反映LOBs买单和卖单的相对分布情况.

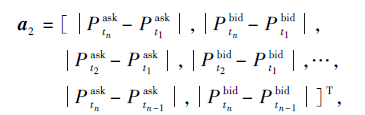
表示第1级与第n级的同向价差和相邻级别的同向价差.

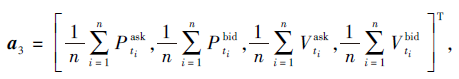
表示卖单或买单的价格均值和挂单量均值.

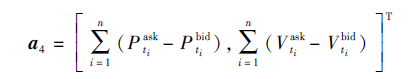
表示累加异向价差, 可反映买单和卖单的不平衡程度.

令分布信息向量

$u_{t}^{2}$ =[ ${a^{T}}_{1}$ , ${a^{T}}_{2}$ , ${a^{T}}_{3}$ , ${a^{T}}_{4}$ ]^T∈ R⁽⁴ⁿ⁺⁶⁾,

表示在时刻t的LOBs分布信息.再令分布信息图像样本向量

$U_{t}^{2}$ =[ $u_{t - k_{1} + 1}^{2}$ , $u_{t - k_{1} + 2}^{2}$ , …, $u_{t}^{2}$ ]^T∈ $R^{k_{1} \times (4 n + 6)}$ ,

其中k₁表示过去时刻分布向量的个数.

订单流包括限价指令、市价指令和撤销指令.3种指令的动态变化不仅会影响LOBs的动态变化, 还会影响投资者的情绪, 甚至影响市场价格, 所以订单流可提供丰富的信息, 有助于分析LOBs的趋势.LOBs和订单流的动态信息可表示为d₁~d₅.

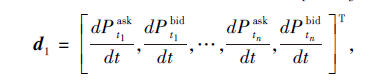
表示LOBs每级价格的导数.

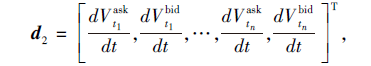
表示LOBs每级挂单量的导数.

d₃=[ $λ_{Δt}^{la}$ , $λ_{Δt}^{lb}$ , $λ_{Δt}^{ma}$ , $λ_{Δt}^{mb}$ , $λ_{Δt}^{ca}$ , $λ_{Δt}^{cb}$ ]^T,

表示六类指令在时间区间[t-Δ t+1, t]的平均强度, 其中, la表示限价卖出指令, lb表示限价买入指令, ma表示市价卖出指令, mb表示市价买入指令, ca表示撤销卖出指令, cb表示撤销买入指令.平均强度

$λ_{Δt}^{type}$ = $\frac{M_{Δt}^{type}}{M_{Δt}^{all}}$ ,

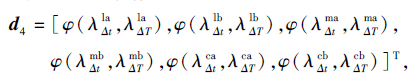
type表示指令的类别, $M_{Δt}^{type}$ 表示指令类别type在时间段Δ t内出现的次数, $M_{Δt}^{all}$ 表示六类指令在时间段Δ t内出现的总次数.

表示六类指令的长期平均强度和短期平均强度的比较值, 其中Δ t< Δ T,

φ (a, b)= $\{\begin{array}{l} 1, & a > b \\ 0, & a \leq b \end{array}$

例如, φ ( $λ_{Δt}^{la}$ , $λ_{ΔT}^{la}$ )表示限价卖出指令的短期平均强度 $λ_{Δt}^{la}$ 和长期平均强度 $λ_{ΔT}^{la}$ 的比较值:如果 $λ_{Δt}^{la}$ > $λ_{ΔT}^{la}$ , 比较值为1; 否则, 比较值为0.

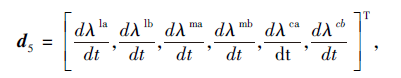
表示每类指令的平均强度变化率.

令动态信息向量

$u_{t}^{3}$ =[ ${d^{T}}_{1}$ , ${d^{T}}_{2}$ , …, ${d^{T}}_{5}$ ]^T∈ R⁽⁴ⁿ⁺¹⁸⁾,

表示在t时刻动态信息的所有特征; 令动态信息图像样本向量

$U_{t}^{3}$ =[ $u_{t - k_{2} + 1}^{3}$ , $u_{t - k_{2} + 2}^{3}$ , …, $u_{t}^{3}$ ]^T∈ $R^{k_{2} \times (4 n + 18)}$ ,

其中k₂表示过去时刻动态信息向量的个数.

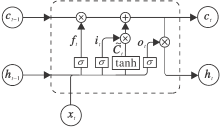
LSTM是在循环神经网络的基础上提出的^[20], 引入门的结构, 能从时间序列中获取时间特征, 并学习时间序列的长期依赖关系^[21].具体如图3所示.

	Figure Option View Download New Window
	图3 LSTM单元结构图Fig.3 Architecture of an LSTM Unit

LSTM单元由3个门(遗忘门f_t、输入门i_t、输出门o_t)和细胞单元C_t组成, 其中, 遗忘门f_t决定在细胞状态中丢弃哪些信息, 输入门i_t决定在细胞状态中保存哪些信息, 输出门o_t产生输出信息.LSTM单元的更新公式可表示为

f_t=σ (W_f[h_t_-1, x_t]+b_f), (1)

i_t=σ (W_i[h_t_-1, x_t]+b_i), (2)

C_t=f_tC_t_-1+i_t ${\dot{C}}_{t}$ , (3)

${\dot{C}}_{t}$ =tanh(W_C[h_t_-1, x_t]+b_C),

o_t=σ (W_o[h_t_-1, x_t]+b_o),

h_t=o_ttanh(C_t),

其中, σ 表示sigmoid函数, x_t表示在t时刻LSTM单元的输入向量, h_t表示输出向量, W_f、W_i、W_C、W_o表示遗忘门、输入门、细胞单元、输出门的权重矩阵, b_f、b_i、b_C、b_o表示遗忘门、输入门、细胞单元、输出门的偏置向量.根据式(1)和式(2), 遗忘门和输入门分别获得删除信息和增加信息的能力.在式(3)中:旧细胞单元与f_t进行点乘, 丢掉要删除的信息; ${\dot{C}}_{t}$ 与i_t进行点乘, 获取需要添加的信息.

在NEM-LOB中的2个LSTM子模型(LSTM I与LSTM II)具有相同结构, 均包含1个变形层和1个LSTM层.其中变形层用于更改输入数据的形状, LSTM层的单元数为16.LSTM I子模型通过学习分布信息得到全局时间特征向量, LSTM II子模型通过学习动态信息得到全局动态特征.

1.3 后端集成策略

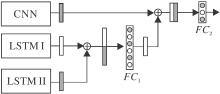
CNN子模型使用LOBs的事实信息生成局部特征, LSTM I子模型用于捕捉LOBs分布信息的全局时间特征, LSTM II子模型用于捕捉LOBs和相应订单流动态信息的全局动态特征.本文期望使用这3种特征(局部特征、全局时间特征和全局动态特征)分析LOBs的未来趋势.为此, 设计后端集成方案, 融合3种特征.NEM-LOB特定的后端集成策略如图4所示.

	Figure Option View Download New Window
	图4 后端集成策略框图Fig.4 Framework of back-end ensemble strategy

LSTM I子模型和LSTM II子模型的输出为相似性质的2个全局特征向量, 这2个向量在行上连接, 得到大小为32× 1的向量.通过全连接层FC₁之后, 生成大小为16× 1的向量, 该向量与CNN子模型的输出, 在列上连接, 形成大小为16× 2的矩阵.最后, NEM-LOB通过全连接层FC₂, 得到每类的概率值, 激活函数为softmax函数.

具体NEM-LOB步骤如下所示.

算法 NEM-LOB

输入 LOBs的事实信息 $U_{t}^{1}$ , 分布信息 $U_{t}^{2}$ ,

订单流与LOBs的动态信息 $U_{t}^{3}$ ,

对应的时间步长m, k₁, k₂

输出训练完毕的网络参数θ

初始化 NEM-LOB网络的所有参数θ ,

设置轮数为N, 批量大小为B

for i=1, 2, …, N do

for i=1, 2, …, ⌊N/B」 do

输入随机选择的B个样本, $U_{t}^{1}$ 、 $U_{t}^{2}$ 、 $U_{t}^{3}$ 分别输入CNN、LSTM I、LSTM II子模型中;

根据自适应矩估计(Adaptive Moment Estima-tion, Adam)优化算法和交叉熵损失函数对网络的参数θ 进行梯度下降更新

end for

2 实验及结果分析

2.1 实验数据集

本文采用基础数据集FI-2010进行实验.FI-2010数据集包含2010年6月1日至6月14日纳斯达克北欧市场中5只芬兰股票的交易数据.在FI-2010数据集上, 一共包含3种标准化方法:z-score标准化、min-max标准化、十进制精度标准化.在z-score标准化的FI-2010数据集上评估NEM-LOB.

在标准化的数据集上, 分析和预测这些股票的未来趋势.令H表示预测区间, 在FI-2010数据集上, H=10, 20, 30, 50, 100.通常, LOBs的趋势可分为3类:上涨(Up)、下跌(Down)、不变(Stationary).简便起见, 令类1为上涨趋势, 类-1为下跌趋势, 类0为不变趋势.

本文模型有多组输入 $U_{t}^{1}$ 、 $U_{t}^{2}$ 、 $U_{t}^{3}$ , 单组输出y_t.多组输入数据分别具有不同的参数:过去时刻事实信息向量的个数m、动态信息向量的个数k₁、分布信息向量的个数k₂.在实验中, 分别设置m=100, k₁=10, k₂=10, 其中m的取值是根据文献[10]、文献[14]、文献[15]设定, 而k₁、k₂的取值是根据经验设定.

单组输出y_t∈ R³是在t时刻输入数据的标签向量:

y_t= $\{\begin{array}{l} {[1, 0, 0]}^{T}, & l_{t} = 1 \\ {[0, 1, 0]}^{T}, & l_{t} = 0 \\ {[0, 0, 1]}^{T}, & l_{t} = - 1 \end{array}$

2.2 实验设置

NEM-LOB是在python环境下实现的, 并使用Keras框架进行训练.CNN子模型中的卷积层Con_i(i=2, 3, 4, 6, 8)和F₉的激活函数为ReLU函数.在后端集成模块中, FC₁的激活函数为ReLU函数, FC₂的激活函数为softmax函数.CNN子模型和2个LSTM子模型均使用随机掩码方法.在实验中, dropout的参数值设置为0.5.Adam优化方法的学习率设置为0.01, 模糊因子的起始值设置为1.使用交叉熵损失函数更新模型的所有参数.

在NEM-LOB的训练过程中, 批量大小设置为64, 共训练200轮.使用准确率(Accuracy, AC)、精确率(Precision, P)、召回率(Recall, R)和F₁值评估NEM-LOB的性能, 则

其中:TP表示预测值为正样本、实际也为正样本的样本个数; FN表示预测值为负样本、实际也为负样本的样本个数; TN表示预测值为正样本、实际为负样本的样本个数; FP预测值为负样本、实际为正样本的样本个数.

在实验过程中, 采用2种数据设置:Setting I和Setting II.在Setting I中, 数据集分为2部分:一部分是包含9天数据的训练集; 另一部分是包含1天数据的测试集, 预测区间H=10, 50, 100.在Setting II中, 数据集同样分为2部分:一部分是包含7天数据的训练集; 另一部分是包含3天数据的测试集, 预测区间H=10, 20, 50.

2.3 预测性能对比

在Setting I中, 对比如下9种模型:岭回归(Ridge Regression, RR)^[7]、单隐层前馈网络(the Single-Hidden Layer Feed-Forward Network, SLFN)^[7]、DeepLOB^[14]、TABN^[14]、多线性判别分析(Multi-linear Discriminant Analysis, MDA)^[22]、神经特征袋(Neural Bag-of-Features, N-BoF)^[23]、时序逻辑特征袋(Temporal Logistic BoF, T-Lo-BoF)^[24]、时序逻辑神经特征袋(Temporal Logistic Neural BoF, TLo-NBoF)^[25]、NEM-LOB.

在Setting I上的实验结果如表1所示, 表中对比模型的结果来自相应的参考文献, -表示没有来自相应参考文献的结果, TABN表示文献[15]的TABL(C).在某些条件下, NEM-LOB的精度相当高.例如, 当H=10时, 精度为90.54%.但由于样本分布的不均匀性, 分类精度存在一定偏差, 因此主要分析F₁值.NEM-LOB的F₁值比DeepLOB平均提高4.35%.此外, 相比MDA、SLFN, NEM-LOB的F₁值分别提高32.21%和45.57%.

表1 各模型在Setting I上的实验结果 Table 1 Experimental results of different models on Setting I %

由于SLFN、MDA、N-BoF、T-LoBoF、TLo-NBoF的相关文献没有提供Setting II的实验结果.因此, 在Setting II中将NEM-LOB与已有的最优2种模型(DeepLOB和TABN)、支持向量机(Support Vector Machine, SVM)^[26]、LSTM^[26]、CNN-I^[10]、CNN-II^[27]进行对比, 结果如表2所示, 表中对比方法的结果也来自相应的参考文献, TABN表示文献[15]中的TABL(C).由表可看到, 当H=20, 50时, 相比Deep-LOB和TABN, NEM-LOB获得更优结果.例如, NEM-LOB在H=20时获得76.40%的F₁值, 明显优于DeepLOB(72.82%).这些结果在一定程度上证实引入LOBs和相关订单流的分布信息和动态信息是有意义和有效的.

表2 各模型在Setting II上的实验结果 Table 2 Experimental results of different models on Setting II %

2.4 计算时间分析

各模型训练单个样本单次反向传播的平均时间(Backward)和预测单个的平均推理时间(Forward)对比如表3所示.TABN、LSTM、DeepLOB、NEM-LOB的训练硬件环境均为GTX1080TI-GPU、32GB.测试硬件环境为i5-9500-CPU、16G.相比TABN、LSTM, NEM-LOB的参数数量和平均计算时间处于劣势, 但从2.3节实验可看出, NEM-LOB的性能明显优于TABN和LSTM.此外, NEM-LOB的计算时间和参数均优于基于深度学习的DeepLOB.

表3 各模型的平均计算时间和参数数量 Table 3 Average computation time and the numbers of parameters of different models

2.5 集成模型与子模型的对比

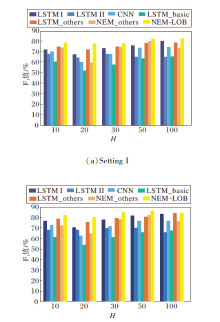
为了显示NEM-LOB的预测性能, 对比NEM-LOB的各个子模型, 并使用F₁值进行评估, 结果如图5所示.对比子模型包括:LSTM I、LSTM II、CNN、使用事实信息的LSTM模型(LSTM_basic)、使用分布和动态信息的LSTM模型(LSTM_others)、结合CNN和LSTM_others的混合模型(NEM_others).由图5可知, LSTM_basic的性能最差, 而针对事实信息的CNN子模型优于LSTM_basic.除此之外, 虽然LSTM_others优于LSTM I和LSTM II, 但与CNN融合之后的性能并不稳定.在7种模型中, NEM-LOB取得最优性能, 说明NEM-LOB可提高子模型的预测能力.

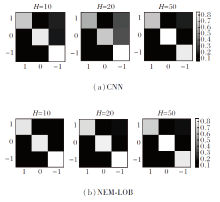
	Figure Option View Download New Window
	图5 各模型在2个数据集上的F₁值对比Fig.5 F₁ values of different models on 2 datasets

除此之外, 采用混淆矩阵对比CNN子模型与NEM-LOB, 混淆矩阵如图6和图7所示.在混淆矩阵中第i行j列的颜色表示实际标签i和预测标签j在实际标签i中所占的样本比例.处于对角线位置的矩阵的颜色较暗, 表示预测正确的样本所占比例相对较小.因此, 对角线矩阵的颜色越浅, 相应模型性能也越优.由图可看到, 无论是在Setting I上还是在Setting II上, 对类1的预测正确比例均有一定程度的提高.除此之外, 在H=20(Setting I)时, 类0对应的矩阵由灰色(CNN)变为白色(NEM-LOB), 说明在应用LOBs和相关订单流的分布信息和动态信息后, NEM-LOB的预测能力优于CNN子模型.

	Figure Option View Download New Window
	图6 CNN子模型和NEM-LOB在Setting I上生成的混淆矩阵Fig.6 Confusion matrices generated by CNN sub-model and NEM-LOB on Setting I

	Figure Option View Download New Window
	图7 CNN子模型和NEM-LOB在Setting II上生成的混淆矩阵Fig.7 Confusion matrices generated by CNN sub-model and NEM-LOB on Setting II

3 结束语

为了更好地预测LOBs的价格波动, 本文提出面向LOBs趋势分析的网络集成模型(NEM-LOB), 采用CNN、LSTM I和LSTM II子模型分别学习3种不同的来自LOBs和相关订单流的信息, 并通过后端集成策略融合3个子模型.在FI-2010数据集上进行大量实验.根据不同的数据划分方式, 构建2种实验设置:Setting I和Setting II.在Setting I上的实验表明, 相比DeepLOB, NEM-LOB的精度和F₁值分别提高12.25%和4.35%.另外, 在Setting II上, 相比DeepLOB, NEM-LOB的F₁值平均提高0.11%.此外, NEM-LOB大幅减少平均计算时间和参数数量.混淆矩阵的结果表明, 加入分布信息和动态信息的后端集成策略显著提高CNN子模型的性能.

虽然NEM-LOB在中长期预测上取得较优效果, 但是在短期预测中, 如在H=10时, NEM-LOB的性能较差.因此, 今后将设计卷积层与集成策略, 提升NEM-LOB对LOBs的短期预测性能.

参考文献

文献选项

[1]	HU G S, HU Y X, YANG K, et al. Deep Stock Representation Learning: From Cand lestick Charts to Investment Decisions // Proc of the International Conference on Acoustics, Speech, and Signal Processing. Washington, USA: IEEE, 2018: 2706-2710. [本文引用:]
[2]	CONT R. Statistical Modeling of High-Frequency Financial Data. IEEE Signal Processing Magazine, 2011, 28(5): 16-25. [本文引用:]
[3]	WEI L J, SHI L. Investor Sentiment in an Artificial Limit Order Market[C/OL]. [2021-03-16]. https: //downloads. hindawi. com/journals/complexity/2020/8581793. pdf. [本文引用:]
[4]	杨宝臣, 郭灿, 王硕. 基于限价指令簿信息的流动性冲击影响. 系统工程, 2017, 35(3): 21-28. (YANG B C, GUO C, WANG S. Order Flows' Liquidity Shock Based on the Order-Driven Market. Systems Engineering, 2017, 35(3): 21-28. ) [本文引用:]
[5]	张传海, 汪璐欹, 彭哲. 限价指令簿信息对价格动态的非对称效应——来自我国A股市场的经验研究. 武汉金融, 2020(3): 18-27. (ZHANG C H, WANG L Q, PENG Z. Asymmetric Effect of Limit Order Book Information on Price Dynamics: An Empirical Study from My Country's A-Shares Market. Wuhan Finance, 2020(3): 18-27. ) [本文引用:]
[6]	TRAN D T, MAGRIS M, KANNIAINEN J, et al. Tensor Representation in High-Frequency Financial Data for Price Change Prediction // Proc of the IEEE Symposium Series on Computational Intelligence. Washington, USA: IEEE, 2017. DOI: DOI:10.1109/SSCI.2017.8280812. [本文引用:]
[7]	NTAKARIS A, MAGRISV M, KANNIAINEN J, et al. Benchmark Dataset for Mid-price Forecasting of Limit Order Book Data with Machine Learning Methods[C/OL]. [2021-03-16]. https: //arxiv. org/pdf/1705. 03233v4. pdf. [本文引用:]
[8]	KERCHEVAL A N, ZHANG Y. Modelling High-Frequency Limit Order Book Dynamics with Support Vector Machines. Quantitative Finance, 2015, 15(8): 1315-1329. [本文引用:]
[9]	NTAKARIS A, KANNIAINEN J, GABBOUJ M, et al. Mid-price Prediction Based on Machine Learning Methods with Technical and Quantitative Indicators[C/OL]. [2021-03-16]. https: //arxiv. org/pdf/1907. 09452v1. pdf. [本文引用:]
[10]	TSANTEKIDIS A, PASSALIS N, TEFAS A, et al. Forecasting Stock Prices from the Limit Order Book Using Convolutional Neural Networks // Proc of the 19th IEEE Conference on Business Informatics. Washington, USA: IEEE, 2017: 7-12. [本文引用:]
[11]	NIÑO J, ARÉVALO A, LEÓN D, et al . Price Prediction with CNN and Limit Order Book Data // Proc of the Workshop on Engineering Applications. Berlin, Germany: Springer, 2018: 124-135. [本文引用:]
[12]	PASSALIS N, TEFAS A, KANNIAINEN J, et al. Adaptive Normalization for Forecasting Limit Order Book Data Using Convolutional Neural Networks // Proc of the IEEE International Confe-rence on Acoustics, Speech, and Signal Processing. Washington, USA: IEEE, 2020: 1713-1717. [本文引用:]
[13]	MÄKINEN Y, KANNIAINEN J, GABBOUJ M, et al . Forecasting Jump Arrivals in Stock Prices: New Attention-Based Network Architecture Using Limit Order Book Data. Quantitative Finance, 2019, 19(12): 2033-2050. [本文引用:]
[14]	ZHANG Z H, ZOHREN S, ROBERTS S. DeepLOB: Deep Convolutional Neural Networks for Limit Order Books. IEEE Transactions on Signal Processing, 2019, 67(11): 3001-3012. [本文引用:]
[15]	TRAN D T, IOSIFIDIS A, KANNIAINEN J, et al. Temporal Attention-Augmented Bilinear Network for Financial Time-Series Data Analysis. IEEE Transactions on Neural Networks and Learning Systems, 2018, 30(5): 1407-1418. [本文引用:]
[16]	NAIK N, MOHAN B R. Intraday Stock Prediction Based on Deep Neural Network. National Academy Science Letters, 2020, 43(2): 241-246. [本文引用:]
[17]	CHOI S P, CHAN Y, LAM S, et al. Analyzing the Importance of Broker Identities in the Limit Order Book through Deep Learning. Big Data, 2021, 9(2): 89-99. [本文引用:]
[18]	GOULD M D, PORTER M A, WILLIAMS S, et al. Limit Order Books. Quantitative Finance, 2013, 13(11): 1709-1742. [本文引用:]
[19]	LI J Y, WANG X T, LIN Y Y, et al. Generating Realistic Stock Market Order Streams. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(1): 727-734. [本文引用:]
[20]	HOCHREITER S, SCHMIDHUBER J. Long Short-Term Memory. Neural Computation, 1997, 9(8): 1735-1780. [本文引用:]
[21]	ZHAO R, WANG K, SU H, et al. Bayesian Graph Convolution LSTM for Skeleton Based Action Recognition // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 6881-6891. [本文引用:]
[22]	TRAN D T, GABBOUJ M, IOSIFIDIS A. Multilinear Class-Speci-fic Discriminant Analysis. Pattern Recognition Letters, 2017, 100: 131-136. [本文引用:]
[23]	PASSALIS N, TSANTEKIDIS A, TEFAS A, et al. Time-Series Classification Using Neural Bag-of-Features // Proc of the 25th European Signal Processing Conference. Washington, USA: IEEE, 2017: 301-305. [本文引用:]
[24]	PASSALIS N, TEFAS A, KANNIAINEN J, et al. Deep Temporal Logistic Bag-of-Features for Forecasting High Frequency Limit Order Book Time Series // Proc of the IEEE International Conference on Acoustics, Speech and Signal Processing. Washington, USA: IEEE, 2019: 7545-7549. [本文引用:]
[25]	PASSALIS N, TEFAS A, KANNIAINEN J, et al. Temporal Logistic Neural Bag-of-Features for Financial Time Series Forecasting Leveraging Limit Order Book Data. Pattern Recognition Letters, 2020, 136: 183-189. [本文引用:]
[26]	TSANTEKIDIS A, PASSALIS N, TEFAS A, et al. Using Deep Learning to Detect Piece Change Indications in Financial Markets // Proc of the 25th European Signal Processing Conference. Washington, USA: IEEE, 2017: 2511-2515. [本文引用:]
[27]	TSANTEKIDIS A, PASSALIS N, TEFAS A, et al. Using Deep Learning for Price Prediction by Exploiting Stationary Limit Order Book Features[C/OL]. [2021-03-16]. https: //arxiv. org/pdf/181009965. pdf. [本文引用:]