引用本文
杜晨杰, 杨宇翔, 伍瀚, 何志伟, 高明煜. 旋转自适应的多特征融合多模板学习视觉跟踪算法. 模式识别与人工智能, 2021,34(9): 787-797
DU Chenjie, YANG Yuxiang, WU Han, HE Zhiwei, GAO Mingyu. Visual Tracking Algorithm Based on Rotation Adaptation, Multi-feature Fusion and Multi-template Learning. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2021,34(9): 787-797.  
Doi: 10.16451/j.cnki.issn1003-6059.202109002
Permissions
Copyright©2021, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
旋转自适应的多特征融合多模板学习视觉跟踪算法
杜晨杰1, 杨宇翔1, 伍瀚1, 何志伟1, 高明煜2
1.杭州电子科技大学 电子信息学院 杭州 310018
2.杭州电子科技大学 浙江省装备电子研究重点实验室 杭州 310018
通信作者:

何志伟,博士,教授,主要研究方向为机器学习、目标跟踪.E-mail:zwhe@hdu.edu.cn.

作者简介:

杜晨杰,博士研究生,主要研究方向为目标检测与跟踪.E-mail:ducj@hdu.edu.cn.

杨宇翔,博士,副教授,主要研究方向为深度学习、目标跟踪.E-mail:yyx@hdu.edu.cn.

伍 瀚,硕士研究生,主要研究方向为目标检测与跟踪.E-mail:wuhan0326@hdu.edu.cn.

高明煜,博士,教授,主要研究方向为视频/图像处理.E-mail:mackgao@hdu.edu.cn.

收稿日期: 2021-04-20 接受日期: 2021-09-02
资助项目: 国家自然科学基金项目(No.61873077,61401129)、浙江省重点研发计划项目(No.2018C01069)资助
摘要

目标发生旋转及遇到外界干扰时会给目标跟踪带来巨大挑战,针对该问题,文中提出旋转自适应的多特征融合多模板学习跟踪算法.首先,构建具有互补特性的多模板学习模型,全局滤波器模板用于跟踪目标,当判定滤波器模板确定全局滤波器模板被污染时,使用修正滤波器模板对全局滤波器模板进行修正.然后,将颜色直方图作为视觉补充信息和VGGNet-19特征图进行自适应融合,提升全局滤波器模板对目标外观的判别能力.最后,提出旋转自适应策略,采用改进的跟踪置信度,估计跟踪框最佳旋转角度,减轻目标旋转带来的全局滤波器模板性能衰退.在OTB-2013、OTB-2015数据集上的实验表明,文中算法的成功率和精确率较高.

关键词: 目标跟踪; 全局滤波器模板; 旋转自适应; 跟踪置信度
中图分类号:TP391.41
Visual Tracking Algorithm Based on Rotation Adaptation, Multi-feature Fusion and Multi-template Learning
DU Chenjie1, YANG Yuxiang1, WU Han1, HE Zhiwei1, GAO Mingyu2
1. School of Electronics and Information Engineering, Hangzhou Dianzi University, Hangzhou 310018
2. Zhejiang Provincial Key Laboratory of Equipment Electronics, Hangzhou Dianzi University, Hangzhou 310018
Corresponding author:
HE Zhiwei, Ph.D., professor. His research interests include machine learning and object tracking.

About Author:
DU Chenjie, Ph.D. candidate. His research interests include object detection and tracking.
YANG Yuxiang, Ph.D., associate profe-ssor. His research interests include deep learning and object tracking.
WU Han, master student. His research interests include object detection and tracking.
GAO Mingyu, Ph.D., professor. His research interests include video/image proce-ssing.

Fund:National Natural Science Foundation of China(No.6187307,61401129), Key Research and Development Program of Zhejiang Province(No.2018C01069)
Abstract

Visual target tracking remains a hard problem due to unpredictable target rotation and external interference. To address this issue, a target tracking algorithm based on rotation adaptation, multi-feature fusion and multi-template learning(RA-MFML) is proposed. Firstly, a multi-template learning model with complementary characteristics is constructed. The global filter template is used for tracking the target. When the global filter template is determined to be contaminated by the decidable filter template, it is corrected by the modified filter template. Then, the color histogram is regarded as visual supplementary information and fused with feature map of VGGNet-19 adaptively. The discriminating ability of the global filter template for object appearance is thus improved. Finally, a rotation adaptation strategy is proposed. The improved tracking confidence is utilized for the estimation of the optimal rotation angle of the tracking box to alleviate performance degradation of the global filter template caused by target rotation. The experiment on OTB-2013 and OTB-2015 datasets demonstrate that RA-MFML is superior in success rate and precision.

Key words: Key Words Target Tracking; Global Filter Template; Rotation Adaptation; Tracking Confidence

本文责任编委 徐 勇

Recommended by Associate Editor XU Yong

视觉目标跟踪是计算机视觉领域一个极具挑战性的重要问题.随着电子设备和人工智能的不断进步, 视觉跟踪在诸多领域中起着至关重要的作用.跟踪器通过估计视频序列中目标位置和尺度以确定目标的运动方向和轨迹[1, 2].然而, 面对背景杂乱、运动模糊、快速运动、遮挡等复杂场景时, 如何实现鲁棒跟踪仍是亟待解决的问题.

近年来, 基于相关滤波器的跟踪算法由于具备较高的计算效率, 已成为目标跟踪领域的研究热点[3].Bolme等[4]将相关滤波引入目标跟踪, 提出快速、自适应训练的最小输出平方误差和跟踪算法(Minimum Output Sum of Squared Error, MOSSE), 但跟踪精度较低、鲁棒性不强.鉴于此种情况, Henri-ques等[5]设计具有高计算效率的核相关滤波器(Kernelized Correlation Filter, KCF), 采用高斯核运算, 将单通道灰度特征扩展到多通道方向梯度直方图特征(Histogram of Oriented Gradients, HOG), 取得170帧/秒的高跟踪速度, 跟踪性能较优.但KCF中目标样本的循环平移会带来边界效应, 并且在遮挡、目标快速运动等场景上的跟踪效果也不理想.

为了克服这些缺点, 学者们提出大量改进算法.Danelljan等[6]提出基于空间正则化的判别相关滤波器(Spatially Regularized Discriminative Correlation Filters, SRDCF), 减轻边界效应带来的负面影响.Wang等[7]设计多尺度超像素和颜色特征引导的核相关滤波器(Multi-scale Superpixels and Color Feature Guided KCF, MSSCF-KCF), 采用优化的目标分量组合和多尺度超像素方法, 提高跟踪器的鲁棒性.Yan等[8]提出双模板自适应的核相关滤波器(Dual-Template-Based Adaptive KCF, DTA-KCF), 用2个不同尺寸的滤波器模板自适应搜索目标, 从中选择更可靠的目标预测位置作为跟踪结果, 有效解决目标快速运动带来的跟踪性能下降问题.然而, 传统相关滤波跟踪算法通常只提取手工特征, 导致目标特征辨识度不高, 限制跟踪器的准确性和稳健性.

受益于卷积神经网络(Convolutional Neural Net-work, CNN)强大的特征提取能力, 结合CNN特征与相关滤波器的跟踪算法表现出良好的跟踪性能, Danelljan等[9]提出利用浅层卷积特征的判别相关滤波器(DeepSRDCF), 跟踪精度达到较高水平.Ma等[10]提出基于层级卷积特征的目标跟踪算法(Hi-erarchical Convolutional Features, CF2), 采用由粗到细(Coarse-to-Fine)的搜索策略, 并融合不同卷积层特征, 提升跟踪精度, 但未考虑目标尺度的变化.为此, Ma等[11]在CF2的基础上提出基于层次相关特征的跟踪器(Hierarchical Correlation Features-Based Tracker, HCFT* ), 添加尺度估计模块, 提升跟踪器应对目标尺度变化的能力, 并引入目标重检测模块, 减轻模型偏离问题.Danelljan等[12]提出基于连续卷积操作跟踪算法(Continuous Convolution Operator Tracker, CCOT), 使用隐式插值模型, 解决连续空间域的学习问题, 实现多分辨率深度特征图的有效集成, 但跟踪速度只有1帧/秒.Choi等[13]提出基于上下文感知深度特征压缩算法(Tracker Based on Con-text-Aware Deep Feature Compression with Multiple Auto-enCoders, TRACA), 用于视觉跟踪, 使用深度特征压缩方法实现高速计算.Wang等[14]将CNN特征集成到相关滤波器中, 设计自适应的模型更新方案, 训练相关滤波器, 使模型鲁棒性得到显著提升.

上述研究工作取得一定的跟踪性能, 但仍存在一些问题:1)当跟踪过程中出现背景杂乱、遮挡、快速运动等干扰因素时, 不可避免地会引入噪声信息, 使跟踪器模板不断积累误差, 性能衰退.2)基于卷积特征的跟踪器难以准确区分目标和相似物体之间的颜色差异[15].3)多数跟踪算法只考虑对目标的位置和尺度进行估计, 而对目标旋转研究不多.

为了解决上述问题, 本文提出旋转自适应的多特征融合多模板学习跟踪算法(Visual Tracking Algorithm Based on Rotation Adaptation, Multi-feature Fusion and Multi-template Learning, RA-MFML).提出多滤波器模板学习模型, 构建具有互补特性的全局滤波器模板(Global Filter Template, GFT)、判定滤波器模板(Decidable Filter Template, DFT)和修正滤波器模板(Modified Filter Template, MFT).全局滤波器模板对目标进行跟踪, 判定滤波器模板用于判断全局滤波器模板是否被污染, 修正滤波器模板对污染的全局滤波器模板进行修正, 提升全局滤波器模板在复杂环境下的抗干扰能力.为了提高全局滤波器模板对目标外观的判别能力, 组合VGGNet-19中3个不同卷积层形成的特征图, 获取丰富的层级特征.再将组合的卷积特征图与颜色直方图进行自适应融合, 使全局滤波器模板能有效区分目标和相似物体之间的颜色差异.最后, 提出旋转自适应策略, 采用改进的跟踪置信度以估计跟踪框最佳旋转角度, 减少跟踪框漂移问题, 使全局滤波器模板在目标旋转场景下的跟踪效果具有鲁棒性.

1 旋转自适应的多特征融合多模板学习跟踪算法

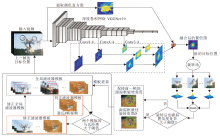
旋转自适应的多特征融合多模板学习跟踪算法(RA-MFML)框架如图1所示.算法包含多模板学习(Multi-template Learning, ML)、多特征融合(Multi-feature Fusion, MF)和旋转自适应(Rotation Adaptation, RA)3部分.在多滤波器模板学习阶段, 构建具有互补特性的全局滤波器模板、判定滤波器模板和修正滤波器模板, 有效提升全局滤波器模板的跟踪鲁棒性.在多特征融合阶段, 融合VGGNet-19特征图和颜色直方图表征目标信息, 提高全局滤波器模板的泛化能力.在旋转自适应阶段, 估计跟踪框最佳旋转角度, 减轻由目标旋转带来的全局滤波器模板性能衰退.

图1 RA-MFML框图Fig.1 Flowchart of RA-MFML

RA-MFML的主要步骤如下.

1)特征提取.使用VGGNet-19提取输入视频的3个卷积层特征, 手工提取颜色直方图特征.

2)多特征融合.将3个卷积层特征通过相关滤波器学习得到3个置信图, 按一定比例进行融合.再将融合后的置信图与颜色直方图进行自适应融合, 用于估计目标位置.

3)旋转自适应.计算跟踪框旋转多个角度后的跟踪置信度, 引入高斯旋转权重约束相邻帧的跟踪框旋转角度变化, 使估计的跟踪框旋转角度贴合目标实际的旋转变化.

4)模板修正和更新.当全局滤波器模板和判定滤波器模板的累计马氏距离大于阈值时, 采用修正滤波器模板对全局模板进行修正, 再在线更新全局、判定和修正滤波器模板.

1.1 多模板学习模型

具有互补特性的多滤波器模板学习模型由全局滤波器模板(GFT)、判定滤波器模板(DFT)和修正滤波器模板(MFT)组成.GFT用于估计目标的位置和旋转变化, 当DFT判断GFT出现污染时, MFT对GFT进行修正.

令前N帧GFT的跟踪结果为

UGN= (uG1, uG2, …, uGN)T,

其中 uGt由第t帧GFT预测的目标位置( xGt, yGt)和平均峰值相关能量(Average Peak Correlation Energy, APCE)[16]APC EGt组成.

UGN的协方差矩阵为

cov( UGN)= cov(xGN, xGN)cov(xGN, yGN)cov(xGN, APCEGN)cov(yGN, xGN)cov(yGN, yGN)cov(yGN, APCEGN)cov(APCEGN, xGN)cov(APCEGN, yGN)cov(APCEGN, APCEGN), (1)

其中,

xGN= (xG1, xG2, …, xGN)T, yGN= (yG1, yG2, …, yGN)T, APCEGN=(APCEG1, APCEG2, …, APCEGN)T

APCE的计算公式如下:

APCE= ‖rmax-rmin‖21W×H(∑w, h‖rw, h-rmin‖2),

其中, rmax、rmin和rw, h分别表示搜索图像特征和滤波器模板互相关得到的响应图分数的最大值、最小值和第w行第h列的值.当后续视频帧(t> N)到来时, 计算 uGt和 uDt之间的马氏距离(Mahalanobis Distan-ce)[17]:

mt= (uGt-uDt)Tcov(UGt)-1(uGt-uDt),

其中 uDt为第t帧的DFT.在跟踪过程中, 每隔k帧计算一次累计马氏距离, 即

Mt= ∑j=t-k+1tmj,

s.t. t=nk+N, n∈ Z+.

将Mt依次存入M中.Mt大于阈值Tht表明最近k帧的GFT被污染.阈值Tht随GFT状态的变化而自适应改变, 即

Tht= ∑j=t-k+1tυ j,

s.t. t=nk+N, n∈ Z+

其中

υ t= (uGt-k-uDt-k)Tcov(UGt)-1(uGt-k-uDt-k).

GFT用于跟踪目标, 每帧都对其进行更新, 即

其中, η G为GFT的学习率, $\hat{α}_{G}^{new}$为GFT新得到的模型.当Mt大于阈值Tht时, 需要使用MFT对GFT进行修正:

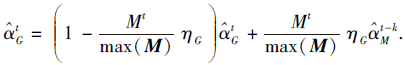
此外, DFT和MFT的更新过程为

其中, n∈ Z+, η D表示DFT的学习率, η M表示MFT的学习率.通过构建具有互补特性的多滤波器模板学习模型, 有效提升GFT在复杂场景下的跟踪鲁棒性.

1.2 多特征融合

在目标跟踪过程中, CNN拥有强大的特征提取能力, 对遮挡、背景杂乱等干扰具有不变性, 鲁棒性较强[18].颜色直方图可区分目标和相似物体的颜色差异.为此, 本文采用在ImageNet上已训练好的VGG-Net-19提取搜索图像的conv3-4、conv4-4、conv5-4这3个层级特征, 通过相关滤波器学习得到3个置信图.再设置3个置信图的权重分别为0.15, 0.3和0.55, 并对它们进行融合, 得到Rconv.

然后与颜色直方图Rcolor进行自适应融合, 得到最终置信图Rf∈ RU× V.多特征融合损失函数如下所示:

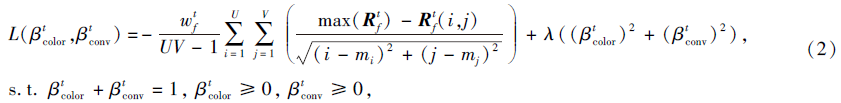
其中, β color表示Rcolor的融合权值, β conv表示Rconv的融合权值, (mi, mj)表示Rf得分最大值坐标, λ 用于控制正则化程度, U× V表示Rf的坐标点个数.

式(2)中

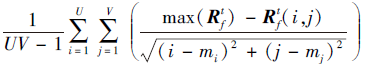
越大, 表明置信图Rf得分最大值位置的斜率平均值越大, 置信图波峰越尖锐, 跟踪性能越优.融合后的置信图

Rft= βcolortRcolort+ βconvtRconvt.

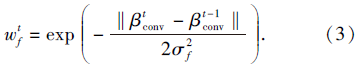
由于跟踪过程中相邻帧目标外观和位置变化有限, 权值 βconvt和 βconvt-1的差值较小, 因此, 本文利用 wft约束相邻帧融合权重的差值:

本文将颜色直方图和VGGNet-19特征图自适应融合后, 置信图更平滑, 波峰更尖锐, 进一步提升全局滤波器模板对目标外观的判别能力.

1.3 旋转自适应

在跟踪过程中, 若目标出现显著的旋转, 会引起跟踪框漂移.Li等[19]提出尺度和旋转相关滤波器(Scale-and-Rotation Correlation Filter, SRCF), 在对数极坐标域上构造相关滤波器, 用于估计目标旋转变化.熊丹等[20]和瑚琦等[21]都采用傅里叶-梅林公式估计目标旋转角度的变化.而本文的旋转自适应策略先计算跟踪框旋转多个角度后的跟踪置信度, 然后引入高斯旋转权重, 对相邻帧的跟踪框旋转角度变化进行约束, 使估计的跟踪框旋转角度贴合目标实际的旋转变化.

本文算法首先定义旋转池(Rotation Pool)如下:

poolt={θ t-1-ns, θ t-1-(n-1)s, …, θ t-1+ns}, s.t. n∈ Z+ (4)

其中, θ t-1表示第t-1帧的跟踪框旋转角度, s表示跟踪框旋转步长.

再针对旋转池中的所有旋转角度, 分别计算跟踪框旋转后置信图得分最大值和平均峰值相关能量.然后, 融合第t帧跟踪框所有旋转角度的 rmaxt和APCEt, 得到跟踪置信度:

ρ t=μ rmaxt+(1-μ )APCEt,

其中,

rmaxt=( rmaxθt-1-ns, rmaxθt-1-(n-1)s, …, rmaxθt-1+ns),

APCEt=(APC Eθt-1-ns, APC Eθt-1-(n-1)s, …, APC Eθt-1+ns), (5)

μ 为权重分配因子.由于置信图得分最大值和平均峰值相关能量的取值区间不同, 融合之前需要对它们进行标准化处理.此外, 由于相邻帧的目标旋转角度变化较小, 引入旋转高斯权重:

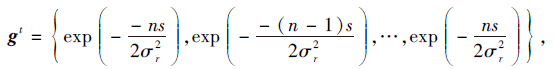
对相邻帧的旋转角度变化进行约束, σ r为旋转区间大小, 即2ns.令

ρgt=max(ρ t☉gt),

获取置信度最高的跟踪框旋转角度θ t.为了进一步提升跟踪稳健性, 本文算法构建相邻帧的跟踪置信度评估模型:

ε = 1, ρgt≥ρgt-10, ρgt< ρgt-1

当ε = 1时, 相比第t-1帧, 当前帧的跟踪置信度得到有效提升, 选择θ t作为跟踪框最佳旋转角度; 否则, 保持前一帧的跟踪框旋转角度.引入旋转自适应策略, 减少由目标旋转带来的跟踪框漂移问题.

2 实验及结果分析

实验使用Matlab 2016b在MatConvNet深度学习库[22]上实现编程. 所有实验在配置为Intel i7-10700 F, 2.9 GHz, NVIDIA GeForce RTX 3070的PC上完成, 本文算法的跟踪速度约为2帧/秒.分别在OTB-2013[23]、OTB-2015[24]数据集上对RA-MFML进行性能评估.

2.1 实验环境

实验设置多特征融合的正则化参数λ =0.1, 多滤波器模板学习模型中η G=η D=η M=0.01, N=20, k=10, 式(3)中σ f=1, 式(4)中n=3.多模板学习的阈值Tht可根据全局模板状态的变化而自适应变化, 多特征融合损失函数中的融合权值 βcolort和 βconvt可根据置信图波峰的尖锐程度而自适应变化.同时部分参数可进行微调, 以适应实际应用场景的需求, 当视频中目标的旋转角度普遍较大时, 可适当增大旋转模板中的旋转步长s, 改善跟踪框漂移的问题.针对遮挡、背景杂乱和相似物体干扰等场景, 可适当减小3个滤波器模板的学习率η G、η D、η M和参数k, 降低外界干扰对模型更新和全局模板污染判定结果的影响.

OTB-2013、OTB-2015数据集分别包含51个和100个视频序列.视频场景有遮挡(Occlusion, OCC)、背景杂乱(Background Clutters, BC)、光照变化(Illumination Variation, IV)、快速运动(Fast Motion, FM)、形变(Deformation, DEF)、尺度变化(Scale Variation, SV)、平面外旋转(Out-of-Plane Rotation, OPR)、平面内旋转(In-Plane Rotation, IPR), 每帧图像至少存在2种挑战场景.

OTB数据集使用一次评估(One-Pass Evalua-tion, OPE)的成功率(Success Rate)和精确率(Preci-sion)作为性能评价标准.

成功率以预测边界框与真实边界框的面积重叠率(Intersection-over-Union, IOU)为基础, 计算在给定重叠率阈值下成功跟踪帧数的占比:

IOU= Rp⋂RgtRp⋃Rgt,

其中, Rp表示预测边界框, Rgt表示真实边界框.成功率越大表示跟踪器的鲁棒性越高.

精确率以预测目标中心位置与真实目标中心位置的中心位置误差(Center Location Error, CLE)为基础, 计算在给定距离阈值下成功跟踪帧数的占比:

CLE= ‖Cp-Cgt‖2,

其中, Cp表示预测目标中心位置, Cgt表示真实目标中心位置.精确率越大表示跟踪精度越高.

2.2 旋转自适应参数分析

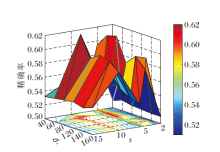
为了获得最佳的旋转区间大小σ r和步长s, 进行16组实验.在实验中, 旋转区间大小σ r依次设置为40, 60, 80, 100, 120, 140, 步长s依次设置为2, 3, 5, 6, 10, 15.选择基准算法HCFT* .跟踪难度较大的18个挑战视频作为测试序列, 包含fleetface、freeman3、bird1、box、human5、human6、matrix、ironman、bolt、couple、tiger2、biker、bolt2、coupon、jump、skating22、trans、panda, 性能指标选择精确率.

σ r 、s不同时的跟踪精度如图2所示.由图可知, 当步长s不变时, 一方面, 随着旋转区间大小σ r逐渐增大, 精确率先增大后减小, 并在σ r= 60时跟踪器获得最大的精确率.另一方面, 旋转区间大小σ r从40增加到60时, 精确率提升非常明显, 说明适当增加旋转池的旋转角度个数, 有利于找到跟踪框最优旋转角度θ t.当旋转区间大小σ r不变时, 在s = 10时取到最大的精确率.因此, 根据图2的实验结果, 为了兼顾OTB-2015数据集的不同视频序列, 后续实验设置旋转区间大小σ r=60, 步长s=10.

图2 σ r和s不同时的跟踪精度Fig.2 Tracking precision with different sizes of σ rand s

在旋转自适应策略中, 将跟踪框旋转所有角度后的rmax和APCE按式(14)融合.为了详尽分析RA-MFML在不同权重μ 下的跟踪性能, 选择OTB-2015数据集上带有旋转挑战的72个测试序列, 包含跟踪难度较大的Bird2、Matrix、MotorRolling、Iron-man等.在实验中, μ =0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8.性能指标选择距离精度(Distance Precision, DP)、重叠精度(Overlap Pre-cision, OP)、中心位置误差(CLE)和视觉目标类重叠率(Visual Object Classes Overlap Ratio, VOR).

μ 不同时, RA-MFML的性能指标值如表1所示.由表可看出, 随着μ 逐渐增大, DP、OP、CLE和VOR都先增大后减小, 当μ = 0.5时, RA-MFML的4个性能指标取到最大值.因此, 按μ = 0.5对响应图得分最大值和平均峰值相关能量进行融合, 可有效提升RA-MFML的整体跟踪性能, 减少由旋转挑战带来的跟踪框漂移问题.

表1 μ 不同时RA-MFML的性能对比 Table 1 Performance comparison of RA-MFML with different μ
2.3 跟踪性能分析

为了验证RA-MFML的优越性能, 选取12种主流跟踪算法在OTB-2013、OTB-2015数据集上进行实验对比.12种对比算法如下:1)孪生网络跟踪器.更深更宽的全卷积孪生网络(Deeper and Wider Full Convolutional Siamese Networks, SiamFC-DW)[25]、孪生候选区域生成网络(Siamese Region Proposal Net-work, SiamRPN)[26]、基于三元组损失的全卷积孪生网络(Triple Loss in Full Convolutional Siamese Net-works, SiamFC-tri)[27]、全卷积孪生网络(Full Convo-lutional Siamese Networks, SiamFC)[28].2)使用卷积特征的相关滤波器跟踪器.DeepSRDCF[9]、CF2[10]、HCF T* [11].3)使用手工特征的相关滤波跟踪器.DTA-KCF[8]、MSSCF-KCF[7]、具有信道和空间可靠性的判别相关滤波器(Discriminative Correlation Filter with Channel and Spatial Reliability, CSRD-CF)[29].4)估计目标旋转的SRCF[19]和具有自适应尺度和旋转估计的鲁棒长期目标跟踪(Robust Long-Term Object Tracking with Adaptive Scale and Rotation Estimation, RLOT)[20].

各算法的成功率曲线和精确率曲线如图3和图4所示.由图可知, RA-MFML的精确率最高, 成功率排名第四.在OTB-2015数据集上, 相比基准算法HCFT* :RA-MFML的成功率从59.3%增加到61.1%, 提升3.04%; 精确率从86.1%提升到89.2%, 提升3.60%.在OTB-2013数据集上, 相比SRCF, RA-MFML的成功率和精确率分别提升15.52%和16.65%.在OTB-2015数据集上, 相比RLOT, RA-MFML的成功率和精确率分别提升6.82%和24.06%.

图3 各算法在2个数据集上的成功率曲线Fig.3 Success rate curves of different algorithms on 2 datasets

图4 各算法在2个数据集上的精确率曲线Fig.4 Precision curves of different algorithms on 2 datasets

各算法在OTB-2015数据集上11种挑战分布的成功率和精确率如图5所示.由图可知, RA-MFML在IPR、OPR、IV、BC、DEF场景下取得优秀性能.

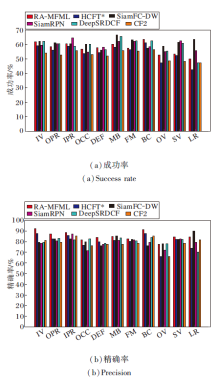图5 各算法在OTB-2015挑战分布下的性能对比Fig.5 Performance comparison of different algorithms with OTB-2015 challenge distribution

为了直观说明RA-MFML在复杂场景下的性能优势, 给出各算法在Bird1、Box、MotorRolling、Skiing、Matrix、Ironman视频上的可视化跟踪结果, 如图6所示.

图6 各算法在OTB-2015数据集的6个挑战视频上的可视化结果Fig.6 Visualization results of different algorithms on 6 challenging sequences from OTB-2015 dataset

由图6可知, Bird1视频存在形变、快速运动等挑战场景, 跟踪难度非常大.第129帧后, 目标形变严重, 有50帧左右目标丢失, 所有对比算法都跟踪失败, 而RA-MFML可保持较高的跟踪鲁棒性.Box视频中:由于背景杂乱、目标旋转等干扰, 第412帧左右, SiamFC和SiamFC-tri难以跟踪目标; 第522帧后, 受遮挡、相似背景干扰, HCFT* 、MSSCF-KCF跟丢目标, 而RA-MFML成功跟踪目标.MotorRolling视频中目标旋转剧烈, 在第120帧左右, SiamFC-DW、SiamFC、DTA-KCF的跟踪框严重漂移, 在后续跟踪过程中无法找回目标.Skiing视频分辨率较低, 跟踪过程出现光照变化、形变和目标旋转等复杂场景, 短时间内旋转角度较大.在第63帧后, SiamFC-DW、SiamRPN、SiamFC-tri、CSRDCF难以适应剧烈的旋转挑战, 而RA-MFML可对目标鲁棒跟踪.Matrix视频背景非常杂乱, 存在目标旋转和遮挡, 第54帧后, 仅RA-MFML和SiamRPN能跟踪目标.Ironman视频存在遮挡、运动模糊和快速运动等复杂场景, 第145帧后, 仅RA-MFML、SiamRPN、CF2能成功跟踪目标.

2.4 消融实验分析

为了验证本文提出的3个关键技术的有效性, 在OTB-2015数据集上对RA-MFML进行消融分析, 结果如表2所示.从整体观察, 基准算法HCFT* 逐一增加多模板学习(ML)、多特征融合(MF)和旋转自适应(RA)后, 成功率和精确率都稳步提升.

表2 RA-MFML在OTB-2015数据集上的消融实验结果 Table 2 Results of ablation experiment of RA-MFML on OTB-2015 dataset

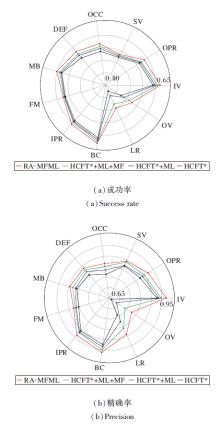
同时对比RA-MFML在11种挑战分布下的成功率和精确率, 如图7所示.相比基准算法HCFT* , 在OCC、SV、OPR、IV、OV、LR、BC、IPR、FM、MB、DEF上:RA-MFML的成功率分别提升5.77%、2.49%、4.27%、4.74%、10.95%、7.52%、3.59%、3.24%、3.26%、1.59%、3.61%、6.05%; 精确率分别提升6.81%、3.05%、5.45%、5.02%、13.60%、10.30%、4.35%、3.26%、3.12%、4.32%、5.28%.因此, 由实验结果可知, 本文的3个关键技术可有效提升跟踪器在复杂场景下的准确性和鲁棒性.

图7 各算法在11种挑战分布上的性能对比Fig.7 Performance comparison of different algorithms with 11 attributes

3 结束语

针对目标发生旋转及遇到外界干扰会给目标跟踪带来巨大的挑战, 本文提出旋转自适应的多特征融合多模板学习目标跟踪算法(RA-MFML).引入多模板学习模型, 提升全局滤波器模板在复杂场景中的跟踪鲁棒性.在此基础上, 融合颜色直方图和VGGNet-19特征图, 提升全局滤波器模板对目标外观的辨别能力.此外, 采用改进的跟踪置信度, 估计目标跟踪框旋转角度, 缓解跟踪框漂移问题.在OTB-2013、OTB-2015数据集上的实验表明, 本文算法能在多个复杂场景下保持跟踪鲁棒性.今后会考虑改进旋转自适应策略, 在实现算法较高跟踪精度的同时, 尽可能减少计算开销.

参考文献
[1] QI Y K, ZHANG S P, QIN L, et al. Hedging Deep Features for Visual Tracking. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(5): 1116-1130. [本文引用:1]
[2] 储珺, 危振, 缪君, 等. 基于遮挡检测和多块位置信息融合的分块目标跟踪算法. 模式识别与人工智能, 2020, 33(1): 59-65.
(CHU J, WEI Z, MIAO J, et al. Block Target Tracking Based on Occlusion Detection and Multi-block Position Information Fusion. Pattern Recognition and Artificial Intelligence, 2020, 33(1): 59-65) [本文引用:1]
[3] 刘巧元, 王玉茹, 张金玲, 等. 基于相关滤波器的视频跟踪方法研究进展. 自动化学报, 2019, 45(2): 265-275.
(LIU Q Y, WANG Y R, ZHANG J L, et al. Research Progress of Visual Tracking Methods Based on Correlation Filter. Acta Automa-tica Sinica, 2019, 45(2): 265-275. ) [本文引用:1]
[4] BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual Object Tracking Using Adaptive Correlation Filters // Proc of the IEEE Computer Society Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2010: 2544-2550. [本文引用:1]
[5] HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-Speed Tracking with Kernelized Correlation Filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. [本文引用:1]
[6] DANELLJAN M, HÄGER G, KHAN F S, et al. Learning Spatially Regularized Correlation Filters for Visual Tracking // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 4310-4318. [本文引用:1]
[7] WANG J, LIU W B, XING W W, et al. Visual Object Tracking with Multi-scale Superpixels and Color-Feature Guided Kernelized Correlation Filters. Signal Processing: Image Communication, 2018, 63: 44-62. [本文引用:2]
[8] YAN J R, ZHONG L C, YAO Y B, et al. Dual-Template Adaptive Correlation Filter for Real-Time Object Tracking. Multimedia Tools and Applications, 2021, 80: 2355-2376. [本文引用:2]
[9] DANELLJAN M, HAGER G, KHAN F S, et al. Convolutional Features for Correlation Filter Based Visual Tracking // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 621-629. [本文引用:2]
[10] MA C, HUANG J B, YANG X K, et al. Hierarchical Convolutional Features for Visual Tracking // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 3074-3082. [本文引用:2]
[11] MA C, HUANG J B, YANG X K, et al. Robust Visual Tracking via Hierarchical Convolutional Features. IEEE Transactions on Pa-ttern Analysis and Machine Intelligence, 2019, 41(11): 2709-2723. [本文引用:1]
[12] DANELLJAN M, ROBINSON A, KHAN F S, et al. Beyond Co-rrelation Filters: Learning Continuous Convolution Operators for Visual Tracking // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 472-488. [本文引用:1]
[13] CHOI J, CHANG H J, FISCHER T, et al. Context-Aware Deep Feature Compression for High-Speed Visual Tracking // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 479-488. [本文引用:1]
[14] WANG Y, WEI X, SHEN H, et al. Adaptive Model Updating for Robust Object Tracking. Signal Processing: Image Communication, 2020, 80. DOI: 10.1016/j.image.2019.115656. [本文引用:1]
[15] GAO T Z, WANG N, CAI J, et al. Explicitly Exploiting Hierarchical Features in Visual Object Tracking. Neurocomputing, 2020, 397: 203-211. [本文引用:1]
[16] WANG M M, LIU Y, HUANG Z Y. Large Margin Object Tracking with Circulant Feature Maps // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 4800-4808. [本文引用:1]
[17] WOJKE N, BEWLEY A, PAULUS D. Simple Online and Realtime Tracking with a Deep Association Metric // Proc of the IEEE International Conference on Image Processing. Washington, USA: IEEE, 2017: 3645-3649. [本文引用:1]
[18] 汤张泳, 吴小俊, 朱学峰. 多空间分辨率自适应特征融合的相关滤波目标跟踪算法. 模式识别与人工智能, 2020, 33(1): 66-74.
(TANG Z Y, WU X J, ZHU X F. Object Tracking with Multi-spatial Resolutions and Adaptive Feature Fusion Based on Correlation Filters. Pattern Recognition and Artificial Intelligence, 2020, 33(1): 66-74. ) [本文引用:1]
[19] LI Y, LIU G Z. Learning a Scale-and -Rotation Correlation Filter for Robust Visual Tracking // Proc of the IEEE International Conference on Image Processing. Washington, USA: IEEE, 2016: 454-458. [本文引用:2]
[20] 熊丹, 卢惠民, 肖军浩, 等. 具有尺度和旋转适应性的长时间目标跟踪. 自动化学报, 2019, 45(2): 289-304.
(XIONG D, LU H M, XIAO J H, et al. Robust Long-Term Object Tracking with Adaptive Scale and Rotation Estimation. Acta Automatica Sinica, 2019, 45(2): 289-304. ) [本文引用:2]
[21] 瑚琦, 李锐, 张薇. 具有旋转特性的目标跟踪算法. 光学学报, 2020, 40(17): 140-147.
(HU Q, LI R, ZHANG W. Target Tracking Algorithm with Rotation Characteristics. Acta Optica Sinica, 2020, 40(17): 140-147. ) [本文引用:1]
[22] VEDALDI A, LENC K. MatConvNet: Convolutional Neural Networks for MATLAB // Proc of the 23rd ACM International Confe-rence on Multimedia. New York, USA: ACM, 2015: 689-692. [本文引用:1]
[23] WU Y, LIM J, YANG M H. Online Object Tracking: A Benchmark // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2013: 2411-2418. [本文引用:1]
[24] WU Y, LIM J, YANG M H. Object Tracking Benchmark. IEEE Tran-sactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. [本文引用:]
[25] ZHANG Z P, PENG H W. Deeper and Wider Siamese Networks for Real-Time Visual Tracking // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2019: 4586-4595. [本文引用:]
[26] LI B, YAN J J, WU W, et al. High Performance Visual Tracking with Siamese Region Proposal Network // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8971-8980. [本文引用:]
[27] DONG X P, SHEN J B. Triplet Loss in Siamese Network for Object Tracking // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2018: 472-488. [本文引用:]
[28] BERTINETTO L, VALMADRE J, HENRIQUES J F, et al. Fully-Convolutional Siamese Networks for Object Tracking // Proc of the European Conference on Computer Vision. Berlin, Germany: Sprin-ger, 2016: 850-865. [本文引用:]
[29] LUKEŽIC A, VOJÍR T, ZAJC L C, et al. Discriminative Correlation Filter with Channel and Spatial Reliability // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 4847-4856. [本文引用:]