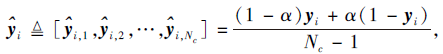形状分类的关键在于提取一个具有高度判别能力的形状描述子, 该形状描述子通常被表示为一个高维的特征向量.因此, 本文提出残差边卷积神经网络, 用于点云分类.网络结构具体如图1 所示, 网络通过1个边卷积(Edge Convolution)及3个残差边卷积块(Residual Edge Convolution Block)分层进行特征提取.将边卷积及堆叠的残差边卷积块提取得到的特征分别记为X₁, X₂, X₃, X₄.再通过密集连接的方式将其拼接, 执行一次卷积操作进行融合, 以充分利用不同层次的特征.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 3D点云分类网络结构图Fig.1 Network structure of 3D point cloud classification

为了获取最终的全局形状描述子f, 本文将全局最大池化和平均池化得到的2个高维向量进行拼接, 保留更多的特征信息.整个过程描述如下:

其中, ‖ 表示拼接操作, * 表示卷积运算, Γ 表示非线性激活函数, $\widetilde{W}$表示融合特征阶段的卷积核权重.

最后形状描述子f被输入到3层全连接网络中, 用于预测最终的分类结果.该全连接网络中前两层网络随机丢弃神经节点的概率为0.5.第三层为线性层, 将目标预测为最终的分类得分.

令

X={x₁, x₂, …, x_N}∈ R^{C× N}

为具有N个点的C维点云.在深度网络中前一层的输出被用作后一层的输入.因此, C通常表示当前层特征的维度.为了捕获点云细致的局部结构特征, 本文根据DGCNN中构图的方式, 将点云构建为一系列的局部图, 并在图上构建边卷积, 结构如图2(a)所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 边卷积与残差边卷积块Fig.2 Edge convolution and residual edge convolution block

首先, 以每个点x_i及它的K个近邻点x_{i, j}∈ N(x_i)构建局部图结构,

N(x_i)={x_{i, j}∶ ‖ x_{i, j}-x_i‖ < δ , j=1, 2, …, K},

其中‖ · ‖ 表示欧几里得范数.每次卷积层都是根据特征空间的距离确定每个点的K近邻, 因此在每层中随特征变化的局部图是动态更新的.通过动态更新的图结构可有效捕获点云在高维空间中的相关性.为了体现邻域点与中心点之间的相关性, 定义图上的节点特征集合:

于是, 边卷积的输出

X^out=Maxpool(Γ (W* H))∈ R^{C'× N},

其中, W为卷积核的权重, Maxpool为对称函数, 保证对任意顺序的输入点集, 输出都保持不变, 从而确保在点云特征提取过程中的置换不变性.

为了强化特征提取能力, 加深网络是一种简单、有效的手段.然而, 简单堆叠卷积层反而会因网络的退化造成特征提取能力的减弱.如图2 (b)所示, 本文在边卷积的基础上, 结合PointNet与残差学习的思想, 构建具有更深层次结构的残差边卷积块.该卷积块的输出为

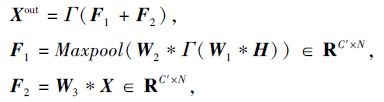
其中, F₁表示从局部图上学习得到的细节特征, F₂表示MLP分支学习到的全局特征, W₁、W₂、W₃为卷积核的权重.

整个卷积块能提取到更深层次的细节特征, 并通过残差学习的方式补充全局特征, 从而丰富点云的特征表示.此外, 残差学习能有效缓解深度网络退化的问题, 构建更深层次的网络, 提高特征提取的能力.此外, 由于在网络特征提取的过程中局部图结构是动态更新的, 因此, 该卷积块能捕获更细致的点对之间的相关性.

对于构造好的残差边卷积神经网络, 采用随机梯度下降算法(Stochastic Gradient Descent, SGD)^[13]训练网络中的权值与偏置.训练网络的损失函数采用光滑的交叉熵损失^[14], 即对样本标签进行软化以获取更光滑的损失函数:

其中, y_i为样本i对应的one-hot编码标签向量,

为软化的标签向量, α 为软化程度, N_c为类别数目, p_{i, j}为预测标签向量的第j个分量.

光滑的损失函数可有效提高模型的泛化能力, 提升网络性能.

实验设备使用一块RTX 6000进行加速运算, 并以Pytorch1.6作为深度学习框架进行网络的搭建与训练.为了公平对比其它方法, 所有的实验结果来源于论文本身.

本文使用整体精度(Overall Accuracy, OA) 和类平均精度(Class-Wise Mean Accuracy, mAcc)作为分类的性能评估指标.

残差边卷积网络中各层的参数如表1所示.表中N表示点的个数, K表示邻域中点的个数, N_c表示类别数, 残差边卷积层的通道数从左到右边依次为卷积核W₁、W₂、W₃的个数.

表1

Table1

表1(Table1)

表1 残差边卷积网络各层参数设置 Table1 Parameter settings of each layer of residual edge convolutional network 输入 尺寸 输出 尺寸 通道数 输入 N - 3 边卷积层 N× K N 64 残差边卷积层 1 N× K N {64, 64, 64} 残差边卷积层 2 N× K N {64, 128, 128} 残差边卷积层 3 N× K N {128, 256, 256} 1× 1 卷积层 N N 1024 最大池化层/ 平均池化层 N 1 2048 全连接层 1 1 {512, 256, Nc}

表1 残差边卷积网络各层参数设置 Table1 Parameter settings of each layer of residual edge convolutional network

另外, 在网络训练阶段, SGD优化器的训练轮数为400, 初始学习率为0.1, 动量系数为0.9, 权重惩罚因子为0.000 1.学习率通过余弦退火函数^[15]衰减到0.001.

本文在ModelNet40^[16]、ScanObjectNN^[17]数据集上进行实验.ModelNet40数据集是3D形状分类任务常用的基准数据集, 包含40个类别的计算机辅助设计(Computer Aided Design, CAD)模型, 总计12 311个.为了公平对比现有算法, 使用相同的方法划分数据集, 9 843个样本用于训练, 2 468个样本用于测试.此外, 与DGCNN^[13]相同, 每个样本被表示为归一化坐标的1 024个点.

ScanObjectNN数据集是真实世界的数据, 样本不仅包含目标本身, 还包含背景信息及噪声干扰.因此, 此数据集更真实、复杂, 具有挑战性.与Model-Net40数据集不同, 每个样本由2 048个坐标归一化的点表示.

在训练阶段, 为了提高样本的多样性, 采用如下操作增强数据:1)[-0.8, 1.25]内的随机各向异性缩放; 2)添加服从N(0, 0.01)分布的随机抖动; 3)随机丢弃部分点 (不超过总点数的12.5%).

本文选择如下算法作为对比方法:PointNet^[6]、点网络加强版(PointNet++)^[7]、ECC^[11]、DGCNN^[12]、蛛网型卷积神经网络(Spider Convolutional Neural Network, SpiderCNN)^[18]、K维树型网络(K-dimen-sional Tree Network, Kd-Net)^[19]、自组织网络(Self-organizing Network, SO-Net)^[20]、点卷积神经网络(PointCNN)^[21]、点卷积(Point Convolution, Point-Conv)^[22]、拓展点卷积神经网络(Point Convolutional Neural Networks by Extension Operators, PCNN)^[23]、环形卷积神经网络(Annularly CNN, A-CNN)^[24]、形状关系卷积(Relation-Shape CNN, RS-CNN)^[25]、几何结构卷积神经网络(Geometric Structure CNN, Geo-CNN)^[26]、连续点卷积(Continuous Convolutions for Point Cloud, ConvPoint)^[27]、点云自适应采样非局部网络(Point Cloud Adaptive Sampling Nonlocal Neural Networks, PointASNL)^[28]、修正的3D费舍尔向量表示(3D Modified Fisher Vector Representation, 3Dm-FV)^[29].各方法在Model-Net40、ScanObjectNN数据集上的性能对比如表2和表3所示, 表中黑体数字表示最优结果.

表2

Table 2

表2(Table 2)

表2 各算法在ModelNet40数据集上的分类性能 Table 2 Classification performance of different algorithms on ModelNet40 dataset 方法 输入格式 点数 mAcc/% OA/% PointNet 坐标 1024 86.2 89.2 PointNet++ 坐标 坐标+法向量 1024 - - 90.7 91.9 ECC 坐标 1024 83.2 87.4 DGCNN 坐标 2048 1024 90.7 90.2 93.5 92.9 SpiderCNN 坐标+法向量 5120 - 92.4 Kd-Net 坐标 32768 - 91.8 SO-Net 坐标+法向量 2048 5120 87.3 90.8 90.9 93.4 PointCNN 坐标 1024 88.1 92.2 PointConv 坐标+法向量 1024 - 92.5 PCNN 坐标 1024 - 92.3 A-CNN 坐标+法向量 1024 90.3 92.6 RS-CNN 坐标 1024 - 92.9 Geo-CNN 坐标+法向量 1024 91.1 93.4 ConvPoint 坐标 1024 88.5 91.8 PointASNL 坐标 坐标+法向量 1024 - - 92.9 93.2 本文算法 坐标 1024 91.23 93.67

表2 各算法在ModelNet40数据集上的分类性能 Table 2 Classification performance of different algorithms on ModelNet40 dataset

表3

Table 3

表3(Table 3)

表3 各算法在ScanObjectNN数据集上的分类性能 Table 3 Classification performance of different algorithms on ScanObjectNN dataset % 3DmFV PointNet PointNet++ SpiderCNN DGCNN PointCNN PointConv 本文算法 bag 39.8 36.1 49.1 43.4 49.4 57.8 52.6 68.6 bin 62.8 69.8 84.4 75.9 82.4 82.9 84.2 85.6 box 15.0 10.5 34.6 12.8 33.1 33.1 35.8 66.2 cabinet 65.1 62.6 77.4 74.2 83.9 83.6 76.8 80.0 chair 84.4 59.0 91.3 89.0 91.8 92.6 91.6 93.3 desk 36.0 50.0 74.0 65.3 63.3 65.3 64.9 62.5 display 62.3 73.0 79.4 74.5 77.0 78.4 79.7 89.9 door 85.2 93.8 85.2 91.4 89.0 84.8 88.7 94.6 shelf 60.6 72.6 72.6 78.0 79.3 84.2 85.1 91.2 table 66.7 67.8 72.6 65.9 77.4 67.4 62.8 67.6 bed 51.8 61.8 75.5 69.1 64.5 80.0 79.5 79.7 pillow 61.9 67.6 81.0 80.0 77.1 80.0 72.8 89.1 sink 46.7 64.2 80.8 65.8 75.0 72.5 73.9 76.5 sofa 72.4 76.7 90.5 90.5 91.4 91.6 90.0 92.6 toilet 61.2 55.3 85.9 70.6 69.4 71.8 73.5 81.2 mAcc 58.1 63.4 75.4 69.8 73.6 75.1 74.1 81.2 OA 63.0 68.2 77.9 73.7 78.1 78.5 77.4 82.4

表3 各算法在ScanObjectNN数据集上的分类性能 Table 3 Classification performance of different algorithms on ScanObjectNN dataset %

在ModelNet40数据集上, 本文算法在OA、mAcc指标上分别达到93.67%和91.3%, 并且仅采用1 024个点的坐标信息就已取得较优结果, 甚至超过以更多点或更多信息作为输入的方法, 如DGCNN、SO-Net、PointASNL等.在ScanObjectNN数据集上, 本文算法不仅在OA、mAcc指标上超出次优方法约4%, 提高点云分类的性能, 而且在多个类别的分类性能上取得最优结果.

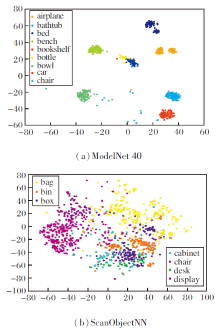
最后, 本文采用T分布随机邻域嵌入(T-distri-buted Stochastic Neighbor Embedding, T-SNE)^[30]对获得的形状描述子进行可视化, 如图3所示.由图可看出, 获得的形状描述子具有良好的判别能力, 可有效分类不同类别.这在很大程度上受益于残差边卷积提取较丰富的特征和构建网络的深层次结构.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 2个数据集上形状描述子T-SNE可视化结果Fig.3 T-SNE visualization results of shape descriptors on 2 datasets

本节讨论网络中不同成分对分类性能的影响.本文构建4组模型的自身消融对比实验.模型A采用原始边卷积进行特征提取.模型B采用串联方式在模型A的基础上堆叠更多层边卷积, 构建更深的特征提取网络.模型C采用残差边卷积块构建深度特征提取网络.模型D在模型C的基础上采用密集连接的方式融合不同层次的特征.实验结果如表4所示.

表4

Table 4

表4(Table 4)

表4 各模型的消融实验结果对比 Table 4 Comparison of ablation experiment results of different models % 模型 ModelNet40 ScanObjectNN mAcc OA mAcc OA A 90.15 92.60 73.21 77.95 B 89.88 91.29 70.25 77.06 C 91.05 93.52 80.92 81.75 D 91.23 93.67 81.24 82.42

表4 各模型的消融实验结果对比 Table 4 Comparison of ablation experiment results of different models %

由表4可看出, 当以简单串联的方式加深网络结构时, 反而会出现网络退化问题, 分类性能欠佳.残差边卷积块能有效改善网络中信息的传递, 一定程度上缓解网络退化的问题, 有效增强特征提取的性能.此外, 采用密集连接的方式能有效融合不同层次的特征, 使最终的形状描述子具有更丰富的特征, 更具判别能力.

在相同的实验环境下, 与DGCNN对比, 分析本文算法的时间复杂度, 具体如表5所示.由表可知, 由于本文算法加深模型深度, 在训练阶段需要花费较多的时间保证模型得到充分的训练.而在测试阶段, 本文算法花费时间与DGCNN仍保持同一水平.结合分类性能提升的幅度来看, 时间复杂度的小幅度提升是可接受的.

表5

Table 5

表5(Table 5)

表5 各算法的时间复杂度分析 Table 5 Time complexity analysis of different methods 算法 训练时间 (每轮)/s 测试时间 (每轮)/s OA /% mAcc /% DGCNN 63 7 92.90 90.20 本文算法 88 9 93.67 91.23

表5 各算法的时间复杂度分析 Table 5 Time complexity analysis of different methods

残差边卷积块涉及的超参数仅有一个邻域节点的数量K, 该参数控制局部图的大小, 即卷积核的大小.于是, 本文通过一组对比实验, 分析不同大小的邻域选择对分类性能的影响, 结果如表6所示.

表6

Table 6

表6(Table 6)

表6 ModelNet40数据集上邻域节点数量对分类性能的影响 Table 6 Effect of the number of neighbor nodes on classification performance on ModelNet40 dataset % K=5 K=10 K=20 K=40 mAcc 88.92 90.02 91.23 91.07 OA 90.83 92.06 93.67 93.32

表6 ModelNet40数据集上邻域节点数量对分类性能的影响 Table 6 Effect of the number of neighbor nodes on classification performance on ModelNet40 dataset %

由表6可知, 当局部图过小时, 由于局部结构特征提取不充分, 分类结果较差.而当局部图过大时, 由于信息的冗余反而使局部特征提取能力下降, 同样影响分类精度.因此, 通过实验发现, 当K=20时, 分类性能达到最优.