引用本文
王森, 危辉, 孟令江. 基于控制点和RGB向量差联合梯度Census变换的立体匹配算法. 模式识别与人工智能, 2022,35(1): 37-50
WANG Sen, WEI Hui, MENG Lingjiang. Stereo Matching Algorithm Based on Control Points, RGB Vector Difference and Gradient Census Transform. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2022,35(1): 37-50.  
Doi: 10.16451/j.cnki.issn1003-6059.202201004
Permissions
Copyright©2022, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于控制点和RGB向量差联合梯度Census变换的立体匹配算法
王森1,2, 危辉1,2, 孟令江1,2
1.复旦大学 计算机科学技术学院 认知算法模型实验室 上海 200438
2.复旦大学 计算机科学技术学院 上海市数据科学重点实验室 上海 200438
通讯作者:

危 辉,博士,教授,主要研究方向为认知科学、人工智能.E-mail:weihui@fudan.edu.cn.

作者简介:

王 森,硕士研究生,主要研究方向为立体视觉.E-mail:19212010029@fudan.edu.cn.

孟令江,博士研究生,主要研究方向为立体视觉.E-mail:ljmeng17@fudan.edu.cn.

收稿日期: 2021-06-07 接受日期: 2021-09-03
资助项目: 国家自然科学基金项目(No.61771146)资助
摘要

为了解决立体匹配算法在弱纹理区域及边界区域匹配精度较低的问题,文中提出基于控制点和RGB向量差联合梯度Census变换的立体匹配算法.首先,使用基于动态时间归整的行匹配算法,寻找最优匹配路径,经过扭曲对齐选取匹配特征点作为控制点.再使用基于RGB向量差代价联合基于梯度Census变换代价作为非控制点的匹配代价,基于梯度Census变换增加像素点的鲁棒性,RGB三向量保留图像三维色彩信息,使求得的代价精度更高.然后,融合求得的控制点与非控制点的匹配代价,作为初始匹配代价,基于RGB三向量差求得针对不同纹理区域的自适应窗口,在该窗口内以一次水平方向和竖直方向代价聚合的方式进行初始代价优化,同时使用多步骤优化减少视差错误率.最后,在Middlebury数据集上对不同区域测试视差错误率和在真实机器人场景上求取视差,将求得的视差利用三维成像原理进行三维重建测试.理论分析和实验表明,文中算法明显降低弱纹理区域和边界的误匹配率.

关键词: 控制点; 动态时间归整(DTW); 梯度Census变换; 立体匹配
中图分类号:TP 391
Stereo Matching Algorithm Based on Control Points, RGB Vector Difference and Gradient Census Transform
WANG Sen1,2, WEI Hui1,2, MENG Lingjiang1,2
1. Laboratory of Algorithms for Cognitive Modeling, School of Computer Science, Fudan University, Shanghai 200438
2. Shanghai Key Laboratory of Data Science, School of Computer Science, Fudan University, Shanghai 200438
Corresponding author:
WEI Hui, Ph.D., professor. His research interests include cognitive science and artificial intelligence.

About Author:
WANG Sen, master student. Her research interests include stereo vision.
MENG Lingjiang, Ph.D. candidate. His research interests include stereo vision.

Fund:National Natural Science Foundation of China(No.61771146)
Abstract

Aiming at the low matching precision of weak texture region and boundary in traditional stereo matching algorithms, a stereo matching algorithm based on control points, RGB vector difference and gradient census transform is proposed. Firstly, a row matching algorithm based on dynamic time warping(DTW) is exploited to find the optimal matching path. The path is distorted and aligned to select matching control points. Then, RGB vector difference cost is combined with gradient Census transform cost as the matching cost of non-control points. The robustness of pixels is enhanced by gradient Census transform, and the three-dimensional color information of the image is retained by the RGB vector. Thus the higher matching precision is achieved. The combination of the matching cost of control points and non-control points is regarded as the initial matching cost. The RGB vector difference is utilized to acquire the adaptive window of different texture areas. The cost aggregation is calculated by the algorithm in a horizontal and vertical directions of an adaptive window. The cost aggregation is employed to optimize the initial cost. Multi-step optimization is employed to reduce the disparity error rate.Finally, the proposed algorithm is validated on Middlebury dataset for different regions and the disparity is calculated in the real scene of robot. The calculated disparity is verified for three-dimensional reconstruction based on the principle of 3D imaging. Both theoretical analysis and experimental results show that the proposed algorithm reduces the matching error rate of weak texture region and boundary significantly.

Key words: Control Points; Dynamic Time Warping(DTW); Gradient Census Transform; Stereo Matching

本文责任编委 汪增福

Recommended by Associate Editor WANG Zengfu

立体匹配是计算机视觉领域的重要研究方向和热门研究领域, 模拟人的两只眼睛的双目立体相机的立体匹配也受到密切关注.

双目立体匹配通过双目相机拍摄左右两幅图像, 通过算法对两幅图像进行匹配, 求取视差图, 根据双目成像原理求出三维世界坐标, 并还原三维场景.因此行业应用非常广泛, 例如:辅助视觉障碍人士避障、自动驾驶、虚拟现实、移动机器人等[1, 2, 3, 4, 5, 6].

双目立体匹配算法分为2种:基于深度学习的立体匹配算法和传统方式的立体匹配算法.基于深度学习的立体匹配算法利用神经网络迭代训练, 判断两幅图像的相似匹配.传统方式的立体匹配算法通过非神经网络迭代训练的方式, 直接计算两幅图像的相似匹配.

基于深度学习的立体匹配算法分为有监督学习的立体匹配算法和无监督学习的立体匹配算法[7].有监督学习的立体匹配算法一般使用激光雷达获得样本的准确视差信息, 作为真值图参与训练.无监督学习的立体匹配算法不需要视差的真值图, 只需要左右图像进行迭代训练.Han等[8]利用孪生网络判断图像块的相似性, 实现立体匹配.Kendall等[9]利用三维卷积网络构建匹配代价, 进行端到端的训练, 实现立体匹配.Menze等[10]提出Disp-Net(Convolu-tional Networks for Disparity, Optical Flow, and Scene Flow Estimation), 利用光流网络, 抽象语义特征, 对不同的特征图辅助监督以完成训练, 实现立体匹配.Seki等[11]利用卷积神经网络(Convolutional Neural Network, CNN)并且加入半全局匹配(Semi-global Matching, SGM)的置信函数进行训练, 对训练后的结果再进行代价聚合处理, 实现立体匹配.

基于深度学习的立体匹配算法由于需要大量的图像进行训练, 计算量巨大, 对电脑硬件要求较高, 训练非常耗时[12], 立体匹配的效果依赖于训练的数据集, 因此不适用于可变场景且硬件成本不高的系统中, 如残障人士避障装置、小型企业级机械臂抓取等.

传统方式的立体匹配算法主要分为局部立体匹配算法和全局立体匹配算法[13].

局部立体匹配算法主要利用算法计算图像的特征角点、边缘、局部平面的信息, 并计算视差.由于参与计算的图像中的区域较少, 鲁棒性较差, 因此得到的视差图较稀疏, 计算精度较低, 但计算速度较快.

全局立体匹配算法主要基于全局能量函数求解全局最优解, 把立体匹配转化为求解全局能量函数最优解的问题, 计算精度较高, 但计算量较大且复杂.

局部立体匹配算法对于初始代价的计算主要有SAD(Sum of Absolute Differences)[14]、SSD(Single Shot Multi-box Detector)[15]、NCC(Normalized Cross Correlation)[16]、自适应权重的学习模型[17]等.然而, 当图像存在光线变化、弱纹理场景、遮挡情况时效果会受到影响.将RGB三通道彩色图像压缩为灰度图, 得到一个灰度值对应的彩色图, 在图像的弱纹理区域会大幅降低匹配准确率, 应保留更多的彩色维度, 使色彩信息更具体、匹配更精确.而使用RGB三向量计算匹配代价, 保留更多的色彩信息, 使像素点之间的匹配结果差异更大, 得到更精确的匹配结果.

Census变换[18]对光照具有较强的鲁棒性, 但Census变换较依赖中心像素, 如果中心像素受到噪声影响, 精度会随之受到影响.Ma等[19]提出改进的Census变换, 为基于领域相关性的匹配算法, 在一定程度上提高效果精度, 但在单一纹理区域和视差不连续的区域表现效果不佳.Lü 等[20]提出基于HSV空间的Census变换, 对光照噪音有一定的鲁棒性, 但丢失很多颜色信息, 在视差不连续区域效果不佳.

为了提高立体匹配的抗噪声性并提高匹配精度, 本文提出基于控制点和RGB向量差联合梯度Census的立体匹配算法.首先, 使用基于动态时间归整(Dynamic Time Warping, DTW)[21]的行匹配算法, 寻找最优匹配路径, 经过扭曲对齐选取匹配特征点作为控制点.再使用基于RGB向量差代价联合基于梯度Census变换代价作为非控制点的匹配代价, 基于梯度Census变换增加像素点的鲁棒性, RGB三向量保留图像三维色彩信息, 求得的代价精度更高.然后, 融合求得的控制点与非控制点的匹配代价, 作为初始匹配代价, 基于RGB三向量差求得针对不同纹理区域的自适应窗口, 在该窗口内以一次水平方向和竖直方向代价聚合的方式进行初始代价优化, 同时使用多步骤优化, 减少视差错误率.最后, 在Middlebury数据集上对不同区域测试视差错误率和在真实机器人场景上求取视差, 将求得的视差利用三维成像原理进行三维重建测试, 理论分析和实验表明, 本文算法明显降低弱纹理区域和边界的误匹配率.

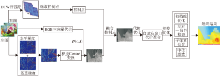
1 基于控制点和RGB向量差联合梯度Census变换的立体匹配算法

本文提出基于控制点和RGB向量差联合梯度Census变换的立体匹配算法.算法主要包括DTW行匹配、控制点计算和选取、初始代价计算、控制点融合、代价聚合、计算视差和视差优化.对于控制点的计算, 使用基于DTW的行匹配算法筛选大量可靠的视差匹配点, 初始代价计算采用RGB三向量的向量差和基于梯度的Cencus变换结合的方式.使用基于RGB颜色三向量的自适应纹理区域进行代价聚合, 使用半全局算法[22]中的扫描线算法对匹配代价进行水平方向和竖直方向代价优化, 采用赢者通吃策略(Winner Take All, WTA)[23]计算视差.最后使用左右一致性校验、子像素拟合、中值滤波计算视差优化.算法具体框图如图1所示.

图1 本文算法框图Fig.1 Framework of the proposed algorithm

1.1 基于动态时间归整的行匹配算法

动态时间归整(DTW)[21]最初是用于衡量两个长度不同时间序列相似度的方法, 是孤立词识别的技术.对于两段不同的语音, 不同人对不同的发音长度不同.通常, 两个语音序列具有相似的形状, 但这些形状在时间上并不是对齐的, 所以在对比它们的相似度之前, 需要将其中一个或两个序列在时间轴上扭曲, 使它们对齐.DTW就是实现这种扭曲的有效方法, 达到特征点与特征点的对齐.DTW不要求样本具有同样的长度及范围, 只要给定样本的起始边界, 保证连续单向进行, 最后可寻找一条路径, 使样本之间的距离总和最小.

在立体匹配时, 需要取左右两图的其中一行进行行匹配, 而由于遮挡、倾斜情况的出现, 会产生不同长度段的匹配, 因此要实现不同长度段的匹配就需要对段进行扭曲对齐匹配.DTW可应用到立体匹配的行匹配过程中, 从中获取匹配的特征点.对于左图像一行序列Q和右图像一行序列C, 令

Q=q1, q2, …, qn, C=c1, c2, …, cn,

其中, n表示图像宽度, 由于左右两图像的宽度确定并相同, 在这里处理的图像认为是行对齐以后的图像, 因此左右两幅图像对应的任意两行的长度均为n.

为了对齐这两个序列, 需要构造n×n的矩阵网格, 矩阵元素(i, j)表示qi到cj的距离:

d(qi, cj)= 13∑t=r, g, b(Iqit-Icjt)2,

其中, Iqit表示左图像某一行点qi处的RGB三通道色度信息, t表示RGB三通道.该矩阵描述序列Q中每点到C中每点之间的相似度, 距离越小相似度越高.

两序列形成的矩阵网格最小的路径定义为W, W中包含的每个元素组成的路径代价最小, 定义的W中第k个元素wk=(i, j)k, 则

W=w1, w2, …, wK, n≤K≤n+n-1,

其中 n为序列Q和C的长度.

根据双目成像原理匹配的特性, 这条路径需要满足如下3个约束条件.

1)边界条件.由于双目相机基线的影响, 左图的起始位置在右图会有一部分不存在, 右图的结束位置在左图会有一部分不存在.假设左图与右图开始为start, 结束匹配为end, 则边界条件

w1=(start, 1), wK(n, end).

2)连续性.假设 wk-1=(a', b'), 对于路径的下个点wk=(a, b), 需要满足

(a-a')and(b-b')≤ 1,

保证序列Q、C中的每个像素都在W中出现.

3)单调性.假设wk-1=(a', b'), 对于路径中下一个点wk=(a, b), 需要满足

0≤ (a-a')and(b-b').

这是因为匹配满足顺序一致性, 已匹配过的像素点后面不会再出现匹配.

匹配问题就变成在该矩阵网格中n×n条路径中找到代价最小的路径:

DTW* (Q, C)=arg min(Q, C)∈{(Qi, Cj)|i=1, 2, …, n, j=1, 2, …, n}∑i=1KWi.

结合连续性和顺序性的约束, 对于像素点(qi, cj), 有3种路径走法:

(qi, cj+1), (qi+1, cj+1), (qi+1, cj).

采用动态规划的方式求最相似路径可将本来O(n3)的复杂度降至O(n2), 定义动态规划转移方程如下:

Mc(qi, cj)=min(Mc(qi-1, cj-1), Mc(qi-1, cj), Mc(qi, cj-1))+d(qi, cj),

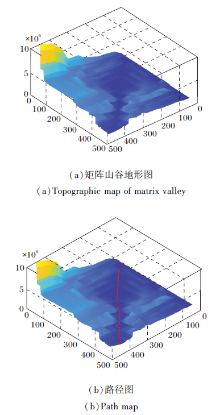
其中Mc为动态转移矩阵.找到的最优路径如图2所示, 以teddy图像为例, (a)表示求得的矩阵网格, 颜色越深表示值越小, 颜色越浅表示值越大, 呈现的结果类似一个复杂的山谷地形.由图可看出, 在复杂的山谷地形中存在一条路径, 这条路径就是求得的最优匹配路径, (b)中红色的线表示找到的路径.

图2 山谷地形路径图Fig.2 Valley path map

1.2 基于控制点融合的立体匹配算法

1.2.1 控制点的作用和选取

Bobick等[24]提出控制点的概念, 最初应用在动态规划立体匹配过程中, 用于处理大遮挡情况, 使用约束和阈值选择算法提高控制点正确匹配的概率, 控制点越多越正确, 修正的效果越优.使用DTW行匹配得到最小路径后, 只需对所求最小路径进行特征选取, 尽可能多地选取可靠的控制点.

DTW行匹配算法寻找最优路径之前必须要给予一个起始点, 以便寻找最优的匹配路径, 最初默认一行中左图的第一个像素点和右图的第一个起始点为匹配点, 之后再逐步过渡到正确匹配.因为算法会导致所求控制点的不可靠, 所以匹配开始会造成很多误差, 需要设置一个截断阈值排除这些错误的起始点, 即

DD={(pi, j, dp)|(dp=i-j)∧ ((i, j)∈ DTW* )∧ dp> α },

其中, (pi, j, dp)为选取的控制点, α 为选取控制点的截断视差阈值, 这里α =10.

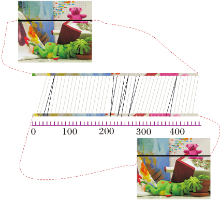
同时, 由于需要使长短不同的段扭曲以达到对齐的目的, 就会出现多对一和一对多的情况.左图Teddy的一行, 与右图Teddy中的某一行进行匹配的情况如图3所示.由于像素太多, 为了清晰描述, 直接以10个像素匹配1次, 图中灰线表示一一匹配的结果, 黑线表示多对一匹配的结果.这些点都认为是误匹配点, 在选择特征点时需剔除, 定义

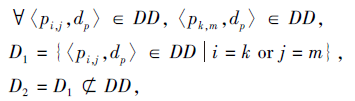
其中, i=k表示左图的点出现的多对一, j=m表示右图的点出现多对一.

图3 行匹配情况Fig.3 Row matching

1.2.2 融合控制点的联合匹配代价

求完控制点后还需要处理非控制点, 而代价计算是立体匹配都要计算的步骤.求取两个像素点之间的代价, 绝对值差(Absolute Difference, AD)[14]为快速计算两像素相似程度的方法, 即求出左右两幅图对应的两个像素值之差的绝对值.由于单个像素点计算会忽略周围的信息, 通常会计算一个像素块内的像素值差的绝对值的和, 常用的计算方式如下:

AD(x, y, i, j)= ∑l=0M-1∑k=0N-1|(A(x+l, y+k)- B(x+i+l, y+j+k))|

其中, A(x+l, y+k)、B(x+i+l, y+j+k)表示当前M×N搜索区域的像素点值, (i, j)表示当前像素块(x, y)内的像素点.以(x, y)作为左图窗口的锚点, 将该窗口覆盖右图的图像区域, 遍历整幅图, 求出不同的差值之和作为AD值.

AD容易受到光照的影响, 边界不清晰.Census变换在光照和边界体现较好的鲁棒性, 但会丢失很多像素点的信息.梯度信息可较好地判定边界, 但对无纹理区域和大面积颜色相似的区域有很多误差.本文提出Census变换方式, 结合RGB三向量差计算代价.对于像素点p, 在视差d下, 根据RGB三通道计算AD的匹配代价:

CAD(px, y, dp)= 13∑i=R, G, B(Ilefti(px, y, dp)-Irighti(px, y, dp))2.

使用RGB向量差的方式表示代价是为了得到更多的颜色信息, 减少噪声对匹配正确性的影响.

传统的Census变换是对比除中心像素点p以外的q组成的匹配窗口:如果q的灰度值大于p, 表示为1; 如果q的灰度值小于p, 表示为0.

本文使用像素的梯度值进行Census变换:如果q的梯度值大于p, 表示为1; 如果q的梯度值小于p, 表示为0.通过Census变换可得到基于中心像素点p的比特序列, 经过Census变换后, 通过汉明(Hamming)距离表示两个像素的相似程度, 汉明距离越小, 相似度越低, 否则相似度越高.定义

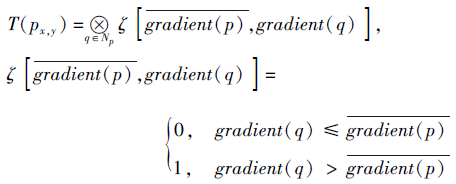
Np表示除中心像素点p以外的匹配窗口内的其它像素, gradient(p)表示像素点p处的梯度, ⊗ 表示异或运算.

得到Census变换的比特序列后, 使用汉明距离计算相似度, 使用左图像窗口的Census变换序列Tleft(px, y)和右图像窗口的Census变换序列Tright(px, y+dp), Census变换的初始匹配代价为

Ccensus(px, y, dp)=Hamming(Tleft(px, y), Tright(px, y, dp)).

由AD匹配代价和基于梯度的Census变换匹配代价可看出, 两者对像素点匹配具有不同的代价标准, 为了让匹配代价能准确描述像素点的特征并控制某一特征占比过于重要而带来误差, 将匹配代价归一化, 融合二者的匹配代价并映射到[0, 1], 即

C(px, y, dp)=ρ (Ccensus(px, y, dp), λcensus)+ρ (CAD(px, y, dp), λAD),

其中, CAD(px, y, dp)为左图像像素p和右图像视差dp的RGB三向量差, Ccensus(px, y, dp)为汉明距离, Census变换窗口取9×7,

λcensus=30, λAD=10, ρ (c, λ)= arctan(-cλ)·2arccos(-1.0).

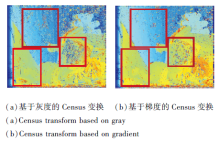
使用灰度值进行Census变换和使用平均值梯度进行Census变换, 效果差别如图4所示.由于基于灰度值的Census变化容易受中心点的像素影响, 中心点的像素值受光照影响较严重, 会带来误差, 而使用梯度值进行Census变换除考虑到变换中心像素四周的情况以外, 同时四周的像素点也考虑四周的周围像素点的信息, 增加像素点匹配的鲁棒性, 减少在低纹理区域像素点的误匹配率.

图4 不同Census变换热值图Fig.4 Different heat maps of different Census transform

求得视差空间图像(Disparity Space Image, DSI)初始视差变化空间后, 还需要将求得的控制点融入初始视差变化空间, 这些控制点是最优代价.将控制点融入DSI视差变化空间, 只需要在DSI空间将控制点的代价值设为最小, 将控制点与代价进行融合, 即

C(px, y, pd)=η, (px, y, pd)∈ D2,

其中, η为当前DSI视差空间中最优的代价值, 为了获得更好效果, 这里取η=0.

加入控制点效果如图5所示.由图可见, 融合控制点和初始代价后有效减少匹配错误率.

图5 初始代价加入控制点前后的效果对比Fig.5 Comparison of initial matching cost with and without control point

1.3 代价聚合优化

1.3.1 基于RGB三向量的自适应聚合窗口

聚合代价的窗口可决定匹配的正确性, 基于固定窗口的代价聚合方式会因为边界误差导致聚合造成误差, 窗口大小不易选取.

为了让立体匹配的结果更正确, 需要根据不同纹理的区域自适应调节聚合窗口的大小, 本文参考文献[25]聚合窗口区域, 在此基础上进行改进, 定义

Dc(p, q)< ∂1, Dc(p, p+(1.0))< ∂1, Ds(p, q)< L1Dc(p, q)< ∂2, Dc(p, p+(1.0))< ∂2, L1< Ds(p, q)< L2

Dc= ∑i=R, G, B(Ii(p)-Ii(q))2.

其中:Dc(p, q)表示像素p、q之间的颜色差异, 使用三向量差异的向量和表示是为了使用更多的颜色信息, 减少误差; ∂1、∂2表示颜色差异的阈值, ∂1> ∂2; p+(1.0)是为了防止穿过边界造成较大的误差, 保证聚合窗口在一片颜色相似的区域; Ds=|q-p|, 表示像素之间的空间距离; L1、L2表示臂长阈值, L2> L1, 当遇到大面积无纹理区域时, 需设置一个更小的颜色阈值, 约束聚合区域确保它们具有相似的颜色特征.

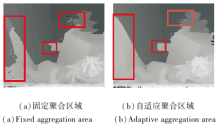
聚合窗口不同时的效果如图6所示.(a)显示固定聚合窗口为7×7时水平方向和竖直方向的聚合效果, (b)为本文方法的自适应聚合窗口水平方向和竖直方向的聚合效果.由图可看出, 由于是窗口, 会因为固定窗口太小或太大导致误差, 同时因为固定窗口包含边界, 也会带来较大误差, 导致聚合效果较差.

图6 不同聚合区域的效果Fig.6 Results of different aggregation areas

1.3.2 代价聚合

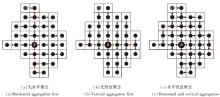
在融合特征点的代价基础上进行代价聚合, 本文参考文献[26]的聚合方式, 在改进的聚合窗口区域进行代价聚合.首先构建自适应聚合窗口, 对像素点p进行水平方向和竖直方向的代价聚合:1)对于象素p的自适应聚合窗口支持区域内所有的像素, 将水平方向上的像素代价值相加, 存储在像素点p的竖直方向作为临时值.2)将1)得到的临时值在像素点p的竖直方向代价相加.如图7(a)所示, 蓝色箭头表示1)中的代价聚合, 橙色箭头表示2)中代价聚合.先竖直方向聚合再水平方向聚合, 如(b)所示.

最后, 为了让最终的聚合代价值在一个较小的可控范围内, 对聚合后的代价进行归一化, 将最终的聚合代价值除以支持区的总像素数.本文算法因为加入控制点, 只需要聚合1次就可得到较精确的结果.最后代价定义如下:

C¯(p, d)= 1N∑s∈Ud(p)C(s, d),

其中, N表示像素p的自适应窗口的总像素数, Ud(p)表示像素p的自适应窗口的DSI视差空间.

图7 不同的代价聚合方式Fig.7 Different cost aggregation ways

1.4 多步骤视差优化

1.4.1 扫描线优化

为了消除模糊的匹配代价, 得到更精确的匹配代价, 在计算视差之前使用基于Hirschmuller的半全局方法的匹配, 进行两方向的扫描线优化, 即水平方向和竖直方向, 更新后的代价为C2(p, d).

再采用WTA策略求解视差, 对于像素点p, 视差可表示为

dp=arg min0≤d≤dmaxC2(p, d).

1.4.2 左右一致性检验

首先计算得到左右两图的视差图.对于左视差图的每个像素Il(x, y), 根据视差值计算该像素右图视差图对应的位置Ir(x, y), 判断视差差值绝对值之差是否小于一个阈值:如果在阈值内, 认为是有效值; 如果超过阈值, 一致性检查不通过, 将像素点的视差值置为无效值.定义如下:

Dp= Dbp, |Dbp-Daq|≤ε, q=Cbm¯(p, Dbp)infinite, 其它,

其中, a为左图像, b为右图像, p、q为左右视差图对应的同名点, ε为视差阈值, 这里ε=1.

1.4.3 子像素拟合优化

由于视差在连续的区域内连续变化, 在DSI视差空间中求解的视差最小单位是1, 造成一定误差.为了让像素的变化更连续, 引入子像素拟合优化[27].子像素拟合优化是根据WTA策略找到最小的视差代价值后, 再记录该最小代价值左边的代价值和右边的代价值, 根据3个代价进行1次一元二次曲线拟合.

由开口向上的二次曲线可知, 存在一个唯一的极小值— — 视差值的子像素位置:

dsub=d+ c1-c22(c1+c2-2c0),

其中, c1表示视差值为d-1的代价值, c2表示视差值为d+1的代价值, c0表示视差值为d的代价值.

1.4.4 中值滤波

在视差优化的最后使用中值滤波平滑最后的视差效果, 可剔除视差图中一些孤立的离群点, 同时填充前面步骤得到的无效点, 得到更优结果.

2 实验及结果分析

为了验证本文算法在边界和弱纹理区域的表现效果, 采用Middlebury测评网站[28, 29]中14组标准图像作为实验对象.实验均在Intel Xeon CPU e5-2640 2.6 GHz 的windows 10环境下运行, 编程语言使用Matlab语言和C++编程语言.对比算法选择跨尺度双边滤波(Cross-Scale Bilateral Filter, CSB-F)[17]、邻域相关信息的改进Census变换(Census Transform Based on the Related Information of Neigh-borhood, RINCensus)[19]、分割树(Segment-Tree, ST)[19]、SGM[22]、非局部代价聚合(Non-local Cost Aggregation, NLCA)[30]、更全面全局匹配(More Global Matching, MGM)[31]、颜色+Census变换+梯度信息(AD+Census+Gradient, CG)[32]、树动态规划(Dynamic Programming on a Tree, TreeDP)[33]、自组织神经网络(Stereo Correspondence by Self-Orga-nizing Neural Network, Stereo-SONN)[34].

SGM、NLCA、MGM、本文算法在8个图像上的对比效果如图8所示.

图8 各算法在8个图像上的效果对比Fig.8 Result comparison of different algorithms on 8 images

除了图像效果, 为了让本文算法更具有说服性, 以Middlebury标准数据集提供的真值图计算匹配误差.Middlebury网站提供误差计算的软件开发工具包(Software Development Kit, SDK), 首先将算法的计算结果与真实的视差图相比, 给定一个误差阈值, 判断匹配得到的视差值大于阈值的像素点占整幅视差图的比重, 即误差

B= 1N∑(x, y)|dc(x, y)-dt(x, y)|> δd,

其中, dc(x, y)表示本文算法计算的视差值, dt(x, y) 表示图像的真实视差图, N表示图像包含的像素总数, δd表示视差误差阈值, 本文取δd=1, 大于该值认为是误差点.

为了使本文算法更具有针对性地验证弱纹理区

域的效果, 根据Middlebury数据集上提供的不同区域划分的图像, 计算不同区域的误匹配率:

Bk= 1Nk ∑(x, y)|dc(x, y)-dt(x, y)|> δd,

其中, Bk表示不同区域的误匹配率, Nk表示不同区域总的像素个数, dc(x, y)表示计算视差, dt(x, y)表示真实视差.

通过误匹配率计算可得到3个区域的误匹配率.

为了验证本文算法的有效性, 对比各算法计算的3个区域的图像误匹配率, 如表1所示, 表中黑体数字表示最优结果.通过对比算法在不同区域的误匹配率可知, 本文算法在非遮挡区域具有较好效果, 在不连续区域误匹配率有一定程度的提高.

表1 各算法在4个图像上的误匹配率对比 Table 1 Disparity error rate comparison of different algorithms on 4 image pairs %

本文算法的误差分布如图9所示, 图(b)中, 灰色表示视差不连续区域误差, 黑色表示无遮挡区域误差.融合控制点后的实验结果更清晰地反映像素的真实视差.

图9 本文算法的误差分布图Fig.9 Disparity error distribution of the proposed algorithm

为了更好地验证本文算法的有效性, 使用Middlebury网站2006数据集上提供的左右两幅真值图, 经过左右一致性检验后得到遮挡图, 对其不同区域计算错误率, 各算法的误匹配率对比如表2所示, 表中黑体数字表示误匹配率最低.由表可知, 本文算法在非遮挡区域平均误匹配率最低(3.2%), 在所有区域的平均误匹配率也最低(8.6%), 这表明本文算法的有效性.

表2 各算法在Middlebury数据集上的误匹配率对比 Table 2 Disparity error rate comparison of different algorithms on Middlebury dataset %

为了更好地验证本文算法在视差不连续区域的效果, 分别对3个区域进行误差分布统计, 针对不同的算法进行对比验证.不同区域的误差数量分布如图10所示.误差统计的区间分为(1, 2]、(2, 3]、(3, 4]、(4, 5]和(5, +¥ ).由图可看出, 相比其它算法, 本文算法在各区域误差数量最低, 且本文算法在视差不连续区域的误差69%以上都集中在(1, 5]中, 而SGM和MGM分别为59%和57%, 由此可知, 本文算法不仅降低视差不连续区域的误差率, 而且在非遮挡区域的效果表现较优.

图10 各算法在不同区域的误差数量分布Fig.10 Disparity error counts of different algorithms on different regions

除了准确率方面, 各算法在14组图像上的平均运行时间如下:本文算法为5.49 s, SGM为34.16 s, NLCA为1.94 s, MGM为2.31 s.本文算法在计算控制点时稍有耗时, 但还有优化空间.控制点的质量决定整个视差图的效果, 在提高正确匹配效率的同时也可能带来误差.

最后在实验室的机器人工业机械臂上进行三维重建实验, 实验所用双目相机型号为SVCamhr-29050彩色工业相机.首先使用双目相机拍摄15组标定板照片进行相机标定, 对双目相机标定使用Matlab 2020a自带的工具箱Stereo Camera Calibrator进行标定和相机参数获取, 使用本文算法获取视差图, 利用相机参数和视差图进行三维重建实验, 各算法实验结果如图11所示.在机器人工业机械臂的真实场景中存在大量的弱纹理区域和反光区域, 图中红色圆圈是弱纹理和反光区域.由图可看出, 本文算法能得到较好的三维重建效果, 在弱纹理区域和反光区域的效果更优.

图11 各算法基于机器人场景的三维重建结果Fig.11 Three-dimensional reconstruction results of robot scene by different algorithms

3 结束语

本文提出基于控制点和RGB向量差联合梯度Census变换的立体匹配算法.针对局部立体匹配算法视差效果较依赖于初始代价的计算, 将控制点融入初始代价计算中, 提高初始代价计算视差的正确率.控制点可提高正确匹配的效率, 但如果对控制点选取不正确也会带来误差.针对基于灰度的Census变换较依赖于中心像素点, 未考虑周围像素的信息, 中心像素点会因为光照而带来误差的问题, 本文提出基于梯度的Census变换算法.为了减少中心像素点带来的误差, 采用平均梯度值代替原有梯度值, 再使用RGB三向量保留更多的色彩信息以计算聚合区域, 并对聚合区域进行一次水平方向和竖直方向代价聚合.最后多步骤优化视差.实验表明本文算法在弱纹理区域和边界区域都有较好效果.今后将考虑优化控制点的选取, 期望更进一步提高获得视差的正确率, 降低误匹配率.

参考文献
[1] WEI H, XU C, JIN Z F. Binocular Matching Model Based on Hie-rarchical V1 and V2 Receptive Fields with Color, Orientation, and Region Feature Information. IEEE Transactions on Biomedical Engineering, 2020, 67(11): 3141-3150. [本文引用:1]
[2] GEIGER A, LENZ P, URTASUN R. Are We Ready for Autonomous Driving? the KITTI Vision Benchmark Suite // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2012: 3354-3361. [本文引用:1]
[3] HAMZAH R A, KADIN A F, HAMID M S, et al. Improvement of Stereo Matching Algorithm for 3D Surface Reconstruction. Signal Processing: Image Communication, 2018, 65: 165-172. [本文引用:1]
[4] ZHAI G D, ZHANG W T, HU W Y, et al. Coal Mine Rescue Robots Based on Binocular Vision: A Review of the State of the Art. IEEE Access, 2020, 8: 130561-130575. [本文引用:1]
[5] TSAI P, CHONDRO P, RUAN S J. Depth-Guided Pixel Dimming with Saliency-Oriented Power-Saving Transformation for Stereoscope AMOLED Displays. IEEE Transactions on Circuits and Systems for Video Technology, 2019, 30(9): 3095-3105. [本文引用:1]
[6] CHONDRO P, YAO Z R, RUAN S J. Depth-Based Dynamic Lightness Adjustment Power-Saving Algorithm for AMOLED in Head-Mounted Display. Optics Express, 2018, 26(25): 33158-33165. [本文引用:1]
[7] LIU P P, KING I, LYU M R, et al. Flow2Stereo: Effective Self-Supervised Learning of Optical Flow and Stereo Matching // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 6647-6656. [本文引用:1]
[8] HAN X F, LEUNG T, JIA Y Q, et al. MatchNet: Unifying Feature and Metric Learning for Patch-Based Matching // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 3279-3286. [本文引用:1]
[9] KENDALL A, MARTIROSYAN H, DASGUPTA S, et al. End-to-End Learning of Geometry and Context for Deep Stereo Regression // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 66-75. [本文引用:1]
[10] MENZE M, GEIGER A. Object Scene Flow for Autonomous Vehicles // Proc of the IEEE Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2015: 3061-3070. [本文引用:1]
[11] SEKI A, POLLEFEYS M. Patch Based Confidence Prediction for Dense Disparity Map[C/OL]. [2021-05-26]. http://www.bmva.org/bmvc/2016/papers/paper023/paper023.pdf. [本文引用:1]
[12] CHENG X L, ZHONG Y R, HARANDI M, et al. Hierarchical Neural Architecture Search for Deep Stereo Matching[C/OL]. [2021-05-26]. https://arxiv.org/pdf/2010.13501v1.pdf. [本文引用:1]
[13] SCHARSTEIN D, SZELISKI R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. International Journal of Computer Vision, 2002, 47(1): 7-42. [本文引用:1]
[14] VANNE J, AHO E, HAMALAINEN T D, et al. A High-Perfor-mance Sum of Absolute Difference Implementation for Motion Estimation. IEEE Transactions on Circuits and Systems for Video Technology, 2006, 16(7): 876-883. [本文引用:2]
[15] LIU W, ANGUELOV D, ERHAN D, et al. SSD: Single Shot Mul-tibox Detector // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 21-37. [本文引用:1]
[16] HIRSCHMÜLLER H, INNOCENT P R, GARIBALDI J. Real-Time Correlation-Based Stereo Vision with Reduced Border Errors. International Journal of Computer Vision, 2002, 47(1): 229-246. [本文引用:1]
[17] YOON K J, KWEON I S. Adaptive Support-Weight Approach for Correspondence Search. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(4): 650-656. [本文引用:2]
[18] LEE J, JUN D, EEM C, et al. Improved Census Transform for Noise Robust Stereo Matching. Optical Engineering, 2016, 55(6). DOI: DOI:10.1117/1.OE.55.6.063107. [本文引用:1]
[19] MA L, LI J J, MA J, et al. A Modified Census Transform Based on the Neighborhood Information for Stereo Matching Algorithm // Proc of the 7th International Conference on Image and Graphics. New York, USA: ACM, 2013: 533-538. [本文引用:3]
[20] LÜ C, LI J H, KOU Q Q, et al. Stereo Matching Algorithm Based on HSV Color Space and Improved Census Transform. Mathematical Problems in Engineering, 2021. DOI: DOI:10.1155/2021/1857327. [本文引用:1]
[21] MÜLLER M. Dynamic Time Warping // MÜLLER M, ed. Information Retrieval for Music and Motion. Berlin, Germany: Sprin-ger, 2007: 69-84. [本文引用:2]
[22] HIRSCHMULLER H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 328-341. [本文引用:2]
[23] 张大禹, 黄灿. 基于WTA立体匹配算法的人体检测方法研究. 电子测试, 2013(5): 66-68.
(ZHANG D Y, HUANG C. The Algorithm of WTA Stereo Matching Based on the Human Detection Method. Electronic Test, 2013(5): 66-68. ) [本文引用:1]
[24] BOBICK A F, INTILLE S S. Large Occlusion Stereo. International Journal of Computer Vision, 1999, 33(3): 181-200. [本文引用:1]
[25] ZHANG K, LU J B, LAFRUIT G. Cross-Based Local Stereo Mat-ching Using Orthogonal Integral Images. IEEE Transactions on Circuits and Systems for Video Technology, 2009, 19(7): 1073-1079. [本文引用:1]
[26] MEI X, SUN X, ZHOU M C, et al. On Building an Accurate Ste-reo Matching System on Graphics Hardware // Proc of the IEEE International Conference on Computer Vision Workshops. Washington, USA: IEEE, 2011: 467-474. [本文引用:1]
[27] YANG Q X, WANG L, YANG R G, et al. Stereo Matching with Color-Weighted Correlation, Hierarchical Belief Propagation, and Occlusion Hand ling // Proc of the IEEE Computer Society Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2006: 2347-2354. [本文引用:1]
[28] SCHARSTEIN D, SZELISKI R, ZABIH R. A Taxonomy and Eva-luation of Dense Two-Frame Stereo Correspondence Algorithms // Proc of the IEEE Workshop on Stereo and Multi-baseline Vision. Washington, USA: IEEE, 2001: 131-140. [本文引用:1]
[29] SCHARSTEIN D, SZELISKI R. High-Accuracy Stereo Depth Maps Using Structured Light // Proc of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2003: 195-202. [本文引用:1]
[30] YANG Q X. A Non-local Cost Aggregation Method for Stereo Mat-ching // Proc of the IEEE Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2012: 1402-1409. [本文引用:1]
[31] FACCIOLO G, DE FRANCHIS C, MEINHARDT E. MGM: A Significantly More Global Matching for Stereovision[C/OL]. [2021-05-26]. http://www.bmva.org/bmvc/2015/papers/paper090/paper090.pdf. [本文引用:1]
[32] ZHU S P, YAN L N. Local Stereo Matching Algorithm with Efficient Matching Cost and Adaptive Guided Image Filter. The Visual Computer, 2017, 33: 1087-1102. [本文引用:1]
[33] VEKSLER O. Stereo Correspondence by Dynamic Programming on a Tree // Proc of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2005, II: 384-390. [本文引用:1]
[34] VANETTI M, GALLO I, BINAGHI E. Dense Two-Frame Stereo Correspondence by Self-Organizing Neural Network // Proc of the 15th International Conference on Image Analysis and Processing. Berlin, Germany: Springer, 2009: 1035-1042. [本文引用:1]
[35] MEI X, SUN X, DONG W M, et al. Segment-Tree Based Cost Aggregation for Stereo Matching // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2013: 313-320. [本文引用:1]